Mapping out spin and particle conductances in a quantum point contact

Significance

Predicting the transport properties of interacting particles in the quantum regime is challenging. A conceptually simple situation is realized by connecting two reservoirs through a quantum point contact. For noninteracting fermions, the conductance is quantized in units of the inverse of Planck’s constant, reflecting the contribution to transport of an individual quantum state. We use a cold atomic Fermi gas to map out the spin and particle conductance in a quantum point contact for increasing attractive interactions and observe remarkable effects of interactions on both spin and particle transport. Our work provides maps of conductance over a wide range of parameters and in the presence of many-body correlations, yielding new insights into the nature of strongly attractive Fermi gases.

Abstract

We study particle and spin transport in a single-mode quantum point contact, using a charge neutral, quantum degenerate Fermi gas with tunable, attractive interactions. This yields the spin and particle conductance of the point contact as a function of chemical potential or confinement. The measurements cover a regime from weak attraction, where quantized conductance is observed, to the resonantly interacting superfluid. Spin conductance exhibits a broad maximum when varying the chemical potential at moderate interactions, which signals the emergence of Cooper pairing. In contrast, the particle conductance is unexpectedly enhanced even before the gas is expected to turn into a superfluid, continuously rising from the plateau at $1/h$ for weak interactions to plateau-like features at nonuniversal values as high as $4/h$ for intermediate interactions. For strong interactions, the particle conductance plateaus disappear and the spin conductance gets suppressed, confirming the spin-insulating character of a superfluid. Our observations document the breakdown of universal conductance quantization as many-body correlations appear. The observed anomalous quantization challenges a Fermi liquid description of the normal phase, shedding new light on the nature of the strongly attractive Fermi gas.

Quantum gas experiments provide a tool to study fundamental concepts in physics, which may be hard to access by other means. Challenges such as the interplay and dynamics of many interacting fermions are addressed by interrogating a specifically tailored quantum many-body system with controlled parameters, an approach referred to as quantum simulation (1). The outcomes can then be used to benchmark theory or even as a direct comparison with different experimental realizations of the same concept. In recent years there has been substantial progress on this path, using cold atomic gases to realize important models of condensed matter physics, formulated to describe the bulk properties of materials (2, 3). Here, neutral fermionic atoms are used to model the electrons in a solid.

In this article we use a quantum gas to study the operation of an entire mesoscopic device, a quantum point contact (QPC), in the presence of interactions between the particles. We observe the transport of a charge neutral quantum degenerate gas of fermionic lithium atoms, which can be prepared in a mixture of two hyperfine states. These states provide a spin degree of freedom and the attractive interaction between them can be tuned continuously from weak to unitary, a feature unique to cold atomic gases. The QPC itself is realized by a suitably shaped optical potential, which consists of a short, one-dimensional channel connected to two large reservoirs (4, 5). Biasing the reservoirs with different chemical potentials can induce a direct current. The ratio of the current to the bias is the conductance of the contact, which is independent of the bias in the linear response regime.

For spinless, noninteracting particles at low temperature, the conductance is quantized in units of $1/h,$ the universal conductance quantum for neutral particles (6). An intuitive understanding thereof can be gained by considering the temporal spacing $\tau =h/\mathrm{\Delta }\mu$ of minimum uncertainty wave packets within one transverse mode and moving through the channel in response to an applied bias $\mathrm{\Delta }\mu$ (7–10). At zero temperature, within one energetically available mode, each wavepacket state is occupied by a single particle in accordance with Pauli’s principle. Hence the maximum current carried by the mode is $I=1/\tau =\mathrm{\Delta }\mu /h$ with $1/h$ being the upper bound for the contribution of a single mode to conductance. This bound, set by Heisenberg’s and Pauli’s principle, holds for all systems where transport proceeds by fermionic quasiparticles, such as Fermi liquids.

In a gas with two spin components, the conductance of each component is quantized in units of $1/h,$ as long as there are no interactions between them. The picture becomes more intricate if collisions between the two components play a role. Studies conducted on solid-state systems have shown that the weak correlations in conventional superconductors yield quantized supercurrents (11, 12) and the emergence of Andreev bound states in mesoscopic conductors (13–15). Besides, in semiconductor systems, the Coulomb repulsion between charge carriers subtly modifies the conductance quantization (16–20), lowering conductance at low density and leading to strong correlations.

To characterize the transport, one may additionally consider the spin current, i.e., the relative current of one component with respect to the other, which is expected to be damped in the presence of interactions (21). Whereas measuring and inducing spin currents in clean mesoscopic conductors is a challenge in solid-state systems, quantum gases naturally allow for spin-resolved observations and manipulations. For example, the damping of spin currents was measured in strongly interacting Fermi gases at high temperature, where many-body effects, in particular pairing, are weak (22–24). In contrast, the total particle current is conserved in collisions, and thus the quantization of particle conductance in the channel should be robust. In fact, it was shown that the applicability of a Fermi liquid description in the leads of the contacts guarantees universal conductance quantization (25–27), regardless of the interaction strength.

Our study of spin and particle conductance of a quantum point contact with tunable interactions uses an atomic Fermi gas in the vicinity of a broad Feshbach resonance, realizing the Bose–Einstein condensate (BEC)–Bardeen–Cooper–Schrieffer (BCS) crossover regime (28). It features a conventional s-wave paired superfluid for strong attraction and low temperatures, as well as a Fermi-liquid phase for weak attraction and high temperatures. The nature of the state in the intermediate regime remains controversial, as it is governed by a nontrivial interplay of pairing and superfluid fluctuations competing with finite temperature properties of the gas (29). This richness makes our system an ideal test bed to study how transport properties change with interactions. On the one hand, a spin-insulating character, not accessible to high-temperature measurements (22), should emerge as a result of s-wave pairing. On the other hand, particle transport directly tests the robustness of conductance quantization as many-body correlations emerge.

System

Implementation.

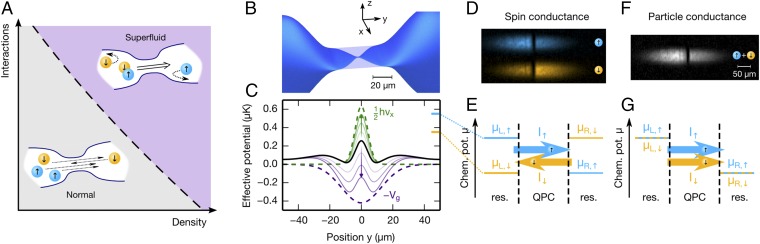
We capture in an elongated harmonic trap a total of $N=9.6\left(3\right)\times {10}^4$ ${}^6\text{Li}$ atoms in each of the lowest and third-lowest hyperfine states, labeled $\downarrow$ and $\uparrow .$ The particles interact via the van der Waals potential, which at the relevant density and energy scales reduces to a contact interaction characterized by the s-wave scattering length a. The scattering length, controlling the interaction strength, is adjusted by setting a homogeneous magnetic field between 673 G and 949 G, covering the regime from $1/k_{\text{F},\text{res}}a=-2.0$ to 0.6, where $k_{\text{F},\text{res}}=\sqrt{2m{E}_{\text{F}}/{\hslash }^2}$ is the Fermi wavevector in the gas, m is the mass of ${}^6\text{Li}$ atoms, and $E_{\text{F}}=k_{\text{B}}{T}_{\text{F}}=\hslash \overline{\omega }{\left(6N\right)}^{1/3}$ is the Fermi energy in the harmonic trap, with $\overline{\omega }$ being the geometric mean of its frequencies. We reach temperatures of 0.15(2) $T_{\text{F}}$ for the strongest and 0.11(2) $T_{\text{F}}$ for the weakest interactions (SI Appendix). For strong interaction, the temperature is low enough to access the superfluid regime, as sketched in Fig. 1A. Starting from the trapped gas, we first imprint a 2D constriction at the center of the cloud, using an off-resonant laser beam operating at a wavelength of 532 nm and shaped in a transverse electromagnetic ${(\text{TEM}}_{01})$-like mode propagating along the x axis and hitting the cloud at its center. This separates the elongated cloud into two reservoirs smoothly connected by a quasi-2D region, with a maximum vertical trap frequency along z of ${\nu }_z=9.2\left(4\right)$ kHz. The quantum point contact itself, depicted in Fig. 1B, is created by imaging a split gate structure on the 2D region, using high-resolution lithography (6). It is characterized by its transverse trapping frequency at the center, ${\nu }_x,$ which is adjustable. The Gaussian envelopes of the beams ensure a smooth connection to the large 3D reservoirs formed at both ends of the cloud (Fig. 1B). An attractive gate potential $V_g$ is realized by a red-detuned laser beam focused on the QPC (6), which tunes the chemical potential in the QPC and its immediate vicinity (Fig. 1C). The left (L) and right (R) reservoirs connected to the QPC contain $N_{i,\sigma }$ atoms and have chemical potentials ${\mu }_{i,\sigma },$ with i = L, R and σ = $\uparrow ,$ $\downarrow .$ Because the gate potential has a waist larger than the QPC, it also increases the density at the entrance and exit points (minima of the effective potential in Fig. 1C), creating a dimple effect that increases the local degeneracy (30).

Fig. 1.

Concept of the experiment. (A) Low-temperature phase diagram of the attractive Fermi gas at fixed temperature. In the normal, weakly interacting phase the two spin components move independently of each other in the QPC. In the superfluid phase large particle currents arise, whereas spin currents are strongly suppressed due to pairing. (B) Three-dimensional impression of the QPC, connected via an intermediate 2D region to large 3D reservoirs (shown only partly). (C) Effective potentials in the central region around the QPC along the transport axis y. It is the sum of the zero-point energy of the QPC (green dashed line: contribution from confinement along x), an attractive gate potential (purple dashed line), and the underlying harmonic trap (Materials and Methods). The black solid line corresponds to the parameters for which the conductance plateau in Fig. 3A is observed. Thin violet lines show how the effective potential evolves when $V_g$ is increased from $0.42\hspace{0.17em}\mathrm{\mu }\mathrm{K}$ to $0.82\hspace{0.17em}\mathrm{\mu }\mathrm{K}$, whereas thin green lines depict the corresponding evolution when ${\nu }_x$ is increased from 13.2 kHz to 25.2 kHz. Note the two local minima of the effective potential at the entrance and exit of the QPC. (D) Absorption images of the $\uparrow$ and $\downarrow$ cloud components prepared before spin conductance measurements. (E) Chemical potentials and currents in the presence of a spin bias. (F) Absorption image of the atoms prepared for the particle transport, with identical bias for $\uparrow$ and $\downarrow .$ (G) Chemical potentials and currents in the presence of a chemical potential bias.

Initialization.

To measure the particle or spin conductances of the QPC, we prepare either an atom number imbalance $\mathrm{\Delta }N=\left(\mathrm{\Delta }{N}_{\uparrow }+\mathrm{\Delta }{N}_{\downarrow }\right)/2\simeq 0.4\hspace{0.17em}N$ or a magnetization imbalance $\mathrm{\Delta }M=\left(\mathrm{\Delta }{N}_{\uparrow }-\mathrm{\Delta }{N}_{\downarrow }\right)/2\simeq 0.25\hspace{0.17em}N,$ with $\mathrm{\Delta }{N}_{\sigma }=N_{\text{L},\sigma }-N_{\text{R},\sigma }.$ These correspond to a chemical potential bias $\mathrm{\Delta }\mu =\left(\mathrm{\Delta }{\mu }_{\uparrow }+\mathrm{\Delta }{\mu }_{\downarrow }\right)/2\simeq 0.21\left(2\right)\mu \ll h{\nu }_z$ or a spin bias $\mathrm{\Delta }b=\left(\mathrm{\Delta }{\mu }_{\uparrow }-\mathrm{\Delta }{\mu }_{\downarrow }\right)/2\simeq 0.24\mu ,$ respectively (Fig. 1 D–G and Materials and Methods). In the weakly interacting regime, we do not find deviations from linear response within our experimental uncertainties (6). For particle transport in the strongly interacting regime, $\left|1/k_{\text{F},\text{res}}a\right|<0.7,$ we observe the emergence of nonlinearities, allowing us to identify the superfluid regime (ref. 31 and SI Appendix). The interaction-dependent chemical potentials ${\mu }_{i,\sigma }$ and the chemical potential at equilibrium μ are extracted from the known equation of state of the tunable Fermi gas (ref. 32 and Materials and Methods). The biases induce a spin current $I_{\sigma }$ and a particle current $I_N$ defined as

$$\{\begin{array}{l}{I}_{\sigma }=-\frac{1}{2}\frac{\text{d}}{\text{d}t}\mathrm{\Delta }M=G_{\sigma }\mathrm{\Delta }b\hfill \\ I_N=-\frac{1}{2}\frac{\text{d}}{\text{d}t}\mathrm{\Delta }N=G_N\mathrm{\Delta }\mu ,\hfill \end{array}$$ [1]

where $G_{\sigma }$ and $G_N$ are the spin and particle conductances, respectively. The currents are estimated by measuring the number of particles transferred after 4 s and 2 s of transport time, respectively, and compared with the bias to obtain the conductances (Materials and Methods).

Spin Transport

Measurements.

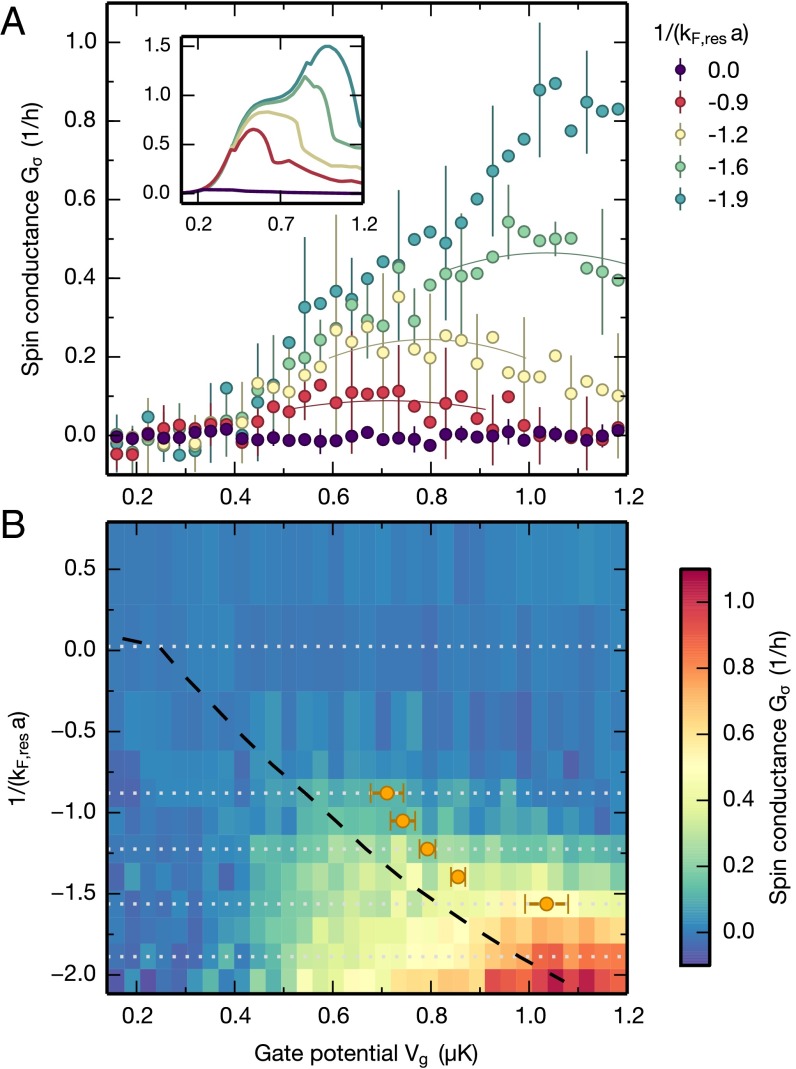
We first investigate the spin conductance $G_{\sigma }$ as a function of gate potential $V_g,$ at fixed ${\nu }_x=23.2\left(2.5\right)$ kHz, but for different interaction strengths. For noninteracting particles, the strength of the gate determines the number of transport channels that are open (6). The results are presented in Fig. 2 A and B. For the weakest interactions, we observe the onset of spin transport as the first channel opens around $V_g=0.4$ μK, followed by a continuous increase of $G_{\sigma }$ up to the largest gate potentials. The second channel is expected to open around $V_g=0.8$ μK. For intermediate interaction strengths $-1.7<\left(1/k_{\text{F},\text{res}}a\right)<-1.0,$ we observe a broad maximum in $G_{\sigma }$ as a function of $V_g.$ The opening of the channel is still indicated by a sharp increase of $G_{\sigma }$ at an interaction-independent value of the gate potential. With increasing interactions, the center of the broad maximum in $G_{\sigma }$ shifts to lower $V_g,$ and its height is reduced. For $1/\left(k_{\text{F},\text{res}}a\right)>-0.5,$ $G_{\sigma }$ vanishes over the entire range of gate potentials. A complete map of $G_{\sigma }$ as a function of interaction strength and gate potential is shown in Fig. 2B. The existence of a maximum in $G_{\sigma }$ and the negative spin transconductance $\text{d}{G}_{\sigma }/\text{d}{V}_g$ for strong interactions indicate the appearance of a spin insulating phase. Indeed, increasing $V_g$ increases the chemical potential in and around the QPC, reducing the relative temperature $T/T_{\text{F}}.$ The decrease of conductance with decreasing temperature is characteristic of an insulating behavior (33).

Fig. 2.

Spin conductance of the attractively interacting Fermi gas. (A) Spin conductance $G_{\sigma }$ as a function of the gate potential $V_g$ for different interaction strengths $1/\left(k_{\text{F},\text{res}}a\right)$ in the reservoirs. Each data point represents the mean over nine measurements and error bars indicate 1 SD plotted for every third point. The thin solid lines are quadratic fits used to identify the maxima in $G_{\sigma }.$ Inset shows $G_{\sigma }$ obtained from a mean-field phenomenological model, reproducing the nonmonotonic behavior of the experimental data. (B) Two-dimensional color plot of $G_{\sigma }$ as a function of $1/\left(k_{\text{F},\text{res}}a\right),$ with cuts of A indicated as gray dotted lines. The points where $G_{\sigma }$ is maximum, obtained from a parabolic fit along $V_g,$ are displayed as orange circles for comparison. The black dashed line represents the superfluid critical line estimated at the entrance and exit regions of the QPC, using the results of ref. 38.

Mean-Field Model.

We use a mean-field approach to capture the phenomenology of the spin transport. It assumes that excitations are noninteracting, fermionic Bogoliubov quasiparticles. Because the Cooper pairs are singlets, these excitations carry the spin current and their populations are controlled by the spin bias. This allows for a generalization of the Landauer approach to spin conductance (SI Appendix). The predictions are shown in Fig. 2A, Inset. The emergence of a maximum as a function of gate potential is reproduced. It results from the competition between the nonlinearly increasing gap at the entrance and exit of the QPC, hindering spin transport, and the opening of conduction channels.

The position of the maximum along the gate potential axis and the shape of the conductance variations are reproduced, but the predictions for the value of the conductance differ by about a factor of 2. This discrepancy could come from interactions between quasiparticles of opposite spin, neglected in the model, in particular inside the contact where the one-dimensional geometry enhances scattering (34).

Particle Transport

Measurements.

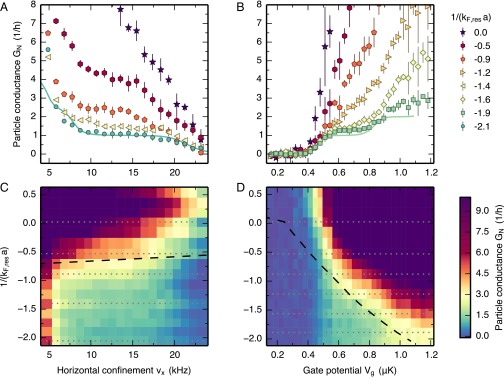
The total particle current is expected to be robust against collisions, because they conserve momentum. However, large interaction effects are observed. We measured $G_N$ for several interaction strengths as functions of $V_g$ and ${\nu }_x.$ Fig. 3A shows the curves for fixed gate potential $V_g=0.42$ μK as a function of horizontal confinement ${\nu }_x.$ For the weakest interaction strength $1/k_{\text{F},\text{res}}a=-2.1,$ $G_N$ shows a distinct plateau at $1/h$ in agreement with the Landauer picture. For the tightest horizontal confinement, ${\nu }_x=23.2$ kHz, the QPC is almost pinched off, whereas when reducing ${\nu }_x$ below 8 kHz, several transverse modes with closely spaced energies get populated.

Fig. 3.

Particle conductance of the attractively interacting Fermi gas. (A and B) Particle conductance $G_N$ as a function of the horizontal confinement frequency ${\nu }_x$ of the QPC, at fixed gate potential $V_g=0.42\hspace{0.17em}\mathrm{\mu }\mathrm{K}$ (A) and as a function of the gate potential $V_g$ at fixed confinement frequency ${\nu }_x=23.2$ kHz (B), for different interaction strengths $1/\left(k_{\text{F},\text{res}}a\right)$ in the reservoirs. The solid lines are theoretical predictions for $1/\left(k_{\text{F},\text{res}}a\right)=2.1$ and 1.9, respectively, based on the Landauer formula including mean-field attraction (SI Appendix). Each data point represents the mean over five measurements and error bars indicate 1 SD. (C and D) Two-dimensional color plot of $G_N$ as a function of interaction strength $1/\left(k_{\text{F},\text{res}}a\right)$ and horizontal confinement (C) or gate potential (D). Both plots contain the cuts of A and B (gray dotted lines) and an estimation of the local superfluid transition at the QPC exits (black dashed line).

For interaction strengths $-2.1<1/(k_{\text{F},\text{res}}a)<-0.5,$ a conductance plateau with a reduced length remains visible in Fig. 3A. The height of this feature continuously increases above the universal value and eventually washes out with increasing interaction strength, leaving a visible shoulder as high as $\sim 4/h$ for $1/\left(k_{\text{F},\text{res}}a\right)=-0.5.$ A similar observation is made when varying $V_g$ at fixed ${\nu }_x=23.2$ kHz, as shown in Fig. 3B. There again, plateau-like features with conductances higher than $1/h$ are observed for interaction strengths $1/\left(k_{\text{F},\text{res}}a\right)<-1.3.$ As interactions are further increased toward the unitary regime [$-0.5<1/\left(k_{\text{F},\text{res}}a\right)\le 0$ for Fig. 3 A and C and $-1.3<1/\left(k_{\text{F},\text{res}}a\right)\le 0$ for Fig. 3 B and D], no conductance plateaus can be distinguished, and $G_N$ increases continuously from zero to large values. Contrary to variations of ${\nu }_x,$ variations of $V_g$ change the density at the entrance and exit of the QPC, which probably causes the disappearance of the plateau already at a lower value of the interaction strength.

The entire crossover from quantized conductance of weakly interacting atoms to its breakdown for strong interactions is mapped out in Fig. 3C for fixed $V_g$ and varying ${\nu }_x$ and in Fig. 3D for fixed ${\nu }_x$ and varying $V_g.$ The latter demonstrates most clearly that the conductance plateau, discernible as a green area, shrinks gradually when the interaction strength is increased from $1/\left(k_{\text{F},\text{res}}a\right)<-2$ to $1/\left(k_{\text{F},\text{res}}a\right)<-1.$ In this regime the plateau width is well predicted by a mean-field model accounting for intra- and intermode attraction in the QPC (SI Appendix). Furthermore, we observe little difference between the unitary and the molecular regime in the experimentally accessible region, $0<1/\left(k_{\text{F},\text{res}}a\right)<0.5,$ where the reservoirs form a condensate of molecules (35).

Superfluid Transition.

In the strongly interacting regime (dark purple regions in Fig. 3 C and D), deviations from a linear response to the bias are observed (36, 37) in agreement with our previous measurements for a QPC in a unitary superfluid (31) (SI Appendix). Indeed, for the temperature imposed by the reservoirs, increasing $V_g$ or the interactions leads to the onset of superfluidity in the minima of the effective potential (Fig. 1C), i.e., at the entrance and exit of the QPC. The local critical temperature at those points thus corresponds to the maximum critical temperature over the entire cloud, and we refer to it as $T_c$ for the remainder of this article. To extract it, we use the state-of-the-art calculation of $T_c/{\tilde{T}}_{\text{F}}\left(1/\left({\tilde{k}}_{\text{F}}a\right)\right)$ (38) in local density approximation, with $k_{\text{B}}{\tilde{T}}_{\text{F}}={\hslash }^2{\tilde{k}}_{\text{F}}^2/\left(2m\right)={\hslash }^2{\left(6{\pi }^{2}n\right)}^{2/3}/\left(2m\right)$ being the Fermi energy of a homogeneous gas with density n. We estimate n at the entrance and exit of the QPC from the trap geometry and the equation of state of the low-temperature, tunable Fermi gas (SI Appendix). The resulting critical line is displayed in Figs. 2B and 3 C and D. It closely tracks the maxima of the spin conductance in Fig. 2B, as well as the disappearance of the conductance plateaus in Fig. 3.

Conductances in the Single-Mode Regime.

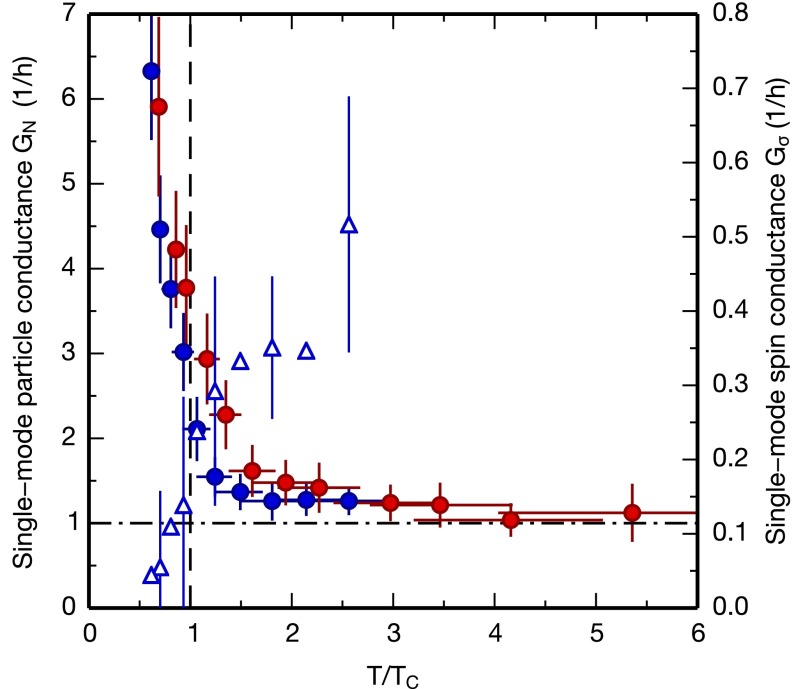
We now focus on the conductances in the single-mode regime, where universal quantization is observed for weak interactions. For this purpose, we display in Fig. 4 the conductances as a function of $T/T_c,$ measured at the position of the plateau center in the weakly interacting regime. These are extracted from Fig. 3C for fixed ${\nu }_x=14.5$ kHz and from Fig. 3D for fixed $V_g=0.64$ μK. We observe that the resulting conductances now coincide within error bars. This demonstrates that $T/T_c$ is a key control parameter of the transition, despite the fact that the two datasets correspond to different geometries in the single-mode regime. The fast increase of particle conductance coincides with a sharp drop in the spin conductance around $T/T_c=1,$ demonstrating directly the intimate connection between pairing and superfluidity. The regime of nonuniversal quantization, with a conductance larger than $1/h$ as identified by our measurement method and accuracy, extends from $T/T_c\sim 1,$ corresponding to the shoulder observed at $\sim 4/h,$ to far above the superfluid transition, up to $T/T_c\sim \mathrm{2.5.}$ This suggests that in this regime, where $T>T_c$ at every point in the cloud, current is not carried by fermionic quasiparticles, challenging a description in terms of Fermi liquids.

Fig. 4.

Particle and spin conductances in the single-mode regime. $G_N$ (solid circles) and $G_{\sigma }$ (open triangles, every second error bar displayed) for various interaction strengths are presented as a function of the reduced temperature $T/T_c,$ which varies due to the dependence of $T_c$ on density and scattering length. Blue data points are obtained from the measurements shown in Figs. 2 and 3 B and D for $V_g=0.64$ μK and ${\nu }_x=23.2$ kHz. Red data points are obtained from the measurements shown in Fig. 3 A and C for $V_g=0.42$ μK and ${\nu }_x=14.5$ kHz. $G_N$ tends to the conductance quantum $1/h$ (horizontal dashed-dotted line) for weak interactions ($T/T_c\gg 1$). Error bars contain statistical and systematic errors (Materials and Methods).

Discussion

A possible interpretation for the anomalously high conductance, i.e., exceeding $1/h$ in the normal, single-mode regime, is the presence of strong superfluid fluctuations in the reservoirs, due to the large critical region around the superfluid transition (39, 40). The critical fluctuations are qualitatively similar to those of the Luttinger liquid in one dimension with attractive interactions in the leads, where they are known to yield an enhanced conductance (25–27). Another possibility is preformed pairs above $T_c$ that could form in particular in the contact region (41), leading to a channel with a bosonic character, where large conductances are expected (42, 43). Evidence for such non-Fermi liquid behavior in the BEC–BCS crossover was found using photoemission spectroscopy (29), in contrast to results based on the equation of state (44, 45). Our findings, covering the attractively interacting regime, complement the observations made with repulsively interacting electrons in solid-state QPCs. Future work could also explore the known conductance anomalies observed in electronic QPCs (19, 20).

Materials and Methods

Preparation of the Cloud.

Interacting Fermi gases are produced by a two-step evaporative cooling procedure. We first create a balanced mixture of the lowest two hyperfine states of ${}^6\text{Li}$ and perform evaporative cooling at a magnetic field of 302 G down to temperatures of the order of the Fermi temperature. A Landau–Zener radio frequency transition then transfers the full population from the second to the third hyperfine state, and the magnetic field is ramped up to 689 G, the center of a Feshbach resonance (46), where the s-wave scattering length diverges. A second step of forced evaporation is then performed using a magnetic field gradient, yielding the low-temperature clouds used for the transport measurements. The magnetic field is then ramped in $200$ ms to the desired value between 673 G and 949 G to vary the interaction strength during transport. In the absence of the point contact and gate beam, the atoms reside in a hybrid trap where the confinement along x and z is ensured by an optical dipole trap and along y by the residual curvature of the magnetic field. The trap frequencies along the x and z directions are $194$ Hz and $157$ Hz, respectively. The trap frequency along y ranges between $28.0\left(5\right)$ Hz and $33.2\left(6\right)$ Hz, depending on the value of the magnetic field.

Creation of the Spin Bias.

To create a symmetric spin bias $\mathrm{\Delta }{\mu }_{\uparrow }=-\mathrm{\Delta }{\mu }_{\downarrow }$ between the two reservoirs (Fig. 1E), we ramp the magnetic field before the Landau–Zener transfer in 10 ms from 302 G down to 52 G, where the lowest and second lowest hyperfine states have different magnetic moments, and apply at the same time a magnetic field gradient along the transport axis. This induces dipole oscillations with different frequencies and different amplitudes for the two states. We wait for roughly one period of the faster oscillation before we abruptly switch on an elliptic repulsive gate laser beam separating the reservoirs (47). The magnetic field is then ramped back to a value close to its initial value, from where we transfer all of the atoms in state $|2\rangle$ to state $|3\rangle ,$ using an adiabatic Landau–Zener radio frequency transfer. After evaporation at the Feshbach resonance, we obtain an opposite atom number imbalance for the two states, $\mathrm{\Delta }{N}_{\uparrow }\simeq -\mathrm{\Delta }{N}_{\downarrow }\simeq 0.25.$ We ensured that this preparation scheme does not increase the temperature compared with the one for the particle transport.

Effective Potential.

For the computation of the conductance we use adiabatic approximation (48, 49), which allows for a separation of longitudinal (y) and transverse (x, z) coordinates. We verified numerically that it is a very good approximation for the geometry of our QPC. In the resulting one-dimensional Schrödinger equation the transverse energy $E_{\perp }\left(y\right)=\left(1/2\right)h{\nu }_x{f}_x\left(y\right)+\left(1/2\right)h{\nu }_z{f}_z\left(y\right)$ acts as an additional potential, with $f_{x,z}\left(y\right)$ describing the spatial variation of the trapping frequencies of the QPC. Together with the gate potential $V_g\left(y\right)=-V_g{f}_g\left(y\right),$ and the harmonic trapping potential $V_{\text{trap}}\left(y\right)=\left(1/2\right)m{\omega }_y^2{y}^2$ along y, and a residual repulsive potential $E_{\text{resid}}\left(y\right)=E_{\text{resid},0}{f}_z^2\left(y\right)$ arising from residual light in the nodal line of the intensity profile of the ${\text{TEM}}_{01}$-like laser mode creating the 2D confinement (50), it forms the effective potential $V_{\text{eff}}=E_{\perp }+V_g+V_{\text{trap}}+E_{\text{resid}},$ which is shown in Fig. 1C. The involved envelope functions are listed in Table 1. The prefactor in $E_{\text{resid}}$ has been calibrated to $E_{\text{resid},0}=0.14\left(7\right)$ μK, using a conductance measurement with only the 2D confinement present. The central maximum in a generic profile $V_{\text{eff}}$ is due to the x confinement of the QPC, and the two minima to each side of it are a result of the combined potential of $E_{\perp }$ and $V_g.$ We define the entrance and exit of the QPC as the position of these minima. They represent the positions of highest density and thus of lowest $T/{\tilde{T}}_{\text{F}}.$

Table 1.

Envelope functions determining the effective potential

Envelope function	Waist	Description
$f_x\left(y\right)=\text{exp}\left(-y^2/w_x^2\right)$	$w_x=5.6\left(6\right)$ μm	QPC, x confinement
$f_z\left(y\right)=\text{exp}\left(-y^2/w_z^2\right)$	$w_z=30\left(1\right)$ μm	QPC, z confinement
$f_g\left(y\right)=\text{exp}\left(-2y^2/w_g^2\right)$	$w_g=25\left(1\right)$ μm	Gate potential

Compressibility and Spin Susceptibility of the Trapped Gas.

To evaluate the interaction-dependent chemical potentials ${\mu }_{\uparrow }$ and ${\mu }_{\downarrow },$ compressibility κ, and spin bias $\mathrm{\Delta }b$ we use the equation of state of the two-component, homogeneous Fermi gas $\mathcal{P}\left({\mu }_{\uparrow },{\mu }_{\downarrow },a\right)$ (32).

Integrating it over the trap provides the thermodynamic potential ${\mathcal{P}}_{\text{trap}}={\displaystyle \int d\overrightarrow{r}\hspace{0.17em}\mathcal{P}\left({\mu }_{\uparrow }-V\left(\overrightarrow{r}\right),{\mu }_{\downarrow }-V\left(\overrightarrow{r}\right),a\right)},$ with $V\left(\overrightarrow{r}\right)$ the known trapping potential (including the QPC region) and ϑ the Heaviside function. The particle number N and the magnetization M in a single reservoir are then given by $N=\left(1/2\right){\left(\partial {\mathcal{P}}_{\text{trap}}/\partial \mu \right)}_b$ and $M=\left(1/2\right){\left(\partial {\mathcal{P}}_{\text{trap}}/\partial b\right)}_{\mu }$ with $\mu =\left({\mu }_{\uparrow }+{\mu }_{\downarrow }\right)/2$ and $b=\left({\mu }_{\uparrow }-{\mu }_{\downarrow }\right)/2.$ The factors of $1/2$ arise because the size of the two identical reservoirs is half of the entire cloud. Given the measured N and M, one can solve numerically for ${\mu }_{\uparrow }$ and ${\mu }_{\downarrow }$ or, equivalently, for μ and b.

The compressibility and spin susceptibility of a single reservoir are given by $\kappa =\left(1/4\right){\left({\partial }^2{\mathcal{P}}_{\text{trap}}/\partial {\mu }^2\right)}_b$ and $\chi =\left(1/4\right){\left({\partial }^2{\mathcal{P}}_{\text{trap}}/\partial b^2\right)}_{\mu },$ respectively. The additional factors of 1/2 the definitions of N and M arise because in our definitions of κ and χ, we require that $\kappa \to {\left(\partial N_{\uparrow (\downarrow )}/\partial {\mu }_{\uparrow (\downarrow )}\right)}_b$ for $b\to 0.$

For a symmetric spin bias, we have $\mathrm{\Delta }b=2b.$ It ranges from $0.18\mu$ to $0.34\mu$ for interaction strengths $-2.0\le 1/\left(k_{\text{F},\text{res}}a\right)\le -0.5,$ corresponding to a mean value of $0.24\mu .$

Extraction of the Conductances.

$G_N$ is determined within linear response as in ref. 6. We use the relation $\mathrm{\Delta }N=\kappa \mathrm{\Delta }\mu ,$ yielding

$$\frac{\text{d}}{\text{d}t}\mathrm{\Delta }N=-\frac{2G_N}{\kappa }\mathrm{\Delta }N.$$ [2]

We indeed observe an exponential decay of $\mathrm{\Delta }N$ as a function of time (except for the deep superfluid regime; SI Appendix). The characteristic time ${\tau }_N$ is related to $G_N$ through $G_N=\kappa /2{\tau }_N.$ To determine $G_N,$ we evaluate κ (see above) and determine ${\tau }_N$ by measuring $\mathrm{\Delta }N$ at $t=0$ and after a transport time of $t_{\text{tr}}=2s.$ From the solution of Eq. 2 we obtain

$$\frac{1}{{\tau }_N}=\frac{1}{t_{\text{tr}}}\hspace{0.17em}\text{ln}\left(\frac{\mathrm{\Delta }N}{N}\left(t=0\right)\right)-\frac{1}{t_{\text{tr}}}\hspace{0.17em}\text{ln}\left(\frac{\mathrm{\Delta }N}{N}\left(t=t_{\text{tr}}\right)\right).$$ [3]

$G_{\sigma }$ is extracted slightly differently: A linear response relation similar to Eq. 2 cannot be established for $\mathrm{\Delta }M$ because the magnetic susceptibility depends in a nonlinear way on b. In particular, χ starts close to zero for low b due to the superfluid gap. We define $G_{\sigma }$ as $G_{\sigma }=I_{\sigma }/\mathrm{\Delta }b.$ We evaluate $\mathrm{\Delta }b$ from the initial magnetization imbalance $\mathrm{\Delta }{M}_0$ (see above) and determine $I_{\sigma }$ from

$$I_{\sigma }=\mathrm{\Delta }{M}_0/\left(2{\tau }_{\sigma }\right),$$ [4]

where ${\tau }_{\sigma }$ is the time constant of the observed exponential decay of the magnetization imbalance $\mathrm{\Delta }M\left(t\right).$ ${\tau }_{\sigma }$ is determined by measuring $\mathrm{\Delta }M/N$ at $t=0$ and after a transport time of $t_{\text{tr}}=4s$ and evaluating

$$\frac{1}{{\tau }_{\sigma }}=\frac{1}{t_{\text{tr}}}\hspace{0.17em}\text{ln}\left(\frac{\mathrm{\Delta }M}{N}\left(t=0\right)\right)-\frac{1}{t_{\text{tr}}}\text{ln}\left(\frac{\mathrm{\Delta }M}{N}\left(t=t_{\text{tr}}\right)\right).$$ [5]

Error Bars.

Error bars in Figs. 2 and 3 are statistical and indicate 1 SD. Error bars in Fig. 4 represent the uncorrelated combination of 1 SD statistical and systematic uncertainties. The systematic uncertainty in the conductance amounts to 11%. It represents the uncorrelated combination of the uncertainties in the compressibility, which are due to the calibration error in the total particle number, an uncertainty in the overall trapping potential, and an uncertainty due to the use of the zero temperature equation of state. The statistical error in $T/T_c$ is due to the determination of T and amounts to 10%. The systematic uncertainty in $T/T_c$ is mainly due to the uncertainty in our estimate of $T_c.$ It is caused by the overall uncertainty in the effective potential, which is due to the uncertainties in ${\nu }_z,$ ${\nu }_x,$ $V_g$ and their spatial dependencies. None of these uncertainties could explain the departure of conductance from $1/h$ observed in Figs. 3 and 4.