Spontaneous wettability patterning via creasing instability

Significance

Surfaces with patterned wettability contrast are important in many applications. Traditional fabrication methods rely on microfabrication technologies, which are generally not cost effective and are difficult to implement on curved surfaces. We show that wettability contrast can be patterned spontaneously on both flat and curved surfaces in a single step process by taking advantage of a reversible creasing instability. Moreover, the domain size, morphology, and wettability contrast can be controlled independently, yielding heterogeneous surfaces that show potential for generating high-throughput parallel microreactors and for harvesting water from humid air. This mechanical self-assembly approach can also lead to other functional materials beyond wettability patterning.

Abstract

Surfaces with patterned wettability contrast are important in industrial applications such as heat transfer, water collection, and particle separation. Traditional methods of fabricating such surfaces rely on microfabrication technologies, which are only applicable to certain substrates and are difficult to scale up and implement on curved surfaces. By taking advantage of a mechanical instability on a polyurethane elastomer film, we show that wettability patterns on both flat and curved surfaces can be generated spontaneously via a simple dip coating process. Variations in dipping time, sample prestress, and chemical treatment enable independent control of domain size (from about 100 to 500 μm), morphology, and wettability contrast, respectively. We characterize the wettability contrast using local surface energy measurements via the sessile droplet technique and tensiometry.

Surfaces that juxtapose local hydrophilic areas with hydrophobic areas show superior performance compared with surfaces with homogeneous wettability in many industrial applications including heat transfer (1), water collecting (2–6), particle separation (7), and microfluidics (8). For instance, developing enhanced water-collecting efficiency has been inspired by the Namib desert beetle, which was reported (2) to have hydrophilic bumps on an overall wax-covered hydrophobic surface. Although the hydrophilic bumps reduce the nucleation/coalescence energy of microdroplets, the overall hydrophobic character of the surface facilitates the spontaneous shedding of water droplets when they grow beyond a certain size.

To achieve surfaces with wettability patterning, traditional fabrication methods such as photolithography and soft lithography have been used. However, these methods are generally not cost-effective, not readily scaled up, require multiple process steps, and are difficult to implement on curved surfaces (3, 9). Recently, mechanical instabilities have been explored as a facile self-assembly approach to endow surfaces with superhydrophobicity (10–12), superhydrophilicity (13), or anisotropic wettability (14). Although mechanical self-assembly provides a low cost route for spontaneous generation of surface patterns, explorations to date have been focused on introducing surface roughness via wrinkling and crumpling instabilities. Here we show that surfaces can be spontaneously patterned with chemical patches with small changes in surface roughness by harnessing a reversible creasing instability (15–17).

A creasing instability develops when a soft polymer network is placed under mechanical compression beyond a certain critical strain, at which point sharp folds spontaneously develop and grow on the deformable free surfaces (18). This process has been linked to the morphology development of the brain (19, 20), electric breakdown of dielectric elastomers (21), and has also been harnessed to prepare switchable surfaces actuated by temperature (22) or electric field (23, 24). Even though the creasing instability develops as a result of large compressive strains, it is elastic in character and reversible (17). Creasing differs from a wrinkling instability in that the surface folds into sharp self-contacts, whereas in the latter case, the surface remains locally smooth. This reversible folding and unfolding of surface self-contacts enables local regions of a creased surface to be reversibly sealed off and then reopened and can be harnessed to coat soft gels and elastomers with different chemical patterns (22).

By taking advantage of this reversible creasing instability, we show in the present study that wettability patterns on both flat and curved surfaces can be generated spontaneously over large areas via a simple dip coating process. Variations in dipping time, sample prestress, and chemical treatment lead to changes in the domain size, the morphology, and the wettability contrast of the heterogeneous surface, respectively. We characterize the wettability contrast using sessile droplet methods and tensiometry. We further show that such scalable and heterogeneous surfaces have potential for generating high-throughput parallel microreactors and for harvesting water from humid air.

Results and Discussion

Spontaneous Patterning of Surfaces with Chemical Patches.

Polyurethane elastomer coatings are generally used to protect surfaces. These coatings are processed from two readily mixable components, with isocyanate groups in the formulation reacting with hydroxyl groups present on the substrates to ensure good adhesion. As shown in Fig. 1A, a polyurethane elastomer film with thickness of ∼1 mm is coated on a flat polystyrene substrate, which is pretreated with a radio frequency oxygen plasma at 18 W for 5 min immediately before coating with the polyurethane, to introduce hydroxyl groups on the polystyrene surface. After curing at room temperature for 24 h, the sample is immersed into a solution that contains poly(ethyl methacrylate) (PEMA)/fluorodecyl polyhedral oligomeric silsesquioxane (fluorodecyl POSS) (80:20 by weight) in Asahiklin 225 solvent (a mixture of 3,3-dichloro-1,1,1,2,2-pentafluoropropane and 1,3-dichloro-1,1,2,2,3-pentafluoropropane) at a total solid content of 3 wt%. The polyurethane film swells by imbibing solvent molecules. In comparison with a freestanding polyurethane film, which swells freely in three dimensions, the surface-bound polyurethane film can swell only in the direction normal to the substrate. As a result, the swollen film is laterally compressed and is in a state of equibiaxial compression (16, 25). Beyond a critical strain of ${\mathit{\epsilon }}_{\mathit{biaxial}}^{\mathit{c}}=0.25$ (26), creases spontaneously form on the surface of the swollen polyurethane film.

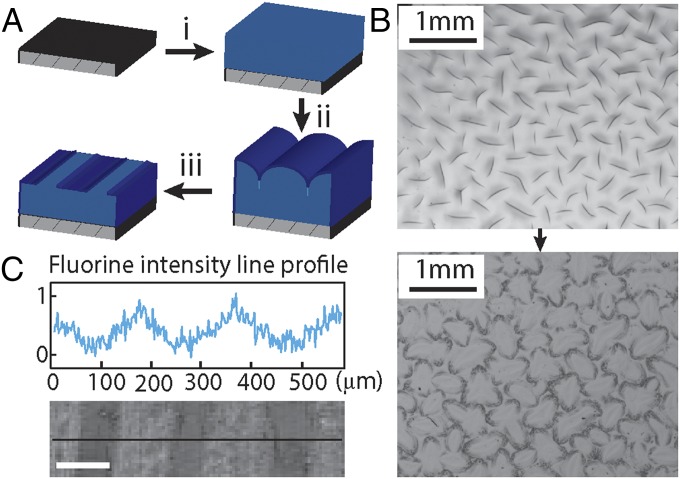
Fig. 1.

Spontaneous surface patterning via reversible creasing instability. (A) The procedure of patterning consists of three steps: (i) coating substrate with a polyurethane elastomer film; (ii) unidirectional swelling of the geometrically constrained polyurethane film in a solution containing poly(ethyl methacrylate)/fluorodecyl POSS in Asahiklin solvent, leading to creases formed on the surface; and (iii) withdrawing the sample from the coating solution resulting in a PEMA/POSS coating to the exposed regions, and evaporation of Asahiklin solvent causing the polyurethane film to deswell, which leads to unfolding of the creases and exposure of the uncoated self-contact regions. (B) Optical micrographs showing creases observed on the polyurethane film surface (Upper) and a patterned surface via reversible creasing (Lower). (C) A fluorine element intensity line profile by EDS showing the deposition of hydrophobic fluorodecyl POSS molecules on the exposed regions. (Scale bar, 100 μm.)

The PEMA/POSS that is dissolved in the Asahiklin solution does not diffuse into the swollen polyurethane elastomer, because diffusion of these molecules into the polyurethane elastomer is thermodynamically unfavorable. The effective network size of the polyurethane elastomer is estimated to be $\mathit{\xi }={\left(k_{b}T/G\right)}^{1/3}\approx 1\hspace{0.5em}\mathrm{nm}$, smaller than the molecular size of the fluorodecyl POSS molecule and that of the PEMA molecule, estimated to be ∼3 and ∼25 nm (i.e., the radius of gyration in good solvent condition), respectively, where $k_{b}T$ is the thermal energy, and $G\approx 1\hspace{0.5em}\mathrm{MP}$ is the shear modulus of the polyurethane film. The large interaction parameter expected between the fluorodecyl POSS molecule and the polyurethane molecule also results in a large enthalpic cost for mixing fluorodecyl POSS with polyurethane. Therefore, we do not expect fluorodecyl POSS and PEMA molecules to diffuse into the polyurethane elastomeric network. At the polyurethane surface, a depletion layer builds up due to the entropic penalty of polymer confinement (27). As the surface of polyurethane elastomer folds into sharp self-contacts at the creased regions, fluorodecyl POSS and PEMA molecules are squeezed out of the creases, preventing the adsorption of PEMA/POSS in the self-contact regions. When the swollen and creased sample is withdrawn from the PEMA/POSS/Asahiklin solution, a thin uniform coating layer of PEMA/POSS is deposited on the exposed region of the creased surface as in a typical viscous withdrawal process (28). As shown in Fig. S1A, a constant withdrawal speed of $\mathit{U}\approx \mathrm{0}\mathrm{.1}\hspace{0.5em}\mathrm{m}/\mathrm{s}$ is applied in the creasing-coating process, corresponding to a capillary number of $Ca=\mathit{\mu }U/\mathit{\sigma }\approx 6.2\mathrm{\times }{10}^{-3}$, where $\mathit{\mu }\approx \mathrm{1}\hspace{0.5em}\mathrm{mPa\cdot s}$ and $\mathit{\sigma }=16.2\hspace{0.5em}\mathrm{mN}/\mathrm{m}$ represents the viscosity and surface tension of the coating solution containing 3wt% PEMA/POSS, respectively. According to Landau–Levich–Derjaguin (28, 29), the expected thickness of the coated solution layer is $h\approx 0.94l_{c}C{a}^{2/3}=32\hspace{0.5em}\mu \mathrm{m}$, where $l_c=\sqrt{\mathit{\sigma }/\mathit{\rho g}}\approx 1\mathrm{\times }{10}^{-3}\hspace{0.5em}\mathrm{m}$ is the capillary length, in which $\rho =1.6\times {10}^3\hspace{0.5em}\mathrm{kg}/{\mathrm{m}}^{\mathrm{3}}$ is the density of the coating solution and $g=9.8\hspace{0.5em}\mathrm{m}/{\mathrm{s}}^{\mathrm{2}}$ is the gravitational acceleration. Because the 3wt% PEMA/POSS/Asahiklin solution has a solid volume fraction of around 3.5%, rapid evaporation of the volatile solvent results in formation of a uniform dry film of PEMA/POSS on the surface with a thickness of $h_{final}=0.035h\approx 1\hspace{0.5em}\mu \mathrm{m}$. This predicted dry film thickness of PEMA/POSS layer is confirmed experimentally by scanning electron microscopy (SEM) imaging of the cross section (Fig. S1B). The cross-sectional image also reveals the clear boundary between the PEMA/POSS layer and the polyurethane elastomer, confirming that no PEMA or POSS molecules diffuse into the polyurethane elastomer. The subsequent slow deswelling of the polyurethane substrate below causes the unfolding of creases, revealing the uncoated self-folding regions (Fig. 1A). Increased amounts of the PEMA/POSS coating solution are trapped at the edge of these folds as a result of contact line pinning and the coffee ring effect (30), leaving additional material deposited at the edge of the creases, as indicated by the darker rims around the uncoated regions shown in Fig. 1B.

Fig. S1.

A thin uniform layer of PEMA/POSS is coated on the exposed surface of a creased polyurethane elastomer via viscous withdrawal from PEMA/POSS/Asahiklin solution. (A) A schematic illustration of the dynamic meniscus in the viscous withdrawal coating process with a vertical withdrawal speed of $U\approx 0.1\hspace{0.5em}\mathrm{m}/\mathrm{s}\mathrm{\cdot }h$ and $l_c$ indicate the thickness of the coated solution layer and the capillary length, respectively. (B) A cross-sectional SEM image of the PEMA/POSS-coated polyurethane elastomer. The thickness of the dry PEMA/POSS layer is about 1 μm, in good agreement with the predicted result by scaling analysis of the viscous withdrawal process. The thickness of the PEMA/POSS layer is measured at five different spots across a surface with lateral dimensions of 5 × 5 cm and the results are within 10% variation, indicating a uniform coating layer is achieved through the viscous withdrawal coating process.

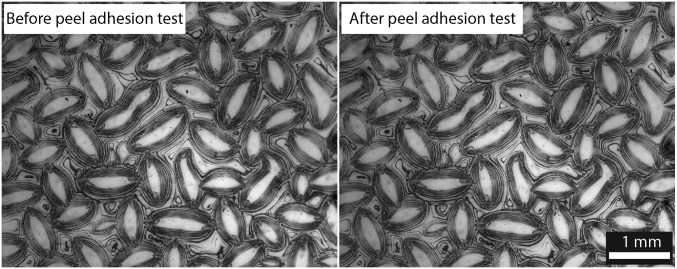
Although this creasing/coating process generates patterned surfaces with regions of chemical contrast, it produces only minimal surface topographical modification. As shown in Fig. S2, a 3D surface profile is obtained by performing a surface scan on the coated polyurethane film (swollen in PEMA/POSS solution for 100 s before withdrawal) with a stylus profilometer. Multiple rings are observed around the unfolded crease, resulting from the competition between dewetting and contact line pinning (31). The root mean square roughness is $R_q=380\hspace{0.17em}\mathrm{nm}$, much smaller than the lateral length scale of the chemical patches, which are on the order of 100 μm. The chemical contrast on the polyurethane surface is characterized via energy dispersive spectroscopy (EDS). As seen in Fig. 1C, the exposed area (outside the self-creased domains) has much higher fluorine element content, whereas the creased regions have minimal fluorine content. This patterned hydrophobic fluorodecyl POSS coating leads to pronounced local surface wettability contrast, which will be characterized and discussed in later sections. PEMA acts as a compatiblizing layer between the POSS and the polyurethane surface that enhances the adhesion of hydrophobic fluorodecyl POSS molecules to the polyurethane elastomer (32). The low-energy POSS molecules reside preferentially at the free surface, whereas the PEMA chains interact with the polyurethane elastomer, creating a strong interface. We confirm the strong adhesion by performing a simple peel adhesion test (Fig. S3).

Fig. S2.

A 3D surface profile by stylus profilometry showing the introduction of a small RMS roughness ($R_q=380\hspace{0.17em}\mathrm{nm}$) to the surface.

Fig. S3.

Peel adhesion test indicates good adhesion strength between the PEMA/POSS layer and the polyurethane elastomer. A strip of tape (3M 371 Carton Sealing Tape) is applied to a PEMA/POSS-coated polyurethane elastomer with finger pressure. The tape is peeled from the sample at a 180° angle. After the peel adhesion test, no apparent change is observed on the coated surface, implying good adhesion between the PEMA/POSS layer and the underlying polyurethane elastomer. PEMA acts as a compatiblizing layer between the POSS and the polyurethane surface that enhances the adhesion of hydrophobic fluorodecyl POSS molecules to the polyurethane elastomer. The low-energy POSS molecules reside preferentially at the free surface, whereas the PEMA chains interact with the polyurethane elastomer, creating a strong interface. Therefore, the interfacial tension between the PEMA/POSS layer and the PU elastomer is estimated to be ${\gamma }_{12}={\gamma }_1+{\gamma }_2-2{\left({\gamma }_1{\gamma }_2\right)}^{1/2}=0.3\hspace{0.5em}\mathrm{mN}/\mathrm{m}$, where ${\gamma }_1=40\mathrm{\pm }5\hspace{0.5em}\mathrm{mN}/\mathrm{m}$ is the surface energy of a typical poly(ether-urethane) (33) and ${\gamma }_2=34\mathrm{\pm }5\hspace{0.5em}\mathrm{mN}/\mathrm{m}$ is the surface energy of PEMA (33).

The success of this wettability patterning approach relies on three factors: swelling of the polyurethane elastomer film beyond the critical strain for creasing; the low surface tension of the PEMA/POSS blend; and the fast evaporation of the volatile solvent (Asahiklin). In another case, we swell a polydimethylsiloxane (PDMS) elastomer film in a solution containing 3 wt% poly(ethyl glycol) (PEO) in chloroform. Creases are formed and chloroform is volatile; however, patterned wettability is not observed. The hydrophilic PEO has a much higher surface tension of 43 mN/m compared with the value for PDMS of 20 mN/m (33), leading to dewetting on crease unfolding (Movie S1 and Fig. S4).

Fig. S4.

Microparticles of PEG deposited on each unfolded crease. When a PDMS (20:1 by weight Sylgard 184 base: cross-linker ratio, fully cured at 80 °C for 24 h) elastomer film with thickness of 1 mm is immersed in a solution containing 3 wt% PEG (Mw = 30 kg/mol) in chloroform, creases spontaneously form on the surface. As chloroform evaporates, the PEG/chloroform solution dewets from the creased PDMS surface, leading to the trapping of the viscous PEG solution at the edge of the creased regions due to the topography of the creased surface and contact line depinning. The creases unfold as the PDMS deswells on further evaporation of chloroform, and the trapped PEG solution droplets shrink and dry into microparticles, as shown in A, where the black dots are PEG microparticles, the white regions are the unfolded creases, and the gray regions are covered with condensed water due to the cooling effects of rapid chloroform evaporation. (B) Fluorescence image showing microparticles of rhodamine-labeled PEG formed through this process.

Modulation of the Size and Morphology of Wettability Patterns.

Both the size and shape of wettability patterns influence performance in applications such as heat transfer (1) and water harvesting (4, 5). In this section, we show that the size and morphology of the wettability contrast pattern can be controlled independently.

The swelling of elastomers in a solvent is a poroelastic process (34). The swollen layer thickness $H$ is governed by the diffusive dynamics of the solvent. In the creasing process, the spacing $W$ between neighboring creases is proportional to the thickness of the swollen layer because that is the only relevant length scale (16). As shown in Movie S2, the small creases that initially nucleate subsequently coarsen as the swollen layer grows in thickness. The spacing of the creases ($W$) can be measured through image analysis. In Fig. 2A, $W^2$ is plotted against the dipping time and the linearity of the plot supports the diffusive nature of the phenomenon, allowing us to obtain an effective diffusion constant $D_{eff}=W^2/t=7.69\mathrm{\times }{10}^{-10}\hspace{0.5em}{\mathrm{m}}^{\mathrm{2}}/\text{s}$. Given that the spacing of the creases ($W$) scales with the initial thickness of the swollen layer ($\tilde{H}$) by a ratio of $W/\tilde{H}\approx 2-2.5$ (16), the effective diffusion constant $D_{eff}$ is reduced by a factor of ${\left(W/\tilde{H}\right)}^2\approx 4-6.25$, which agrees well with the diffusivity of $D\approx 1.3\mathrm{\times }{10}^{-10}\hspace{0.5em}{\text{m}}^2/\text{s}$ resulting from tracking the thickness change during the swelling of a free-standing polyurethane film (Fig. S5). Guided by the diffusion analysis, noncoated hydrophilic regions of different sizes can therefore be achieved by controlling the swelling time. Although micrographs in Fig. 2B show patches of three different sizes ranging from 100 to 500 μm, we note that this process has the potential to generate smaller patterns, down to the tens of nanometer scale (35, 36). Successful processing of very small patterns relies on a thin polyurethane layer, the thickness of which imposes an upper bound for the evolving pattern size, and on a very fast solvent evaporation rate to prevent the viscous coating solution from migrating laterally onto the uncoated regions during the simultaneous deswelling of the elastomeric film and the unfolding of creases.

Fig. 2.

Modulating the size of patterned patches by controlling the swelling time. (A) The spacing ($W$) between neighboring creases is proportional to the swollen layer thickness ($H$), which is controlled by the swelling time ($t$). An effective diffusion constant ($D_{eff}=7.69\mathrm{\times }{10}^{-10}\hspace{0.17em}{\mathrm{m}}^{\mathrm{2}}/s$) for the swelling of the elastomer by the solvent can be obtained by plotting $W^2$ as a function of $t$. (B) Micrographs showing three different pattern sizes resulting from three different swelling times.

Fig. S5.

Volumetric swelling of a freestanding polyurethane film and estimation of the diffusivity. (A) A polyurethane film with an initial thickness of $\tilde{h}\left(0\right)\approx 1.6\hspace{0.5em}\mathrm{mm}$ reaches equilibrium volumetric swelling ratio [$Vol\left(\mathrm{\infty }\right)/Vol\left(0\right)=3.2$, determined by tracking the weight change during swelling] at about 30,000 s in Asahiklin 225 solvent. By contrast, a polystyrene substrate does not change its weight or volume after prolonged immersion in Asahiklin 225 solvent, indicating immiscibility between polystyrene and Asahiklin 225. (B) The diffusivity ($D$) is obtained by tracking the change in thickness of the freestanding polyurethane film during swelling. Using the inset equation^§ in Fig. S5B, fitting the dimensionless thickness change $\left[\tilde{h}\left(t\right)-\tilde{h}\left(0\right)\right]/\tilde{h}\left(0\right)$ during the initial period of swelling, as a function of $\sqrt{t}/\tilde{h}\left(0\right)$, where $t$ is the swelling time and $\tilde{h}\left(t\right)$ is the thickness of the polyurethane film at the swelling time $t$. This analysis gives a value of $D\approx 1.3\mathrm{\times }{10}^{-10}\hspace{0.17em}{\mathrm{m}}^2/s$, in good agreement with the diffusion constant estimated by tracking the spacing of creases in a substrate-attached polyurethane film during constrained swelling. ^§Equation 30 in ref. 58.

Constrained swelling always leads to equibiaxial compression in the polyurethane elastomer coating. The polyurethane film has a swelling ratio of ${\lambda }_0=1.47$ (measured from the change in dimensions of a free standing polyurethane film) in 3wt% PEMA/POSS/Asahiklin solution. Taking the free swelling state as the reference state, the compressive strains induced in the film by constrained swelling are ${\epsilon }_x={\epsilon }_y=1-1/{\lambda }_0=0.32$, which is above the critical strain of ${\epsilon }_{bioxial}^c=0.25$ required for creases to form (26). In Fig. 3, the experimental image on the bottom shows a similar morphology to that on the top based on the theoretical predictions (highlighted by the blue square) (37). Globally, the patterns that form are randomly oriented due to the in-plane stress symmetry, whereas locally, the short striped creases are arranged in a mostly perpendicular fashion to their neighbors, to most effectively release the compressive energy in plane. Breaking the in-plane stress symmetry yields patterns with different morphology (37). Specifically, we can put the polyurethane elastomer film under precompression by gluing it to a prestretched substrate and subsequently releasing the prestretch, followed by immersing it in the PEMA/POSS/Asahiklin solution. Working on jointly, the amplitude of precompression and the swelling ratio determine the final stress state in the polyurethane elastomer, leading to creases with different morphologies. Applying a precompression of ${\lambda }_{\mathit{x}}^{\prime }=0.85$ in the x direction, followed by subsequent swelling, led to a strain state with the ratio of in-plane strains ${\epsilon }_y/{\epsilon }_x=0.64$ (Fig. S6). As highlighted by the red square in Fig. 3, the micrograph on the bottom shows long stripe patterns along the less compressed (y) direction, in good agreement with the corresponding range of theoretical predictions shown on the top. The two examples provided here demonstrate that the morphology of our wettability patterning can be tuned by controlling the initial stress state in the elastomeric surface layer.

Fig. 3.

Modulating the morphology of patterned patches by precompression. (Upper Row) Images show the predicted morphology of creases at different stress states. Reproduced with permission from ref. 37, copyright (2013) American Physical Society. (Lower Row) Micrographs show the morphology of patterned patches obtained under different stress states (Left: ${\epsilon }_y/{\epsilon }_x=1$; Right: ${\epsilon }_y/{\epsilon }_x=0.62$), in good agreement with the theoretical results at similar stress states on the top, as highlighted in the red and blue squares. The level of overall compression denoted by ${\lambda }_x\sqrt{{\lambda }_y}$ in experiments is close to that ($0.54$) in the theoretical results.

Fig. S6.

A schematic illustration of the principal stretches in the polyurethane elastomer film in the unswelled state, the free swelling state (stress-free reference state) and the precompressed patterning state. Taking the equilibrium free swelling state as the stress-free reference state, we can calculate the stress state in the patterned state by evaluating the principal stretches in the elastomer: ${\lambda }_x={\lambda }_x^{\prime }/{\lambda }_0$, ${\lambda }_y={\lambda }_y^{\prime }/{\lambda }_0$, where ${\lambda }_0$ and $\lambda \prime$ represent the principal stretch in the free swelling state and the patterning state with respect to the unswelled state. If we assume incompressibility of the cross-linked polyurethane elastomer, then ${\lambda }_y^{\prime }=1/\sqrt{{\lambda }_x^{\prime }}$. In the nonprecompressed state, ${\lambda }_y^{\prime }={\lambda }_x^{\prime }=1$, and the polyurethane film has a swelling ratio of ${\lambda }_0=1.47$ (measured from the change in dimensions of a free standing polyurethane film) in 3 wt% PEMA/POSS/Asahiklin solution. The substrate-attached polyurethane film is therefore under equibiaxial compression and the compressive strains induced in the film by constrained swelling are ${\epsilon }_x={\epsilon }_y=1-1/{\lambda }_0=0.32$, which is above the critical strain of ${\epsilon }_{biaxial}^c=0.25$ required for creases to form (26). In this equibiaxial state, ${{\epsilon }_y/\epsilon }_x=1$ and ${\lambda }_x\sqrt{{\lambda }_y}=0.56$. When we apply a precompression of ${\lambda }_x^{\prime }=0.85$ in the x direction, the principal stretch in the orthogonal y direction can be calculated: ${\lambda }_y^{\prime }=1/\sqrt{{\lambda }_x^{\prime }}=1.08$. We can use these values to calculate the strain in the patterned state: ${\lambda }_x={\lambda }_x^{\prime }/{\lambda }_0=0.58$, ${\epsilon }_x=0.42$ and ${\lambda }_y={\lambda }_y^{\prime }/{\lambda }_0=0.73$, ${\epsilon }_y=0.27$. Therefore, in this state, the ratio of in-plane strains is ${\epsilon }_y/{\epsilon }_x=0.64$ and ${\lambda }_x\sqrt{{\lambda }_y}=0.50$.

Characterization of the Wettability of the Patterned Surfaces.

We next characterize the wettability of the patterned surfaces using the sessile droplet technique and tensiometry. Water contact angle were measured on the uncoated polyurethane surface and a surface uniformly coated with PEMA/POSS via the sessile droplet technique. The advancing and receding contact angles for water on the uncoated polyurethane are ${\theta }_a=88\mathrm{\pm }2°$ and ${\theta }_r=32\mathrm{\pm }1°$, respectively. On the uniformly coated PEMA/POSS surface prepared by spin coating the 3 wt% Asahiklin solution, the advancing and receding contact angles for water are ${\theta }_a=124\mathrm{\pm }1°$ and ${\theta }_r=118\mathrm{\pm }1°$ respectively, in good agreement with a previous study (32). We note that elastocapillarity can affect the apparent contact angle of liquid drops on soft elastomers (38). The polyurethane elastomer used here has a shear modulus of $G_{PU}\approx 1\hspace{0.5em}\mathrm{MPa}$, and the water surface tension is ${\gamma }_{\mathit{LV}}=72.8\hspace{0.5em}\mathrm{mN}/\mathrm{m}$, so the elastocapillary length is of order ${\gamma }_{\mathit{LV}}/G_{PU}\approx 70\hspace{0.5em}\mathrm{nm}$, much smaller than the radius of the sessile droplet. For this relatively stiff polyurethane elastomer, elastocapillarity has a negligible influence on the apparent contact angle (39).

To visualize the patterned wettability contrast directly on the polyurethane surface, we observe a 20-μL droplet rolling down a patterned surface tilted at 60°. As shown in Movie S3, capillary fingers continuously form and pinch off in the hydrophilic regions as the water droplet recedes along the inclined surface. The capillary finger breakup and the average surface contact angle can be measured by tensiometry. As illustrated in Fig. 4A, in these tensiometric experiments, force and relative position data are collected while a container of probe liquid is raised and lowered at a constant velocity such that the liquid contact line advances (or recedes) across the solid surface at a controlled velocity. In the quasi-static limit, when viscous forces are negligible, the net force acting on the sample results from a combination of interfacial and buoyant forces and is given by $F=p{\gamma }_{LV}\cos \theta -{\rho }_{L}gAd$, where $p$, ${\gamma }_{LV}$, $\theta$, ${\rho }_L$, $g$, $A$, and $d$ represent the perimeter length of the cross section, the liquid surface tension, the liquid-surface contact angle, the liquid density, the gravitational acceleration, the cross-sectional area, and the immersion depth, respectively (40). Three advancing and receding cycles are recorded at an immersion velocity of $0.1\hspace{0.5em}\mathrm{mm}/\mathrm{s}$ (Fig. 4A). Linear regression to the advancing and receding force measurements gives rise to the average advancing and receding angles. Although the measured receding contact angle is $104\mathrm{\pm }2°$, there is a decrease of advancing contact angle from $147\mathrm{\pm }1°$ in the first advancing cycle to $136\mathrm{\pm }3°$ in the second and third advancing cycles, reflecting a small amount of water absorption by the polyurethane elastomer. The patterned surface has a larger water advancing contact angle compared with the flat PEMA/POSS surface, due to the introduction of surface roughness, following the swelling/deswelling/evaporation process.

Fig. 4.

Tensiometry measurements of the patterned surfaces and formation of microdroplets due to capillary finger breakup. (A) Tensiometry measurements on a patterned surface for three advancing and receding cycles. (B) An enlarged view of the tensiometric force curve for the first receding measurement shows sawtooth waves corresponding to the stick-slip of capillary fingers at the receding contact line. The Upper Inset figure shows the power spectrum of a 1D Fourier transform of the sawtooth waves, with a primary peak at 300 μm, in good agreement with the spacing between creases shown in the Lower Left Inset optical micrograph. (C) Brine (1.37 M sodium chloride) and (D) hexadecane microdroplets deposited on hydrophilic regions due to capillary finger breakup. (E) Water rivulets breaking into short ellipsoidal droplets on nontreated hydrophilic regions. (F) Continuous water rivulets adhere to oxygen plasma-treated hydrophilic regions with high fidelity. (Scale bars, 250 μm.)

In these experiments, the meniscus advances at U = $0.1\hspace{0.5em}\mathrm{mm}/\mathrm{s}$, corresponding to a capillary number of $Ca=\mu U/{\gamma }_{LV}=1.4\mathrm{\times }{10}^{-6}$, where $\mu$ represents the viscosity of the liquid. At this small capillary number, capillary fingers form and break up, without leaving visible droplets in the hydrophilic regions. Such stick-slip behavior of a moving contact line on chemically patterned surfaces has been observed before both computationally (41) and experimentally (42). The stick-slip capillary finger formation and breakup is captured in the advancing and receding force-displacement curves as sawtooth patterns. Fig. 4B shows an enlarged view of the first receding force curve. 1D Fourier transformation of this signal yields a characteristic wavelength of 300 μm, corresponding well to the average spacing of creases as shown in the inset of Fig. 4B. The agreement between the periodicity of the sawtooth patterns and the average spacing of creases is further confirmed in Fig. S7, where a sample with an 800-μm average spacing of creases is tested under the same conditions. However, as recorded in Movie S4, when the patterned sample is withdrawn from a water bath at a speed of U=$40\hspace{0.5em}\mathrm{mm}/\mathrm{s}$, corresponding to a much larger capillary number of $Ca=5.6\mathrm{\times }{10}^{-4}$, the elongated capillary fingers leave a microdroplet in each hydrophilic domain. Fig. 4 C and D shows that brine (1.37 M sodium chloride) and oil microdroplets can be deposited in the hydrophilic regions through this process, suggesting that this simple immersion/emersion process can be used to prepare microreactors in parallel. We demonstrate this concept in Fig. S8 by synthesizing magnetic microparticles. The deposited microdroplets have radii on the order of tens of microns, which evaporate quickly. The relatively lower vapor pressure of brine solutions allows for reliable measurement of the size of the deposited droplets through optical microscopy. The diameters of brine microdroplets deposited in the hydrophilic regions at a withdrawal speed of $U=40\hspace{0.5em}\mathrm{mm}/\mathrm{s}$ are narrowly distributed in size with a mean diameter of $38\mathrm{\pm }4\hspace{0.17em}\mu \mathrm{m}$ (Fig. S9). We note that the volume ($V$) of each deposited microdroplet should be a function of the capillary number ($Ca$), the receding contact angle (${\theta }_r$), and the characteristic length ($L$) of the hydrophilic domain through Landau–Levich dynamics (43). However, the detailed characterization of the appropriate functional form $V=f\left(Ca,{\theta }_r,L\right)$ is beyond the scope of the current study. Patterning droplets on a surface can also be influenced by other factors such as substrate stiffness (44) and surface roughness (45, 46). Our coating process generates a substrate stiffness contrast. Although the uncoated polyurethane has a shear modulus of $G_{PU}\approx 1\hspace{0.5em}\mathrm{MPa}$, the coated 1-μm PEMA/POSS layer has a shear modulus of $G_{PEMA/POSS}\approx 1\hspace{0.5em}\mathrm{GPa}$ (47). The deposited droplets have radii on the order of tens of microns, three and six orders of magnitude larger than the elastocapillary lengths on polyurethane substrate (${\gamma }_{LV}/G_{PU}\approx 70\hspace{0.17em}\mathrm{nm}$) and on PEMA/POSS layer (${\gamma }_{LV}/G_{PEMA/POSS}\approx 0.7\hspace{0.17em}\mathrm{nm}$), respectively. Therefore, substrate stiffness effects or “durotaxis” is not to be expected in our current experiments (44). Surface roughness can also result in stick-slip motion in moving contact lines (45, 46). The rough corners and sharp edges can cause pinning of contact lines, and subsequent release of pinning from these surface features leads to sudden slipping of the contact lines. Our coated surface has an RMS roughness of $R_q=380\hspace{0.5em}\mathrm{nm}$, which is two to three orders of magnitude smaller than the lateral length scale (∼100–500 μm) of the hydrophilic regions, implying the effect of surface roughness is probably small. However, quantitative deconvolution of the effect of the wettability contrast from the effect of the surface roughness on microdroplet deposition in the current experiment is not possible with the information available.

Fig. S7.

An enlarged view of the tensiometric force curve for the first receding measurement shows sawtooth waves corresponding to the stick-slip of capillary fingers at the receding contact line. The Upper Inset figure shows the power spectrum of a 1D Fourier transform of the sawtooth waves, with a primary peak at 800 μm, in good agreement with the spacing between creases shown in the Lower Left Inset optical micrograph. The large spectral noise observed in the power spectrum is due to the limited number of creases that can be probed in the tensiometry measurement. Nevertheless, this data in conjunction with Fig. 4B together confirm that stick-slip periodicity in tensiometry measurement matches the average spacing of creases.

Fig. S8.

Parallel microreactors through capillary finger breakup. (A) A patterned surface is immersed in a solution containing iron (II) chloride and iron (III) chloride mixture (1:2 ratio by weight FeCl₂: FeCl₃). (B) Withdrawing at a speed of $U=40\hspace{0.5em}\mathrm{mm}/\mathrm{s}$ leads to a microdroplet deposited on each hydrophilic region. (C) Magnetic microparticles are synthesized by incubation in the vapor phase above saturated ammonia water for 24 h at room temperature (21 °C).

Fig. S9.

Narrow distribution in size of the entrained brine microdroplets. (A) Brine (1.37 M sodium chloride) microdroplets deposited on the hydrophilic regions due to local dewetting of the aqueous thin film formed during viscous withdrawal at a withdrawal speed of $U=40\hspace{0.5em}\mathrm{mm}/\mathrm{s}$. (B) The bar plot quantifies the narrow size distribution ($38\mathrm{\pm }4\hspace{0.5em}\mu \mathrm{m}$ in diameter) of the entrained brine microdroplets shown in A.

The wettability contrast between the coated and the uncoated regions can be enhanced by improving the hydrophilicity of the polyurethane surface before the coating step. A 3-min oxygen plasma treatment (radio frequency plasma at 18 W) reduces the water advancing angle on the polyurethane surface from ${\theta }_a=88\mathrm{\pm 2°}$ to $58\mathrm{\pm }1°$, and the receding angle from ${\theta }_r=32\mathrm{\pm 1°}$ to $8\mathrm{\pm }2°$, as measured by the sessile droplet technique. Fig. 4 E and F shows a surface patterned with long stripes by applying a precompression of ${\lambda }_x^{\prime }=0.85$ before the coating process, as discussed in the previous section. For the polyurethane surface without oxygen plasma treatment (Fig. 4E), the water filaments that develop during withdrawal break into small ellipsoidal drops due to dewetting and the Rayleigh–Plateau instability, whereas on the oxygen plasma-treated surface (Fig. 4F), water filaments remain as continuous rivulets in good registry with the hydrophilic regions. Although the oxygen plasma treatment enhances the wetting contrast, it also tends to slightly alter the morphology of creases and the wettability patterns (Fig. S10), probably due to changes in the surface roughness, surface energy, and the mechanical properties of the polyurethane induced by the oxygen plasma (48, 49).

Fig. S10.

Changes in coating morphology due to the oxygen-plasma treatment. Micrographs showing the coating pattern on the as-prepared polyurethane surface (A) and on the oxygen-plasma treated polyurethane surface (B). Each surface was swollen for 100 s in the coating solution before withdrawal. Hydrophilic patterns with larger length-to-width aspect ratio are observed in B, indicating that longer and shallower creases are formed on the oxygen-plasma treated surface. Although the low-intensity oxygen plasma promotes oxygen-containing groups on the surface, leading to lower water contact angles, it also slightly changes the surface roughness and the mechanical properties of the polyurethane (48, 49), which are probably responsible for the morphology change.

We probe the local modifications to the wettability by performing local contact angle measurements, delivering water microdroplets (volume ≤ 0.02 μL) precisely to different regions (Fig. S11). The local measurements show good agreement with water contact angles measured previously on bulk surfaces, confirming that the coating process does not significantly change the water contact angles in the uncoated creased regions.

Fig. S11.

Local contact angle measurement by the sessile microdrop method illustrating local wettability contrast. Water microdroplets are precisely delivered to the uniformly coated hydrophobic region (A); the uncoated hydrophilic region (B); and the oxygen-plasma treated hydrophilic region (C). The exact location and the relative size of microdrops to the crease pattern size are revealed from the top view optical micrographs presented in the Bottom Row. The advancing contact angle is measured by dynamically incrementing water volume (Top Row), whereas the receding contact angle is measured when the contact line depins as the water microdrops evaporate (Middle Row). The advancing contact angle and receding contact angle are measured to be 127 ± 2° and 114 ± 1° for A; 87 ± 1° and ∼35° for B; and 76 ± 2° and ∼20° for C, respectively.

Water Condensation on Patterned Surfaces.

One of the motivations for patterning surfaces with wettability contrast is to enhance water collection efficiency. Whereas Namib desert beetles are believed to use hydrophilic bumps distributed on a hydrophobic background to harvest fog droplets (2), it is also argued that enhanced dew condensation can be another potential mechanism for these beetles to collect water (50). We also investigated the water condensation behavior on our patterned surfaces. As shown in Movie S5 and Fig. 5, a patterned surface is equilibrated to −20 °C in a freezer for 30 min before performing a water condensation experiment at 21 °C and 40% relatively humidity. Water condensation from the air to the cold surface is monitored in situ by an optical microscope operated in reflection mode. Initially, tiny water droplets condense on the entire surface due to the large subcooling. These droplets grow, coarsen, and coalesce much faster in the hydrophilic regions. The free energy barrier $\mathrm{\Delta }G$ for the formation of a water nucleus on a flat surface depends strongly on the contact angle $\theta$: $\mathrm{\Delta }G=\pi {\gamma }_{LV}{r}_c^2\left(2-3\cos \theta +{\cos }^3\theta \right)/3$, where $r_c$ is the critical radius of a water nucleus (51). The critical radius in the current experiment is calculated to be $r_c=0.75\hspace{0.5em}\mathrm{nm}$ using the Kelvin equation: $\ln \left(S\right)=2{\gamma }_{LV}/\left(n_L{k}_{b}T{r}_c\right)$ (52), where $S=5$ is the saturation ratio of water vapor pressure in the experiment; defined by the ratio of water vapor pressure in the environment to the dew point at the cold surface, $n_L$ is the number of molecules per unit volume of water, and $k_{b}T$ is the thermal energy. The nucleation rate $J$ depends on the nucleation energy barrier in an inverse exponential form $J=J_0\exp \left(-\mathrm{\Delta }G/k_{b}T\right)=J_0\exp \left[\pi {\gamma }_{LV}{r}_c^2\left(3\cos \theta -2-{\cos }^3\theta \right)/3k_{b}T\right]$, where $J_0$ is a kinetic constant. Therefore, based on this expression, the nucleation rate in the more hydrophilic regions $\left({\theta }_{adv}=88°\right)$ is ∼10 orders of magnitude higher than that in the coated regions $\left({\theta }_{adv}=127°\right)$. Additional materials deposited at the rim of the hydrophilic regions increase the roughness, and therefore the level of hydrophobicity at the rim. Therefore, the tiny water droplets that initially condense at the rim quickly coalesce to form droplets that sit on the nearby hydrophilic regions. The regions near the boundaries of the creases thus reflect more light and appear to turn white quickly, an observation that can be explained by a mobile coalescence mechanism on a superhydrophobic surface. It is known that coalescence of microdroplets condensed on a superhydrophobic surface can induce out-of-plane jumping, which is powered by the released surface energy on drop coalescence (53). This type of mobile coalescence mechanism allows only condensed droplets with diameters smaller than 10 μm to sit on a superhydrophobic surface (53). As illustrated in Fig. S12, although microdroplets larger than this critical size at the rim jump and coalesce to form droplets in the nearby hydrophilic regions, water microdroplets still remain in the flat hydrophobic regions and scatter light. Therefore, these flat hydrophobic regions appear dark, whereas the rim regions appear white in the optical micrographs (Fig. 5). The difference in water condensation rate in different regions on the patterned surface offers potential for using such patterned surfaces to enhance the efficiency of harvesting and collection of dew water condensing from humid air (SI Methods).

Fig. 5.

Optical micrographs showing the temporal evolution of condensation of water droplets from the air [at room temperature (21 °C) and 40% relative humidity] onto a cold patterned surface (−20 °C). The volume of the water droplets deposited on the uncoated, hydrophilic regions is many orders of magnitude higher than the volume of water microdrops deposited on the coated hydrophobic regions, reflecting the influence of local patterning in the surface wettability on local droplet nucleation rate. (Scale bar, 200 μm.)

Fig. S12.

A schematic illustration of water condensation on the patterned surface. Water droplets condensed in the hydrophilic region grow into large drops. Water microdroplets condensed at the superhydrophobic rim can jump out of plane (as indicated by the arrows), powered by the excess surface energy released on microdroplet coalescence. Water microdroplets remain in the flat hydrophobic regions and scatter light. Therefore, these regions still appear dark during bright field microscopy, whereas the rim regions appear white in the optical micrographs (cf Fig. 5).

Spontaneous Patterning on Curved Surfaces.

Traditional techniques for patterning surfaces with spatial wettability contrast include vapor deposition (8), photolithography (3), and soft lithography (54, 55). Although photolithography can only be used to pattern flat substrates, soft lithography using flexible molds or masks fabricated via photolithography can work on cylindrical or conical surfaces, i.e., curved surfaces with zero Gaussian curvature (54, 55). However, such techniques cannot be applied to surfaces with nonzero Gaussian curvature such as spherical or saddle surfaces. Essentially, the flexible molds or masks in use have zero Gaussian curvature. Distortions including stretching and compression have to be applied when a flat mask is mapped onto a surface with a nonzero Gaussian curvature (56). A microspraying system offers the possibility to operate and pattern wettability to arbitrarily curved surfaces (57); however, it requires precise and sophisticated maneuvering of the spray head in three dimensions and should be difficult and costly to scale up.

Our crease coating approach includes the capability of producing patterned wettability on any arbitrarily curved surface and on a wide variety of materials. As shown in Fig. 6, both a cylindrical surface (Fig. 6A) and a spherical surface (Fig. 6B) can be patterned readily. Our approach relies on the conformal coating of arbitrary surfaces with a well-adhered layer of polyurethane elastomer. Chemical reactivity with hydroxyl groups present on the surface of a variety of substrate materials ensures good adhesion of the polyurethane elastomer layer. Therefore, this patterning approach works on a variety of materials, such as plasma treated polystyrene mentioned in previous sections, oxidized steel (Fig. 6A), and glass (Fig. 6B). The patterning is primarily a chemical process with the introduction of very small incremental surface roughness as discussed previously. Consequently, it only slightly reduces light transmission when applied to a transparent substrate. As shown in Fig. 6B, the coated spherical glass lens remains highly transparent.

Fig. 6.

Spontaneous wettability patterning on curved surfaces: (A) a cylindrical steel rod surface (15 mm in diameter), which has a mean curvature of $H=1/2\left(1/R_1+1/R_2\right)=0.067\hspace{0.5em}{\text{mm}}^{-1}$ and a Gaussian curvature of $K=1/\left(R_1{R}_2\right)=0$, and (B) a spherical glass lens surface (8 mm in radius, 2 mm in thickness at the apex of the lens), with $H=0.125\hspace{0.5em}{\text{mm}}^{-1}$ and $K=0.0156\hspace{0.5em}\mathrm{m}{\mathrm{m}}^{-2}$. (Scale bars, 500 μm.) ($R_1$ and $R_2$ are the two principal radii of a curved surface.)

SI Methods

Spontaneous Patterning of Flat and Curved Surfaces with Chemical Patches.

All of the patterned samples with wettability contrast were prepared by immersing substrate-bonded polyurethane films in a solution that contains PEMA/fluorodecyl POSS (80:20 by weight) in Asahiklin solvent (AK225; Asahi Glass Company) at a total solid content of 3 wt%. PEMA (Mw = 515 kg/mol) obtained from Sigma-Aldrich was used without further purification, and fluorodecyl POSS was obtained from NBD Nanotechnologies as a gift. To prepare polyurethane film-coated surfaces, Clear Flex 50 polyurethane precursors A and B (obtained from Smooth-On) were thoroughly mixed at a weight ratio of 1:2, followed by vacuum degassing to remove air bubbles. They were then poured on flat polystyrene substrates or molded onto steel rod surfaces and spherical glass lens surfaces and cured at room temperature for 24 h. All of the polyurethane films have a thickness ranging from 0.3 to 1 mm. The polystyrene substrates were treated with radio frequency oxygen plasma at 18 W for 5 min immediately before coating with polyurethane to introduce hydroxyl groups on the polystyrene surface and therefore to promote bonding of the polyurethane coating to the substrate.

The polyurethane film-coated substrates were withdrawn vertically at a speed of $U\approx 0.1\hspace{0.5em}\mathrm{m}/\mathrm{s}$ from PEMA/fluorodecyl POSS/Asahiklin solution after immersing them for a certain period and left in a fume hood to evaporate residual solvent, leading to simultaneous deswelling of the polyurethane film and exposure of the uncoated self-contacting regions. An upright optical microscope (ZEISS Axioplan2) equipped with a CCD camera (AxioCam HRC) was used to record the patterned surfaces.

To characterize roughness of the patterned surface, stylus profilometry (Dektak XT stylus profiler with 2-μm B-type stylus) was used to probe the topography. The patterned chemical contrast was confirmed by EDS and was associated with micrographs obtained from scanning electron microscope (SEM; JEOL 6010LA).

Modulation of the Size and Morphology of Wettability Patterns.

To modulate the size and spacing of the wettability patterns, we controlled the swelling time of the polyurethane films in the coating solution. An inverted optical microscope (Nikon Eclipse TE2000-S) equipped with a CMOS camera (Pixelink PL-B741) was used to monitor in situ the size of creases as a function of swelling time.

To control the morphology of the wettability patterns, we apply a prestress to the polyurethane films. A cast polyurethane film with a thickness of 0.7 mm was peeled off a polystyrene Petri dish and cut into 2- × 5-cm rectangular pieces. One piece was glued to a prestretched high modulus polyurethane tape (3M 8663 polyurethane protective tape, obtained from Uline) Releasing the prestretch imposes a compression in the top polyurethane film. This bilayer film can then be glued to a rigid polystyrene or glass substrate, followed by immersion in the coating solution to pattern the wettability contrast.

Characterization of Wettability.

The wettability contrast was characterized by sessile droplet methods and tensiometry. Water contact angle measurements were performed using a ramé-hart model 590 goniometer after vertically dispensing sessile droplets (2 ≤ volume ≤ 12 μL) of deionized water ($\gamma =72.8\hspace{0.17em}\mathrm{mN}/\mathrm{m}$) on various surfaces. Advancing water contact angles were measured as deionized water was supplied via syringe, whereas receding contact angles were measured as deionized water was removed via syringe. Measurements were taken over three or more different locations on each surface, and the reported uncertainties are SDs associated with the measurement of these independent contact angle values. Tensiometric force measurements were made using a DCAT 11 (Data Physics Instruments) tensiometer. The samples are probed at a velocity of $0.1\hspace{0.5em}\mathrm{mm}/\mathrm{s}$ and at a temperature of $20°\mathrm{C}$, with a total immersion depth of $\mathrm{\Delta }Z=15\hspace{0.17em}\mathrm{mm}$.

To enhance the wettability contrast between the coated regions and the noncoated regions, the samples were pretreated with radio frequency oxygen plasma (Harrick Plasma PDC-32G) at 18 W for 3 min before immersing them in the Asahiklin solution.

The local distribution of contact angles on the patterned films were measured using a microscopic contact angle meter (KYOWA MCA-3) by delivering deionized water microdroplets (volume ≤ 0.02 μL) precisely to individual hydrophilic and hydrophobic regions through a glass capillary micropipette with an inner diameter of 5 μm.

Water Condensation on Patterned Surfaces.

A coated sample was equilibrated to −20 °C in a freezer for 30 min before carrying out the water condensation experiment at room temperature (21 °C) and 40% relatively humidity. The condensation of water from the air to the surface was monitored in situ with a 5× objective on an upright optical microscope (ZEISS Axioplan2 imaging) equipped with a CCD camera (AxioCam HRC) operated in the reflection mode.

Water Condensation on Surfaces with Different Wetting Properties.

Side-by-side water vapor condensation was compared on three different surfaces: (i) a crease-patterned surface (the size of hydrophilic domains is around 500 μm and the area fraction of the hydrophilic regions is about 0.20), (ii) an unpatterned uniformly hydrophilic polyurethane surface, and (iii) a homogeneously coated hydrophobic polyurethane surface (the homogeneously hydrophobic surface was prepared by spin-coating PEMA/POSS solution onto a polyurethane substrate). All three samples were equilibrated to −20 °C in a freezer for 30 min, followed by being placed on a digital scale to measure the weight of condensed water from the air at ambient temperature of 24 °C and 40% relative humidity over a period of 90 s. The mass of water condensed on the unpatterned hydrophilic polyurethane surfaces is ∼26 ± 2 mg for a surface area of 40 cm², whereas water condensed on the homogeneously coated hydrophobic polyurethane surface is ∼17 ± 2 mg in mass for the same surface area and same exposure time (90 s). As expected, strong surface hydrophobicity reduces the nucleation rate. However, when the amount of condensed water was measured on the crease-patterned surface, it returned to essentially the same amount as collected on the uniformly hydrophilic surface even though now about 80% of the surface is hydrophobic. These experiments show that patterning hydrophilic domains on hydrophobic background does not reduce the amount of water condensation, compared with that on a hydrophilic surface. The water droplets that nucleate and grow on the patterned surface are bigger than on the uniformly hydrophilic surface, and their positions are also passively controlled, so that they form only on the hydrophilic domains. These bigger and patterned droplets provide potential for enhancing water-collection efficiency.

Conclusions

In summary, exploiting the reversible creasing instability of swollen elastomers provides a facile self-assembly approach to spontaneously pattern both flat and curved surfaces with wettability contrasts having a characteristic feature scale from about 100 to 500 μm. The patterning is primarily a chemical process with little change in the surface roughness. Variations in dipping time, prestress, and chemical treatment allow for independent control of the domain size, the morphology, and the wettability contrast, respectively. Such heterogeneous surfaces show potential for constructing high-throughput parallel microreactors and for harvesting and collecting water from humid air.

Methods

All of the patterned samples with wettability contrast are prepared by immersing substrate-bonded polyurethane films in a solution that contains 3 wt% PEMA/fluorodecyl POSS (80:20 by weight) in Asahiklin solvent (AK225). The polyurethane film-coated substrates are withdrawn vertically at a speed of $U\approx 0.1\hspace{0.5em}\mathrm{m}/\mathrm{s}$ from the coating solution after immersing them for a certain period and left in a fume hood to evaporate residual solvent, leading to simultaneous deswelling of the polyurethane film and exposure of the uncoated self-contacting regions. More details can be found in SI Methods.