Dexter energy transfer pathways

Significance

Controlling the dynamics of excitons—including their transport, fission, fusion, and free carrier generation—presents a central challenge in energy science, optoelectronics, and photobiology. We develop a coupling-pathway theory for triplet energy transfer, a process controlled by the structure of the medium between donor and acceptor sites, and find two competing coupling pathway mechanisms. At shorter distances or high tunneling gaps, the electron and hole move sequentially from donor to acceptor, accessing donor–acceptor charge-transfer exciton virtual states; at longer distances or lower tunneling gaps, virtual exciton states of the bridge mediate the transport. Molecular design strategies can leverage these competing mechanisms and their distinctive dependences on molecular structure.

Abstract

Energy transfer with an associated spin change of the donor and acceptor, Dexter energy transfer, is critically important in solar energy harvesting assemblies, damage protection schemes of photobiology, and organometallic opto-electronic materials. Dexter transfer between chemically linked donors and acceptors is bridge mediated, presenting an enticing analogy with bridge-mediated electron and hole transfer. However, Dexter coupling pathways must convey both an electron and a hole from donor to acceptor, and this adds considerable richness to the mediation process. We dissect the bridge-mediated Dexter coupling mechanisms and formulate a theory for triplet energy transfer coupling pathways. Virtual donor–acceptor charge-transfer exciton intermediates dominate at shorter distances or higher tunneling energy gaps, whereas virtual intermediates with an electron and a hole both on the bridge (virtual bridge excitons) dominate for longer distances or lower energy gaps. The effects of virtual bridge excitons were neglected in earlier treatments. The two-particle pathway framework developed here shows how Dexter energy-transfer rates depend on donor, bridge, and acceptor energetics, as well as on orbital symmetry and quantum interference among pathways.

A compelling challenge in supramolecular chemistry is to direct the flow, fission, and fusion of excitons in molecular assemblies (1–4). When donor or acceptor species undergo a spin change during energy transfer, a two-particle or Dexter interaction enables the energy transfer because the Förster (dipole–dipole) coupling is spin forbidden (5). Developing design principles for Dexter energy transfer is a considerable challenge compared with that of single-electron (hole) transfer because of the combinatorial growth in the number of mediating (virtual) two-particle states with system size (6–9). As with single-particle (electron or hole) transfer, Dexter energy transfer arises from donor–acceptor coupling mediated by molecular species (10). Here, we develop a coupling pathway theory for bridge-mediated Dexter energy transfer and explore the relative contributions of bridge and donor–acceptor charge-transfer excitons to the transport.

A wide variety of critical chemical systems rely on bridge-mediated Dexter transfer of triplet excitons. The lowest-energy electronic excited states of transition metal complexes used for solar-energy harvesting are often high spin, and the excitation energy usually flows to a low-spin ground state acceptor (3). In the electro-optics underpinning light-emitting diodes based on metal-containing chromophores, the exchange of energy between low- and high-spin excited states is crucial for device efficiency (11). As well, protection of biological light-harvesting machinery from damage induced by sensitized singlet oxygen formation relies on a Dexter energy transfer quenching mechanism (12). The strong dependence of the Dexter coupling on the bridge structure indicates that triplet energy-transfer materials offer additional control (compared with the case for Förster energy transfer) through the manipulation of the bridge-mediated coupling.

Dexter’s 1953 analysis of spin-forbidden excitation energy transfer between donor (D) and acceptor (A) moieties in contact invoked coupling via the electron–electron Coulomb operator (5). However, most Dexter systems of interest today involve chemically bridged species. In addition to the two-electron interaction identified by Dexter, one-electron interactions (applied to second or higher order) also couple D to A. The term “Dexter coupling” is now understood to arise from both one- and two-electron interactions that may be mediated by a bridge (see Two-State EnT Kinetics), and two-state approximations to the Dexter coupling that include both contributions are well known (13). Pioneering kinetic studies of bridge-mediated Dexter energy transport in molecules have been reported by Closs et al. (14), Albinsson et al. (15), Harriman et al. (16), and Spieser (10); and considerable recent attention has turned to Dexter energy transfer at nanoparticle–molecule junctions (4). Despite the crucial role played by bridge-mediated Dexter energy transfer, a general framework to assess coupling pathway-mediated Dexter interactions and their interferences is lacking. We formulate a theory for bridge-mediated Dexter coupling pathways that allows the appraisal of specific coupling mechanisms.

Our description of Dexter coupling pathways relies on a configuration-interaction single-excitations (CIS) framework, motivated by schemes used to assess bridge-mediated interactions for single-electron/hole transfer (6, 7), adapted here to track the coupled motion of two particles. Pathway decompositions allow molecular-level understanding of energy, orbital symmetry, and interference effects on energy-transfer rates. The framework developed here allows analysis of Dexter-pathway coupling mechanisms in the language of virtual exciton pathways mediated by the bridge. We find that Dexter pathways through short bridges with high tunneling-energy gaps are dominated by charge-transfer virtual exciton intermediates [donor–acceptor charge-transfer excitons (DAE)] with one particle (electron or hole) on D and the other on A. The coupling in this short-distance high-barrier regime is consistent with an early conjecture of Closs et al. (14) and with the picture of Harcourt et al. (13). At longer distances or lower bridge energy gaps, however, bridge-localized virtual excitons (without DAE intermediates) dominate the Dexter coupling. These virtual excited states of the bridge, or bridge excitons (BE), are characterized by electron-hole pairs localized on the bridge. We provide formulas to assess the BE contribution to the Dexter coupling, because the earlier theories did not account for these BE intermediates.

We denote the donor, bridge, and acceptor chemical fragments in the energy transfer (EnT) system as D, B, and A, respectively. To describe the electron/hole charge distributions in these regions we use a $+,-$ notation. For an exciton with both the hole and the electron localized in a single D, B, or A region, we use $R^{\mathrm{\mp }}$ ($R=D$, B, or A, where the plus sign indicates a hole, and the minus sign indicates an electron). For an exciton with electron and hole localized in separate regions R and $R\prime ,$ we use $R^{+}{R\prime }^{-}.$ A specific exciton state (configuration) with hole in orbital i and excited electron in orbital x is denoted $|i,x\rangle .$ Specific excited-electron orbitals $x,y$ are denoted with the $*$ notation.

Two-State EnT Kinetics

Nonadiabatic triplet-to-triplet (tr) EnT is well described in the golden-rule approximation when the (resonant) donor and acceptor electronic transitions are at much lower energies than all other electronic transitions. The golden rule rate is

$$k=\frac{2\pi }{\hslash }{\left|V_{\text{tr}}\right|}^2\text{FC},$$ [1]

where $V_{\text{tr}}$ is the bridge-mediated donor–acceptor coupling and FC is the Franck–Condon factor associated with molecular and medium polarization that brings the donor and acceptor excitation energies into coincidence (17, 18).

A commonly used expression for the bridge-mediated Dexter coupling is given in Eq. 2 (19). We find that Eq. 2 does not capture these crucial BE contributions to the Dexter coupling, and we provide more general formulas that account for the BE contributions. The approximate Dexter coupling between D-centered $\left(|\mathbf{D},\mathbf{D}*\rangle \right)$ and A-centered $\left(|\mathbf{A},\mathbf{A}*\rangle \right)$ triplet excited states is

$$V_{\text{tr}}\mathrm{\simeq }2\frac{\langle \mathbf{D}\left|{\widehat{V}}^h\right|\mathbf{A}\rangle \langle \mathbf{D}*\left|{\widehat{V}}^e\right|\mathbf{A}*\rangle }{\mathrm{\Delta }{E}_{\text{CT}}}-\left(\mathbf{D}\mathbf{A}|\mathbf{D}*\mathbf{A}*\right).$$ [2]

$|\mathbf{D}\rangle ,$ $|\mathbf{D}*\rangle ,$(and $|\mathbf{A}\rangle ,$ $|\mathbf{A}*\rangle$) denote hole-occupied and electron-occupied diabatic orbitals that are mostly localized on the D (and A) fragments with tails on B. These orbitals can be written in a basis of zeroth-order hole or electron orbitals that are fully localized on D, B, or A fragments; i.e., $|\mathbf{D}\rangle \simeq |d\rangle +|{\delta }_D^{\text{br}}\rangle ,$ $|\mathbf{D}*\rangle \simeq |d*\rangle +|{\delta }_{D\ast }^{\text{br}}\rangle ,$$|\mathbf{A}\rangle \simeq |a\rangle +|{\delta }_A^{\text{br}}\rangle ,$ and $|\mathbf{A}*\rangle \simeq |a*\rangle +|{\delta }_{A\ast }^{\text{br}}\rangle ,$ where $|d\rangle$ $\left(|d*\rangle \right)$ and $|a\rangle$ $\left(|a*\rangle \right)$ are the zeroth-order D-localized and A-localized basis orbitals and $|{\delta }^{\text{br}}\rangle$ are the bridge tails.

In Eq. 2, $\langle \mathbf{D}\left|{\widehat{V}}^h\right|\mathbf{A}\rangle$ is the bridge-mediated hole-tunneling matrix element between $|\mathbf{D}\rangle$ and $|\mathbf{A}\rangle ,$ and $\langle \mathbf{D}*\left|{\widehat{V}}^e\right|\mathbf{A}*\rangle$ is the bridge-mediated electron-tunneling matrix element between $|\mathbf{D}*\rangle$ and $|\mathbf{A}*\rangle$ (${\widehat{V}}^h$ and ${\widehat{V}}^e$ denote the hole- and electron-tunneling operators of the one-electron Hamiltonian). $\mathrm{\Delta }{E}_{\text{CT}}$ is the energy difference between the triplet donor–acceptor charge-transfer exciton state $|\mathbf{D},\mathbf{A}*\rangle$ (or $|\mathbf{A},\mathbf{D}*\rangle$) and the triplet donor state $|\mathbf{D},\mathbf{D}*\rangle .$ In the CT states, a hole occupies the $|\mathbf{D}\rangle$ $\left(|\mathbf{A}\rangle \right)$orbital and an electron the $|\mathbf{A}*\rangle$ $\left(|\mathbf{D}*\rangle \right)$ orbital. $\left(\mathbf{D}\mathbf{A}|\mathbf{D}*\mathbf{A}*\right)$ is the Coulomb exchange integral $\left(\mathbf{D}\mathbf{A}|\mathbf{D}*\mathbf{A}*\right)=k{\displaystyle \int d{\mathbf{r}}_{1}d{\mathbf{r}}_2{\mathrm{\Psi }}_D\left({\mathbf{r}}_1\right){\mathrm{\Psi }}_A\left({\mathbf{r}}_1\right)r_{12}^{-1}{\mathrm{\Psi }}_{D*}\left({\mathbf{r}}_2\right){\mathrm{\Psi }}_{A*}\left({\mathbf{r}}_2\right)}$ $\left(k=e^2/4\pi {\mathit{ϵ}}_0\right)$ (5, 19). Eq. 2 indicates that $|\mathbf{D},\mathbf{D}*\rangle$ and $|\mathbf{A},\mathbf{A}*\rangle$ are coupled by both a one-electron/hole Hamiltonian operator (to second order) and a two-electron Coulomb Hamiltonian operator (to first order) (5, 19).

In Eq. 2, $\langle \mathbf{D}\left|{\widehat{V}}^h\right|\mathbf{A}\rangle$ and $\langle \mathbf{D}*\left|{\widehat{V}}^e\right|\mathbf{A}*\rangle$ are the couplings that cause hole or electron D-to-A CT reactions mediated by through-bridge tunneling (7). There are numerous approaches to compute these couplings (6, 17, 18, 20). Diabatization approaches compute the diabatic orbitals $|\mathbf{D}\rangle$ $\left(|\mathbf{D}*\rangle \right)$ and $|\mathbf{A}\rangle$ $\left(|\mathbf{A}*\rangle \right)$ and then obtain the matrix elements of ${\widehat{V}}^h$ and ${\widehat{V}}^e$ (14, 21–23). Green’s function (GF) strategies based on the Löwdin projection technique (7) express $\langle \mathbf{D}\left|{\widehat{V}}^h\right|\mathbf{A}\rangle$ and $\langle \mathbf{D}*\left|{\widehat{V}}^e\right|\mathbf{A}*\rangle$ in terms of the zero-order $|d\rangle ,$$|d*\rangle$and $|a\rangle ,$$|a*\rangle$ orbitals mentioned above; i.e., $\langle \mathbf{D}\left|{\widehat{V}}^h\right|\mathbf{A}\rangle =\langle d\left|{\widehat{V}}^h{\widehat{G}}_B{\widehat{V}}^h\right|a\rangle$ and $\langle \mathbf{D}*\left|{\widehat{V}}^e\right|\mathbf{A}*\rangle =\langle d*\left|{\widehat{V}}^e{\widehat{G}}_B{\widehat{V}}^e\right|a*\rangle ,$ where ${\widehat{G}}_B={\left(E_t{\widehat{I}}_B-{\widehat{H}}_B\right)}^{-1}$ is the single-particle bridge GF (${\widehat{H}}_B$ is the bridge Hamiltonian and $E_t$ is the electron- or hole-tunneling energy).

The GF approach is useful to interpret $\langle \mathbf{D}\left|{\widehat{V}}^h\right|\mathbf{A}\rangle$ $\left(\langle \mathbf{D}*\left|{\widehat{V}}^e\right|\mathbf{A}*\rangle \right)$ as a sum of through-bridge hole (electron)-coupling pathways (7), symbolized by $D^{\mp }BA\to D^{-}{B}^{+}A\to D^{-}B{A}^{+}$ $\left(D^{\mp }BA\to D^{+}{B}^{-}A\to D^{+}B{A}^{-}\right).$ Thus, the first term in Eq. 2 describes the contribution of single-particle transfer (SPT) pathways to the triplet-EnT coupling $V_{\text{tr}}$ ($D^{\mp }BA\to D^{+}{B}^{-}A\to D^{+}B{A}^{-}\to D{B}^{+}{A}^{-}\to DB{A}^{\mp }$ and $D^{\mp }BA\to D^{-}{B}^{+}A\to D^{-}B{A}^{+}\to$$D{B}^{-}{A}^{+}$$\to DB{A}^{\mp }$). Eq. 2 suggests that this contribution always involves DAE virtual intermediates with charge distributions $D^{+}B{A}^{-}$ or $D^{-}B{A}^{+}.$ We formulate a general GF approach to analyze $V_{\text{tr}}$ in terms of more general triplet exciton tunneling pathways. We show that Eq. 2 excludes an important class of triplet BE virtual mediating states $\left(D{B}^{\mp }A\right).$ For long bridges or low bridge tunneling barriers, these BE pathways dominate the Dexter coupling.

Characteristics of the Dexter Coupling

Experimental and theoretical studies of Dexter transport have been carried out in rigid and flexible molecules, in polymers, in polymer assemblies, and in metal–organic frameworks (3, 24, 25). Dexter rates drop approximately exponentially with distance (10), and Eq. 2 suggests a distance decay constant equal to the sum of the electron and hole superexchange decay constants (14). Experimental studies of Harriman found that some Dexter rates decay with exponential decay constants as small as 0.1 Å⁻¹ for Ru(II)–Os(II) terpyridyl complexes linked by 1,4-diethynylene-2,5-dialkoxy-benzene bridges (16). Albinsson et al. found exponential decay constants of 0.45 Å⁻¹ for phenylene ethynelene linked porphyrins (15). For alkane linkers, Closs et al. found large decay exponents, 2.8 Å⁻¹ (14). Computed decay constants as large as 3.4–3.8 Å⁻¹ were reported by Curutchet and Voityuk for through-solvent Dexter transport (26). Experimental and theoretical studies clearly indicate that Dexter couplings depend on the structure and energetics of the bridge.

CIS Model in a Localized Basis

We use a CIS approach (27) to describe the tr Dexter coupling. CIS methods were found to describe tr EnT couplings accurately in earlier studies (21–23). We use an orthogonal basis of natural localized molecular orbitals (NLMOs) that are mostly two-center bonding (e.g., σ and π) and two-center antibonding orbitals (e.g., $\sigma *$ and $\pi *$) with occupations of two and zero, respectively (28). A triplet CIS configuration is defined as $|i,x\rangle \equiv {\widehat{\mathit{\psi }}}_{x\mathrm{\uparrow }}^{\mathrm{†}}{\widehat{\psi }}_{i\downarrow }|{\mathrm{\Phi }}_0\rangle ,$ where ${\widehat{\psi }}_{i\downarrow }$ destroys a spin-down electron (creates a hole) in occupied NLMO spatial orbital i $\left({\varphi }_i\left(\mathbf{r}\right)\right),$ and ${\widehat{\psi }}_{x\uparrow }^{\mathrm{†}}$ creates a spin-up electron in virtual NLMO spatial orbital x $\left({\varphi }_x\left(\mathbf{r}\right)\right).$ $|{\mathrm{\Phi }}_0\rangle$ is a ground-state restricted Hartree–Fock Slater determinant [linear combinations of $|i,x\rangle$ must be used for triplet states (29)].

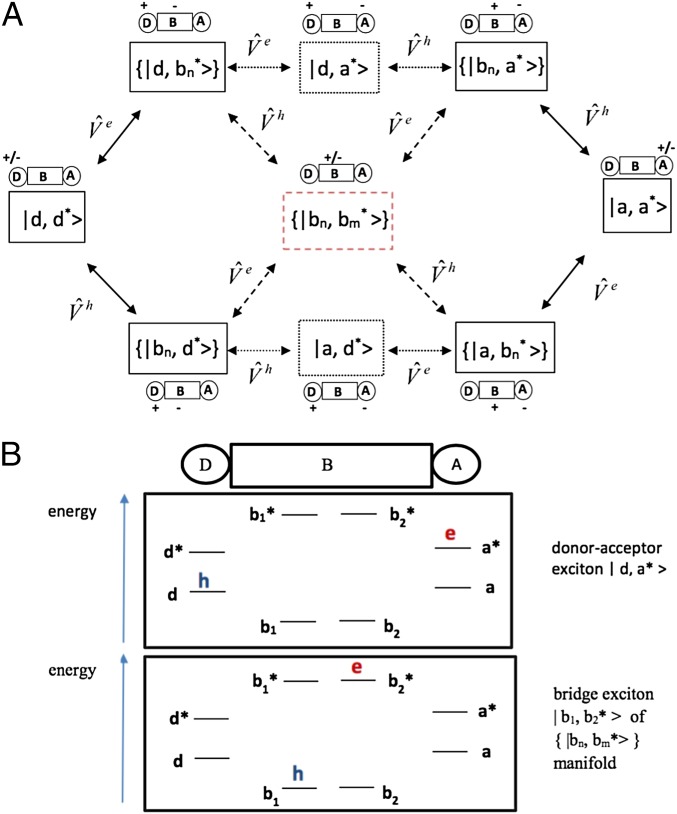
The NLMO representation for i and x produces an intuitive interpretation of a triplet basis state $|i,x\rangle$ as an exciton with hole and electron localized on different (D, B, A) molecular segments. The $|i,x\rangle$ basis set can be divided into different groups (Fig. 1). $|d,d*\rangle$ and $|a,a*\rangle$ describe triplet exciton states with the electron and hole entirely localized in D and A regions, respectively. $|d,a*\rangle$ and $|a,d*\rangle$ describe DAE states with a hole on D (orbital $|d\rangle$) and an electron on A (orbital $|a*\rangle$) or the reverse (an electron on $|d*\rangle$ and a hole on $|a\rangle$). There is a set of states $\left\{|d,b_n^{\mathrm{\ast }}\rangle \right\}$ with an electron on B (one of the $\left\{|b_n^{\mathrm{\ast }}\rangle \right\}$ NLMOs) and a hole on D, as well as a set $\left\{|a,b_n^{\mathrm{\ast }}\rangle \right\}$ with an electron on B and a hole on A. (In Fig. 1, braces $\{\hspace{0.17em}\}$ denote multiple $|i,x\rangle$). The $\left\{|b_n,d^{\mathrm{\ast }}\rangle \right\}$ and $\left\{|b_n,a^{\mathrm{\ast }}\rangle \right\}$ sets contain all states with a hole on B and an electron on either D or A. Finally, $\left\{|b_n,b_m^{\mathrm{\ast }}\rangle \right\}$ contains all BE basis states with both an electron and a hole on B. We establish a framework to understand how these sets of configurations mediate the Dexter coupling (Fig. 1).

Fig. 1.

(A) Schematic view of the electron-then-hole DAE pathways (upper route via $|d,a*\rangle$), hole-then-electron DAE pathways (lower route via $|a,d*\rangle$), and mixed electron/hole bridge-exciton BE pathways (routes through the center block of the bridge-exciton states $\left\{|b_n,b_m^{*}\rangle \right\}$). The DAE pathways (upper and lower routes, dotted lines) avoid the BE manifold $\left\{|b_n,b_m^{*}\rangle \right\}.$ The BE pathways (dashed lines to and from the center block) avoid $|d,a*\rangle$ and $|a,d*\rangle$. (B) Schematic diagrams of hole- and electron-occupied orbitals in the DAE state $|d,a*\rangle$ and in a BE state $|b_1,b_2^{*}\rangle .$ For example, NLMO orbitals $|b_1\rangle$ and $|b_2^{*}\rangle$ could correspond to the first σ bond and the second $\sigma *$ antibond of the alkane bridge in Fig. 2A.

The Hamiltonian elements among CIS basis states are (29)

$$H_{ix,jy}=\langle i,x\left|\widehat{H}\right|j,y\rangle ={\delta }_{i,j}{F}_{x,y}-{\delta }_{x,y}{F}_{i,j}-\left(ij|xy\right),$$ [3]

where $F_{i,j}$ and $F_{x,y}$ are Fock matrix elements that arise from the (mean field) Hartree–Fock theory. Each diagonal Fock matrix element $F_{i,i}$ ($F_{x,x}$) corresponds to the energy of the NLMO i (x); each off-diagonal Fock matrix element $F_{i,j}$ ($F_{x,y}$) corresponds to the electronic interaction between orbital i and orbital j (orbital x and orbital y) (28, 29)

$$\left(ij|xy\right)=k{\displaystyle \int d{\mathbf{r}}_{1}d{\mathbf{r}}_2{\varphi }_i\left({\mathbf{r}}_1\right){\varphi }_j\left({\mathbf{r}}_1\right)r_{12}^{-1}{\varphi }_x\left({\mathbf{r}}_2\right){\varphi }_y\left({\mathbf{r}}_2\right)}.$$ [4]

$\left(k=e^2/4\pi {\mathit{ϵ}}_0\right)$ are Coulomb matrix elements. It is useful to separate the CIS Hamiltonian matrix elements (Eq. 3) into diagonal ${\widehat{h}}^{\left(\text{di}\right)}$ and off-diagonal $\widehat{V}$ parts

$$h_{ix,ix}^{\left(\text{di}\right)}\equiv \langle i,x\left|{\widehat{h}}^{\left(\text{di}\right)}\right|i,x\rangle =F_{x,x}-F_{i,i}-\left(ii|xx\right),$$ [5]

and

$$V_{ix,jy}\equiv \langle i,x\left|\widehat{V}\right|j,y\rangle =V_{ix,jy}^{\left(1p\right)}+V_{ix,jy}^{\left(2p\right)}.$$ [6]

${\widehat{h}}^{\left(\text{di}\right)}$ (Eq. 5) contains the electron and hole NLMO orbital energies ($F_{x,x}$ and $-F_{i,i},$ respectively) and the electron–hole Coulomb attraction energy, $-\left(ii|xx\right).$ The off-diagonal interaction (Eq. 6) contains one-particle $\left(V_{ix,jy}^{\left(1\hspace{0.17em}p\right)}\right)$ and two-particle $\left(V_{ix,jy}^{\left(2\hspace{0.17em}p\right)}\right)$ components. $V_{ix,jy}^{\left(1\hspace{0.17em}p\right)}={\delta }_{i,j}{F}_{x,y}-{\delta }_{x,y}{F}_{i,j}$ (Fig. 1). These Fock matrix elements $F_{i,j}$ and $F_{x,y}$ describe, e.g., the through-bond (or through–anti-bond) interactions familiar in electron-transfer theory. $V_{ix,jy}^{\left(2\hspace{0.17em}p\right)}=-\left(ij|xy\right)$ is the two-electron pure exchange interaction.

The term BE used for the $\left\{|b_n,b_m^{\mathrm{\ast }}\rangle \right\}$ CIS basis states does not imply that a physical BE state in a molecular system corresponds to a single $|b_n,b_m^{\mathrm{\ast }}\rangle .$ Physical BE states are eigenstates of the Hamiltonian submatrix involving the BE basis states, i.e., the submatrix with elements $\langle b_n,b_m^{\mathrm{\ast }}\left|\widehat{H}\right|b_k,b_l^{\mathrm{\ast }}\rangle .$ These eigenstates, which are linear combinations of the $|b_n,b_m^{\mathrm{\ast }}\rangle ,$ are denoted $|{\mathrm{\Psi }}_L^{b{b}^{\mathrm{\ast }}}\rangle$ (eigenenergies $E_L^{b{b}^{\mathrm{\ast }}}$).

Exact EnT Splittings in Model Compounds

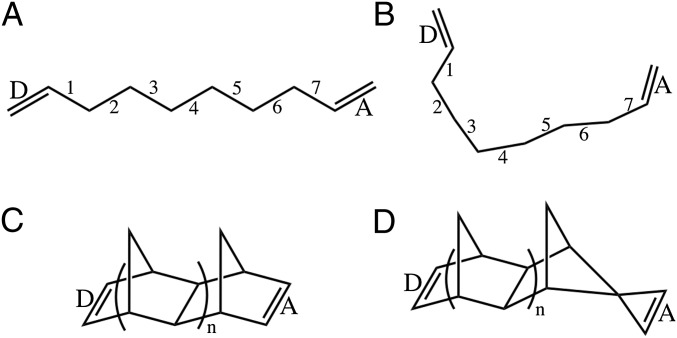
We focus on a simple set of n-alkyl–bridged dienes and norbornanes (Fig. 2) to study bridge-mediated EnT couplings, including their distance, energy-gap, molecular-conformation, and coupling-pathway dependence. For all of the molecules in Fig. 2 we choose the donor and acceptor segments to be the left (L) and right (R) C=C bonds, and we set $|d,d*\rangle =|{\pi }_L,{\pi }_L^{\mathrm{\ast }}\rangle$ and $|a,a*\backslash \rangle =|{\pi }_R,{\pi }_R^{\mathrm{\ast }}\rangle .$ These states are quasi-resonant with each other and are off-resonance with the other $|i,x\rangle ,$ ensuring that the $|d,d*\rangle$ to $|a,a*\rangle$ Dexter coupling is an entirely virtual process. We then scan the energy difference $\langle d,d*\left|\widehat{H}\right|d,d*\rangle -\langle a,a*\left|\widehat{H}\right|a,a*\rangle$ until we find two eigenstates $|{\mathrm{\Psi }}_{\pm }\rangle$ of $\widehat{H}$ (Eq. 3) given by $|{\mathrm{\Psi }}_{\mathrm{\pm }}\rangle \simeq \left(1/\sqrt{2}\right)\left[|d,d*\rangle \pm |a,a*\rangle \right]+|{\delta }_{\pm }\rangle ,$ where $|{\delta }_{\pm }\rangle$ is small, and it contains the contribution to $|{\mathrm{\Psi }}_{\pm }\rangle$ of all $|i,x\rangle$ other than $|d,d*\rangle$ and $|a,a*\rangle .$ In this virtual coupling (tunneling) regime, the energy eigenvalues $E_{\pm }$ of $|{\mathrm{\Psi }}_{\pm }\rangle$ are near each other and are separated from the other energy eigenvalues. This setup provides a definition of an “exact” coupling V_tr between $|d,d*\rangle$ and $|a,a*\rangle$ as one-half of the splitting computed by diagonalizing the full Hamiltonian matrix $\tilde{H}$ in Eq. 3:

$$V_{\text{tr}}\equiv \left(E_{+}-E_{-}\right)/2.$$ [7]

Fig. 1 shows that the bridge-mediated $|d,d*\rangle$-to-$|a,a*\rangle$ EnT coupling can be mediated by the virtual states $|d,a*\rangle$ and $|a,d*\rangle$ (DAE) or the virtual-state manifold $\left\{|b_n,b_m^{\mathrm{\ast }}\rangle \right\}$ (BE). We therefore define the exact tr EnT coupling mediated by DAE as $V_{\text{tr}}^{\left(\text{dae}\right)}\equiv \left(E_{+}^{\left(\text{dae}\right)}-E_{-}^{\left(\text{dae}\right)}\right)/2,$ where $E_{\pm }^{\left(\text{dae}\right)}$ are obtained by diagonalizing the $\tilde{H}$ matrix (Eq. 3) with all elements containing the $|b_n,b_m^{\mathrm{\ast }}\rangle$ states in Fig. 1 set to zero. By construction, $V_{\text{tr}}^{\left(\text{dae}\right)}$ is thus mediated by DAE rather than by BE. Similarly, we define the exact $\text{tr}$ EnT coupling mediated by BE as $V_{\text{tr}}^{\left(\text{be}\right)}\equiv \left(E_{+}^{\left(\text{be}\right)}-E_{-}^{\left(\text{be}\right)}\right)/2,$ where $E_{\pm }^{\left(\text{be}\right)}$ are obtained by diagonalizing the $\tilde{H}$ matrix with all elements containing the $|d,a*\rangle$ and $|a,d*\rangle$ states in Fig. 1 set to zero.

Fig. 2.

(A) Alkyl-bridged diene model compound with seven bridging σ bonds. The alkane bridge is planar, and the left and right C=C bonds are twisted approximately ${60}^{\text{o}}$ in opposite directions out of the CC-bonded bridge plane. These double bonds are taken to be the D and A. In our computations (Fig. 3), the number of bridge σ bonds is varied from 4 to 13. (B) Example of disordered alkyl-bridged diene model compound with seven bridging σ bonds used in the computations of Tables S1 and S2. (C) Norbornyl bridged diene model compound with two parallel C=C bonds (D and A). These compounds with n = 1, 2 are used in the computations shown in Tables S3 and S4. (D) Norbornyl bridged diene model compound with orthogonal C=C bonds (D and A) with symmetry-forbidden triplet EnT.

Contributions of DAE and BE Virtual Intermediates to the Dexter Coupling

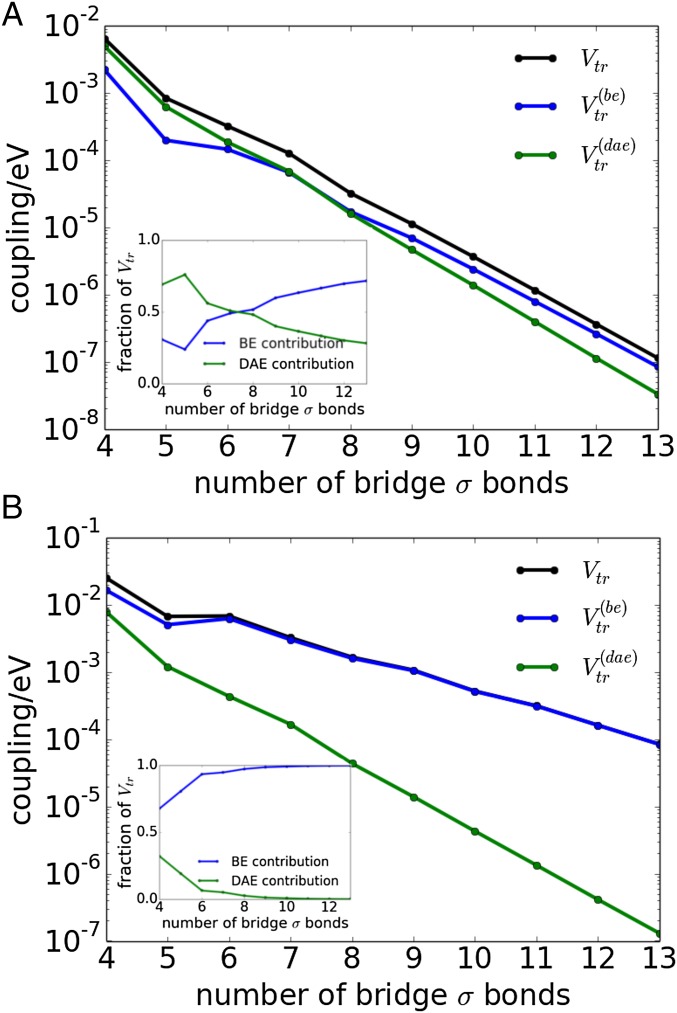
In our quantum computations, we used restricted Hartree–Fock methods implemented in Gaussian 09 (30) with a 6–31G basis. Fig. 3A shows $V_{\text{tr}},$ $V_{\text{tr}}^{\left(\text{dae}\right)},$ and $V_{\text{tr}}^{\left(\text{be}\right)}$ as a function of bridge length for the extended alkane systems of Fig. 2A. Fig. 3A, Inset indicates the relative magnitude of the DAE and BE contributions [$V_{\text{tr}}^{\left(\text{dae}\right)}/\left(V_{\text{tr}}^{\left(\text{dae}\right)}+V_{\text{tr}}^{\left(\text{be}\right)}\right),$ as well as the contribution of $V_{\text{tr}}^{\left(\text{be}\right)}/\left(V_{\text{tr}}^{\left(\text{dae}\right)}+V_{\text{tr}}^{\left(\text{be}\right)}\right),$ respectively] as a function of bridge length. Figs. 2A and 3A show that the BE contribution in extended alkane bridges with more than seven to eight CC bonds is larger than the DAE contribution. The relative BE contribution is larger for bridges with smaller tunneling barriers. To explore this switching effect, we shift the energies of all bridge NLMO diagonal Fock matrix elements, $F_{x,x}=F_{b_n^{\mathrm{\ast }},b_n^{\mathrm{\ast }}}$ and $F_{i,i}=F_{b_n,b_n}$ in Eq. 5, so that the energy gaps $\text{aver}(F_{b_n^{\mathrm{\ast }},b_n^{\mathrm{\ast }}})-F_{d\ast ,d\ast }$ and $F_{d,d}-\text{aver}(F_{b_n,b_n})$ are reduced (aver indicates the average value). We ensure that the energy-shifted systems remain in the tunneling regime. That is, we can still find two eigenstates $|{\mathrm{\Psi }}_{\pm }\rangle$ of $\tilde{H}$ (Eq. 3) equally delocalized over $|d,d*\rangle$ and $|a,a*\rangle$ with small amplitude on the bridge. Then, we compute $V_{\text{tr}},$ $V_{\text{tr}}^{\left(\text{dae}\right)},$ and $V_{\text{tr}}^{\left(\text{be}\right)},$ using the new CIS Hamiltonian. Fig. 3B shows $V_{\text{tr}},$ $V_{\text{tr}}^{\left(\text{dae}\right)},$ and $V_{\text{tr}}^{\left(\text{be}\right)}$ as a function of bridge length for the extended alkane structures used in Fig. 2A, where we have set the $\text{aver}\left(F_{b_n^{\mathrm{\ast }},b_n^{\mathrm{\ast }}}\right)-F_{d\ast ,d\ast }=6.15\hspace{0.5em}\text{eV}$ and $F_{d,d}-\text{aver}\left(F_{b_n,b_n}\right)=6.35\hspace{0.5em}\text{eV}$ [compared with the original values $\text{aver}\left(F_{b_n^{\mathrm{\ast }},b_n^{\mathrm{\ast }}}\right)-F_{d\ast ,d\ast }=11.32\hspace{0.5em}\text{eV}$ and $F_{d,d}-\text{aver}\left(F_{b_n,b_n}\right)=11.52\hspace{0.5em}\text{eV}$ in Fig. 3A]. For the seven-bond bridge in Fig. 3B, the lowest BE eigenstate $|{\mathrm{\Psi }}_{L_{\text{min}}}^{bb\ast }\rangle$ is $2.2\hspace{0.5em}\text{eV}$ above $|d,d*\rangle ,$ whereas the DAE state $|d,a*\rangle$ is $10.8\hspace{0.5em}\text{eV}$ above $|d,d*\rangle$ (as opposed to values of $12.4\hspace{0.5em}\text{eV}$ and $10.8\hspace{0.5em}\text{eV},$ respectively for the seven-bond bridge in Fig. 3A). Therefore, for the lower barrier systems in Fig. 3B, the BE contribution dominates the coupling for all bridge lengths, becoming more than two orders of magnitude larger than the DAE contribution for longer bridges. Fig. 3B shows that the BE contribution produces large $V_{\text{tr}}$ matrix elements of the order ${10}^{-2}$–${10}^{-3}\hspace{0.5em}\text{eV}.$

Fig. 3.

(A) Dexter coupling and the BE and DAE contributions to the couplings for linear alkanes (Fig. 2A) as a function of bridge length. (B) Same structures as in A, where the average energy gaps $\text{aver}\left(F_{b_n^{\mathrm{\ast }},b_n^{\mathrm{\ast }}}\right)-F_{d\ast ,d\ast }$ and $F_{d,d}-\text{aver}\left(F_{b_n,b_n}\right)$ are lowered.

To investigate the effects of molecular conformations on the alkane systems, we sampled structures by choosing random torsional angles and optimizing these conformations with restricted Hartree–Fock methods using a 6–31G basis set (RHF/6–31G). The folded structures thus generated (Fig. 2B) were used to compute $V_{\text{tr}}$ values and the DAE and BE coupling contributions as a function of energy gap. In Table S1, we show $V_{\text{tr}},$ $V_{\text{tr}}^{\left(\text{dae}\right)},$ and $V_{\text{tr}}^{\left(\text{be}\right)}$ for five folded alkanes with seven CC bonds that have $\text{aver}\left(F_{b_n^{\mathrm{\ast }},b_n^{\mathrm{\ast }}}\right)-F_{d\ast ,d\ast }=11.32\hspace{0.5em}\text{eV}$ and $F_{d,d}-\text{aver}(F_{b_n,b_n})=11.52\hspace{0.5em}\text{eV}$. Table S2 shows $V_{\text{tr}},$ $V_{\text{tr}}^{\left(\text{dae}\right)},$ and $V_{\text{tr}}^{\left(\text{be}\right)}$ for the structures in Table S1 with lowered the energy gaps to $\text{aver}\left(F_{b_n^{\mathrm{\ast }},b_n^{\mathrm{\ast }}}\right)-F_{d\ast ,d\ast }=6.15\hspace{0.5em}\text{eV}$ and $F_{d,d}-\text{aver}\left(F_{b_n,b_n}\right)=6.35\hspace{0.5em}\text{eV}$ (the same energy gap as in Fig. 3B). In most cases, the BE contribution is greater than or approximately equal to the DAE contribution. The Dexter couplings for the conformationally sampled alkane bridges are smaller compared with the couplings for the extended alkane bridges (for the seven-CC bond bridge, $V_{\text{tr}}=1.27\times {10}^{-4}\hspace{0.5em}\text{eV}$ in Fig. 3A, and for the partially folded seven-CC bond bridges in Table S1, $\langle V_{\text{tr}}\rangle =1.67\times {10}^{-5}\hspace{0.5em}\text{eV}$).

Table S1.

Total Dexter coupling and BE and DAE contributions of seven-bond folded alkanes (Fig. 2B)

Conformation	$V_{\text{tr}},$ eV	$V_{\text{tr}}^{\left(\text{be}\right)},$ eV	$V_{\text{tr}}^{\left(\text{dae}\right)},$ eV
Conf1	$5.07\times {10}^{-7}$	$1.10\times {10}^{-6}$	$1.25\times {10}^{-6}$
Conf2	$8.90\times {10}^{-7}$	$9.36\times {10}^{-7}$	$1.48\times {10}^{-7}$
Conf3	$1.66\times {10}^{-5}$	$1.42\times {10}^{-6}$	$1.46\times {10}^{-5}$
Conf4	$2.06\times {10}^{-5}$	$9.77\times {10}^{-6}$	$1.38\times {10}^{-5}$
Conf5	$4.47\times {10}^{-5}$	$1.27\times {10}^{-5}$	$2.89\times {10}^{-5}$

Table S2.

Total Dexter coupling and BE and DAE contributions of seven-bond folded alkanes (Fig. 2B) with lowered average energy gaps compared with the values for Table S1 (main text)

Conformation	$V_{\text{tr}},$ eV	$V_{\text{tr}}^{\left(\text{be}\right)},$ eV	$V_{\text{tr}}^{\left(\text{dae}\right)},$ eV
Conf1	$2.14\times {10}^{-4}$	$2.17\times {10}^{-4}$	$1.33\times {10}^{-6}$
Conf2	$4.67\times {10}^{-5}$	$4.68\times {10}^{-5}$	$1.58\times {10}^{-7}$
Conf3	$2.34\times {10}^{-5}$	$4.26\times {10}^{-5}$	$1.58\times {10}^{-5}$
Conf4	$2.68\times {10}^{-4}$	$2.43\times {10}^{-4}$	$2.46\times {10}^{-5}$
Conf5	$1.60\times {10}^{-4}$	$1.12\times {10}^{-4}$	$3.41\times {10}^{-5}$

The trends in the coupling mechanism apply to more complex bridged structures. Tables S3 and S4 show $V_{\text{tr}},$ $V_{\text{tr}}^{\left(\text{dae}\right)},$ and $V_{\text{tr}}^{\left(\text{be}\right)}$ for norbonyl bridged systems (Fig. 2C) where, as with the linear alkanes, we choose the donor and acceptor segments to be the L and R C=C bonds, and we set $|d,d*\rangle =|{\pi }_L,{\pi }_L^{\mathrm{\ast }}\rangle$ and $|a,a*\rangle =|{\pi }_R,{\pi }_R^{\mathrm{\ast }}\rangle .$ In Table S3, we examine two bridge lengths with $n=\mathrm{1,2}$ (Fig. 2C). In Table S4, we use the same structures as in Table S3 with lowered energy gaps. The $\text{aver}\left(F_{b_n,b_n}\right)$ values are increased by 4.90 eV and the $\text{aver}\left(F_{b_n^{\mathrm{\ast }},b_n^{\mathrm{\ast }}}\right)$ values are lowered by 4.90 eV. The splittings shown in Tables S3 and S4 indicate that the BE contribution dominates the Dexter coupling as the chain length grows and the tunneling barrier drops. As a final example, we consider a norbonyl system with orthogonal donor/acceptor C=C bonds (Fig. 2D). In this structure, the Dexter coupling is symmetry forbidden ($V_{\text{tr}}=2.10\times {10}^{-13}\hspace{0.5em}\text{eV}$) and both BE and DAE contributions are symmetry forbidden [$V_{\text{tr}}^{\left(\text{dae}\right)}=3.70\times {10}^{-13}\hspace{0.5em}\text{eV}$ and $V_{\text{tr}}^{\left(\text{be}\right)}=1.53\times {10}^{-13}\hspace{0.5em}\text{eV},$ within the numerical noise].

Table S3.

$V_{\text{tr}},$ $V_{\text{tr}}^{\left(\text{be}\right)},$ and $V_{\text{tr}}^{\left(\text{dae}\right)}$ for the polynorbornyl bridged model compounds with n = 1, 2 (see Fig. 2C for the molecular structures)

Number of bridge units	$V_{\text{tr}},$ eV	$V_{\text{tr}}^{\left(\text{be}\right)},$ eV	$V_{\text{tr}}^{\left(\text{dae}\right)},$ eV
n = 1	$4.00\times {10}^{-2}$	$9.86\times {10}^{-3}$	$2.91\times {10}^{-2}$
n = 2	$2.42\times {10}^{-3}$	$8.65\times {10}^{-4}$	$1.48\times {10}^{-3}$

The edge D, A C=C bonds are parallel.

Table S4.

$V_{\text{tr}},$ $V_{\text{tr}}^{\left(\text{be}\right)},$ and $V_{\text{tr}}^{\left(\text{dae}\right)}$ for the polynorbornyl bridged model compounds with n = 1, 2 (see Fig. 2C for the molecular structures) with parallel D, A C=C bond fragments

Number of bridge units	$V_{\text{tr}},$ eV	$V_{\text{tr}}^{\left(\text{be}\right)},$ eV	$V_{\text{tr}}^{\left(\text{dae}\right)},$ eV
n = 1	$1.13\times {10}^{-1}$	$5.89\times {10}^{-2}$	$4.36\times {10}^{-2}$
n = 2	$2.39\times {10}^{-2}$	$2.01\times {10}^{-2}$	$2.70\times {10}^{-3}$

For these computations the energy gaps were lowered compared to their values in Table S3 (main text).

To summarize, the splitting computations find that the Dexter coupling is mediated by BE virtual states, rather than by DAE virtual states; i.e., $V_{\text{tr}}\mathrm{\simeq }{V}_{\text{tr}}^{\left(\text{be}\right)}$ and $V_{\text{tr}}^{\left(\text{be}\right)}>V_{\text{tr}}^{\left(\text{dae}\right)}$ for low tunneling energy gaps and/or long bridges. The distance at which the transition from DAE to BE dominance occurs is structure and energy gap dependent.

Triplet-EnT Pathways

Having established the importance of BE contributions to the Dexter coupling $V_{\text{tr}},$ we return to our consideration of Eq. 2. Our focus is the first single-particle transfer (SPT) term, which is a product of D-to-A electron transfer (ET) and hole transfer (HT) couplings. To understand the contributions of this term to $V_{\text{tr}},$ we develop a general GF pathway description of $V_{\text{tr}},$ $V_{\text{tr}}^{\left(\text{dae}\right)}$ and $V_{\text{tr}}^{\left(\text{be}\right)},$ using Löwdin (effective Hamiltonian) projection methods that are applicable to tunneling matrix element computations. Below, $T_{\text{tr}},$ $T_{\text{tr}}^{\left(\text{dae}\right)},$ and $T_{\text{tr}}^{\left(\text{be}\right)}$ denote the Löwdin projection (GF) expressions for $V_{\text{tr}},$ $V_{\text{tr}}^{\left(\text{dae}\right)},$ and $V_{\text{tr}}^{\left(\text{be}\right)},$ respectively. The Löwdin projection expression for $V_{\text{tr}}$ is given by

$$\begin{array}{c}{T}_{\text{tr}}\equiv \langle d,d*|{\widehat{H}}^{\text{ef}}\left(E_t\right)|a,a*\rangle ,\\ {\widehat{H}}^{\text{ef}}\left(E_t\right)\hspace{0.17em}=\hspace{0.17em}\widehat{P}\widehat{H}\widehat{P}+\widehat{P}\widehat{H}\widehat{Q}\widehat{\mathcal{G}}\left(E_t\right)\widehat{Q}\widehat{H}\widehat{P},\end{array}$$ [8]

where $\widehat{P}=|d,d*\rangle \langle d,d*|+|a,a*\rangle \langle a,a*|$ is the projection operator for the DAE subspace and $\widehat{Q}=\widehat{I}-\left(|d,d*\rangle \langle d,d*|+|a,a*\rangle \langle a,a*|\right)$ is the projection operator for the complementary subspace containing all exciton states $|i,x\rangle$ other than $|d,d*\rangle$ and $|a,a*\rangle .$ Given the subspace grouping of Fig. 1

$$\widehat{Q}={\widehat{Q}}_{db*}+{\widehat{Q}}_{bd*}+{\widehat{Q}}_{ba*}+{\widehat{Q}}_{ab*}+{\widehat{Q}}_{da*}+{\widehat{Q}}_{ad*}+{\widehat{Q}}_{bb*},$$ [9]

where ${\widehat{Q}}_{db*}={\displaystyle {\sum }_n|d,b_n^{*}\rangle \langle d,b_n^{*}|,}$ ${\widehat{Q}}_{d{a}^{\ast }}=\left|d,a^{\ast }\rangle \langle d,a^{\ast }\right|,etc.{\widehat{Q}}_{b{b}^{\ast }}={\displaystyle {\sum }_{n,m}\left|b_n,b_m^{\ast }\rangle \langle b_n,b_m^{\ast }\right|}$ is the projection operator for the BE subspace, etc. $\widehat{\mathcal{G}}\left(E\right)={\left[E\widehat{Q}-\widehat{Q}\widehat{H}\widehat{Q}\right]}^{-1}$ is the exact GF for the CIS Hamiltonian (Eq. 3) in the $\widehat{Q}$ subspace $\left(\widehat{Q}\widehat{H}\widehat{Q}\right).$ $E_t$ is the tunneling energy that can be adjusted so that $T_{\text{tr}}$ is infinite order in perturbation theory so that $T_{\text{tr}}=V_{\text{tr}}$ (e.g., refs. 7 and 31 and Supporting Information). We also define $T_{\text{tr}}^{\left(\text{dae}\right)}$ and $T_{\text{tr}}^{\left(\text{be}\right)}$ in the same way that we defined $V_{\text{tr}}^{\left(\text{dae}\right)}$ and $V_{\text{tr}}^{\left(\text{be}\right)}$ (Eqs. S6 and S7). That is, we use equations identical to Eq. 8 where we zero out all $\widehat{H}$ matrix elements that contain $|d,a*\rangle$ and $|a,d*\rangle$ states [for $T_{\text{tr}}^{\left(\text{be}\right)}$] or all $\widehat{H}$ matrix elements containing $|b_n,b_m^{*}\rangle$ [for $T_{\text{tr}}^{\left(\text{dae}\right)}$]. The important conclusion is that for all systems in Fig. 2 and all tunneling energy gaps, we can reproduce the splitting-derived $V_{\text{tr}},$ $V_{\text{tr}}^{\left(\text{dae}\right)},$ and $V_{\text{tr}}^{\left(\text{be}\right)}$ values, using the Löwdin GF expressions for $T_{\text{tr}},$ $T_{\text{tr}}^{\left(\text{dae}\right)},$ and $T_{\text{tr}}^{\left(\text{be}\right)},$ respectively, thus confirming that the Löwdin projection method is applicable (Tables S5–S8).

Table S5.

Couplings for a linear alkane system with a bridge of seven CC bonds (Fig. 2A) as a function of energy gap $\mathrm{\Delta }E$

$\mathrm{\Delta }{E}_1,\mathrm{\Delta }{E}_2,$ eV	$T_{\text{tr}},$ eV	$V_{\text{tr}},$ eV
6.32, 6.52	$2.60\times {10}^{-3}$	$2.52\times {10}^{-3}$
11.32, 11.52	$1.22\times {10}^{-4}$	$1.27\times {10}^{-4}$

$\mathrm{\Delta }{E}_1=\text{aver}\left(F_{b_n*,b_n*}\right)-F_{d\ast ,d\ast },$ $\mathrm{\Delta }{E}_2=F_{d,d}-\text{aver}\left(F_{b_n,b_n}\right).$

Table S8.

Single-particle component to the Dexter couplings (i.e., using a CIS Hamiltonian with no pure exchange) as a function of energy gap for the linear alkane systems in Table S5

$\mathrm{\Delta }{E}_1,\mathrm{\Delta }{E}_2,$ eV	$T_{\text{tr}\left(\text{ne}\right)},$ eV	$V_{\text{tr}\left(\text{ne}\right)},$ eV
6.32, 6.52	$5.59\times {10}^{-3}$	$5.41\times {10}^{-3}$
11.32, 11.52	$1.55\times {10}^{-4}$	$1.53\times {10}^{-4}$

Table S6.

BE contribution to the Dexter couplings as a function of energy gap for the linear alkane systems in Table S5

$\mathrm{\Delta }{E}_1,\mathrm{\Delta }{E}_2,$ eV	$T_{\text{tr}}^{\left(\text{be}\right)},$ eV	$V_{\text{tr}}^{\left(\text{be}\right)},$ eV
6.32, 6.52	$2.93\times {10}^{-3}$	$2.32\times {10}^{-3}$
11.32, 11.52	$6.04\times {10}^{-5}$	$6.59\times {10}^{-5}$

Table S7.

DAE contribution to the Dexter coupling as a function of energy gap for the linear alkane systems in Table S5

$\mathrm{\Delta }{E}_1,\mathrm{\Delta }{E}_2,$ eV	$T_{\text{tr}}^{\left(\text{dae}\right)},$ eV	$V_{\text{tr}}^{\left(\text{dae}\right)},$ eV
6.32, 6.52	$1.65\times {10}^{-4}$	$1.72\times {10}^{-4}$
11.32, 11.52	$6.27\times {10}^{-5}$	$6.81\times {10}^{-5}$

Donor—Acceptor Exciton vs. Bridge-Exciton Triplet-EnT Pathways

We derive a generalized GF expression for the first (SPT) term of Eq. 2. This term contains electron-transfer ${\widehat{V}}^e$ and hole-transfer ${\widehat{V}}^h$ off-diagonal operators. Therefore, in Eq. 8, we replace the total CIS Hamiltonian $\widehat{H}$ (Eq. 3) with a Hamiltonian ${\widehat{H}}^{\left(\text{ne}\right)}$ where the pure exchange terms $\left(ij|xy\right)$ in the off-diagonal elements $V_{ix,jy}$ of Eq. 6 are ignored (ne means no exchange). Therefore, ${\widehat{H}}^{\left(\text{ne}\right)}={\widehat{h}}^{\left(\text{di}\right)}+{\widehat{V}}^e+{\widehat{V}}^h,$ where ${\widehat{h}}^{\left(\text{di}\right)}$ is the diagonal part of the CIS Hamiltonian (Eq. 5) [containing the Coulomb attraction terms $-\left(ii|xx\right)$], and $\langle i,x|{\widehat{V}}^e|j,y\rangle ={\delta }_{i,j}{F}_{x,y},$ $\langle i,x|{\widehat{V}}^h|j,y\rangle =-{\delta }_{x,y}{F}_{i,j}.$ Replacing $\widehat{H}$ by ${\widehat{H}}^{\left(\text{ne}\right)}$ in $T_{\text{tr}}$ (Eq. 8), we obtain pathway expressions for the SPT components of the total Dexter coupling, of the DAE-mediated coupling, and of the BE-mediated coupling. These expressions (Eqs. S15, S19, and S21) are denoted $T_{\text{tr}\left(\text{ne}\right)},$ $T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{dae}\right)},$ and $T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{be}\right)},$ respectively, to emphasize that they do not include the effects of pure-exchange interactions in transferring electrons and holes. The final result is

$$T_{\text{tr}\left(\text{ne}\right)}=T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{dae}\right)}+T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{be}\right)},$$ [10]

where $T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{dae}\right)}$ in Eq. 10 describes DAE pathways and is given by

$$\begin{array}{l}{T}_{\text{tr}\left(\text{ne}\right)}^{\left(\text{dae}\right)}\simeq \frac{\langle dd*|{\widehat{V}}^e{\widehat{G}}_{db*}{\widehat{V}}^e|da*\rangle \langle da*|{\widehat{V}}^h{\widehat{G}}_{ba*}{\widehat{V}}^h|aa*\rangle }{E_t-E_{da*}}\hspace{0.17em}\\ \hspace{1em}\hspace{1em}\hspace{1em}+\frac{\langle dd*|{\widehat{V}}^h{\widehat{G}}_{bd*}{\widehat{V}}^h|ad*\rangle \langle ad*|{\widehat{V}}^e{\widehat{G}}_{ab*}{\widehat{V}}^e|aa*\rangle }{E_t-E_{ad\ast }}\end{array}$$ [11]

(Eq. S25). $T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{be}\right)}$ in Eq. 10 describes BE pathways

$$\begin{array}{l}{T}_{\text{tr}\left(\text{ne}\right)}^{\left(\text{be}\right)}\simeq \langle dd*|{\widehat{V}}^e{\widehat{G}}_{db*}{\widehat{V}}^h{\widehat{G}}_{bb*}{\widehat{V}}^e{\widehat{G}}_{ba*}{\widehat{V}}^h|aa*\rangle \hspace{0.17em}\\ +\langle dd*|{\widehat{V}}^h{\widehat{G}}_{bd*}{\widehat{V}}^e{\widehat{G}}_{bb*}{\widehat{V}}^h{\widehat{G}}_{ab*}{\widehat{V}}^e|aa*\rangle \hspace{0.17em}\\ +\langle dd*|{\widehat{V}}^e{\widehat{G}}_{db*}{\widehat{V}}^h{\widehat{G}}_{bb*}{\widehat{V}}^h{\widehat{G}}_{ab*}{\widehat{V}}^e|aa*\rangle \hspace{0.17em}\\ +\langle dd*|{\widehat{V}}^h{\widehat{G}}_{bd*}{\widehat{V}}^e{\widehat{G}}_{bb*}{\widehat{V}}^e{\widehat{G}}_{ba*}{\widehat{V}}^h|aa*\rangle \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\end{array}$$ [12]

(Eq. S26). $E_t$ is the exciton tunneling energy. The ${\widehat{G}}_K$ are ${\widehat{H}}^{\left(\text{ne}\right)}$ GFs for the individual subspaces K of virtual intermediate states shown in Fig. 1. ${\widehat{G}}_K\left(E_t\right)={\left[E_t{\widehat{Q}}_K-{\widehat{Q}}_K{\widehat{H}}^{\left(\text{ne}\right)}{\widehat{Q}}_K\right]}^{-1},$ where the ${\widehat{Q}}_K$ are the projection operator components of Eq. 9.

The DAE contribution $T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{dae}\right)}$ in Eq. 11 is the generalized GF pathway expression for the first (SPT) component of Eq. 2. It describes EnT as a sequence of two complete D-to-A electron and hole tunneling steps (first term, $D^{\mp }BA\to D^{+}{B}^{-}A\to D^{+}B{A}^{-}\to D{B}^{+}{A}^{-}\to DB{A}^{\mp };$ second term, $D^{\mp }BA\to D^{-}{B}^{+}A\to D^{-}B{A}^{+}\to D{B}^{-}{A}^{+}\to DB{A}^{\mp }$). In the framework of Fig. 1, Eq. 11 contains all of the upper and lower tunneling paths connecting $|d,d*\rangle$ to $|a,a*\rangle$ via virtual DAE states $|a,d*\rangle$ and $|d,a*\rangle ,$ respectively (avoiding the BE manifold $|b_n,b_m^{\ast }\rangle$). $\langle dd*|{\widehat{V}}^e{\widehat{G}}_{db*}{\widehat{V}}^e|da*\rangle$ and $\langle ad*|{\widehat{V}}^e{\widehat{G}}_{ab\ast }{\widehat{V}}^e|aa*\rangle$ are the bridge-mediated electron tunneling matrix elements for photo-excited electron transfer from $|d*\rangle$ to $|a*\rangle .$ Similarly, $\langle da*|{\widehat{V}}^h{\widehat{G}}_{ba*}{\widehat{V}}^h|aa*\rangle$ and $\langle dd*|{\widehat{V}}^h{\widehat{G}}_{bd*}{\widehat{V}}^h|ad*\rangle$ are the bridge-mediated hole tunneling matrix elements for photo-excited hole transfer from $|a\rangle$ to $|d\rangle .$ These matrix elements include the influence of electron–hole Coulomb attraction.

The bridge exciton contribution, $T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{be}\right)}$ (Eq. 12), describes all tunneling pathways from $|d,d\ast \rangle$ to $|a,a\ast \rangle$ through the virtual BE manifold $|b_n,b_m^{*}\rangle$ in Fig. 1 (avoiding the DAE states) (first two terms, $D^{\mp }BA\to D^{+}{B}^{-}A\to D{B}^{\mp }A\to D{B}^{+}{A}^{-}\to DB{A}^{\mp }$ and $D^{\mp }BA\to D^{-}{B}^{+}A\to D{B}^{\mp }A\to D{B}^{-}{A}^{+}\to DB{A}^{\mp };$ last two terms, $D^{\mp }BA\to D^{+}{B}^{-}A\to D{B}^{\mp }A\to D{B}^{-}{A}^{+}\to DB{A}^{\mp }$ and $D^{\mp }BA\to D^{-}{B}^{+}A\to D{B}^{\mp }A\to D{B}^{+}{A}^{-}\to DB{A}^{\mp }).$).

Rapid Growth in the Number of Bridge-Exciton Intermediate States with Chain Length

Ignoring pure exchange when computing the Dexter coupling is not generally sound. For the systems studied in Fig. 2A, the average exchange contribution to the Dexter coupling in the long chain limit (Fig. 2A) is about 25% of $V_{\text{tr}}.$ The analysis above finds that the SPT component of the Dexter coupling contains DAE and BE pathway terms that are of the same order in ${\widehat{V}}^e$ and ${\widehat{V}}^h.$ Therefore, DAE and BE pathways must both be considered; it is not appropriate to retain only $T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{dae}\right)}$ (which is analogous to the first term in Eq. 2) without keeping the $T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{be}\right)}$ term as well. For bridges with N bonding/antibonding orbitals ($|b_n\rangle ,$ $|b_m^{*}\rangle$), the number of BE CIS configurations $|b_n,b_m^{*}\rangle$ is at least $N^2.$ Therefore, the number of BE eigenstates $|{\mathrm{\Psi }}_L^{bb\ast }\rangle$ of the submatrix $\langle b_n,b_m^{*}|\widehat{H}|b_k,b_l^{*}\rangle$ (or $\langle b_n,b_m^{*}|{\widehat{H}}^{\left(\text{ne}\right)}|b_k,b_l^{*}\rangle$) is also $N^2.$ In Eq. 12 for $T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{be}\right)},$ ${\widehat{G}}_{bb\ast }={\displaystyle {\sum }_{L=1}^{N^2}\left(|{\mathrm{\Psi }}_L^{bb\ast }\rangle \langle {\mathrm{\Psi }}_L^{bb\ast }|\right)/\left(E_t-E_L^{bb\ast }\right)}$ (where $E_L^{bb\ast }$ is the eigenvalue of BE eigenstate $|{\mathrm{\Psi }}_L^{bb\ast }\rangle$). As the bridge length N grows, the number of possible BE virtual intermediates $|{\mathrm{\Psi }}_L^{bb\ast }\rangle$ grows as $N^2$ (as opposed to the two DAE intermediates $|d,a*\rangle$ and $|a,d*\rangle$ in Eq. 11). Thus, BE pathways are important for long bridge lengths or low energy gaps, where omitting the BE contribution to the Dexter coupling may introduce errors of one to two orders of magnitude.

Conclusions

We have found that bridge-exciton tunneling pathways dominate triplet energy transfer mediation in the long-distance/small tunneling gap regime accessed in many molecular structures of current interest. As well, we have developed a coupling pathway description for bridge-mediated triplet Dexter coupling. The Dexter coupling is exponentially sensitive to donor–acceptor distance and to bridge structure, suggesting that these EnT rates and their directionality may be manipulated by the bridge structure. As with bridge-mediated electron and hole transfer, control can be realized by using pathway interference effects, bridge energetics, and through-bond/through-space coupling trade-offs. The theory enables an atomic-level description for the origins of Dexter coupling, a necessary step toward controlling Dexter coupling interactions in a wide range of systems of current interest in energy science and molecular biophysics.

The most significant result of the Dexter pathway analysis is the demonstration that virtual bridge-exciton intermediate states (Fig. 1, center) can dominate the EnT coupling for long bridges and low tunneling-energy bridges. This BE-mediated coupling, and thus the Dexter coupling, cannot be expressed as a simple product of electron and hole donor-to-acceptor tunneling steps. Indeed, Curutchet and Voityuk’s studies of Dexter couplings through solvent found Dexter decay exponents to be smaller than the sum of the electron- and hole-mediated superexchange coupling decay exponents (26). The coupling pathway dissections introduced here are sufficiently general to enable the further development of structure–function relations for Dexter energy-transfer interactions.

Pathway Analysis

The full CIS Hamiltonian $\widehat{H}$ of the system in the local NLMO representation is

$$\langle i,x|\widehat{H}|j,y\rangle ={\delta }_{i,j}{F}_{x,y}-{\delta }_{x,y}{F}_{i,j}-\left(ij|xy\right).$$ [S1]

To proceed with the Löwdin projection method we write the identity operator in the $|i,x\rangle$ basis as a sum of projection operators, $\widehat{I}=\widehat{P}+\widehat{Q},$ where

$$\widehat{P}=|d,d*\rangle \langle d,d*|+|a,a*\rangle \langle a,a*|$$ [S2]

and $\widehat{Q}={\widehat{Q}}_1+{\widehat{Q}}_2,$ with

$${\widehat{Q}}_1={\widehat{Q}}_{db*}+{\widehat{Q}}_{bd*}+{\widehat{Q}}_{ba*}+{\widehat{Q}}_{ab*},$$ [S3]

$${\widehat{Q}}_2={\widehat{Q}}_{da*}+{\widehat{Q}}_{ad*}+{\widehat{Q}}_{bb*}.$$ [S4]

In the equation above the ${\widehat{Q}}_K$ are projection operators for the bridging subspaces of Fig. 1 (main text); e.g., ${\widehat{Q}}_{db\ast }={\displaystyle {\sum }_n|d,b_n^{*}\rangle \langle d,b_n^{*}|},$ ${\widehat{Q}}_{bb\ast }={\displaystyle {\sum }_{n,m}|b_n,b_m^{*}\rangle \langle b_n,b_m^{*}|},$ etc.

From the above definitions, and using the projection technique, we can obtain a GF expression ($T_{\text{tr}}$) for the splitting-derived total EnT coupling ($V_{\text{tr}}$). This is done by deriving an effective two-state Hamiltonian ${\widehat{H}}^{\text{ef}}$ defined on the subspace $\widehat{P}$ of $|d,d*\rangle$ with $|a,a*\rangle .$ The off-diagonal matrix element ($|d,d*\rangle$-to-$|a,a*\rangle$) of ${\widehat{H}}^{\text{ef}}$ is $T_{\text{tr}};$ i.e.,

$$T_{\text{tr}}=\langle d,d*|{\widehat{H}}^{\text{ef}}\left(E_t\right)|a,a*\rangle ;\hspace{1em}\widehat{P}{\widehat{H}}^{\text{ef}}\left(E_t\right)\widehat{P}=\widehat{P}\widehat{H}\widehat{P}+\widehat{P}\widehat{H}\widehat{Q}\widehat{\mathcal{G}}\left(E_t\right)\widehat{Q}\widehat{H}\widehat{P},$$ [S5]

where the GF $\widehat{\mathcal{G}}\left(E_t\right)={\left[E_t\widehat{Q}-\widehat{Q}\widehat{H}\widehat{Q}\right]}^{-1}$ is infinite order in all matrix elements of $\widehat{Q}\widehat{H}\widehat{Q}.$ Here $E_t$ is the tunneling energy; i.e., $E=E_t^{\left(0\right)},$ where $E_t^{\left(0\right)}=\langle d,d*|\widehat{H}|d,d*\rangle =\langle a,a*|\widehat{H}|a,a*\rangle$ as a first approximation. $E_t$ can be improved iteratively, e.g., $E_t^{\left(1\right)}=\left(\langle d,d*|{\widehat{H}}^{\text{ef}}\left(E_t^{\left(0\right)}\right)|d,d*\rangle +\langle a,a*|{\widehat{H}}^{\text{ef}}\left(E_t^{\left(0\right)}\right)|a,a*\rangle \right)/2$ (7, 31), in which case the above expression for $T_{\text{tr}}$ also becomes infinite order in all matrix elements of $\widehat{P}\widehat{H}\widehat{Q}.$ With the iterative readjustment of $E_t,$ Eq. S5 can reproduce the value of $V_{\text{tr}}$ in the tunneling limit.

The Löwdin projection expression $T_{\text{tr}}^{\left(\text{be}\right)}$ for the splitting-derived $V_{\text{tr}}^{\left(\text{be}\right)}$ is obtained by an equation similar to Eq. S5 where $\widehat{H}$ is replaced by ${\widehat{H}}^{\left(\text{be}\right)},$ the CIS Hamiltonian in the $|i,x\rangle$ representation with DAE states $|d,a*\rangle$ and $|a,d*\rangle$ deleted. Therefore

$$T_{\text{tr}}^{\left(\text{be}\right)}=\langle d,d*|{\widehat{H}}_{\text{be}}^{\text{ef}}\left(E_t\right)|a,a*\rangle ;\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\widehat{P}{\widehat{H}}_{\text{be}}^{\text{ef}}\left(E_t\right)\widehat{P}=\widehat{P}{\widehat{H}}^{\left(\text{be}\right)}\widehat{P}+\widehat{P}{\widehat{H}}^{\left(be\right)}\widehat{Q}{\left[E_t\widehat{Q}-\widehat{Q}{\widehat{H}}^{\left(\text{be}\right)}\widehat{Q}\right]}^{-1}{\widehat{H}}^{\left(be\right)}\widehat{Q}\widehat{P}.$$ [S6]

Similarly, the Löwdin projection expression $T_{\text{tr}}^{\left(\text{dae}\right)}$ for the splitting-derived $V_{\text{tr}}^{\left(\text{dae}\right)}$ is

$$T_{\text{tr}}^{\left(\text{dae}\right)}=\langle d,d*|{\widehat{H}}_{\text{dae}}^{\text{ef}}\left(E_t\right)|a,a*\rangle ;\hspace{0.17em}\widehat{P}{\widehat{H}}_{\text{dae}}^{\text{ef}}\left(E_t\right)\widehat{P}=\widehat{P}{\widehat{H}}^{\left(\text{dae}\right)}\widehat{P}+\widehat{P}{\widehat{H}}^{\left(dae\right)}\widehat{Q}{\left[E_t\widehat{Q}-\widehat{Q}{\widehat{H}}^{\left(\text{dae}\right)}\widehat{Q}\right]}^{-1}{\widehat{H}}^{\left(dae\right)}\widehat{Q}\widehat{P},$$ [S7]

where ${\widehat{H}}^{\left(\text{dae}\right)}$ is the CIS Hamiltonian in the $|i,x\rangle$ representation with all BE states $|b_n,b_m^{*}\rangle$ deleted.

To derive single particle pathway contributions to the EnT coupling, we define a Hamiltonian operator without pure exchange $\left(ij|xy\right)$ interactions as

$${\widehat{H}}^{\left(\text{ne}\right)}={\widehat{h}}^{\left(\text{di}\right)}+{\widehat{V}}^{\left(1p\right)},$$ [S8]

where ${\widehat{h}}^{\left(\text{di}\right)}$ is the diagonal part and ${\widehat{V}}^{\left(1p\right)}={\widehat{V}}^e+{\widehat{V}}^h$ is the off-diagonal part. The matrix elements of the diagonal Hamiltonian are given by

$$\langle i,x\left|{\widehat{h}}^{\left(\mathit{di}\right)}\right|i,x\rangle =F_{x,x}-F_{i,i}-\left(ii|xx\right)$$ [S9]

(Eq. 5 of main text). The matrix elements of the off-diagonal Hamiltonian ${\widehat{V}}^{\left(1p\right)}$ are given by the electron or hole transfer terms

$$\langle i,x|{\widehat{V}}^e|j,y\rangle ={\delta }_{i,j}{F}_{x,y},\hspace{1em}\langle i,x|V^h|j,y\rangle =-{\delta }_{x,y}{F}_{i,j}.$$ [S10]

The exact (spitting-derived) $V_{\text{tr}\left(\text{ne}\right)},$ $V_{\text{tr}\left(\text{ne}\right)}^{\left(\text{dae}\right)},$ and $V_{\text{tr}\left(\text{ne}\right)}^{\left(\text{be}\right)}$ are computed from diagonalization of ${\widehat{H}}^{\left(\text{ne}\right)}$ [by analogy to $V_{\text{tr}},$ $V_{\text{tr}}^{\left(\text{dae}\right)},$ and $V_{\text{tr}}^{\left(\text{be}\right)}$]. We obtain GF expressions $T_{\text{tr}\left(\text{ne}\right)},$ $T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{dae}\right)},$ and $T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{be}\right)}$ for $V_{\text{tr}\left(\text{ne}\right)},$ $V_{\text{tr}\left(\text{ne}\right)}^{\left(\text{dae}\right)},$ and $V_{\text{tr}\left(\text{ne}\right)}^{\left(\text{be}\right)}.$

Replacing $\widehat{H}$ by ${\widehat{H}}^{\left(\text{ne}\right)}$ in Eq. S5 gives

$$T_{\text{tr}\left(\text{ne}\right)}\left(E_t\right)=\langle d,d*|{\widehat{H}}^{\left(\text{ne}\right)}|a,a*\rangle +\langle d,d*|{\widehat{H}}^{\left(\text{ne}\right)}\widehat{Q}{\widehat{\mathcal{G}}}^{\left(\text{ne}\right)}\left(E_t\right)\widehat{Q}{\widehat{H}}^{\left(\text{ne}\right)}|a,a*\rangle ,$$ [S11]

where the GF ${\widehat{\mathcal{G}}}^{\left(\text{ne}\right)}\left(E_t\right)={\left[E_t\widehat{Q}-\widehat{Q}{\widehat{H}}^{\left(\text{ne}\right)}\widehat{Q}\right]}^{-1}.$ To proceed further, we ignore the direct matrix element $\langle d,d*|{\widehat{H}}^{\left(\text{ne}\right)}|a,a*\rangle ,$ which is zero for long-distance EnT. We then get

$$T_{\text{tr}\left(\text{ne}\right)}\left(E_t\right)=\langle d,d*|{\widehat{V}}^{\left(1p\right)}\widehat{Q}{\widehat{\mathcal{G}}}^{\left(\text{ne}\right)}\left(E_t\right)\widehat{Q}{\widehat{V}}^{\left(1p\right)}|a,a*\rangle .$$ [S12]

Using again the projection technique for ${\widehat{Q}}_1{\widehat{\mathcal{G}}}^{\left(\text{ne}\right)}\left(E_t\right){\widehat{Q}}_1$ in Eq. S12,

$${\widehat{Q}}_1\widehat{\mathcal{G}}\left(E_t\right){\widehat{Q}}_1={\left[E{\widehat{Q}}_1-{\widehat{Q}}_1{\widehat{H}}^{\left(\text{ne}\right)}{\widehat{Q}}_1-{\widehat{Q}}_1\widehat{R}\left(E_t\right){\widehat{Q}}_1\right]}^{-1}.$$ [S13]

In the equation above ${\widehat{Q}}_1{\widehat{H}}^{\left(\text{ne}\right)}{\widehat{Q}}_1={\widehat{H}}_{db*}^{\left(\text{ne}\right)}+{\widehat{H}}_{bd*}^{\left(\text{ne}\right)}+{\widehat{H}}_{ba*}^{\left(\text{ne}\right)}+{\widehat{H}}_{ab*}^{\left(\text{ne}\right)},$ where ${\widehat{H}}_K^{\left(\text{ne}\right)}={\widehat{Q}}_K{\widehat{H}}^{\left(\text{ne}\right)}{\widehat{Q}}_K$ denotes the full Hamiltonians for these subspaces [${\widehat{H}}^{\left(\text{ne}\right)}$ is given in Eq. S8]. ${\widehat{Q}}_1\widehat{R}\left(E\right){\widehat{Q}}_1$ is a resolvent operator given

$${\widehat{Q}}_1\widehat{R}\left(E\right){\widehat{Q}}_1={\widehat{Q}}_1{\widehat{V}}^{\left(1e\right)}{\widehat{Q}}_2{\left[E{\widehat{Q}}_2-{\widehat{Q}}_2{\widehat{H}}^{\left(\text{ne}\right)}{\widehat{Q}}_2\right]}^{-1}{\widehat{Q}}_2{\widehat{V}}^{\left(1e\right)}{\widehat{Q}}_1$$ [S14]

that can be written as a sum of two resolvent operators ${\widehat{R}}^{\left(\text{dae}\right)}$ and ${\widehat{R}}^{\left(\text{be}\right)}$ describing effective couplings between the $\left\{|d,b_n^{*}\rangle \right\}$ $\left(\left\{|b_n,d*\rangle \right\}\right)$ and $\left\{|b_n,a*\rangle \right\}$ $\left(\left\{|a,b_n^{*}\rangle \right\}\right)$ subspaces mediated by the DAE ($\text{dae}$) and BE ($\text{be}$), respectively.

In summary, the GF expression $T_{\text{tr}\left(\text{ne}\right)}$ for the splitting-derived EnT coupling $V_{\text{tr}\left(\text{ne}\right)}$ is

$$T_{\text{tr}\left(\text{ne}\right)}\left(E_t\right)=\langle d,d*|\left({\widehat{V}}^e{\widehat{Q}}_{db*}+{\widehat{V}}^h{\widehat{Q}}_{bd*}\right){\widehat{\mathcal{G}}}^{\left(\text{ne}\right)}\left(E_t\right)({\widehat{Q}}_{a{b}^{\ast }}{\widehat{V}}^e+{\widehat{Q}}_{b{a}^{\ast }}{\widehat{V}}^h)|a,a*\rangle ,$$ [S15]

where $\langle i,x|{\widehat{V}}^e|j,y\rangle ={\delta }_{ij}{F}_{x,y},$ $\langle i,x|{\widehat{V}}^h|j,y\rangle =-{\delta }_{x,y}{F}_{i,j},$ $E_t$ is the tunneling energy, and

$$\begin{array}{l}{\widehat{\mathcal{G}}}^{\left(\text{ne}\right)}\left(E_t\right)={\left[E_t\left({\widehat{Q}}_{db\ast }+{\widehat{Q}}_{bd\ast }+{\widehat{Q}}_{ba\ast }+{\widehat{Q}}_{ab\ast }\right)-\left({\widehat{H}}_{db\ast }^{\left(\text{ne}\right)}+{\widehat{H}}_{bd\ast }^{\left(\text{ne}\right)}+{\widehat{H}}_{ba\ast }^{\left(\text{ne}\right)}+{\widehat{H}}_{ab\ast }^{\left(\text{ne}\right)}+{\widehat{R}}^{\left(\text{dae}\right)}+{\widehat{R}}^{\left(\text{be}\right)}\right)\right]}^{-1}.\end{array}$$ [S16]

${\widehat{R}}^{\left(\text{dae}\right)}$ and ${\widehat{R}}^{\left(\text{be}\right)}$ are resolvent operators that describe effective couplings between the $\left\{|d,b_n^{*}\rangle \right\}$ $\left(\left\{|b_n,d*\rangle \right\}\right)$ and $\left\{|b_n,a*\rangle \right\}$ $\left(\left\{|a,b_n^{*}\rangle \right\}\right)$ subspaces mediated by the DAE (dae: $|d,a*\rangle$ and $|a,d*\rangle$) and BE (be: $\left\{|b_n,b_m^{*}\rangle \right\}$), respectively. The resolvents are

$$\begin{array}{l}{\widehat{R}}^{\left(\text{dae}\right)}\left(E_t\right)={\widehat{Q}}_{db*}{\widehat{V}}^e{\widehat{Q}}_{da*}{\widehat{G}}_{da*}\left(E_t\right){\widehat{Q}}_{da*}{\widehat{V}}^h{\widehat{Q}}_{ba*}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\widehat{Q}}_{bd*}{\widehat{V}}^h{\widehat{Q}}_{ad*}{\widehat{G}}_{ad*}\left(E_t\right){\widehat{Q}}_{ad*}{\widehat{V}}^e{\widehat{Q}}_{ab*},\end{array}$$ [S17]

and

$$\begin{array}{l}{\widehat{R}}^{\left(\text{be}\right)}\left(E_t\right)={\widehat{Q}}_{db*}{\widehat{V}}^h{\widehat{Q}}_{bb*}{\widehat{G}}_{bb*}\left(E_t\right){\widehat{Q}}_{bb*}{\widehat{V}}^e{\widehat{Q}}_{ba*}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.5em}\hspace{0.5em}+{\widehat{Q}}_{bd*}{\widehat{V}}^e{\widehat{Q}}_{bb*}{\widehat{G}}_{bb*}\left(E_t\right){\widehat{Q}}_{bb*}{\widehat{V}}^h{\widehat{Q}}_{ab*}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.5em}\hspace{0.5em}+{\widehat{Q}}_{db*}{\widehat{V}}^h{\widehat{Q}}_{bb*}{\widehat{G}}_{bb*}\left(E_t\right){\widehat{Q}}_{bb*}{\widehat{V}}^h{\widehat{Q}}_{ab*}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.5em}\hspace{0.5em}\hspace{0.5em}+{\widehat{Q}}_{bd*}{\widehat{V}}^e{\widehat{Q}}_{bb*}{\widehat{G}}_{bb*}\left(E_t\right){\widehat{Q}}_{bb*}{\widehat{V}}^e{\widehat{Q}}_{ba*},\end{array}$$ [S18]

where ${\widehat{G}}_K\left(E_t\right)={\left[E_t{\widehat{Q}}_K-{\widehat{Q}}_K{\widehat{H}}^{\left(\text{ne}\right)}{\widehat{Q}}_K\right]}^{-1}$ are the GFs for the subspaces ${\widehat{Q}}_K.$

From Eq. S15, we can obtain an exact expression for the effective EnT coupling mediated by the DAE (and not the BE) denoted $T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{dae}\right)}$ if we remove ${\widehat{R}}^{\left(\text{be}\right)}$ (the bridge-exciton contribution) from $\widehat{\mathcal{G}}$ in Eq. S16. Namely,

$$T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{dae}\right)}\equiv \langle d,d*|\left({\widehat{V}}^e{\widehat{Q}}_{db*}+{\widehat{V}}^h{\widehat{Q}}_{bd*}\right){\widehat{\mathcal{G}}}^{\left(\text{dae}\right)}\left(E_t\right)\left({\widehat{Q}}_{a{b}^{\ast }}{\widehat{V}}^e+{\widehat{Q}}_{b{a}^{\ast }}{\widehat{V}}^h\right)|a,a*\rangle ,$$ [S19]

where

$${\widehat{\mathcal{G}}}^{\left(\text{dae}\right)}\left(E_t\right)={\left[E_t\left({\widehat{Q}}_{db\ast }+{\widehat{Q}}_{bd\ast }+{\widehat{Q}}_{ba\ast }+{\widehat{Q}}_{ab\ast }\right)-\left({\widehat{H}}_{db\ast }^{\left(\text{ne}\right)}+{\widehat{H}}_{bd\ast }^{\left(\text{ne}\right)}+{\widehat{H}}_{ba\ast }^{\left(\text{ne}\right)}+{\widehat{H}}_{ab\ast }^{\left(\text{ne}\right)}+{\widehat{R}}^{\left(\text{dae}\right)}\right)\right]}^{-1}.$$ [S20]

Similarly, we can obtain an exact expression for the EnT coupling mediated by BE (and not DAE) denoted $T_{tr\left(ne\right)}^{\left(be\right)}$ if we remove the DAE contribution $\left[{\widehat{R}}^{\left(\text{dae}\right)}\right]$ from ${\widehat{\mathcal{G}}}^{\left(\text{ne}\right)}$ in Eq. S16; i.e.,

$$T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{be}\right)}\equiv \langle d,d*|\left({\widehat{V}}^e{\widehat{Q}}_{db\ast }+{\widehat{V}}^h{\widehat{Q}}_{bd\ast }\right){\widehat{\mathcal{G}}}^{\left(\text{be}\right)}\left(E_t\right)\left({\widehat{Q}}_{a{b}^{\ast }}{\widehat{V}}^e+{\widehat{Q}}_{b{a}^{\ast }}{\widehat{V}}^h\right)|a,a*\rangle ,$$ [S21]

where

$${\widehat{\mathcal{G}}}^{\left(\text{be}\right)}\left(E_t\right)={\left[E_t\left({\widehat{Q}}_{db\ast }+{\widehat{Q}}_{bd\ast }+{\widehat{Q}}_{ba\ast }+{\widehat{Q}}_{ab\ast }\right)-\left({\widehat{H}}_{db\ast }^{\left(\text{ne}\right)}+{\widehat{H}}_{bd\ast }^{\left(\text{ne}\right)}+{\widehat{H}}_{ba\ast }^{\left(\text{ne}\right)}+{\widehat{H}}_{ab\ast }^{\left(\text{ne}\right)}+{\widehat{R}}^{\left(\text{be}\right)}\right)\right]}^{-1}.$$ [S22]

To simplify the expression for $T_{\text{tr}\left(\text{ne}\right)}$ we write ${\mathcal{G}}^{\left(\text{ne}\right)}$ in Eq. S16 as

$$\begin{array}{c}{\widehat{\mathcal{G}}}^{\left(\text{ne}\right)}\left(E_t\right)={\left[{\widehat{G}}^{-1}\left(E_t\right)-\left({\widehat{R}}^{\left(\text{dae}\right)}+{\widehat{R}}^{\left(\text{be}\right)}\right)\right]}^{-1},\\ {\widehat{G}}^{-1}\left(E_t\right)={\widehat{G}}_{db\ast }^{-1}\left(E_t\right)+{\widehat{G}}_{bd\ast }^{-1}\left(E_t\right)+{\widehat{G}}_{ba\ast }^{-1}\left(E_t\right)+{\widehat{G}}_{ab\ast }^{-1}\left(E_t\right),\end{array}$$ [S23]

where ${\widehat{G}}_K\left(E_t\right)={\left[E_t{\widehat{Q}}_K-{\widehat{Q}}_K{\widehat{H}}^{\left(\text{ne}\right)}{\widehat{Q}}_K\right]}^{-1}$ are the GFs for the subspaces ${\widehat{Q}}_K.$ To first order in ${\widehat{R}}^{\left(\text{dae}\right)}+{\widehat{R}}^{\left(\text{be}\right)},$ ${\widehat{\mathcal{G}}}^{\left(\text{ne}\right)}\left(E_t\right)\simeq \widehat{G}\left(E_t\right)+\widehat{G}\left(E_t\right)\left({\widehat{R}}^{\left(\text{dae}\right)}+{\widehat{R}}^{\left(\text{be}\right)}\right)\widehat{G}\left(E_t\right).$ Substituting this approximate equation into Eq. S15 gives

$$T_{\text{tr}\left(\text{ne}\right)}\simeq T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{dae}\right)}+T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{be}\right)},$$ [S24]

where

$$\begin{array}{l}{T}_{tr\left(ne\right)}^{\left(dae\right)}\simeq \frac{\langle dd*|{\widehat{V}}^e{\widehat{G}}_{db\ast }{\widehat{V}}^e|da*\rangle \langle da*|{\widehat{V}}^h{\widehat{G}}_{ba\ast }{\widehat{V}}^h|aa*\rangle }{E_t-E_{da*}}\\ \hspace{1em}\hspace{1em}\hspace{1em}+\frac{\langle dd*|{\widehat{V}}^h{\widehat{G}}_{bd\ast }{\widehat{V}}^h|ad*\rangle \langle ad*|{\widehat{V}}^e{\widehat{G}}_{ab\ast }{\widehat{V}}^e|aa*\rangle }{E_t-E_{ad*}}\end{array}$$ [S25]

is the lowest-order [in ${\widehat{R}}^{\left(dae\right)}$] expression for the D-A exciton contribution to $T_{tr\left(ne\right)}$ and

$$T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{be}\right)}\simeq \langle dd*|{\widehat{V}}^e{\widehat{G}}_{db\ast }{\widehat{V}}^h{\widehat{G}}_{bb\ast }{\widehat{V}}^e{\widehat{G}}_{ba\ast }{\widehat{V}}^h|aa*\rangle +\langle dd*|{\widehat{V}}^h{\widehat{G}}_{bd\ast }{\widehat{V}}^e{\widehat{G}}_{bb\ast }{\widehat{V}}^h{\widehat{G}}_{ab\ast }{\widehat{V}}^e|aa*\rangle +\langle dd*|{\widehat{V}}^e{\widehat{G}}_{db\ast }{\widehat{V}}^h{\widehat{G}}_{bb\ast }{\widehat{V}}^h{\widehat{G}}_{ab\ast }{\widehat{V}}^e|aa*\rangle +\langle dd*|{\widehat{V}}^h{\widehat{G}}_{bd\ast }{\widehat{V}}^e{\widehat{G}}_{bb\ast }{\widehat{V}}^e{\widehat{G}}_{ba\ast }{\widehat{V}}^h|aa*\rangle$$ [S26]

is the lowest-order [in ${\widehat{R}}^{\left(\text{be}\right)}$] expression for the bridge exciton contribution to $T_{tr}^{\left(ne\right)}.$

The terms $\langle dd*|{\widehat{V}}^e{\widehat{G}}_{db\ast }{\widehat{V}}^e|da*\rangle$ and $\langle ad*|{\widehat{V}}^e{\widehat{G}}_{ab\ast }{\widehat{V}}^e|aa*\rangle$ in the expression for $T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{dae}\right)}$ are the bridge-mediated electron tunneling matrix elements. Similarly, $\langle da*|{\widehat{V}}^h{\widehat{G}}_{ba\ast }{\widehat{V}}^h|aa*\rangle$ and $\langle dd*|{\widehat{V}}^h{\widehat{G}}_{bd*}{\widehat{V}}^h|ad*\rangle$ are the bridge-mediated hole tunneling matrix elements. Strictly speaking, these matrix elements describe excited-state bridge-mediated electron and hole transfer DA couplings, rather than electron- or hole-shift DA couplings.

For the compounds under study and for all energy gaps mentioned in the main text (Figs. 2 and 3), we find that $T_{\text{tr}},$ $T_{\text{tr}}^{\left(\text{dae}\right)},$ and $T_{\text{tr}}^{\left(\text{be}\right)}$ approximate well the splitting-derived $V_{\text{tr}},$ $V_{\text{tr}}^{\left(\text{dae}\right)},$ and $V_{\text{tr}}^{\left(\text{be}\right)}$ even within one iteration with $E_t=E_t^{\left(0\right)}$ or $E_t^{\left(1\right)}=\left(\langle d,d*|{\widehat{H}}^{\text{ef}}\left(E_t^{\left(0\right)}\right)|d,d*\rangle +\langle a,a*|{\widehat{H}}^{\text{ef}}\left(E_t^{\left(0\right)}\right)|a,a*\rangle \right)/2.$ This also holds for the $T_{\text{tr}\left(\text{ne}\right)},$ $V_{tr\left(ne\right)}^{\left(be\right)},$ and $T_{\text{tr}\left(\text{ne}\right)}^{\left(\text{be}\right)}$ to the splitting-derived $V_{\text{tr}\left(\text{ne}\right)},$ $V_{\text{tr}\left(\text{ne}\right)}^{\left(\text{dae}\right)},$ and $V_{tr(ne)}^{\left(\mathit{be}\right)}$ values. Examples are given in Tables S5–S8.

Tables S1–S4 are Dexter coupling computations on the folded alkane systems (Fig. 2B) and the polynorbornyl bridged systems Fig. 2C).