Bidirectional prefrontal-hippocampal interactions support context-guided memory

Abstract

We compared the dynamics of hippocampal and prefrontal interactions in rats as they used spatial contexts to guide the retrieval of object memories. Upon context entry, functional connectivity analysis indicated a flow of contextual information from the hippocampus to prefrontal cortex. Conversely, upon the onset of object sampling, the direction of information flow reversed, consistent with prefrontal control over the retrieval of context-appropriate hippocampal memory representations.

The hippocampus is critical to memory for events within the spatial and temporal context in which they occur¹, and the prefrontal cortex supports the cognitive control of memory by suppressing context-inappropriate memories^2–5. The prefrontal cortex and hippocampus interact via oscillatory synchronization in the theta band^6–11 and here we explored the functional dynamics of this interaction in rats performing a context-guided memory task that is dependent on both areas⁵.

On each trial animals explored one of two distinct spatial contexts (1 & 2; the context exploration period), then were presented with and sampled two objects (A & B; the object sampling period; Fig. 1). In Context 1, object A was rewarded and not object B, whereas in Context 2, B was rewarded, not A. We recorded local field potentials (LFPs) in the dorsal (dHPC) and ventral (vHPC) hippocampus and the medial prefrontal area (mPFC) and identified maximal PFC-HPC coherence at 7–12 Hz during the initial second of both the context exploration and object sampling periods (Supplementary Fig. 1). During each period, overall local neuronal activity was phased locked to theta in each area (context exploration: 172 mPFC cells, Rayleigh test z = 40.51, p = 2.52e–18; 130 dHPC cells, z = 417.49, p = 3.17e–182; 60 vHPC cells, z = 39.15, p = 9.40e–18; object sampling: 175 mPFC cells, z = 23.07, p = 9.49e–11; 109 dHPC cells, z = 7.45e–140; 34 vHPC cells, z= 2.72e–4), and in each area substantial proportions of individual active (at least 50 spikes) cells were phase-locked to local theta during context exploration (mPFC 30.23%, dHPC 73.08%, vHPC 71.51%) and during object sampling (mPFC 38.29%, dHPC 47.71%, vHPC 43.4%). Also, the firing patterns of individual neurons with task-relevant activity was well correlated with theta during context exploration and during object sampling, confirming that each LFP recording reflects local oscillations of relevant neural activity at each trial phase (Supplementary Table 1; Buzsaki et al.¹²).

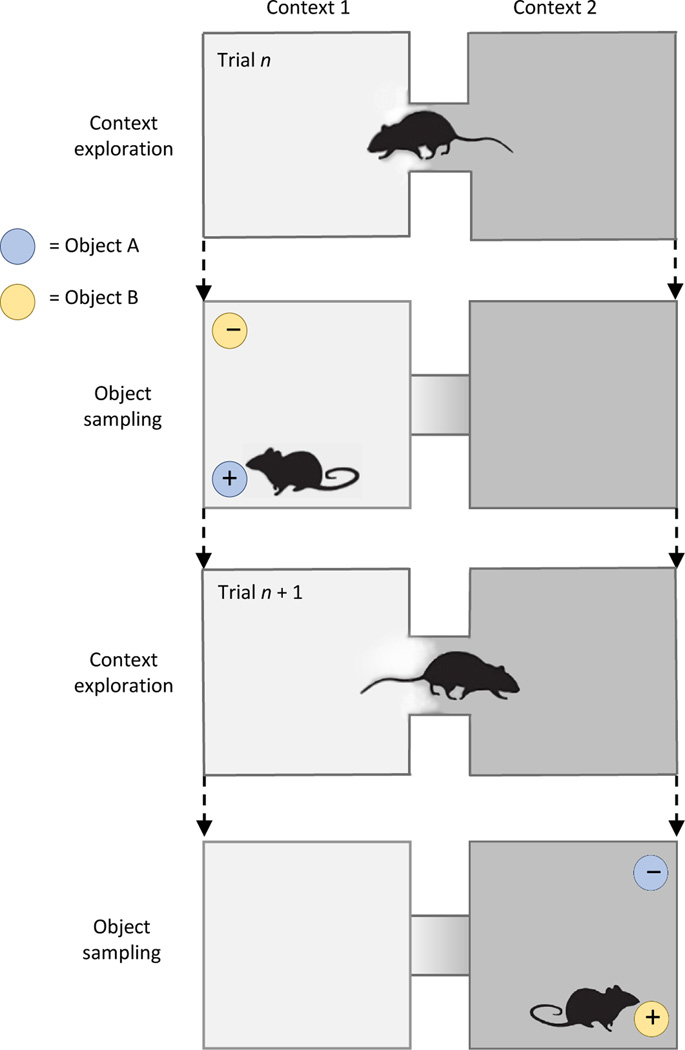
Figure 1.

The context-guided memory task and model of functional hippocampal– prefrontal pathways. + = rewarded, − = non-rewarded.

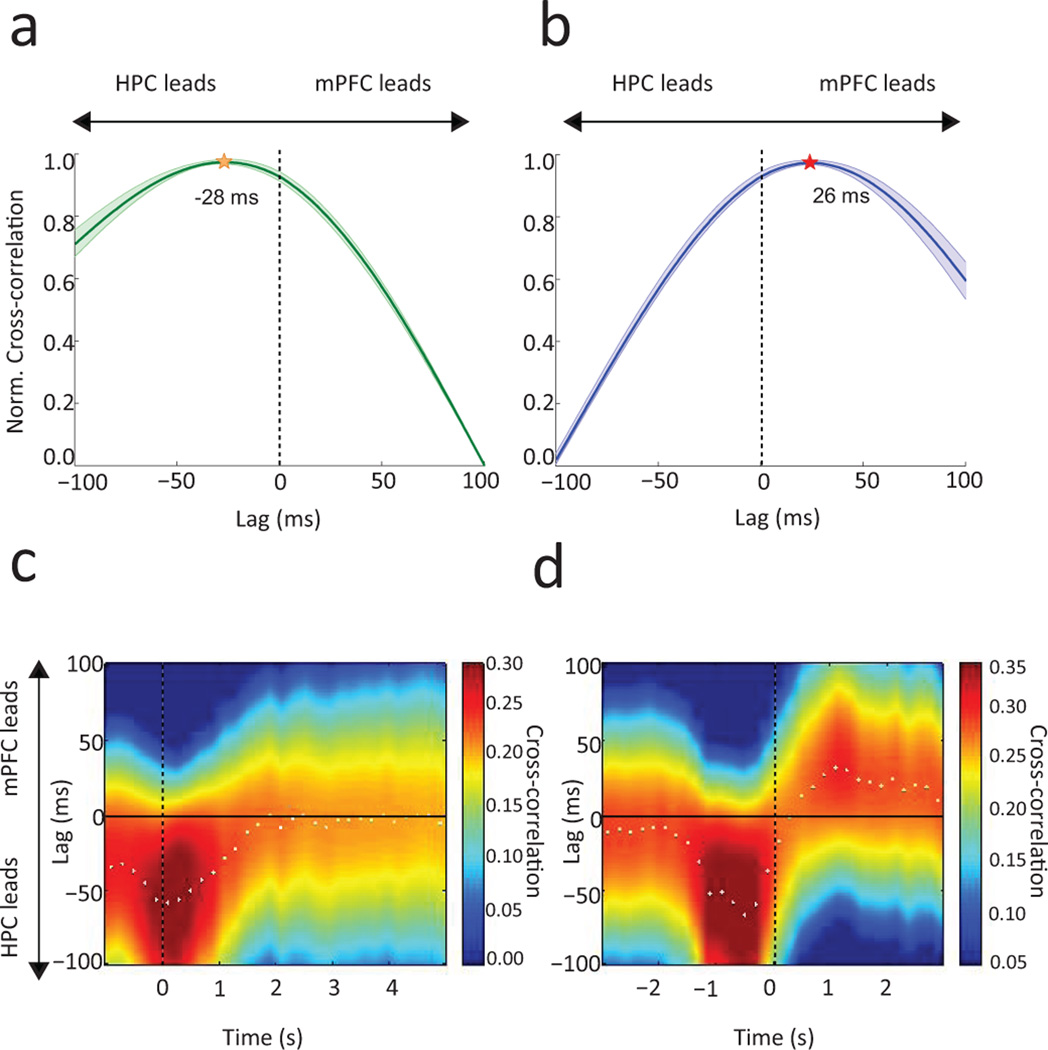
Functional connectivity was characterized by the maximum theta-amplitude cross correlation across serial temporal shifts, indicating the direction and timing of communication from one area to another¹³. In well-trained animals, during the initial 1 s of context exploration, theta in both dHPC and vHPC led that in mPFC (dHPC: 28 ± 7 ms, z₁₈ = 4.95, p = 1.29e⁻⁴; vHPC: 23 ± 8.06 ms, W₁₂ = 0, p = 0.0011; dHPC-to-mPFC versus vHPC-to-mPFC leads: 5 ± 7.41 ms, z₃₀ = 0.33, p = 0.7358). The overall HPC lead significantly differed from zero (28 ± 5.40 ms, z₂₁ = 4.02, p = 5.95e⁻⁵; Fig. 2a) and was observed in each subject (Supplementary Fig. 2a & Supplementary Table 2). Functional connectivity reversed during the initial 1 s of object sampling, such that mPFC theta led that in dHPC by 25 ± 4.26 ms (z₁₈ = 3.63, p = 2.74e⁻⁴) and vHPC by 30 ± 6.25 ms (W₁₂ = 78, p = 2.55e⁻⁴; dHPC vs vHPC lags: 5 ± 4.60 ms, z₃₀ = 0.78, p = 0.5671). The overall mPFC lead over HPC was significantly above zero (26 ± 4.55 ms, z₂₁ = 3.93, p = 8.52e⁻⁵; Fig. 2b) and was observed in each subject (Supplementary Fig. 2b & Supplementary Table 2). Furthermore, the switch in direction was significant in the overall average (z₄₂ = 3.92, p = 8.83e⁻⁵) and observed for both dHPC and vHPC in each subject (Supplementary Table 2). We confirmed the main results using Granger causality analysis (Supplementary Fig. 3). Notably, a coherence peak between PFC and HPC was also observed at 2–5 Hz (Supplementary Fig. 1c) but there was no significant lag/lead in this band during either context exploration or object sampling (Context: PFC leads by 6.10 ± 7.51ms, Wilcoxon signed-rank, z₂₁ =1.02, p = 0.3051; Object: HPC leads by 8.00 ± 10.57, z₂₁ = −0.80, p = 0.4206). Finally, an additional analysis of functional connectivity along the long axis of the hippocampus in animals with electrodes at both sites (n = 3) showed that dHPC leads vHPC by an average of 18.44 ± 5.84 ms during context exploration (Wilcoxon signed-rank, W₉ = 1, p = 0.0078).

Figure 2.

Normalized correlations between instantaneous theta amplitude across a range of shifts between LFPs recorded in hippocampus (HPC) and prefrontal cortex (mPFC). Group average lag/lead relations during accurate performance following learning in the context exploration (a,c) and object sampling (b,d) periods. (a,b) Correlations between LFP amplitude patterns in HPC and mPFC over a series of temporal shifts for each trial phase. Shading indicates S.E.M. across sessions (n=21). (a) During context exploration the HPC lead significantly differed from zero (Wilcoxon signed-rank test, z₂₁ = 4.02, p = 5.95e⁻⁵). (b) During object sampling the direction of functional connectivity reversed (z₄₂ = 3.92, p = 8.83e⁻⁵) such that PFC led HPC (z₂₁ = 3.93, p = 8.52e⁻⁵). (c–d) Sliding 1 s correlation windows advanced at 200 ms temporal shifts throughout the occurrence each trial phase. Dotted line denotes (c) the moment of entry into a context and (d) the onset of object sampling. White dots indicate peak correlation for each window.

Importantly, PFC-HPC lag/lead relations were not correlated with movement speed during either context exploration of object sampling (Supplementary Fig. 4). Furthermore, during 1 s periods of immobility in context exploration when speed (17.1 ± 0.6 cm/s) did not differ from that observed during object sampling (17.5 ± 0.6 cm/s; Wilcoxon rank-sum, z₃₅₅₄ = 1.13, p = 0.8739), vHPC theta led that in mPFC by 15.0 +/− 5.4 ms W₁₂ = 4.5, p = 0.0039). Theta in dHPC did not lead or lag that in mPFC (lead = 8.0 +/− 7.09 ms, z₁₈ = 1.02, p = 0.3059) during these periods of immobility, but the vHPC lead over mPFC significantly differed from the opposite lead of mPFC over vHPC during object sampling (W₁₂ = 0, p =4.88e⁻⁴), confirming the switch in functional connectivity between context exploration and object sampling even when movement speeds are equivalently slow for both periods. These findings, combined with the observation that strong lag/leads are observed only during correct trials despite identical behavioral responses and equivalent movement speeds on error trials (see below), indicate that the switches in functional connectivity reflect differences in the cognitive processes engaged in these behaviors rather than a direct consequence of differences in motor patterns.

Additional analyses of these post-learning data using a sliding window of cross correlations showed that the HPC lead over mPFC was maximal at −400 to +600ms after context entry (Fig. 2c). As animals approached the objects HPC led again, then, just as object sampling began, the direction of communication flipped and mPFC maximally led HPC during the ensuing 500–1500 ms of object sampling (Fig. 2d).

Strong bidirectional connectivity between the hippocampus and prefrontal cortex predicted memory accuracy in trials performed as animals were learning the task, even when overt behavior was closely matched between correct trials and errors (see Online Methods). On correct trials, during context exploration, HPC led by 22 ± 9.13 ms (z₂₆ = 3.30, p = 9.56e⁻⁴) and during object sampling, mPFC led by 29 ± 6.35 ms (z₂₆ = 3.28, p = 0.0010), and each animal showed these directions of functional connectivity (Supplementary Fig. 2c–d & Supplementary Table 3), consistent with the findings at the end of training. On errors, differences between context exploration and object sampling were observed in each subject (Supplementary Table 3) but there was more variability in the peak lags/leads in both trial phases (Supplementary Fig. 2e–f) and there were no significant leads or lags in the group data (context: HPC lead 7 ± 10.30 ms; z₂₆ = 0.52, p = 0.5969; object: mPFC lead 11 ± 10.81 ms; z₂₆ =1.41, p = 0.1567).

These observations support a model of bidirectional interaction in which initially the hippocampus sends contextual information to prefrontal cortex, then prefrontal cortex guides successful retrieval of memories in the hippocampus⁵. Notably, the timing of communication in each direction is approximately one gamma cycle (22–30 ms; equivalent to 33–45Hz), thought to reflect local network processing^14,15. Thus, extending recent proposals^11,16–18, prefrontal-hippocampal communication may involve multiplexing sequential gamma informational “packets” within a theta-driven “carrier”, and these multiplexed communications are exchanged in both directions at a lead of one packet, perhaps via bidirectional multisynaptic pathways through the nucleus reuniens or perirhinal and lateral entorhinal cortex⁵. Consistent with multiplexing oscillations supporting memory, successful learning of this task is correlated with strong theta-gamma synchrony in the hippocampus¹⁹ as well as in human context-dependent memory²⁰.

Online Methods

Subjects

13 Male Long-Evans rats (Charles River, age = 6–18 months) weighing between 250–350 g were individually housed on 12 hr light/dark cycle and restricted to 85% of their ad libitum feeding body weight with ad libitum access to water during behavioral training. Seven rats were used in the LFP analyses and six were used to determine relations between spiking activity and local LFPs. All rats were trained and tested in the context-guided memory task during the light period of the cycle. Procedures were conducted in accordance to National Institutes of Health (NIH) and Boston University Institutional Animal Care and Use Committee (IACUC) standards. Sample sizes for each condition of this study are similar to those generally employed in the field (at least 4 rats for each dHPC-mPFC and vHPC-mPFC LFP comparison and 6 rats for each local spike-phase comparison) and were not predetermined by a sample size calculation.

Surgical preparation

Anesthesia was induced by 4% isoflurane inhalation and was maintained at 1.5 – 2% throughout surgery. For LFP recording at multiple sites, single tungsten wire electrodes (50 µm) were implanted into mPFC (3.5 mm anterior, 0.75 mm lateral, 3.6 mm ventral with a 10 degree lateral-to-medial angle), dHPC (3 mm posterior, 2 mm lateral, 2.8 mm ventral) and vHPC (5.6 mm posterior, 5 mm lateral, 7.5 mm ventral, with a 10 degree medial to lateral angle). dHPC and vHPC electrodes were attached to micro-drives and were gradually lowered into the corresponding CA1 pyramidal layer over the course of 2 weeks post-surgery. For single neuron recording, head stages containing 12–24 independently movable tetrodes were aimed at one of the above locations. Each tetrode was composed of four 12.5 µm nichrome wires with the tips gold-plated to bring the impedance to 200 kΩ at 1 kHz. Two scull screws implanted overlying the cerebellum served as ground and reference. Procedures were conducted in accordance to National Institutes of Health (NIH) and Boston University Institutional Animal Care and Use Committee (IACUC) standards.

Behavioral training

The recordings from HPC and mPFC were acquired from rats as they performed a context-guided object-reward association task that required subjects to select one of two objects presented simultaneously within each of two distinctive spatial contexts differing in multiple features²¹ (Fig. 1). The objects consisted of identical terra cotta pots with unique digging media and odors. On each trial, the rats initially entered and explored one context (designated the context exploration period). Because the animals reliably explored the context only during the initial few seconds of this period, we focused our analyses on the initial 1 s of this period, except where noted. At the end of 10 s, the animal was constrained to the rear of the context using a manually placed divider while two objects were placed at the two forward corners of the context. Then the divider was removed and the animal was allowed to sample the objects. Animals were allowed to explore each object (designated the object sampling period) multiple times. When presented in Context 1, Object A was rewarded in either of the two positions, and Object B was not. When presented in Context 2, Object B was rewarded in either position, and Object A was not. Thus, subjects were required to use the current context to guide learning and retrieval of distinct context-dependent reward associations for the same objects. A trial ended when the animal eventually chose one of the objects by digging in the medium and retrieving the reward if it has made the correct choice or finding no reward on errors. Rats learned each of three context-guided object associations to an 80% correct performance criterion (requiring 3–4 100-trial training sessions), after which each rat further performed the same problem for 3 additional post-learning recording sessions (100 trials each). Data from post-learning and learning sessions were analyzed separately (see below). Position data was acquired by tracking light emitting diodes attached to the rat’s head stage using Cineplex Digital Capture System (Plexon), and behavioral sampling events were marked offline with Cineplex Editor (Plexon). Identification of behavioral flags was blind to trial types; identification of correct and error trials and analyses of neural data and statistics was automated.

Randomization

For each trial, the rewarded object position (left versus right) within a particular context was randomized. Each trial was randomly assigned to one of the two contexts, with constraints predetermining that 20% of all trials would repeat contextual conditions.

Electrophysiological Recordings

Local field potentials (LFPs) were recorded at 1000 Hz, while spiking activity (for phase-spike and selectivity index analyses) was captured at 400–8000 Hz and digitized to 40 kHz using a Multichannel Acquisition Processor (Plexon). Single clusters were manually isolated using Offline Sorter (Plexon) waveform dimensions (relative amplitudes across each wire, peak to valley difference, and waveform width). Identified units were screened for inter-spike intervals found to be shorter than the neuronal refractory period (< 2 ms).

Histological Procedures

Electrode tip lesions were generated by passing 40 µA current through each recording wire for 30 s or until the connection was severed. Rats then received an overdose of Euthasol and were perfused intracardially with 10% formalin phosphate following 0.9% saline. Brains were extracted and left in 30% sucrose solution for 48 hrs. Frozen coronal sections (40 µm) were collected from each relevant region and stained with cresyl violet. Electrode tip lesion locations were confirmed within mPFC (PL/ IL), dHPC, or vHPC²². Rats with successful placement of at least two electrode sites (n=7) were used in the LFP analyses, and all rats with single site tetrode recordings (n=6) contributed to data that determined relations between spiking activity and local LFPs.

LFP analysis

We initially analyzed LFP data on three 100 trial sessions for each well trained animal (91–100% correct performance in post-learning sessions) then subsequently also compared data collected during the course of learning (3–4 sessions for each animal) where there were substantial errors as well as correct trials (43–78% correct performance; see Supplementary Materials).

Power spectra and coherence between brain regions were determined using the Chronux toolbox multitaper functions using 3 tapers and a time-bandwidth product of 2 (http://www.chronux.org/²³). The trial-averaged multitaper frequency spectrum was calculated (mtspecgram.m) using a 500 ms window slid across the defined behavioral epoch in 10 ms increments. LFP coherence was calculated (coherencyc.m) across the first 1 s of each event.

To obtain an overall group measure of leads and lags, hippocampal and mPFC LFP signals spanning 1 s following context entry or arrival at an object were concatenated for each animal (n = 7) and each post-learning session (n = 3 per animal) composing a total of 21 sessions. These signals were then zero-phase filtered for the theta frequency (7–12 Hz) using a third-order Butterworth filter, converted to instantaneous amplitude signals by the Hilbert transform, and the mean amplitude was subtracted to eliminate each signal’s DC component. Pearson cross correlations were performed to compare values of hippocampal and mPFC amplitudes at 1 ms steps for the 1 s period; these correlations were performed over a +100 to −100 ms range of 1 ms temporal shifts between the signals¹³ (Fig. 2a,b). The r-values for each lag/lead relationship were normalized to the minimum and maximum values so that differences among individual subjects were minimized, and mean r-values across the 21 sessions were computed and visualized for each lag/lead (Fig. 2a,b). The distribution of correlations across lags/leads was examined to identify the lag or lead with the peak r-value for each session. A Wilcoxon Signed Rank test was performed on the sample of peak lags/leads (n=21) to verify that each distribution’s median differed significantly from zero. A paired Wilcoxon Rank Sum test was used to confirm that the difference between lags/leads during context exploration and item sampling reliably differed. Separate analyses were also performed on correct trials and on error trials during the earlier learning sessions.

The temporal dynamics of lag/lead relations during behavioral events were visualized by computing cross-correlations of theta amplitudes between hippocampal and mPFC LFP traces within 1000 ms data windows over 200 ms temporal shifts (Fig. 2c,d).

The same analyses were performed to compare lag/lead relations between LFPs in the dorsal and ventral hippocampus during the context exploration period in 3 of the 7 rats.

To characterize lags and leads for individual subjects, LFP waveforms from 1 s context exploration or object sampling events were concatenated across all three post-learning sessions for each subject before performing the cross-correlation of instantaneous theta-filtered amplitudes as described above, which reveals a single peak lead/lag value (Supplementary Table 1) and curve (Supplementary Fig. 2) for each subject in its combined post-learning sessions.

Granger Causality

LFP data recorded from mPFC and HPC during corresponding behavioral epochs were analyzed for G-Causality in the frequency domain using the Multivariate Granger Causality (MVGC) Toolbox ²⁴). Model order was estimated using Bayesian Information Criterion (BIC) to a maximum of 100 lags for both Context Exploration and Object Sampling epochs for each session. Subsequently, LFP signals were converted to auto-covariance data using MVGC routines (tsdata_to_var.m, var_to_autocov.m). Finally, Pairwise spectral GC was performed on the observed auto-covariance sequences (autocov_to_spwcgc.m), and statistical directionality for 1–25 Hz GC-traces and peak GC-values were tested using Two-way ANOVAs and paired Wilcoxon rank sum tests respectively for each behavioral epoch (Supplementary Fig. 3).

Analysis of correct trials versus errors

We assessed the extent to which functional connectivity predicted accurate behavioral responses during sessions when animals were acquiring the task, and therefore produced substantial errors as well as correct responses. To match overt behavior during correct and incorrect trials, we compared the subset of correct trials in which animals appropriately responded to the rewarded object against error trials in which animals incorrectly responded to the non-rewarded object, and used equal numbers of trials (range = 15–40) matched for movement speed during both context exploration (correct: 51 +/− 1.2 cm/s, error: 51 +/− 1.2 cm/s; z₁₄₀₆ = 0.47, p = 0.6320) and object sampling (correct: 16.2 +/− 0.6 cm/s, error: 17.4 +/− 1.2 cm/s; z₁₄₀₆ = 0.77, p = 0.4449). To quantify differences between mean cross-correlation lags of correct versus incorrect trials, instantaneous amplitudes were obtained for HPC and mPFC theta traces for 1000 ms periods when PFC-HPC interactions were maximal (context exploration: −400 to +600 ms; object sampling: 500 to 1500 ms; Fig 2c,d) on subsequently correct trials and errors. As described above, cross-correlations of HPC to mPFC theta amplitudes were performed over a range of lags for each learning session, where animals required different numbers of sessions before reaching the performance criterion (range = 3–4; n = 26 total sessions). Cross-correlation values for each time lag were normalized to the mean session minimum and maximum r-values for each lag. Peak lags were then obtained for each session. Wilcoxon signed rank tests were used to verify that peak lags differed from zero, and a paired Wilcoxon rank sum test was used to verify within-trial type differences in the peak lags of conditional context versus object sampling means.

The analysis described above was additionally performed on LFP waveforms concatenated across all sessions of each subject. Between-subject variability during correct and erroneous behaviors are portrayed in Supplementary Fig. 2(c–f) & Supplementary Table 2.

Spike-Phase Analysis

In separate animals single neurons and LFPs in each region (n = 2 per region) were recorded and single units isolated with standard methods (see above). Single unit phase-locking to the locally recorded theta rhythm was assessed using the Circ-Stats Toolbox²⁵. Phase modulation of combined spiking activity in each region to local theta was calculated using Rayleigh’s test on the resultant vector length to provide a z-statistic and p-value (matlab circ_rtest, alpha = 0.05). In addition, the same calculations were performed on individual units and the proportion of phase-locked units was counted in each region.

Selectivity Index (SI)

We also performed a spike-phase analysis on individual neurons whose firing rates discriminated the major task dimensions during the context exploration and object sampling periods. Discrimination of the two contexts during context exploration and of the contexts, objects, and reward values of objects during object sampling was measured using a selectivity index that compared firing rates during 1 s periods:

• SI = (FR₁ − FR₂) / (FR₁ + FR₂)

where FR₁ and FR₂ represent mean firing rates across multiple trials for each condition (during context exploration: context 1 versus context 2; during object sampling: context 1 vs context 2, or object A vs object B, or rewarded vs non-rewarded object samplings). SI chance level was determined using a random permutation procedure, wherein, for each permutation, a mean firing rate was computed from single trial firing rates that were randomly assigned to a particular condition. Cells were declared to be significantly selective for a dimension if their observed SI value exceeded 99% of the SI values produced by permutated firing rate means.

Code availability

Analysis specific code is available upon request, and is easily accessible as a series of published matlab scripts: cross-correlations of instantaneous amplitudes¹³, spectral power and coherence comparisons (www.chronux.org²³), granger causality²⁴, and spike-phase modulation²⁵.

Statistical Analysis

Because peak cross-correlation lead/lags were not normally distributed by chi-squared goodness-of-fit testing (all p’s < 0.0001), a Wilcoxon signed rank test was employed for determining significance. Similarly, a Wilcoxon rank sum test was used for between-group comparisons of (1) cross-correlations lead/lags, (2) peak granger causality differences, and (3) all behavioral running speed comparisons (though note that all effects remained when using equivalent parametric statistics). Z-statistics are given for appropriately large sample sizes (n>15), otherwise Wilcoxon test statistic (W) is reported. A two-sample F-test was used to ensure that all between groups comparisons had similar variance. A two-way ANOVA was employed to analyze the differences in directionality across complete (1–25 Hz) granger causality traces. Rayleigh’s z statistic was employed to test spike-phase associations for non-uniformity. All tests were two-tailed (α = 0.05). A Supplementary Methods Checklist is available.

Data Availability

The data that support these findings are available from the corresponding author upon request.