Likelihood Ratio and Score Tests to Test the Non-inferiority (or Equivalence) of the Odds Ratio in a Crossover Study with Binary Outcomes

Abstract

We consider the non-inferiority (or equivalence) test of the odds ratio (OR) in a crossover study with binary outcomes to evaluate the treatment effects of two drugs. To solve this problem, Lui and Chang (2011) proposed both an asymptotic method and a conditional method based on a random effects logit model. Kenward and Jones (1987) proposed a likelihood ratio test (LRT_M) based on a log linear model. These existing methods are all subject to model misspecification. In this paper, we propose a likelihood ratio test (LRT) and a score test that are independent of model specification. Monte Carlo simulation studies show that, in scenarios considered in this paper, both the LRT and the score test have higher power than the asymptotic and conditional methods for the non-inferiority test; the LRT, score and asymptotic methods have similar power and they all have higher power than the conditional method for the equivalence test. When data can be well described by a log linear model, the LRT_M has the highest power among all the five methods (LRT_M, LRT, score, asymptotic and conditional) for both non-inferiority and equivalence tests. However, in scenarios for which a log linear model does not describe the data well, the LRT_M has the lowest power for the non-inferiority test and has inflated type I error rates for the equivalence test. We provide an example from a clinical trial that illustrates our methods.

1. Introduction

The crossover study has a long history in clinical trials and has been widely used to compare the effects of a new treatment and an existing treatment particularly for relatively stable chronic diseases such as asthma and hypertension. Unlike a conventional parallel-group trial, in a crossover study, each patient serves as his/her own control. Thus, crossover studies avoid the need to control for confounding variables (e.g. age and sex) and increase the efficiency of study. Crossover studies also require fewer subjects compared to the corresponding parallel group study; and thus reduce the costs of recruiting more subjects, especially when subjects are scarce or expensive to obtain. In the two-period crossover study, subjects are randomly selected to enter one of two sequences: 1). they receive treatment A followed by treatment B; 2). they receive treatment B followed by treatment A. There usually is a washout period between the two treatments to reduce the chance that the effect of the first treatment is carried over to the second treatment. The treatment effect of the drugs, period effect and carryover effect are of interest. In this paper, our primary focus is the testing problem for the treatment effect and we assume there is no carryover effect. We hypothesize that the efficacy of the new treatment is not worse (not inferior) or equivalent to the efficacy of the standard treatment and that the new treatment has other advantages (for example, less toxic, lower cost or easier to carry out, etc.).

The binary outcome crossover study is considered here. The complete data that would result from such a study can be summarized in a 2 by 4 table given in Table 1. The subjects who receive the treatment in the order AB will be denoted as group 1 and those in the order BA as group 2. In the table, the column name is defined as the responses of two treatments. Here “1” indicates positive response and “0” indicates negative response. For example, the pair (1,0) in group 1 indicates that the response is positive for treatment A and negative for treatment B. The entry $n_{10}^{(1)}$, for example, is the number of patients in group 1 who had a (1,0) response. The other entries in the table are defined in a similar way and the sizes of the two groups are given by the marginal totals N₁ and N₂. Associated with each entry $n_{ij}^{(k)}$ is the corresponding probability ${\pi }_{ij}^{(k)}$ that the patient has that outcome.

Table 1.

Treatment Groups by Ordered Responses table in crossover study with binary outcome (“1” indicates positive response and “0” indicates negative response)

Treatment Groups	Ordered	Responses	Total
	(0,0)	(0,1)		(1,0)	(1,1)
1(AB)	$n_{00}^{(1)}$	$n_{01}^{(1)}$	$n_{10}^{(1)}$	$n_{11}^{(1)}$	N1
2(BA)	$n_{00}^{(2)}$	$n_{01}^{(2)}$	$n_{10}^{(2)}$	$n_{11}^{(2)}$	N2

The risk difference (RD) between the two treatments has been used to test the non-inferiority (or equivalence) of the new treatment versus the standard treatment in this setting [1, 2]. However, the non-inferiority (or equivalence) margin for the RD depends heavily on the response rate for the standard treatment, which makes it difficult to select a fixed constant non-inferiority (or equivalence) margin. To alleviate this concern, the odds ratio (OR) has been recommended by Lui and Chang [3] and Gart and Thomas [4] as an alternative measure for tests of non-inferiority (or equivalence) for binary outcomes.

In order to provide statistical inference for the crossover study, different models have been proposed. These include the random effects logit model (Ezzet and Whitehead [5]) and the log linear model (Kenward and Jones [6]). Interestingly, in both models, the treatment effect can be estimated by the OR from the 2 by 4 table (see Table 1) without model assumptions about the entry proportions. Lui and Chang [3] proposed both an asymptotic method and a conditional method to test non-inferiority (or equivalence) of the OR based on the random effects logit model in Ezzet and Whitehead [5]. Kenward and Jones [6] provided a likelihood ratio test (LRT_M) to test the OR based on the log linear model, that is equivalent to the logit model [5] when the random effects are ignored. All these methods are subject to model misspecification. In this paper, we propose a likelihood ratio (LRT) and a score test to evaluate the non-inferiority (or equivalence) of the OR without these model assumptions. Our method is model free, and thus is more robust to model misspecification and provides extra efficiency for tests of the OR.

We introduce these non-inferiority and equivalence tests for the OR in Section 1. In Section 2, we provide the statistical framework and introduce the methods used in Lui and Chang [3] and Kenward and Jones [6]. Then we introduce our proposed LRT and score test methods in Section 3. We compare the type I error rates and power for all of these methods using Monte Carlo simulation in Section 4 and provide the sample size calculation in Section 5. An example is given in Section 6. Finally, we discuss the results and provide some recommendations in Section 7.

2. Statistics Framework and Model Based Methods [3, 6]

For the first row (AB) of Table 1, the four random cell counts $(n_{00}^{(1)},n_{01}^{(1)},n_{10}^{(1)},n_{11}^{(1)})$ with sum N₁ are assumed to have a multinomial distribution with probabilities $({\pi }_{00}^{(1)},{\pi }_{01}^{(1)},{\pi }_{10}^{(1)},{\pi }_{11}^{(1)})({\mathrm{\Sigma }}_{i,j\in \{0,1\}}{\pi }_{ij}^{(1)}=1)$. Similarly, the second row (BA) cell counts $(n_{00}^{(2)},n_{01}^{(2)},n_{10}^{(2)},n_{11}^{(2)})$ with sum N₂ are assumed to have multinomial distribution $({\pi }_{00}^{(2)},{\pi }_{01}^{(2)},{\pi }_{10}^{(2)},{\pi }_{11}^{(2)})({\mathrm{\Sigma }}_{i,j\in \{0,1\}}{\pi }_{ij}^{(2)}=1)$. Let $\varphi =\frac{{\pi }_{01}^{(1)}/{\pi }_{10}^{(1)}}{{\pi }_{01}^{(2)}/{\pi }_{10}^{(2)}}=\frac{{\pi }_{01}^{(1)}{\pi }_{10}^{(2)}}{{\pi }_{10}^{(1)}{\pi }_{01}^{(2)}}$ be the OR of a positive response rate of B over A. Please notice that, in Lui and Chang’s [3], they defined the OR as the square root of the OR defined here. In this paper, we consider the following non-inferiority test (1) [3]

$$H_0:\varphi \le {\varphi }_l\text{ versus }{H}_1:\varphi >{\varphi }_l$$ (1)

and equivalence test (2) [3]:

$$H_0:\varphi \le {\varphi }_l\text{ or}\ge {\varphi }_u\text{ versus }{H}_1:{\varphi }_l<\varphi <{\varphi }_u$$ (2)

where 0 < ϕ_l < 1 and we set ϕ_l = 0.5 [3]. We also set ϕ_u = 1/ϕ_l in this paper.

To test (1) and (2), Lui and Chang [3] used a random effects logit model; Kenward and Jones [6] used a log linear model. When the random effect terms are ignored in Lui and Chang’s logit model [3], the logit model is equivalent to Kenward’s log linear model [6]. For convenience in this paper, we only consider the log linear model [6].

In the section below on simulation, we describe some scenarios for which the log linear model does not adequately describe the data. In such scenarios, methods based on the log linear model lose power for tests of the OR due to loss of efficiency for the non-inferiority test and have high type I error inflation for the equivalence test. In Section 3, we provide a likelihood ratio test (LRT) and a score test which do not depend on any model assumptions.

3. Test Statistics

3.1. Likelihood Ratio Test (LRT) Statistic

We first consider the LRT statistic for non-inferiority test (1).

Suppose we have a 2 × 2 binary outcome sample $n_{ij}^{(k)}$; i, j = 0, 1; k = 1, 2 with ${\mathrm{\Sigma }}_{i,j\in \{0,1\}}{n}_{ij}^{(k)}=N_k$, k = 1, 2 as in Table 1. Assume $n_{ij}^{(k)}~\mathit{\text{Multinom}}({\pi }_{ij}^{(k)})$; i, j = 0, 1; k = 1, 2 with natural constraints ${\mathrm{\Sigma }}_{i,j\in \{0,1\}}{\pi }_{ij}^{(k)}=1$; k = 1, 2.

Let $\mathit{\theta }=({\pi }_{00}^{(1)},{\pi }_{01}^{(1)},{\pi }_{10}^{(1)},{\pi }_{11}^{(1)},{\pi }_{00}^{(2)},{\pi }_{01}^{(2)},{\pi }_{10}^{(2)},{\pi }_{11}^{(2)};n_{00}^{(1)},n_{01}^{(1)},n_{10}^{(1)},n_{11}^{(1)},n_{00}^{(2)},n_{01}^{(2)},n_{10}^{(2)},n_{11}^{(2)})$, the likelihood function is given as:

$$L(\mathit{\theta })={\mathrm{\Pi }}_{k\in \{1,2\}}{\mathrm{\Pi }}_{i,j\in \{0,1\}}\frac{N_1!N_2!}{n_{ij}^{(k)}!}{\pi }_{ij}^{(k)n_{ij}^{(k)}}$$

where ${\mathrm{\Sigma }}_{i,j\in \{0,1\}}{\pi }_{ij}^{(k)}=1$, k = 1, 2 are two constraints for parameters, and ${\mathrm{\Sigma }}_{i,j\in \{0,1\}}{n}_{ij}^{(k)}=N_k$. When we take the logarithm on both sides, we have

$$\text{log }L(\mathit{\theta })=\text{log }\left({\mathrm{\Pi }}_{k\in \{1,2\}}{\mathrm{\Pi }}_{i,j\in \{0,1\}}\frac{N_1!N_2!}{n_{ij}^{(k)}!}\right)+{\mathrm{\Sigma }}_{k\in \{1,2\}}{\mathrm{\Sigma }}_{i,j\in \{0,1\}}{n}_{ij}^{(k)}\text{ log }{\pi }_{ij}^{(k)}.$$

With the following reparameterization

$$\varphi =\frac{{\pi }_{01}^{(1)}{\pi }_{10}^{(2)}}{{\pi }_{10}^{(1)}{\pi }_{01}^{(2)}}$$ (3)

$$M_1=1-{\pi }_{00}^{(1)}-{\pi }_{11}^{(1)}$$

and

$$M_2=1-{\pi }_{00}^{(2)}-{\pi }_{11}^{(2)},$$

we have

$$\text{log }L=\text{log }\left(\frac{N_1!N_2!}{{\mathrm{\Pi }}_{k\in \{1,2\}}{\mathrm{\Pi }}_{i,j\in \{0,1\}}{n}_{ij}^{(k)}}\right)+n_{00}^{(1)}\text{ log }{\pi }_{00}^{(1)}+n_{01}^{(1)}\text{ log }\left(\frac{\varphi (M_2-{\pi }_{10}^{(2)})M_1}{{\pi }_{10}^{(2)}+\varphi (M_2-{\pi }_{10}^{(2)})}\right)+n_{10}^{(1)}\text{ log }\left(\frac{{\pi }_{10}^{(2)}{M}_1}{{\pi }_{10}^{(2)}+\varphi (M_2-{\pi }_{10}^{(2)})}\right)+n_{11}^{(1)}\text{ log }{\pi }_{11}^{(1)}$$

$$n_{00}^{(2)}\text{ log }{\pi }_{00}^{(2)}+n_{01}^{(2)}\text{ log}(M_2-{\pi }_{10}^{(2)})+n_{10}^{(2)}\text{ log }{\pi }_{10}^{(2)}+n_{11}^{(2)}\text{ log }{\pi }_{11}^{(2)}.$$

This is a function of six independent parameters $(\varphi ;{\pi }_{10}^{(2)},{\pi }_{00}^{(1)},{\pi }_{11}^{(1)},{\pi }_{00}^{(2)},{\pi }_{11}^{(2)})$ where ϕ is parameter of interest.

Let $a=n_{10}^{(2)}-n_{01}^{(1)}+{\varphi }_l(n_{10}^{(1)}-n_{01}^{(2)});b=-(n_{01}^{(1)}+n_{01}^{(2)});c={\varphi }_l(n_{10}^{(1)}+n_{10}^{(2)});m_1=(n_{01}^{(1)}+n_{10}^{(1)})/N_1$ and $m_2=(n_{01}^{(2)}+n_{10}^{(2)})/N_2$. And A = −a + b + c; B = a * m₂ − 2cm₂; $C={\mathit{\text{cm}}}_2^2$. Then the restricted maximum likelihood estimate (RMLE) of ${\pi }_{10}^{(2)}$ under ϕ = ϕ_l is the smaller root of the quadratic equation $A{({\pi }_{10}^{(2)})}^2+B{\pi }_{10}^{(2)}+C=0$. The RMLE’s of the other parameters are given by ${\tilde{\pi }}_{01}^{(1)}=\frac{{\varphi }_l(m_2-{\tilde{\pi }}_{10}^{(2)})m_1}{{\tilde{\pi }}_{10}^{(2)}+{\varphi }_l(m_2-{\tilde{\pi }}_{10}^{(2)})};{\tilde{\pi }}_{10}^{(1)}=\frac{{\tilde{\pi }}_{10}^{(2)}{m}_1}{{\tilde{\pi }}_{10}^{(2)}+{\varphi }_l(m_2-{\tilde{\pi }}_{10}^{(2)})};{\tilde{\pi }}_{01}^{(2)}=m_2-{\tilde{\pi }}_{10}^{(2)};{\tilde{\pi }}_{00}^{(1)}=\frac{n_{00}^{(1)}}{N_1};{\tilde{\pi }}_{11}^{(1)}=\frac{n_{11}^{(1)}}{N_1};{\tilde{\pi }}_{00}^{(2)}=\frac{n_{00}^{(2)}}{N_2};{\tilde{\pi }}_{11}^{(2)}=\frac{n_{11}^{(2)}}{N_2}$. The unrestricted maximum likelihood estimates (MLE’s) are ${\hat{\pi }}_{ij}^{(k)}=\frac{n_{ij}^{(k)}}{N_k}$; i, j = 0, 1; k = 1, 2.

Consider the following form of LRT statistic:

$$LRT=\frac{{\text{sup}}_{H_0:\varphi \le {\varphi }_l}\text{ log }L}{{\text{sup}}_{H_0\cup H_1}\text{log }L}$$

that can be calculated by using the above estimates of RMLE’s and unrestricted MLE’s.

If ϕ < ϕ_l, then LRT → 0; if ϕ = ϕ_l, “the asymptotic distribution of LRT is that of a chance variable which is zero half the time and which behaves like χ² with one degree of freedom the other half of the time” [7]. Denote δ(0) as the distribution of the random variable with probability mass 1 at point zero. Then the random variable with distribution $\frac{1}{2}\delta (0)+\frac{1}{2}{\chi }_1^2$ is non-negative. To be conservative, $\frac{1}{2}\delta (0)+\frac{1}{2}{\chi }_1^2$ will be used to calculate p-values for the LRT.

In order to do equivalence test (2), we conduct two non-inferiority tests H_a0 : ϕ ≤ ϕ_l versus H_a1 : ϕ > ϕ_l and H_b0 : ϕ ≥ 1/ϕ_l versus H_b1 : ϕ < 1/ϕ_l by using two one-sided tests procedure [8].

3.2. Score Test Statistic

Non-inferiority score test is considered first. In order to deduce this score test, we need to obtain the information matrix first (see detailed calculation in Appendix). The information matrix $I_{6\times 6}(\varphi ,{\pi }_{10}^{(2)},{\pi }_{00}^{(1)},{\pi }_{11}^{(1)},{\pi }_{00}^{(2)},{\pi }_{11}^{(2)})$ can be partitioned as

$$I_{6\times 6}(\varphi ,{\pi }_{10}^{(2)},{\pi }_{00}^{(1)},{\pi }_{11}^{(1)},{\pi }_{00}^{(2)},{\pi }_{11}^{(2)})=I(\varphi ,\mathit{\beta })=\left(\begin{array}{cc}{I}_{\varphi \varphi }(\varphi ,\mathit{\beta })\hfill & I_{\varphi \mathit{\beta }}(\varphi ,\mathit{\beta })\hfill \\ I_{\mathit{\beta }\varphi }(\varphi ,\mathit{\beta })\hfill & I_{\mathit{\beta }\mathit{\beta }}(\varphi ,\mathit{\beta })\hfill \end{array}\right)$$ (4)

where the elements $I_{\varphi \varphi }=-E\left(\frac{{\partial }^2\mathit{\text{ log }}L}{\partial {\varphi }^2}\right)$ is a scalar, $\mathit{\beta }={({\pi }_{10}^{(2)},{\pi }_{00}^{(1)},{\pi }_{11}^{(1)},{\pi }_{00}^{(2)},{\pi }_{11}^{(2)})}^T,I_{\mathit{\beta }\varphi }(\varphi ,\mathit{\beta })=I_{\varphi \mathit{\beta }}{(\varphi ,\mathit{\beta })}^T=-E\left(\frac{{\partial }^2\mathit{\text{ log }}L}{\partial \varphi \partial \mathit{\beta }}\right)$ is a 5 × 1 matrix, $M=-E(\frac{{\partial }^2\mathit{\text{ log }}L}{\partial \mathit{\beta }\partial {\mathit{\beta }}^T})$ is a 5×5 symmetric matrix.

Let β̂^T be the RMLE under the null hypothesis. Then the general score test for testing H₀ can be computed as

$$S_{\varphi }=S_{\varphi }^T(\varphi ,\mathit{\beta })I_{\varphi \varphi }^{-1}{S}_{\varphi }(\varphi ,\mathit{\beta })$$

where the score vector is given by:

$$S_{\varphi }(\varphi ,\mathit{\beta })={\frac{\partial \mathit{\text{log}}l}{\partial \varphi }|}_{({\varphi }_l,{\hat{\mathit{\beta }}}^T)}=n_{01}^{(1)}/{\varphi }_l-(n_{01}^{(1)}+n_{10}^{(1)}){\tilde{\pi }}_{01}^{(2)}/{({\tilde{\pi }}_{10}^{(2)}+{\varphi }_l{\tilde{\pi }}_{01}^{(2)})}^2.$$

From equation (4), the inverse of the Fisher information matrix for ϕ is given by:

$$I_{\varphi \varphi }^{-1}=I_{\varphi \varphi }(\varphi ,\mathit{\beta })-I_{\varphi \mathit{\beta }}{(\varphi ,\mathit{\beta })}^T{I}_{\mathit{\beta }\mathit{\beta }}{(\varphi ,\mathit{\beta })}^{-1}{I_{\varphi \mathit{\beta }}(\varphi ,\mathit{\beta })|}_{({\varphi }_l,{\hat{\mathit{\beta }}}^T)}.$$

Under the null hypothesis, the asymptotic distribution of the score statistic is chi-squared with one degree of freedom.

As in LRT, we also use two one sided tests procedure [8] to conduct the equivalence score test (2).

4. Monte Carlo Simulation

We conducted a simulation study to examine the type I error rates and power of the proposed LRT and score test, the existing asymptotic method [3], conditional method [3] and LRT_M [6] under the following three different scenarios. In Scenario 1), data comes from log linear model [6] with the basic probability of success set to be 0.2 and the period effect set to be 0.5; in Scenario 2), we set ${\pi }_{00}^{(1)}=0.5,{\pi }_{11}^{(1)}=0.2,{\pi }_{00}^{(2)}=0.5,{\pi }_{11}^{(2)}=0.1,{\pi }_{01}^{(2)}=0.35,{\pi }_{10}^{(2)}=0.05$; in Scenario 3), ${\pi }_{00}^{(1)}=0.5,{\pi }_{11}^{(1)}=0.2,{\pi }_{00}^{(2)}=0.4,{\pi }_{11}^{(2)}=0.1,{\pi }_{01}^{(2)}=0.4,{\pi }_{10}^{(2)}=0.1$. We evaluated the fit of the log linear model [6] in scenarios 2 and 3 by deviance goodness of fit tests. In the scenarios considered, the log linear model did not adequately describe the data.

We take Scenario 1 (non-inferiority test) as an example to illustrate our simulation procedure. For a given sample size (N₁, N₂) and a true odds ratio, we generated 10,000 repeated samples from the log linear model with basic probability of success 0.2 and period effect 0.5. We calculated the theoretical p-values for LRT and score test using the asymptotic distribution under the null derived in Section 3. We used $\frac{1}{2}\delta (0)+\frac{1}{2}{\chi }_1^2$ as the asymptotic null distribution for the LRT and used ${\chi }_1^2$ as the asymptotic null distribution for the score test. Then, by computing the proportion of times for which the null hypothesis was rejected (p ≤ 0.05), we obtained the estimated type I error rate when the true ϕ ≤ ϕ_l and power when true ϕ > ϕ_l for all the five methods. Then, similar procedures were used for data generated from Scenarios 2 and 3. Finally, we summarized the type I error rates and power for all methods based on scenario 1 in Figure 1 and those based on Scenarios 2 and 3 in Figure 2. Similar procedures were conducted in the equivalence test. The simulation results for equivalence test based on Scenario 1 are shown in Figure 3 and those based on Scenarios 2 and 3 are shown in Figure 4. This simulation study was conducted using R software.

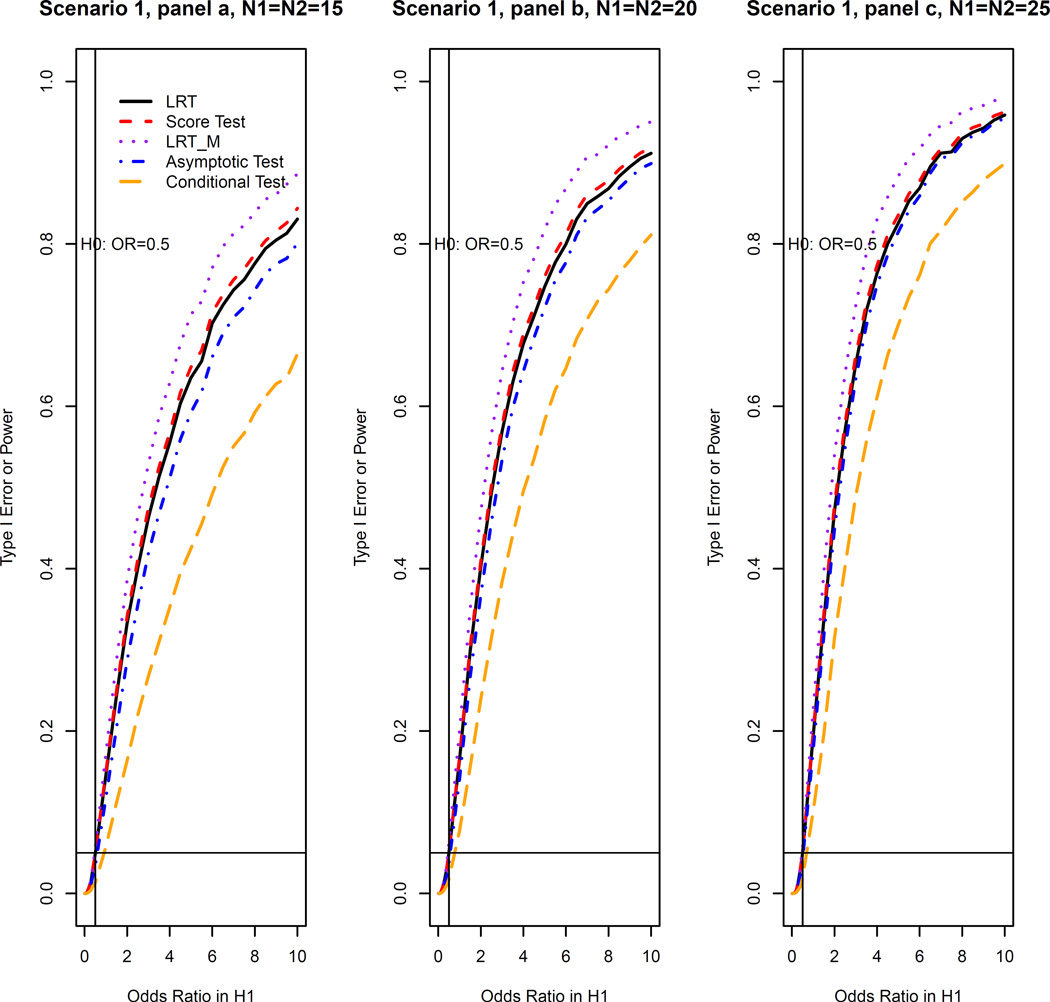
Figure 1.

Type I error rates and power of OR test at the 5% nominal significance level for all methods for the non-inferiority test (Scenario I: data simulated from log linear model [6] with the basic probability of success set to be 0.2 and the period effect set to be 0.5).

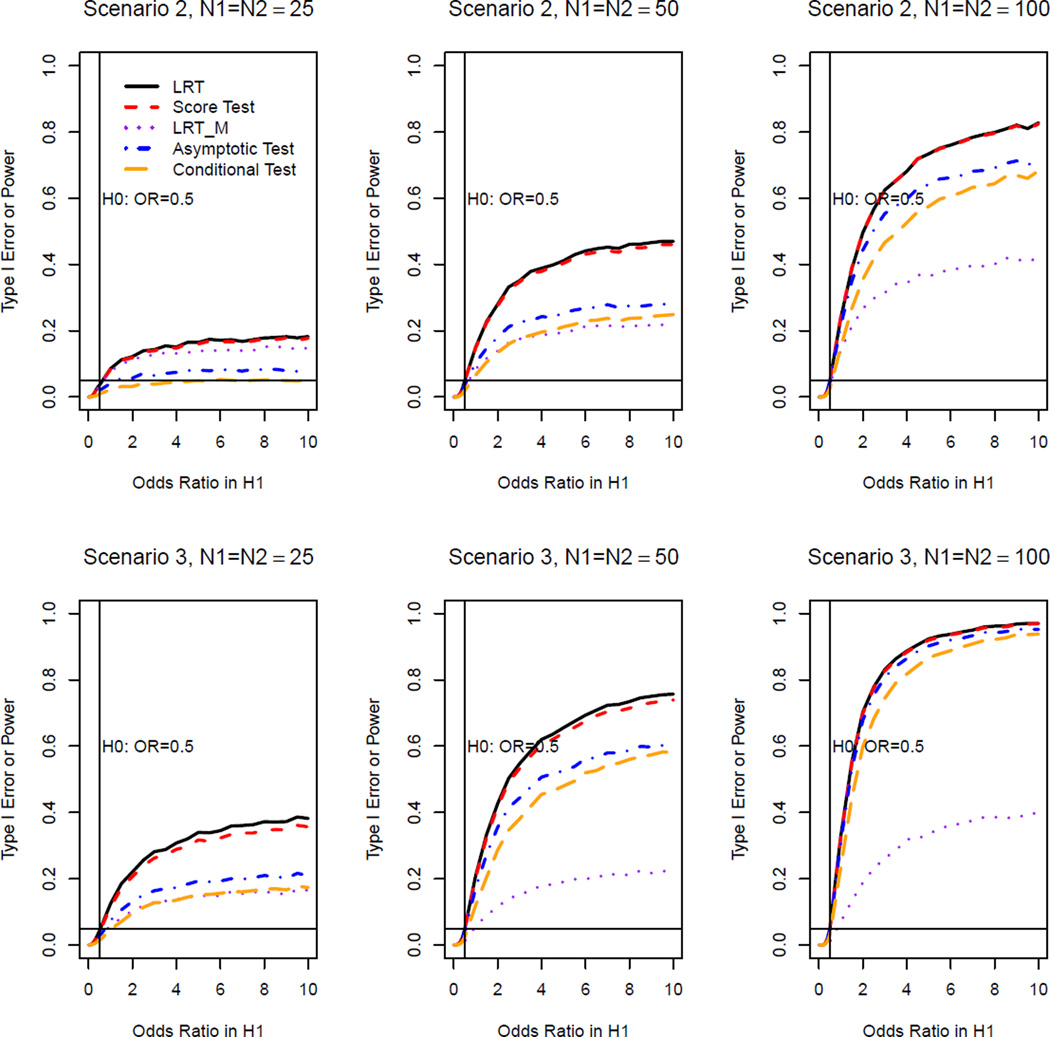
Figure 2.

Type I error rates and power of OR test at the 5% nominal significance level for all methods for the non-inferiority test(Scenario II (top): ${\pi }_{00}^{(1)}=0.5,{\pi }_{11}^{(1)}=0.2,{\pi }_{00}^{(2)}=0.5,{\pi }_{11}^{(2)}=0.1,{\pi }_{01}^{(2)}=0.35,{\pi }_{10}^{(2)}=0.05$; Scenario III (bottom): ${\pi }_{00}^{(1)}=0.5,{\pi }_{11}^{(1)}=0.2,{\pi }_{00}^{(2)}=0.4,{\pi }_{11}^{(2)}=0.1,{\pi }_{01}^{(2)}=0.4,{\pi }_{10}^{(2)}=0.1$

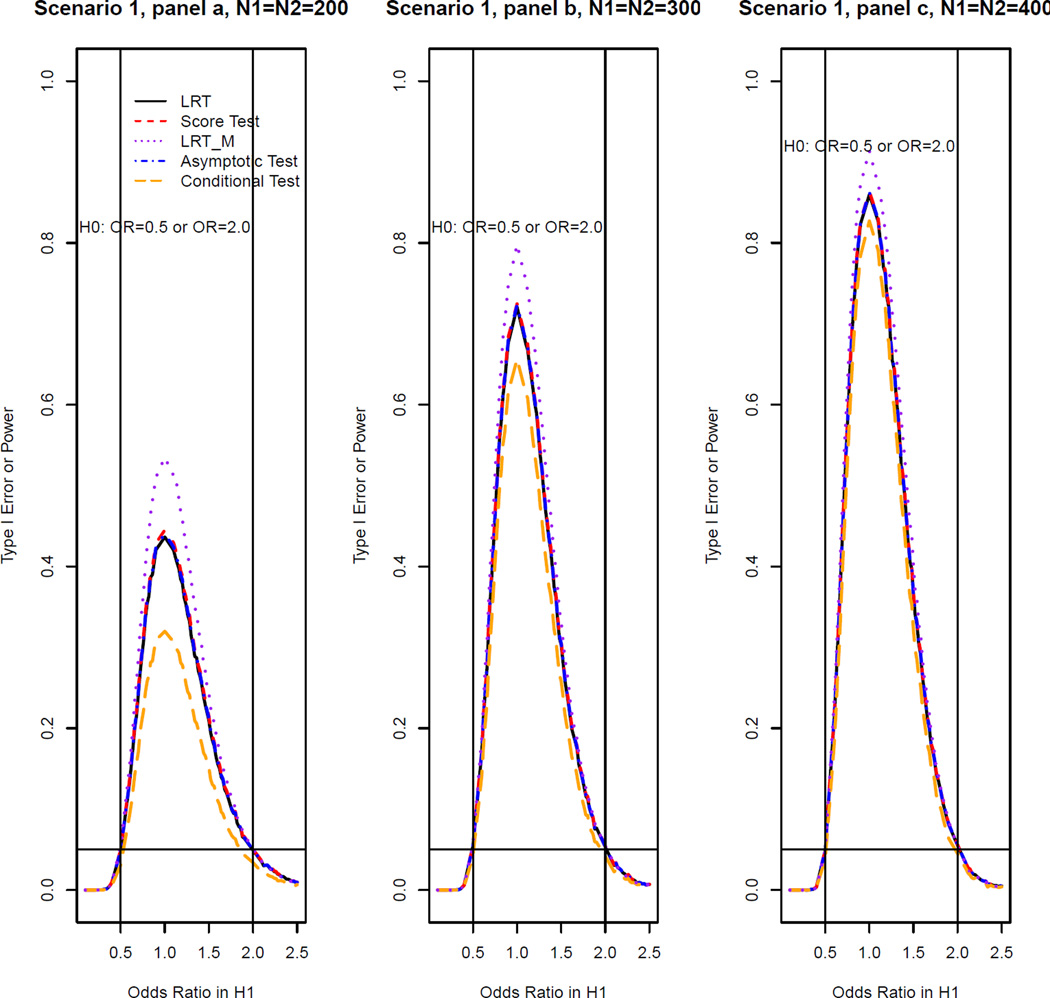
Figure 3.

Type I error rates and power of OR test at the 5% nominal significance level for all methods for the equivalence test (Scenario I: data simulated from log linear model [6] with the basic probability of success set to be 0.2 and the period effect set to be 0.5).

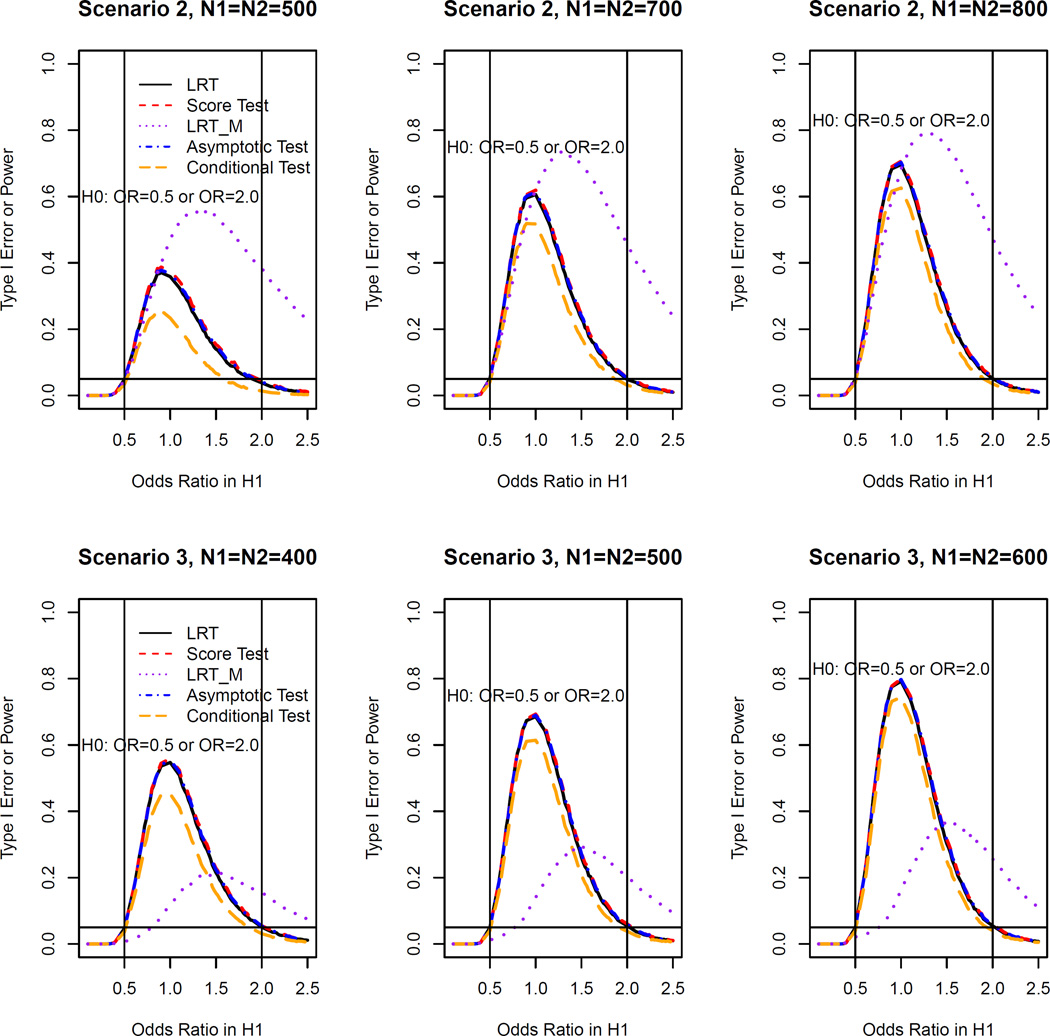
Figure 4.

Type I error rates and power of OR test at the 5% nominal significance level for all methods for the equivalence test (Scenario II (top): ${\pi }_{00}^{(1)}=0.5,{\pi }_{11}^{(1)}=0.2,{\pi }_{00}^{(2)}=0.5,{\pi }_{11}^{(2)}=0.1,{\pi }_{01}^{(2)}=0.35,{\pi }_{10}^{(2)}=0.05$; Scenario III (bottom): ${\pi }_{00}^{(1)}=0.5,{\pi }_{11}^{(1)}=0.2,{\pi }_{00}^{(2)}=0.4,{\pi }_{11}^{(2)}=0.1,{\pi }_{01}^{(2)}=0.4,{\pi }_{10}^{(2)}=0.1$

Figures 1 and 2 show that, for the non-inferiority test, all methods can maintain the nominal type I error in these three scenarios. We note from Figures 1 and 2 that, our LRT and score test methods achieve greater power than the asymptotic method of Lui and Chang [3] (not to be confused with the asymptotic distribution of the LRT and score test). The larger the sample size, the closer the power of the asymptotic method is to the power of our methods. We also note that our LRT and score test methods and the Lui and Chang’s asymptotic method always have greater power than the conditional method. It is well known that the conditional test method is conservative and hence loses power. The LRT, score and asymptotic test methods are generally more efficient than the conditional test method. The most interesting observation is the behavior of the LRT_M. When the data can be described by a log linear model, the LRT_M method based on the model has greater power than all other methods (See Fig 1 for Scenario 1). However, when the data cannot be described by the log linear model, the LRT_M method based on the log linear model loses power. In particular, the power is even lower than the asymptotic and conditional methods as shown in Figure 2 for Scenarios 2 and 3.

We did simulations to investigate the relationship between goodness of fit of the log linear model and power loss of the LRT_M compared to the LRT (defined as (power of LRT-power of LRT_M)/power of LRT_M) when a log linear model does not describe data well. In Scenario 2, for a given true odds ratio, we simulated 10,000 repeated samples, fit a log linear model to each sample to obtain the deviance of the model fitting, and calculated the mean of these deviances to estimate the average goodness of fit for the log linear model. For the same true odds ratio, we also calculated the powers of LRT_M and LRT to obtain the power loss. We did calculations on 50 true odds ratios with N₁ = N₂ = 50. By doing linear regression for the power losses on the corresponding deviances, we found that, there is a significant increase of power loss with the increase of deviance. That is to say, the worse the fit of the log linear model, the more power loss of the LRT_M compared to our proposed LRT for the non-inferiority test. Since our score test has similar power as the LRT, we also expect that, the worse the fit of the log linear model, the more power loss of the LRT_M compared to the score test.

Figures 3 and 4 show the simulation results for equivalence test. The LRT, score and asymptotic methods have similar power in all scenarios considered and they all outperform the conditional test. In Scenario 1 when the data can be described by a log linear model, as in the non-inferiority test, LRT_M has the greatest power (See Figure 3). However, in Scenarios 2 and 3 for which the data cannot be described by a log linear model, the LRT_M has high type I error rate inflation (see Figures 3 and 4). Furthermore, LRT, score, asymptotic and conditional methods all obtain the highest power at true ϕ = 1 as expected, while LRT_M does not. From this inconsistent behavior of the LRT_M, we can see that it cannot be used in scenarios for which a log linear model does not describe data well.

5. Sample Size Calculation

Sample sizes required for 80% power in Scenario 2 with ${\pi }_{00}^{(1)}=0.5,{\pi }_{11}^{(1)}=0.2,{\pi }_{00}^{(2)}=0.5,{\pi }_{11}^{(2)}=0.1,{\pi }_{01}^{(2)}=0.35,{\pi }_{10}^{(2)}=0.05$ are shown in Table 2 for non-inferiority test and Table 3 for equivalence test.

Table 2.

Sample Size required by the five methods to achieve 80% power with significance level 5% for listed true ϕ (OR) values in non-inferiority test

		Test		Statistics
True ϕ	LRT	Score	Asym	Conditional	LRTM
0.8	1362	1344	1376	1476	1804
0.9	907	902	904	1000	1312
1.0	676	676	684	760	1066
1.1	548	538	542	614	870
1.2	458	448	454	516	776

Table 3.

Sample Size required by the five methods to achieve 80% power with significance level 5% for listed true ϕ (OR) values in equivalence test

		Test		Statistics
True ϕ	LRT	Score	Asym	Conditional	LRTM
0.8	1370	1344	1366	1484	1812
0.9	1022	1005	1020	1090	1320
1.0	969	962	968	1064	1052
1.1	1092	1066	1085	1202	890
1.2	1410	1406	1410	1516	831

As expected, for the non-inferiority test, the required sample size decreases as ϕ increases. Obviously, the sample sizes required by LRT_M are larger than the sample sizes required by other methods because in this scenario, the log linear model does not fit the simulated data. The sample sizes obtained for the LRT, score and asymptotic method are necessarily smaller than conditional method which is conservative. Furthermore, the sample sizes obtained for LRT and score methods are comparable. For the equivalence test, the required sample size is highest when true ϕ = 1 for all methods except the LRT_M. The LRT, score and asymptotic methods require similar sample size for all situations. The conditional method still requires greater sample size than the LRT, score and asymptotic methods. The LRT_M method also behaves poorly as it does in the Monte Carlo simulation study.

6. Clinical Trial Example

Consider the example conducted by 3M-Riker in Lui and Chang’s [3]. This crossover study was designed to compare two inhalation devices (A and B) delivering salbutamol [5]. The randomized 139 patients in Group 1 used device A followed by device B and the 140 patients in Group 2 used the devices in reverse order. Patients were asked to evaluate the features of each device and to respond either “Yes” or “No” to each device. The summary of patients’ responses was listed in Table 4. A “1” represents a “Yes” response and a “0” represents a “No” response. We are interested in testing the non-inferiority (or equivalence) of device A versus device B with respect to the patient preference rate (instead of device B versus A) [3].

Table 4.

Treatment Groups by Ordered Responses table in a crossover study for inhalation devices A and B delivering salbutamol

Treatment Groups	Ordered	Responses	Total
	(0,0)	(0,1)		(1,0)	(1,1)
1(AB)	57	15	41	26	139
2(BA)	54	32	16	38	140

Suppose we choose a clinically acceptable non-inferior margin 0.8 for the OR. When we conducted a non-inferiority test for the OR on this study, we obtained the p-values 1.67 × 10⁻⁶, 1.96 × 10⁻⁶, 4.39 × 10⁻⁶, 3.68 × 10⁻⁶, 1.09 × 10⁻⁵ for the LRT, score, asymptotic, conditional and LRT_M respectively. All these small p-values show strong evidence that the patients’ preference rate for device A is non-inferior to that of device B. When fitting a log linear model on this data, we obtained deviance ${\chi }_3^2=22.23$ (p < 0.001). Thus, a log linear model does not describe the data well and for this reason the LRT_M has a greater p-value than LRT and score methods.

For the equivalence test, all the LRT, score, asymptotic, conditional methods do not reject the null hypothesis that the patients’ preference rates for devices A and B are different. Due to the high type I error inflation rates for the LRT_M when a log linear model does not fit the data, it is not appropriate to apply LRT_M in this study.

7. Discussion

In this paper, we proposed a likelihood ratio test and a score test to solve the non-inferiority (or equivalence) testing problem for the odds ratio in a crossover study. Both methods are independent of model assumptions. We compared our tests with Lui and Chang’s asymptotic method and conditional method [3] that are based on random effects model. For the non-inferiority test, our proposed LRT and score tests achieve higher power than asymptotic [3] and they have closer and more comparable power as the sample size gets larger. For the equivalence test, the LRT and score and asymptotic methods have similar power. This occurs because the asymptotic method is actually a Wald test. Engle [9] showed that, the larger the sample size, the closer the power of all three tests because they are asymptotically equivalent. We also compared the LRT and score tests to Kenward’s LRT_M method which is based on a log linear model assumption [6]. The LRT_M achieves higher power than the LRT and score test when the log linear model holds; but behaves poorly when the log linear model does not hold. From the Neyman-Pearson Lemma, LRT_M is the most powerful test when the log linear model holds, but the LRT_M loses good behavior when this model assumption does not hold due to the loss of precision in the estimation of parameters.

We focused on treatment effects for a crossover study in our paper. If we use the $\mathit{\text{OR}}=\frac{{\pi }_{01}^{(1)}/{\pi }_{10}^{(1)}}{{\pi }_{10}^{(2)}/{\pi }_{01}^{(2)}}$ which results from switching ${\pi }_{01}^{(2)}$ and ${\pi }_{10}^{(2)}$ in (3), we can extend our LRT and score methods to the non-inferiority (or equivalence) test to incorporate period effects.

The LRT and score test methods in this paper can only be used for crossover study with two periods. It will be an interesting topic to do further research on expanding them to crossover study with more than two periods.

Appendix

Information Matrix for the Score Test

Denote

$$Q_1={\pi }_{10}^{(2)}+{\varphi }_l(M_2-{\pi }_{10}^{(2)})={\pi }_{10}^{(2)}+{\varphi }_l{\pi }_{01}^{(2)},$$

$$Q_2=N_1({\pi }_{01}^{(1)}+{\pi }_{10}^{(1)})$$

and

$$Q_3=(N_1{\pi }_{01}^{(1)}+N_2{\pi }_{01}^{(2)})/{({\pi }_{01}^{(2)})}^2.$$

Then the elements of the information matrix $I_{6\times 6}(\varphi ,{\pi }_{10}^{(2)},{\pi }_{00}^{(1)},{\pi }_{11}^{(1)},{\pi }_{00}^{(2)},{\pi }_{11}^{(2)})$ are

$$I_{\varphi \varphi }=E(-\frac{{\partial }^2\mathit{\text{log}}l}{{\partial }^2\varphi })=N_1{\pi }_{01}^{(1)}/{\varphi }_l^2-Q_2{{\pi }_{01}^{(2)}}^2/Q_1^2$$

$$I_{\varphi {\pi }_{10}^{(2)}}=I_{{\pi }_{10}^{(2)}\varphi }=E(-\frac{{\partial }^2\mathit{\text{log}}l}{\partial \varphi \partial {\pi }_{10}^{(2)}})=-Q_2{M}_2/Q_1^2$$

$$I_{\varphi {\pi }_{00}^{(2)}}=I_{{\pi }_{00}^{(2)}\varphi }=E(-\frac{{\partial }^2\mathit{\text{log}}l}{\partial \varphi \partial {\pi }_{00}^{(2)}})=I_{\varphi {\pi }_{11}^{(2)}}=I_{{\pi }_{11}^{(2)}\varphi }=E(-\frac{{\partial }^2\mathit{\text{log}}l}{\partial \varphi \partial {\pi }_{11}^{(2)}})=-Q_2{\pi }_{10}^{(2)}/Q_1^2$$

$$I_{{\pi }_{10}^{(2)}{\pi }_{10}^{(2)}}=E(-\frac{{\partial }^2\mathit{\text{log}}l}{{\partial }^2{\pi }_{10}^{(2)}})=Q_3-{(1-{\varphi }_l)}^2{Q}_2/Q_1^2+(N_1{\pi }_{10}^{(1)}+N_2{\pi }_{10}^{(2)})/{{\pi }_{10}^{(2)}}^2$$

$$I_{{\pi }_{00}^{(2)}{\pi }_{10}^{(2)}}=I_{{\pi }_{10}^{(2)}{\pi }_{00}^{(2)}}=E(-\frac{{\partial }^2\mathit{\text{log}}l}{\partial {\pi }_{10}^{(2)}\partial {\pi }_{00}^{(2)}})=I_{{\pi }_{10}^{(2)}{\pi }_{11}^{(2)}}=I_{{\pi }_{11}^{(2)}{\pi }_{10}^{(2)}}=E(-\frac{{\partial }^2\mathit{\text{log}}l}{\partial {\pi }_{10}^{(2)}\partial {\pi }_{11}^{(2)}})=Q_3+{\varphi }_l(1-{\varphi }_l)Q_2/Q_1^2$$

$$I_{{\pi }_{00}^{(1)}{\pi }_{00}^{(1)}}=E(-\frac{{\partial }^2\mathit{\text{log}}l}{{\partial }^2{\pi }_{00}^{(1)}})=N_1/{\pi }_{00}^{(1)}+Q_2/M_1^2$$

$$I_{{\pi }_{00}^{(1)}{\pi }_{11}^{(1)}}=I_{{\pi }_{11}^{(1)}{\pi }_{00}^{(1)}}=E(-\frac{{\partial }^2\mathit{\text{log}}l}{\partial {\pi }_{00}^{(1)}\partial {\pi }_{11}^{(1)}})=Q_2/M_1^2$$

$$I_{{\pi }_{11}^{(1)}{\pi }_{11}^{(1)}}=E(-\frac{{\partial }^2\mathit{\text{log}}l}{{\partial }^2{\pi }_{11}^{(1)}})=N_1/{\pi }_{11}^{(1)}+Q_2/M_1^2$$

$$I_{{\pi }_{00}^{(2)}{\pi }_{00}^{(2)}}=E(-\frac{{\partial }^2\mathit{\text{log}}l}{{\partial }^2{\pi }_{00}^{(2)}})=N_2/{\pi }_{00}^{(2)}+Q_3-Q_2{\varphi }_l^2/Q_1^2$$

$$I_{{\pi }_{00}^{(2)}{\pi }_{11}^{(2)}}=I_{{\pi }_{11}^{(2)}{\pi }_{00}^{(2)}}=E(-\frac{{\partial }^2\mathit{\text{log}}l}{\partial {\pi }_{00}^{(2)}\partial {\pi }_{11}^{(2)}})=Q_3-Q_2{\varphi }_l^2/Q_1^2$$

$$I_{{\pi }_{11}^{(2)}}=E(-\frac{{\partial }^2\mathit{\text{log}}l}{{\partial }^2{\pi }_{11}^{(2)}})=N_2/{\pi }_{11}^{(2)}+Q_3-Q_2{\varphi }_l^2/Q_1^2$$

$$I_{{\pi }_{10}^{(2)}{\pi }_{00}^{(1)}}=I_{{\pi }_{00}^{(1)}{\pi }_{10}^{(2)}}=I_{{\pi }_{10}^{(2)}{\pi }_{11}^{(1)}}=I_{{\pi }_{11}^{(1)}{\pi }_{10}^{(2)}}=I_{{\pi }_{00}^{(1)}{\pi }_{00}^{(2)}}=I_{{\pi }_{00}^{(2)}{\pi }_{00}^{(1)}}=I_{{\pi }_{00}^{(1)}{\pi }_{11}^{(2)}}=I_{{\pi }_{11}^{(2)}{\pi }_{00}^{(1)}}=I_{{\pi }_{11}^{(1)}5}=I_{{\pi }_{00}^{(2)}{\pi }_{11}^{(1)}}=I_{{\pi }_{11}^{(1)}{\pi }_{11}^{(2)}}=I_{{\pi }_{11}^{(2)}{\pi }_{11}^{(1)}}=0.$$