Skip to main content
PMC home page
Nature Communications logoLink to Nature Communications
. 2016 Jul 22;7:12262. doi: 10.1038/ncomms12262

A disorder-enhanced quasi-one-dimensional superconductor

A P Petrović 1,a,*, D Ansermet 1,*, D Chernyshov 2, M Hoesch 3, D Salloum 4,5, P Gougeon 4, M Potel 4, L Boeri 6, C Panagopoulos 1,b
PMCID: PMC4961838  PMID: 27448209

Abstract

A powerful approach to analysing quantum systems with dimensionality d>1 involves adding a weak coupling to an array of one-dimensional (1D) chains. The resultant quasi-1D (q1D) systems can exhibit long-range order at low temperature, but are heavily influenced by interactions and disorder due to their large anisotropies. Real q1D materials are therefore ideal candidates not only to provoke, test and refine theories of strongly correlated matter, but also to search for unusual emergent electronic phases. Here we report the unprecedented enhancement of a superconducting instability by disorder in single crystals of Na2−δMo6Se6, a q1D superconductor comprising MoSe chains weakly coupled by Na atoms. We argue that disorder-enhanced Coulomb pair-breaking (which usually destroys superconductivity) may be averted due to a screened long-range Coulomb repulsion intrinsic to disordered q1D materials. Our results illustrate the capability of disorder to tune and induce new correlated electron physics in low-dimensional materials.

Inline graphicDisorder localizes electrons, which is usually detrimental to the onset of superconductivity. Here, Petrović et al. report a disorder-enhanced superconducting instability in quasi-one dimensional Na2-dMo6Se6 and suggest that this effect may originate from an intrinsically screened Coulomb repulsion.

Weakly-interacting electrons in a three-dimensional (3D) periodic potential are well-described by Landau–Fermi liquid theory1, in which the free electrons of a Fermi gas become dressed quasiparticles with renormalized dynamical properties. Conversely, in the one-dimensional (1D) limit a Tomonaga–Luttinger liquid (TLL) is formed2,3, where single-particle excitations are replaced by highly correlated collective excitations. So far, it has proved difficult to interpolate theoretically between these two regimes, either by strengthening electron–electron (e−–e−) interactions in 3D, or by incorporating weak transverse coupling into 1D models4,5. The invariable presence of disorder in real materials places further demands on theory, particularly in the description of ordered electronic ground states. Q1D systems such as nanowire ropes, filamentary networks or single crystals with uniaxial anisotropy therefore represent an opportunity to experimentally probe what theories aspire to model: strongly correlated electrons subject to disorder in a highly anisotropic 3D environment.

Physical properties of q1D materials may vary considerably with temperature. TLL theory is expected to be valid at elevated temperatures, since electrons cannot hop coherently perpendicular to the high-symmetry axis and q1D systems behave as decoupled arrays of 1D filaments. Phase-coherent single-particle hopping can only occur below temperature Tx≤t⊥ (where t⊥ is the transverse hopping integral), at which a dimensional crossover to an anisotropic quasi-3D (q3D) electron liquid is anticipated4,6. The properties of such q3D liquids remain largely unknown, especially the role of electronic correlations in determining the ground state. At low temperature, a TLL is unstable to either density wave (DW) or superconducting fluctuations, depending on whether the e−–e− interaction is repulsive (due to Coulomb forces) or attractive (from electron–phonon coupling). Following dimensional crossover, the influence of such interactions in the q3D state is unclear. As an example, electrical transport in the TLL state of the q1D purple bronze Li0.9Mo6O17 is dominated by repulsive e−–e− interactions7,8, yet a superconducting transition occurs for temperatures below 1.9 K.

Disorder adds further complication to q1D materials due to its tendency to localize electrons at low temperature. For dimensionality d≤2, localization occurs for any non-zero disorder; in contrast, for d>2 a critical disorder is required and a mobility edge separates extended from localized states. The question of whether a mobility edge can form in q1D materials after crossover to a q3D liquid state is open, as is the microscopic nature of the localized phase. Disorder also renormalizes e−–e− interactions, leading to a dynamic amplification of the Coulomb repulsion9 and a weaker enhancement of phonon-mediated e−–e− attraction, that is, Cooper pairing10,11,12,13. We therefore anticipate that disorder should strongly suppress superconductivity in q1D materials, unless the Coulomb interaction is unusually weak or screened.

In this work, we show that the q1D superconductor Na2−δMo6Se6 provides a unique environment in which to study the interplay between dimensionality, electronic correlations and disorder. Although Na2−δMo6Se6 is metallic at room temperature, the presence of Na vacancy disorder leads to electron localization and a divergent resistivity ρ(T) at low temperature, prior to a superconducting transition. In contrast with all other known superconductors, the onset temperature for superconducting fluctuations Tpk is positively correlated with the level of disorder. Normal-state electrical transport measurements also display signatures of an attractive e−–e− interaction, which is consistent with disorder-enhanced superconductivity. A plausible explanation for these phenomena is an intrinsic screening of the long-range Coulomb repulsion in Na2−δMo6Se6, arising from the high polarizability of disordered q1D materials. The combination of disorder and q1D crystal symmetry constitutes a new recipe for strongly correlated electron liquids with tunable electronic properties.

Results

Crystal and electronic structure of Na2−δ Mo6Se6

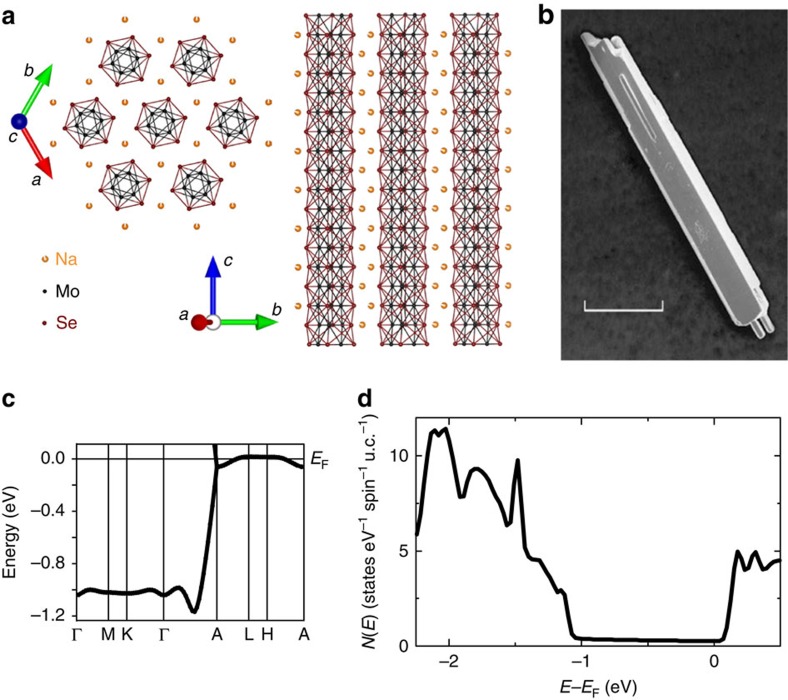
Na2−δMo6Se6 belongs to the q1D M2Mo6Se6 family14 (M=Group IA alkali metals, Tl, In) which crystallize with hexagonal space group P63/m. The structure can be considered as a linear condensation of Mo6Se8 clusters into infinite-length (Mo6Se6)∞ chains parallel to the hexagonal c-axis, weakly coupled by M atoms (Fig. 1a). The q1D nature of these materials is apparent from the needle-like morphology of as-grown crystals (Fig. 1b; see Methods for growth details). Ab initio calculations (Supplementary Note I) using density functional theory reveal an electronic structure which is uniquely simple among q1D metals. A single spin-degenerate band of predominant Mo dxz character crosses the Fermi energy EF at half-filling (Fig. 1c, Supplementary Fig. 1), creating a 1D Fermi surface composed of two sheets lying close to the Brillouin zone boundaries at ±π/c (where c is the c-axis lattice parameter). The warping of these sheets (and hence the coupling between (Mo6Se6)∞ chains) is controlled by the M cation, yielding values for t⊥ ranging from 230 K (M=Tl) to 30 K (M=Rb) (Supplementary Fig. 2). In addition to tuning the dimensionality, M also controls the ground state: M=Tl, In are superconductors15,16, while M=K, Rb become insulating at low temperature16,17.

Figure 1. Quasi-one-dimensional crystal and electronic structures in Na2−δMo6Se6.

Figure 1

Open in a new tab

(a) Hexagonal crystal structure of Na2−δMo6Se6, viewed perpendicular and parallel to the c-axis. From synchrotron X-ray diffraction experiments, we measure the a- and c-axis lattice parameters to be 8.65 Å and 4.49 Å, respectively at 293 K (Supplementary Note II). (b) Electron micrograph of a typical Na2−δMo6Se6 crystal. Scale bar, 300 μm. (c) Calculated energy-momentum dispersion of the conduction band within the hexagonal Brillouin zone, highlighting the large bandwidth and minimal dispersion perpendicular to the chain axis. (d) Electronic density of states N(E) around the Fermi level in Na2Mo6Se6.

Within the M2Mo6Se6 family, M=Na is attractive for two reasons. First, we calculate an intermediate t⊥=120 K, suggesting that Na2−δMo6Se6 lies at the threshold between superconducting and insulating instabilities. Second, the combination of the small Na cation size and a high growth temperature (1750 °C) results in substantial Na vacancy formation during crystal synthesis. Since the Na atoms are a charge reservoir for the (Mo6Se6)∞ chains, these vacancies will reduce EF and lead to an incommensurate band filling. Despite the reduction in carrier density, the density of states N(EF) remains constant for Na1.5→2.1 (Fig. 1d, Supplementary Note I). Energy-dispersive X-ray (EDX) spectrometry on our crystals indicates Na contents from 1.7 to 2, comfortably within this range. This is confirmed by synchrotron X-ray diffraction (XRD) on three randomly-chosen crystals: structural refinements reveal Na deficiencies of 11±1%, 11±2% and 13±4% (that is, δ=0.22, 0.22, 0.26), but the (Mo6Se6)∞ chains remain highly ordered. No deviation from the M2Mo6Se6 structure is observed between 293 and 20 K, ruling out any lattice distortions such as the Peierls transition, which often afflicts q1D metals. To probe the Na vacancy distribution, we perform diffuse X-ray scattering experiments on the δ=0.26 crystal. No trace of any Huang scattering (from clustered Na vacancies) or structured diffuse scattering from short-range vacancy ordering is observed (Supplementary Fig. 3, Supplementary Note II). Na vacancies therefore create an intrinsic, random disorder potential in Na2−δMo6Se6 single crystals.

Normal-state electrical transport

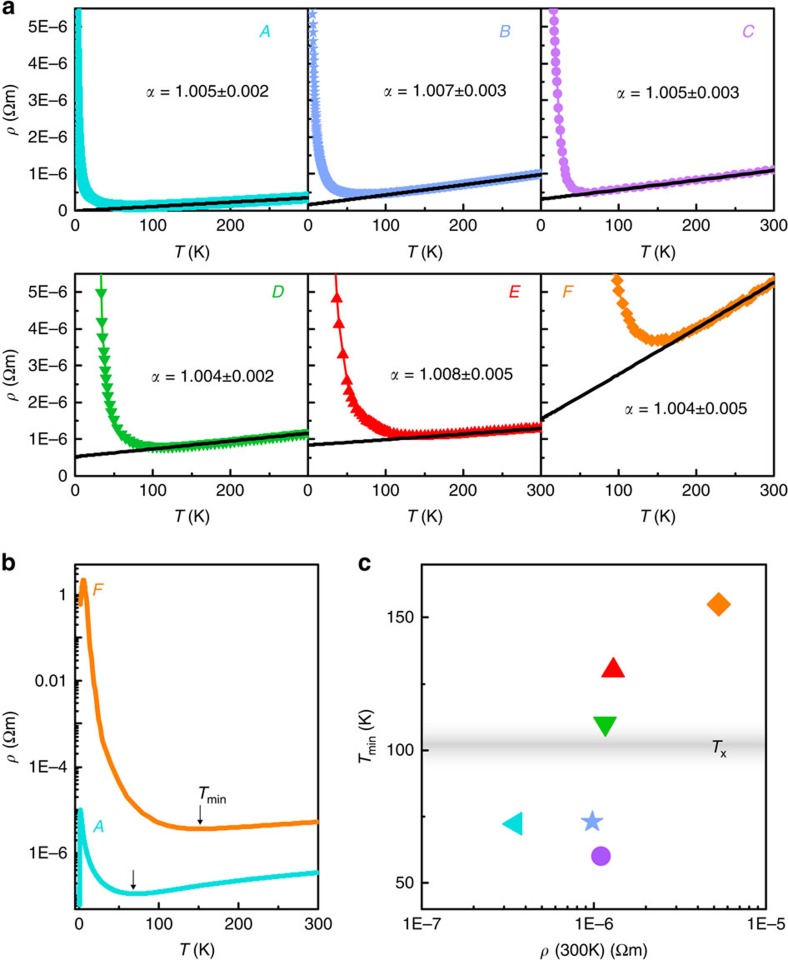
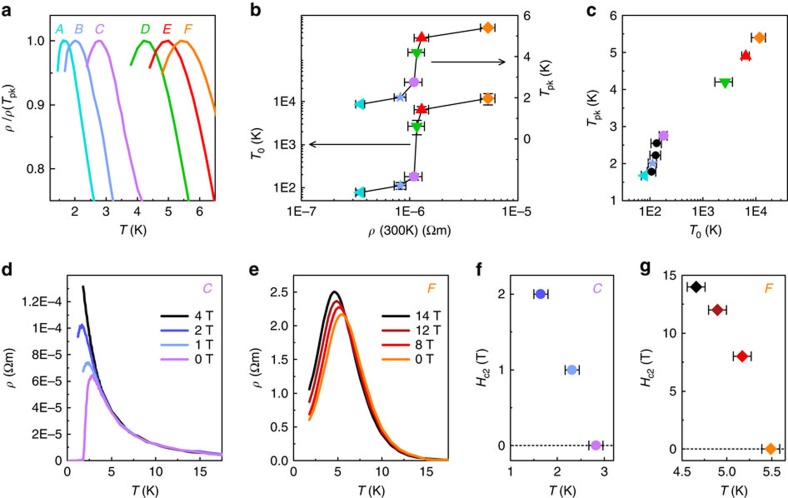
We first examine the electrical transport at high energy for signatures of disorder and one-dimensionality. The temperature dependence of the resistivity ρ(T) for six randomly-selected Na2−δMo6Se6 crystals A–F is shown in Fig. 2a. ρ(300 K) increases by >1 order of magnitude from crystal A to F (Fig. 2b): such large differences between crystals cannot be attributed to changes in the carrier density due to Na stoichiometry variation and must instead arise from disorder. Despite the variance in ρ(300 K), the evolution of ρ(T) is qualitatively similar in all crystals. On cooling, ρ(T) exhibits metallic behaviour before passing through a broad minimum at Tmin and diverging at lower temperature. Tmin falls from 150 K to ∼70 K as ρ(300 K) decreases (Fig. 2c), suggesting that the divergence in ρ(T) and the disorder level are linked.

Figure 2. Power laws and minima in the normal-state resistivity ρ(T).

Figure 2

Open in a new tab

(a) ρ(T) for crystals A–F, together with power-law fits ρ∝Tα (black lines, fitting range 1.5Tmin<T<300 K). Tmin corresponds to the minimum in ρ(T) for T>Tpk. (b) ρ(T) plotted on a semi-logarithmic scale for crystals A and F: ρF≈105ρA as T→Tpk. (c) Evolution of Tmin with ρ(300 K), which is a measure of the disorder in each crystal. The horizontal shading indicates the estimated6 single-particle dimensional crossover temperature Tx∼104 K, obtained using 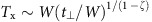Inline graphic, where W is the conduction bandwidth (Supplementary Note I), 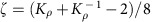Inline graphic and Kρ=3/2. No anomaly is visible in ρ(T) at Tx, suggesting either that Tx may be further renormalized due to competing charge instabilities8, or that signatures of Tomonaga–Luttinger liquid behaviour may persist even for T<Tx (ref. 6).

Upturns or divergence in ρ(T) have been widely reported in q1D materials and variously attributed to localization18,19,20,21,22, multiband TLL physics23, DW formation24,25, incipient density fluctuations16 and proximity to Mott instabilities8. Differentiating between these mechanisms has proved challenging, in part due to the microscopic similarity between localized electrons and randomly-pinned DWs in 1D. We briefly remark that the broad minimum in ρ(T) in Na2−δMo6Se6 contrasts strongly with the abrupt jumps in ρ(T) for nesting-driven DW materials such as NbSe3 (ref. 26), while any Mott transition will be suppressed due to the non-stoichiometric Na content.

Instead, a disordered TLL provides a natural explanation for this unusual crossover from metallic to insulating behaviour. At temperatures T≳t⊥, power-law behaviour in ρ(T) is a signature of TLL behaviour in a q1D metal. Fitting ρ∝Tα in the high-temperature metallic regime of our crystals consistently yields 1<α<1.01 (Fig. 2a). In a clean half-filled TLL, this would correspond to a Luttinger parameter Kρ=(α+3)/4∼1, that is, non-interacting electrons. However, disorder renormalizes the e−–e− interactions: for a commensurate chain of spinless fermions, α=2Kρ−2 and a critical point separates localized from delocalized ground states at Kρ=3/2 (ref. 6). Our experimental values for α therefore indicate that Na2−δMo6Se6 lies close to this critical point. Although the effects of incommensurate band filling on a disordered TLL remain unclear, comparison with clean TLLs suggests that removing electrons reduces Kρ. For 1<Kρ<3/2, ρ(T) is predicted to be metallic at high temperature, before passing through a minimum at Tmin (which rises with increasing disorder) and diverging at lower temperature. These features are consistently reproduced in our data.

Within the disordered TLL paradigm, our high-temperature transport data indicate that the e−–e− interaction is attractive, that is, Kρ>1. This implies that electron–phonon coupling dominates over Coulomb repulsion and suggests that the Coulomb interaction may be intrinsically screened in Na2−δMo6Se6. A quantitative analysis of the low-temperature divergence in ρ(T) provides further support for the influence of disorder, as well as a weak/screened Coulomb repulsion. We have attempted to fit ρ(T) using a wide variety of resistive mechanisms: gap formation (Arrhenius activation), repulsive TLL power laws, weak and strong localization (Supplementary Fig. 4, Supplementary Note III). Among these models, only Mott variable range hopping27 (VRH) consistently provides an accurate description of our data. VRH describes charge transport by strongly-localized electrons: in a d-dimensional material 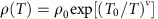Inline graphic, where T0 is the characteristic VRH temperature (which rises as the disorder increases) and ν=(1+d)−1. Although Mott's original model assumed that hopping occurred via inelastic electron–phonon scattering, VRH has also been predicted to occur via e−–e− interactions in disordered TLLs28.

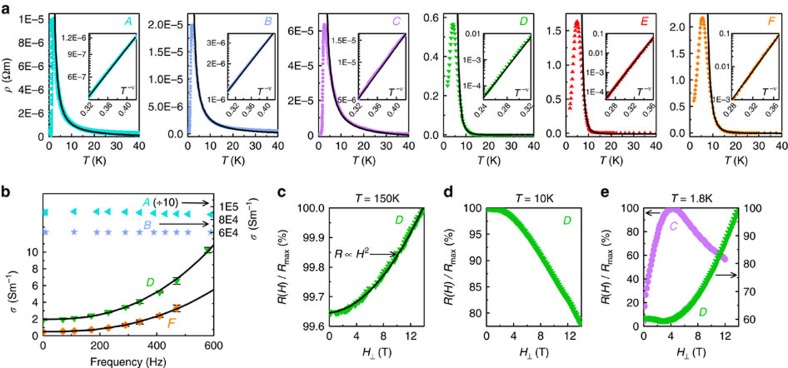
Figure 3a displays VRH fits for crystals A–F, while fits to ρ(T) in three further crystals which cracked during subsequent measurements are shown in Supplementary Fig. 5. All our crystals yield values for d ranging from 1.2 to 1.7 (Supplementary Table I), in good agreement with the d=1.5 predicted for arrays of disordered conducting chains29. Coulomb repulsion in disordered materials opens a soft (quadratic) gap at EF, leading to VRH transport with d=1 regardless of the actual dimensionality. We consistently observe d>1, implying that localized states are present at EF and no gap develops in Na2−δMo6Se6. A small paramagnetic contribution also emerges in the dc magnetization below Tmin and rises non-linearly with 1/T (Supplementary Fig. 6). Similar behaviour has previously been attributed to a progressive crossover from Pauli to Curie paramagnetism due to electron localization (Supplementary Note IV).

Figure 3. Influence of electron localization on the low-temperature electrical transport.

Figure 3

Open in a new tab

(a) Low-temperature divergence in the electrical resistivity ρ(T) for six Na2−δMo6Se6 crystals A–F. Black lines are least-squares fits using a variable range hopping (VRH) model (Supplementary Note III). T0 (and hence the disorder) rises monotonically from crystal A→F. Insets: ρ(T−v) plotted on a semi-logarithmic scale; straight lines indicate VRH behaviour. (b) Frequency-dependent conductivity σ(ω) in crystals A, B, D and F (data points). Error bars correspond to the s.d. in the measured conductivity, that is, our experimental noise level. For the highly-disordered crystals D and F, the black lines illustrate the 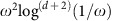Inline graphic trend predicted30 for strongly-localized electrons (using d=1). Data are acquired above Tpk, at T=4.9, 4.9, 4.6, 6 K for crystals A, B, D and F, respectively. (c–e) Normalized perpendicular magnetoresistance (MR) in crystal D (see Methods for details of the magnetic field orientation). At 150 K (c), the effects of disorder are weak and ρ∝H2 due to the open Fermi surface. In the VRH regime at 10 K (d), magnetic fields delocalize electrons due to a Zeeman-induced change in the level occupancy34, leading to a large negative MR. For T<Tpk (e), the high-field MR is positive as superconductivity is gradually suppressed. The weak negative MR below H=3 T may be a signature of enhanced quasiparticle tunnelling: in a spatially-inhomogeneous superconductor, magnetic field-induced pair-breaking in regions where the superconducting order parameter is weak can increase the quasiparticle density and hence reduce the electrical resistance. MR data from crystal C are shown for comparison: here the disorder is lower and H∼4 T destroys superconductivity.

Although ρ(T) exhibits VRH divergence in all crystals prior to peaking at Tpk, a dramatic increase in ρ(Tpk) by 4 orders of magnitude occurs between crystals C and D. This is reminiscent of the rapid rise in resistivity on crossing the mobility edge in disordered 3D materials. Our data are therefore suggestive of a crossover to strong localization and the existence of a critical disorder or ‘q1D mobility edge'. Such behaviour may also originate from proximity to the Kρ=3/2 critical point. Interestingly, the critical disorder approximately correlates with the experimental condition Tmin≈Tx, where Tx is the estimated single-particle dimensional crossover temperature (Fig. 2c). This suggests a possible role for dimensional crossover in establishing the mobility edge.

Further evidence for criticality is seen in the frequency dependence of the conductivity σ(ω) within the divergent ρ(T) regime (Fig. 3b). For crystals with sub-critical disorder, σ(ω) remains constant at low frequency, as expected for a disordered metal. In contrast, σ(ω) in samples with super-critical disorder rises with frequency, following a ω2ln2(1/ω) trend. This is quantitatively compatible with both the Mott–Berezinskii formula for localized non-interacting electrons in 1D30 and the expected behaviour of a disordered chain of interacting fermions6,31. The strong variation of σ(ω) even at sub-kHz frequencies implies that the localization length ξL is macroscopic, in contrast with the 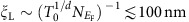Inline graphic expected from Mott VRH theory32. However, it has been predicted that the relevant localization lengthscale for a weakly-disordered q1D crystal is the Larkin (phase distortion) length, which may be exponentially large29.

The evolution of the magnetoresistance (MR) ρ(H) with temperature also supports a localization scenario. Above Tmin, ρ(H) is weakly positive and follows the expected H2 dependence for an open Fermi surface (Fig. 3c). At lower temperature, the divergence in ρ(T) correlates with a crossover to strongly negative MR within the VRH regime (Fig. 3d). The presence of a soft Coulomb gap at EF would lead to a positive MR within the VRH regime33; in contrast, our observed negative MR in Na2−δMo6Se6 corresponds to a delocalization of gapless electronic states34 and provides additional evidence for a screened Coulomb interaction. The MR switches sign again below Tpk and becomes positive (Fig. 3e): as we shall now demonstrate, this is a signature of superconductivity.

Superconducting transitions in Na2−δ Mo6Se6

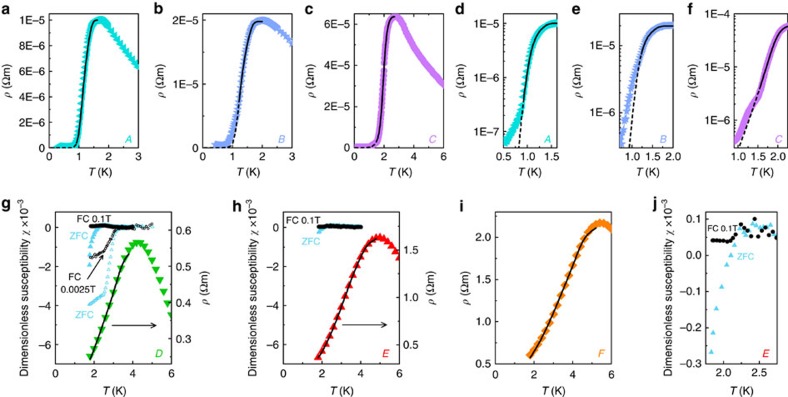
The presence of a superconducting ground state15,16,35 in Tl2Mo6Se6 and In2Mo6Se6 implies that the peak in ρ(T) <6 K is likely to signify the onset of superconductivity in Na2−δMo6Se6. On cooling crystals A–C in a dilution refrigerator, we uncover a two-step superconducting transition characteristic of strongly anisotropic q1D superconductors35,36,37,38 (Fig. 4a–c). Below Tpk, superconducting fluctuations initially develop along individual (Mo6Se6)∞ chains and ρ(T) is well-described by a 1D phase slip model (Supplementary Note V). Subsequently, a weak hump in ρ(T) emerges (Fig. 4d–f) at temperatures ranging from ∼ 0.95 K (crystal A) to ∼ 1.7 K (crystal C). This hump signifies the onset of transverse phase coherence due to inter-chain coupling. Cooper pairs can now tunnel between the chains and a Meissner effect is expected to develop, but we are unable to observe this since 1.7 K lies below the operational range of our magnetometer. Analysis of the current–voltage characteristics indicates that a phase-coherent superconducting ground state is indeed established at low temperature (Supplementary Fig. 7, Supplementary Note VI). We estimate an anisotropy 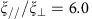Inline graphic in the coherence length, which is lower than the experimental values for Tl2Mo6Se6 and In2Mo6Se6 (13 and 17, respectively16) in spite of the smaller t⊥ in Na2−δMo6Se6 (Supplementary Fig. 2; see Methods for magnetic field orientation details). This anisotropy is also far smaller than the measured conductivity ratio at 300 K: 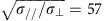Inline graphic. 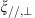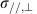In comparison, close agreement is obtained between the anisotropies in Inline graphic and Inline graphic for Li0.9Mo6O17 (ref. 39), where the effects of disorder are believed to be weak8. The disparate anisotropies in Na2−δMo6Se6 arise from a strong suppression of 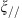Inline graphic, thus illustrating the essential role of disorder in controlling the low-temperature properties of Na2−δMo6Se6.

Figure 4. Resistive and magnetic superconducting transitions in Na2−δMo6Se6.

Figure 4

Open in a new tab

(a–c) Electrical resistivity ρ(T<6 K) for crystals A–C. Coloured points represent experimental data; black lines are fits to a 1D model incorporating thermal and quantum phase slips (Supplementary Note V). (d–f) Zoom views of ρ(T) in crystals A–C, plotted on a semi-logarithmic scale. The low-temperature limit of our 1D phase slip fits is signalled by a hump in ρ(T), highlighted by the transition from solid to dashed black fit lines: this corresponds to the onset of transverse phase coherence. In quasi-one-dimensional (q1D) superconductors, such humps form due to finite-size or current effects during dimensional crossover38. (g–i) ρ(T<6K) for the highly-disordered crystals D–F. Coloured points represent experimental data; black lines are fits to the same 1D phase slip model as in a–c, which accurately reproduces the broad superconducting transitions due to an increased quantum phase slip contribution (Supplementary Note V). Inhomogeneity and spatial fluctuations of the order parameter are expected to blur the characteristic hump in ρ(T) at dimensional crossover, thus explaining its absence from our data as the disorder rises. In g and h, we also plot zero-field-cooled/field-cooled (ZFC/FC) thermal hysteresis loops displaying the Meissner effect in the magnetic susceptibility χ(T); j shows a zoom view of the susceptibility in crystal E. Data were acquired with the magnetic field parallel to the crystal c-axis and a paramagnetic background has been subtracted. The small diamagnetic susceptibilities 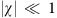Inline graphic are due to emergent pairing inhomogeneity creating isolated superconducting islands11; 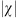Inline graphic is further decreased by the large magnetic penetration depth perpendicular to the c-axis in q1D crystals.

Although superconducting fluctuations are observed regardless of the level of disorder in Na2−δMo6Se6, it is important to identify whether phase-coherent long-range order develops in crystals D–F which exhibit super-critical disorder. In Fig. 4g–i, we demonstrate that ρ(T) in these samples still follows a 1D phase slip model, albeit with a strongly enhanced contribution from quantum phase slips due to the increased disorder40 (Supplementary Note V). The fitting parameters for our 1D phase slip analysis are listed in Supplementary Table II. A weak Meissner effect also develops in the magnetization below ∼ 3.5 K in crystals D and E (Fig. 4g,h,j), but is rapidly suppressed by a magnetic field. Low transverse phase stiffness is common in q1D superconductors: for example, bulk phase coherence in carbon nanotube arrays is quenched by 2–3 T, yet pairing persists up to 28 T36. The superconducting volume fraction corresponding to the magnitude of this Meissner effect is also unusually low: <0.1%. Magnetic measurements of the superconducting volume fraction in q1D materials invariably yield values <100%, since the magnetic penetration depth λab normal to the 1D axis can reach several microns16 and diamagnetic flux exclusion is incomplete. For a typical Na2−δMo6Se6 crystal of diameter d∼100 μm, we estimate that a 0.1% volume fraction would require λc∼10 μm, which seems excessively large. Conversely, an array of phase-fluctuating 1D superconducting filaments would not generate any Meissner effect at all. We therefore attribute the unusually small Meissner signal to inhomogeneity in the superconducting order parameter, which is predicted to emerge in the presence of intense disorder11,12,41,42. In an inhomogeneous superconductor, Meissner screening is achieved via Josephson coupling between isolated superconducting islands43. Within a single super-critically disordered Na2−δMo6Se6 crystal, we therefore anticipate the formation of multiple Josephson-coupled networks comprising individual superconducting filaments. The total magnitude of the diamagnetic screening currents flowing percolatively through each network will be much smaller than that in a homogeneous sample due to the smaller d/λab ratio, thus diminishing the Meissner effect.

Enhancement of superconductivity by disorder

We have established a clear influence of disorder on electrical transport in Na2−δMo6Se6 (Figs 2 and 3) and demonstrated that the peak in ρ(T) at Tpk corresponds to the onset of superconductivity (Fig. 4). Let us now examine the effects of disorder on the superconducting ground state. Figure 5a illustrates Tpk rising monotonically from crystal A to F. Plotting Tpk as a function of ρ(300 K) (which is an approximate measure of the static disorder in each crystal), we observe a step-like feature between crystals C and D, that is, at the critical disorder (Fig. 5b). Strikingly, the characteristic VRH temperature T0 which we extract from our ρ(T) fits (Fig. 3a) displays an identical dependence on ρ(300 K). This implies that disorder controls both the superconducting ground state and the insulating tendency in ρ(T) at low temperature. The positive correlation between Tpk and T0 (Fig. 5c) confirms that the onset temperature for superconducting fluctuations (and hence the pairing energy Δ0) is enhanced by localization in Na2−δMo6Se6. A concomitant increase in the transverse coherence temperature (Supplementary Note VI) implies that some enhancement in the phase stiffness also occurs.

Figure 5. Disorder controls the divergent electrical resistivity and enhances superconductivity.

Figure 5

Open in a new tab

(a) Zoom view of the temperature-dependent electrical resistivity ρ(T) at the onset of superconductivity in all crystals, normalized to ρ(Tpk). (b) Evolution of the characteristic variable range hopping temperature T0 and the superconducting onset temperature Tpk with ρ(300 K). The step at 10−6 Ω m corresponds to the critical disorder, that is, the quasi-one-dimensional mobility edge. Error bars in ρ(300 K) are determined from the experimental noise level and our measurement resolution for the crystal dimensions. The error in T0 corresponds to its s.d., obtained from our variable range hopping fitting routine. (c) Tpk versus T0 for each crystal, confirming the positive correlation between superconductivity and disorder. Data from three additional crystals which broke early during our series of measurements (Supplementary Note III) are also included (black circles). (d,e) Suppression of superconductivity with magnetic field H perpendicular to the c-axis for crystals C (d) and F (e). (f,g) Upper critical field Hc2(T), equivalent to Tpk(H), for crystals C (f) and F (g). Error bars in Hc2(T) correspond to the error in determining the maximum in ρ(T,H). 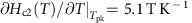Inline graphic and 24 T K−1 for C and F, respectively.

Super-critical disorder furthermore enables superconducting fluctuations to survive in high magnetic fields (Fig. 5d–g). In crystal C (which lies below the q1D mobility edge), superconductivity is completely quenched at all temperatures (that is, Tpk→0) by H=4 T (Fig. 5d,f). A giant negative MR reappears for H>4 T (Fig. 3e), confirming that superconductivity originates from pairing between localized electrons. In contrast, the peak at ρ(Tpk) in the highly-disordered crystal F is strikingly resistant to magnetic fields (Fig. 5e,g): at T=4.6 K, our observed Hc2=14 T, which exceeds the weak-coupling Pauli pair-breaking limit HP=3 T by a factor >4 (see Supplementary Note VII for a derivation of HP(T)). A similar resilience is evident from the positive MR in crystal D, which persists up to at least 14 T at 1.8 K (Fig. 3e). Triplet pairing is unlikely to occur in Na2−δMo6Se6 (since scattering would rapidly suppress a nodal order parameter) and orbital limiting is also suppressed (since vortices cannot form across phase-incoherent filaments). Our data therefore suggest that disorder lifts HP, creating anomalously strong correlations which raise the pairing energy Δ0 (refs 10, 11) above the weak-coupling 1.76 kBTpk. A direct spectroscopic technique would be required to determine the absolute enhancement of Δ0, since spin-orbit scattering from the heavy Mo ions will also contribute to raising HP.

Discussion

The emergence of a superconducting ground state in Na2−δMo6Se6 places further constraints on the origin of the normal-state divergence in ρ(T). Our electronic structure calculations indicate that the q1D Fermi surface of Na2−δMo6Se6 is almost perfectly nested: any incipient electronic DW would therefore gap the entire Fermi surface, creating clear signatures of a gap in ρ(T) and leaving no electrons at EF to form a superconducting condensate. In contrast, our VRH fits and MR data do not support the formation of a DW gap, and a superconducting transition occurs at low temperature. Electrons must therefore remain at EF for all T>Tpk, indicating that ρ(T) diverges due to disorder-induced localization rather than any other insulating instability.

It has been known since the 1950s that an s-wave superconducting order parameter is resilient to disorder44,45, provided that the localization length ξL remains larger than the coherence length (that is, the Cooper pair radius). However, experiments have invariably shown superconductivity to be destroyed by disorder, due to enhanced Coulomb pair-breaking9, phase fluctuations42,46,47 or emergent spatial inhomogeneity10,48. In particular, increasing disorder in Li0.9Mo6O17 (one of the few q1D superconductors extensively studied in the literature) monotonically suppresses superconductivity49. Therefore, the key question arising from our work is why the onset temperature for superconductivity rises with disorder in Na2−δMo6Se6, in contrast to all other known materials?

Disorder acts to enhance the matrix element for e−–e− interactions. This may be explained qualitatively by considering that all conduction electron wavefunctions experience the same disorder-induced potential, developing inhomogeneous multifractal probability densities50 and hence becoming spatially correlated. Such enhanced correlations have been predicted to increase the Cooper pairing energy10: in the absence of pair-breaking by long-ranged Coulomb interactions, this will lead to a rise in the superconducting transition temperature11,12,13,51,52. A proposal to observe this effect in superconducting heterostructures with built-in Coulomb screening51 (by depositing superconducting thin films on substrates with high dielectric constants) has not yet been experimentally realised. However, our VRH dimensionality d>1 (Fig. 3a) and negative MR (Fig. 3d,e) both point towards a weak or screened Coulomb repulsion, while the power laws and broad minima in ρ(T) at high temperature (Fig. 2a) indicate a Luttinger parameter Kρ>1. These results all imply that e−–e− interactions in Na2−δMo6Se6 are attractive. (For comparison, Kρ∼0.25 in Li0.9Mo6O17 and the e−–e− interaction is repulsive7,8.) Phonon-mediated coupling—the Cooper channel—therefore appears to dominate over the Coulomb repulsion in Na2−δMo6Se6, suggesting that the usual disorder-induced Coulomb pair-breaking may be avoided. Below the q1D mobility edge, our rise in Tpk is quantitatively compatible with a weak multifractal scenario (Supplementary Fig. 8, Supplementary Note VIII), providing a possible explanation for the enhancement of superconductivity which merits further theoretical attention.

The fact that no experimental examples of q1D materials with attractive e−–e− interactions have yet been reported poses the question why Na2−δMo6Se6 should be different. Although strong electron–phonon coupling is known to play an important role in the physics of molybdenum cluster compounds16,53, we propose that the disordered q1D nature of Na2−δMo6Se6 may instead play the dominant role, by suppressing the Coulomb repulsion. In the presence of disorder, a q1D material can be regarded as a parallel array of ‘interrupted strands'54, that is, a bundle of finite-length nanowires. The electric polarizability of metallic nanoparticles is strongly enhanced relative to bulk materials55, although this effect is usually cancelled out by self-depolarization. The geometric depolarization factor vanishes for q1D symmetry, leading to giant dielectric constants ɛ which rise as the filament length increases56. This effect was recently observed in Au nanowires57, with ɛ reaching 107. In Na2−δMo6Se6, we therefore anticipate that the long-range Coulomb repulsion in an individual (Mo6Se6)l filament (l<∞) will be efficiently screened by neighbouring filaments29. This intrinsic screening provides a natural explanation for attractive e−–e− interactions and suppresses Coulomb pair-breaking in the superconducting phase.

It has been suggested that impurities can increase the temperature at which transverse phase coherence is established in q1D superconductors58. This effect cannot be responsible for our observed rise in Tpk, which corresponds to the onset of 1D superconducting fluctuations on individual (Mo6Se6)l filaments. We also point out that the finite-size effects which influence critical temperatures in granular59 or nanomaterials60 are not relevant in Na2−δMo6Se6: quantum confinement is absent in homogeneously-disordered crystalline superconductors and hence no peaks form in N(EF). These mechanisms are discussed in detail in Supplementary Note IX.

In summary, we have presented experimental evidence for the enhancement of superconductivity by disorder in Na2−δMo6Se6. The combination of q1D crystal symmetry (and the associated dimensional crossover), disorder and incommensurate band filling in this material poses a challenge to existing 1D/q1D theoretical models. Although the normal-state electrical resistivity of Na2−δMo6Se6 is compatible with theories for disordered 1D systems with attractive e−–e− interactions, we establish several unusual low-temperature transport properties which deserve future attention. These include a resistivity which diverges following a q1D VRH law for all levels of disorder, the existence of a critical disorder or q1D mobility edge where Tmin≈Tx, and a strongly frequency-dependent conductivity σ(ω)∼ω2 in crystals with super-critical disorder. At temperature Tpk, 1D superconducting fluctuations develop, and a phase-coherent ground state is established via coupling between 1D filaments at lower temperature. As the disorder rises, Tpk increases: in our most-disordered crystals, the survival of superconducting fluctuations in magnetic fields at least four times larger than the Pauli limit suggests that the pairing energy may be unusually large.

We conclude that deliberately introducing disorder into q1D crystals represents a new path towards engineering correlated electron materials, in remarkable contrast with the conventional blend of strong Coulomb repulsion and a high density of states. Beyond enhancing superconductivity, the ability to simultaneously modulate band filling, disorder and dimensionality promises a high level of control over emergent order, including DWs and magnetic phases. More generally, Na2−δMo6Se6 and other similar interrupted strand materials may be ideal environments in which to study the evolution of many-body electron localization beyond the non-interacting Anderson limit.

Methods

Crystal growth and initial characterization

A series of Na2−δMo6Se6 crystals was grown using a solid-state synthesis procedure. The precursor materials were MoSe2, InSe, Mo and NaCl, all in powder form. Before use, the Mo powder was reduced under H2 gas flowing at 1,000 °C for 10 h, to eliminate any trace of oxygen. The MoSe2 was prepared by reacting Se with H2-reduced Mo in a ratio 2:1 inside a purged, evacuated and flame-baked silica tube (with a residual pressure of ∼10−4 mbar argon), which was then heated to ∼700 °C for 2 days. InSe was synthesized from elemental In and Se in an evacuated sealed silica tube at 800 °C for 1 day. Powder samples of Na2−δMo6Se6 were prepared in two steps. First, In2Mo6Se6 was synthesized from a stoichiometric mixture of InSe, MoSe2 and Mo, heated to 1,000°C in an evacuated sealed silica tube for 36 h. Second, an ion exchange reaction of In2Mo6Se6 with NaCl was performed at 800 °C, using a 10% NaCl excess to ensure total exchange as described in ref. 61. All starting reagents were found to be monophase on the basis of their powder XRD patterns, acquired using a D8 Bruker Advance diffractometer equipped with a LynxEye detector (CuKα1 radiation). Furthermore, to avoid any contamination by oxygen and moisture, the starting reagents were kept and handled in a purified argon-filled glovebox.

To synthesize single crystals, a Na2−δMo6Se6 powder sample (of mass ∼5 g) was cold-pressed and loaded into a molybdenum crucible, which had previously been outgassed at 1,500 °C for 15 min under a dynamic vacuum of ∼10−5 mbar. The Mo crucible was subsequently sealed under a low argon pressure using an arc-welding system. The Na2−δMo6Se6 powder charge was heated at a rate of 300 °C h−1 up to 1,750 °C, held at this temperature for 3 h, then cooled at 100 °C h−1 down to 1,000 °C and finally cooled naturally to room temperature within the furnace. Crystals obtained using this procedure have a needle-like shape with length up to 4 mm and a hexagonal cross-section with typical diameter ≤150 μm. Initial semi-quantitative microanalyses using a JEOL JSM 6400 scanning electron microscope equipped with an Oxford INCA EDX spectrometer indicated that the Na contents ranged between 1.7 and 2, that is, up to 15% deficiency. The Na deficiency results from the high temperatures used during the crystal growth process coupled with the small size of the Na ion: it cannot be accurately controlled within the conditions necessary for crystal growth.

Since In2Mo6Se6 is known to be superconducting below 2.85 K16, it is important to consider the possibility of In contamination in our samples. The Na/In ion exchange technique used during synthesis is known to be highly efficient61,62 and In2Mo6Se6 decomposes above 1,300 °C, well below our crystal growth temperature (1,750 °C). This precludes the presence of any superconducting In2Mo6Se6 (or In-rich (In,Na)2Mo6Se6) filaments in our crystals. Diffuse X-ray scattering measurements accordingly reveal none of the Huang scattering or disk-like Bragg reflections which would be produced by such filaments. Furthermore, EDX spectrometry is unable to detect any In content in our crystals, while inductively-coupled plasma mass spectrometry indicates a typical In residual of <0.01%, that is, <0.0002 In atoms per unit cell. The electronic properties of Na2−δMo6Se6 crystals will remain unaffected by such a tiny In residual in solid solution.

Electrical transport measurements

Before all measurements, the as-grown crystal surfaces were briefly cleaned with dilute hydrochloric acid (to remove any residue from the Mo crucible and hence minimize the contact resistance), followed by distilled water, acetone and ethanol. Four Au contact pads were sputtered onto the upper surface and sides of each crystal using an Al foil mask; 50 μm Au wires were then glued to these pads using silver-loaded epoxy cured at 70 °C (Epotek E4110). Special care was taken to thoroughly coat each end of the crystal with epoxy, to ensure that the measurement current passed through the entire crystal. All contacts were verified to be Ohmic at room temperature before and after each series of transport measurements, and at T=4 K after cooling. Typical contact resistances were of the order of 2 Ω at 300 K. The transverse conductivity σ⊥ was estimated at room temperature using a four-probe technique, with contacts on opposite hexagonal faces of a single crystal. The temperature dependence of the transverse resistivity ρ⊥(T) has never been accurately measured in M2Mo6Se6 due to the exceptionally large anisotropies, small crystal diameters and high fragility, even in the least anisotropic Tl2Mo6Se6 which forms the largest crystals15.

Low-frequency four-wire ac conductivity measurements were performed in two separate cryogen-free systems: a variable temperature cryostat and a dilution refrigerator, both of which may be used in conjunction with a superconducting vector magnet. The ac conductivity was measured using a Keithley 6100 current source, a Stanford SRS850 lock-in amplifier with input impedance 10 MΩ and (for low resistances, that is, weakly-disordered samples) a Stanford SR550 preamplifier with input impedance 100 MΩ. Data from several crystals were cross-checked using a Quantum Design Physical Property Measurement System with the standard inbuilt ac transport hardware: both methods generate identical, reproducible data. With the exception of the frequency-dependence studies in Fig. 3b, all the transport data which we present in our manuscript are acquired with an ac excitation frequency of 1 Hz, that is, we are measuring in the dc limit. At 1 Hz, the phase angle remained zero at all temperatures in all crystals. Therefore, no extrinsic capacitance effects are present in our data.

The typical resistance of a weakly-disordered crystal lies in the 1–10 Ω range. In contrast, the absolute resistances of crystals D–F at Tpk are 41.9 kΩ, 33.7 kΩ and 27.6 kΩ, respectively: the crystal diameter increases from D to F, thus explaining the rise in resistivity despite a fall in resistance. These values remain much smaller than our lock-in amplifier input impedance, ruling out any current leakage in highly-disordered crystals. Our measurement current Iac=10 μA leads to a maximum power dissipation <10 μW. This is negligible compared with the ∼2 mW cooling power at 2 K on our cryostat cold finger and we may hence rule out any sample heating effects in our data.

We acquire transverse magnetotransport data (Fig. 3c–e, Fig. 5d–g) with the magnetic field perpendicular to both the c-axis and the crystal faces, that is, at 30° to the hexagonal a axis. Q1D Bechgaard salts and blue/purple bronzes exhibit monoclinic crystal symmetry, and hence strong anisotropies along all three crystallographic axes. In contrast, M2Mo6Se6 crystallize in a hexagonal lattice: any azimuthal (⊥c) anisotropy in Na2−δMo6Se6 will therefore reflect this hexagonal symmetry. In Tl2Mo6Se6, this anisotropy has been variously reported to be small or entirely absent: it is at least an order of magnitude lower than the polar anisotropy at low temperature63. Our conclusions regarding the reduced low-temperature anisotropy in Na2−δMo6Se6 are therefore robust.

In common with most highly 1D materials, Na2−δMo6Se6 crystals are extremely fragile, with a tendency to split into a forest of tangled fibres if mishandled. The crystals therefore exhibit a finite experimental lifetime, with thermal cycling from 2 K to room temperature presenting a particular risk to their structural integrity: this explains why we were unable to obtain complete data sets in crystals A–F (the MR ρ(H) at high temperature in crystal C and χ(T) in Crystal F are missing, for example).

Data availability

The authors declare that the data supporting the findings of this study are available within the article and its Supplementary Information files.

Additional information

How to cite this article: Petrović, A. P. et al. A disorder-enhanced quasi-one-dimensional superconductor. Nat. Commun. 7:12262 doi: 10.1038/ncomms12262 (2016).

Supplementary Material

Supplementary Information

Supplementary Figures 1-8, Supplementary Tables 1-2, Supplementary Notes 1-9 and Supplementary References

ncomms12262-s1.pdf (1.9MB, pdf)

Acknowledgments

We thank Alexei Bosak (Beamline ID28, ESRF Grenoble) for assistance with data collection and processing, and Igor Burmistrov, Vladimir Kravtsov, Tomi Ohtsuki and Vincent Sacksteder IV for stimulating discussions. The Swiss-Norwegian Beamlines (ESRF Grenoble) are acknowledged for beam time allocation. This work was supported by the National Research Foundation, Singapore, through Grant NRF-CRP4-2008-04.

Footnotes

Author contributions A.P.P. and C.P. conceived the project; D.S., P.G. and M.P. grew the crystals; D.C. performed the XRD measurements with M.H. and A.P.P.; D.A. carried out the transport experiments; A.P.P. and D.A. analysed the data; L.B. contributed the electronic structure calculations; A.P.P., D.A. and C.P. wrote the paper with input from all the authors; C.P. supervised the entire project.

References

  1. Landau L. D. The theory of a Fermi liquid. Sov. Phys. JETP 3, 920–925 (1957). [Google Scholar]
  2. Tomonaga S.-I. Remarks on Bloch's method of sound waves applied to many-fermion problems. Prog. Theor. Phys. 5, 544–569 (1950). [Google Scholar]
  3. Luttinger J. M. An exactly soluble model of a many-fermion system. J. Math. Phys. 4, 1154–1162 (1963). [Google Scholar]
  4. Boies D., Bourbonnais C. & Tremblay A.-M. One-particle and two-particle instability of coupled Luttinger liquids. Phys. Rev. Lett. 74, 968–971 (1995). [DOI] [PubMed] [Google Scholar]
  5. Carr S. T. & Tsvelik A. M. Superconductivity and charge-density waves in a quasi-one-dimensional spin-gap system. Phys. Rev. B 65, 195121 (2001). [Google Scholar]
  6. Giamarchi T. Quantum Physics in One Dimension Clarendon Press, (2003). [Google Scholar]
  7. Wakeham N. et al. Gross violation of the Wiedemann-Franz law in a quasi-one-dimensional conductor. Nat. Commun. 2, 396 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Chudzinski P., Jarlborg T. & Giamarchi T. Luttinger-liquid theory of purple bronze Li0.9Mo6O17 in the charge regime. Phys. Rev. B 86, 075147 (2012). [Google Scholar]
  9. Finkel'stein A. M. Superconducting transition temperature in amorphous films. JETP Lett. 45, 46–49 (1987). [Google Scholar]
  10. Ghosal A., Randeria M. & Trivedi N. Inhomogeneous pairing in highly disordered s-wave superconductors. Phys. Rev. B 65, 014501 (2001). [Google Scholar]
  11. Feigel'man M. V., Ioffe L. B., Kravtsov V. E. & Yuzbashyan E. A. Eigenfunction fractality and pseudogap state near the superconductor-insulator transition. Phys. Rev. Lett. 98, 027001 (2007). [DOI] [PubMed] [Google Scholar]
  12. Feigel'man M. V., Ioffe L. B., Kravtsov V. E. & Cuevas E. Fractal superconductivity near localization threshold. Ann. Phys. 325, 1390–1478 (2010). [Google Scholar]
  13. Kravtsov V. E. Wonderful life at weak Coulomb interaction: increasing of superconducting/superfluid transition temperature by disorder. J. Phys. Conf. Ser. 376, 012003 (2012). [Google Scholar]
  14. Potel M. et al. New pseudo-one-dimensional metals: M2Mo6Se6 (M=Na, In, K, Tl), M2Mo6S6 (M=K, Rb, Cs), M2Mo6Te6 (M=In, Tl). J. Solid State Chem. 35, 286–290 (1980). [Google Scholar]
  15. Armici J. C. et al. A new pseudo-one-dimensional superconductor: Tl2Mo6Se6. Solid State Commun. 33, 607–611 (1980). [Google Scholar]
  16. Petrović A. P. et al. Phonon mode spectroscopy, electron–phonon coupling, and the metal-insulator transition in quasi-one-dimensional M2Mo6Se6. Phys. Rev. B 82, 235128 (2010). [Google Scholar]
  17. Tarascon J. M., DiSalvo F. J. & Waszczak J. V. Physical properties of several M2Mo6X6 compounds. Solid State Commun. 52, 227–231 (1984). [Google Scholar]
  18. Sato M., Matsuda Y. & Fukuyama H. Localization and superconductivity in Li0.9Mo6O17. J. Phys. C Solid State Phys. 20, L137–L142 (1987). [Google Scholar]
  19. Narduzzo A., Enayati-Rad A., Horii S. & Hussey N. E. Possible coexistence of local itinerancy and global localization in a quasi-one-dimensional conductor. Phys. Rev. Lett. 98, 146601 (2007). [DOI] [PubMed] [Google Scholar]
  20. Enayati-Rad A., Narduzzo A., Rullier-Albenque F., Horii S. & Hussey N. E. Irradiation-induced confinement in a quasi-one-dimensional metal. Phys. Rev. Lett. 99, 136402 (2007). [DOI] [PubMed] [Google Scholar]
  21. Khim S. et al. Enhanced upper critical fields in a new quasi-one-dimensional superconductor Nb2PdxSe5. New J. Phys. 15, 123031 (2013). [Google Scholar]
  22. Lu Y. F. et al. Superconductivity at 6K and the violation of Pauli limit in Ta2PdxS5. J. Phys. Soc. Jpn. 83, 023702 (2014). [Google Scholar]
  23. dos Santos C. et al. Electrical transport in single-crystalline Li0.9Mo6O17: a two-band Luttinger liquid exhibiting Bose metal behavior. Phys. Rev. B 77, 193106 (2008). [Google Scholar]
  24. dos Santos C., White B., Yu Y.-K., Neumeier J. & Souza J. Dimensional crossover in the purple bronze Li0.9Mo6O17. Phys. Rev. Lett. 98, 266405 (2007). [DOI] [PubMed] [Google Scholar]
  25. Xu X. et al. Directional field-induced metallization of quasi-one-dimensional Li0.9Mo6O17. Phys. Rev. Lett. 102, 206602 (2009). [DOI] [PubMed] [Google Scholar]
  26. Ong N. P. & Monceau P. Anomalous transport properties of a linear-chain metal: NbSe3. Phys. Rev. B 16, 3443–3455 (1977). [Google Scholar]
  27. Mott N. F. Conduction in non-crystalline materials. Phil. Mag. 19, 835–852 (1969). [Google Scholar]
  28. Nattermann T., Giamarchi T. & Le Doussal P. Variable-range hopping and quantum creep in one dimension. Phys. Rev. Lett. 91, 056603 (2003). [DOI] [PubMed] [Google Scholar]
  29. Fogler M. M., Teber S. & Shklovskii B. I. Variable-range hopping in quasi-one-dimensional electron crystals. Phys. Rev. B 69, 035413 (2004). [Google Scholar]
  30. Klein A., Lenoble O. & Müller P. On Mott's formula for the ac-conductivity in the Anderson model. Ann. Math. 166, 549–577 (2007). [Google Scholar]
  31. Fukuyama H. & Lee P. A. Dynamics of the charge-density wave. I. Impurity pinning in a single chain. Phys. Rev. B 17, 535–541 (1978). [Google Scholar]
  32. Shklovskii B. I. & Efros A. L. Electronic Properties of Doped Semiconductors Springer-Verlag (1984). [Google Scholar]
  33. Efros A. L. & Shklovskii B. I. Coulomb gap and low temperature conductivity of disordered systems. J. Phys. C Solid State Phys. 8, L49–L51 (1975). [Google Scholar]
  34. Fukuyama H. & Yosida K. Negative magnetoresistance in the Anderson localized states. J. Phys. Soc. Jpn. 46, 102–105 (1979). [Google Scholar]
  35. Bergk B. et al. Superconducting transitions of intrinsic arrays of weakly coupled one-dimensional superconducting chains: the case of the extreme quasi-1D superconductor Tl2Mo6Se6. New J. Phys. 13, 103018 (2011). [Google Scholar]
  36. Wang Z., Shi W., Lortz R. & Sheng P. Superconductivity in 4-Angstrom carbon nanotubes - a short review. Nanoscale 4, 21–41 (2012). [DOI] [PubMed] [Google Scholar]
  37. He M. et al. 1D to 3D dimensional crossover in the superconducting transition of the quasi-one-dimensional carbide superconductor Sc3CoC4. J. Phys. Condens. Matter 27, 075702 (2015). [DOI] [PubMed] [Google Scholar]
  38. Ansermet D. et al. Reentrant phase coherence in superconducting nanowire composites. ACS Nano 10, 515–523 (2016). [DOI] [PubMed] [Google Scholar]
  39. Mercure J.-F. et al. Upper critical magnetic field far above the paramagnetic pair-breaking limit of superconducting one-dimensional Li0.9Mo6O17 single crystals. Phys. Rev. Lett. 108, 187003 (2012). [DOI] [PubMed] [Google Scholar]
  40. Altomare F. & Chang A. One-Dimensional Superconductivity in Nanowires Wiley (2013). [Google Scholar]
  41. Ghosal A., Randeria M. & Trivedi N. Role of spatial amplitude fluctuations in highly disordered s-wave superconductors. Phys. Rev. Lett. 81, 3940–3943 (1998). [Google Scholar]
  42. Dubi Y., Meir Y. & Avishai Y. Nature of the superconductor-insulator transition in disordered superconductors. Nature 449, 876–880 (2007). [DOI] [PubMed] [Google Scholar]
  43. Beloborodov I. S., Lopatin A. S., Vinokur V. M. & Efetov K. B. Granular electronic systems. Rev. Mod. Phys. 79, 469–518 (2007). [Google Scholar]
  44. Abrikosov A. A. & Gor'kov L. P. Superconducting alloys at finite temperatures. Sov. Phys. JETP 36, 319–320 (1959). [Google Scholar]
  45. Anderson P. W. Theory of dirty superconductors. J. Phys. Chem. Solids 11, 26–30 (1959). [Google Scholar]
  46. Kapitulnik A. & Kotliar G. Anderson localization and the theory of dirty superconductors. Phys. Rev. Lett. 54, 473–476 (1985). [DOI] [PubMed] [Google Scholar]
  47. Fisher M. P. A. Quantum phase transitions in disordered two-dimensional superconductors. Phys. Rev. Lett. 65, 923–926 (1990). [DOI] [PubMed] [Google Scholar]
  48. Bouadim K., Loh Y. L., Randeria M. & Trivedi N. Single- and two-particle energy gaps across the disorder-driven superconductor-insulator transition. Nat. Phys. 7, 884–889 (2011). [Google Scholar]
  49. Matsuda Y., Sato M., Onoda M. & Nakao K. On the anomalous transport properties of Li0.9Mo6O17. J. Phys. C Solid State Phys. 19, 6039–6052 (1986). [Google Scholar]
  50. Aoki H. Critical behaviour of extended states in disordered systems. J. Phys. C Solid State Phys. 16, L205–L208 (1983). [Google Scholar]
  51. Burmistrov I. S., Gornyi I. V. & Mirlin A. D. Enhancement of the critical temperature of superconductors by Anderson localization. Phys. Rev. Lett. 108, 017002 (2012). [DOI] [PubMed] [Google Scholar]
  52. Mayoh J. & Garca-Garca A. M. Global critical temperature in disordered superconductors with weak multifractality. Phys. Rev. B 92, 174526 (2015). [Google Scholar]
  53. Fischer Ø. Chevrel phases: superconducting and normal state properties. Appl. Phys. 16, 1–28 (1978). [Google Scholar]
  54. Kuse D. & Zeller H. Evidence for one-dimensional metallic behavior in K2Pt(CN)4Br0.3.(H2O)n. Phys. Rev. Lett. 27, 1060–1063 (1971). [Google Scholar]
  55. Gor'kov L. P. & Eliashberg G. M. Minute metallic particles in an electromagnetic field. Sov. Phys. JETP 21, 940–947 (1965). [Google Scholar]
  56. Rice M. J. & Bernasconi J. Gor'kov-Eliashberg effect in one-dimensional metals? Phys. Rev. Lett. 29, 113–116 (1972). [Google Scholar]
  57. Saha S. K., DaSilva M., Hang Q., Sands T. & Janes D. B. A nanocapacitor with giant dielectric permittivity. Nanotechnology 17, 2284–2288 (2006). [Google Scholar]
  58. Efetov K. B. & Larkin A. I. Effect of fluctuations on the transition temperature in quasi-one-dimensional superconductors. Sov. Phys. JETP 39, 1129–1134 (1974). [Google Scholar]
  59. Abeles B., Cohen R. W. & Cullen G. W. Enhancement of superconductivity in metal films. Phys. Rev. Lett. 17, 632–634 (1966). [Google Scholar]
  60. Bose S. et al. Observation of shell effects in superconducting nanoparticles of Sn. Nat. Mater. 9, 550–554 (2010). [DOI] [PubMed] [Google Scholar]
  61. Potel M., Gougeon P., Chevrel R. & Sergent M. Labilité des cations dans les chalcogénures ternaires de molybdène: voies d'accès à de nouvelles synthèses. Rev. Chim. Min. 21, 509–536 (1984). [Google Scholar]
  62. Tarascon J. M., Hull G. W. & DiSalvo F. J. A facile synthesis of pseudo one-monodimensional ternary molybdenum chalcogenides M2Mo6X6 (X=Se,Te; M=Li,Na..Cs). Mater. Res. Bull. 19, 915–924 (1984). [Google Scholar]
  63. Lepetit R., Monceau P., Potel M., Gougeon P. & Sergent M. Superconductivity of the linear chain compound Tl2Mo6Se6. J. Low Temp. Phys. 56, 219–235 (1984). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Figures 1-8, Supplementary Tables 1-2, Supplementary Notes 1-9 and Supplementary References

ncomms12262-s1.pdf (1.9MB, pdf)

Data Availability Statement

The authors declare that the data supporting the findings of this study are available within the article and its Supplementary Information files.

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES