Abstract.
Magnetic resonance-guided high intensity focused ultrasound treatment of the liver is a promising noninvasive technique for ablation of liver lesions. For the technique to be used in clinical practice, however, the issue of liver motion needs to be addressed. A subject-specific four-dimensional liver motion model is presented that is created based on registration of dynamically acquired magnetic resonance data. This model can be used for predicting the tumor motion trajectory for treatment planning and to indicate the tumor position for treatment guidance. The performance of the model was evaluated on a dynamic scan series that was not used to build the model. The method achieved an average Dice coefficient of 0.93 between the predicted and actual liver profiles and an average vessel misalignment of 3.0 mm. The model performed robustly, with a small variation in the results per subject. The results demonstrate the potential of the model to be used for MRI-guided treatment of liver lesions. Furthermore, the model can possibly be applied in other image-guided therapies, for instance radiotherapy of the liver.
Keywords: liver motion model, magnetic resonance imaging, registration, dynamic data
1. Introduction
Magnetic resonance-guided high intensity focused ultrasound (MR-HIFU) heating is a new noninvasive technique for ablative tumor treatment and local drug delivery. It is currently routinely used in the clinic for the ablation of uterine fibroids 1–5 and as a palliative treatment for painful bone metastases.6–11 Furthermore, MR-HIFU could potentially be applied to treat lesions in abdominal organs. Although such procedures are still in the developmental stage, clinical case studies have already been performed,12,13 indicating the need for reliable motion compensation.
During HIFU ablation, a focused ultrasound beam is used to heat tumor tissue. The deposited energy causes temperature elevation in the tissue and finally induces coagulative necrosis and apoptosis of tumor cells. In MR-HIFU, the temperature is monitored by MR temperature mapping, which is most commonly realized by fast multistack two-dimensional (2-D) MR image acquisition. For application of MR-HIFU to liver tumor ablation, one major obstacle is liver motion. The liver moves and deforms considerably during breathing. Since targeted therapy on moving organs requires knowledge of the tumor position for multiple phases of the respiratory cycle, it would be beneficial to have that information available before and during treatment. Image-guided therapies often rely on real-time imaging to provide information about the tumor position.14–16 The beam geometry can be updated during treatment according to the tumor motion, or gated therapy can be performed. In the case of a continuous updating process, fast image registration can be performed to track the tumor, possibly aided by fiducial markers that are implanted near the tumor. A different approach is to use a model that predicts the tumor position. This model can be built offline prior to treatment and does not necessarily depend on imaging during treatment. Also, treatment planning can be improved by using such a model to assess the feasibility of MR-HIFU treatment for a specific patient and to optimize the beam geometry. During treatment, the model could be used to either adjust the ultrasound beam according to the tumor position or to modulate the power in case of gated therapy.
The liver moves during the respiratory cycle. From earlier studies, it is known that the most significant component of liver motion is translation in the feet-head (FH)-direction. This translation was shown to vary between human subjects from 10 to 30 mm during normal breathing.17 In addition, translation was found to range from 1 to 12 mm in the anterior–posterior (AP)-direction and from 1 to 3 mm in the left-right (LR)-direction.17–19 Furthermore, friction with surrounding organs can cause an additional local deformation of up to 3 mm.20 Finally, there is a small continuous change of position of the liver over time, called drift.20,21 This drift is mainly caused by gravity and muscle relaxation. The drift predominantly occurs in the superior direction when in a supine position,20,22 but a small drift in other directions was also described in Ref. 23. The mean magnitude of the drift was found to vary between 2.4 and 7.1 mm over time periods of more than an hour by Ref. 22. However, the maximum displacement caused by the drift can be larger than 15 mm.20,22
In the literature, several liver motion models have been introduced which may be divided into subject-specific models and population-based models. Approaches for population-based models used statistical modeling 21 or biomechanical modeling.24 Although these models show promising results, it is difficult to adjust such a model to subject-specific deviations. Samei et al. 25 combined free-breathing four-dimensional (4-D) MRI acquisition with nonrigid registration to create an exemplar model that could be adapted to an unseen subject. The robustness of this exemplar model to outliers in the breathing pattern was demonstrated. However, such a model needs input from many different subjects in order to capture all possible intersubject variations in the motion pattern. A significant improvement was shown by combining the exemplar model with a subject-specific model based on principal component analysis. In Preiswerk et al.,26 a population-based statistical model (as described in their previous work21) was combined with information from 2-D ultrasound sequences on which tracking of manually placed landmarks was performed. It was shown that this method could predict the motion of the right liver lobe accurately. Given the large intersubject variability in liver motion,17,27 building a subject-specific model offline prior to treatment will ensure that the model is tuned to the characteristics of that patient. Patients undergoing liver treatment may show a nonaverage liver motion pattern, due to the presence of tumors varying in location and size, cirrhosis, or a history of liver surgery. Such deviations are not an issue for a patient-specific model, since this is exclusively built on data of that patient.
Subject- or patient-specific models have been investigated by Rohlfing et al. 28 and Siebenthal et al.18 Both studies used registration of dynamic MRI data of a single patient to obtain a patient-specific model. In Ref. 28, a prospectively gated three-dimensional (3-D) MRI protocol was used, depicting the liver in ten different stages in the breathing cycle. Although such a scanning protocol provides accurate information on liver motion, the duration of the data acquisition of is considerable, whereas time is often limited in clinical practice. In Ref. 18, multi2-D + t MRI acquisition was used, which yielded a collection of unsorted 2-D images. A retrospective slice stacking method was developed based on navigator frames that were acquired in between the 2-D slices. On these frames, regions of interest were selected manually to calculate the displacements. The motion correction method proposed in Ref. 29 also used retrospective slice stacking based on image similarities. In Ref. 30, a slice stacking method was proposed using manifold learning. This technique was shown to outperform methods based on one-dimensional (1-D) pencil beam navigators and image-based methods. In Ref. 31, the liver motion was predicted by creating a look-up table of liver states during an average motion cycle, based on optical-flow registration of 2-D liver images. This method was developed for 2-D motion prediction. In Ref. 32, a subject-specific statistical model was proposed, based on free-form registration and principal component analysis. In Ref. 33, nonrigid registration of six 3-D MRI volumes was performed to obtain a liver motion model. The reference 3-D MRI volume was then registered to 2-D intraoperative ultrasound images acquired during free breathing. For this registration, the model was used to constrain the alignment. More recently, a method that used external information on the breathing depth combined with ultrasound speckle information was developed to predict the liver motion.34 For each ultrasound frame, a motion vector was determined by the model. This motion vector was assumed to be valid for the entire image such that local deformations were ignored. Furthermore, in Ref. 35, an extensive overview of respiratory motion models in general is given, describing their use, the data acquisition, the fitting methods, and issues that arise when using such models.
In this paper, we describe a clear and fast method to obtain a subject-specific 4-D liver motion model. In our approach, 2-D dynamic data are used in a similar way to the abovementioned methods to build a motion model of the entire liver. In contrast to these methods, the data acquisition is performed at six locations in the liver only and does not include navigator frames, which reduces the amount of data and the total acquisition time considerably. The building of the model is automatic; it does not require any manually selected regions of interest or landmarks, as in Ref. 18. The model includes nonrigid deformations to accurately describe the motion of the entire liver.
2. Materials and Methods
2.1. Data Acquisition
MRI scans were obtained of 18 healthy volunteers, aged from 20 to 30 years. In accordance with local regulations in the hospital, the volunteers were screened for contraindications and informed about possible risks. All MRI scans were acquired on a clinical 1.5-T MR scanner (Achieva, Philips Healthcare Best, The Netherlands). The volunteers were scanned in a prone position, as would most likely be the position during MR-HIFU treatment of the liver. For each volunteer, a transverse 3-D T1-weighted spoiled gradient echo scan with spectral attenuated inversion recovery (SPAIR) fat suppression was acquired during a breathhold at inspiration, with the following scan parameter settings: , flip angle 30 deg, acquired voxel size , slice gap (overcontiguous slices), acquisition matrix , half-scan in-plane factor 0.7 and through-plane factor 0.85, and acquisition time 22.5 s. In addition, a series of 200 dynamically acquired multislice scans with six slices was recorded. This was a dynamic multislice sagittal spoiled gradient echo scan with SPAIR fat suppression, with the following parameter settings: , flip angle 30 deg, acquired in-plane voxel size , slice thickness 8 mm, temporal resolution 1800 ms, acquisition matrix , six slices, 200 dynamics, and total acquisition time 369 s. The six slices were placed at equidistant locations in the liver, with a 15-mm gap in between them. The dynamics were acquired interleaved over these six locations during free breathing, at an interval of 1.8 s. The volunteers did not receive breathing instructions, other than to breathe normally. In total, 1200 dynamics were acquired, resulting in 200 dynamics at each location. Finally, an additional sagittal single 2-D dynamic sequence was acquired, which was identical to the scan acquired with the dynamic protocol mentioned above with the same orientation. This series consisted of 150 dynamics and was acquired at a different location in the liver, for validation of the model, as will be explained in Sec. 2.3. For one volunteer, this evaluation sequence was performed in both the sagittal and the coronal direction.
2.2. Methods
The aim was to obtain a model of one average motion cycle of the entire liver. This average motion cycle should consist of a number of deformations that could be applied to a 3-D liver volume obtained from other data to show the entire liver in a specific state.
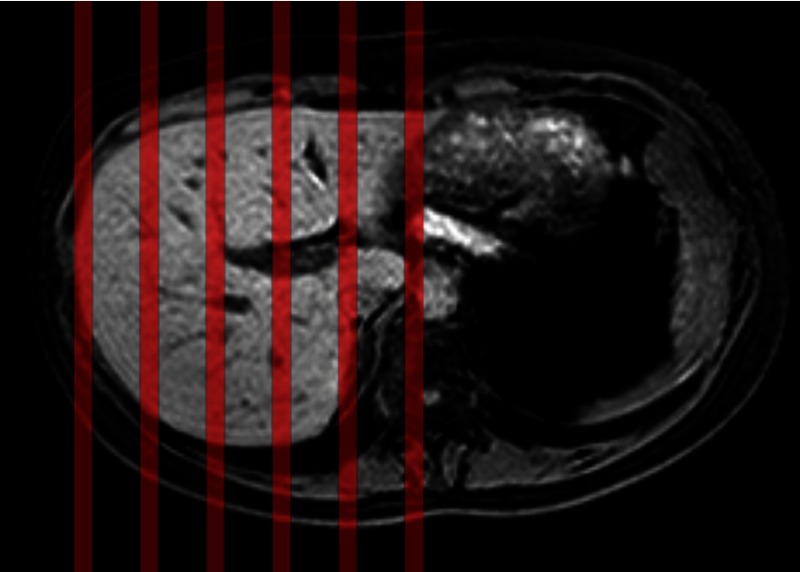
Dynamic 2-D data were available at six equidistant locations in the liver (see Figs. 1 and 2). They were acquired over a total time interval of 369 s. In this short time interval, the drift in liver motion was considered negligible. Since the dynamic data at these six locations were not acquired at the same point in time, they needed to be reordered, such that dynamics from different locations belonging to the same state of the liver could be grouped together. It was assumed that the translation of the liver in FH-direction, both magnitude and direction, indicated the state of the liver at a particular time point. The translation value and the motion direction were used to cluster the data, such that each cluster corresponded to a specific state of the liver during an average respiratory cycle. For each cluster, a 3-D deformation field was calculated by registration of the dynamic data. The FH-translation value and direction of an unseen slice could then be used to look up the corresponding state in the model, such that the liver deformation could be predicted. This model is an extension of our previous work,36 including more volunteers and introducing improvements in the method. One of the most significant changes was the inclusion of gradient magnitude images in the registration process, which considerably increased robustness. Also, registrations were now actually performed in 2-D, in contrast to our previous work, where the registration process was implemented in 3-D while blocking motion in the LR-direction. This yielded a significant speed-up in building the model, from 30 to 2.5 h. Furthermore, the grouping process was simplified, which resulted in a reduction of the computation time and less variation in the number of clusters that were obtained for each subject. Finally, the evaluation of the vessel center alignment was performed by automatic calculation of the center of mass of each vessel crosscut, instead of selecting the center positions manually.
Fig. 1.
Series of 200 dynamics were acquired at six equidistant locations in the liver, indicated by the red lines.
Fig. 2.
Examples of dynamic slices at the six locations in the liver.
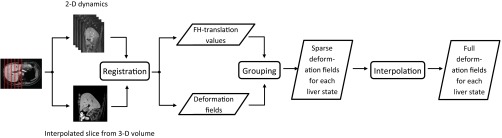
Our method consisted of three main stages (see Fig. 3).
Fig. 3.
Pipeline of the model building process.
-
1.
Registration: Registration was performed of the 3-D liver volume to each dynamic at each location. This resulted in 200 deformation fields at each of the six locations.
-
2.
Grouping: The deformation fields were grouped based on the translation of a dynamic in FH-direction. Each group then contained deformation fields from all six locations, belonging to the same state of the liver.
-
3.
Interpolation: These deformation fields were averaged for every location and interpolated in 3-D, to yield a 3-D deformation field for every cluster. The liver was then deformed according to these 3-D deformation fields, to obtain a look-up table of the liver for all possible states.
Each stage is explained in more detail later.
2.2.1. Stage 1: registration
The 3-D breathhold image of the liver was registered to the dynamics at each location. For this process, liver masks were created manually on every first dynamic slice. These masks served as a sampling region during registration, so that the focus was on the liver and possible distortions from the surrounding moving organs and ribs were avoided. The masks were, therefore, not accurate liver segmentations, but rather regions of interest that also included the outer contours of the liver.
In addition, gradient magnitude images were calculated of the 2-D dynamics by convolution with the derivative of a Gaussian kernel with . These gradient magnitude images were included in parts of the registration process, to force alignment of the inner structures as well as the liver boundary.
The registration process consisted of two phases. First, the liver volume was registered to the first dynamic at each of the six locations. Then, each first dynamic was registered to the other 199 dynamics at that location.
For all registrations, the publicly available elastix toolkit was used.37 A multiresolution strategy was adopted. The multiresolution pyramid was constructed by downsampling with a factor of 2, starting from the original image. Simultaneously, the image was smoothed by convolution with a Gaussian kernel, with increasing with a factor of 2 at each step, starting from for the original image. Multiresolution registration was then performed from coarse to fine. In each resolution step, optimization ran for a maximum of 1000 iterations. Mutual information was used as the metric for registration of the intensity images, implemented as in Ref. 38. The histograms that were built to calculate the mutual information contained bins. For registration of the corresponding gradient magnitude images, normalized cross correlation was used. When both images were registered simultaneously, these metrics were combined into a single cost function by adding their normalized values. For all registrations, a random coordinate sampler was used, with the number of samples defined for each resolution separately, using more samples for higher resolutions.
Registration phase 1: volume to first dynamic
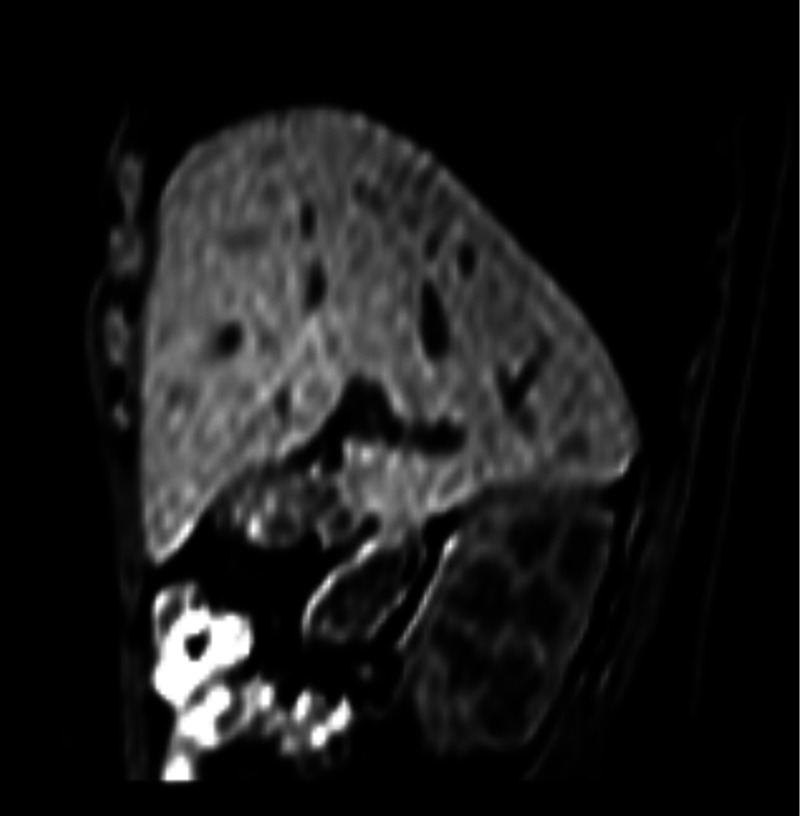
During registration of the volume to the first dynamic at each location, motion in the lateral direction was not accounted for. The 3-D registration problem (3-D volume to 2-D slice) could, therefore, be converted to a 2-D registration, since the lateral location of the slice in the 3-D volume was already known. A 2-D interpolated slice was taken from the 3-D volume at each of the six locations where dynamics were acquired, using the scanner coordinates to determine the location (see Fig. 4). These six slices were then registered to the first dynamic of each corresponding dynamic sequence.
Fig. 4.
Example of a 2-D interpolated slice taken from the 3-D breathhold image.
First, rigid registration of the volume slice to the first dynamic was performed, followed by deformable registration using a B-spline transformation model to capture local deformations. In both the rigid and the deformable registration steps, the liver masks defined the region of interest, meaning that all samples were drawn in this region.
The rigid registration step was performed only on the intensity images, using mutual information as a metric. Gradient magnitude images were not included in this step, since the edge images of the interpolated slice and the dynamic differed considerably outside the liver, owing to differences in contrast between the 2-D and 3-D scan sequences. These differences in the edge images would disturb the registration process. Rigid registration was performed at four resolutions, using a random coordinate sampler drawing 750, 1500, 3000, and 6000 samples from the lowest to the highest resolution.
During deformable registration, the gradient magnitude images were included to improve alignment of the inner structures of the liver. It was assumed that the rigid registration step had aligned the livers sufficiently, so that possible distorting edges outside the liver were not located in the region of interest anymore. Because the intensity images were registered simultaneously with the gradient magnitude images, a combined cost function of mutual information and cross correlation was used, as described in Sec. 2.2.1. Two resolutions were used, with 1024 and 2048 samples. The grid spacing of the B-spline control point grid was 80 by in the lower resolution and 40 by in the final resolution.
Finally, at each of the six locations in the liver, a deformation field was obtained describing the transformation from the volume to the first dynamic of that location. This deformation field did not have a physical meaning, but was merely a mapping to the domain of the dynamic sequences.
Registration phase 2: first dynamic to other dynamics
In this phase, for each of the six dynamic series, the first dynamic was registered to the other 199 dynamics. As these dynamics were all acquired at the same lateral location in the liver and lateral motion was neglected, this registration was performed in 2-D.
Again, rigid registration was followed by deformable registration for each dynamic, using the masks on the first dynamics as a region of interest. Because this time all images were obtained from the same scan sequence, no disturbing edges were expected in the gradient magnitude images. Therefore, a combined cost function was used to perform simultaneous registration of the intensity image and the gradient magnitude image in both steps.
The rigid registration step was again performed in four resolutions, using 750, 1500, 2250, and 3000 samples in each resolution. The deformable registration step used a B-spline transformation model in two resolutions, with 1024 and 2048 samples. Again, the control point grid spacing was 80 by in the lower resolution and 40 by in the final resolution.
This registration phase yielded a deformation field for every dynamic, describing the transformation of the first dynamic to this particular dynamic. This resulted in deformation fields.
Combination of the deformation fields
Finally, the deformation fields obtained in phase 1 were concatenated with each of the deformation fields from phase 2, to yield a single 2-D deformation field for every dynamic at every location. Each of these 1200 deformation fields described the transformation for the corresponding 2-D volume slice to a specific dynamic.
2.2.2. Stage 2: grouping
The liver motion model should contain a sufficient number of states to represent the motion of the liver with the breathing cycle. For this purpose, the deformation fields were divided into groups representing a particular stage of the liver motion cycle. The spread of the groups over the motion range was such that each state of the liver was represented by at least one dynamic at every location. Each group should contain deformation fields from all six locations in order to form a 3-D liver motion field for a particular state. The inspiration states were separated from the expiration states.
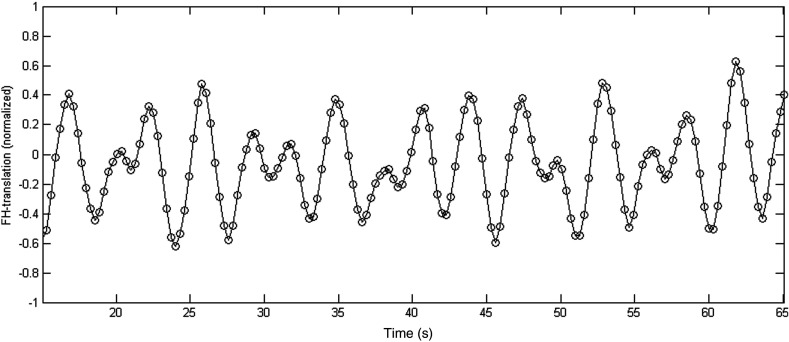
For each dynamic, the FH translation value was taken from the rigid registration step in the second registration phase (Sec. 2.2.1). To perform separate grouping of the inspiration and expiration states, first all FH-values from every location were normalized between and , rejecting outliers of more than two standard deviations from the average, to correct for differences in the range of translation for each location in the liver. Next, these data points were all plotted over time and smoothed by local regression using weighted linear least squares and a second degree polynomial model. Figure 5 shows the smoothed data. The gradient at each of these data points was used to label the points as inspiration or expiration.
Fig. 5.
A typical subset of smoothed data points representing the normalized FH-translation values of the dynamics from all locations over time. The values were normalized between and , with mean value 0.
For both sets (inspiration and expiration), the same grouping procedure was used. Groups were formed based on rounding the abovementioned normalized values to 0.1 mm. Dynamics that had the same FH-value after normalization and rounding were grouped together. If a group did not contain at least one dynamic from every location, that particular cluster was merged with the closest neighboring group. This typically occurred for extreme states that were not reached at all locations during scanning. Consequently, the number of liver motion cycle stages obtained in the model could differ per subject. The grouping process resulted in 15 to 20 groups with one or more deformation fields at all six locations in the liver. This was sufficient for a typical motion range of maximally 30 mm, as this would result in a maximum difference of 2 mm per group.
2.2.3. Stage 3: interpolation
For each group, deformation fields from the same location were averaged, such that each group contained six average deformation fields, corresponding to the six slices in the liver. Then a 3-D deformation field was calculated over the entire liver for each cluster. This field was obtained by cubic spline interpolation between the six averaged deformation fields in each cluster. This resulted in a 3-D deformation field for each cluster, describing the liver deformation in a specific stage of the motion cycle.
2.3. Evaluation
To evaluate the performance of the model, the data acquired using the 2-D single dynamic sequence of 150 images was used, which was not included in the model construction. This resembled the practical situation of obtaining fast 2-D images during therapy at the location of the tumor. An assessment was made of the accuracy of predicting the deformation of this unseen dataset, which corresponds to the prediction error during actual HIFU treatment. When synchronization with the breathing signal is needed, a navigator echo can be acquired at the diaphragm. In this way, a navigator signal can be obtained which is represented by a 1-D image, from which the motion in a specific direction can be calculated using the contrast between the diaphragm and the lung. Most scanners contain software that can automatically detect this translation, usually by edge detection. In our approach, such a navigator signal was simulated for each dynamic by taking the middle column of the sagittal slices, which always clearly depicted the diaphragm.
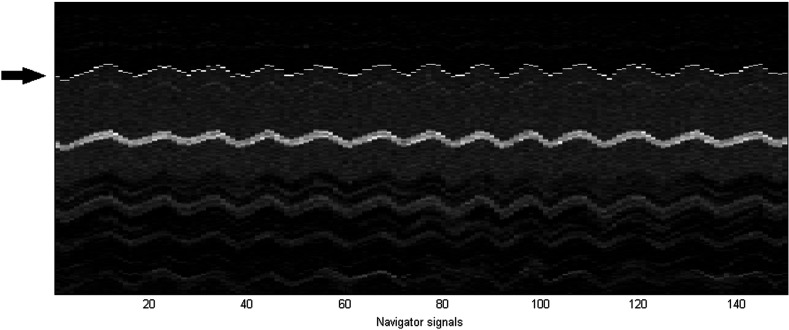
The first navigator was manually placed on the diaphragm, as would be done in practice prior to acquisition. Then each of the 149 subsequent navigator signals was registered to the first one, minimizing the sum of squared differences (SSD) between the two signals. A maximum shift of five voxels between two neighboring signals was allowed, in order to guarantee correct registration of the diaphragm edge. In Fig. 6, the 1-D navigator signals and the diaphragm positions obtained by registration are shown.
Fig. 6.
An example of the navigator signals in a typical dataset. The 1-D navigator signals are the 150 columns in this image. The periodic motion of the liver is clear from this image. The arrow points to the position of the diaphragm. This position was obtained by registering each subsequent column to the first one, and the results are indicated in white. It can be appreciated that the boundary of the liver is detected correctly. The bright structure in the middle of the liver is a blood vessel.
The resulting values were again normalized to match the translation values on which clustering was performed. By comparing each value with its neighbors and calculating the gradient, it was determined automatically whether the dynamic was taken during inspiration or expiration. For each dynamic, the normalized FH-value together with the inspiration/expiration label was used to find the closest cluster in the model. The 3-D deformation field belonging to this particular cluster was used to deform the liver volume. A 2-D interpolated slice was taken from this volume at the position of the evaluation series, using the scanner coordinates to determine the exact location. This slice, showing the liver deformation predicted by the model, was then compared with the actual evaluation slice.
The performance of the model was evaluated by calculating the Dice coefficient of the predicted and actual liver masks, the median of the surface distance of these masks, and by measuring the distance between the predicted and actual center positions of the largest vessels. The Dice coefficient indicates the prediction accuracy for the entire liver, whereas the surface distance is a more informative measure of the accuracy of the predicted liver shape. The vessel misalignment indicates the error in predicting the position of the inner structures of the liver. The latter is especially valuable, since the purpose of the model is prediction of the tumor position. It is expected that misalignment of the vessels is similar to misalignment of a tumor. Because the size of the entire dataset was large, with 150 evaluation dynamics per volunteer, evaluation was only performed on randomly chosen subsets of 30 dynamics per subject. For these dynamics, a manual liver segmentation was created by the first author, to automatically calculate the Dice score. These masks were also used for calculating the surface distance in combination with a Euclidean distance transform. In addition, the distance between the vessel centers was calculated on the same subset of 30 slices. First, a threshold was put on the slices manually to roughly segment the blood vessel profiles. Then landmark annotations were placed on vessels that were visible in both slices, with a maximum of five vessels, as demonstrated in Fig. 7. The centers of mass of these vessel profiles were calculated automatically and the Euclidean distance between them was determined. Because the dynamics on which evaluation was performed were chosen randomly for each subject, it was assumed that these results were representative for the entire dataset. For the last volunteer, evaluation was performed on both the coronal and the sagittal sequence.
Fig. 7.
Landmark annotation of vessel profiles that are visible on both (a) the actual slice and (b) the predicted slice.
3. Results
The results of the comparison of the predicted and actual liver profiles are given in Table 1. The Dice scores ranged from 0.86 to 0.96, with a mean of 0.93. For all volunteers, a standard deviation of 0.02 or less was obtained in the Dice coefficient, indicating that results varied minimally over the different dynamics. The average median surface displacement of the liver masks was calculated over the 30 evaluation dynamics for each subject. This measure varied between 1.1 and 4.5 mm, with a mean value of 2.0 mm over all subjects.
Table 1.
Dice coefficient and median surface displacement in mm of predicted versus actual liver profiles.
| Volunteer | Dice coefficient () | Median surface displacement (mm) () |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| 15 | ||
| 16 | ||
| 17 | ||
| 18 | ||
| average |
In Table 2, the results for vessel misalignment are presented. An average vessel misalignment of 3.0 mm was obtained. The number of vessels on which distance measurements were performed varied per slice, because some slices depicted more vessels than others. Often, on the predicted slice, which was a deformed version from the 3-D volume, more vessels were visible than on the dynamic slices. The number of visible vessels also varied between slices. Consequently, evaluation was performed on one vessel in 2% of the slices, on two vessels in 8% of the slices, three vessels (33%), four vessels (26%) or five vessels (31%).
Table 2.
Vessel misalignment between predicted and actual slices.
| Volunteer | Vessel misalignment (mm) () |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| Average |
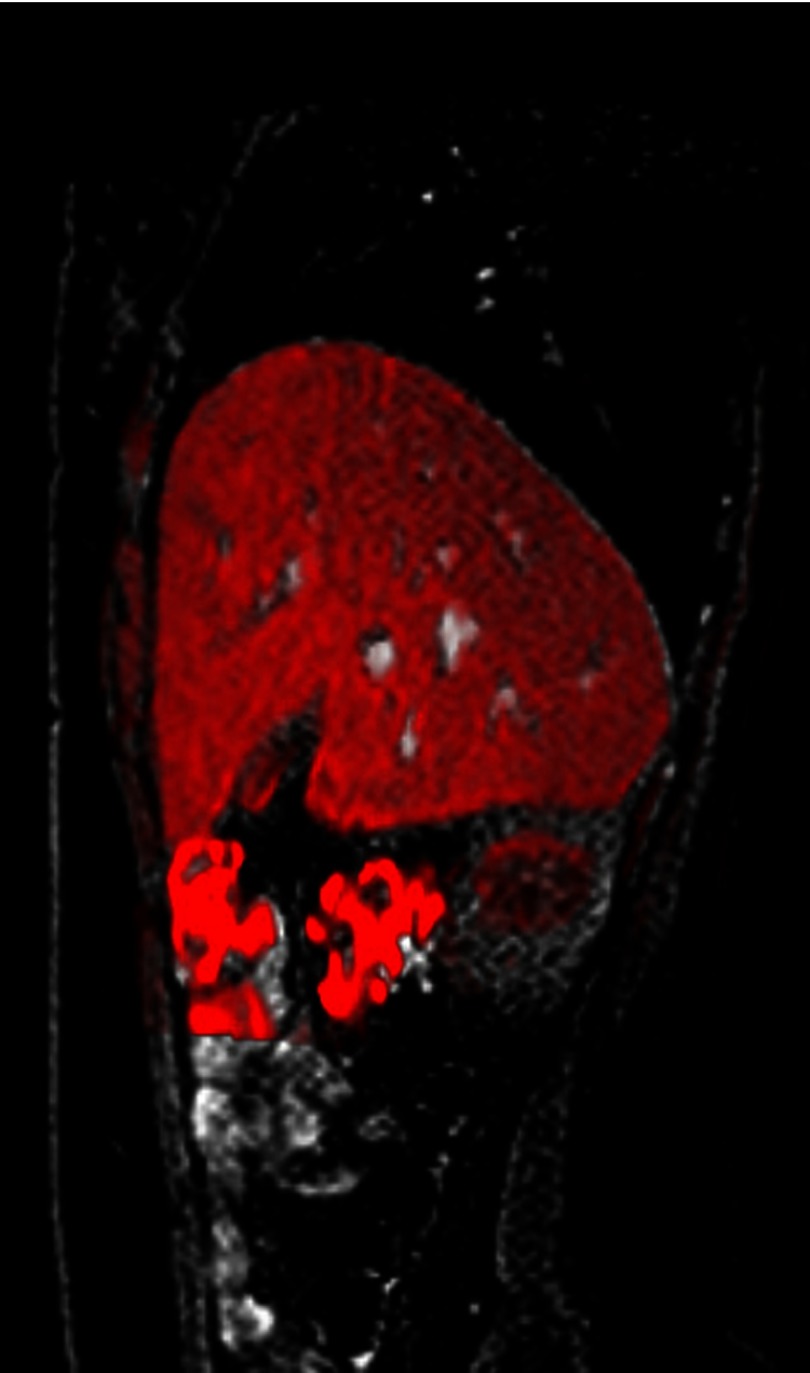
In Fig. 8, a dynamic slice is shown with the predicted slice for this dynamic overlaid in red.
Fig. 8.
Still image from a movie showing the predicted slice (in red) overlaid on the original dynamic. It can be seen that the shape and the vessel positions are accurately matched. (Video 1, MPEG, 438 kB) [URL: http://dx.doi.org/10.1117/1.JMI.3.1.015002.1].
An additional evaluation was performed for volunteer 18 in the coronal direction. The results are presented in Table 3.
Table 3.
Comparison of the vessel misalignment in the sagittal and coronal series.
| Direction | Dice | Median surface displacement (mm) () | Vessel misalignment (mm) () | |||
|---|---|---|---|---|---|---|
| FH | AP | LR | Euclidean | |||
| Sagittal | N/A | |||||
| Coronal | N/A | |||||
4. Discussion
We developed a subject-specific liver motion model based on registration of dynamic MR data. The model was based on 1200 deformation fields, obtained from 200 dynamics at six locations in the liver, which were typically acquired in 369 s. The dynamic MR acquisition protocol was derived from a standard clinical liver imaging sequence. Therefore, the temporal resolution of 300 ms could not be decreased without compromising the image resolution and consequently the registration accuracy. Similarly, a relationship exists between the slice thickness and the gap between the dynamic slice locations. A larger slice thickness allows a larger coverage of the liver, while a smaller slice thickness yields a more accurate local deformation field. In addition, the total imaging time should be kept as low as possible. To acquire dynamic images equidistantly over the entire liver while limiting the total acquisition time, dynamics were acquired at six locations with a slice thickness of 8 mm. As a consequence of the interleaved scan protocol, a minimal gap of 15 mm was necessary to avoid signal saturation in neighboring slices. For practical use of this model, it would be feasible to investigate the possibilities for optimizing the data acquisition. A more sophisticated sequence design could allow fast image acquisition, thereby increasing the temporal resolution and reducing the total scan time.
Data were obtained of healthy volunteers. We expect that the model will perform similarly on patient data as it did on data of healthy volunteers, since the model captures subject-specific liver deformations, without making prior assumptions about global liver motion.
The volunteers were instructed to breathe normally. They did not obtain further instructions on their breathing, such as deep or shallow breaths or variations in the frequency. The purpose was to build a motion model in which natural variations are captured. Extreme situations were, therefore, not included. On the other hand, it is possible that an occasional deep breath occurred during dynamic imaging. To deal with such situations, outliers were excluded from the model by not taking into account positions that were outside two standard deviations of the average position.
Next to breathing, several other unpredictable factors influence liver motion, such as bowel movements, stomach filling, and additional motion of surrounding organs. The extent of these influences varies for different locations in the liver. To eliminate errors introduced by these factors, motion fields are averaged by the clustering process for similar phases in the breathing cycle. Possibly, motion of the rib cage affects the liver motion fields close to the ribs. In practice, tumors located at these sites would not be eligible for HIFU treatment due to safety issues with near field heating at the ribs. In addition, the rib cage motion should be synchronized with the liver motion, as they are both caused by breathing. Therefore, these motion fields should be reproducible and captured by the model.
When the liver moves during breathing, it slides along other organs and the rib cage. Without introducing specific constraints in the registration method, sliding motion is not captured during registration. This work did not specifically address this problem, because our interest was mainly in internal deformation of the liver, since these are the most probable target locations to be treated with HIFU. However, to minimize errors introduced by sliding motion, we used a mask of the liver during registration, such that information of voxels in neighboring organs did not influence the liver deformation field.
The output of the model was a look-up table representing 15 to 20 different possible liver states. The grouping of the deformation fields was an iterative process and the number of obtained clusters varied depending on the spread of the FH-values in the data. Grouping the data eliminated variations due to registration errors, thereby increasing the robustness of the model. Although temporal accuracy was limited by this approach, the number of states in the model was still sufficient for accurate performance.
The average Dice coefficient obtained on all volunteers was 0.93. In addition, the standard deviation of the Dice score was low, which suggests that the performance of the model is robust. This was also confirmed by the median surface displacement, which had an average value of 2.0 mm over all subjects.
The average vessel misalignment over all volunteers was 3.0 mm. This is quite satisfactory, given that the size of a typical focal area in a clinical MR-HIFU system is . Moreover, in practice, an additional margin around the tumor target area is taken, both for safety reasons and to avoid tumor spread. However, the standard deviation of vessel misalignment was high. Results varied considerably between slices from the same volunteer. One reason for this was that the number of vessels that were visible, and on which evaluation could thus be performed, varied over the slices. Secondly, this variability could originate from errors introduced during evaluation. Although an attempt was made during acquisition to place the evaluation slice at a location free of vessel bifurcations and sudden changes in directions, variations in shape of the cross sections of the visible vessels could still be present because of out-of-plane motion or signal differences. In these cases, the calculated center of mass of the thresholded vessel profile could deviate from the actual vessel center.
These errors might be reduced by using a different approach in a practical situation. In this work, the model was built on the entire liver. In practice, it would probably suffice to model only the portion of the liver surrounding the tumor. The slice thickness could be reduced and the slices could be placed closely around the ablation area. This could possibly yield an increase in accuracy.
The additional evaluation in the coronal direction for volunteer 18 showed that the average error in the coronal series was 3.0 mm, compared with an average error of 2.5 mm in the sagittal series. Since motion in the LR-direction was not included in the model, it should be expected that a small error in this direction would occur. The errors in FH- and AP-direction were 2.0 mm and 1.1 mm, respectively. The average error in the LR-direction was 1.7 mm. This indicates that the prediction error in all three directions was comparable, even though the motion in LR-direction was not compensated for. At least for this volunteer, neglecting the motion in LR-direction was considered reasonable.
The main goal of this work was to explore the possibility of building an accurate liver motion model. The results show a sufficiently accurate prediction of both the rigid displacement and the deformation of the liver at the evaluation sequence. The model was evaluated for 18 volunteers for a single slice location in the liver. This location was not included in the construction of the model. To avoid undesired heating of surrounding organs, clinical HIFU treatment is preferably performed on tumors located sufficiently far from organ boundaries. To reflect this, the sagittal evaluation sequence was recorded at a location roughly in the middle of the liver. The image-based navigator used for evaluation could in practice be replaced by an external signal, such as a respiratory belt or a navigator signal.
The deformation fields that were used to build the model only contained motion in the FH-direction and AP-direction; we assumed motion in the LR-direction to be negligible. Including the LR-direction in the model would require additional data for building the model. Such a full 3-D solution seems infeasible for use during treatment, in view of the additional time it would cost to build the model. Furthermore, introducing additional degrees of freedom in the registration problem could lead to deterioration in the robustness of the model.
The computational cost of the model was, for a large part, caused by the extensive number of registrations. Computations were performed on a duo-quad core Xeon system. It is important to note that some parts of the code in elastix were not implemented in a multithreaded fashion, so that not all cores were used at all times. The registration of the volume to the first dynamic took approximately 50 s. The registration of the first dynamic to each of the other dynamics took 45 s. This resulted in a total registration time per volunteer of , which is . The averaging and clustering of the deformation fields took around 2 min. The interpolation of the deformation fields in 3-D took . These offline calculations could probably be accelerated by implementation on graphics processing units. Once the model had been built, its use as a look-up table was very fast, taking only . This makes use of the model in real-time applications attractive.
The main benefit of the proposed model lies in the fact that it does not require complex MR acquisition techniques or additional hardware. It was shown that even when no external breathing signal was recorded, the model could still be applied to accurately predict spatial motion. This liver motion model can, therefore, be used for treatment planning to indicate the pattern of tumor motion during regular breathing. Treatment strategies and parameters can be adjusted based on this predicted pattern.
In theory, the model could also be used during treatment to predict the tumor position in real-time. However, several additional practical issues should be addressed to that end. First of all, real-time tracking of the displacement of the liver should be available, either by acquiring a navigator signal or by using external sensors to capture the breathing cycle, such as a respiratory belt or possibly an ultrasound image. Second, for use during treatment, it is necessary to predict the translation ahead of time, so that the expected deformation can be searched for in the look-up table based on this translation, before the liver actually reaches this point and the HIFU beam geometry can be updated accordingly. Next, to match the calculated deformations to the liver volume during treatment, an initial registration would be necessary to obtain a correspondence with the volume that was used to build the model. Furthermore, the drift in the liver motion, as mentioned in Sec. 1, cannot be ignored during lengthy treatment procedures, which may take over an hour. Finally, an important issue with the use of the model during treatment would be sudden changes in the breathing pattern, in case of which a recalibration of the model might be required.
5. Conclusion
A 4-D liver motion model based on registration of dynamic MRI data was presented. The model proved successful in predicting the liver deformation during regular breathing. With an average Dice coefficient of 0.93, the profile of the liver was accurately predicted. The average error in the prediction of the blood vessel center positions was 3.0 mm. It is expected that tumor misalignment will be similar to vessel misalignment, therefore, this figure indicates the expected error of the predicted tumor position during HIFU treatment. For a HIFU focal area size of a few and the use of a significant additional safety margin, this result appears promising. The model thus seems valuable for use in the planning of HIFU treatment of liver lesions, to indicate the expected motion pattern of the target. The model also has potential for treatment guidance, since it may predict the motion of the liver in real time, provided that the breathing pattern of the patient is regular. The setup of the model makes detection of patient motion or deviations in breathing possible, which contributes to the safety of the treatment.
Supplementary Material
Acknowledgments
This work was financially supported by the project Mediate (Patient Friendly Medical Intervention) in the framework of the EU research program ITEA (Information Technology for European Advancement).
Biographies
Yolanda H. Noorda is a PhD candidate at the Image Sciences Institute, University Medical Center Utrecht, The Netherlands. She received her BSc degree in physics and astronomy and mathematics at Utrecht University in 2009 and her MSc degree in biomedical image sciences at Utrecht University in 2010. Her research focuses on image processing for image-guided procedures, involving motion modeling, image registration, and image segmentation.
Lambertus W. Bartels received his MSc in applied physics at Eindhoven University of Technology in 1997 and his PhD at Utrecht University in 2001. He is an associate professor of MRI physics, (co) author of more than 100 refereed scientific articles and 4 books, and supervisor of 18 PhD theses. He coordinates and teaches several courses in medical imaging physics. His main research interests are MRI methods for planning, guidance, and evaluation of therapy.
Max A. Viergever is professor of medical imaging at Utrecht University (since 1988) and founder/director of the Image Sciences Institute of the University Medical Center Utrecht. He (co)authored >650 refereed scientific articles, (co) authored/edited 18 books, supervised >130 PhD theses and >150 MSc theses. He was editor-in-chief of the IEEE Transactions on Medical Imaging (2002–2008). He is Honorary Senator of the University of Ljubljana, received the IEEE-EMBS Academic Career Achievement Award and the MICCAI Enduring Impact Award.
Josien P.W. Pluim is professor of medical image analysis at Eindhoven University of Technology and holds a part-time appointment at the UMC Utrecht. She received her MSc degree in computer science at the University of Groningen in 1996 and received her PhD at Utrecht University in 2001. She was chair of SPIE Medical Imaging Image Processing in 2006–2009, is associate editor of five international journals (incl. JMI), and a member of the MICCAI board of directors.
References
- 1.Tempany C. M. C., et al. , “MR imaging-guided focused ultrasound surgery of uterine leiomyomas: a feasibility study,” Radiology 226, 897–905 (2003). 10.1148/radiol.2271020395 [DOI] [PubMed] [Google Scholar]
- 2.Hesley G. K., Gorny K. R., Woodrum D. A., “MR-guided focused ultrasound for the treatment of uterine fibroids,” Cardiovasc. Intervent. Radiol. 36, 5–13 (2013). 10.1007/s00270-012-0367-3 [DOI] [PubMed] [Google Scholar]
- 3.Ikink M., et al. , “Mid-term clinical efficacy of a volumetric magnetic resonance-guided high-intensity focused ultrasound technique for treatment of symptomatic uterine fibroids,” Eur. Radiol. 23, 3054–3061 (2013). 10.1007/s00330-013-2915-x [DOI] [PubMed] [Google Scholar]
- 4.Stewart E., et al. , “Clinical outcomes of focused ultrasound surgery for the treatment of uterine fibroids,” Fertil. Steril. 85, 22–29 (2006). 10.1016/j.fertnstert.2005.04.072 [DOI] [PubMed] [Google Scholar]
- 5.Voogt M., et al. , “Uterine fibroid embolisation for symptomatic uterine fibroids: a survey of clinical practice in Europe,” Cardiovasc. Intervent. Radiol. 34, 765–773 (2011). 10.1007/s00270-010-9978-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Catane R., et al. , “MR-guided focused ultrasound surgery (MRgFUS) for the palliation of pain in patients with bone metastases—preliminary clinical experience,” Ann. Oncol. 18, 163–167 (2007). 10.1093/annonc/mdl335 [DOI] [PubMed] [Google Scholar]
- 7.Gianfelice D., et al. , “Palliative treatment of painful bone metastases with MR imaging-guided focused ultrasound,” Radiology 249, 355–363 (2008). 10.1148/radiol.2491071523 [DOI] [PubMed] [Google Scholar]
- 8.Hurwitz M. D., et al. , “Magnetic resonance-guided focused ultrasound for patients with painful bone metastases: phase III trial results,” J. Natl. Cancer Inst. 106, dju082 (2014). 10.1093/jnci/dju082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Liberman B., et al. , “Using MR-guided focused ultrasound surgery: a multicenter study,” Ann. Surg. Oncol. 16, 140–146 (2009). 10.1245/s10434-008-0011-2 [DOI] [PubMed] [Google Scholar]
- 10.Napoli A., et al. , “Primary pain palliation and local tumor control in bone metastases treated with magnetic resonance-guided focused ultrasound,” Invest. Radiol. 48, 351–358 (2013). 10.1097/RLI.0b013e318285bbab [DOI] [PubMed] [Google Scholar]
- 11.Huisman M., et al. , “Feasibility of volumetric MRI-guided high intensity focused ultrasound (MR-HIFU) for painful bone metastases,” J. Ther. Ultrasound 2, 16 (2014). 10.1186/2050-5736-2-16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Anzidei M., et al. , “Magnetic resonance-guided focused ultrasound ablation in abdominal moving organs: a feasibility study in selected cases of pancreatic and liver cancer,” Cardiovasc. Intervent. Radiol. 37, 1611–1617 (2014). 10.1007/s00270-014-0861-x [DOI] [PubMed] [Google Scholar]
- 13.Okada A., et al. , “A case of hepatocellular carcinoma treated by MR-guided focused ultrasound ablation with respiratory gating,” Magn. Reson. Med. Sci. 5, 167–171 (2006). 10.2463/mrms.5.167 [DOI] [PubMed] [Google Scholar]
- 14.Dawson L. A., Jaffray D. A., “Advances in image-guided radiation therapy,” J. Clin. Oncol. 25, 938–946 (2007). 10.1200/JCO.2006.09.9515 [DOI] [PubMed] [Google Scholar]
- 15.Ma C. M. C., Paskalev K., “In-room CT techniques for image-guided radiation therapy,” Med. Dosim. 31, 30–39 (2006). 10.1016/j.meddos.2005.12.010 [DOI] [PubMed] [Google Scholar]
- 16.Balter J. M., Kessler M. L., “Imaging and alignment for image-guided radiation therapy,” J. Clin. Oncol. 25, 931–937 (2007). 10.1200/JCO.2006.09.7998 [DOI] [PubMed] [Google Scholar]
- 17.Clifford M., et al. , “Assessment of hepatic motion secondary to respiration for computer assisted interventions,” Comput. Aided Surg. 7, 291–299 (2002). 10.3109/10929080209146038 [DOI] [PubMed] [Google Scholar]
- 18.von Siebenthal M., et al. , “4D MR imaging of respiratory organ motion and its variability,” Phys. Med. Biol. 52, 1547–1564 (2007). 10.1088/0031-9155/52/6/001 [DOI] [PubMed] [Google Scholar]
- 19.Chui C., et al. , “Combined compression and elongation experiments and non-linear modelling of liver tissue for surgical simulation,” Med. Biol. Eng. Comput. 42, 787–798 (2004). 10.1007/BF02345212 [DOI] [PubMed] [Google Scholar]
- 20.von Siebenthal M., et al. , “Inter-subject modelling of liver deformation during radiation therapy,” Lect. Notes Comput. Sci. 4791, 659–666 (2007). 10.1007/978-3-540-75757-3_80 [DOI] [PubMed] [Google Scholar]
- 21.Preiswerk F., et al. , “A Bayesian framework for estimating respiratory liver motion from sparse measurements,” Lect. Notes Comput. Sci. 7029, 207–214 (2012). 10.1007/978-3-642-28557-8_26 [DOI] [Google Scholar]
- 22.von Siebenthal M., et al. , “Systematic errors in respiratory gating due to intrafraction deformations of the liver,” Med. Phys. 34, 3620–3629 (2007). 10.1118/1.2767053 [DOI] [PubMed] [Google Scholar]
- 23.Sharp G. C., et al. , “Assessing residual motion for gated proton-beam radiotherapy,” J. Radiat. Res. 48, A55–A59 (2007). 10.1269/jrr.48.A55 [DOI] [PubMed] [Google Scholar]
- 24.Nguyen T.-N., et al. , “Adapting liver motion models using a navigator channel technique,” Med. Phys. 36(4), 1061–1073 (2009). 10.1118/1.3077923 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Samei G., Tanner C., Székely G., “Predicting liver motion using exemplar models,” Lect. Notes Comput. Sci. 7601, 147–157 (2012). 10.1007/978-3-642-33612-6_16 [DOI] [Google Scholar]
- 26.Preiswerk F., et al. , “Model-guided respiratory organ motion prediction of the liver from 2D ultrasound,” Med. Image Anal. 18, 740–751 (2014). 10.1016/j.media.2014.03.006 [DOI] [PubMed] [Google Scholar]
- 27.Davies S., et al. , “Ultrasound quantitation of respiratory organ motion in the upper abdomen,” Brit. J. Radiol. 67, 1096–1102 (1994). 10.1259/0007-1285-67-803-1096 [DOI] [PubMed] [Google Scholar]
- 28.Rohlfing T., et al. , “Modeling liver motion and deformation during the respiratory cycle using intensity-based nonrigid registration of gated MR images,” Med. Phys. 31, 427–432 (2004). 10.1118/1.1644513 [DOI] [PubMed] [Google Scholar]
- 29.Dikaios N., et al. , “MRI-based motion correction of thoracic PET: initial comparison of acquisition protocols and correction strategies suitable for simultaneous PET/MRI systems,” Eur. Radiol. 22, 439–446 (2012). 10.1007/s00330-011-2274-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Baumgartner C. F., et al. , “High-resolution dynamic MR imaging of the thorax for respiratory motion correction of PET using groupwise manifold alignment,” Med. Image Anal. 18, 939–952 (2014). 10.1016/j.media.2014.05.010 [DOI] [PubMed] [Google Scholar]
- 31.de Senneville B., Mougenot C., Moonen C., “Real-time adaptive method for treatment of mobile organs by MRI-controlled high-intensity focused ultrasound,” Magn. Reson. Med. 57, 319–330 (2007). 10.1002/mrm.21124 [DOI] [PubMed] [Google Scholar]
- 32.Blackall J., et al. , “A statistical model of respiratory motion and deformation of the liver,” Lect. Notes Comput. Sci. 2208, 1338–1340 (2001). 10.1007/3-540-45468-3_219 [DOI] [Google Scholar]
- 33.Blackall J. M., et al. , “Alignment of sparse freehand 3-D ultrasound with preoperative images of the liver using models of respiratory motion and deformation,” IEEE Trans. Med. Imaging 24, 1405–1416 (2005). 10.1109/TMI.2005.856751 [DOI] [PubMed] [Google Scholar]
- 34.Yang M., et al. , “Subject-specific real-time respiratory liver motion compensation method for ultrasound-mri/ct fusion imaging,” Int. J. Comput. Assist. Radiol. Surg. 10, 517–529 (2014). 10.1007/s11548-014-1085-x [DOI] [PubMed] [Google Scholar]
- 35.McClelland J., et al. , “Respiratory motion models: a review,” Med. Image Anal. 17, 19–42 (2013). 10.1016/j.media.2012.09.005 [DOI] [PubMed] [Google Scholar]
- 36.Noorda Y. H., et al. , “A patient specific 4D MRI liver motion model based on sparse imaging and registration,” Proc. SPIE 8671, 86710S (2013). 10.1117/12.2008061 [DOI] [Google Scholar]
- 37.Klein S., et al. , “Elastix: a toolbox for intensity based medical image registration,” IEEE Trans. Med. Imaging 29, 196–205 (2010). 10.1109/TMI.2009.2035616 [DOI] [PubMed] [Google Scholar]
- 38.Mattes D., et al. , “Nonrigid multimodality image registration,” Proc. SPIE 4322, 1609–1620 (2001). 10.1117/12.431046 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.