Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Jul 27;6:30469. doi: 10.1038/srep30469

Problems encountered when defining Arctic amplification as a ratio

Alistair Hind 1,2,3,a, Qiong Zhang 2,3, Gudrun Brattström 1,3
PMCID: PMC4962034  PMID: 27461918

Abstract

In climate change science the term ‘Arctic amplification’ has become synonymous with an estimation of the ratio of a change in Arctic temperatures compared with a broader reference change under the same period, usually in global temperatures. Here, it is shown that this definition of Arctic amplification comes with a suite of difficulties related to the statistical properties of the ratio estimator itself. Most problematic is the complexity of categorizing uncertainty in Arctic amplification when the global, or reference, change in temperature is close to 0 over a period of interest, in which case it may be impossible to set bounds on this uncertainty. An important conceptual distinction is made between the ‘Ratio of Means’ and ‘Mean Ratio’ approaches to defining a ratio estimate of Arctic amplification, as they do not only possess different uncertainty properties regarding the amplification factor, but are also demonstrated to ask different scientific questions. Uncertainty in the estimated range of the Arctic amplification factor using the latest global climate models and climate forcing scenarios is expanded upon and shown to be greater than previously demonstrated for future climate projections, particularly using forcing scenarios with lower concentrations of greenhouse gases.

When the magnitude of zonally averaged surface temperature change at high latitudes exceeds globally averaged temperature changes in response to climate forcings on interannual or longer time scales, we often refer to this as polar amplification, of which Arctic amplification is the northern part. At least, this is the definition considered in the IPCC (Intergovernmental Panel on Climate Change) fifth assessment report (AR5)1, which broadly reflects the current standing of the scientific community on the state of climate research. Arctic amplification is evident in instrumental observations2, climate model simulated temperatures3,4 as well as historical occurrences based on palaeoclimatic evidence5,6. It is often claimed that the near surface of the Northern Hemisphere high latitudes are warming at rates roughly double those of the global average in recent decades, particularly in the autumn/winter7,8,9,10. Similar degrees of amplification also occur in climate model simulations of future projections forced with higher greenhouse gas concentrations1,11,12,13. These results however are frequently based on the analysis of different time-periods, different regional definitions and include different treatments of uncertainty. Motivation for this article comes in many respects from a lack of standardized results in Arctic amplification analysis, which can result in confusion regarding the uncertainty of the amplification factor.

The myriad of potential and known causes, feedbacks or drivers involved in this amplification process are not the topic of interest in this article. For a comprehensive overview of that topic we refer the reader to Serreze & Barry14, as well as Lu & Cai15 and Pithan & Mauritsen4. Neither will we presently cover issues pertaining to palaeoclimatic reconstructions of Arctic amplification. Here the problem of defining Arctic amplification itself is dealt with, attempting a synthesis of present definitions discussing the pitfalls and benefits with these approaches. Various aspects of complexity in the distribution of the ratio estimator statistic are discussed, in the context of current research focusing on Arctic amplification. Rather than being just a case of statistical detail, we stress that understanding of the behavior of the uncertainty in the ratio estimator involves fundamental concepts regarding the scientific questions being addressed. An approach to develop confidence intervals for ratio estimators is demonstrated, which as an example based on results from IPCC AR5, gives a clearer picture of how uncertainty in Arctic amplification in future projections from climate models is related to the degree of external radiative forcing. The range of definitions used to quantify the Arctic amplification factor are reviewed, as well as comparatively underused alternative definitions to the ratio estimator when considering the concept of amplification of temperatures at higher latitudes.

Ratio Estimators

The ratio estimator approach to defining Arctic amplification is most often expressed as the mean change in Arctic temperatures (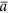Inline graphic) divided by the global change (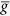Inline graphic) over a period of interest, so that an estimate of Arctic amplification (r), capable of being either positive (a change to warmer climate) or negative (a change to colder climate), can be represented as:

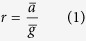graphic file with name srep30469-m3.jpg

Note that global and Arctic changes in temperature 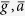Inline graphic can be considered over any length of time, using any time resolution, however it is often multi-decadal trends or changes, based on seasonally or annually averaged data that are considered in the examples given in this article. Despite that eq. 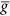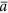(1) is often used to define Arctic amplification, many may not be aware that the probability distribution of this ratio estimator can exhibit a complicated behavior, even if uncertainties in Inline graphic and Inline graphic are well quantified16,17,18. This complicated probability distribution for ratio estimators can occur if the denominator in a given ratio estimator, for the purposes of this article–global temperature change (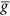Inline graphic), is close to 0 relative to its distribution. This makes estimation of uncertainty bounds (or confidence intervals) for ratio estimators problematic. The Fieller method or “Fieller’s theorem” is a practiced solution known in statistics for specifying confidence intervals for ratios and can be used to illustrate this complicated behavior19. Note that there are other possible approaches to confidence intervals for ratios, however provided the means of the numerator and denominator are approximately normally distributed, Fieller’s theorem is a practical solution, even for smaller sample sizes20.

The derivation of confidence intervals for ratios using Fieller’s theorem is described more thoroughly in the ‘Methods detail’ section at the end of this article, where most importantly we see that “bounded” confidence intervals can only be obtained when the denominator tends to be significantly different from 021. Where the denominator is likely to not be significantly different from 0, then the absolute value of the ratio estimator may be arbitrarily inflated or even change signs. Note that if the numerator, in this case Arctic temperature change (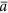Inline graphic), is not significantly different from 0 either, then essentially any value of the Arctic amplification factor is possible.

Ratio of Means or Mean Ratio

The ratio estimator presented so far is also known as the ‘Ratio of Means’ estimator (rR), which functions literally as the ratio of two estimated means:

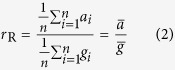graphic file with name srep30469-m9.jpg

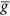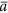The sample mean global (Inline graphic) and Arctic (Inline graphic) temperature changes can be estimated from climate models i (in an ensemble of size n) for example. Contrast this with the ‘Mean Ratio’ estimator (rM), where an estimation of mean Arctic amplification is made based on the ratio estimate of each individual model simulation i:

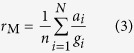graphic file with name srep30469-m12.jpg

At first glance, the differences between eqs (2) and (3) may appear trivial, however these estimators ask different scientific questions when estimates are based on climate model ensembles (or alternative observational datasets). We use Winton12 (abbreviated as WN) as an example of the ‘Mean Ratio’ estimator approach to Arctic amplification though there are other examples in the literature11,22. In WN twelve model simulations taken from the CMIP4 (Coupled Model Intercomparison Project) ensemble were used to estimate an Arctic amplification factor, where the models were allowed to reach a quasi-equilibrium state after being subjected to a doubling of carbon dioxide (CO2) (Fig. 1). They first calculated the Arctic amplification of each of their individual twelve (n = 12) ensemble members 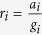Inline graphic, then formed sample mean ratio and uncertainty statistics of the distribution based on the model spread of these ratios (eq. (3), column 3 in Fig. 1). This particular example in WN corresponds to an investigation of the average Arctic amplification factor in a climate model ensemble after responding to a simulated doubling of CO2. If however a ‘Ratio of Means’ estimator (eq. (2)) approach is used in WN, the investigation becomes quite conceptually different in regards to both the amplification factor and the uncertainty therewith. Using a ‘Ratio of Means’ approach would rather mean investigating how the average Arctic temperature change response to a simulated doubling of CO2 is comparable with the global average. In other words, the estimated uncertainty in the Arctic amplification factor using a ‘Mean Ratio’ approach is based on the spread of individual climate model or data-set Arctic amplification factors (ri), whereas the estimated uncertainty for the ‘Ratio of Means’ approach compares the spread of Arctic temperature changes (ai) from different climate models or data-sets with the respective spread of global changes (gi). Hence, Fieller’s theorem for deriving confidence intervals for ratios corresponds to the Ratio of Means estimator exclusively. The difference between the ‘Mean Ratio’ and ‘Ratio of Means’ approaches applied to WN’s model ensemble are illustrated in Fig. 1 (column 3 against column 4), where it can clearly be seen that the uncertainty increases using the latter approach.

Figure 1. Based on Winton’s12 (WN) Fig. 1, where mean global and Arctic temperature change as well as Arctic amplification factors are presented for a doubling of carbon dioxide (CO2) equilibrium experiment based on twelve climate model simulations from CMIP4 (first three columns).

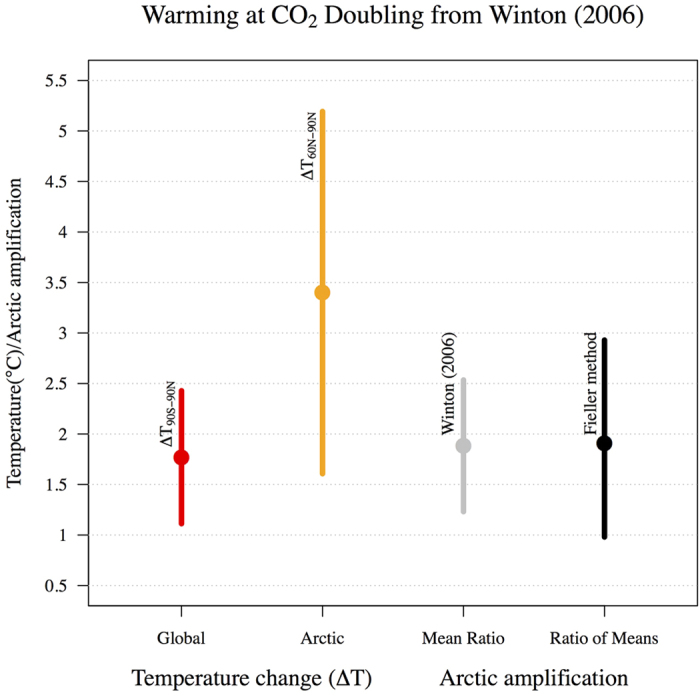
Figure 1

Open in a new tab

Note that the original figure presented respective standard deviations, whereas here we present the 90% confidence interval ranges. The fourth column of data is a Ratio of Means definition of Arctic amplification with model spread calculated using the methodology presented in Fieller19 as opposed to the Mean Ratio approach employed by the original authors (column 3).

If an average ratio estimate of Arctic amplification is sought, both the Mean Ratio and Ratio of Means will likely provide similar results (rM ~ rR), provided denominator values close to 0 are considered extremely unlikely. For example, compare the similar mean Arctic amplification factors calculated using both approaches in columns 3 and 4 of Fig. 1 (Mean Ratio and Ratio of Means respectively). If however global temperature changes are likely close to 0 relative to the distribution of Inline graphic, then rM can be sensitive to outlying values in any individual model Arctic amplification factor (ri) due to the fact that the Mean Ratio estimator (rM) gives equal weighting to individual ratio estimates in the ensemble. Consider expressing eq. (1) in the form 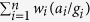Inline graphic, in which case 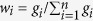Inline graphic for the Ratio of Means (rR) and when w = 1/n we have the Mean Ratio (rM). 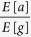It is clear the latter ratio estimator gives equal weighting to each individual ratio Inline graphic, even if individual ratios may be highly inflated (see Supplementary Information). Furthermore, Rao et al.23 demonstrated through a second-order Taylor expansion of the ratio estimator that as sample size n increases, the expected value of the Ratio of Means (E[rR]) approaches Inline graphic, whereas the expected Mean Ratio statistic (E[rM]) does not. As a result the Mean Ratio (rM) can be considered an inconsistent estimator of Inline graphic24 (demonstrated in Supplementary Information).

There are certainly conceptual differences between the Ratio of Means (rR) and Mean Ratio (rM) estimators of Arctic amplification. As demonstrated using WN’s data in the above example, the Ratio of Means gives larger confidence intervals than the Mean Ratio (Fig. 1) as it encompasses intermodel (from a multi-model ensemble encompassing several different physical climate models) uncertainty in both the Arctic and global temperature change estimates, instead of intermodel uncertainty in the Arctic amplification factor itself. Each individual multi-model ensemble member has a particular climate sensitivity to a given radiative forcing25, which means that resulting Arctic and global temperature changes can be compared for different individual model climate sensitivities within the multi-model ensemble when using the Ratio of Means approach. It is important to understand that here we are discussing uncertainty in the spread of a climate model ensemble, not the statistical uncertainty, or precision, of the ratio estimators themselves. The statistical uncertainty relates to how precisely a given sample ratio estimator Inline graphic represents a true population ratio 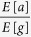Inline graphic, in which case the Ratio of Means is actually less statistically uncertain than the Mean Ratio26.

If a given analysis wishes to investigate how the projected temperature change in the Arctic compares with global changes, then confidence intervals for the Ratio of Means seems appropriate, as you would be most interested in comparing estimates of changes in both regions, even if it is perhaps the case that no individual member of the model or data-set ensemble is capable of producing results at the tails of the distribution. The Mean Ratio approach on the other hand, only allows Arctic and global regions to be compared for a given individual model or data-set, with the same climate sensitivity. Given the conceptual differences in these approaches, deciding which is more appropriate to use is rather dependent on the nature of the specific analysis question. The Mean Ratio certainly seems appropriate when comparing the individual Arctic amplification factors of members in a climate model ensemble or in different data-sets, however the aforementioned statistical inconsistency and susceptibility to outliers can be problematic, unless it is known that the denominator is unlikely to be close to 0 within its distribution.

Confidence Intervals for Arctic Amplification in the IPCC Fifth Assessment Report (AR5)

In IPCC AR5 projected future Arctic amplification based on the CMIP5 climate model ensemble is claimed to be “between 2.2–2.4 times the global average warming for 2081–2100 compared to 1986–2005” (see Table 12.2 in IPCC AR527). This range of future projected Arctic amplification factors is based on the Ratio of Means estimate of four multi-model ensembles with different forcing scenarios known as Representative Concentration Pathways (RCPs), which are labeled as RCP2.6, RCP4.5, RCP6 and RCP8.5. The RCP numbers approximately refer to the maximum projected total global radiative forcing effect (Wm2) they are predicted to achieve before 2100, although RCP2.6 would likely peak around 3 Wm2 and significantly earlier than 210028. Figure 2 shows the multi-model mean Arctic (orange/yellow) and global (red) temperature changes projected for the period 2081–2100 in contrast with those simulated for 1986–2005 using the four RCP scenarios. The 90% confidence intervals for the spread of Arctic and global temperatures are presented here as provided in Table 12.2 of IPCC AR5 and are essentially very similar for all RCP forcing scenarios. Here, we apply the Fieller method in an attempt to give representative confidence intervals at a 90% significance level for projected Arctic amplification using the Ratio of Means approach, based on the model spread for each RCP forcing scenario (black in Fig. 2). The RCP4.5 and RCP6 simulated future scenarios show a similar uncertainty in the Arctic amplification factor, with potential values ranging from approximately 1.2–3.8 at a 90% significance level (second and third columns in Fig. 2), whereas the RCP8.5 scenario has a somewhat smaller uncertainty, ranging from 1.5–3 (fourth column in Fig. 2). On the other hand, for the RCP2.6 simulated future scenarios an Arctic amplification factor of less than 1 or even negative values are quite possible. In other words, the Arctic region may be able to undergo temperature changes in opposition to the direction of any global changes if the global radiative forcing follows the RCP2.6 pathway. It generally seems as though the uncertainty bounds calculated for future projected Arctic amplification factors indicate that higher numbered RCP forcing experiments (analogous to higher greenhouse gas concentrations) show less uncertainty than the lower RCP experiments. This is perhaps not an unexpected result given that higher greenhouse gas forcings would be expected to increasingly overcome differences in the physical models and internal climate variability.

Figure 2. Projected simulated future temperature change between 2081–2100 and 1986–2005 from IPCC AR5 based on the respective Representation Concentration Pathways (RCPs, which are projected future forcing scenarios).

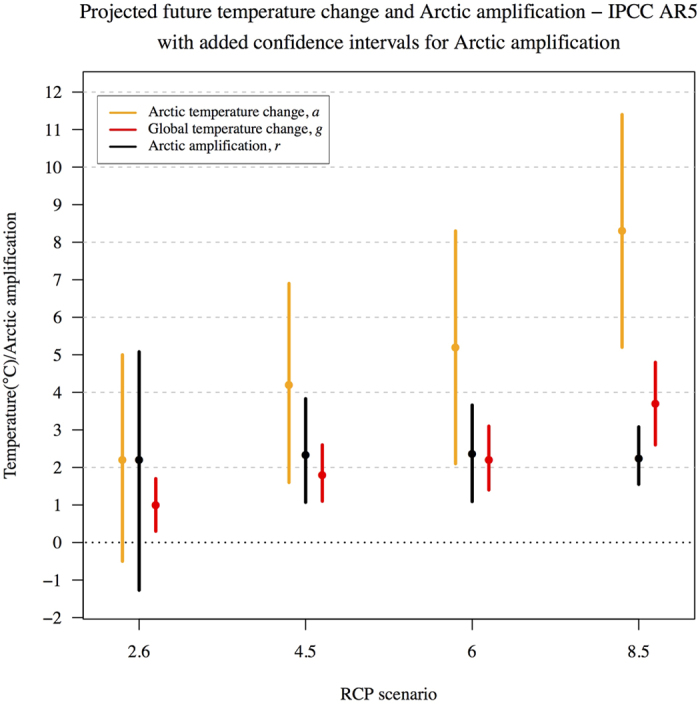
Figure 2

Open in a new tab

The global (red) and Arctic (orange) mean change and intervals at the 90% confidence level (Gaussian assumption), as well as Ratio of Means Arctic amplification factors, are provided for each RCP forcing scenario based on the CMIP5 climate model ensemble data published in IPCC AR5. The authors provide the additional Arctic amplification (black) confidence intervals calculated using the Fieller method19, based on the CMIP5 model ensemble statistics. Note that the ensemble size differs for each forcing scenario (n = 32, 42, 25, 39 for RCP2.6, RCP4.5, RCP6, RCP8.5 respectively).

The potential for negative Arctic amplification factors in the spread of the RCP2.6 pathway simulations above is due to the fact that spread of the projected future global changes for this scenario ensemble is quite close to 0 at its lower end (first column in Fig. 2). Consider the hypothetical case of an additional projected radiative forcing scenario that would be weaker than RCP2.6, with mean temperature changes of 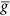Inline graphic = 0.5 °C and 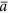Inline graphic = 1.1 °C (compared to 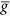Inline graphic = 1.0 °C and 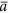Inline graphic = 2.2 °C in the case of RCP2.6), and with the same model uncertainty in 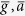Inline graphic as RCP2.6 (a not unreasonable assumption given the similarity in model uncertainty for the four RCP forcing scenarios as seen in Fig. 2). For this hypothetical weaker RCP scenario it is impossible to generate bounded confidence intervals for Arctic amplification at all using the Fieller method, in which case the corresponding mean Arctic amplification factor (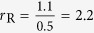Inline graphic) is rendered uninterpretable. This is simply because if the distribution of the denominator 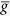Inline graphic is close to 0, then artificially inflated values of Arctic amplification are possible that cannot be meaningfully interpreted20. The range of 2.2–2.4 presented in IPCC AR5 is a simple representation of four mean values based on the Ratio of Means estimator for each RCP forcing scenario and does not represent the full model uncertainty in future projected Arctic amplification; nor does it link uncertainty with different RCP radiative forcing scenarios as the confidence intervals calculated here for Arctic amplification clearly show in Fig. 2. Naturally, one must also consider the confidence level used to generate these statistics as increasing the confidence level will increase the chance of uninterpretable uncertainties in the ratio estimator, by increasing the width of the distribution of the denominator 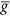Inline graphic. In the hypothetical case above, a number for an Arctic amplification factor can be generated from the mean temperature change statistics 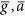Inline graphic despite the result being essentially meaningless given the uncertainty.

Defining the Arctic

There are a great deal of choices that can be made when investigating the nature of Arctic amplification in climate models or gridded observational datasets. A sample of studies from the literature that more or less focus on defining Arctic amplification are presented in Table 1. Note that we do not include investigations considering palaeodata given the markedly reduced data coverage. IPCC AR5 defines the Arctic as 67.5–90°N27 for example, in contrast with a slightly different definition in IPCC AR429 of 65–90°N. There is also the issue of whether annual or seasonal data is used, given that Arctic amplification tends to be stronger during the autumn/winter months8,9,30. The reference region used in these analyses are included as well, namely if global or Northern Hemisphere temperature changes were used.

Table 1. A summary of key articles and reports relating to Arctic amplification and their respective areal definitions of the Arctic region; and whether the global or Northern Hemispheric (NH) temperature changes were used as a reference.

Definition of Arctic amplification
Reference Arctic region Season Relative to
IPCC (2007) AR4 [s. 249]29 >65°N ann global
IPCC (2013) AR5 [s. 1055]27 ≥67.5°N ann global
Bekryaev et al. (2010)2 ≥60°N all NH
Chylek et al. (2009)38 ≥64°N all global
Crook et al. (2011)44 * ≥60°N all global
Graversen et al. (2008)7 ** >65°N Nov–Feb NH
Hazeleger et al. (2012)34 ≥70°N ann global
Holland & Bitz (2003)11 ≥75°N ann global
Hwang et al. (2011)22 >70°N ann global
Kelly (1982)50 65°N–85°N ann NH
Screen & Simmonds (2010)9,51 ** ≥70°N Oct–Jan global
Wang et al. (2007)52 ≥60°N ann global
Winton (2006, 2008)12,39 ≥60°N ann global
Open in a new tab

We refer to the seasons used in defining Arctic amplification emphasized in the main body of the articles in question. ‘all’ corresponds to where results for all four seasons of Arctic amplification are clearly published in the article (note that in IPCC AR5 November-December is emphasized as a period of peak amplification but results are not produced anywhere explicitly in the main text).

*Difference between polar and tropical regions normalized by global temperature changes.

**Emphasizing rather the near surface air temperature change of the Arctic region (950–1000 hPa) compared with the entire tropospheric column (below around 300 hPa); in addition to Arctic amplification based on surface temperatures alone.

Spatial resolution of gridded data, as well as climate model specific factors, may influence the choice of region used to represent Arctic temperatures in order to generate Arctic amplification statistics. It is however rare in the literature that any justification of these choices are stated when regional averaging occurs. An investigation could certainly be undertaken to see how sensitive the Arctic amplification factor is to particular averaging choices made. There are cases in the literature where reference is made to more emphatic changing temperatures at higher latitudes as meaning Arctic amplification, but it is left to the reader to interpret what constitutes high latitudes (see Serreze & Francis31 or Yamanouchi32 for example). Consider one of the earliest multi-model ensemble estimated ranges given for Arctic amplification in Holland & Bitz11 (abbreviated as HB). A specific range of simulated polar warming for the Arctic region was claimed to be 1.5–4.5 times the global mean warming for a doubling of carbon dioxide (2 × CO2) in HB; and has been used as a benchmark for comparison with other Arctic amplification studies (s. 904 in IPCC AR433). Hazeleger et al.34 used this 1.5–4.5 range to corroborate their simulated Arctic amplification factor of 2.5, however this was for an Arctic averaged over 70–90°N, whereas the stated HB range was actually the maximum and minimum calculated from 5° zonal bands. The 1.5–4.5 range quoted from HB is naturally larger than one would expect for amplification factors based on averaging over the entire Arctic region. A simple area-weighted averaging using HB’s data indicates rather a range of 1.8–2.7 for the Arctic region defined for 70–90°N, as an example of how Hazeleger et al.34 could have more fairly compared their results with the earlier example in HB.

Discussion

An important distinction exists between the various analyses of Arctic amplification made so far; and that is whether they are considering changes in temperature as an equilibrium or transient climate response. Looking at annual to decadal temperature changes in observational data, or climate model simulations where radiative forcings are time dependent, is necessarily the reflection of a transient climate response, whereas an equilibrium climate response would require longer time scales so that the deep oceans have time to equilibriate with a given radiative forcing35. For example, the future projected temperature changes from IPCC AR5 are transient responses to the RCP radiative forcing scenarios, whereas the simulated doubling of CO2 concentrations in WN12 represent an equilibrium response, given that they wait for the climate model system to more or less equilibriate with a prescribed change in radiative forcing. Climate models that are run to some form of quasi-equilibrium, inherently tend to display an Arctic amplification (or more generally polar amplification)36. In contrast, transient simulations or indeed the observed climate system, may very well undergo periods where the global change is close to 0 or where there is no Arctic amplification at all and the global changes exceed changes in the Arctic (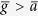Inline graphic). For example, Polyakov37 found observational evidence for a cooling Arctic during periods of warming in the Northern Hemisphere at large during the 20th century whereas Chylek et al.38 found inflated Arctic amplification factors based on meteorological station data for the period 1940–1970, largely because the global temperature change for that period was very close to 0. Indeed, the concept of an amplification factor defined as a ratio can be questioned for shorter term transient responses in the climate system.

Bekryaev et al.2 (abbreviated as BV) recognized some of the complexity of the ratio estimator approach to Arctic amplification (specifically, where the denominator approaches 0) and suggest that Arctic amplification should rather be defined by the ordinary least squares (OLS) linear regression of temperature in the Arctic Ta(t) on to Northern Hemispheric temperature (labeled Tg(t) here for simplicity) in the form Ta(t) = rCTg(t) + b, where rC represents the Arctic amplification factor. Based on 42 historical runs from the CMIP3 model ensemble, BV found this linear regression approach to Arctic amplification to be stable over the model spread when compared with ratio estimation. A linear relationship between the Arctic and global temperatures certainly seems to exist based on equilibrium projection results of climate model ensembles39, but it is not clear whether this linearity can be assumed for a transient response of the climate system on shorter timescales (such as decadal) as well. Sensitivity to the choice of time period could also be investigated. An important issue with OLS regression of Arctic (dependent variable) on to global or hemispheric temperatures (independent variable) is that uncertainty is only assumed in Arctic temperatures, whereas uncertainty exists in both a and g (i.e. an errors-in-variables problem40). It seems reasonable to assume that uncertainty in hemispheric or global temperatures is at least within an order of magnitude of Arctic uncertainty12. We would suggest treating the covariates and independent variable in a more geometrically symmetrical manner, such as in total least squares (TLS) regression41, or a weighted TLS42 when it is known that the uncertainties are likely of a different size. Note that one could just as easily consider global temperatures as a linear function of Arctic temperatures instead, then the estimated regression coefficient (rc) would be larger than using the BV approach; and different errors-in-variables models like TLS or weighted TLS would be somewhere in between.

An early framing of Arctic amplification by Callendar43 was to compare higher and lower latitude bands, where the “temperature difference for 1921–1950 minus 1891–1920 for the latitude zone 60–73°N was 0.81 °C, compared with 0.39 °C for the band spanning 25–60°N”. However, consideration of Arctic amplification in terms of latitudinal differences in changes of temperature is uncommon in the literature, at least as a measured quantity. Notably, Crook et al.44 defined amplification as the difference in warming between polar and tropical regions for various physical contributions to polar amplification (such as radiative forcings and horizontal heat transports). Arctic or more generally, polar amplification exists where horizontal heat transport between polar and equatorial regions causes a latitudinal difference in temperature distribution that would not be predicted by local net radiation balances45. Considering this physical definition of amplification, a latitudinal difference in temperature changes perhaps seems more relevant to studies focusing on Arctic (or polar) amplification than using either hemispheric or global temperature changes as a reference. An issue would then be justification of what constitutes the Arctic or tropical regions of course. One way to distinguish the Arctic and tropical regions could be based on either side of where the (annually or seasonally) averaged meridional wind component v is equal to 0. This would at least allow the data-set or climate model to more decide where the higher and lower latitude regions lie.

Summary

An attempt has been made to draw attention to many aspects that can potentially lead to confusion in defining Arctic amplification using a ratio estimator (r), and in particular, quantification of its uncertainty. When Arctic amplification is defined as a ratio estimator, it is usually the case that the numerator is representative of a change in temperatures over the Arctic (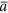Inline graphic) and the denominator is a reference change, such as in global temperatures (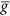Inline graphic). If the global temperature change is near to 0 the amplification factor can become artificially inflated and hence both statistically and physically meaningless; if Arctic temperature change is also near to 0 then essentially any value of Arctic amplification is possible.

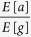Here, a distinction is made between the ‘Mean Ratio’ and ‘Ratio of Means’ estimators, which can also result in a misattribution of uncertainty in Arctic amplification. For a climate model ensemble, a sample uncertainty can easily be derived using the Mean Ratio estimator by looking at the model spread of the individual climate model’s Arctic amplification factors Inline graphic, however the Mean Ratio estimator is statistically inconsistent, in that regardless of how large a model ensemble or set of alternative observational data are used, this statistic will not converge on the “expected” value of the Arctic amplification factor expressed as Inline graphic, unlike the Ratio of Means estimator which does. Using a sample uncertainty based on the model spread of both Arctic and global temperature changes, confidence intervals can be derived for the Ratio of Means estimator using ‘Fieller’s theorem’19. The uncertainty derived from the Ratio of Means estimate of Arctic amplification in a multi-model ensemble tends to be larger than when using the Mean Ratio estimator, as demonstrated here on the climate model ensemble of Winton12. We speculate that the main reason for this increased uncertainty is that for the Ratio of Means estimator, changes in Arctic temperatures can be compared with global changes from two different climate models potentially possessing different climate sensitivities to radiative forcing. Therefore, if individual model Arctic amplification factors are calculated, as is done to define the Mean Ratio estimator, then uncertainty is conceptually limited by the range of individual model ensemble member climate sensitivities.

The IPCC fifth assessment report (AR5) presents the most up-to-date projections of future changes in Arctic temperatures to be some 2.2–2.4 those of projected global changes comparing the end of the 21st century with the recent past27. We emphasize that this range of future temperature changes with respect to latitude presented in IPCC AR5 can be misleading. The IPCC AR5 report’s claimed 2.2–2.4 range of future projected Arctic amplification is actually just the range of the four mean amplification factors for four differently forced climate model ensembles (RCPs). These four mean values are calculated in IPCC AR5 using the Ratio of Means estimator. Here, it is demonstrated using Fieller’s theorem that the uncertainty in the Arctic amplification factor differs greatly between the four different RCP forcing experiments. In fact, the uncertainty in the amplification factor is more complicated than the 2.2–2.4 range presented in IPCC AR5 suggests, with lower greenhouse gas emitting future scenarios having greater uncertainty than the experiments with higher projected radiative forcing. In the case of RCP2.6, the future scenario with the lowest projected anthropogenic emissions and radiative forcing, the Arctic amplification factor could likely be less than 0 or even have a negative value due to the spread of future projected global temperature changes being close to 0 for this particular experiment, comparing the recent past with the end of the 21st century. This would understandably have both global and regional implications for mitigation and adaptation strategies under future climate change.

The fact that increased CO2 equilibrium temperature response experiments, recent future projected scenarios in IPCC AR5, as well as surface temperature observations over recent decades have all roughly shown a doubling of the rate of warming in the Arctic region compared with global temperature changes, has perhaps masked potential discussion regarding the ratio estimator as a suitable definition for the concept of amplification itself. The uncertainty in an Arctic (or polar) amplification factor expressed as a ratio is clearly far from trivial when changes in global temperature are near 0, such as can easily be observed in the climate system on inter-annual to decadal time-scales, or as can occur in transient climate model simulations.

Methods Detail

Fieller’s theorem

Consider Arctic and global temperature change where eq. (1) is expressed in the form 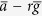Inline graphic. Following the derivation of Franz21, dividing 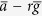Inline graphic by an estimate of its standard deviation gives the following statistic:

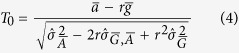graphic file with name srep30469-m38.jpg

where 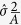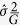Inline graphic, Inline graphic are the variance estimators for a change in Arctic and global temperatures respectively and 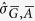Inline graphic represents an estimate of their covariance. If both 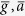Inline graphic are assumed to be normally distributed, then so is the term 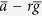Inline graphic, which consists of the difference of two normal variables. Note that normality is assumed for 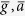Inline graphic regardless of the number of observations (or model ensemble members). The T0 estimator therefore approximates a Student t-distribution, given that we are standardizing the mean of our normal data by a standard deviation which is itself estimated from the data. The distribution of T0 will resemble a normal distribution more and more as the number of observations increases. 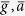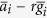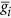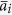T0 follows a t-distribution exactly (again, assuming the data is normally distributed for Inline graphic) given that observations are of the form Inline graphic (as in Fieller’s theorem), which are independent for different i observations (or model ensemble members if you will) and require neither dependence or independence between the paired observations Inline graphic and Inline graphic (paired because they come from the same climate model). These criteria are met in the case of the example model ensemble experiments used in this article.

To obtain approximate confidence intervals for r, one can calculate the set of r values for which the corresponding T0 values lie within the upper and lower (1 − α) quantiles of the t-distribution (these quantiles are denoted as tq here and can be obtained from R function qt or Matlab function nctinv, where the degrees of freedom are specified as n − 2, n being the ensemble size). This can be expressed in terms of the inequalities −tq ≤ T0 ≤ tq, the solving of which for r leads to the following confidence limits20:

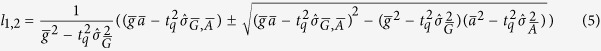graphic file with name srep30469-m49.jpg

where l1 and l2 give “bounded” confidence intervals provided that the denominator, global temperature change (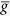Inline graphic), is different from 0 at significance level α. Otherwise a confidence set is obtained which only excludes the values between l1 and l2 (“unbounded/exclusive” case) or else a confidence set is obtained that does not exclude any values at all (“unbounded” case)20,21. 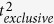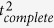Two quantities can be used to determine which class of confidence intervals within Fieller’s theorem are available for a given r, namely Inline graphic and Inline graphic, defined below as:

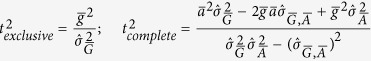graphic file with name srep30469-m53.jpg

and which in the formulation of von Luxburg & Franz20 gives unbounded/exclusive confidence intervals if 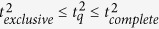Inline graphic and unbounded confidence intervals where 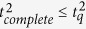Inline graphic, otherwise bounded confidence intervals can be determined. The Fieller’s theorem confidence interval sets can be summarized as:

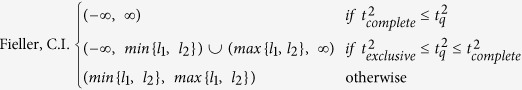graphic file with name srep30469-m56.jpg

Note that the expression under the root sign in the numerator of eq. (5) will always be non-negative (as long as the correlation of errors in 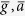Inline graphic are not negatively correlated) whenever the denominator 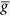Inline graphic is significantly different from 0. 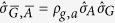Inline graphic from eq. (4) allows for correlation between the ratio denominator and estimator via ρg,a. We used a correlation coefficient of ρg,a = 0.6 taken from the approximate correlation between the annual mean temperature series of the Arctic (60–90°N) and global regions based on HadCRUT446,47 and GISTEMP48,49 data, to the nearest 0.05. Note that the dimensions of the confidence intervals were largely insensitive to the choice of ρg,a used, within the scope of the results given by the various observational datasets.

Additional Information

How to cite this article: Hind, A. et al. Problems encountered when defining Arctic amplification as a ratio. Sci. Rep. 6, 30469; doi: 10.1038/srep30469 (2016).

Supplementary Material

Supplementary Information
srep30469-s1.pdf (934.7KB, pdf)

Acknowledgments

This research was funded by the Swedish Research Council (grant C0592401; P.I. Gudrun Brattström at the Department of Mathematics, Stockholm University). We thank the Griffin project members for useful discussions relating to this research and particularly Ekaterina Fetisova for enlightenment regarding the literature on confidence intervals for ratio estimators, based on her licentiate thesis work.

Footnotes

Author Contributions A.H. wrote the paper, G.B. provided some coding of Fieller’s theorem and practical advice, as well as double checking of statistical details. Q.Z. helped focus the manuscript.

References

  1. IPCC authors. In Climate Change: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (eds Stocker T. F. et al.) Ch. 5, 396–398 (Cambridge University Press, NY, USA, 2013). [Google Scholar]
  2. Bekryaev R. V., Polyakov I. V. & Alexeev V. A. Role of Polar Amplification in Long-Term Surface Air Temperature Variations and Modern Arctic Warming. J. Clim. 23, 3888–3906 (2010). [Google Scholar]
  3. Manabe S. & Stouffer R. J. Sensitivity of a global climate model to an increase of CO2 concentration in the atmosphere. J. Geophys. Res-Oceans 85, 5529–5554 (1980). [Google Scholar]
  4. Pithan F. & Mauritsen T. Arctic amplification dominated by temperature feedbacks in contemporary climate models. Nature Geosci. 7, 181–184 (2014). [Google Scholar]
  5. Masson-Delmotte V. et al. Past and future polar amplification of climate change: climate model intercomparisons and ice-core constraints. Clim. Dynam. 26, 513–529 (2006). [Google Scholar]
  6. Miller G. H. et al. Arctic amplification: can the past constrain the future? Quat. Sci. Rev. 29, 1779–1790 (2010). [Google Scholar]
  7. Graversen R. G., Mauritsen T., Tjernström M., Källén E. & Svensson G. Vertical structure of recent Arctic warming. Nature 451, 53–57 (2008). [DOI] [PubMed] [Google Scholar]
  8. Serreze M. C., Barrett A. P., Stroeve J. C., Kindig D. N. & Holland M. M. The emergence of surface-based arctic amplification. The Cryosphere 3, 11–19 (2009). [Google Scholar]
  9. Screen J. A. & Simmonds I. The central role of diminishing sea ice in recent Arctic temperature amplification. Nature 464, 1334–1337 (2010). [DOI] [PubMed] [Google Scholar]
  10. Cowtan K. & Way R. G. Coverage bias in the HadCRUT4 temperature series and its impact on recent temperature trends. Q. J. R. Meteorol. Soc. 140, 1935–1944 (2014). [Google Scholar]
  11. Holland M. M. & Bitz C. M. Polar amplification of climate change in coupled models. Clim. Dynam. 21, 221–232 (2003). [Google Scholar]
  12. Winton M. Amplified Arctic climate change: what does surface albedo feedback have to do with it? Geophys. Res. Lett. 33, L03701 (2006). [Google Scholar]
  13. Stroeve J. C. et al. The Arctic’s rapidly shrinking sea ice cover: a research synthesis. Clim. Chang. 110, 1005–1027 (2012). [Google Scholar]
  14. Serreze M. C. & Barry R. G. Processes and impacts of arctic amplification: A research synthesis. Glob. Planet. Chang. 77, 85–96 (2011). [Google Scholar]
  15. Lu J. & Cai M. Quantifying contributions to polar warming amplification in an idealized coupled general circulation model. Clim. Dynam. 34, 669–687 (2010). [Google Scholar]
  16. Marsaglia G. Ratios of normal variables and ratios of sums of uniform variables. Biometrika 60, 193–204 (1965). [Google Scholar]
  17. Hinkley D. V. On the ratio of two correlated normal random variables. Biometrika 56, 635–639 (1969). [Google Scholar]
  18. Hinkley D. V. Correction: On the ratio of two correlated normal random variables. Biometrika 57, 638 (1970). [Google Scholar]
  19. Fieller E. C. Some Problems in Interval Estimation. J. R. Stat. Soc. B 16, 175–185 (1954). [Google Scholar]
  20. von Luxburg U. & Franz V. H. A Geometric approach to confidence sets for ratios: Fieller’s theorem, generalizations and bootstrap. Stat. Sinica 19, 1095–1117 (2009). [Google Scholar]
  21. Franz V. Ratios: A short guide to confidence limits and proper use (Cornell University Library, 2007). [Google Scholar]
  22. Hwang Y. T., Frierson D. M. W. & Kay J. E. Coupling between Arctic feedbacks and changes in poleward energy transport. Geophys. Res. Lett. 38, L17704 (2011). [Google Scholar]
  23. Rao C. R. Advanced Statistical Methods in Biometrical Research, 154–155 (Wiley, NY, USA, 1952). [Google Scholar]
  24. Rao T. J. Mean of ratios or ratio of means or both? J. Stat. Plan. Infer. 102, 129–138 (2002). [Google Scholar]
  25. Knutti R. & Hegerl G. C. The equilibrium sensitivity of the Earth’s temperature to radiation changes. Nature Geosci. 1, 735–743 (2008). [Google Scholar]
  26. Formenti M. Mean of Ratios or Ratio of Means: statistical uncertainty applied to estimate Multiperiod Probability of Default (Cornell University Library, 2014). [Google Scholar]
  27. IPCC authors. In Climate Change: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (eds Stocker T. F. et al.) Ch. 12, 1055 (Cambridge University Press, NY, USA, 2013). [Google Scholar]
  28. Meinshausen M. et al. The RCP greenhouse gas concentrations and their extensions from 1765 to 2300. Clim. Chang. 109, 213–241 (2011). [Google Scholar]
  29. IPCC authors. In Climate Change: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change (eds Solomon S. et al.) Ch. 3, 249 (Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2007). [Google Scholar]
  30. Cohen J. et al. Recent Arctic amplification and extreme mid-latitude weather. Nature Geosci. 7, 627–637 (2014). [Google Scholar]
  31. Serreze M. C. & Francis J. A. The Arctic Amplification Debate . Clim. Chang. 76, 241–264 (2006). [Google Scholar]
  32. Yamanouchi T. Early 20th century warming in the Arctic: A review. Polar Science 5, 53–71 (2011). [Google Scholar]
  33. IPCC authors. In Climate Change: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change (eds Solomon S. et al.) Ch. 11, 904 (Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2007). [Google Scholar]
  34. Hazeleger W. et al. EC-Earth V2.2: description and validation of a new seamless earth system prediction model. Clim. Dynam. 39, 2611–2629 (2012). [Google Scholar]
  35. Winton M., Griffies S. M., Samuels B. L., Sarmiento J. L. & Frölicher T. L. Connecting Changing Ocean Circulation with Changing Climate. J. Clim. 26, 2268–2278 (2010). [Google Scholar]
  36. Hall A. D. The role of surface albedo feedback in climate. J. Clim. 17, 1550–1568 (2004). [Google Scholar]
  37. Polyakov I. V. et al. Trends and variations in Arctic Climate System. Eos Trans. AGU 83, 547–548 (2002). [Google Scholar]
  38. Chylek P., Folland C. K., Lesins G., Dubey M. K. & Wang M. Arctic air temperature change amplification and the Atlantic Multidecadal Oscillation. Geophys. Res. Lett. 36, L14801 (2009). [Google Scholar]
  39. Winton M. Sea Ice-Albedo Feedback and Nonlinear Arctic Climate Change In Arctic Sea Ice Decline: Observations, Projections, Mechanisms, and Implications (eds DeWeaver E. T. et al.) 114 (American Geophysical Union, Washington, D.C., USA, 2008). [Google Scholar]
  40. Durbin J. Errors in Variables. Rev. Inst. Int. Stat. 22, 23–32 (1954). [Google Scholar]
  41. Nievergelt Y. Total Least Squares: State-of-the-Art Regression in Numerical Analysis. SIAM Rev. 36, 258–264 (1994). [Google Scholar]
  42. Markovsky I., Rastello M. L., Premoli A., Kukush A. & van Huffel S. The element-wise weighted total least-squares problem. Comput. Stat. Data An. 50, 181–209 (2006). [Google Scholar]
  43. Callendar G. S. Temperature fluctuations and trends over the earth. Q. J. R. Meteorol. Soc. 87, 1–12 (1961). [Google Scholar]
  44. Crook J. A., Forster P. M. & Stuber N. Spatial Patterns of Modeled Climate Feedback and Contributions to Temperature Response and Polar Amplification. J. Clim. 24, 3575–3592 (2011). [Google Scholar]
  45. Pierrehumbert R. T. Principles of Planetary Climate (Cambridge University Press, Cambridge, United Kingdom, 2010). [Google Scholar]
  46. Kennedy J. J., Rayner N. A., Smith R. O., Parker D. E. & Saunby M. Reassessing biases and other uncertainties in sea surface temperature observations measured in situ since 1850: 1. Measurement and sampling uncertainties. J. Geophys. Res. 116, D14104 (2011). [Google Scholar]
  47. Morice C. P., Kennedy J. J., Rayner N. A. & Jones P. D. Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: the HadCRUT4 dataset. J. Geophys. Res. 117, D08101 (2012). [Google Scholar]
  48. Hansen J., Ruedy R., Sato M. & Lo K. Global surface temperature change. Rev. Geophys. 48, RG4004 (2010). [Google Scholar]
  49. GISTEMP Team. GISS Surface Temperature Analysis. Available at: http://data.giss.nasa.gov/gistemp/. Accessed: 25th September 2015.
  50. Kelly P. M., Jones P. D., Sear C. B., Cherry S. G. & Tavakol R. K. Variations in Surface Air Temperature: Part 2. Arctic Regions, 1881–1980. Mon. Weather Rev. 110, 71–83 (1982). [Google Scholar]
  51. Screen J. A. & Simmonds I. Increasing fall-winter energy loss from the Arctic Ocean and its role in Arctic temperature amplification. Geophys. Res. Lett. 37, L16707 (2010). [Google Scholar]
  52. Wang M. et al. Intrinsic versus Forced Variation in Coupled Climate Model Simulations over the Arctic during the Twentieth Century. J. Clim. 30, 1093–1107 (2007). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep30469-s1.pdf (934.7KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES