Abstract
Image-based computational modeling is becoming an increasingly used clinical tool to provide insight into the mechanisms of reentrant arrhythmias. In the context of ischemic heart disease, faithful representation of the electrophysiological properties of the infarct region within models is essential, due to the scars known for arrhythmic properties. Here, we review the different computational representations of the infarcted region, summarizing the experimental measurements upon which they are based. We then focus on the two most common representations of the scar core (complete insulator or electrically passive tissue) and perform simulations of electrical propagation around idealized infarct geometries. Our simulations highlight significant differences in action potential duration and focal effective refractory period (ERP) around the scar, driven by differences in electrotonic loading, depending on the choice of scar representation. Finally, a novel mechanism for arrhythmia induction, following a focal ectopic beat, is demonstrated, which relies on localized gradients in ERP directly caused by the electrotonic sink effects of the neighboring passive scar.
Keywords: arrhythmia, scar, infarct, monodomain, computational modeling
Introduction
Ischemic heart disease (IHD) remains a significant cause of mortality and morbidity, primarily due to associated ventricular arrhythmias.1 When coronary vessels become occluded in IHD, the restricted blood supply can lead to the formation of localized regions of necrotic collagenous scar and fibrosis within the myocardial tissue.2 The associated structural and electrophysiological changes that occur in and around these scarred regions provide a highly arrhythmic substrate, facilitating both the formation and sustainment of reentrant waves of electrical excitation that characterize self-sustaining ventricular tachycardia circuits.
Infarct scars usually comprise of nonconducting, dense fibrotic tissue surrounded by remodeled,3 yet still viable, myocardium that constitutes the peri-infarct zone (PZ). In some cases, the otherwise dense scar may be transcended by channels, or isthmuses, of surviving tracts of myocardium interspersed with patchy fibrosis (Fig. 1A and B).4 Electrical activation may still propagate through these channels, but the wavefront is forced to take tortuous, zigzag propagation pathways around the fibrotic regions,5,6 significantly slowing activation. The resulting conduction delay associated with these conduits of activation provides the prerequisite for successful self-sustained reentry; such mechanisms underlie the majority of incidences of scar-related ventricular arrhythmias.4,7
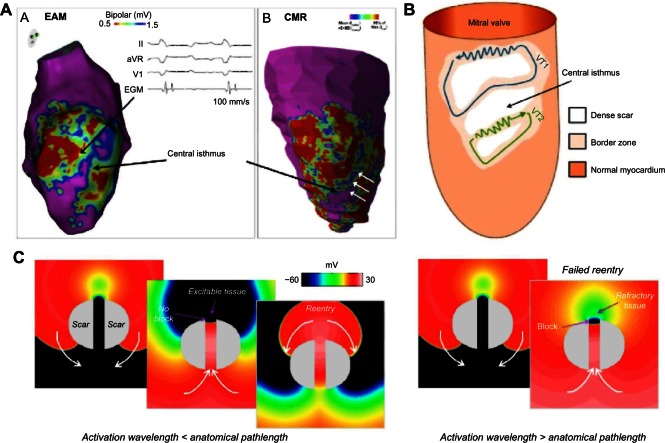
Figure 1.
Surviving central isthmus transcending dense scar and its role as an arrhythmic substrate. (A) A direct comparison of an electroanatomical voltage map with corresponding contrast-enhanced h MR data, highlighting close correspondence of central isthmus identified by both methods (reproduced from Ref. 8, with permissions). The white arrows show the central isthmus. (B) A schematic of the reentrant wavefront propagation through slow-conducting isthmuses associated with dense scar (reproduced from Ref. 9 with permissions). (C) Simulated reentrant activation patterns through a central isthmus transcending a dense scar. The left images show successful reentry in which the activation wavelength is less than the anatomical path length provided by the scar (ie, an excitable gap exists); the right images show unsuccessful reentry in which the activation wavelength is greater than the anatomical path length.
Here, we review the important aspects of the electro-physiological functioning of the infarcted area (both the PZ and scar core) and discuss how these functional properties have been represented within previous computational models of IHD. Such models are increasingly being used to elucidate important mechanisms that underlie reentrant arrhythmias in the setting of structural heart disease,10 helping understand and guide therapeutic interventions. In the second part of the paper, we highlight the potential differences in the overall electrophysiological function of this region, depending on the specific modeling representation. We use this strategy to suggest how parameters and properties of the scar may have important arrhythmogenic implications, particularly with respect to transcending isthmuses of conduction due to its key role in arrhythmic risk in the context of IHD.
Review of Current Modeling Strategies for Representing Infarct Regions
Image-based computational models of infarct scar
Recent advances in magnetic resonance (MR) imaging protocols and contrast agents have allowed us to identify and quantify infarct scarred regions.11,12 Careful analysis of the acquired imaging data allows delineation of both necrotic infarct scar and PZ (alternatively termed gray zone or border zone), which have been shown to correlate well with postmortem histological analysis.13 The availability of such high-resolution clinical, and preclinical, imaging data of this nature has facilitated the representation of scar within image-based computational ventricular models. Necrotic scar and PZ regions may be separately identified, or segmented, within the image stack, and such information directly translated over to the resulting geometrical computational models created from the images.14 Scar and PZ regions have also been included into ventricular models using specific algorithms, based on known clinical scar anatomy.15,16 Once the scar is identified, the use of unique identifiers associated with individual regions in the computational domain allow different electrophysiological properties to be assigned to the regions associated with necrotic and PZ tissue.
Many groups have used a similar approach to generate computational ventricular models, including regions of infarct scar.16–23 These models have been used to understand how the altered electrophysiological properties represented by the scar and PZ interact with activation wavefronts to induce and sustain arrhythmias,17,18,23 and consequently inform and guide catheter ablation therapies.16,19,20 Models of this nature have also been used to understand how externally applied electrical fields interact with the conductivity discontinuities represented by the scar to shed light on the mechanisms of defibrillation21 in the context of patients with myocardial infarction, who represent the vast majority of patients receiving such therapies. All these studies have concluded that the specific presence of an infarct scar significantly influences cardiac arrhythmias and antiarrhythmia therapies. Thus, accurate representation of scar within models – both geometrically and parametrically – is essential to better understand scar-related arrhythmias and to advance therapies against them.
Geometrical identification and representation of infarct from imaging data
Necrotic scar and the surrounding PZ tissue are normally identified (or segmented) from MR imaging data sets as differences in intensities in contrast-enhanced images. Alternatively, preclinical diffusion tensor imaging may also be used to identify infarct regions as having less anisotropic water diffusion.14 In the more common case of contrast-enhanced MR data, threshold methods such as the full-width half-maximum method or the standard deviation method24 are frequently used to segment scar and PZ in a (semi-) automated manner (Fig. 1A shows a comparison between scar delineated via contrast-enhanced imaging and via electroanatomical mapping). Although these methods have been analyzed in detail, there remains debate as to their accuracy in delineating these complex heterogeneous tissue regions, which has also led to the development of use of more advanced scar segmentation methods.25 Two recent computational studies have highlighted the importance of accurately identifying scar and PZ regions within imaging data for translation into computational image-based models. Both the resolution of the initial MR data (comparing typical clinical vs preclinical resolutions)17 and the size of the identified PZ18 were shown to influence the dynamics of induced episodes of ventricular tachycardia within the generated models. In both cases, the exact pattern of the reentry (figure-of-eight, focal) and location of the reentrant core varied as the specific geometry of the scar and/or PZ was altered, highlighting the importance of accurately identifying these regions within image-based models for clinical application.
Arrhythmogenic properties of PZ regions and their representation within models
Following their assignment within computational models, the three different tissue regions (healthy myocardium, necrotic scar, and PZ) are parameterized with associated electrophysiological properties, both in terms of differences in active cell properties and passive conductivities.
Ionic remodeling in the PZ
Surviving cardiomyocytes within the PZ are known to have remodeled electrophysiological properties,3 corresponding to a downregulation of numerous individual ion channels and transport processes. Downregulation of INa and ICaL causes reduced excitability, lowers action potential amplitude, decreases upstroke velocity, and consequently slows conduction. A reduction in repolarizing potassium currents (IKr, IKs, and Ito) causes action potential duration (APD) prolongation, which can lead to the formation of early after depolarizations. The majority of specific measurements performed on the downregulation of ionic currents in PZ have been obtained from single-cell patch-clamp experiments on epicardial border zone cells of canine infarct models. These data have reported a decrease of 38%,26 30%,27 and 20%27 from normal value in peak INa, peak IKr, and peak IKs, respectively. In addition to these changes based on canine infarct border zone measurements, changes to the conductances of the sodium–calcium exchange (upregulated by 132%) and ICaL (decreased to 31%) have been reported from the PZ of rabbit infarct tissue.28 Trayanova et al first implemented these reductions in ionic conductances, which have been generally replicated in the majority of other studies seeking to represent ionic remodeling in PZ regions using physiologically detailed ionic models.16–23 However, it should be noted that the epicardial border zone of the canine infarct model exists due to collateral circulation in this species. Consequently, cells from this region may be functionally different to the PZ regions in other species including human, defined as the tissue surrounding the scar on all sides, at the junction of healthy myocardium and dense scar. Other studies using phenomenological cell models within image-based geometric models have opted for tuning the associated parameters within healthy tissue and PZ based on optical mapping29 or clinical electrogram22 recordings.
The effects on the action potential at the single-cell level due to the documented ionic remodeling of isolated PZ cells appear to be at odds with the expected behavior of cells within the PZ region at the tissue/organ level. The presence of PZ, as quantified by contrast-enhanced MR, has been consistently correlated with the incidence of cardiac arrhythmias and related sudden death,30 suggesting that the specific electrophysiological properties of PZ tissue facilitates reentry. A crucial factor determining the propensity of a scar to act as a reentrant substrate, however, is its ability to fit a reentrant wavefront within the corresponding anatomical reentrant circuit that it provides.4,16,31,32 Electrical wavelength in this context depends upon conduction velocity and refractory period.31,32 Conduction through PZ tissue introduces a significant delay, due to the zigzag pathways it is forced to take as it negotiates around fibrotic bundles.2,5,6 This delay is crucial in the context of surviving isthmuses of conduction transcending dense infarct scars, as it allows tissue at the exit site time to recover, in order to be reactivated by the reentrant wavefront [Fig. 1C (left panel)]. Although this slowed conduction reduces wavelength, this may be negated if PZ tissue was to have the prolonged APDs as measured in single-cell experiments (depending on the relative magnitude of these effects).3 In light of this, it becomes difficult to reconcile the arrhythmogenic effect of PZ tissue with the antiarrhythmic effect of prolonged APD (in the context of increased wavelength and arrhythmia sustenance). However, the effects of electrotonic coupling at the tissue level are well known to significantly alter the action potential characteristics relative to their behavior as isolated single cells,33 smoothing out heterogeneities in action potential duration and shape between neigh-boring tissue regions with heterogeneous ionic properties.34,35 Therefore, differences in electrophysiological tissue properties of neighboring scar, combined with these electrotonic modulating effects, may act to alter the action potential and refractory properties of PZ cells relative to their behavior when isolated, facilitating a more arrhythmic tissue-level substrate.
Slowed conduction within the PZ
Slowing of conduction within the PZ is thought to be one of the major factors governing its strong association with increased arrhythmic risk, particularly key for propagation through surviving isthmus regions, which often provide reentrant pathways. A number of factors, identified by experimental imaging and measurements, are thought to affect conduction within the PZ, both in terms of its absolute speed and also its anisotropy. Although the reduced sodium conductance assigned to PZ cells within models described above partly acts to reduce conduction velocity due to its effects on upstroke velocity, significant changes to electrotonic cell-to-cell (passive) conductivity properties also occur. Unlike the ionic changes, however, these effects have been less consistently represented within computational models of the PZ.
The presence of interstitial and patchy replacement fibrosis in infarcted PZ regions has the effect of separating myocyte bundles, removing their direct side-to-side electrical connections by insulating them from one another.6 Conduction transverse to the fiber direction is thus significantly slowed, as activation proceeds in a zigzag pattern between the patchy collagenous septa.5,6 At the macroscopic scale, conduction anisotropy is therefore increased as longitudinal connections between myocytes are not effected. The overall effect of this conduction disturbance is very often represented in computational models of the PZ by reducing the transverse conductivity within the PZ tissue by 90%, yet leaving the fiber direction conductivity unaltered.17,19–21
Gap junction remodeling is known to be apparent in and around scarred regions, with specific changes to the distribution and density of the Cx43 isoform (the key ventricular gap junction protein related to electrotonic current flow) implicating conduction.36 Overall, Cx43 has been shown to be downregulated in the presence of fibrosis.2,36,37 Such a downregulation may be thought to reduce conductivity uniformly within the fiber and transverse directions, and thus could explain the isotropic reduction in conduction in the PZ imposed within some recent computational models.16,18 However, the effect of downregulated Cx43 on conductivity is not clear,38 as there is thought to be a high degree of redundancy, with only very large reductions in Cx43 causing conduction slowing.39,40 Thus, basing reductions in conductivities assigned to computational models upon experimentally measured levels of Cx43 downregulation may not be entirely appropriate.
Lateralization of Cx43 – the alteration of the distribution of the protein to the sides of the myocytes, away from the intercalated disks – has been shown to be a prominent feature of surviving myocytes within the PZ surrounding infarct scar tissue in the human ventricle,41 as well as in the presence of fibrosis in heart failure.37 A recent comprehensive modeling study (which examined the role of different types of fibrosis representation within MR-derived human atria models) used these findings to reduce fiber conductivity while increasing conduction transverse to the fiber direction (as has been witnessed in atrial mapping experiments).42 In addition to decreasing combined conductivity, such an approach has the effect of decreasing conduction anisotropy and is contrary to the reduction in transverse conduction (increasing anisotropy) imposed to represent muscle bundle isolation by interstitial fibrosis, as described above. However, representing gap junction lateralization by decreasing anisotropy has not been implemented by studies constructing ventricular models of fibrotic regions in the PZ. Furthermore, recent experimental results also suggest that, despite the witnessed redistribution of connexin under fibrotic conditions, the lateralized Cx43 may in fact be nonfunctional,36 explaining the lack of change in patterns of anisotropic conduction witnessed in similar scenarios.43 Thus, using measurement of changes in Cx43 distributions in PZ tissue to inform conductivity corresponding changes in models may also be misleading.
Experimental imaging studies have highlighted significant disruption to myofiber orientation within PZ in rat,6 mouse,41 and pig8 infarct models. A similar reduction in structural anisotropy (for water diffusion) is often used as a marker to delineate infarcted regions (including the PZ) from healthy myocardium in diffusion-tensor MRI signals based on relatively lower values of fractional anisotropy.14 Macroscopically (or in an averaged sense), fiber disarray would suggest a reduction in effective conduction anisotropy. Thus, as models represent electrical activation as a continuum, reduced, isotropic conduction may provide the most consistent representation of PZ conduction changes applied within computational models. However, we also highlight that PZ regions typically represent relatively small areas of tissue within models; thus, representing overall combined reduction in conductivity in this region will provide the most important aspect of arrhythmogenicity, with the specifically assigned anisotropy playing a secondary role.
Arrhythmogenic properties of scar core and its representation within computational models
Passive electrical properties of the scar core
Representation of the electrophysiological properties of the necrotic infarct region itself is also not consistent within the literature. Largely, this is due to the fact that the specific electrophysiological properties of the scar are not fully understood. Although necrotic scar may be considered as entirely inactive, acellular tissue, recent experimental optical mapping studies have suggested that propagation of activation into large infarct regions may occur.44–46 One possible explanation for this phenomena is that surviving bundles of myocytes penetrate into the nectotic scar, carrying electric impulses and giving rise to detectable optical signals (which may scatter through the more optically transparent scar tissue), identified as propagation.44 An alternative explanation is that myofibloblasts, although nonexcitable with only passive membrane properties, may be fully electrically connected to neighboring PZ myocytes and could potentially passively transmit propagation across large necrotic regions.47–49 Such an effect has been demonstrated in vitro on cultured preparations, which showed how bridges of myofibroblasts can transmit across distances of up to 300 µm.50 Ultimately, a combination of surviving myocyte bundles with coupled myofibroblasts may offer the most likely explanation for possible large-scale electrotonic conduction of activation across dense scar regions. The existence of an extensive network of passively electrically coupled myofibroblasts across otherwise dense necrotic scar may have acute effects upon the electrophysiological properties of the surrounding surviving myocardial tissue, with important arrhythmogenic implications. Measuring these fundamental properties experimentally, and using computational models to facilitate a deeper mechanistic understanding of their subsequent effects, will no doubt represent an important direction of research in the combing years, particularly in light of the growing interest in targeting scar and PZ regions with pharmacological or direct stem cell treatments.48
Modeling the scar as an insulator
In terms of representing the scar within computational models, despite the above evidence highlighting the important passive properties of the scar, the consensus from the majority of work in this field (lead by the pioneering work by the Trayanova et al) has been to represent the necrotic scar purely as an insulator.16,19–22,29,51 In a monodomain representation, this con sequently means that the scar tissue is represented as an internal boundary (as it has no intracellular domain and no membrane potential – it is acellular). In a bidomain model,51 it may be represented as a bath (only having an extracellular space) with low conductivity relative to the conductive blood (usually represented to be present in other bath regions such as inside the ventricular cavities and vessels).52 In such a representation, the scar provides no electrotonic load to surrounding PZ tissue, and the PZ cells are effectively uncoupled from the scar. The presence of this isolating boundary around the scar core significantly reduces the electrotonic loading of neighboring PZ cells, relative to those adjoining the healthy tissue where coupling is high, which may lead to differences in the action potential characteristics and refractoriness of PZ cells dependent on their specific anatomical location in the infarct region.53,54
Representing the passive properties of the scar
Some recent studies have modeled the dense scar in a different manner, not treating the tissue as entirely acellular, but instead seeking to account for the passive conductive properties of the necrotic tissue,17,18,23 which may be thought to represent the averaged effect of electrotonically coupled myofibroblasts, as discussed above. The study by McDowell et al (2011)23 modeled small discrete clusters of myofibroblasts as individual randomly distributed finite elements (assigned myofibroblast ionic properties,55 resting potential −49 mV) embedded within the rest of the scar, which was represented as an insulator. Two scenarios (80% or 0% of the scar region, by volume, was modeled as myofibroblast clusters) were chosen, thus effectively representing the scar as a high electrotonic passive load or no passive electrotonic load (complete insulator), respectively. Myofibloblast regions within the scar were assigned isotropic conductivities, 50% reduced relative to healthy (fiber direction) conductivity. The studies by Deng et al.17 and Ringenberg et al.18 chose to model the scar as having entirely passive membrane properties. In such a scenario, the passive ionic model (equivalently a resistor–capacitor circuit) must be assigned both a membrane resistance and a resting membrane potential (Vrest). The choice of Vrest made by Ringenberg et al (2014)18 was −60 mV, presumably representing the elevated resting potential of myofibroblasts, known to be of this order.55 In contrast to the McDowell et al study, in this work, the scar core region has preserved conduction anisotropy, although conduction in each respective direction was reduced by a much greater degree, to just 5% of the values in healthy myocardium.
Electrotonic effects on APD and refractoriness of PZ cells
Depending on whether the scar core is represented as a pure insulator16,19–21 or with passive conductive properties17,18,23 will significantly affect the associated electrotonic loading imposed upon neighboring PZ cells. Electrotonic loading is known to affect action potential upstroke and duration of cells, giving rise to the modulation of transmural gradients in these quantities at the tissue level, relative to isolated cell properties due to coupling at the tissue level.33–35 Differences in electrotonic loading have also been recently shown to significantly affect refractoriness, introducing large gradients in effective refractory period (ERP) that are sufficient to initiate unidirectional block under focal ectopic stimuli.53,54 Thus, potential differences in the representation of scar within computational models (insulator vs passive) may have significant effects on both the APD and refractoriness of PZ cells. Understanding these effects may help to shed light on the arrhythmogenic properties of the scar and the associated reentrant pathways through conducting isthmuses and better inform the specific parameter choices when constructing image-based models.
It is the purpose of this article to perform a series of idealized experiments and analytical analysis to present the potential significant differences that specific choices of scar representation have on the local electrophysiological behavior of infarcted regions. Our findings show that an entirely necrotic scar facilitates the PZ region, and the corresponding isthmus, to maintain their assigned higher APD; however, as the scar becomes passive, electrotonic effects drag down this elevated APD, as the scar acts like a current sink. Depending on the conductivity properties of the regions and their geometry, this can result in lower APD values within the isthmus (flanked by scar either side) than in healthy myocardium, although often a region of refractory tissue remains at the isthmus entrance/exit, as shown to be the case clinically.56 This analysis leads us to conclude that a necrotic region with passive electrical properties (perhaps representing a network of coupled myofibroblasts) could facilitate arrhythmias to a greater degree than entirely necrotic scar, a consideration for future modeling endeavors in this area.
Methods
Computational methods
The Cardiac Arrhythmia Research Package57 finite element solver was used to solve the monodomain partial differential equations for cardiac electrodynamics:58
| (1) |
where σm is the bulk conductivity tensor, Vm is the transmembrane potential, β is the surface area to volume ratio of the myocyte, Cm is the membrane capacitance, Iion is the sum of the individual ionic currents, and Is is the stimulus current density. The boundary condition on the surface of the myocardium (∂Ω) associated with Equation (1) is
| (2) |
The conductivity was chosen to be isotropic (σm ≡ σm I, where I is the identity tensor), reflecting observed myofiber disarray in the vicinity of the infarct scar,6,8,14,41 and in all simulations, structured quadrilateral finite elements with an edge length of 50 µm and a time step of 20 µs were used. Active ionic currents were represented by a widely used human ventricular cell model,59 and passive tissue was represented as a resistor–capacitor network with a specific resting potential Vrest.
Computational models
Geometries
A square template domain of edge length 4 cm, resulting in 640,000 quadrilateral (two-dimensional [2D]) finite elements, was used to create geometries representing isthmus channels surrounded by circular segments, representing islands of scar (passive or necrotic) with a surviving isthmus region. A transition region consisting of PZ cells surrounded the isthmus and scar region. A schematic of the computational models is shown in Figure 2.
Figure 2.
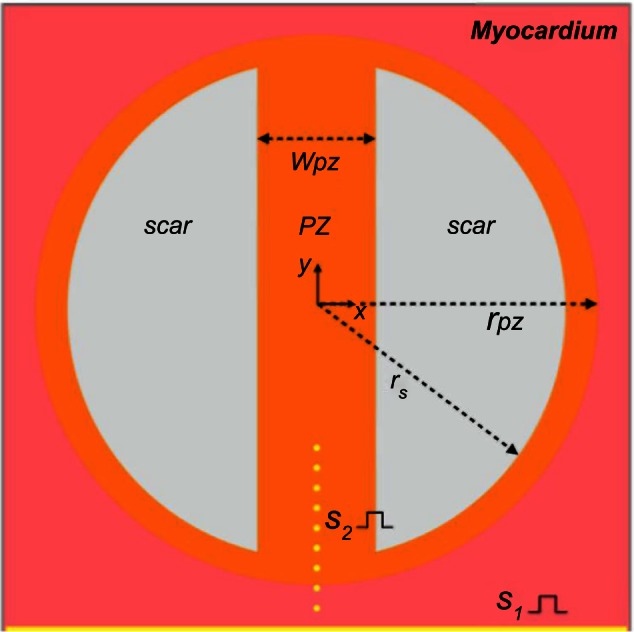
Schematic of the computational domain. Inside healthy myocardium (pink) is a circular region representing the PZ (orange) of radius rPZ, which contains two circular segments of radius rs representing the scar (gray). The PZ region contains an isthmus of width wPZ, which separates the scar regions. The sites of S1 and S2 stimuli are represented in yellow. S1 stimuli are applied to all nodes along the lower surface of the domain, and S2 stimuli are applied to small clusters of nodes (of radius 50 µm) along the line of symmetry.
The radii of the scar and PZ were set to rs = 15 mm and rPZ = 17 mm, respectively, giving an isthmus length of 30 mm and a transition distance of 2 mm between the scar and healthy tissue. The width of the isthmus wPZ was varied between 2, 4, and 8 mm, to investigate the effects of the computational representation of the scar on the electrophysiological dynamics in the PZ region. All chosen dimensions were based on experimentally observed values.60,61
Tissue representation
The various electrophysiological regions in the computation models were represented by the human ventricular cell model by ten Tusscher et al.59, with various conductivities and ion channel alterations. These are listed in Table 1, where tissue and ion channel conductivities are represented as a fraction of their maximum value in healthy tissue (healthy tissue conductivity was set to 0.15 S/m), based upon other modeling studies.17,18,23
Table 1.
Electrophysiological representation of various tissue regions.
| REGION | TISSUE CONDUCTIVITY | CELLULAR MODIFICATION |
|---|---|---|
| Healthy myocardium | 1.0 | None |
| PZ | 0.25 | 0.38 × gNa, 0.2 × gKs, 0.3 × gKr and 0.31 × gCaL |
| Passive scar | 0.05 | Vrest = −60 mV |
| Necrotic scar | 0.0 | N/A |
Note: Numbers without units multiply the maximum healthy conductivities.
The scar tissue is represented in two ways: passive refers to a resistor–capacitor network with no active ionic currents (Iion = Vm/Rm in Equation (1)) with properties (unless otherwise stated) given in Table 1 and necrotic refers to an internal boundary in the computational domain, where the no-flux boundary condition (2) is satisfied at the interface.
Computational protocols
Stimulation protocols
Before performing tissue-level simulations, single cells representing the PZ and healthy myocardium (Table 1) were prepaced 100 times at a basic cycle length of 500 ms. The resultant ionic state vectors (η in equation (1)) were then applied to all reaction source terms in the appropriate regions in the tissue (Fig. 2). In order to set up preexisting gradients in refractoriness, the tissue was then prepaced from the S1 site (the bottom yellow line in Fig. 2) five times at the same basic cycle length of 500 ms. All APD measurements were taken on the sixth S1 beat, and all ERP measurements were taken after the fifth S1 wave had passed the S2 pacing sites.
APD
The APD was calculated by computing the difference in time from the maximum rate of upstroke until 90% repolarization for a normalized action potential (normalized by the maximum transmembrane potential during the action potential).
ERP
The ERP was calculated at discrete S2 stimulus points in the tissue (Fig. 2) using the bisection algorithm, with a tolerance of 1 ms, taking into account the activation time of the tissue. The criterion for the bisection search was a successful action potential propagation following a point stimulation (of fixed strength) at the S2 site, at a given time after prior activation from the S1 wave. The details of the bisection scheme used to compute ERP are discussed in more detail in Ref. 54.
Results
Wave propagation patterns and APD for passive and necrotic scars
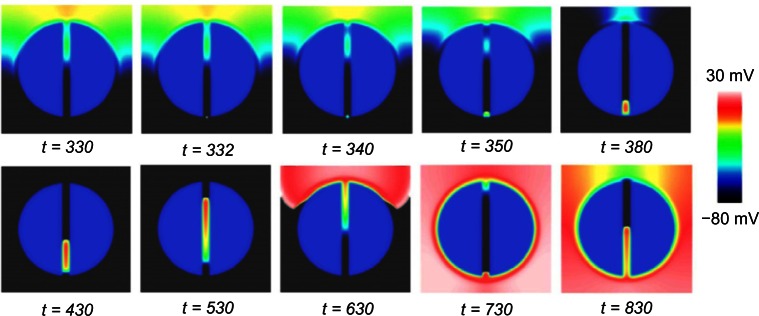
Snapshots of the wave propagation pattern and 2D colormaps of the APD for both the necrotic and passive scars are shown in Figure 3.
Figure 3.

Wave propagation pattern at different times (A) and APD colormap (B) for the necrotic (upper row) and passive scar (lower row) representations, for the case with the isthmus width of 4 mm.
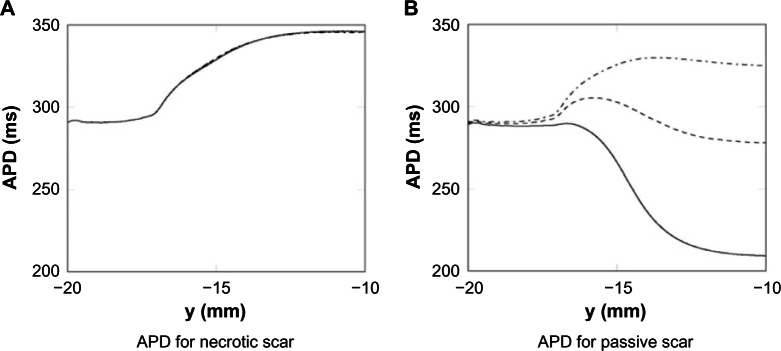
In Figure 3A, the excitation wavefront can be seen to propagate quickly through the healthy myocardium and slowly through the PZ due to its lower conductivity and reduced gNa. In Figure 3B, the APD is significantly lower in the boundary layer of the PZ, compared with the necrotic scar, due to the electro-tonic interactions of the PZ tissue in proximity with the passive scar. The APD in the isthmus of the necrotic scar is significantly longer than in the healthy tissue due to the remodeling of the ionic currents in the PZ tissue (Table 1). In the passive scar case, the APD at the isthmus entrance/exit is seen to be raised relative to its value elsewhere in the tissue; this is due to the competition between the ionic current remodeling in the PZ (raising the single-cell APD) and the electrotonic interaction of the trans-membrane potential with the passive scar with a resting potential of −60 mV (acting to lower the APD of proximal tissue).
Effects on APD of different scar parameters
Here, the effects on the APD along the line of symmetry of the domain are investigated for both necrotic and passive scar representations, for different isthmus widths and passive scar parameters.
APD for different isthmus widths
The effects of the different isthmus widths, for both the necrotic and passive scars, on the APD are shown in Figure 4. Figure 4 shows that the thickness of the isthmus has little effect on the APD for the necrotic scar (A), but significantly affects the APD for the passive scar (B). The negligible effect on APD in the necrotic case is due to the no-flux boundary condition on the tissue–scar interface; the APD is unaffected by the scar, and thus, the thickness of the isthmus does not change the APD along the center. The large effect on APD in the passive scar case is due to the relative influence of the passive scar on the PZ tissue due to the assigned resting potential of the scar, because there is no boundary condition assigned to the PZ–passive scar interface. The thinner the isthmus, the greater the transmembrane current flux from the isthmus to the passive scar, which acts to shorten the APD.
Figure 4.
APD measured along the centerline of the passive and necrotic scar domains for the 2 mm—, 4 mm ----, and 8 mm -.-.-. isthmuses.
Influence of passive scar properties on APD
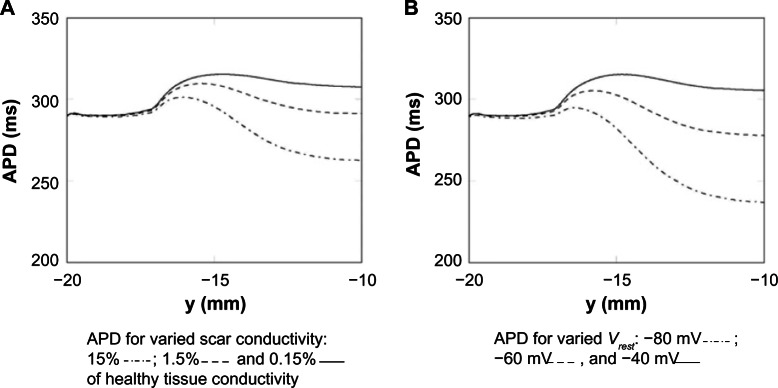
The effect of different passive scar properties (conductivity and Vrest) on the APD along the centerline, for a fixed isthmus width (4 mm), was investigated. Keeping the resting potential fixed at −60 mV, the conductivity of the scar was varied by three orders of magnitude: 15%, 1.5%, and 0.15% of the healthy myocardium. Keeping the conductivity of the scar fixed at 5% of the healthy myocardium, the resting potential was varied in increments of 20 mV: −80 mV (close to the resting potential of the healthy myocardium), −60 mV, and −40 mV. These results are shown in Figure 5. It can be seen from Figure 5A and B that the APD is relatively constant until the transition to PZ tissue (at y = −17 mm) when it starts to increase, due to the raised APD in the PZ from the altered ionic conductivities, then starts to decrease inside the isthmus due to electrotonic influences from the enclosing scar and rapidly approaches a steady value at y = −10 mm. The electrotonic interaction between the scar and isthmus, due to increasing scar conductivity, acts to decrease the APD along the centerline. This is due to the relative influence of the boundary layer between the scar and isthmus on the point at which the APD is measured – the higher the scar conductivity the greater the space constant λ and thicker the boundary layer; therefore, the scar acts like more of an electrotonic current sink, reducing the APD at the center of the isthmus. As the passive scar conductivity vanishes, the passive scar acts like an insulator and the computational representation is equivalent to that of the dense necrotic scar.
Figure 5.
APD measured along the centerline for a passive scar with 4 mm isthmus and varied scar parameters. (A) The scar resting potential is kept fixed at −60 mV. (B) The scar conductivity is kept fixed at 5% of the healthy tissue conductivity.
The large effect on APD of the varied scar Vrest is due to the fact that the magnitude of the electrotonic current sink (which acts to shorten APD), from the isthmus to the scar, during the plateau phase of the action potential is proportional to the difference between the plateau potential (approximately 20 mV) and the scar potential Vrest. Therefore, the APD inside the isthmus is approximately inversely proportional to Vplateau − Vrest, in other words as Vrest becomes more negative the APD reduces commensurately.
The magnitude of the electrotonic current sink, caused by the scar, which acts to shorten APD, may be calculated for a one-dimensional (1D) or cylindrical isthmus, surrounded by an infinite scar, using an exact solution to the steady-state monodomain equations (temporal derivatives vanish in Equation~(1)). Figure 6 shows the electrotonic current at the origin of a one-dimensional isthmus as a function of Vplateau − Vrest and scar conductivity, for a plateau potential of 20 mV. Figure 6 shows how the magnitude of the electrotonic current Im increases as the electrotonic driving force Vplateau − Vrest increases, and its dependence on the scar conductivity. When the conductivity of the scar tends to zero, the electrotonic current remains small even for large values of Vplateau − Vrest.
Figure 6.
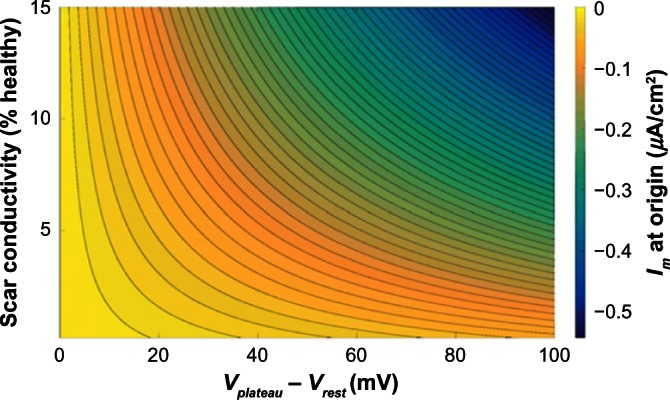
Electrotonic current Im at the origin of a 1D isthmus of width 4 mm surrounded by an infinite scar with varying resting potential Vrest, assuming a fixed plateau potential in the isthmus of Vplateau = 20 mV, from an exact solution to the steady-state isotropic monodomain equations. Contour lines are plotted at increments of 0.01 µA/cm2.
ERP for passive and necrotic scars
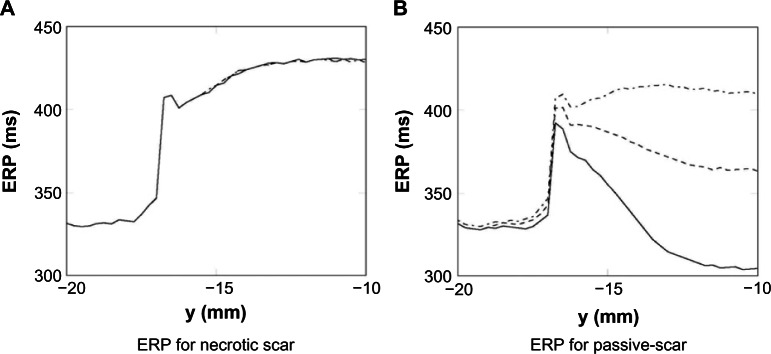
The ERP, while known to depend on the specific nature of the S2 stimulus, provides an indication of the likelihood of wave propagation upon spontaneous depolarization of bundles of surviving myocytes. The ERP was calculated at points along the line of symmetry (as shown in Fig. 2). The ERP for the necrotic and passive scars (with tissue properties given in Table 1) is shown in Figure 7. In both the necrotic and passive scars, Figure 7 shows how the ERP increases significantly at the interface between the healthy tissue and PZ tissue (at y = −17 mm); this is due to the ionic remodeling of the fast sodium current (Table 1), reducing the excitability of the PZ. In the necrotic scar case, the ERPs for each of the isthmus widths are identical (within the tolerance of the bisection search), and after the initial increase at the healthy–PZ interface, the ERP reduces slightly before increasing inside the isthmus. In the passive scar case, the different isthmus widths significantly affect the ERP; after the initial increase at the healthy–PZ interface, the ERP reduces slightly, before decreasing for the 2 and 4 mm widths, and increasing for the 8 mm isthmus width.
Figure 7.
ERP measured along the centerline of the necrotic (A) and passive (B) scars with different isthmus thickness; 2 mm—, 4 mm ----, and 8 mm -.-.-.
Discussion
The first part of this study reviewed the current approaches taken in the construction of computational models, which aim to represent the electrophysiological changes that occur in regions of infarct scar.
The specific manner by which both the scar core and the PZ of surviving myocardium that surrounds it are modeled was described, summarizing the physiological research that has motivated the computational representations, and important differences in infarct representations between different studies were highlighted.
In the second part of this work, key differences in the functional electrophysiological behavior of tissue within, and in the vicinity of the scar, were highlighted, which are dependent upon the scar representation chosen in the model.
Specifically, localized differences in both APD and ERP were observed and it was shown that the dynamics of wavefront propagation around the scar and the mechanisms driving arrhythmogenesis in these regions are different, depending on the scar representation.
Effect on APD of scar representation
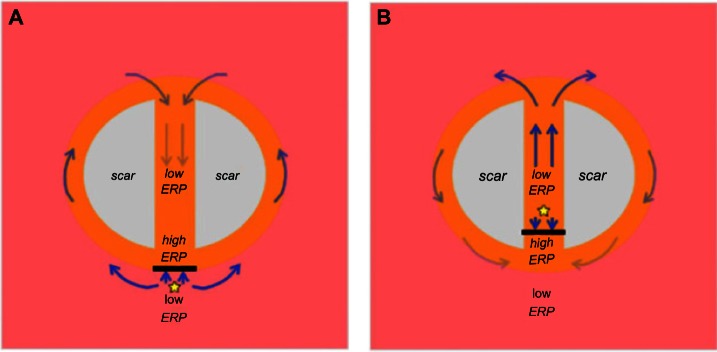
The core of the infarct scar is most consistently represented in models as being necrotic (ie, a perfect insulator).16,19–22,29,51 In this case, the boundaries of the scar act like an insulating boundary to intracellular current flux. Within an isthmus, which is flanked on either side by scar, the tissue therefore experiences a relatively low electrotonic loading. Consequently, the PZ tissue within the isthmus, which has a high APD at the single-cell level due to remodeling of various ion channels, maintains this high APD as it is surrounded by only similar PZ tissue or insulating boundary (as shown in Fig. 4A). Thus, the APD of the tissue here is close to its value at the single-cell level. As propagation is along the axis of the isthmus, reducing the isthmus width did not alter the APD, as the insulating boundary is parallel to the wave propagation direction. At the mouth of the isthmus, however, the PZ tissue neighbors the healthy tissue with a lower APD. Thus, electrotonic effects result in a more rapid repolarization and slightly less prolonged APD of the tissue at the entry/exit site of the isthmus, relative to the isthmus center.
A distinctive difference is immediately evident in the case where the scar core is represented as passive tissue. Although not the norm, some recent previous studies17,18,23 have chosen to represent the scar in this manner, presumably to replicate the effect of electrotonically coupled myofibroblasts, for which experimental evidence is mounting.47,48 Representing a scar as tissue with passive properties significantly changes the electro-physiological behavior of the nearby PZ. The passive scar acts as an electrotonic current source or sink, depending on the sign of the difference between the membrane potentials in the scar and in the PZ. The effect of this current source or sink action is most evident in the isthmus, which is surrounded on both sides by scar. Here, the plateau potential and APD are reduced. For example, as shown in Figure 4, at the center of the isthmus (of width 4 mm), the APD in the case of passive scar tissue was ≈280 ms, much shorter than its isolated single-cell value (and the corresponding value in the case of insulating scar) of ≈345 ms.
As in the case of the necrotic scar, in the passive case, the APD at the mouth of the isthmus differs to that within the isthmus itself; however, here, the APD is seen to be raised relative to its value within the isthmus center, as opposed to reduced in the necrotic case; this can be seen clearly in Figures 3B and 4B. Tissue at the exit and entry sites of the isthmus is no longer flanked on both sides by passive scar, and thus is less affected by the corresponding electrotonic current effects, relative to tissue in the isthmus center. Consequently, the APD of tissue in this region is less abbreviated and is closer to its single-cell value. This effect gives rise to a biphasic shape to the APD along the centerline of the isthmus, with an increase in APD near the mouth (approaching from the distal healthy tissue with lower APD), followed by a decrease to a minimum within the isthmus itself (Fig. 3B).
Implications for arrhythmias
The identified effect of a raised APD at the isthmus mouth, accompanied by a reduced APD within the isthmus itself, may have important implications for arrhythmia genesis and sustenance. As highlighted in “Effects on APD of different scar parameters” section, if APD is raised throughout the length of the isthmus (as in the necrotic case), this seems counterintuitive with respect to the fixed anatomical circuit provided by the scar enabling a viable reentrant pathway (Figs. 8 and 9).
Figure 8.
Mechanism of arrhythmia induction following capture of a focal ectopic beat due to ERP gradients within the isthmus. (A) Focal ectopic occurs at the mouth of the isthmus, distal to the scar itself (ie, just outside main isthmus). Capture is blocked from directly entering the isthmus at the mouth due to the high ERP and is forced around the outer boundary of the scar where ERP is lower, entering the isthmus from the opposite side. In this time, tissue within the isthmus center has sufficiently recovered, and a reentrant circuit is established. (B) Focal ectopic occurs at the mouth of the isthmus, proximal to the scar itself (ie, just inside the isthmus). Capture is blocked from exiting the isthmus at the mouth due to the high ERP, but is allowed to propagate along the isthmus itself, exiting at the opposite end. Activation then proceeds to propagate around the scar boundary and reenters the isthmus, setting up a reentrant circuit.
Figure 9.
Formation of a reentrant circuit upon premature focal 2 ms S2 stimulus in a spatiotemporal region with a gradient in ERP (as shown in Fig. 7B). Time units are in milliseconds.
We have shown here that, despite assigning the isolated cells in the isthmus-elevated APDs through downregulation of various ionic conductances, the possible passive effects of the scar may act to pull-down APD, shortening wavelength, and making the formation of a sustained reentrant circuit more likely.
We further demonstrated that these effects were highly sensitive to the passive nature of the scar, specifically, its assigned conductivity and the effective resting potential (Fig. 5). Thus, the degree of myofibroblast proliferation throughout the scar, combined with the level at which viable electrotonic coupling with healthy myocytes is established, may govern the degree to which the scar acts like a passive electrotonic current sink. Such considerations therefore suggest further experimental investigations to understand exactly how these parameters may govern the degree to which a particular scar may act as a more dangerous arrhythmic substrate.
Refractory tissue at the mouth of an isthmus is known to be an important perquisite in facilitating the initial conduction block that leads to reentry.57 If tissue at the entry to the isthmus remains refractory when a more premature beat arrives, it blocks and the isthmus is initially protected from excitation. The blocked wave instead travels around the outside of the scar and enters the isthmus from the distal side, initiating a reentrant circuit (as shown in the left panel in Fig. 8). This mechanism therefore relies on this initial conduction block at the isthmus mouth due to increased refractoriness of the isthmus mouth relative to its immediate neighbors. Here, we have demonstrated that such an effect is possible, both in the case of the scar acting as a necrotic insulator and also when acting as a passive conductor, due to the noted regions of elevated APD at the entry/exit sites. However, as discussed above, in the passive case, the APD throughout the isthmus length (including the entry/exit sites) is lower than in the necrotic case, as shown clearly in Figure 3, due to the above-mentioned electrotonic sink effects. Thus, when the initially blocked wavefront enters the isthmus from the distal end (which would now be excitable again in the time taken for the wavefront to propagate around the outer boundaries of the scar), it is more likely to be able to successfully propagate through the isthmus, exiting out of the proximal mouth and reentering. Therefore, the passive scar may provide a more dangerous reentrant substrate due to the shorter electrical wavelength it provides.
Effect on ERP of scar core representations
ERP and APD represent fundamentally very different quantities. ERP, although related to APD, requires two separate stimuli for evaluation (S1 and S2) and can only be reliably calculated at the stimulus site itself; it thus depends upon the nature of the second stimulus (strength, duration, etc.). ERP also depends upon the refractoriness of the tissue to be re-excited by the S2, whereas APD depends only upon the repolarization characteristics of the membrane potential levels.
In our recent studies,53,54 we have highlighted the vital role that local electrotonic loading plays in governing ERP following focal stimuli. In the absence of significant differences in APD, large variations were seen in ERP due to differences in electrotonic loading brought about by the heterogeneity in local tissue structure. Such fine-scale structural heterogeneities included proximity to nearby insulating boundaries (tissue surfaces and intramural vessel cavities),53 or rapid tissue expansions within PZ regions.54 As ERP depends sensitively on the nature of the S2 stimulus, sites that experience low electrotonic loading better confine the S2 stimulus current, with less of it diffusing away due to current sink effects. Thus, more of the S2 stimulus current may be used to capture the focally stimulated region, meaning capture is possible at higher levels of refractoriness (shorter coupling intervals), reducing ERP. Conversely, in high loading regions (surrounded only by well-coupled tissue, for example), less of the applied stimulus current is available for capture, and thus, the tissue is harder to excite, requiring longer coupling intervals, lengthening ERP.
Here, we have demonstrated that differences in structural and excitability properties in and around the scar region lead to important variations in ERP and depend sensitively upon the exact manner in which they are represented in computational models. The transition between healthy tissue and PZ tissue at the mouth of the isthmus results in a sharp rise in ERP, both when the scar is represented necrotically and passively. First, this is because the PZ has reduced excitability due to a markedly reduced sodium current conductance (downregulated to 40% – Table 1), making it harder to re-excite the tissue. Second, in both passive and necrotic representations, APD was lengthened at the isthmus mouth, leading to a delayed repolarization phase and prolonged refractoriness.
In the case of the passive scar, the electrotonic current sink effect of the scar acts to reduce APD within the isthmus, reducing ERP commensurately. However, the same effect acts to dissipate the S2 focal stimulus current, making capture harder, which increases ERP. Although Figures 4B and 7B show that the passive effects on APD seem to dominate the ERP, the passive effects on the S2 are apparent; for example, there is a difference in APD at the isthmus center between a 4 mm isthmus (with higher loading) and an 8 mm isthmus (with lower loading) of ≈50 ms, whereas the corresponding difference in ERPs is less, at ≈40 ms. This relative reduction in ERP is because the stimulus current is more confined for the wider isthmus case.
Implications for arrhythmias
Focal stimuli from spontaneously activated groups of cells are known to represent an important arrhythmogenic risk.62,63 Spontaneous beats are suggested to be more likely in the neighborhood of infarct regions, due to the ionic remodeling in these areas, which is known to facilitate early and delayed afterdepolarizations,3,62 along with the cellular uncoupling and changes in anisotropy due to fibrosis.62,64 However, the exact mechanism by which focal capture of an isolated region of tissue facilitates the induction of a sustained reentrant circuit remains unknown.
We have demonstrated in our previous recent studies how significant differences in ERP (driven by fine-scale structural heterogeneity) can occur within spatially localized regions. The resulting high ERP gradients were shown to facilitate unidirectional block of focal stimuli, such that propagation is prevented in the direction of high ERP, but allowed in the direction of low ERP.53,54 In this study, we have highlighted significant gradients in ERP along the isthmus, present both when the scar is represented as necrotic and as passive tissue. Both cases showed a large ERP increase in the transition from healthy to PZ tissue near the isthmus mouth (explained above). Capture of a focal stimulus around the time of the local ERP would therefore exploit this gradient; propagation would be blocked from propagating into the isthmus, instead being forced to propagate around the scar border, entering the isthmus instead from its distal end. Block of such a premature beat, in which the isthmus is initially protected from excitation due to elevated refractoriness near the isthmus entrance, has been shown clinically to be an important mechanism of arrhythmia initiation in this context56 and is demonstrated schematically in Figure 8A. In the passive scar case, our work has highlighted an additional novel mechanism of arrhythmia induction. In Figure 7B, a second steep gradient in ERP was seen further into the isthmus center, as ERP falls from its relatively high value at the isthmus mouth, to lower values within the isthmus center (depending on the isthmus width). A focal stimulus capturing just inside the isthmus may thus be blocked from propagating out of the isthmus (as ERP is high at the mouth), but may propagate further through the isthmus, out of the distal side (where the tissue has now recovered in the intervening time), reentering back around the scar. This novel proposed mechanism is highlighted schematically in Figure 8B and was found to occur readily in the thinnest isthmus. A low-strength S2 stimulus of 2 ms duration was applied along the centerline at y = −15 mm at approximately the observed ERP (of 330 ms). The stimulus captured in one direction only, causing unidirectional propagation and establishing a reentrant circuit, as shown in Figure 9.
Dependence upon passive properties
Mounting experimental evidence suggests that scar core may indeed have important passive properties, driven by myofibroblast proliferation and coupling.47,48 Nonetheless, representing the scar as passive within a computational model is fraught with difficulties with respect to faithful parameterization of properties such as the passive tissue conductivity, resting membrane potential, and whether to explicitly include myofibroblast cell models.
An important aspect of this study has demonstrated how the localized changes in both APD and ERP described above depend sensitively upon the specific choice of associated passive parameters, in combination with the width of the isthmus. Such sensitivity analysis is important as the exact passive behavior of the scar is not yet well measured and will differ significantly between individual infarcts. The analytical result in “Influence of passive scar properties on APD” section demonstrated how the electrotonic current sink effect of the passive scar is affected by the conductivity of the scar and the potential difference between the PZ and the scar. This result is intuitive and shows that the current sink effect is greater for a larger potential difference and scar conductivity, and it is to lower the APD in the PZ region. Another result, not shown in this work, is that the electrotonic current sink effect is larger for thinner isthmuses.
In the 2D simulations of “Results” section, increasing the scar conductivity increased the electrotonic current sink effect of the scar, significantly reducing the APD within the isthmus. Likewise, lowering the assigned passive resting membrane potential of the scar increased the electrotonic current flow away from the PZ region, increasing repolarization and abbreviating APD. For fixed tissue conductivity of the PZ, varying the width of the isthmus simply changes the relative amount of isthmus tissue affected passively by the scar. For isthmuses with widths less than a few length constants, the center of the isthmus becomes appreciably affected. If a relatively large proportion of the isthmus has its APD significantly shortened, this may thus reduce the associated activation wavelength for a wave traveling through the isthmus, increasing its ability to act as an arrhythmogenic substrate.
Similar effects on APD have also been examined in a previous study by McDowell et al.23 who explicitly represented islands of myofibroblasts (of varying densities) within both the scar as well as within the PZ itself. The authors showed that the electrotonic current sink effect of the myofibroblasts act to shorten APD around the scar, increasing arrhythmia propensity. However, as the electrotonic current sink effects were increased, the region became more protected against arrhythmia initiation, as the coupled myofibroblast regions elevated the resting potential of neighboring myocardium, reducing excitability and blocking propagation. In this study, we have focused primarily on the isthmus region and specific changes in electrophysiological properties (APD and ERP) that may affect arrhythmogenesis in this area.
Clinical implications of computational scar representation
Computational modeling, in general, reduces experimental costs and, provided the model is physiologically faithful, aids in mechanistic understanding. It has long been accepted that the monodomain and bidomain representations of the cardiac syncytium are, in the macroscopic sense, faithful representations of reality. The use of computational modeling to understand the electrophysiological environment of the infarct scar is still relatively immature; however, recent works20,65 demonstrate that computational modeling of the infarct region is clinically useful and may be of significant future benefit for patients if applied routinely in the clinic.
Personalized computational models have recently been shown to significantly outperform traditional predictors of future arrhythmic events.65 The computational geometries (generated from contrast-enhanced patient MR images) in Ref. 65 include regions of PZ and isthmuses surrounded by scar tissue, which was assigned zero conductivity (referred to as necrotic scar in this work). Similar approaches were also used in the study by Ashikaga et al.20 in which personalized models were used to successfully (retrospectively) predict targets for catheter ablation in patients. As we have described in this work, the electrophysiological dynamics in the infarct region, and thus the likelihood of the infarct region providing a lethal arrhythmogenic substrate and the subsequent dynamics, may be modulated by the specific modeling choices in the infarct region.
Conclusions
It is currently unknown to what extent the scar core of an infarcted region should be considered as entirely necrotic (insulating) or passive (containing coupled myofibroblasts). We have highlighted that representing either the insulating or passive properties of the scar can give rise to significant variations in local spatial patterns of both repolarization and refractoriness to secondary stimuli.
Both necrotic and passive representations of the scar give rise to localized high gradients in both APD and ERP at the mouth of the isthmus, which may provide important mechanisms for unidirectional block of either premature sinus beats or spontaneous focal ectopics. However, a passive scar core reduces APD further within the isthmus center, reducing activation wavelength, potentially explaining its ability to contain a viable reentrant circuit over an entirely necrotic scar in which a high APD is maintained throughout the isthmus length.
This study suggests further lines of experimental investigations aimed to more faithfully determine the electro-physiological properties of both the scar core itself, and the surrounding PZ and healthy myocardium to better understand its potential as a lethal arrhythmic substrate.
Footnotes
ACADEMIC EDITOR: Thomas E. Vanhecke, Editor in Chief
PEER REVIEW: Four peer reviewers contributed to the peer review report. Reviewers’ reports totaled 758 words, excluding any confidential comments to the academic editor.
FUNDING: This work was supported by the National Institute for Health Research Biomedical Research Centre at Guy’s and St Thomas’ National Health Service Foundation Trust and King’s College London, in addition to the Centre of Excellence in Medical Engineering funded by the Wellcome Trust and Engineering and Physical Sciences Research Council (EPSRC; WT 088641/Z/09/Z). The views expressed are those of the author(s) and not necessarily those of the National Health Service, the National Institute for Health Research, or the Department of Health. The authors acknowledge the British Heart Foundation under project grant number PG/14/66/30927. The authors confirm that the funder had no influence over the study design, content of the article, or selection of this journal.
COMPETING INTERESTS: Authors disclose no potential conflicts of interest.
Paper subject to independent expert blind peer review. All editorial decisions made by independent academic editor. Upon submission manuscript was subject to anti-plagiarism scanning. Prior to publication all authors have given signed confirmation of agreement to article publication and compliance with all applicable ethical and legal requirements, including the accuracy of author and contributor information, disclosure of competing interests and funding sources, compliance with ethical requirements relating to human and animal study participants, and compliance with any copyright requirements of third parties. This journal is a member of the Committee on Publication Ethics (COPE).
Author Contributions
Conceived and designed the experiments: MB, AC. Analyzed the data: MB, AC. Wrote the first draft of the manuscript: MB. Contributed to the writing of the manuscript: AC. Agree with manuscript results and conclusions: MB, AC. Jointly developed the structure and arguments for the paper: MB, AC. Made critical revisions and approved final version: MB, AC. Both authors reviewed and approved of the final manuscript.
REFERENCES
- 1.Lopshire JC, Zipes DP. Sudden cardiac death better understanding of risks, mechanisms, and treatment. Circulation. 2006;114(11):1134–6. doi: 10.1161/CIRCULATIONAHA.106.647933. [DOI] [PubMed] [Google Scholar]
- 2.de Jong S, van Veen TAB, van Rijen HVM, de Bakker JMT. Fibrosis and cardiac arrhythmias. J Cardiovasc Pharmacol. 2011;57(6):630–8. doi: 10.1097/FJC.0b013e318207a35f. [DOI] [PubMed] [Google Scholar]
- 3.Nattel S, Maguy A, Le Bouter S, Yeh YH. Arrhythmogenic ion-channel remodeling in the heart: heart failure, myocardial infarction, and atrial fibrillation. Physiol Rev. 2007;87(2):425–56. doi: 10.1152/physrev.00014.2006. [DOI] [PubMed] [Google Scholar]
- 4.Stevenson WG. Ventricular tachycardia after myocardial infarction: from arrhythmia surgery to catheter ablation. J Cardiovasc Electrophysiol. 1995;6(10):942–50. doi: 10.1111/j.1540-8167.1995.tb00370.x. [DOI] [PubMed] [Google Scholar]
- 5.de Bakker JM, van Capelle FJ, Janse MJ, et al. Slow conduction in the infarcted human heart. ’Zigzag’ course of activation. Circulation. 1993;88(3):915–26. doi: 10.1161/01.cir.88.3.915. [DOI] [PubMed] [Google Scholar]
- 6.Rutherford SL, Trew ML, Sands GB, LeGrice IJ, Smaill BH. High-resolution 3-dimensional reconstruction of the infarct border zone: impact of structural remodeling on electrical activation. Circ Res. 2012;111(3):301–11. doi: 10.1161/CIRCRESAHA.111.260943. [DOI] [PubMed] [Google Scholar]
- 7.Asirvatham SJ, Stevenson WG. Editor’s perspective: the isthmus of uncertainty. Circ Arrhythm Electrophysiol. 2014;7(1):175–7. doi: 10.1161/CIRCEP.114.001425. [DOI] [PubMed] [Google Scholar]
- 8.Tschabrunn CM, Roujol S, Nezafat R, et al. A swine model of infarct-related reentrant ventricular tachycardia: electroanatomic, magnetic resonance, and histopathological characterization. Heart Rhythm. 2016;13(1):262–73. doi: 10.1016/j.hrthm.2015.07.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tanawuttiwat T, Nazarian S, Calkins H. The role of catheter ablation in the management of ventricular tachycardia. Eur Heart J. 2016;37(7):594–609. doi: 10.1093/eurheartj/ehv421. [DOI] [PubMed] [Google Scholar]
- 10.Clayton RH, Bishop MJ. Computational models of ventricular arrhythmia mechanisms: recent developments and future prospects. Drug Discov Today Dis Models. 2014;14:1–6. [Google Scholar]
- 11.Setser RM, Bexell DG, O’Donnell TP, et al. Quantitative assessment of myocardial scar in delayed enhancement magnetic resonance imaging. J Magn Reson Imaging. 2003;18(4):434–41. doi: 10.1002/jmri.10391. [DOI] [PubMed] [Google Scholar]
- 12.Kwong RY, Farzaneh-Far A. Measuring myocardial scar by CMR. JACC Cardiovasc Imaging. 2011;4(2):157–60. doi: 10.1016/j.jcmg.2010.12.004. [DOI] [PubMed] [Google Scholar]
- 13.Kim RJ, Fieno DS, Parrish TB, et al. Relationship of MRI delayed contrast enhancement to irreversible injury, infarct age, and contractile function. Circulation. 1999;100(19):1992–2002. doi: 10.1161/01.cir.100.19.1992. [DOI] [PubMed] [Google Scholar]
- 14.Vadakkumpadan F, Arevalo H, Prassl AJ, et al. Image-based models of cardiac structure in health and disease. Wiley Interdiscip Rev Syst Biol Med. 2010;2(4):489–506. doi: 10.1002/wsbm.76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cardone-Noott L, Bueno-Orovio A, Minchole A, et al. Computing in Cardiology Conference (CinC) Vol. 2014. IEEE; Cambridge, MA: 2014. A computational investigation into the effect of infarction on clinical human electrophysiology biomarkers; pp. 673–6. [Google Scholar]
- 16.Hill YR, Child N, Hanson B, et al. Investigating a novel activation-repolarisation time metric to predict localised vulnerability to reentry using computational modelling. PLoS One. 2016;11(3):e0149342. doi: 10.1371/journal.pone.0149342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Deng D, Arevalo H, Pashakhanloo F, et al. Accuracy of prediction of infarct-related arrhythmic circuits from image-based models reconstructed from low and high resolution MRI. Front Physiol. 2015;6:282. doi: 10.3389/fphys.2015.00282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ringenberg J, Deo M, Filgueiras-Rama D, et al. Effects of fibrosis morphology on reentrant ventricular tachycardia inducibility and simulation fidelity in patient-derived models. Clin Med Insights Cardiol. 2014;8(Suppl 1):1–13. doi: 10.4137/CMC.S15712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Arevalo H, Plank G, Helm P, Halperin H, Trayanova N. Tachycardia in post-infarction hearts: insights from 3D image-based ventricular models. PLoS One. 2013;8(7):e68872. doi: 10.1371/journal.pone.0068872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ashikaga H, Arevalo H, Vadakkumpadan F, et al. Feasibility of image-based simulation to estimate ablation target in human ventricular arrhythmia. Heart Rhythm. 2013;10(8):1109–16. doi: 10.1016/j.hrthm.2013.04.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Rantner LJ, Arevalo HJ, Constantino JL, Efimov IR, Plank G, Trayanova NA. Three-dimensional mechanisms of increased vulnerability to electric shocks in myocardial infarction: altered virtual electrode polarizations and conduction delay in the peri-infarct zone. J Physiol. 2012;590(18):4537–51. doi: 10.1113/jphysiol.2012.229088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Relan J, Chinchapatnam P, Sermesant M, et al. Coupled personalization of cardiac electrophysiology models for prediction of ischaemic ventricular tachycardia. Interface Focus. 2011;1(3):396–407. doi: 10.1098/rsfs.2010.0041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.McDowell KS, Arevalo HJ, Maleckar MM, Trayanova NA. Susceptibility to arrhythmia in the infarcted heart depends on myofibroblast density. Biophys J. 2011;101(6):1307–15. doi: 10.1016/j.bpj.2011.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Flett AS, Hasleton J, Cook C, et al. Evaluation of techniques for the quantification of myocardial scar of differing etiology using cardiac magnetic resonance. JACC Cardiovasc Imaging. 2011;4(2):150–6. doi: 10.1016/j.jcmg.2010.11.015. [DOI] [PubMed] [Google Scholar]
- 25.Lu Y, Yang Y, Connelly KA, Wright GA, Radau PE. Automated quantification of myocardial infarction using graph cuts on contrast delayed enhanced magnetic resonance images. Quant Imaging Med Surg. 2012;2(2):81–6. doi: 10.3978/j.issn.2223-4292.2012.05.03. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Pu J, Boyden PA. Alterations of Na+ currents in myocytes from epicardial border zone of the infarcted heart: a possible ionic mechanism for reduced excitability and postrepolarization refractoriness. Circ Res. 1997;81(1):110–9. doi: 10.1161/01.res.81.1.110. [DOI] [PubMed] [Google Scholar]
- 27.Jiang M, Cabo C, Yao JA, Boyden PA, Tseng G. Delayed rectifier K currents have reduced amplitudes and altered kinetics in myocytes from infarcted canine ventricle. Cardiovascular Res. 2000;48(1):34–43. doi: 10.1016/s0008-6363(00)00159-0. [DOI] [PubMed] [Google Scholar]
- 28.Litwin SE, Li J, Bridge JHB. Na-Ca exchange and the trigger for sarcoplasmic reticulum Ca release: studies in adult rabbit ventricular myocytes. Biophys J. 1998;75(1):359–71. doi: 10.1016/S0006-3495(98)77520-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pop M, Sermesant M, Mansi T, et al. Correspondence between simple 3-D MRI-based computer models and in-vivo EP measurements in swine with chronic infarctions. IEEE Trans Biomed Eng. 2011;58(12):3483–6. doi: 10.1109/TBME.2011.2168395. [DOI] [PubMed] [Google Scholar]
- 30.Zaman S, Kovoor P. Sudden cardiac death early after myocardial infarction: pathogenesis, risk stratification, and primary prevention. Circulation. 2014;129(23):2426–35. doi: 10.1161/CIRCULATIONAHA.113.007497. [DOI] [PubMed] [Google Scholar]
- 31.Comtois P, Kneller J, Nattel S. Of circles and spirals: bridging the gap between the leading circle and spiral wave concepts of cardiac reentry. Europace. 2005;7:S10–20. doi: 10.1016/j.eupc.2005.05.011. [DOI] [PubMed] [Google Scholar]
- 32.Panfilov AV. Is heart size a factor in ventricular fibrillation? Or how close are rabbit and human hearts? Heart Rhythm. 2006;3(7):862–4. doi: 10.1016/j.hrthm.2005.12.022. [DOI] [PubMed] [Google Scholar]
- 33.Cherry EM, Fenton FH. Effects of boundaries and geometry on the spatial distribution of action potential duration in cardiac tissue. J Theor Biol. 2011;285(1):164–76. doi: 10.1016/j.jtbi.2011.06.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bishop MJ, Vigmond EJ, Plank G. The functional role of electrophysiological heterogeneity in the rabbit ventricle during rapid pacing and arrhythmias. Am J Physiol Heart Circ Physiol. 2013;304(9):H1240–52. doi: 10.1152/ajpheart.00894.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Colli Franzone P, Pavarino LF, Scacchi S, Taccardi B. Modeling ventricular repolarization: effects of transmural and apex-to-base heterogeneities in action potential durations. Math Biosci. 2008;214(1–2):140–52. doi: 10.1016/j.mbs.2008.06.006. [DOI] [PubMed] [Google Scholar]
- 36.Severs NJ, Bruce AF, Dupont E, Rothery S. Remodelling of gap junctions and connexin expression in diseased myocardium. Cardiovasc Res. 2008;80(1):9–19. doi: 10.1093/cvr/cvn133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Glukhov AV, Fedorov VV, Kalish PW, et al. Conduction remodeling in human end-stage nonischemic left ventricular cardiomyopathy. Circulation. 2012;125(15):1835–47. doi: 10.1161/CIRCULATIONAHA.111.047274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Akar FG, Tomaselli GF. Conduction abnormalities in nonischemic dilated cardiomyopathy: basic mechanisms and arrhythmic consequences. Trends Cardiovas Med. 2005;15(7):259–64. doi: 10.1016/j.tcm.2005.08.002. [DOI] [PubMed] [Google Scholar]
- 39.Morley GE, Vaidya D, Samie FH, Lo C, Delmar M, Jalife J. Characterization of conduction in the ventricles of normal and heterozygous Cx43 knockout mice using optical mapping. J Cardiovasc Electrophysiol. 1999;10(10):1361–75. doi: 10.1111/j.1540-8167.1999.tb00192.x. [DOI] [PubMed] [Google Scholar]
- 40.Stein M, van Veen TAB, Hauer RNW, de Bakker JMT, van Rijen HVM. A 50 coupling affects conduction velocity restitution and activation delay in the mouse heart. PLoS One. 2011;6(6):e20310. doi: 10.1371/journal.pone.0020310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Smith JH, Green CR, Peters NS, Rothery S, Severs NJ. Altered patterns of gap junction distribution in ischemic heart disease. An immunohistochemical study of human myocardium using laser scanning confocal microscopy. Am J Pathol. 1991;139(4):801. [PMC free article] [PubMed] [Google Scholar]
- 42.Dhein S, Rothe S, Busch A, et al. Effects of metoprolol therapy on cardiac gap junction remodelling and conduction in human chronic atrial fibrillation. Br J Pharmacol. 2011;164(2b):607–16. doi: 10.1111/j.1476-5381.2011.01460.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Akar FG, Spragg DD, Tunin RS, Kass DA, Tomaselli GF. Mechanisms underlying conduction slowing and arrhythmogenesis in nonischemic dilated cardio-myopathy. Circ Res. 2004;95(7):717–25. doi: 10.1161/01.RES.0000144125.61927.1c. [DOI] [PubMed] [Google Scholar]
- 44.Walker NL, Burton FL, Kettlewell S, Smith GL, Cobbe SM. Mapping of epicardial activation in a rabbit model of chronic myocardial infarction. J Cardiovasc Electrophysiol. 2007;18(8):862–8. doi: 10.1111/j.1540-8167.2007.00858.x. [DOI] [PubMed] [Google Scholar]
- 45.Saba S, Mathier MA, Mehdi H, et al. Dual-dye optical mapping after myocardial infarction: does the site of ventricular stimulation alter the properties of electrical propagation? J Cardiovasc Electrophysiol. 2008;19(2):197–202. doi: 10.1111/j.1540-8167.2007.00998.x. [DOI] [PubMed] [Google Scholar]
- 46.Ripplinger CM, Lou Q, Li W, Hadley J, Efimov IR. Panoramic imaging reveals basic mechanisms of induction and termination of ventricular tachycardia in rabbit heart with chronic infarction: implications for low-voltage cardioversion. Heart Rhythm. 2009;6(1):87–97. doi: 10.1016/j.hrthm.2008.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Rog-Zielinska EA, Norris RA, Kohl P. The living scar–cardiac fibroblasts and the injured heart. Trends Mol Med. 2016;22(2):99–114. doi: 10.1016/j.molmed.2015.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ongstad E, Kohl P. Fibroblast–myocyte coupling in the heart: potential relevance for therapeutic interventions. J Mol Cell Cardiol. 2016;91:238–46. doi: 10.1016/j.yjmcc.2016.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Quinn TA, Camelliti P, Siedlecka U, et al. Abstract 11749: Cell-specific expression of voltage-sensitive protein confirms cardiac myocyte to non-myocyte electrotonic coupling in healed murine infarct border tissue. Circulation. 2014;130(2):11749. [Google Scholar]
- 50.Gaudesius G, Miragoli M, Thomas SP, Rohr S. Coupling of cardiac electrical activity over extended distances by fibroblasts of cardiac origin. Circ Res. 2003;93(5):421–8. doi: 10.1161/01.RES.0000089258.40661.0C. [DOI] [PubMed] [Google Scholar]
- 51.Street AM, Plonsey R. Propagation in cardiac tissue adjacent to connective tissue: two-dimensional modeling studies. IEEE Trans Biomed Eng. 1999;46(1):19–25. doi: 10.1109/10.736748. [DOI] [PubMed] [Google Scholar]
- 52.Bishop MJ, Plank G. Representing cardiac bidomain bath-loading effects by an augmented monodomain approach: application to complex ventricular models. IEEE Trans Biomed Eng. 2011;58(4):1066–75. doi: 10.1109/TBME.2010.2096425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Bishop MJ, Connolly A, Plank G. Structural heterogeneity modulates effective refractory period: a mechanism of focal arrhythmia initiation. PLoS One. 2014;9(10):e109754. doi: 10.1371/journal.pone.0109754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Connolly A, Trew M, Smaill B, Plank G, Bishop M. Local gradients in electrotonic loading modulate the local effective refractory period: implications for arrhythmogenesis in the infarct border zone. IEEE Transactions in Biomedical Engineering. 2015;62(9):2251–9. doi: 10.1109/TBME.2015.2421296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.MacCannell KA, Bazzazi H, Chilton L, Shibukawa Y, Clark RB, Giles WR. A mathematical model of electrotonic interactions between ventricular myocytes and fibroblasts. Biophys J. 2007;92(11):4121–32. doi: 10.1529/biophysj.106.101410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Segal OR, Chow AWC, Peters NS, Davies DW. Mechanisms that initiate ventricular tachycardia in the infarcted human heart. Heart Rhythm. 2010;7(1):57–64. doi: 10.1016/j.hrthm.2009.09.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Vigmond E, Hughes M, Plank G, Leon LJ. Computational tools for modeling electrical activity in cardiac tissue. J Electrocardiol. 2003;36:69–74. doi: 10.1016/j.jelectrocard.2003.09.017. [DOI] [PubMed] [Google Scholar]
- 58.Henriquez CS. Simulating the electrical behavior of cardiac tissue using the bidomain model. Crit Rev Biomed Eng. 1992;21(1):1–77. [PubMed] [Google Scholar]
- 59.ten Tusscher KH, Noble D, Noble PJ, Panfilov AV. A model for human ventricular tissue. Am J Physiol Heart Circ Physiol. 2003;286(4):H1573–89. doi: 10.1152/ajpheart.00794.2003. [DOI] [PubMed] [Google Scholar]
- 60.de Chillou C, Groben L, Magnin-Poull I, et al. Localizing the critical isthmus of postinfarct ventricular tachycardia: the value of pace-mapping during sinus rhythm. Heart Rhythm. 2014;11(2):175–81. doi: 10.1016/j.hrthm.2013.10.042. [DOI] [PubMed] [Google Scholar]
- 61.Mountantonakis SE, Park RE, Frankel DS, et al. Relationship between voltage map “channels” and the location of critical isthmus sites in patients with post-infarction cardiomyopathy and ventricular tachycardia. J Am Coll Cardiol. 2013;61(20):2088–95. doi: 10.1016/j.jacc.2013.02.031. [DOI] [PubMed] [Google Scholar]
- 62.Nguyen TP, Qu Z, Weiss JN. Cardiac fibrosis and arrhythmogenesis: the road to repair is paved with perils. J Mol Cell Cardiol. 2014;70:83–91. doi: 10.1016/j.yjmcc.2013.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Xie Y, Sato D, Garfinkel A, Qu Z, Weiss JN. So little source, so much sink: requirements for afterdepolarizations to propagate in tissue. Biophys J. 2010;99(5):1408–15. doi: 10.1016/j.bpj.2010.06.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Wilders R, Wagner MB, Golod DA, et al. Effects of anisotropy on the development of cardiac arrhythmias associated with focal activity. Pflügers Arch. 2000;441(2–3):301–12. doi: 10.1007/s004240000413. [DOI] [PubMed] [Google Scholar]
- 65.Arevalo HJ, Vadakkumpadan F, Guallar E, et al. Arrhythmia risk stratification of patients after myocardial infarction using personalized heart models. Nat Commun. 2016;7:11437. doi: 10.1038/ncomms11437. [DOI] [PMC free article] [PubMed] [Google Scholar]