Uncertainty in assessment of radiation-induced diffusion index changes in individual patients

Abstract

The purpose of this study is to evaluate repeatability coefficients of diffusion tensor indices to assess whether longitudinal changes in diffusion indices were true changes beyond the uncertainty for individual patients undergoing radiation therapy (RT). Twenty-two patients who had low-grade or benign tumors and were treated by partial brain radiation therapy (PBRT) participated in an IRB-approved MRI protocol. The diffusion tensor images in the patients were acquired pre-RT, week 3 during RT, at the end of RT, and 1, 6, and 18 months after RT. As a measure of uncertainty, repeatability coefficients (RC) of diffusion indices in the segmented cingulum, corpus callosum, and fornix were estimated by using test–retest diffusion tensor datasets from the National Biomedical Imaging Archive (NBIA) database. The upper and lower limits of the 95% confidence interval of the estimated RC from the test and retest data were used to evaluate whether the longitudinal percentage changes in diffusion indices in the segmented structures in the individual patients were beyond the uncertainty and thus could be considered as true radiation-induced changes. Diffusion indices in different white matter structures showed different uncertainty ranges. The estimated RC for fractional anisotropy (FA) ranged from 5.3% to 9.6%, for mean diffusivity (MD) from 2.2% to 6.8%, for axial diffusivity (AD) from 2.4% to 5.5%, and for radial diffusivity (RD) from 2.9% to 9.7%. Overall, 23% of the patients treated by RT had FA changes, 44% had MD changes, 50% had AD changes, and 50% had RD changes beyond the uncertainty ranges. In the fornix, 85.7% and 100% of the patients showed changes beyond the uncertainty range at 6 and 18 months after RT, demonstrating that radiation has a pronounced late effect on the fornix compared to other segmented structures. It is critical to determine reliability of a change observed in an individual patient for clinical decision making. Assessments of the repeatability and confidence interval of diffusion tensor measurements in white matter structures allow us to determine the true longitudinal change in individual patients.

1. Introduction

Diffusion tensor imaging (DTI) has been increasingly investigated as an imaging biomarker for detecting physiological and pathological changes in white matter before they appear on conventional imaging (Padhani et al 2009). Previous studies have suggested that a change in a diffusion index of brain white matter structures following radiation therapy is an indicator of radiation-induced neurotoxicity (Sundgren and Cao 2009, Wang et al 2009, Assaf and Pasternak 2008, Nagesh et al 2008, Chapman et al 2012, Chapman et al 2013, Nazem-Zadeh et al 2012a). These studies have examined changes in diffusion indices such as fractional anisotropy (FA) as an index of fiber integrity, mean diffusivity (MD) as an index of overall diffusivity, radial diffusivity (RD) as an index of demyelination, and axial diffusivity (AD) as an index of fiber degradation/degeneration (Song et al 2003, Wheeler-Kingshott and Cercignani 2009). A radiation-induced change of a diffusion index in a structure has been shown to depend on received radiation dose, the intrinsic properties of the structure, and the time of the study. In general, a decrease in FA and an increase in MD and RD would be expected, while different directions of changes have been reported for AD (Nagesh et al 2008, Chapman et al 2012, Chapman et al 2013, Nazem-Zadeh et al 2012a, Song et al 2003). The reproducibility of an imaging biomarker must be tested in order to determine whether an observed imaging change in an individual patient is a ‘true change’, i.e., a change beyond the level of uncertainty in the measurement (Barnhart and Barboriak 2009).

Longitudinal changes in diffusion indices have conventionally been studied as the mean of a group of patients, instead of an individual patient (Nagesh et al 2008, Chapman et al 2012, Chapman et al 2013, Nazem-Zadeh et al 2012a, Mabbott et al 2006, Chua et al 2009). Analysis of a diffusion index change in an individual patient is valuable in the context of individualizing radiation treatment: for example, decreasing radiation dose in a patient who shows high risk for white matter toxicity. However, whether an individual patient has a true change cannot be determined from the mean of changes observed in a group of patients. Even though a group of patients has a statistically significant mean change, some individuals in the group may not have true changes. Conversely, observing a statistically insignificant mean change from a group of patients does not imply that there is no individual with a true change. In order to assess an individual change, one must determine how large a change can be considered as a true change. If an ‘uncertainty range’ can be estimated from test–retest data, an individual patient's change can be compared to this uncertainty range. In longitudinal imaging studies, this uncertainty range has been defined as the repeatability or reproducibility coefficient (RC). Several studies have estimated the RC of diffusion indices in kidney (with RC of 14.6% and 10.3% for FA and 3.3% and 3.6% for MD in renal cortex and medulla, respectively) (Cutajar et al 2011), muscle (with RC ranging from 12.9% to 33% for FA and 7.3% to 14.6% for MD in different forearm muscles) (Froeling et al 2010), intervertebral disc (with RC for MD ranging from 4.6% to 24.1% in different disc locations) (Beattie et al 2008), whole brain in healthy subjects (with RC of 7.7% for FA and 5.4% for MD) (Cercignani et al 2003) and the tumor volume in patients with glioblastoma (with RC of 8.7% for FA and 5.2% for MD) (Paldino et al 2009). The broad range of RC suggests that many factors can influence the RC, including imaging acquisition, data preprocessing, segmentation methods, and characteristics of the structures under study. The estimated RC is essential to determine how reliable a longitudinal individual change is for potential use in clinical decision making.

The goal of this study was to estimate the uncertainty of longitudinal changes in diffusion indices in three white matter structures that may be valuable for assessment of radiation-related neurotoxicity. Using a test–retest diffusion tensor dataset of twelve patients, we estimated the uncertainty in diffusion indices of fornix and cingulum (limbic circuit structures known to be involved in emotional functions associated with memory) (Ghia et al 2007), and corpus callosum (involved in the coordination of cognitive, motor, and sensory functions between the cerebral hemispheres) (Llufriu et al 2012, Davatzikos et al 2003), which were segmented based upon previously developed methods (Nazem-Zadeh et al 2012a, Nazem-Zadeh et al 2011, Nazem-Zadeh et al 2012b). We then demonstrated the concept of how to apply the estimated RC and the confidence to evaluate longitudinal changes in diffusion indices of the same white matter structures in individual patients with low-grade gliomas or benign tumors treated by fractionated partial brain radiation.

2. Materials and methods

2.1. Human subjects and image acquisition

Test–retest diffusion tensor datasets of twelve patients with glioblastoma (GBM) from the National Biomedical Imaging Archive (NBIA) database were used to estimate the RC of diffusion indices in the cingulum, fornix, and corpus callosum. The patients were selected to have the diffusion weighted images without distortion, severe edema, and mass effect on the white matter structures of interest. The time interval between the test and retest studies was two days for ten patients and one day for two patients. The diffusion weighted images (DWIs) and one set of b₀ null images (with b-value = 0 s/mm²) were acquired at 12 non-collinear diffusion gradient directions on a 3T MRI system (Avanto, Siemens, Erlangen, Germany) with a matrix of 128 × 128, a voxel size of 1.71 × 1.71 × 5 mm³, and b-value of 1000 s mm⁻².

Twenty-two patients who had either a low-grade or benign CNS tumor and were treated using a standard 6-week fractionated partial brain radiation therapy (PBRT) (a median dose of 54 Gy) were enrolled in an IRB-approved prospective DT-MRI protocol. The DT images were acquired pre-RT, week 3 during RT, at the end of RT (6 weeks), and 1, 6, and 18 months after the completion of RT. The first ten patients were scanned on a 1.5T MRI system (Signa, GE, Milwaukee, WI, USA), and the next 12 patients were scanned on a 3T MRI system (Achieva, Philips, Eindhoven, The Netherlands). DWIs plus one set of b₀ null images were acquired along 15 diffusion gradient directions in the Philips scanner and along 9 diffusion gradient directions in the GE scanner with b-value = 1000 s mm⁻², with an image matrix of 128 × 128 and a voxel size of 1.75 × 1.75 × 2 mm³ for the Philips scanner and an image matrix of 128 × 128 and a voxel size of 2.5 × 2.5 × 4 mm³ for the GE scanner. The DT images in the 22 patients did not have distortion, severe edema, or mass effect white matter structures of interest. Segmented white matter structures were excluded from individual time samples where/when severe edema or mass effect was present. Patient characteristics are presented in table 1. The individual longitudinal changes in diffusion indices of the patients were assessed using the estimated RC.

Table 1.

The characteristics of patients.

Patient#	Sex	Age @ pre-RT	Scanner	Primary tumor	Location
1	F	38	Philips	Meningioma	Left occipital lobe
2	F	27	Philips	Low grade glioma	Left frontal lobe
3	M	44	Philips	Diffuse oligodendroglioma grade II	Right parietal lobe
4	F	56	Philips	Gemistocytic astrocytoma grade II	Left frontal lobe
5	M	48	Philips	Macroadenoma	Pituitary
6	M	56	Philips	Macroadenoma	Pituitary
7	F	44	Philips	Macroadenoma	Pituitary
8	F	59	Philips	Macroadenoma	Pituitary
9	F	57	Philips	Meningioma	Left temporal lobe
10	M	48	Philips	Meningioma	Right fronto-temporal
11	F	47	Philips	Macroadenoma	Pituitary
12	F	54	Philips	Meningioma	Left parietal lobe
13	M	34	GE	Gemistocytic astrocytoma grade II	Right temporal
14	M	64	GE	Macroadenoma	Pituitary
15	M	55	GE	Meningioma	Left temporal lobe
16	M	29	GE	Craniopharyngioma	Pituitary
17	F	25	GE	Low grade glioma grade II	Left fronto- temporal
18	M	72	GE	Macroadenoma	Pituitary
19	M	31	GE	Diffuse astrocytoma grade II	Left fronto-temporal
20	M	56	GE	Astrocytoma grade II	Left frontal lobe
21	M	39	GE	Mixed oligoastrocytoma grade II	Right fronto-temporal
22	M	44	GE	Macroadenoma	Pituitary

2.2. Image pre-processing

Before segmenting the white matter structures of interest, the diffusion weighted images for both datasets were prepared through intra- and inter-series co-registration, interpolation to a homogeneous voxel size of 1.75 × 1.75 × 1.75 mm³, gradient correction for the Philips scanner, and tensor calculation (Nazem-Zadeh et al 2012a) FA, MD, RD (the mean of the two smaller eigenvalues of the tensor), and AD (the largest eigenvalue of the tensor) were calculated. The principal diffusion direction (PDD) (the eigenvector corresponding to the largest eigenvalue of the tensor) was also calculated from the tensor for segmentation purposes.

2.3. Segmentation of white matter structures of interest

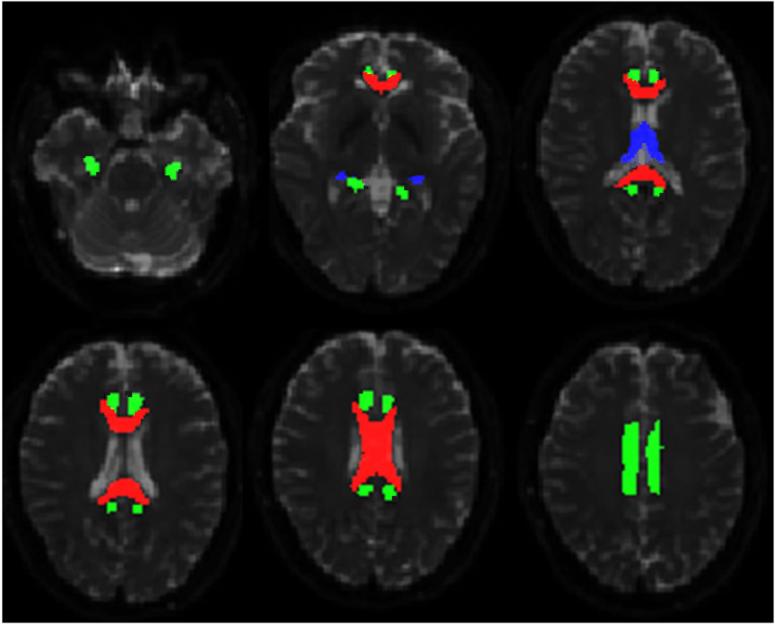
We segmented the bilateral cingulum and its sub-regions (anteroinferior, superior, and posteroinferior), the fornix, and the corpus callosum and its sub-regions (genu, body, and splenium) for both datasets, using previously described fiber tracking/segmentation methods (Nazem-Zadeh et al 2012a, Nazem-Zadeh et al 2012b). In brief, the cingulum was segmented using an automatic seed-based segmentation algorithm (Nazem-Zadeh et al 2012a). For each seed point, a 2-dimensional region of interest (ROI) was automatically extracted, and then fiber tracking was performed between the consecutive extracted ROIs. The segmentation results were post-processed through a morphological operation to achieve a connected and smoothed segmented three-dimensional structure. Using the highest curvature points of the cingulum medial axis, the cingulum was divided into three sub-regions as anteroinferior, superior, and posteroinferior sub-regions. The fornix was segmented by multiple ROI tractography after manually depicting three coronal ROIs on the body, one axial ROI at the most posterior part, and one terminating axial ROI at the inferior part of the fornix (Nazem-Zadeh et al 2012a). The corpus callosum was segmented using a level-set algorithm based on local tensor similarities measured between the neighbor voxels of a growing surface boundary (Nazem-Zadeh et al 2012b). Figure 1 displays the segmented cingulum, fornix, and corpus callosum overlaid on b₀ null axial images of a patient.

Figure 1.

The segmented corpus callosum (red/mid-gray), cingulum (green/light-gray), and fornix (blue/dark gray) overlaid on b₀ axial images.

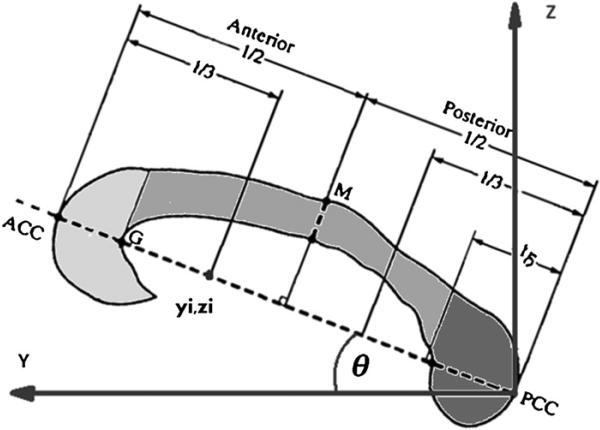
After segmenting the whole corpus callosum, the corpus callosum was segmented into three sub-regions of genu, body, and splenium (figure 2). First, we determined the longitudinal axis of corpus callosum by connecting a line between its most anterior and posterior points in the mid-sagittal plane (ACC and PCC in figure 2). Next, we accounted for a possible rotation along the longitudinal axis (y-direction in figure 2) (Nazem-Zadeh et al 2012b), and then calculated the planes perpendicular to the longitudinal axis passing through the Witelson (Witelson 1989) dividing points (y_i, z_i) (figure 2). Finally, the rostrum was combined with the genu, and the body sub-regions were merged together.

Figure 2.

Witelson sub-divisions of the corpus callosum, with rotation on its longitudinal axis with respect to the anterior-posterior direction. Sub-divisions were eventually merged into genu (light gray), body (medium gray), and splenium (dark gray).

2.4. Repeatability coefficient

To determine true changes in the diffusion indices for individual subjects, we measured the level of uncertainty of the diffusion indices by estimating the RC values of FA, MD, AD, and RD within the fornix, the cingulum and its three sub-regions, and corpus callosum and its three sub-region as follows:

Let I_ik be the index observed value for the ith subject and kth replication, i = 1, 2 . . . , n, k = 1, 2 . . . , K (in our test and retest dataset, n = 12, k = 2) as:

$$I_{ik}∕{\mu }_i=1+{\epsilon }_{ik}$$ (1)

which relates I_ik to its true value μ_i for each subject through a residual relative error ε_ik with the within-subject variance ${\sigma }_w^2=\mathrm{var}\left({\epsilon }_{ik}\right)$ in a normalized ANOVA model. The within- and between-subject means of squares (WMS and BMS) with χ² distributions of n(K – 1) and n – 1 degrees of freedom are (Barnhart and Barboriak 2009):

$$WMS=\frac{1}{n(K-1)}\sum _{i=1}^n\sum _{k=1}^k{\left[\frac{I_{ik}-{\stackrel{‒}{I}}_i}{{\stackrel{‒}{I}}_i}\right]}^2$$ (2)

and

$$BMS=\frac{K}{n-1}\sum _{i=1}^n{\left[\frac{\overline{I_i}-\stackrel{‒}{I}}{\stackrel{‒}{I}}\right]}^2$$ (3)

respectively, where Ī_i is the mean over replications for ith subject, and Ī is the mean over all observations. The within-subject variance can be estimated by $\widehat{{\sigma }_w^2}=WMS$. Rewriting the equation (2) for K = 2, we have

$$\widehat{{\sigma }_w^2}=1∕n\sum _{i=1}^{n}1∕2{\left[\frac{I_{it}-I_{ir}}{(I_{it}+I_{ir})∕2}\right]}^2$$ (4)

where t and r denote test and retest, respectively. We define SND_i (Squared Normalized Difference between test and retest indices of the ith subject as $1∕2{\left[\frac{I_{it}-I_{ir}}{(I_{it}+I_{ir})∕2}\right]}^2$ hereafter. Therefore, equation (4) will be simplified to a sample mean of SND_i over the subjects.

$$\widehat{{\sigma }_w^2}=1∕n\sum _{i=1}^{n}SN{D}_i$$ (5)

The standard error of SND can be also estimated as

$${\sigma }_{\widehat{{\sigma }_w^2}}=\frac{{\sigma }_{SND}}{\sqrt{n}},\widehat{{\sigma }_{SND}}=\sqrt{\frac{1}{n-1}\sum _{i=1}^n{(SN{D}_i-\overline{SND})}^2}\to \widehat{{\sigma }_{\widehat{{\sigma }_w^2}}}=\sqrt{\frac{1}{n(n-1)}\sum _{i=1}^n{(SN{D}_i-\overline{SND})}^2}.$$ (6)

The RC is given by RC = 2.77σ_w, which defines the 95% confidence interval (CI) of the normalized measurements to determine whether a change in an individual patient is a true change (Barnhart and Barboriak 2009). The 95% confidence interval (CI) of the estimated RC is given by

$$R{C}_L=2.77\sqrt{\frac{n.WMS}{{\chi }_n^2\left(0.975\right)}},R{C}_U=2.77\sqrt{\frac{n.WMS}{{\chi }_n^2\left(0.025\right)}},\widehat{RC}\epsilon (R{C}_L,R{C}_U).$$ (7)

Assuming there is no change in a structure between test and retest due to disease progression or therapy, any change has to be due to random and/or systematic errors that could have originated from imaging device, image acquisition, patient re-positioning, image processing and analysis, and/or subject physiological variation.

To determine whether the within-subject variation of the test and retest data was within expectation compared to the between-subjects variation, an F-score was calculated as a ratio:

$$F(n-1,n(K-1))=\frac{BMS}{WMS}.$$ (8)

A significant F-score indicates that the within-subject variation in the test–retest data is significantly smaller than the between-subject variation.

2.5. True individual longitudinal changes

We evaluated whether the longitudinal change in each diffusion index of each segmented structure in each individual patient who was treated by PBRT for a tumor was a true change using the 95% CI of estimated RC. To accomplish this, we calculated a percentage change (I_t%) in FA, MD, AD, or RD in a segmented white matter structure of a patient from baseline scan to follow-up scan t (t = 3 or 6 weeks during RT, or 1 month, 6 months or 18 months after RT). Considering an interval (–δ_c, δ_c) within which there is essentially no change, three possible scenarios could occur for I_t% (Barnhart and Barboriak 2009). In the first scenario, I_t% is confidently considered to have no change if the interval (I_t%–RC_L, I_t% + RC_U) is contained inside the interval(–δ_c, δ_c). In the second scenario, an individual patient is considered to have a true change with 95% confidence if the interval (I_t%–RC_L, I_t%+RC_U) lies outside the interval (–δ_c, δ_c) and does not contain zero. For a single direction of change, the requirement for a true change is reduced to I_t% ≥ RC_L for a positive change or I_t% < –RC_U for a negative change (Barnhart and Barboriak 2009). In the third scenario, if the interval (I_t% – RC_L, I_t% + RC_U) and the interval (–δ_c, δ_c) overlap but do not contain one another, we are unable to confidently determine whether there is a true change or not.

We also tested the significance of mean percentage changes in diffusion indices over the patient group using pairwise t-test statistics for the same set of PBRT data. Any change with p-value less than 0.05 was considered statistically significant.

3. Results

3.1. RC ranges of DTI indices in the segmented structures

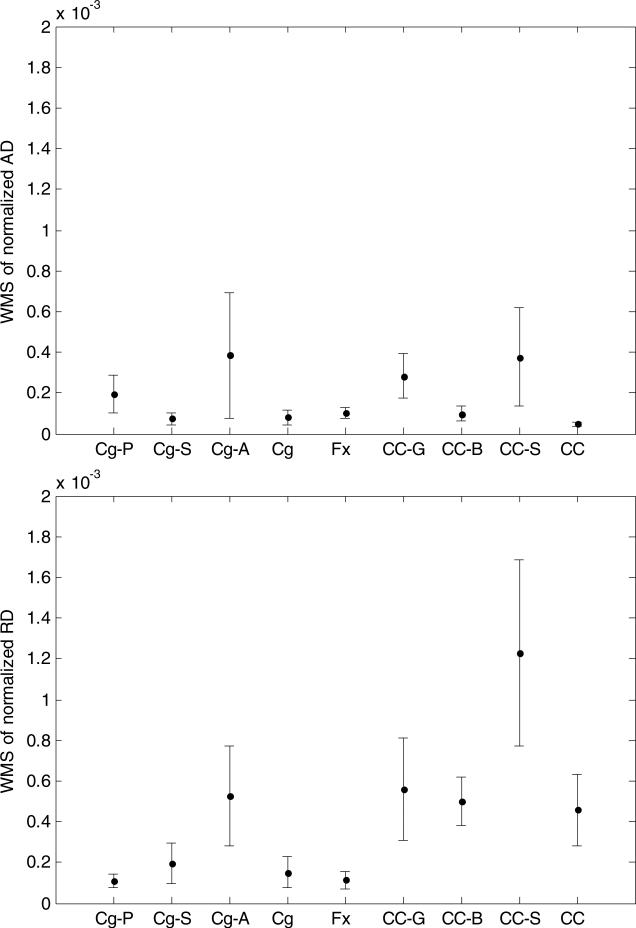
We evaluated the within-subject variance (the sample mean of SND) in the segmented structures, from which the estimated RC and their variations come. For FA, large within-subject variance and standard error were observed in the cingulum anteroinferior sub-region, the corpus callosum body, and the fornix, compared to those in the corpus callosum splenium, and the cingulum superior and posteroinferior sub-regions (figure 3). The cingulum anteroinferior sub-region, the corpus callosum body, and the fornix had estimated RC of 9.6%, 8.6%, and 7.9%, respectively; while the corpus callosum splenium, and the cingulum superior and posteroinferior sub-regions had RC of 5.3%, 5.3%, and 6.0%, respectively. Considering the whole segmented structures, the cingulum had the smallest (4.3%) and the fornix had the largest (7.9%) estimated RC. Among the sub-regions of the cingulum, the anteroinferior sub-region had the largest estimated RC (9.6%). Among the sub-regions of the corpus callosum, the body sub-region had the largest estimated RC (8.6%).

Figure 3.

WMS (within-subject mean of squares) of the normalized diffusion indices of FA, MD, AD, and RD for the cingulum sub-regions of posteroinferior (Cg P), superior (Cg S), and anteroinferior (Cg A), the entire cingulum (Cg), the fornix (Fx), the corpus callosum sub-regions of genu (CC G), body (CC B), splenium (CC S), and the whole corpus callosum (CC). The error bar is the standard error of the SND given in equation (6).

For MD, AD, and RD, the estimated within-subject variance and RC were large in the cingulum anteroinferior sub-region and the corpus callosum splenium, compared to the cingulum posteroinferior and superior sub-regions, fornix, and corpus callosum body. Table 2 shows the estimated RC of the diffusion indices, and the Dice coefficients and overlapping volumes of segmented structure volumes from test and retest data. For RD, the fornix had the smallest (2.8%) and the corpus callosum had the largest (5.9%) estimated RC among the whole structures. In the cingulum, the anteroinferior sub-region had the largest estimated RC (6.4%). In the corpus callosum, the splenium had the largest estimated RC (9.7%). In general, AD had the smallest estimated RC and FA had the largest ones. Note that fornix, corpus callosum body, and cingulum anteroinferior sub-region had the three smallest Dice coefficients among the segmented structures, which is consistent with their relative large RC (table 2) and variance of SND for FA (figure 3(a)).

Table 2.

The estimated RC% and its confidence interval within the structures. The first four rows: the estimated RC% and its confidence interval (RC_L%, RC_U%) for each diffusion index and each structure; the 5th row: the mean and standard error of the Dice coefficient; the last row: the mean and standard error of the overlapping structure volumes in mm³ between the test and retest data from the 12 patients. The structures under study are: the cingulum sub-regions of posteroinferior (Cg P), superior (Cg S), and anteroinferior (Cg A), the entire cingulum (Cg), the fornix (Fx), the corpus callosum sub-regions of genu (CC G), body (CC B), splenium (CC S), and the entire corpus callosum (CC).

	Cg P	Cg S	Cg A	Cg	Fx	CC G	CC B	CC S	CC
RC%(FA)	6.0(4.3,10.0)	5.3(3.8,8.8)	9.6(6.9,15.8)	4.3(3.1,7.1)	7.9(5.7,13.1)	6.5(4.7,10.7)	8.6(6.2,14.2)	5.3(3.8,8.8)	6.1(4.3,10.0)
RC%(MD)	3.1(2.2,5.1)	2.8(2.0,4.6)	6.2(4.4,10.2)	2.9(2.1,4.8)	2.2(1.6,3.7)	5.2(3.7,8.5)	5.1(3.7,8.4)	6.8(4.9,11.2)	3.8(2.7,6.3)
RC%(AD)	3.9(2.8,5.1)	2.4(1.7,3.9)	5.5(3.9,9.0)	2.5(1.8,4.1)	2.8(2.0,4.6)	4.7(3.3,7.7)	2.7(1.9,4.5)	5.4(3.9,8.9)	1.9(1.4,3.1)
RC%(RD)	2.9(2.1,5.1)	3.9(2.8,4.6)	6.4(4.6,10.5)	3.4(2.4,5.6)	3.0(2.1,4.9)	6.6(4.7,10.8)	6.2(4.4,10.2)	9.7(7.0,16.0)	5.9(4.3,9.8)
Dice%	95.1 ± 2.2	97.0 ± 1.2	92.3 ± 5.4	96.1 ± 1.7	84.7 ± 2.3	97.4 ± 2.0	90.9 ± 2.5	96.5 ± 2.0	95.3 ± 1.0
Volume(mm3)	2257 ± 131	4317 ± 311	610 ± 81	7183 ± 404	1234 ± 99	3008 ± 456	3614 ± 324	4044 ± 524	10666 ± 657

3.2. Evaluation of the within-subject variation

We compared the within- and between-subject variations using F-statistics. Table 3 presents the F-score and p-value of the F-test. All the F-scores are greater than 11.6 and p-values are less than 0.0001, indicating that the within-subject variation in the test–retest data is significantly smaller than the between-subject variation, and the test–retest dataset is valid for estimating the RC.

Table 3.

Between-subject variation versus within-subject variation in the test–retest data. The white matter structures under the study are: cingulum sub-regions of posteroinferior (Cg P), superior (Cg S), and anteroinferior (Cg A), the entire cingulum (Cg), fornix (Fx), corpus callosum sub-regions of genu (CC G), body (CC B), splenium (CC S), and the entire corpus callosum (CC).

		Cg P	Cg S	Cg A	Cg	Fx	CC G	CC B	CC S	CC
FA	F-ratio	31.8	52.1	32.1	43.0	53.8	116.3	60.8	38.8	31.0
	p-value	4.E-07	2.E-08	4.E-07	7.E-08	2.E-08	2.E-10	9.E-09	1.E-07	4.E-07
MD	F-ratio	46.1	121.1	127.1	50.4	401.1	175.3	38.2	18.5	60.9
	p-value	4.E-08	2.E-10	1.E-10	3.E-08	1.E-13	2.E-11	1.E-07	8.E-06	9.E-09
AD	F-ratio	14.8	76.0	96.4	34.7	127.9	61.6	57.8	11.6	86.7
	p-value	3.E-05	2.E-09	6.E-10	2.E-07	1.E-10	8.E-09	1.E-08	9.E-05	1.E-09
RD	F-ratio	84.9	105.9	166.3	61.4	317.8	256.4	67.6	28.0	60.0
	p-value	1.E-09	3.E-10	2.E-11	8.E-09	5.E-13	2.E-12	5.E-09	8.E-07	1.E-08

3.3. Evaluation of longitudinal percentage changes in diffusion indices in individual patients

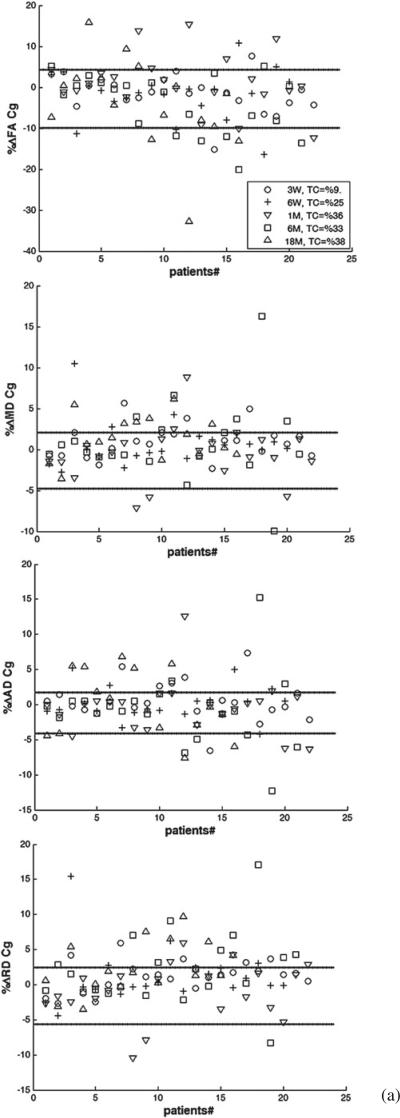
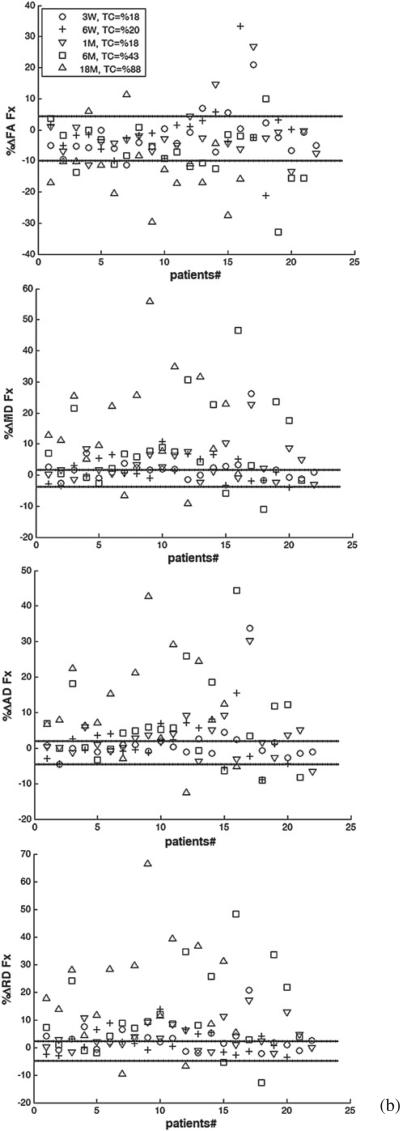
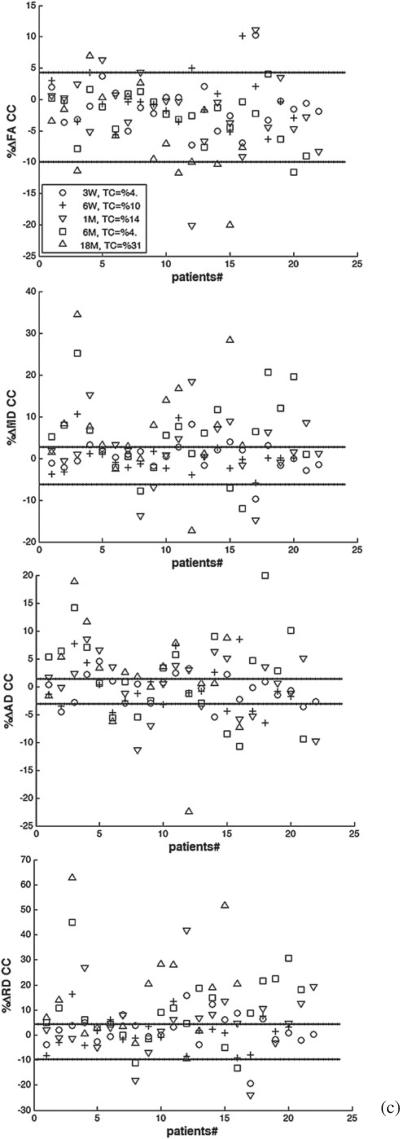
We determined whether the longitudinal percentage change in each diffusion index of each segmented structure of each patient who received PBRT was beyond the 95% CI (–RC_U, RC_L) of the estimated RC. Figure 4 shows the percentage changes in FA, MD, AD, and RD of the whole structures of cingulum, fornix, and corpus callosum, for individual patients at all time points compared to (–RC_U, RC_L). Considering all time points and structures, 23%, 44%, 50%, and 50% of the patients experienced changes beyond (–RC_U, R_L) for FA, MD, AD and RD, respectively. However, the number of the patients who had changes in diffusion indices beyond the uncertainty range increased over time. For all the structures under study, the number of the patients who had true FA changes increased from 11% at week 3 during RT, to 18% at the end of RT, 22% at 1 month, 27% at 6 months, and 46% at 18 months after RT, indicating that radiation effects on the diffusion indices became more pronounced over time.

Figure 4.

The individual percentage changes in FA, MD, AD, and RD in the cingulum (a), the fornix (b), and the corpus callosum (c) in the patients who underwent PBRT from pre-RT to week 3 during RT (3 W, circle), end of RT (6 W, plus), 1 month (1 M, downward-pointing triangle), 6 months (6 M, square) and 18 months (18 M, upward-pointing triangle) after RT. TC indicates the percentage of the patients who had changes beyond the uncertainty. The lines show the estimated –RC_U and RC_L (minus upper limit and lower limit of RC), respectively. If a diffusion index percentage change is larger than RC_L or smaller than –RC_U, we consider it a true change.

Table 4 shows the percentages of patients with longitudinal percentage changes beyond (–RC_U, RC_L) for each diffusion index in each segmented structure at each time point. As can be seen, as early as at week 3 during RT, 22% or more of the patients had FA changes beyond the uncertainty range in the cingulum posteroinferior and anteroinferior sub-regions, which are greater than in other structures or sub-regions at that time point. At the end of RT, 1 month, and 6 months after RT, all cingulum sub-regions showed FA changes beyond the uncertainty range in more than 25%, 45%, and 38% of the patients, respectively, which are again greater than in other structures. At 18 months after RT, both the fornix and all cingulum sub-regions showed FA changes beyond the uncertainty range for more than 50% of the patients, which is greater than in the corpus callosum sub-regions. Note that due to the large estimated RC and associated variance in FA in the fornix, the number of the patients who had the FA changes beyond the uncertainty range at early follow-ups was small even though the individual percentage FA changes were large. At 6 months and 18 months after RT, the fornix showed the greatest number of patients with percentage changes in MD, AD, and RD beyond the uncertainty range, indicating the pronounced late radiation effects on the fornix. Furthermore, the majority of the patients (from 55% to 100%) had post RT percentage changes in RD beyond the uncertainty range in the fornix, the cingulum posteroinferior, and the corpus callosum body sub-regions, suggesting demyelination is prominent in these structures.

Table 4.

The percentages of the patients who had changes beyond the uncertainty ranges. The white matter structures under study are: the cingulum sub-regions of posteroinferior (Cg P), superior (Cg S), and anteroinferior (Cg A), the fornix (Fx), the corpus callosum sub-regions of genu (CC G), body (CC B), and splenium (CC S).

FA	3-W into RT	at the end of RT	1-M following RT	6-M following RT	18-M following RT
Cg P	23	35	46	43	62
Cg S	9	25	46	38	54
Cg A	29	32	48	40	50
Fx	9	15	14	24	54
CC G	9	20	27	19	23
CC B	9	10	18	19	23
CC S	9	15	23	5	23

MD	3-W into RT	at the end of RT	1-M following RT	6-M following RT	18-M following RT
Cg P	50	45	32	52	46
Cg S	14	25	18	43	39
Cg A	11	0	22	12	30
Fx	50	45	55	81	92
CC G	46	15	55	48	69
CC B	32	28	47	61	58
CC S	5	10	27	52	39

AD	3-W into RT	at the end of RT	1-M following RT	6-M following RT	18-M following RT
Cg P	41	25	9	38	39
Cg S	32	30	50	38	69
Cg A	19	11	14	25	42
Fx	23	55	50	76	100
CC G	32	20	46	52	69
CC B	64	50	82	76	77
CC S	0	20	18	48	23

RD	3-W into RT	at the end of RT	1-M following RT	6-M following RT	18-M following RT
Cg P	64	45	73	71	69
Cg S	18	25	14	48	39
Cg A	14	11	33	30	50
Fx	50	40	545	86	100
CC G	32	35	55	62	85
CC B	32	40	59	71	77
CC S	27	20	46	62	46

Given the large (–RC_L, RC_U)intervals of FA in the fornix, cingulum anteroinferior, and corpus callosum body sub-regions, many patients had changes within the uncertainty range. However, assuming a 6% RC (equal to the estimated RC of FA in the cingulum posteroinferior sub-region) for all the white matter structures of interest, the numbers of the patients who had the FA changes in the fornix beyond a 6% uncertainty interval increased to 18% at week 3 during RT, to 20% at the end of RT, to 18% 1 month after RT, to 43% 6 months after RT, and to 85% 18 months after RT (table 5). Similar trends were observed in the cingulum anteroinferior and corpus callosum body using a 6% uncertainty interval, illustrating the impact of the uncertainty of a parameter on assessment of an individual change.

Table 5.

The percentages of patients with the FA percentages changes beyond a threshold of 6%. The white matter structures under study are: the cingulum sub-regions of posteroinferior (Cg P), superior (Cg S), and anteroinferior (Cg A), the fornix (Fx), the corpus callosum sub-regions of genu (CC G), body (CC B), and splenium (CC S).

FA	3-W during RT	at the end of RT	1-M after RT	6-M after RT	18-M after RT
Cg P	23	35	46	43	62
Cg S	9	25	37	19	39
Cg A	52	74	71	60	58
Fx	18	20	18	43	85
CC G	9	20	27	24	39
CC B	23	15	27	29	46
CC S	9	10	18	0	23

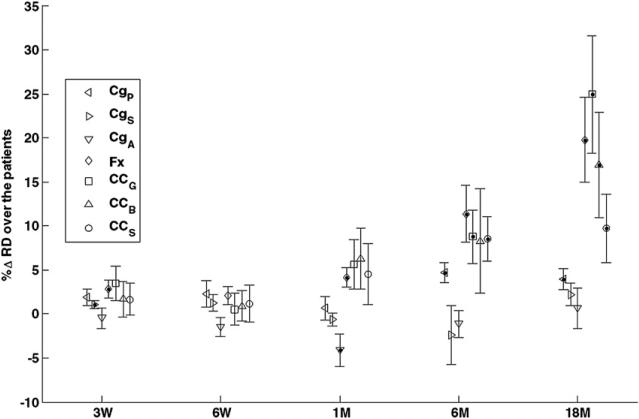
We tested the significance of group mean percentage changes in diffusion indices from the patients who received PBRT. The histogram of the percentage changes in diffusion indices suggested a distribution close to normal. Figure 5 shows the means and standard errors of the percentage changes in RD in the structures under study at all time points. As anticipated, the group means reached significance at the later time points when more patients had individual changes beyond the uncertainty. However, comparing figure 5 with table 4, whether a group-mean change was significant or not did not differentiate who had significant individual changes, showing that different statistical analyses are required by two different tasks.

Figure 5.

The means and standard errors of the percentage changes in RD of the cingulum sub-regions of posterior (Cg_P, left-pointing triangles), superior (Cg_S, right – pointing triangles), and anterior (Cg_A, downward-pointing triangles), the fornix (Fx, diamonds), and the corpus callosum sub-regions of genu (CC_G, s, squares), body (CC_B, upward-pointing triangles), and splenium (CC_S, circles) in the patients who underwent PBRT from pre-RT to week 3 during RT, end of RT, 1 month, 6 months and 18 months after RT. The dots inside symbols indicate significant changes.

4. Discussion

In this study, we estimated repeatability coefficients as a measure of uncertainty of a change. We determined the 95% CIs of the repeatability coefficients of diffusion indices in the segmented cingulum and its sub-regions, corpus callosum and its sub-regions, and fornix using test–retest diffusion tensor datasets. The 95% CI of the estimated RC of diffusion indices provided a statistical reference to determine longitudinal changes beyond uncertainty in individual patients who underwent partial brain RT.

We consider the present work to be a demonstration of the concept, rather than establishing particular RC estimates and confidence intervals. Several factors can affect the accuracy and confidence of the estimated RC, including systematic errors and random errors. The systematic errors include differences between scanners, diffusion imaging protocols, preprocessing methods, structure segmentation methods, and characteristics of white matter structures. The random errors include scanner hardware noise, patient repositioning error, and idiosyncrasies of subjects. Random effects as a group can be reduced by averaging multiple measurements or increasing the number of subjects. However, each systematic error always creates a measurement bias in the same direction, which affects the exchangeability of measurements obtained from the different scanners. On the other hand, random errors affect the reproducibility of measurements. In order to assess the exchangeability of diffusion indices between different scanners or image acquisition protocols, a same group of subjects should be imaged using different scanners with the same protocols, or different protocols on the same scanner. Statistical analysis of these differences allows us to determine whether the indices can be used interchangeably across platforms and protocols. However, to test reproducibility of the DTI indices, repeated scans have to be performed on the same scanner and using the same protocol. To test both interexchangeability and reproducibility, repeated measures have to be done in a group of subjects on various scanners, using different protocols, and with the number of the subjects that are justified statistically. This will involve in a large number of repeated scans, which has not been done up to date. However, to gain our understanding of these questions, several studies have probed the problems from various points of view. By testing normal subjects on two different vendor scanners (Cercignani et al 2003), found that the fractional anisotropy and to some extent the mean diffusivity were different by the use of different scanners, and less noticeably by the use of different image acquisition protocols. However, the reproducibility of the DTI indices observed from a same scanner was not tested in this early study. Using a phantom and a single subject (Zhu et al 2011) showed that inter-scanner variations from a single vendor, although small, affect the fractional anisotropy and mean diffusivity, while intra-scanner variations are approximately 10–50% smaller than inter-scanner ones in eight of the ten tested ROIs (Ferrell et al 2007). investigated the effect of the signal to noise ratio (SNR) as a parameter of image acquisition protocols on the reproducibility of diffusion indices and found an upward bias of fractional anisotropy as the SNR decreased. Using simulated DTI data, Jones (2004) and Zhu et al (2009) found that the number of diffusion gradient directions has an effect on the estimation of fractional anisotropy. In our study, there were differences in image acquisition protocols and SNR between the test–retest and radiation therapy data sets, which could affect the RC estimates across systems. However, in our work, diffusion index measurements were averaged over many voxels in the extracted structures, reducing the effect of differences in SNR between scanner systems. Also, influence of systemic biases on the relative reproducibility of DTI indices obtained on a same scanner is minimal. This has been verified in our data (data not shown). Therefore, in our study, longitudinal (repeated) scans for each individual patient were done on the same scanner. However, previous studies have showed that poor calibration of a system could produce systemic biases over time (Zhu et al 2011, Nagy et al 2007). Our research scanners are calibrated monthly. Also, our control group had a test–retest interval of one or two days. Future studies would benefit by including a control test–retest group with a similar time interval. Finally, we noticed that baseline diffusion indices varied across patients, possibly due to many reasons, including age and sex. By normalizing the diffusion indices to their baseline values, we minimized the effects of cross-subject (and to some extent the effect of cross-scanner) variation and made the comparison between structures more meaningful.

The segmentation process can also introduce errors in the estimated RC. To minimize the RC variation due to segmentation, we analyzed the overlapping volumes of segmented structures between test and retest data. However, different geometry and diffusivity complexity in different structures can result in variation of the estimated RC. The larger structures with greater anisotropy usually have more reliable estimates of RC, because a large number of voxels in the structure leads to a stable mean of diffusion index measures. The structure size effect on the RC accuracy was also the main reason why we merged corpus callosum body sub-divisions into a single body sub-region. However, consolidating sub-structures to achieve smaller RC variations may diminish clinical utility of the results. Low anisotropy can also decrease accuracy in estimating RC, for example in the fornix. Low anisotropy in the fornix also challenged the consistency of the segmented volumes from the test and retest data, as indicated by a low Dice coefficient between the two segmented volumes. Although fairly small values of RC were estimated for AD and RD in the fornix, these indices are related to FA in a non-linear manner and might still lead to a fairly high estimated RC for FA. The large estimated RC of FA in the fornix, the anteroinferior sub-region and the corpus callosum body are unlikely to be due to choice of scanner and protocols, and most likely due to the challenges from low anisotropy, small diameter of the fiber bundles and the shape and characteristics of the structure. Co-registration was used to minimize errors caused by the segmentation process, however the accuracy of image registration can be confounded by subject repositioning, noise, spatial resolution, partial volume averaging, and data interpolation, even without any gross anatomy changes. The fine structure of white matter fibers results in diffusion tensor indices, particularly FA, being highly sensitive to partial volume averaging occurred during data interpolation. Reproducibility of a diffusion index in a small structure or a structure with a large variation in the index could be worse than a large structure, and thereby the estimated RC could be large. This is also reflected in our relatively large RC estimates for the fornix.

To decide whether a diffusion index change is a true change, we used the 95% CI of the estimated RC of that index, but not the estimated RC, which is a conservative approach. The number of subjects in the test and retest data has an impact on the RC estimation and the 95% CI of the estimate. As we mentioned in the Methods section, we used the 95% confidence interval of the estimated RC to define the uncertainty range. By increasing the number of subjects in the test–retest dataset, the RC will be estimated more accurately and the confidence interval will be narrowed. As the number of subjects approaches infinity, the estimated RC and the upper and lower limits of its confidence interval approach the true RC ($\widehat{RC}$, RC_L, RC_U → RC), and the condition of a true change approaches > |RC|, and the condition of no change approaches < |RC|. Likewise, the probability that a patient falls into the undetermined range (third scenario mentioned in the Methods section) approaches zero. The equation $\frac{{\chi }_{n(K-1)}^2\left(\alpha \right)}{n(K-1)}⩾{\left(\frac{RC}{{\delta }_C}\right)}^2$ can be used to determine the number of subjects needed to calculate the confidence interval at the level of 1 – α (Barnhart and Barboriak 2009).

Analysis of diffusion index changes in individual patients is valuable in the context of customizing radiation treatment, for example, by decreasing dose in a patient showing unusually high white matter toxicity. We have demonstrated how to use estimated repeatability coefficients to evaluate imaging biomarkers for assessing radiation-induced neurotoxicity. The concept can be applied to other imaging biomarkers for therapy assessment.