Dissociable behavioural outcomes of visual statistical learning

Abstract

Statistical learning refers to the extraction of probabilistic relationships between stimuli and is increasingly used as a method to understand learning processes. However, numerous cognitive processes are sensitive to the statistical relationships between stimuli and any one measure of learning may conflate these processes; to date little research has focused on differentiating these processes. To understand how multiple processes underlie statistical learning, here we compared, within the same study, operational measures of learning from different tasks that may be differentially sensitive to these processes. In Experiment 1, participants were visually exposed to temporal regularities embedded in a stream of shapes. Their task was to periodically detect whether a shape, whose contrast was staircased to a threshold level, was present or absent. Afterwards, they completed a search task, where statistically predictable shapes were found more quickly. We used the search task to label shape pairs as “learned” or “non-learned”, and then used these labels to analyse the detection task. We found a dissociation between learning on the search task and the detection task where only non-learned pairs showed learning effects in the detection task. This finding was replicated in further experiments with recognition memory (Experiment 2) and associative learning tasks (Experiment 3). Taken together, these findings are consistent with the view that statistical learning may comprise a family of processes that can produce dissociable effects on different aspects of behaviour.

An important cognitive function is to learn associative relationships between stimuli in our environment. However, our perceptual systems are oversatu-rated in terms of the number of stimuli we can attend to and remember. Thus, learning to associate stimuli into coherent perceptual objects may seem like a hopeless endeavour. One way that people learn associative relationships between environmental patterns is through statistical learning, a ubiquitous process that involves learning patterns among stimuli organized according to probabilistic relationships. It can occur extremely quickly in experimental settings, after only a few minutes (Aslin, Saffran, & Newport, 1998; Kim, Seitz, Feenstra, & Shams, 2009; Saffran, Aslin, & Newport, 1996), and without explicit awareness (Fiser & Aslin, 2002; Kim et al., 2009). Statistical learning has been found to underlie basic aspects of language development (Saffran et al., 1996; Saffran & Thiessen, 2003; Yang, 2004), as well as other aspects of cognitive development and psychology. For instance, it occurs in both children and adults (Saffran, Johnson, Aslin, & Newport, 1999), operates in multiple modalities (Conway & Christiansen, 2005), helps bind both features and objects (Turk-Browne, Isola, Scholl, & Treat, 2008), transfers across spatial and temporal dimensions (Turk-Browne & Scholl, 2009), defines the scale of visual objects (Fiser & Aslin, 2001, 2005), and can even alter our perception of stimuli (Chalk, Seitz, & Seriès, 2010).

Among the wide array of statistical learning studies, there is an equally wide array of exposure (acquisition of learning) and testing (assessment of learning) procedures. Exposure can occur passively with auditory stimuli (Saffran et al., 1996), passively with visual stimuli (Fiser & Aslin, 2001), actively with a cover task related to the stimuli (Toro, Sinnett, & Soto-Faraco, 2005), and actively with a cover task unrelated to the stimuli (Saffran, Newport, Aslin, Tunick, & Barrueco, 1997). Testing procedures used to assay learning include familiarity tests (e.g., Fiser &Aslin, 2001, 2002; Saffran et al., 1999; Turk-Browneet al., 2008), reaction time tests (Hunt & Aslin, 2001; Kim et al., 2009; Turk-Browne, Jungé, & Scholl, 2005), and functional magnetic resonance imaging (e.g., Karuza et al., 2013; Schapiro, Gregory, Landau, McCloskey, & Turk-Browne, 2014; Schapiro, Kustner, & Turk-Browne, 2012; Turk-Browne, Scholl, Chun, & Johnson, 2009).

Researchers often alternate between measures of statistical learning without differentiating between the general interpretations of the outcomes (Turk-Browne et al., 2008, 2005). For example, results obtained using a reaction time task have been discussed in the same terms as those obtained using a two-interval forced choice task with relation to what they reveal about statistical learning (Turk-Browne et al., 2008, 2005). Additionally, results from paradigms as varied as the learning of visuo-spatial patterns, visuo-temporal patterns, and audio-temporal patterns, are all labelled with the general name of “statistical learning” with little discussion of distinctions in the learning rate, mechanisms, and constraints (Fiser & Aslin, 2005; Saffran et al., 1999; Zhao, Al-Aidroos, & Turk-Browne, 2013). These results are sometimes explicitly theorized to represent the same underlying learning mechanism (Kirkham, Slemmer, & Johnson, 2002; Perruchet & Pacton, 2006) or occasionally theorized to stem from different cognitive mechanisms (Conway & Christiansen, 2005), but more often the literature has not discussed in detail what exactly statistical learning is.

Further, despite the myriad procedures that have been used to investigate statistical learning, researchers rarely address the possibility that different systems may be engaged and responsible for the learning observed across studies. Here we address the possibility that statistical learning comprises multiple cognitive processes. A “process” refers to a series of steps to achieve a particular end (http://www.merriam-webster.com), and by “multiple processes” we mean that different systems act at once upon the stimuli—independently, cooperatively, or competitively—and that each can achieve its own end and learn independently.

Growing evidence suggests that numerous cognitive processes are sensitive to statistical relationships and that learning in even simple tasks can involve simultaneous dissociable processes (Frost, Siegelman, Narkiss, & Afek, 2013; Le Dantec, Melton, & Seitz, 2012; Zhao et al., 2013; Zhao, Ngo, McKendrick, & Turk-Browne, 2011). The consolidation of statistical learning has both sleep-dependent and time-dependent components (Durrant, Taylor, Cairney, & Lewis, 2011) and may lead to perceptual learning in addition to associative learning (Barakat, Seitz, & Shams, 2013). In artificial grammar learning (AGL) paradigms, which are closely related to statistical learning paradigms, fMRI studies have revealed different neural networks subserving the recognition of items and the learning of the grammar (Fletcher, Büchel, Josephs, Friston, & Dolan, 1999; Lieberman, Chang, Chiao, Bookheimer, & Knowlton, 2004; Seger, Prabhakaran, Poldrack, & Gabrieli, 2000) and dissociable overlapping networks of implicit and explicit learning during AGL have been demonstrated (Yang & Li, 2012). Similarly, in statistical learning paradigms, different time-courses of medial temporal lobe and striatal activation have been observed, which might correspond to competing memory systems at work (Durrant, Cairney, & Lewis, 2013; Turk-Browne et al., 2009; Turk-Browne, Scholl, Johnson, & Chun, 2010).

In the present study, we investigate how the utilization of multiple tasks that assay statistical learning may reveal different underlying cognitive processes. This involves using a novel “item analysis” approach in which we quantify statistical learning with two different tests per experiment and then relate the amount of learning in each test on an item-by-item basis. This approach enables a more detailed characterization of statistical learning than is typically possible in studies using a single outcome measurement. Moreover, by using multiple tests of statistical learning, we can also examine whether learning manifests itself in a stable way across different behaviours for a given item. Although measuring different behavioural tasks does not provide conclusive evidence for or against multiple processes per se, this approach might nevertheless produce evidence useful for evaluating our hypothesis.

A single-process model of statistical learning predicts that multiple tests should reveal the same qualitative pattern of results. If one measure is more sensitive to learning than another, a single-process model would predict significant results from the more sensitive measure(s) and diminished or null results from the less sensitive measure(s). However, across three experiments, we found reversals between different behavioural outcomes of statistical learning; that is, qualitative patterns of learning opposite to each other. These findings undermine an implicit assumption in the field that a common process underlies all manifestations of statistical learning.

Experiment 1

Our first experiment was an investigation of whether different tasks can reveal different statistical learning outcomes from the same exposure. We conducted an item-level analysis where, for each statistical regularity (e.g., a single pair of items for a participant), we compared learning for that regularity across two outcome measures. Specifically, we used a search post-test to categorize regularities as “learne” or “non-learned”, and then examined performance for these categorized regularities during a detection task conducted concurrent with exposure.

In the detection task, a continuous stream of shapes was presented and participants responded to a periodic tone as to whether a shape was present or absent. This task occurred while participants learned the statistical regularities and then continued for a period of time after learning could reasonably be assumed to have occurred. In the search task, which occurred after the detection task, participants were presented with a target shape at the beginning of each trial and responded as soon as that shape appeared in a rapid-serial visual presentation (RSVP) of distractors and a target.

These tasks are described more fully below, but insofar as different measures of statistical learning reveal the same underlying process, then learned regularities from the search task should exhibit the same signatures of learning in the detection task. Alternatively, there may be no relationship or a negative relationship between learning effects during the detection task and the search task, which would be consistent with the existence of multiple processes in statistical learning that manifest different behavioural outcomes.

Methods

Participants

Thirty-seven undergraduates at the University of California, Riverside, aged 18–24 (24 females), were included in this study. The number of participants was determined based on how many students could be recruited for this study within one 10-week quarter in the UC Riverside undergraduate subject pool. This method introduces no statistical bias, as at no point were data analysed in order to determine when to cease data collection. Inclusion required completion of all experimental procedures without technical errors and with responses to at least 70% of targets in both tasks (a criterion derived from pilot data). Inability to complete both tasks satisfactorily resulted in the exclusion of seven participants beyond the 37 included in the study. The data of these participants were not analysed beyond the point of determining their response rates and, importantly, these subject exclusion criteria are not related to the differential performance between items that form the critical analyses in this study. Participants received credit toward partial fulfilment of course requirements for an introductory psychology course, gave written informed consent as approved by the Human Research Review Board, and had normal or corrected-to-normal vision. These criteria also apply to the subsequent experiments reported below.

Stimuli

The stimuli consisted of 15 shapes that were novel to the participants. These shapes were adapted from or made to resemble shapes used in previous statistical learning studies (Fiser & Aslin, 2001; Turk-Browne et al., 2005), subtending approximately 2.5° visually, and were randomly grouped into five triplets on a participant-by-participant basis (see Figure 1(A)).

Figure 1.

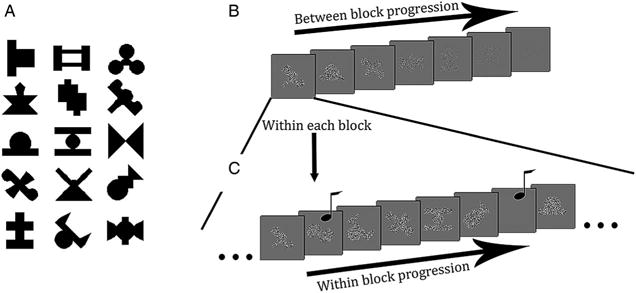
(A) 15 shapes used in Experiment 1, shown here grouped into five example triplets. (B) Example of block progression and of stimuli at different contrasts. (C) Example of progression within a single block. Stimuli appear onscreen sequentially and musical notes indicate the occurrence of the periodic tone, which instructs participants to respond whether a shape was or was not onscreen.

Apparatus

All stimuli were displayed on a 40.96 cm wide ViewSonic PF817 CRT monitor connected to an Apple Mac Pro computer running OSX 10.6.8. Mediating the connection from monitor to computer was a Bits + + digital video processor (Cambridge Research Systems) that enables a 14-bit DAC, allowing for a 64-fold increase in the display’s possible contrast values. Sennheiser HD 650 headphones, plugged into an AudioFire 2 (Echo Digital Audio) audio interface, were used to present the auditory stimuli. Participants’ heads were restrained with a chin rest and forehead bar 69.22 cm from the screen. Stimuli were controlled by custom code written in Matlab, using the Psychophysics Toolbox (http://psychtoolbox.org).

Detection task

During exposure, participants performed a detection task on a stream of shapes appearing one at a time. Unbeknownst to them, the 15 shapes were grouped into five triplets, e.g., if shapes A, B, and C were grouped together, they always occurred in the order of A–B–C. Triplets for each participant were mixed pseudorandomly within the presentation blocks, preserving relations within triplets and equating overall exposure of triplets. In each of the 20 exposure blocks, the five triplets were presented 18 times. The shapes were presented one at a time in the centre of the screen, on a grey background, with duration of 300 ms and ISI of 100 ms. Shapes were filled with spatial white noise with pixel values above or below the grey background and thus were always presented at the same mean luminance as the background (54 cd/m²). The luminance range was scaled according to a staircase (see Figure 1(B) and Figure 2(B)). The duration of each block was 1.8 minutes and, with breaks between blocks, the exposure phase typically lasted 40–45 minutes.

Figure 2.

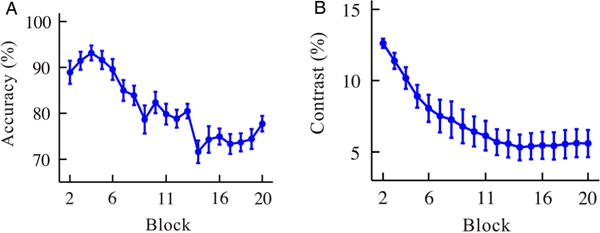
(A) Mean accuracy as a function of block number. (B) Contrast levels at each block, averaged over the 37 participants of Experiment 1. The ordinate displays the proportion contrast, above or below the background. The first block was a practice block and was not analysed. Error bars in both figures represent between-subjects standard error of the mean (SEM).

Within every block, each shape was paired twice with a tone that signalled the participants to press “1” on the keyboard if a shape was visible on the screen or “2” if there was no visible shape (Figure 1 (C)). All shapes were used once as a “present” target (i.e., visible and requiring a “1” response from the participant) and once as an “absent” target (i.e., invisible and requiring a “2” response). That is, when a shape was an “absent” target, we presented a grey patch the same colour and contrast as the background (and thus invisible) during the shape’s normal presentation period. When the tone sounded the participant had to report whether there was a shape present or whether there was no shape present. To temporally distribute responses, 1–3 filler triplets were placed between triplets containing a target.

To ensure that the detection task was engaging and challenging, the contrast of the shapes was adjusted using a block-wise staircase (Le Dantec et al., 2012). If mean accuracy in the prior block was greater than .80, contrast was adjusted according to the formula C′= (C/(P − .75) + 1), where C′ is the new contrast level for the upcoming block, C is the current contrast level, and P is the mean performance for the completed block. If mean accuracy for the block was .70 or less, then contrast was adjusted according to the formula C′=C∗(1 − (P − .75)) with the constraint that the minimum value of P was set to .50 (i.e., chance level). This staircase brought participants’ performance to an average of 75% accuracy (see Figure 2(A)) and converged after approximately 10 blocks.

To measure statistical learning, we examined data after the staircase on contrast converged. Based upon pilot experiments, and verified in the present experiment, this occurred after block 10. Thus, all analyses use only data from the second half of the detection task, blocks 11–20, where the change in contrast between blocks is minimal (see Figure 2(B)). The use of these later blocks ensured that there was minimal variance in stimulus contrast and subject performance and that there was sufficient time for the statistical regularities to be learned. As such, our analysis of blocks 11–20 is akin to post-tests used in other studies of statistical learning. For staircasing purposes, accuracy was calculated over both present and absent targets but, because we were interested only in how statistical learning occurs for visible shapes and the effect of the absence of a shape is unknown, analyses were performed only on present targets. Since present trials had higher accuracy than absent trials overall, accuracy in subsequent analyses was slightly greater than the 75% level.

In both the detection task and in the search task (below), RTs more than two standard deviations from the mean of each subject were excluded from analyses.

Search task

Immediately following exposure, a “search task”, adapted from previous studies (Kim et al., 2009; Turk-Browne et al., 2005), was performed. At the beginning of each trial of the search task, a target shape (one of the 15 seen in the exposure phase) was displayed at the top of the screen and the participant pressed any key to begin the trial. After the target shape disappeared, a pseudorandomly ordered stream of the five triplets was shown at the same sequential presentation rate as in exposure, with the constraint that the triplet containing the target could not be the first or last triplet shown in that trial. The participant’s task was to press the space bar as soon as the target shape appeared. Each of the 15 shapes served as a target once per block, and all shapes were displayed at a suprathreshold contrast level. The search task consisted of six blocks with 15 trials each, which lasted 12 minutes total.

Analysis of shape groupings

The goal of the study was to determine statistical learning on an item level–that is, at the level of individual shape groupings—and determine whether different shape groupings were learned in different ways (see “Analysis of learned and non-learned pairs”, below). To determine the proper items to use in the ultimate analyses, we first examined whether participants learned the full configuration of the triplets or whether participants learned two pairs—the first/second shape pair (pair 1) and the second/third shape pair (pair 2; Fiser & Aslin, 2002, 2005; Hunt & Aslin, 2001). We based this analysis on the search task, which is a more standard measure of visual statistical learning (Baker, Olson, & Behrmann, 2004; Hunt & Aslin, 2001; Olson & Chun, 2001; Turk-Browne et al., 2005) than the detection task, which we introduce for the first time in this paper. In this analysis, a negative correlation of r = −0.5 is expected by chance, simply because the same second-position RT is the negative part of the subtraction for pair 1 and the positive part of the subtraction for pair 2. Response latency in the search task measures the degree to which a target can be predicted based on associations with the preceding item(s) and previous studies using this task found monotonic decreases in RT as item position increases (e.g., Campbell, Healey, Lee, Zimerman, & Hasher, 2012; Kim et al., 2009; Turk-Browne et al., 2005, 2010). Insofar as a triplet has been well learned, there are strong associations between all items and the associative strength from the first to second item and the second to third item should be correlated. Thus, if the full triplet structure were learned, the RT differences between items 1 and 2 would correlate with RT differences between items 2 and 3 significantly more positively than r=−0.5. However, we found an even more negative correlation between the effects for the two pairs (r=−0.77, p<.00001), which was more negative than all but 8.37% of iterations in non-parametric randomization test (i.e., randomly assigning the observed distribution of RTs to different triplet positions 10,000 times and computing the correlation in each iteration). We also ran additional correlational analyses and simulations on the difference between the first two items of the triplet and the difference between the first and last items of the triplet. Here we found a correlation of r=0.47, which is almost identical to the value of r = 0.50 that is expected by chance. These analyses suggest a failure to learn at the triplet level and the trend in the opposite direction suggests that learning of the two pairs—which shared an element—may be competitive (see also Fiser & Aslin, 2002) rather than cooperative.

Given that the evidence suggested that learning did not occur on the level of the triplets, subsequent analyses were restricted to pairs and, in particular, to the first pair of each triplet. The restriction of analyses to the first pair also provides uniformity across the studies, as Experiment 3 only included pairs (which were all first pairs, by definition). In addition, because the first pair appeared before the second, this decision helps mitigate any complications that might arise due to the possible competition between the pairs. For example, if there are negative interactions between pair 1 and pair 2 then including pair 2 in the analysis would introduce a lack of independence, which could complicate the interpretation of learning comparisons between the detection and search tasks. Of note, the correlational analysis described here is intended to determine which items should be included in subsequent comparisons of learning between the two tasks and does not itself argue for or against the multiple-process hypothesis of statistical learning.

Analysis of learned and non-learned pairs

A key novelty of the present study is that we split each participant’s pairs into those that were learned and those that were not learned. We did this based on the search task, which represents the more typical measure of statistical learning and where the standard analysis is to compute the mean RT for all first position shapes and compare that to the mean RT for all second position shapes. Instead of averaging over all shapes in each position, our analysis conserved information about the pairings that the shapes were assigned to for each participant. Each pair for a participant was classified as “learned” if the mean RT during the search task was lower for the second position shape of that pair than for the first position (Figure 3, solid blue lines, negative slope). If the mean RT was not lower for the second position shape of a pair, then it was classified as “non-learned” (Figure 3, dashed red lines, zero or positive slope). Although this classification method may not capture all of the nuances of the extent to which a pair was learned, it provides a simple dichotomous measure of learning from the search task that can then be related to the independent data from the detection task (see Figure S1 for confirmation that this analysis is reliable and consistent with the number of times that the second position RTs are faster than those of the first position RTs within each of the six blocks of the search task).

Figure 3.

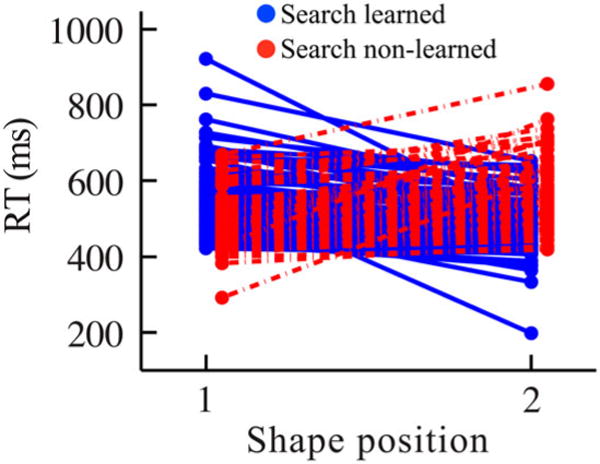
Mean RTs of each pair across participants for the search task of Experiment 1. “Search learned” were pairs showing learning in the search task in terms of a faster RT for the second vs. first shape (102 pairs, solid blue lines, negative slope). “Search non-learned” were pairs not showing learning (78 pairs, dashed red lines, flat or positive slope). N = 36 participants (one participant, comprising five pairs, omitted from figure for clarity, due to RTs greater than 1000 ms).

To analyse learning of each pair separately (averaging across repetitions of each item in the detection and search tasks), we employed a modified 2 × 2 (position: first/second × learning status: learned/non-learned) factorial ANOVA (see Supplemental data “Statistical analyses” for details). After the interaction had been calculated, we used planned paired-samples t-tests to analyse the simple effects of position across learned and non-learned pairs.Because the search and detection tasks were independent of one another, using this method to analyse the pairs did not raise any issues of spurious dependencies between the results of the search task and the results of the detection task. Additionally, we modelled these results using 10,000 permutations of the data to discover how often we would expect results similar to those reported below, in which the detection task reveals opposite patterns of RT than the search task. The resulting likelihood was less than 0.1% (p < .001) of obtaining an effect similar to this by chance.

Results and discussion

As a basic measure of statistical learning, we examined first vs. second shape position performance in the search and detection tasks. In accordance with the literature, the search task showed significantly faster RTs (Figure 4; planned one-tailed paired t-test, t(36) = 1.69, p = .05, Cohen’s d = 0.28) for the second (520.0 ms) compared to the first position (535.0 ms) of pairs. However, in the detection task no effect of position (see Supplemental data), was observed in terms of RTs (666.7 vs. 674.5 ms, respectively; t(36) = 1.08, p = .29, Cohen’s d = 0.18) or accuracy for second vs. first positions (85.6 vs. 84.8%, respectively; t(36) = 0.69, p = .50, Cohen’s d = 0.12).

Figure 4.

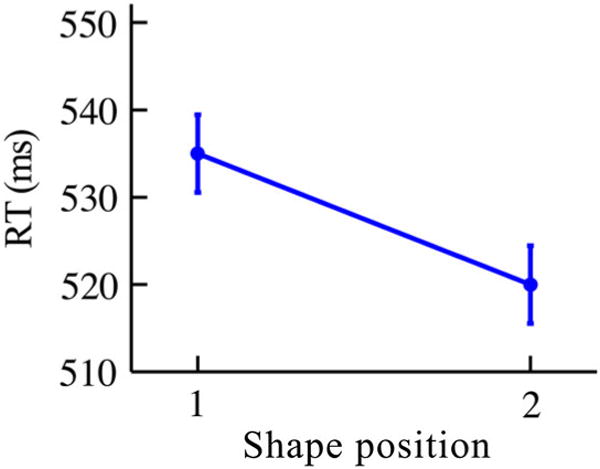
Mean RT in the search task of Experiment 1. Error bars reflect ±1 within-subjects SEM (Loftus & Masson, 1994). N = 37.

Although an overall effect of statistical learning was observed in the search task, the significance of this effect was borderline. This raises the question of whether all pairs were learned weakly and to the same extent, or whether some pairs were learned and others were not. This question gets to the heart of our multiple-process hypothesis and, as can be seen in Figure 3, evidence suggests that there was considerable variability across pairs in the search RT effect, with some pairs showing an effect consistent with learning and others showing the opposite. This variability may just be noise, unrelated to performance in the detection task for the same items. Alternatively, it may reflect true differences in item-level learning, such that our labelling of pairs as learned or non-learned retains meaning in the detection task.

To test the multiple-process hypothesis, we examined whether learned pairs from the search task (Figure 3, solid blue lines) elicited different performance in the detection task than non-learned pairs (Figure 3, dashed red lines). For results of this experiment and of Experiment 2 using the full triplet structure, see Supplemental data. This pair-wise analysis differs from typical analyses in studies of statistical learning, in that we allow for the possibility that participants did not learn each pair that they were exposed to in the same manner.

This analysis revealed a dramatic and counterintuitive negative relationship between the detection task from exposure and the search task from the post-test (Figure 5). The pairs classified as learned in the search task (N = 106 pairs, or 212 shapes) and the pairs classified as non-learned in the search task (N = 79, or 158 shapes) showed a significant interaction (position × learning status) for RT (F(1,366) = 7.00, p = .0085, η² = 0.019) although not accuracy (F(1,366) = 1.36, p = .24, η² = 0.0037) in the detection task. For RTs, non-learned pairs (i.e., those not showing learning in the search task) did show learning in the detection task, with faster responses for second vs. first positions (645.7 vs. 670.7 ms, respectively; t(78) = 2.42, p = .018, Cohen’s d = 0.27). This finding of learning in the detection task for pairs not showing learning in the search task cannot be explained by a speed-accuracy tradeoff, as accuracy was numerically higher for the second vs. first positions (87.7 vs. 85.6%, respectively) of the non-learned pairs (t(78) = 1.46, p = .15, Cohen’s d = 0.16). In contrast, learned pairs (i.e., those showing learning in the search task) exhibited no learning in the detection task for second vs. first RTs (684.3 vs. 677.9 ms, respectively; t(105) = 0.79, p = .43, Cohen’s d = 0.076) or accuracy (84.0 vs. 84.2%, respectively; t(105) = 0.22, p = .82, Cohen’s d = 0.015). Notably, the reliable decrease in RT for non-learned second position in the detection task implies that statistical learning occurred for those pairs, as there was no information available to the participant about the upcoming shape except for the statistical regularities governing the presentations. These data, showing a dissociation between statistical learning as manifested in the detection and search tasks, are consistent with the predictions of the multiple-process hypothesis.

Figure 5.

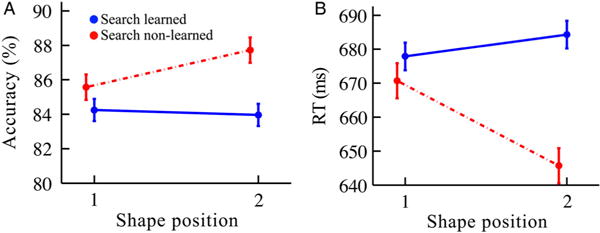
Detection task results in Experiment 1 split by the search task, in terms of (A) accuracy and (B) RT. “Search learned” were pairs that demonstrated learning in the subsequent search task (solid blue lines). “Search non-learned” were pairs that did not demonstrate learning in the subsequent search task (dashed red lines). Error bars reflect ±1 within-subjects SEM. N = 37. (N of pairs in blue curves = 106; N of pairs in red curves = 79.)

Experiment 2

Although Experiment 1 provides initial support for the multiple-process hypothesis, the counter-intuitive nature of the result compelled us to replicate the finding. Furthermore, to better understand the dissociation between learning on the detection and search tasks, and to validate the dissociation, in Experiment 2 we replaced the search task with a recognition task, in which participants were asked to judge whether a sequence had occurred during exposure or not, and to rate their confidence in the judgment.

The recognition task was selected as potentially being more sensitive to different components of memory than the classically described two-alternative-forced-choice familiarity test in statistical learning (e.g., Fiser & Aslin, 2002). Research indicates that familiarity and recognition judgments may correspond to different aspects of encoded memories (Wixted, 2007; Yonelinas, 1994) and we hypothesized that different memory judgments might map onto the learned/non-learned dissociations seen in Experiment 1. For example, pairs rated with “Remember” (see Methods below) might correspond to the learned pairs of Experiment 1 and pairs rated as “Familiar” might correspond to the non-learned pairs. However, regardless of information gained from the ratings, the main purpose of this experiment was to replicate the results of Experiment 1 and generalize the dissociation of statistical learning measures using a different learning measure.

Methods

Participants

Forty-one undergraduates at the University of California, Riverside, aged 18–22 (26 females), participated in this experiment (sample size again determined by how many students could be recruited within a quarter from the UC Riverside undergraduate subject pool). Inability to complete both tasks satisfactorily resulted in the exclusion of four participants beyond the 41 included in the study. As in Experiment 1, if participants were excluded then their data were not analysed beyond determining their response rate.

Stimuli and apparatus

The stimuli and display apparatus were identical to Experiment 1, except for the differences noted here. Stimuli were displayed on a 48.26 cm wide Sony Trinitron CRT monitor connected to an Apple Mac mini computer running OSX 10.5.6. Mediating the connection from monitor to computer was a Data-pixx processor (VPixx Technologies) that enables a 16-bit DAC, allowing for a 256-fold increase in the display’s possible contrast values. Responses were collected using a RESPONSEPixx button box (VPixx Technologies) that enables microsecond precision of response latency measurement. Tones were presented using a small speaker placed behind the monitor. Participants’ heads were restrained with a chin rest 69.85 cm from the screen.

Detection task

The exposure and detection task were identical to Experiment 1.

Recognition task

A recognition task was used instead of the search task for the post-test. Responses were provided on a multidimensional “New/Old” and “Familiar/Remember” scale (Figure 6; adapted from Ingram, Mickes, & Wixted, 2012). On this scale, participants reported with a single response whether a sequence was new or old, rated their confidence, and, in the case of old responses, whether they recollected any details surrounding prior experiences with the sequence. If participants recalled any such details, for example a specific instance when that sequence occurred, they responded with the “R” scale for remember. If they did not recall specific details but simply had a feeling that they had seen the sequence before, they responded with the “F” scale for familiar. Stickers were placed on the number-pad of the keyboard to match the scale shown in Figure 6.

Figure 6.

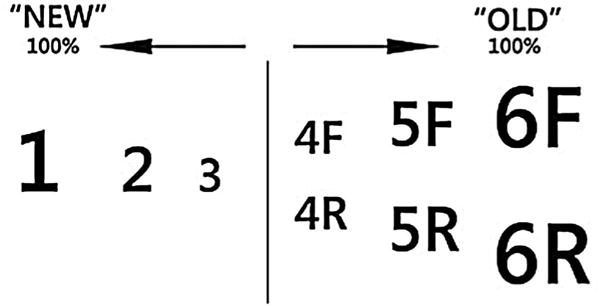
Response scale used during the recognition task. “F” stands for “Familiar” and “R” stands for “Remember”. Size of numbers and letters corresponds to confidence levels, with 1 and 6 being the most confident in a “New” or “Old” response, respectively.

In each of 10 trials, participants were exposed to a sequence of three of the shapes seen during exposure, presented with the same SOA and ISI as before. After the last shape was displayed, a response query appeared on screen and participants reported whether that sequence (i.e., those three shapes in that exact order) had occurred during exposure. The 10 trials consisted of the five intact triplets, which had occurred repeatedly during exposure, and five rearranged triplets, which contained the same exposed shapes but in an order that could not have occurred during exposure. After obtaining the recognition judgments, we confined our multiple-process analyses to the first two shapes, i.e., the first pair, of each triplet for the reasons provided in Experiment 1.

Results and discussion

To test the multiple-process hypothesis, we coded the detection task performance according to whether an intact pair was correctly identified as “Old” in the recognition task (“Recognition learned”) or incorrectly identified as “New” (“Recognition non-learned”). Consistent with the hypothesis (see Figure 7), learned pairs (N = 139 pairs, or 278 shapes) and non-learned pairs (N = 66 pairs, or 132 shapes) showed a significant interaction (position × learning status) for RT (F(1,406) = 10.41, p = .0014, η² = 0.025) and a marginal interaction for accuracy (F(1,406) = 2.90, p = .089, η² = 0.007). Learned pairs (i.e., those that were correctly identified in the recognition task) showed a significant drop in detection accuracy for the second vs. first positions (87.2 vs. 90.6%, respectively; t(138) = 3.15, p = .002, Cohen’s d = 0.27) and no significant difference in RT for the second vs. first positions (603.4 vs. 601.0 ms, respectively; t(138) = 0.41, p = .68, Cohen’s d = 0.036). For non-learned pairs (i.e., those that were not correctly identified in the recognition task), RT showed a significant decrease for the second vs. first positions (579.9 vs. 608.4 ms, respectively; t(65) = 3.32, p = .0015, Cohen’s d = 0.41) and no significant difference in accuracy for the second vs. first positions (90.8 vs. 91.1%, respectively; t(65) = 0.20, p = .84, Cohen’s d = 0.024). These results conceptually replicate those of Experiment 1 and suggest that, unlike the detection task, the recognition task from this experiment and the search task from Experiment 1 may tap into the same statistical learning process—at least based on their shared opposition to the detection task.

Figure 7.

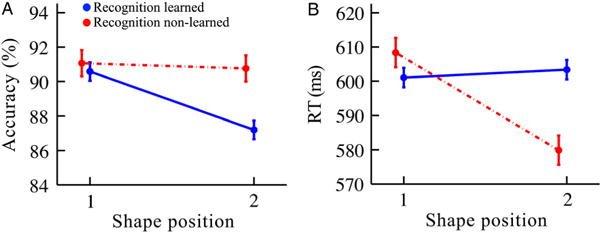
Detection task results in Experiment 2 split by the recognition task, in terms of (A) accuracy and (B) RT. “Recognition learned” were pairs correctly identified in the subsequent recognition task (solid blue lines). “Recognition non-learned” were pairs not correctly identified in the subsequent recognition task (dashed red lines). Error bars reflect ±1 within-subjects SEM. N = 41. (N of pairs in blue curves = 139; N of pairs in red curves = 66.)

To understand these results in greater detail, learned pairs were further subdivided into “Familiar” or “Remember” retrieval modes (Figure 8). Treating learning status as a three-level factor (Familiar, N = 78 pairs, or 156 shapes; Remember, N = 61 pairs, or 122 shapes; and New, N = 66, or 132 shapes), there was a significant interaction (position × learning status) for RT (F(2,404) = 5.44, p = .0047, η² = 0.026) and a marginal interaction for accuracy (F(2,404) = 2.40, p = .092, η² = 0.011). The decrease in accuracy for the second position vs. the first position in learned pairs was driven by Familiar (84.7 vs. 89.4%, respectively; t(77) = 2.89, p = .005, Cohen’s d = 0.33) but not Remember pairs (90.3 vs. 92.1%, respectively; t(60) = 1.35, p = .18, Cohen’s d = 0.17). The difference in RT for the second position as compared to the first was not reliable for Familiar (615.7 vs. 616.8 ms, respectively; t(77) = 0.13, p = .90, Cohen’s d = 0.015) nor Remember (587.5 vs. 580.9 ms, respectively; t(60) = 0.90, p = .37, Cohen’s d = 0.11) pairs. As reported above, only the non-learned pairs showed a decrease in RT for the second position.

Figure 8.

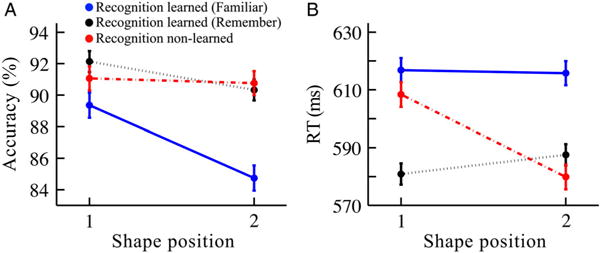
Detection task results in Experiment 2 split by the Familiar/Remember ratings in the recognition task, in terms of (A) accuracy and (B) RT. “Recognition learned (Familiar)” were pairs correctly identified in the subsequent recognition task and given a “Familiar” rating (solid blue lines). “Recognition learned (Remember)” were pairs correctly identified in the subsequent recognition task and given a “Remember” rating (dotted black lines). “Recognition non-learned” were pairs not correctly identified in the subsequent recognition task (dashed red lines). Error bars reflect ±1 within-subjects SEM. N = 41. (N of pairs in blue curves = 78; N of pairs in black curves = 61; N of pairs in red curves = 66).

These results suggest a potential dissociation between remembered and familiar pairs with the primary distinction being faster and more accurate detection for the remembered pairs. Although we had hypothesized that a familiar/remember dissociation might be linked to the learned/non-learned dissociation seen in Experiment 1, the data did not support this hypothesis. Instead, both the familiar and remember pairs are consistent with the learned pairs of Experiment 1 and the results as a whole replicate the learned/non-learned dissociation found in Experiment 1.

Experiment 3

Although Experiment 2 replicated Experiment 1, it failed to provide additional clarity about the mechanisms underlying our results. Experiment 3 was run for this purpose, to determine whether the facilitation for the second shape position in the search task reflects an enhanced representation of the second shape, the learning of an association between the first and second shapes, or a combination of the two.

Statistical learning is typically assumed to reflect an association between stimuli A and B, where perceiving A enables one to predict the subsequent appearance of B (Schapiro et al., 2012). However, recent work suggests that statistical learning can give rise to an enhanced salience of the second stimulus of a pair even outside of its exposed context, and that this enhanced salience can account for second position effects in the search task (Barakat et al., 2013). We therefore examined whether learning in the detection and search tasks reflects an associative and/or representational form of learning. If learning is associative, then replacing the second shape with an out-of-context shape (a misplaced second shape or a foil, see Methods below) should result in slower RTs. On the other hand, if the learning reflects an enhanced representation of the second shape, then misplaced second shapes should elicit speeded responses even when presented out of context; in contrast, foils, which are shapes not shown during exposure, should receive no such benefit. A combination of associative effects and enhancement is also possible.

Methods

Participants

Fifty-six undergraduates at the University of California, Riverside, aged 17–32 (25 females), participated in this experiment (sample size again determined by how many students could be recruited within a quarter from the UC Riverside undergraduate subject pool). Inability to complete both tasks satisfactorily resulted in the exclusion of five participants beyond the 56 included in the study. As in Experiments 1 and 2, if participants were excluded then their data were not analysed beyond determining their response rate.

Stimuli and apparatus

The stimuli and apparatus were identical to Experiment 2, except that three additional shapes were used to accommodate the conditions of this experiment.

Detection task

The detection task during exposure was the same as Experiment 1, except as noted. First, the stimulus regularities in Experiment 3 consisted of six pairs rather than five triplets. Second, in blocks 11–20, one of five conditions occurred when a target appeared on the screen (blocks 1–10 were the same as in Experiment 1 other than the use of pairs rather than triplets). The two “intact” target conditions were the same as in the previous experiments and as in the first 10 blocks of the current experiment: the target was either the correct first or second shape of a pair. The two “foil” target conditions involved six foil shapes that were never shown in the first half of exposure. Foils could occur as targets in either the first or second position of a pair with equal frequency. That is, in each of the latter 10 blocks, each of the six foil items occurred in place of the first item of a pseudorandomly determined intact pair and during a different trial would also appear in place of the second item of a pseudorandomly determined intact pair. The particular foil used with each pair was randomized and counterbalanced across blocks. The “mismatched” condition replaced a pair’s second shape with the second shape from a different pair as was done in Barakat et al. (2013). That is, a shape that had been seen in the first half of the exposure task occupying a second position appeared as a target after a different first shape. All conditions and shapes were counterbalanced to equate the exposure of shapes and pairs.

As in Experiment 1, there were 20 blocks of exposure. In the first 10 blocks, all pairs were presented as intact pairs. Each shape position of the six pairs was used as a target twice, resulting in 24 pairs that contained a target. In half of these, the target was present and in the other half, the target was absent. The shape used as the target was counterbalanced. A total of 1–3 intact filler pairs were presented between target-containing pairs, which amounted to a total of 72 pairs, or 144 shapes, per block. In the second 10 blocks, there were 60 targets per block, again half present and half absent. The 30 present targets consisted of six instances of each of the following: intact first position, intact second position, foil first position, foil second position, and mismatched second position. Combined with 1–3 intact filler pairs between each target-containing pair, this amounted to a total of 180 pairs, or 360 shapes, per block.

Search task

The search task was similar to Experiment 1, except as noted. There were five blocks of 30 trials each. Within a block, every shape from each condition (first and second intact, first and second foil, mismatch) was used once as a target, including the six foils when the trial called for one of those two conditions. Given that the mismatched condition required the second shape of a pair to be replaced with another pair’s second shape, the pair from which the second shape was drawn could not be displayed on that trial (or else the target would be displayed twice in a single trial, once as an intact second shape and once as a mismatched second shape). Thus, each trial of the search task displayed five of the pairs instead of all six. The omitted pair was counterbalanced across trials and, when the mismatched condition occurred, the missing pair was always the pair from which the replacement shape had been drawn.

Results and discussion

Search task

We first sought overall evidence of statistical learning in the search task (Figure 9). The intact pairs showed reliably faster RTs for the second vs. first positions (424.7 vs. 441.9 ms, respectively; t(55) = 5.38, p < .0001, Cohen’s d = 0.72). The second position foils (422.0 ms) and mismatched second shapes (429.9 ms) were also found more quickly than the first intact shape (441.9 ms; t(55) = 5.93, p < .0001, Cohen’s d = 0.80 and t(55) = 3.64, p = .0006, Cohen’s d = 0.48, respectively). Furthermore, RTs were faster for second position vs. first position foils (422.0 vs. 434.9 ms, respectively; t(55) = 4.14, p = .00012, Cohen’s d = 0.55), suggesting that there may have been some learning for position, regardless of item presented. These results demonstrate that statistical learning occurred and replicate the findings of Barakat et al. (2013), showing a benefit for shapes in the second position even outside of their pair context.

Figure 9.

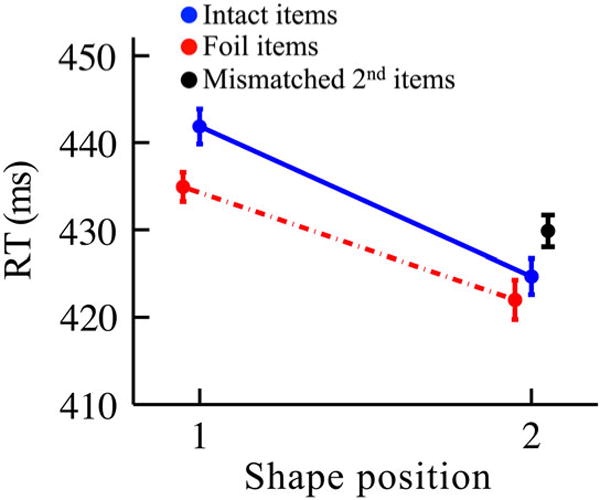
RTs in the search task of Experiment 3. “Intact items” were shapes from conditions in which the pairs were presented intact (solid blue line). “Foil items” were shapes from conditions in which pairs were presented with either the first or second shape replaced with a foil unseen in the first 10 blocks of exposure (dashed red line). Note that the foil items were not matched as the intact items were; the dashed line is only to demonstrate the difference between the two position RTs. “Mismatched 2nd items” were shapes from the condition in which the second shape of a pair was replaced with the second shape of another pair (black point). Error bars reflect ±1 within-subjects SEM. N = 56.

However, our primary interest was to test the multiple-process hypothesis by examining performance in the detection task. As in Experiment 1, we split pairs according to whether they displayed a negative slope (learned) or a flat/positive slope (non-learned) in the search task. We did this separately for each condition.

Learned vs. non-learned pairs—intact conditions

For intact conditions, learning was measured as intact first shape RT minus intact second shape RT, resulting in N = 179 learned pairs, or 358 shapes, and N = 157 non-learned pairs, or 314 shapes. Results for the intact pairs replicated those of Experiment 1 (Figure 10) and provide additional support for the multiple-process hypothesis. Although neither interaction (position × learning status) reached significance (accuracy: F(1,668) < 0.1, p = .95, η² < 0.001; RT: F(1,668) = 1.01, p = .31, η² = 0.0015), non-learned pairs showed a simple RT effect for second vs. first position in the detection task (542.6 vs. 553.6 ms, respectively; t(156) = 2.24, p = .026, Cohen’s d = 0.18), whereas learned pairs did not (556.6 vs. 561.0 ms, respectively; t(178) = 0.92, p = .36, Cohen’s d = 0.068). There was no effect in accuracy for second vs. first in either learned pairs (89.0 vs. 88.7%, respectively; t(178) = 0.25, p = .80, Cohen’s d = 0.020) or non-learned pairs (88.3 vs. 87.9%, respectively; t(156) = 0.32, p = .75, Cohen’s d = 0.027).

Figure 10.

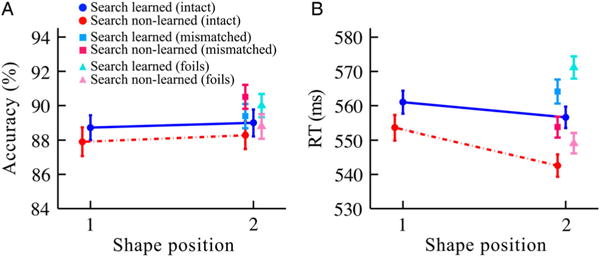
Detection task results for intact, foil, and mismatched conditions in Experiment 3 split by the search task, in terms of (A) accuracy and (B) RT. “Search learned” circles were intact pairs that showed evidence of learning in the subsequent search task. “Search non-learned” circles were intact pairs that did not show learning in the subsequent search task. “Search learned” triangles were foils following an intact first shape that showed learning in the subsequent search task. “Search non-learned” triangles were foils following an intact first shape that did not show learning in the subsequent search task. “Search learned” squares were mismatched second shapes following an intact first shape that showed learning in the subsequent search task. “Search non-learned” squares were mismatched second shapes following an intact first shape that did not show learning in the subsequent search task. Error bars reflect ±1 within-subjects SEM. N = 56. (N of blue pairs in each condition = 179; N of red pairs in each condition = 157.)

Learned vs. non-learned pairs—foil and mismatched conditions

As in the search task, analyses of the foil and mismatched conditions in the detection task can provide additional evidence on whether the faster performance for second shapes is an associative effect rather than just a speeded response for any item presented after a learned first item. The foil and mismatched conditions indicated that both the learned and non-learned pairs displayed some learning in the detection task (Figure 10). However, the nature of these effects differed. For the learned pairs, the overall pattern was slower RTs for second shapes relative to intact first shapes. This was only significant for foil second shapes (571.2 vs. 561.0 ms; t(178) = 2.10, p = .037, Cohen’s d = 0.16), not mismatched second shapes (564.1 vs. 561.0 ms; t(178) = 0.70, p = .49, Cohen’s d = 0.052). Comparing just second positions of the learned pairs, RTs were significantly slower for foil vs. intact shapes (571.2 vs. 556.6 ms, respectively; t(178) = 3.14, p = .002, Cohen’s d = 0.23) and marginally slower for mismatched vs. intact shapes (564.1 vs. 556.6 ms, respectively; t(178) = 1.68, p = .094, Cohen’s d = 0.12). These results provide support for the hypothesis that associative learning occurred between the first and second positions of the learned pairs.

For the non-learned pairs, the overall pattern was equivalent RTs for second shapes relative to first intact shapes. This was true for both foil second shapes (549.1 vs. 553.6 ms; t(156) = 0.91, p = .36, Cohen’s d = 0.072) and mismatched second shapes (553.8 vs. 553.6 ms; t(156) = 0.04, p = .97, Cohen’s d = 0.0033). Comparing just second positions, RTs were significantly slower for mismatched vs. intact shapes (553.8 vs. 542.6 ms, respectively; t(156) = 2.41, p = .017, Cohen’s d = 0.19) and not significantly different for foil vs. intact shapes (549.1 vs. 542.6 ms, respectively; t(156) = 1.46, p = .15, Cohen’s d = 0.12). This can be considered a lack of facilitation for the mismatched second shapes and is also suggestive of associative learning being displayed in the detection task for the non-learned-pairs.

Considering the learned and non-learned pairs together, our data are consistent with the associative learning hypothesis. Whenever the second shape in a pair is replaced, the response is slowed. Using this measure of learning, there was a comparable magnitude of associative learning displayed in the detection task for both learned pairs (11.1 ms) and non-learned pairs (8.9 ms). However, the manner in which the violation of the associative prediction manifested itself (slowing for learned but a lack of speeding for non-learned) provides further evidence of dissociation between detection and search measures of statistical learning. Combined with the pattern of results for the intact conditions, which are analogous to the conditions of Experiments 1 and 2 and replicate those patterns of results, these data again are consistent with the predictions of the multiple-process hypothesis for statistical learning.

General discussion

For most studies of statistical learning, a single test is used to index learning. Here we show that this approach underestimates the extent of learning that has taken place. Specifically, we found that statistical learning can be reflected in multiple behavioural tasks and, critically, that these tasks do not provide redundant information. One aspect of learning was revealed in the search task, where lower latencies were found for predictable shapes. A dissociated aspect of learning was observed in the detection task, again indicated by better performance for predictable shapes, but only for those items that did not display learning in the search task. Similar results were obtained for recognition memory judgments, where correctly recognized regularities did not show a detection effect, and other regularities showed a detection effect but were forgotten in the recognition test, and the results were obtained again with the intact pairs of Experiment 3.

This manner of double dissociation of performance across tasks is classically taken as evidence for different processes in cognitive research (Chun, 1997; Gabrieli, Fleischman, Keane, Reminger, & Morrell, 1995) and defies the alternative explanation that different tasks will naturally have different sensitivities because of the starkly opposite results seen in the dependent variables of the compared tasks. If the tasks were merely displaying different levels of sensitivities for the same process, we would expect similar results for both tasks, albeit with different effect sizes. Instead we observe results that consistently demonstrate one pattern for one task and an opposite pattern for another task. The observed search, recognition, and detection effects cannot be explained by individual shapes or happenstance groupings of the shapes, as these were randomized and counterbalanced across participants. Furthermore, in Experiment 3, we provided evidence that dissociable patterns of learning for different pairs (positive vs. negative second position RT effects) can be observed within the same detection task. The question then becomes: why is learning expressed differently depending on the task?

A logical answer is that there are multiple processes that underlie different aspects of visual statistical learning. Moreover, to account for the observation that any given regularity is only reflected in one task, these systems may compete with each other. Neuroscientific investigations of statistical learning are consistent with this interpretation. Specifically, statistical learning is supported by at least two memory systems in the brain, the hippocampus and the striatum (Durrant et al., 2013; Schapiro et al., 2014, 2012; Turk-Browne et al., 2009, 2010). These systems have been shown to compete with each other during learning (Packard, 1999; Poldrack et al., 2001; but see Sadeh, Shohamy, Levy, Reggev, & Maril, 2011). The left inferior frontal cortex also supports statistical learning (Karuza et al., 2013; Turk-Browne et al., 2009), and it has been suggested that learning in frontal cortex differs from the striatum in terms of the speed of learning (Pasupathy & Miller, 2005). Different learning processes in the hippocampus, striatum, and frontal cortex may therefore occur at different rates and produce different kinds of behavioural effects (e.g., the hippocampus may underlie recognition judgments). Identifying other specific mechanisms that might underlie these processes will require future experimental and theoretical work. A first step could be to generalize existing computational models of statistical learning to account for multiple behavioural measures. Currently, these models account for either recognition (e.g., TRACX, French, Addyman, & Mareschal, 2011; PARSER, Perruchet & Vinter, 1998) or prediction (e.g., SRN, Cleeremans & McClelland, 1991; Elman, 1990), but not both.

An intriguing result from Experiment 2 is the difference in performance for regularities that were given “Familiar” versus “Remember” ratings. As discussed above, the dissociation seen in the detection task for familiar/remember pairs did not mirror the dissociation seen for learned/non-learned pairs as we had hypothesized it might. However, the fact that there is a visible difference between explicitly given “Familiar” and “Remember” ratings suggests that participants are able to effectively rank their implicit memories of the regularities and indicates a shade of grey between classic notions of implicit and explicit knowledge (Bertels, Franco, & Destrebecqz, 2012). This explicit sense of the richness of retrieval is intriguing because statistical learning is often thought to be an implicit process (Kim et al., 2009). Indeed, out of 134 participants, not a single participant reported consciously detecting any pattern to the shapes displayed in the experiment. Ultimately the familiar/remember aspect of this experiment failed to reveal a further dissociation of learning patterns across pairs but, nevertheless, Experiment 2 provided compelling results regarding differences in processing between “Remembered” and “Familiar” pairs which warrants further study.

Experiment 3 provides evidence that the learning in both the detection and search tasks is associative. The results for the detection task as split by the search task show that when the second shape of a pair is replaced with a shape that it does not normally occur with, there is a slowing of RT (learned pairs) or a lack of facilitation (non-learned pairs). As discussed above, this different pattern of results for learned and non-learned pairs provides further evidence that the detection and search tasks are measuring two separate learning processes. This does not rule out the possibility that perceptual enhancement of the second shape also occurred (Barakat et al., 2013). Of note, RTs for mismatched second shapes were faster than for intact first shapes in the search task. Thus, a mix of associative and enhancement effects can jointly determine performance in statistical learning tasks.

In sum, the data presented here provide evidence that visual statistical learning might be composed of dissociable processes that can be revealed through different behavioural tasks. While it is possible that the different tasks used in the experiments reveal different aspects of a complex memory representation, the multiple-process model is consistent with neuroscience research showing that there are multiple brain systems that are sensitive to statistical regularities in the environment (Schapiro & Turk-Browne, 2015). Together, these findings challenge a common assumption that different operational methods of measuring statistical learning are interchangeable in terms of their interpretation. We caution against treating different measures of statistical learning as equivalent, since this not only discards useful variance in the data, but also gives the false impression that statistical learning is a single process rather than a multifaceted collection of processes. Our findings are useful in that they provide a foundation for future research in statistical learning that should more routinely use multiple tasks and seek to clarify dissociations of learning and the brain structures that underlie these dissociated processes.