Abstract
Biomass gasification technology has been rapidly developed recently. But fire and poisoning accidents caused by gas leakage restrict the development and promotion of biomass gasification. Therefore, probabilistic safety assessment (PSA) is necessary for biomass gasification system. Subsequently, Bayesian network-bow-tie (BN-bow-tie) analysis was proposed by mapping bow-tie analysis into Bayesian network (BN). Causes of gas leakage and the accidents triggered by gas leakage can be obtained by bow-tie analysis, and BN was used to confirm the critical nodes of accidents by introducing corresponding three importance measures. Meanwhile, certain occurrence probability of failure was needed in PSA. In view of the insufficient failure data of biomass gasification, the occurrence probability of failure which cannot be obtained from standard reliability data sources was confirmed by fuzzy methods based on expert judgment. An improved approach considered expert weighting to aggregate fuzzy numbers included triangular and trapezoidal numbers was proposed, and the occurrence probability of failure was obtained. Finally, safety measures were indicated based on the obtained critical nodes. The theoretical occurrence probabilities in one year of gas leakage and the accidents caused by it were reduced to 1/10.3 of the original values by these safety measures.
Introduction
Biomass has been rapidly developed as a renewable energy source in recent years [1], and it has tremendous potential in solving future shortage of energy [2]. In China, the capacity of biomass energy increased from 2.2 GW [3] to 3 GW [4] between 2004 and 2015. Biomass energy usage is increasing in other countries as well [5–7]. As one of the most widely available energy sources [8], conversion of biomass resource includes biodiesel, biomass to liquid (BTL), biomass gasification, etc [9,10]. Recently, biomass gasification stations have been constructed and put into operation massively in rural areas of China. They are used to reduce the burning of crop straw, which causes air pollution [11]. And more importantly, agriculture wastes can be made into green energy via biomass gasification. However, hydrogen (H2), carbon monoxide (CO), and methane (CH4) which are produced by biomass gasification are flammable and CO has high poisonousness [12]; leakage of biomass gasification gas will lead to accidental fires and poisoning incidents [13,14]. Because the development and promotion of biomass gasification is restricted by their danger, therefore, PSA is necessary for biomass gasification system, and effective safety measures are needed to reduce the risks associated with gas leakage.
Biomass gasification system is complicated, various causes may lead to gas leakage, and gas leakage will cause multifarious consequences as well. Bow-tie analysis is a quantitative method which includes fault tree analysis (FTA) and event tree analysis (ETA, [15]). So the deduction and induction function of bow-tie analysis makes it possible to investigate the causes and consequences referred to gas leakage. As a concise and effective quantitative risk assessment (QRA) methodology, Paolo [16] applied bow-tie analysis to baseline risk assessment tool (BART), and they utilized bow-tie analysis for identification and assessment of any potential hazards and associated risks. Because bow-tie analysis can clearly display the links between causes, loss event (LE), conditional events (CE), and outcome events (OE), Chen [17] considered bow-tie analysis as an effective tool to identify environmental risk source. The application of bow-tie analysis is broad based on its characteristic. It can be applied in risk management of sea ports and offshore terminals [18], risk evaluation for natural gas industry [19], risk assessment of hexane distillation installation [20]. However, the focus of bow-tie analysis is displaying the whole scenario of accidents, identifying and assessing the potential causes and consequences. Causes which are more critical to the consequences based on the logical links and occurrence probabilities of themselves cannot be readily obtained by bow-tie analysis. Therefore, as a method widely used in PSA [21], bow-tie analysis can be mapped into BN to achieve the goal. Some research are involved in mapping bow-tie analysis into BN. Badreddine and Amor [22] took advantage of dynamic analysis function of BN to improve a bow-tie model. They constructed bow-tie diagrams in an automatic and dynamic way to implement the appropriate preventive and protective barriers in a dynamic system. Khakzad [23] made dynamic risk analysis of a physical reliability periodically updating system, the failure probabilities of safety barriers of bow-tie were periodically updated by using Bayesian theorem, and the probabilities of the consequences were estimated by the improved bow-tie analysis. They considered that the bow-tie's limitations resulting from its static constituents can be relaxed by mapping bow-tie analysis into BN [24]. Majeed [25] used bow-tie analysis and BN to confirm the critical elements of the well integrity model. In their study, the posterior probability was obtained by Bayesian theorem, then the critical elements were confirmed by the ratio of posterior probability to prior probability. All in all, bow-tie analysis mapping into BN can make dynamic risk analysis, and the critical elements of system can be confirmed by the calculation of posterior probability using Bayesian theorem. However, PSA importance measures can be introduced as well [26], because the conditional probability can be calculated by Bayesian theorem, BN can be fitted with these importance measures well, the importance measures can be computed accurately and easily. Thus the BN-bow-tie analysis is not only displaying the accidents scenarios of biomass gasification, but also making PSA to confirm the critical causes of accidents by adding the importance measures.
In order to make PSA of biomass gasification system, the reliability data is needed. Standard reliability data sources [27] can provide some common reliability data. Lopez [28] used the standard reliability data sources to confirm the probability of base event (BE) of FTA in liquefied natural gas (LNG) industry. Similarly, Khakzad [24] confirmed the failure probability in bow-tie analysis of a mixing tank system by referring to the standard reliability data sources. In addition, some reliability data cannot be obtained from currently available data. As fuzzy methods are widely used in risk analysis [29,30], fuzzy methods based on expert judgment can be the way to obtain reliability data [31,32]. However, fuzzy methods are practical and flexible in application for many fields. The fuzzy logic can be coupled with regression, nearest neighbor method, and artificial neural networks to construct a predictive model, and this model can be utilized effectively to make predicting demand for natural gas and energy cost savings in public buildings [33]. In Rodger's study [34], the fuzzy logic can cooperate with BN to implement probabilistic estimation, meanwhile, the method proposed by Rodger used the fuzzy clustering to produce a funnel diagram to make a clear and systematic demonstration for the relevance in supply chain backorder aging, unfilled backorders, and customer wait time. Moreover, Rodger [35] made a comprehensive study of group decision making, weighted average, linguistic terms, and fuzzy logic, in their study, a fuzzy induced linguistic ordered weighted averaging approach which can provide further insight and linguistic simplicity for decision makers was proposed to evaluate the risk in the supply chain. The fuzzy numbers reflect the linguistic expression of expert judgments to estimate events, for instance, if the expert judgment of a failure is 'about very low', the triangular number is introduced to indicate the judgment, and the trapezoidal number can indicate the judgment 'about very low to low'. Then fuzzy numbers can be converted to fuzzy failure rate (FFR, [36,37]), and the occurrence probability of failure is obtained. Ferdous [38] used triangular numbers to define expert judgments in the confirmation of occurrence probability in bow-tie analysis. In a fuzzy Bayesian network, triangular numbers were employed by Li [39] in quantitative human reliability analysis (HRA) frameworks. Ramzali [40] used expert judgment to obtain the failure probability of safety barriers in offshore drilling system, in their study, fuzzy numbers were introduced to reflect expert judgments. Various aggregation methods of fuzzy numbers are available. Bardossy [41] proposed a simple and effective approach to aggregate fuzzy numbers when they include only triangular or trapezoidal numbers. Hsu and Chen [42] proposed similarity aggregation method (SAM), when the fuzzy numbers were all triangular numbers or trapezoidal numbers, SAM was utility in aggregating fuzzy numbers with considering expert weighting [40,43]. Lin and Wang (Lin and Wang 1997) proposed an approach to aggregate fuzzy numbers including both triangular and trapezoidal numbers. However, fuzzy numbers based on expert judgment may be triangular or trapezoidal numbers, and the character of experts will affect their judgments as well. Therefore, in this study, Lin and Wang's method [44] was improved, the improved method can aggregate fuzzy numbers including both triangular and trapezoidal numbers, and expert weighting was also considered simultaneously. So it will make the occurrence probability of failure to be more objective, and the PSA of biomass gasification system to be more reliable.
This study identified the biomass gasification system by bow-tie analysis, causes of gas leakage and consequences resulted in gas leakage were obtained. Meanwhile, failure data was partly obtained from standard reliability data sources. For the failure data was not available from the existing data, fuzzy method based on expert judgment was employed to obtain the failure data. The fuzzy numbers which reflected the linguistic expression of expert judgments included both triangular and trapezoidal numbers, and an improved method was proposed to obtain the fuzzy failure data with considering the expert weighting. Then bow-tie analysis was mapping into BN (BN-bow-tie) to make PSA, three importance measures were introduced, and the critical nodes to accidents were obtained by computing the importance measures. Finally, safety measures aiming at the critical nodes were proposed, and the reduction of occurrence probabilities of accidents was calculated.
Methods
Model
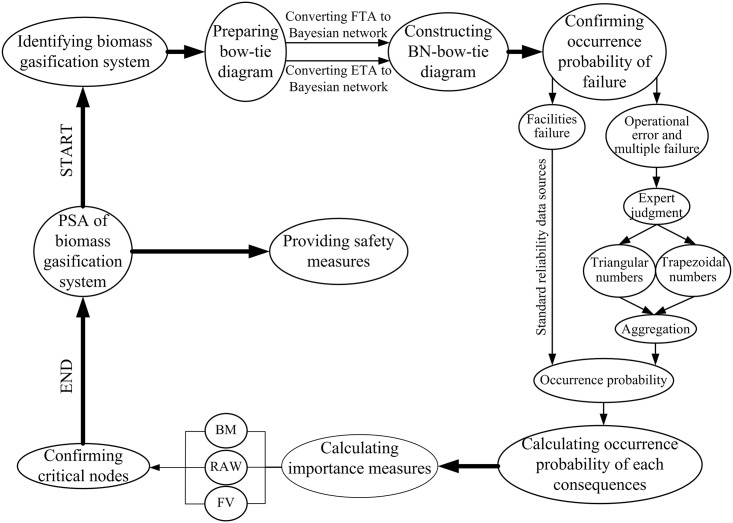
Bow-tie analysis was used to display the accidents scenarios of a system from an LE. Causes of LE can be found by FTA of bow-tie analysis; consequences that result in LE can be identified by ETA of bow-tie analysis. In this proposed approach, FTA and ETA of bow-tie were transformed into BN to make the BN-bow-tie analysis. Units that give rise to accidents are more easily could be obtained. With this approach, the explicit occurrence probability of failure was needed. The occurrence probability of facilities failure was obtained from standard reliability data sources [27]. The occurrence probability of operational error cannot be confirmed from existing data. Then fuzzy methods based on expert judgment were used to achieve these occurrence probabilities. Subsequently, variable consequences were predicted by BN-bow-tie analysis. Finally, the critical nodes related to the consequences was obtained. Flowchart of the methodology was showed below (Fig 1).
Fig 1. Proposed methodology.
BN-bow-tie Analysis
Bow-tie was combined with FTA and ETA, and FTA and ETA were converted to BN. The algorithm of the logical relationship was identical to FTA and ETA. FTA in bow-tie was used to calculate LE as well as top event (TE) occurrence probability. If the occurrence probability of the basic event (BE) was obtained, the occurrence probability of the TE was also obtained. When the logical relationship of events was AND-gate, all events occured, and the TE occured. Eq 1 was used to calculate TE occurrence probability.
| (1) |
If the logical relationship of events was OR-gate, only one of these events, the TE, was occurrence. Eq 2 was used to calculate TE occurrence probability.
| (2) |
The occurrence probability of TE of FTA was defined to be that of LE. Meanwhile, the occurrence probability of an initiating event (IE) of ETA was equal to that of LE. Eq 3 was used to calculate occurrence probability of OE in ETA.
| (3) |
BN is an inference approach that was combined with graph theory and probability theory. BN analysis of BN was based on the Bayesian theorem (Eq 4).
| (4) |
According to the Bayesian theorem, three importance measures were introduced in the new methodology. So that events can be evaluated by their logical relationship and their occurrence probability in BN. The three importance measures were described below [26].
Birnbaum measure (BM)
BM measured increment of TE occurrence probability when BE occurred (Eq 5).
| (5) |
where P(TE|BE = 1) denoted the occurrence probability of TE when a BE occurred, P(TE|BE = 0) denoted the occurrence probability of TE when a BE didn't occur.
Risk achievement worth (RAW)
RAW evaluated the influence of BE for TE when it was considered with the occurrence probability of BE. RAW was adjusted by the occurrence probability of TE and BE. In this article, Eq 6 was used to calculate RAW.
| (6) |
where P(BE) denoted the occurrence probability of BE, P(TE) denoted the occurrence probability of TE under no conditions.
Fussel-Vesely (FV)
FV was used to describe the BE contribution to the failure of the system (Eq 7).
| (7) |
In the proposed methodology, the critical nodes which triggered accidents more easily were obtained by calculating these importance measures.
Confirming Occurrence Probability by Fuzzy Methods
In this approach, the occurrence probability of each BE was needed in BN-bow-tie analysis. BEs were divided into three classes: facilities failure, operational error and multiple failure, and multiple failure included facilities failure and operational error. The occurrence rate of facilities failure was obtained from standard reliability data resources, subsequently, occurrence rate was converted to occurrence probability by Eq 8. Because the occurrence probability of operational error and multiple failure could not be confirmed by existing data resources, the fuzzy methods based on expert judgment were used to estimate occurrence probabilities of operational error and multiple failure.
| (8) |
where F denoted the occurrence probability of failure, λ denoted the occurrence rate of failure.
The fuzzy methods involved aggregating the different judgment of different experts, expert weighting was considered and triangular fuzzy numbers or trapezoidal fuzzy numbers proposed by experts were estimated to calculate FFR [44], and FFR was converted to the occurrence probability of operational error and multiple failure.
The following steps were used to confirm occurrence probability based on expert judgment.
1. Confirm the weighting of each expert. The weighting of each expert was partitioned by age, education background, years of service, and professional position (Table 1, [40,43]).
Table 1. Weighting Score of Different Expert Factors.
| Factors | Classification | Weighting Score |
|---|---|---|
| Age (a) | < 30 years old | 1 |
| 30–39 years old | 2 | |
| 40–49 years old | 3 | |
| ≥ 50 years old | 4 | |
| Education background(b) | High school | 1 |
| Junior college | 2 | |
| Bachelor | 3 | |
| Master | 4 | |
| PhD | 5 | |
| Service year (c) | < 5 years | 1 |
| 5–10 years | 2 | |
| 11–20 years | 3 | |
| 21–30 years | 4 | |
| ≥ 30 years | 5 | |
| Professional Position (d) | Worker | 1 |
| Technician | 2 | |
| Junior academic/engineer | 3 | |
| Senior academic/engineer | 4 |
Eq 9 showed the calculation of the total weighting score of each expert, and the weighting of each expert was calculated by Eq 10.
| (9) |
where Su denoted the total weighting score of an expert.
| (10) |
where M denoted the number of experts.
2. Judgment of occurrence probabilities were classified as nonoccurrence, absolute low, very low, low, fairly low, medium, fairly high, high, very high, absolute high or occurrence. The level value of each classification were defined from 0 to 1 (Table 2, [29,45]). Then corresponding triangular numbers or trapezoidal numbers proposed by experts were used to judge occurrence probabilities of events.
Table 2. Level Value of Each Classification.
| Judgment of Occurrence Probabilities Classification | Level Value |
|---|---|
| Nonoccurrence | 0 |
| Absolute low | 0.1 |
| Very low | 0.2 |
| Low | 0.3 |
| Fairly low | 0.4 |
| Medium | 0.5 |
| Fairly high | 0.6 |
| High | 0.7 |
| Very high | 0.8 |
| Absolute high | 0.9 |
| Occurrence | 1 |
3. Aggregate the fuzzy numbers. When the fuzzy numbers were all triangular number or trapezoidal number, Eq 11 was used to calculate the aggregated fuzzy number of experts for one event [42].
| (11) |
where denoted the aggregated fuzzy numbers of M experts' judgment, Wu denoted the weighting of expert.
Assume was triangular number and was trapezoidal number, calculation of was showed as below (Eqs 12 and 13). Then Eqs 14 and 15 were used to calculate the value of [30].
| (12) |
| (13) |
| (14) |
| (15) |
4. If the fuzzy numbers included both triangular number and trapezoidal number. Algorithm of the aggregation proposed by Lin and Wang [44] was employed, furthermore, experts weighting were considered to improve the method. The following example was introduced to illustrate the algorithm.
Assume was triangular number proposed by expert 1 and was trapezoidal number proposed by expert 2. Experts weightings of them were W1 and W2, respectively. The membership function of them were;
α-cut method [44,46] was employed to aggregate the fuzzy numbers, meanwhile, expert weighting was also considered (Eq 16).
| (16) |
where denoted α-cut for membership function of the aggregated fuzzy number , Wu denoted expert weighting, denoted α-cut for membership function of , n was the number of fuzzy numbers.
Then α-cut for membership function of and were;
Set α = (x−a11)/(a12−a11), and x can be either x1 or x2, so it can be obtained that x1 = (a12−a11)α+a11, and by this analogy, the α-cut values of and was calculated as;
was computed as (Eqs 12 through 16);
Set , we can obtained that;
Then, the membership function of the aggregated fuzzy number can be obtained;
After that, the aggregated fuzzy number of and was achieved;
Moreover, when the number of fuzzy numbers was more than two, aggregation algorithm was similar to the procedure above.
5. After the aggregated fuzzy number was confirmed, centroid-index method (Eq 17, [36]) was used to deal with the fuzzy number, then the fuzzy possibility score (FPS) was obtained. Assume was triangular number and was trapezoidal number. Eq 18 was used to calculate FPS when fuzzy number was triangular number, and Eq 19 was used to calculate trapezoidal number.
| (17) |
where X is the defuzzified output, g(x) is the membership function, and x is the output variable.
| (18) |
| (19) |
6. Finally, Eq 20 converted the FPS to FFR [37], and FFR was converted to occurrence probability of operational error and multiple failure (Eq 8).
| (20) |
Results
Biomass Gasification System
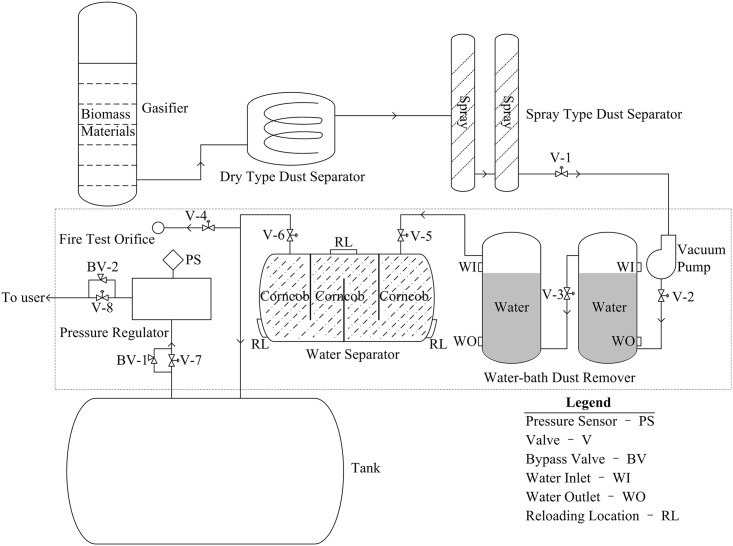
The biomass gasification system included a gasifier, dry type dust separator (DTDS), spray type dust separator (STDS), vacuum pump (VP), water-bath dust remover (WBDR), water separator (WS), tank, and pressure regulator (PR) (Fig 2). Biomass materials were burned in the gasifier with insufficient oxygen, and biomass gasses (hereafter referred to as “gas”) including CO, H2 and CH4 were produced by chemical reactions. The gas went into the DTDS, where most dust was separated. The VP was located between the STDS and WBDR. The gas was flowed into the STDS by the VP and was cleaned by the spray in the STDS. The WBDR provided further decontamination. Valve 2 (V-2) controlled the input of gas for the first WBDR, and valve 3 (V-3) controlled another. There was a water inlet (WI) and water outlet (WO) on the WBDR, and water in the WBDR was replaced through WI and WO. Waste water was discharged from the WO, and fresh water was injected into the WBDR from the WI such that the liquid level was below the WI. After the WBDR, the gas arrived at the WS, where the inlet and outlet were controlled by valve 5 (V-5) and valve 6 (V-6). Residual water in the gas was absorbed by corncobs in the WS, which were replaced via three reloading locations (RL). There was a fire test orifice (FTO) setting after WS that tested the ignitability of gas at the beginning of production; FTO was controlled by valve 4 (V-4). Finally, the cleaned gas was stored in an external tank. Gas was released from the tank into the PR, which contained a bypass valve 1 (BV-1) installed in parallel with valve 7 (V-7) of the PR. BV-1 ensured that if V-7 was plugged, gas in tank would be released to maintain a safe pressure level. The pressure was monitored by a pressure sensor (PS). Valve 8 (V-8) was located after the PR, and bypass valve 2 (BV-2) was installed in parallel with V-8. Hence, when V-8 was plugged, the gas was transferred from BV-2.
Fig 2. Biomass gasification system.
Analysis of Gas Leakage in the Biomass Gasification System
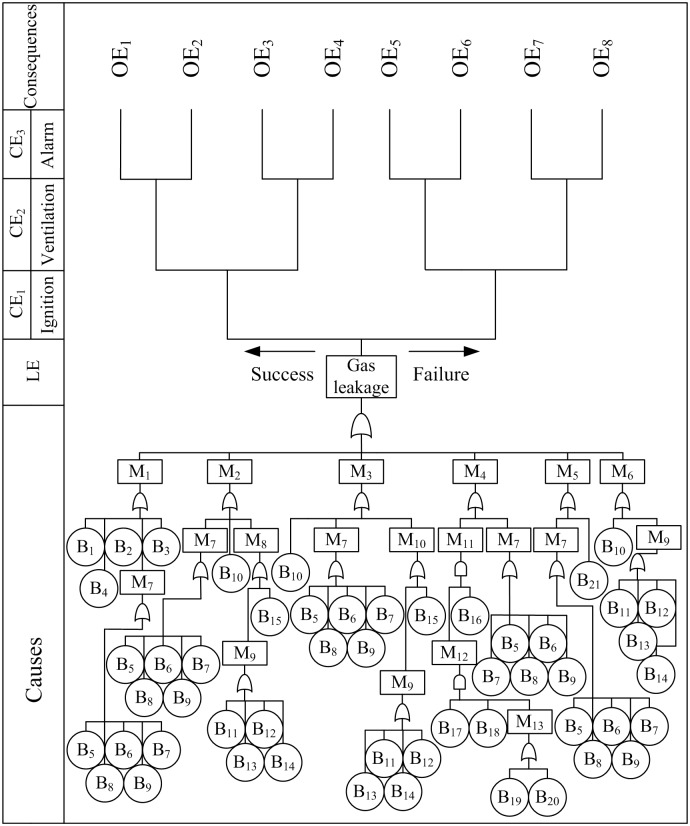
As mentioned previously, the devices and pipelines before and after the VP were under the condition of negative and positive pressure during production process, respectively. No leakage could occur in the areas with the condition of negative pressure. And the tank was external to the system, then the parts where gas leakage would be considered were encircled by the dashed line in Fig 2. Gas leakage was set as the TE to make FTA. Meanwhile, ventilation system and alarm system were placed in the system. Then set them and ignition as CEs, and gas leakage was set as the IE to make ETA. Various OEs were obtained by the conditions of the CEs. Finally, gas leakage was set to be the LE, bow-tie analysis connected the FTA and ETA by the LE (Fig 3, Table 3). Eight OEs were predicted depending on the success or failure of CEs (Fig 3, Table 4). Gas ignition would occur if CE1 was success but not if CE1 was failure.
Fig 3. Diagram of bow-tie analysis for gas leakage.
Table 3. Details of Bow-tie Components in Fig 3.
| Event | Symbol | Logic Link Type | Failure Model |
|---|---|---|---|
| Gas leakage | Gas leakage | OR-gate | ------ |
| Gas leakage of VP | M1 | OR-gate | ------ |
| Gas leakage of WBDR | M2 | OR-gate | ------ |
| Gas leakage of WS | M3 | OR-gate | ------ |
| Gas leakage of PR | M4 | OR-gate | ------ |
| Gas leakage of FTO | M5 | OR-gate | ------ |
| Gas leakage of pipelines | M6 | OR-gate | ------ |
| Gas leakage of valve | M7 | OR-gate | ------ |
| Gas leakage of WI | M8 | OR-gate | ------ |
| Flange failure | M9 | OR-gate | ------ |
| Gas leakage of RL | M10 | OR-gate | ------ |
| Gas leakage by high pressure | M11 | AND-gate | ------ |
| High pressure | M12 | AND-gate | ------ |
| Manual pressure relief failure | M13 | OR-gate | ------ |
| VP Seal Failure | B1 | ------ | Facilities failure |
| Cylinder liner failure | B2 | ------ | Facilities failure |
| Breakage of VP | B3 | ------ | Facilities failure |
| Wear of VP | B4 | ------ | Facilities failure |
| Valve Seal Failure | B5 | ------ | Facilities failure |
| Gaskets failure | B6 | ------ | Facilities failure |
| Seat rings failure | B7 | ------ | Facilities failure |
| Breakage of valve | B8 | ------ | Facilities failure |
| Wear of valve | B9 | ------ | Facilities failure |
| Material failure | B10 | ------ | Facilities failure |
| Breakage of flange | B11 | ------ | Facilities failure |
| Erosion | B12 | ------ | Facilities failure |
| Looseness | B13 | ------ | Facilities failure |
| Wear of flange | B14 | ------ | Facilities failure |
| Flange isn't tightly clipped | B15 | ------ | Operational error |
| Leakage | B16 | ------ | Facilities failure |
| V-8 plugged | B17 | ------ | Facilities failure |
| BV-2 is failed to open on demand | B18 | ------ | Facilities failure |
| Operational error | B19 | ------ | Operational error |
| PS is failed to function on demand | B20 | ------ | Facilities failure |
| V-4 is not closed | B21 | ------ | Operational error |
| Ignition | CE1 | ------ | Multiple failure |
| Ventilation | CE2 | ------ | Multiple failure |
| Alarm | CE3 | ------ | Multiple failure |
Table 4. OE Analysis.
| Event | Symbol | Event | Symbol |
|---|---|---|---|
| Gas stays in room briefly | OE1 | Poisoning, minor casualties | OE2 |
| Fire, minor property damage | OE3 | Fire and poisoning, major property damage, major casualties | OE4 |
| Gas stays in room briefly | OE5 | Poisoning, minor casualties | OE6 |
| Gas accumulation in room | OE7 | Poisoning, major casualties | OE8 |
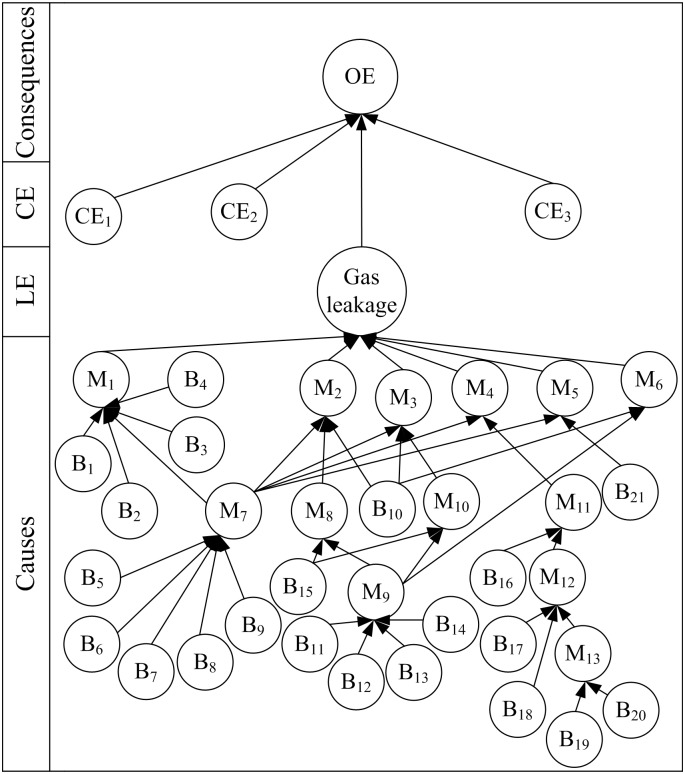
BN-Bow-Tie Model of Gas Leakage
The BN-bow-tie model of gas leakage was established by converting FTA and ETA into BN (Fig 4).
Fig 4. BN-bow-tie diagram of gas leakage.
Confirming Occurrence Probability of Each Basic Event and Conditional Event
Occurrence probability of facilities failure in the biomass gasification system was retrieved from a standard reliability data resource (Eq 8, Table 5, [27]).
Table 5. Occurrence Probability of Facilities Failure.
| Event | Symbol | Occurrence Rate (d-1) | Occurrence Probability (in 1 year) |
|---|---|---|---|
| VP Seal Failure | B1 | 4.443e-4 | 1.497e-1 |
| Cylinder Liner Failure | B2 | 1.018e-5 | 3.709e-3 |
| Breakage of VP | B3 | 8.384e-5 | 3.014e-2 |
| Wear of VP | B4 | 6.787e-4 | 2.194e-1 |
| Valve Seal Failure | B5 | 4.305e-6 | 1.570e-3 |
| Gasket Failure | B6 | 6.578e-6 | 2.398e-3 |
| Seat Ring Failure | B7 | 5.038e-6 | 1.837e-3 |
| Breakage of valve | B8 | 1.900e-6 | 6.933e-4 |
| Wear of valve | B9 | 6.242e-6 | 2.276e-3 |
| Material Failure | B10 | 2.942e-6 | 1.073e-3 |
| Breakage of flange | B11 | 9.660e-7 | 3.525e-4 |
| Erosion | B12 | 1.194e-5 | 4.349e-3 |
| Looseness | B13 | 3.956e-5 | 1.434e-2 |
| Wear of Flange | B14 | 1.142e-5 | 4.160e-3 |
| Leakage | B16 | 1.332e-4 | 4.746e-2 |
| V-8 Plugged | B17 | 1.462e-8 | 5.336e-6 |
| BV-2 Fails to Open on Demand | B18 | 5.040e-6 | 1.838e-3 |
| PS Fails to Function on Demand | B20 | 6.660e-5 | 2.402e-2 |
Note: all data was obtained from OREDA (2002) [27].
The other occurrence probabilities were confirmed by expert judgment. Five experts were invited to make judgment (Table 6). The weighting of each expert was calculated by Table 1 and Eqs 9 through 10 (Table 7).
Table 6. Description of Experts.
| Expert | Age (years) | Education | Service (years) | Professional Position |
|---|---|---|---|---|
| 1 | 55 | High school | 22 | Worker |
| 2 | 36 | Master | 11 | Technician |
| 3 | 40 | Bachelor | 18 | Junior engineer |
| 4 | 47 | PhD | 14 | Senior engineer |
| 5 | 50 | PhD | 21 | Senior academic |
Table 7. Weighting of Experts.
| Expert | Weighting Score | Total Weighting Score | Weighting | |||
|---|---|---|---|---|---|---|
| Age | Education | Service | Professional Position | |||
| 1 | 4 | 1 | 4 | 1 | 10 | 0.154 |
| 2 | 2 | 4 | 3 | 2 | 11 | 0.169 |
| 3 | 3 | 3 | 3 | 3 | 12 | 0.185 |
| 4 | 3 | 5 | 3 | 4 | 15 | 0.231 |
| 5 | 4 | 5 | 4 | 4 | 17 | 0.261 |
| Total | 16 | 18 | 17 | 14 | 65 | 1 |
Each expert gave judgment based on Table 2 to the events which belonged to the failure mode of operational error or multiple failure, and the corresponding fuzzy numbers were obtained (Table 8). Then the fuzzy numbers were aggregated by Eqs 11 through 16 (Table 9). Finally, the aggregated fuzzy numbers were converted to FPS and FFR by Eqs 17 through 20 (Table 9), and FFR was converted to occurrence probability by Eq 8 (Table 9).
Table 8. Experts Judgment of Operational Error and Multiple Failure.
| Event | Fuzzy numbers proposed by each expert | ||
|---|---|---|---|
| Flange is not tightly clipped (B15) | Expert1 | Expert 2 | Expert 3 |
| (0.2,0.3,0.4,0.5) | (0.1,0.2,0.3,0.5) | (0.2,0.3,0.4,0.5) | |
| Expert 4 | Expert 5 | ||
| (0.1,0.2,0.3,0.4) | (0.1,0.2,0.3,0.5) | ||
| Operational error (B19) | Expert 1 | Expert 2 | Expert 3 |
| (0.1,0.2,0.3,0.5) | (0.2,0.3,0.4) | (0.1,0.3,0.4,0.5) | |
| Expert 4 | Expert 5 | ||
| (0.2,0.3,0.4,0.5) | (0.2,0.3,0.5) | ||
| V-4 is not closed (B21) | Expert 1 | Expert 2 | Expert 3 |
| (0.2,0.3,0.4) | (0.1,0.3,0.4,0.5) | (0.1,0.2,0.3,0.4) | |
| Expert 4 | Expert 5 | ||
| (0.1,0.3,0.5) | (0.1,0.3,0.4,0.5) | ||
| Ignition (CE1) | Expert 1 | Expert 2 | Expert 3 |
| (0.1,0.3,0.4) | (0,0.2,0.3,0.4) | (0.1,0.2,0.4) | |
| Expert 4 | Expert 5 | ||
| (0.1,0.2,0.3,0.5) | (0.1,0.2,0.3) | ||
| Ventilation(CE2) | Expert 1 | Expert 2 | Expert 3 |
| (0.1,0.3,0.4,0.5) | (0.1,0.2,0.3,0.4) | (0,0.1,0.2,0.3) | |
| Expert 4 | Expert 5 | ||
| (0,0.1,0.3,0.4) | (0.1,0.2,0.3,0.4) | ||
| Alarm(CE3) | Expert 1 | Expert 2 | Expert 3 |
| (0.1,0.2,0.3,0.5) | (0.1,0.2,0.3,0.4) | (0,0.1,0.3,0.4) | |
| Expert 4 | Expert 5 | ||
| (0,0.1,0.2) | (0,0.1,0.2,0.3) | ||
Table 9. FPS, FFR and Occurrence Probability Calculations of Operational Error and Multiple Failure.
| Event | Aggregated fuzzy numbers | FPS | FFR (d-1) | Occurrence Probability of failure (in 1 year) |
|---|---|---|---|---|
| Flange is not tightly clipped (B15) | (0.1339, 0.2339, 0.3339, 0.4769) | 0.2966 | 8.542e-4 | 2.679e-1 |
| Operational error (B19) | (0.1661, 0.2846, 0.3416, 0.4831) | 0.3202 | 1.103e-3 | 3.314e-1 |
| V-4 is not closed (B21) | (0.1154, 0.2815, 0.3430, 0.4661) | 0.2990 | 8.773e-4 | 2.740e-1 |
| Ignition (CE1) | (0.0831, 0.2154, 0.2554, 0.3970) | 0.2383 | 4.080e-4 | 1.384e-1 |
| Ventilation (CE2) | (0.0584, 0.1738, 0.2969, 0.3969) | 0.2309 | 3.661e-4 | 1.251e-1 |
| Alarm (CE3) | (0.0323, 0.1323, 0.2277, 0.3431) | 0.1845 | 1.675e-4 | 5.931e-2 |
Occurrence Probability of LE and OE Updating
Occurrence probability of LE gas leakage and OEs were determined by Eqs 1 through 3, and the occurrence probabilities of them were listed in Table 10.
Table 10. Occurrence Probability of Gas Leakage and OEs.
| Symbol | Occurrence Probability (in 1 year) |
|---|---|
| Gas Leakage | 6.702e-1 |
| OE1 | 7.634e-2 |
| OE2 | 4.813e-3 |
| OE3 | 1.092e-2 |
| OE4 | 6.883e-4 |
| OE5 | 4.753e-1 |
| OE6 | 2.997e-2 |
| OE7 | 6.796e-2 |
| OE8 | 4.285e-3 |
Discussion
The occurrence probability of gas leakage in one year was 6.702e-1 (Table 10), and occurrence probabilities of accidents would be reduced when ventilation and alarm system were present and functional. However, present and functional ventilation or alarm system can't avoid minor accidents, their occurrence probabilities like OE3 and OE6 still remained relatively high. Although ventilation and alarm system were necessary to lessen the impact of gas leakage in biomass gasification system. But the key to avoid accidents was reducing the occurrence probability of gas leakage. Thus, the critical nodes of causes for gas leakage was determined by BN-bow-tie analysis, and the corresponding safety measures were proposed according to the critical nodes.
Confirming the Critical Nodes of Causes
To find the critical nodes of causes, the importance measures of each event was calculated by Eqs 4 through 7 (Table 11). The rank of events based on importance measures was obtained by the methods listed below.
Table 11. Calculations of Importance Measures.
| Symbol | Importance Measure | ||
|---|---|---|---|
| BM | RAW | FV | |
| B1 | 3.878e-1 | 8.662e-2 | 8.662e-2 |
| B2 | 3.310e-1 | 1.832e-3 | 1.832e-3 |
| B3 | 3.400e-1 | 1.529e-2 | 1.529e-2 |
| B4 | 4.224e-1 | 1.383e-1 | 1.383e-1 |
| B5 | 3.303e-1 | 7.736e-4 | 7.743e-4 |
| B6 | 3.305e-1 | 1.183e-3 | 1.183e-3 |
| B7 | 3.304e-1 | 9.055e-4 | 9.056e-4 |
| B8 | 3.300e-1 | 3.413e-4 | 3.417e-4 |
| B9 | 3.305e-1 | 1.122e-3 | 1.123e-3 |
| B10 | 3.301e-1 | 5.285e-4 | 5.297e-4 |
| B11 | 3.299e-1 | 1.735e-4 | 1.746e-4 |
| B12 | 3.312e-1 | 2.149e-3 | 2.150e-3 |
| B13 | 3.346e-1 | 7.158e-3 | 7.159e-3 |
| B14 | 3.311e-1 | 2.055e-3 | 2.056e-3 |
| B15 | 4.504e-1 | 1.800e-1 | 1.800e-1 |
| B16 | 0 | 0 | 0 |
| B17 | 1.000e-5 | 7.961e-11 | 0 |
| B18 | 0 | 0 | 0 |
| B19 | 0 | 0 | 0 |
| B20 | 0 | 0 | 0 |
| B21 | 4.542e-1 | 1.857e-1 | 1.857e-1 |
- If the amount of events was “n”, the normalized weighting R* was calculated by the importance measures Ii and Eq 21.
(21) - After the normalized weighting R* of each importance measure was calculated, the total weighting was calculated by Eq 22.
(22) Finally, events were ranked from maximum to minimum by total weighting , and the critical nodes of causes was found by the rank. The results are shown in Table 12.
Table 12. Rank of Events.
| Rank | Symbol | Normalization Weighting (R*) | Total Weighting () | ||
|---|---|---|---|---|---|
| 1 | B21 | 7.976 | 29.751 | 29.750 | 67.477 |
| 2 | B15 | 7.910 | 28.846 | 28.845 | 65.601 |
| 3 | B4 | 7.418 | 22.156 | 22.156 | 51.730 |
| 4 | B1 | 6.810 | 13.878 | 13.878 | 34.566 |
| 5 | B3 | 5.971 | 2.450 | 2.450 | 10.871 |
| 6 | B13 | 5.875 | 1.147 | 1.147 | 8.169 |
| 7 | B12 | 5.816 | 0.344 | 0.344 | 6.504 |
| 8 | B14 | 5.815 | 0.329 | 0.329 | 6.473 |
| 9 | B2 | 5.812 | 0.293 | 0.294 | 6.399 |
| 10 | B6 | 5.805 | 0.189 | 0.190 | 6.184 |
| 11 | B9 | 5.804 | 0.180 | 0.180 | 6.164 |
| 12 | B7 | 5.802 | 0.145 | 0.145 | 6.092 |
| 13 | B5 | 5.800 | 0.124 | 0.124 | 6.048 |
| 14 | B10 | 5.797 | 0.085 | 0.085 | 5.967 |
| 15 | B8 | 5.795 | 0.055 | 0.055 | 5.905 |
| 16 | B11 | 5.793 | 0.028 | 0.028 | 5.849 |
| 17 | B17 | ≈0 | ≈0 | 0 | ≈0 |
| 18 | B16 | 0 | 0 | 0 | 0 |
| 19 | B18 | 0 | 0 | 0 | 0 |
| 20 | B19 | 0 | 0 | 0 | 0 |
| 21 | B20 | 0 | 0 | 0 | 0 |
| Total | 100 | 100 | 100 | 100 | |
The total weighting of B21 (V-4 is not closed), B15 (flange is not tightly clipped), B4 (wear of VP) and B1 (VP seal failure) was much higher than others; they were the critical nodes of causes. Because accidents were mainly caused by these nodes, the occurrence probabilities of accidents could be reduced effectively by implementing corresponding safety measures. If B21, B15, B4 and B1 were implemented with measures to ensure safety, the occurrence probabilities was reduced to 1/10.3 of the original values (Table 13).
Table 13. Occurrence Probabilities of Accidents when Critical Nodes are Ensured Safety.
| Symbol | Occurrence Probability (in 1 year) |
|---|---|
| Gas Leakage | 6.527e-2 |
| OE1 | 7.435e-3 |
| OE2 | 4.688e-4 |
| OE3 | 1.063e-3 |
| OE4 | 6.703e-5 |
| OE5 | 4.628e-2 |
| OE6 | 2.918e-3 |
| OE7 | 6.618e-3 |
| OE8 | 4.173e-4 |
Providing Safety Measures for Critical Nodes
B21 (V-4 is not closed) and B15 (flange is not tightly clipped) were operational errors. To eliminate these errors, a safety check was added to make sure that flange was tightly clipped before production. Additionally, the V-4 manual valve was replaced with a self-closing valve. Both B4 (wear of VP) and B1 (VP seal failure) are facilities failures; the VP safety checks should be improved and the VP seals replaced at regular intervals.
Conclusions
In biomass gasification system, facilities failure data can be obtained from standard reliability data sources, and operational error data can be confirmed by fuzzy methods based on expert judgment. These reliability data can be used to make probabilistic safety assessment (PSA) of biomass gasification system.
Bow-tie analysis was employed to evaluate gas leakage from biomass gasification stations. When ventilation and alarm systems were present and functional, the occurrence probabilities of accidents caused by gas leakage were reduced, but they were inefficient in reducing the occurrence probabilities of minor accidents. Therefore, the occurrence probability of gas leakage must be lessened to reduce the exposure to associated accidents caused by gas leakage.
By mapping bow-tie analysis into BN (BN-bow-tie), the critical nodes of accidents causes were identified. These critical nodes of gas leakage were as follows: V-4 is not closed, the flange is not tightly clipped, wear of VP, and VP seal failure. If safety measures were implemented at these nodes, the occurrence probabilities of accidents were reduced to 1/10.3 of the original values.
To reach the safety goal, safety checks should be added. The manual V-4 valve should be replaced with a self-closing valve, and the VP seals should be replaced periodically.
Data Availability
Data are available from the Offshore Reliability Data Handbook. 4th ed. whose authors may be contacted at oreda@sintef.no.
Funding Statement
The authors have no support or funding to report.
References
- 1.Demirbas A. Biomass gasification for power generation in Turkey. Energy Sources, Part A: Recovery, Utilization, and Environment Effects. 2006; 28(5): 433–45. 10.1080/009083190913584 [DOI] [Google Scholar]
- 2.Christoforou EA, Fokaides PA. A review of quantification practices for plant-derived biomass potential. International Journal of Green Energy. 2015; 12(4): 368–378. 10.1080/15435075.2014.880147 [DOI] [Google Scholar]
- 3.Cherni JA, Kentish J. Renewable energy policy and electricity market reforms in China. Energy Policy. 2007; 35: 3616–3629. 10.1016/j.enpol.2006.12.024 [DOI] [Google Scholar]
- 4.Zhang O, Yu SK, Liu PK. Development mode for renewable energy power in China: Electricity pool and distributed generation units. Renewable and Sustainable Energy Reviews. 2015; 44: 657–668. 10.1016/j.rser.2015.01.020 [DOI] [Google Scholar]
- 5.Flamos A, Georgallis PG, Doukas H, Psarras J. Using biomass to achieve European Union energy targets-a review of biomass status, potential, and supporting policies. International Journal of Green Energy. 2011; 8(4): 411–428. 10.1080/15435075.2011.576292 [DOI] [Google Scholar]
- 6.Sam C, Aira H, Reeli K, Sanna S, Dalia S, Arta D. Progress in renewable electricity in Northern Europe towards EU 2020 targets. Renewable and Sustainable Energy Reviews. 2015; 52: 1768–1780. 10.1016/j.rser.2015.07.165 [DOI] [Google Scholar]
- 7.Petinrin JO, Mohamed S. Renewable energy for continuous energy sustainability in Malaysia. Renewable and Sustainable Energy Reviews. 2015; 50: 967–981. 10.1016/j.rser.2015.04.146 [DOI] [Google Scholar]
- 8.Sharma S, Sheth PN. Air-steam biomass gasification: Experiments, modeling and simulation. Energy Conversion and Management. 2016; 110: 307–318. 10.1016/j.enconman.2015.12.030 [DOI] [Google Scholar]
- 9.Ogunkoya D, Fang TG. Engine performance, combustion, and emissions study of biomass to liquid fuel in a compression-ignition engine. Energy Conversion and Management. 2015; 95: 342–351. 10.1016/j.enconman.2015.02.041 [DOI] [Google Scholar]
- 10.Gao XY, Zhang YN, Li BX, Yu XY. Model development for biomass gasification in an entrained flow gasifier using intrinsic reaction rate submodel. Energy Conversion and Management. 2016; 108: 120–131. 10.1016/j.enconman.2015.10.070 [DOI] [Google Scholar]
- 11.Cao GL, Zhang XY, Wang YQ, Zheng FC. Estimation of emissions from field burning of crop straw in China. Chinese Science Bulletin. 2007; 53 (5): 784–790. 10.1007/s11434-008-0145-4 [DOI] [Google Scholar]
- 12.Sreejith CC, Muraleedharan C, Arun P. Thermo-chemical analysis of biomass gasification by Gibbs free energy minimization model-part: II (optimization of biomass feed and steam to biomass ratio). International Journal of Green Energy. 2013; 10(6): 610–639. 10.1080/15435075.2012.709203 [DOI] [Google Scholar]
- 13.Cummer KR, Brown RC. Ancillary equipment for biomass gasification. Biomass & Bioenergy. 2002; 23: 113–128. 10.1016/S0961-9534(02)00038-7 [DOI] [Google Scholar]
- 14.Lv XJ, Lu CH, Zhu XJ, Weng YW. Safety analysis of a solid oxide fuel/gas turbine hybrid system fueled with gasified biomass. Journal of Fuel Cell Science and Technology. 2015; 12(1): 1–6. 10.1115/1.4029084 [DOI] [Google Scholar]
- 15.de Dianous V, Fievez C. ARAMIS project: A more explicit demonstration of risk control through the use of bow-tie diagrams and the evaluation of safety barrier performance. Journal of Hazardous Materials. 2006; 130(3): 220–233. 10.1016/j.jhazmat.2005.07.010 [DOI] [PubMed] [Google Scholar]
- 16.Paolo C, Stefano P, Annamaria P. Baseline risk assessment tool: a comprehensive risk management tool for process safety. Process Safety Progress. 2011; 30(3): 251–260. 10.1002/prs.10464 [DOI] [Google Scholar]
- 17.Chen QQ, Jia Q, Yuan ZW, Huang L. Environmental risk source management system for the petrochemical industry. Process Safety and Environmental Protection. 2014; 92: 251–260. 10.1016/j.psep.2013.01.004 [DOI] [Google Scholar]
- 18.Mokhtari K, Ren J, Roberts C, Wang J. Application of a generic bow-tie based risk analysis framework on risk management of sea ports and offshore terminals. Journal of Hazardous Materials. 2011; 192(2): 465–475. 10.1016/j.jhazmat.2011.05.035 [DOI] [PubMed] [Google Scholar]
- 19.Lu LL, Liang W, Zhang LB, Zhang H, Lu Z, Shan JZ. A comprehensive risk evaluation method for natural gas pipelines by combining a risk matrix with a bow-tie model. Journal of Natural Gas Science and Engineering. 2015; 25: 124–133. 10.1016/j.jngse.2015.04.029 [DOI] [Google Scholar]
- 20.Markowski A, Kotunia A. Bow-tie model in layer of protection analysis. Process Safety and Environmental Protection. 2011; 89(4): 205–213. 10.1016/j.psep.2011.04.005 [DOI] [Google Scholar]
- 21.Kaki A, Salo A, Talluri S. Disruptions in supply networks: A probabilistic risk assessment approach. Journal of Business Logistics. 2015; 36(3): 273–287. 10.1111/jbl.12086 [DOI] [Google Scholar]
- 22.Badreddine A, Amor NB. A Bayesian approach to construct bow tie diagrams for risk evaluation. Process Safety and Environmental Protection. 2013; 91: 159–171. 10.1016/j.psep.2012.03.005 [DOI] [Google Scholar]
- 23.Khakzad N, Khan F, Amyotte P. Dynamic risk analysis using bow-tie approach. Reliability Engineering and System Safety. 2012; 104: 36–44. 10.1016/j.ress.2012.04.003 [DOI] [Google Scholar]
- 24.Khakzad N, Khan F, Amyotte P. Dynamic safety analysis of process systems by mapping bow-tie into Bayesian network. Process Safety and Environmental Protection. 2013; 91(1–2): 46–53. 10.1016/j.psep.2012.01.005 [DOI] [Google Scholar]
- 25.Majeed A, Khan F, Khakzad N. Risk-based safety analysis of well integrity operations. Safety Science. 2016; 84: 149–160. 10.1016/j.ssci.2015.12.009 [DOI] [Google Scholar]
- 26.van der Borst M, Schoonakker H. An overview of PSA importance measures. Reliability Engineering and System Safety. 2001; 72(3): 241–245. 10.1016/S0951-8320(01)00007-2 [DOI] [Google Scholar]
- 27.Orissa Renewable Energy Development Agency (OREDA). Offshore Reliability Data Handbook. 4th ed Trondheim: OREDA; 2002. [Google Scholar]
- 28.Lopez RA, Saud Y, Vaez N. Assessment of the likelihood of exceeding the flare capacity of multiple LNG processing trains. Process Safety Progress. 2015; 34: 250–258. 10.1002/prs.11719 [DOI] [Google Scholar]
- 29.Chen SM, Chen JH. Fuzzy risk analysis based on ranking generalized fuzzy numbers with different heights and different spreads. Expert Systems with Applications. 2009; 36(3): 6833–6842. 10.1016/j.eswa.2008.08.015 [DOI] [Google Scholar]
- 30.Chen SM, Sanguansat K. Analyzing fuzzy risk based on a new fuzzy ranking method between generalized fuzzy numbers. Expert Systems with Applications. 2011; 38(3): 2163–2171. 10.1016/j.eswa.2010.08.002 [DOI] [Google Scholar]
- 31.Dubois D, Prade H. Ranking fuzzy numbers in the setting of possibility theory. Information Science. 1983; 30(3): 183–224. 10.1016/0020-0255(83)90025-7 [DOI] [Google Scholar]
- 32.Chen SJ, Chen SM. Fuzzy risk analysis based on similarity measures of generalized fuzzy numbers. IEEE Transactions on Fuzzy Systems. 2003; 11(1): 45–56. 10.1109/TFUZZ.2002.806316 [DOI] [Google Scholar]
- 33.Rodger JA. A fuzzy nearest neighbor neural network statistical model for predicting demand for natural gas and energy cost savings in public buildings. Expert Systems with Applications. 2014; 41(4): 1813–1829. 10.1016/j.eswa.2013.08.080 [DOI] [Google Scholar]
- 34.Rodger JA. Application of a fuzzy feasibility Bayesian network probabilistic estimation of supply chain backorder aging, unfilled backorders, and customer wait time using stochastic simulation with Markov blankets. Expert Systems with Applications. 2014; 41(16): 7005–7022. 10.1016/j.eswa.2014.05.012 [DOI] [Google Scholar]
- 35.Rodger JA, Pankaj P, Gonzalez SP. Decision making using a fuzzy induced linguistic ordered weighted averaging approach for evaluating risk in a supply chain. International Journal of Advanced Manufacturing Technology. 2014; 70(1–4): 711–723. 10.1007/s00170-013-5311-4 [DOI] [Google Scholar]
- 36.Yager RR. Ranking fuzzy subsets over the unit interval. In Proceedings of 17th IEEE international conference on decision and control. San Diego, California. 1978; 1435–1437. org/10.1109/CDC.1978.268154.
- 37.Onisawa T. An approach to human reliability in man-machine systems using error possibility. Fuzzy sets and system. 1988; 27: 87–103. 10.1016/0165-0114(88)90140-6 [DOI] [Google Scholar]
- 38.Ferdous R, Khan F, Sadiq R, Amyotte P, Veitch B. Handling and updating uncertain information in bow-tie analysis. Journal of Loss Prevention in the Process Industries. 2012; 25(1): 8–19. 10.1016/j.jlp.2011.06.018 [DOI] [Google Scholar]
- 39.Li PC, Chen GH, Dai LC, Zhang L. A fuzzy Bayesian network approach to improve the quantification of organizational influences in HRA frameworks. Safety Science. 2012; 50(7): 1569–1583. 10.1016/j.ssci.2012.03.017 [DOI] [Google Scholar]
- 40.Ramzali N, Lavasani MRM, Ghodousi J. Safety barriers analysis of offshore drilling system by employing Fuzzy Event Tree Analysis. Safety Science. 2015; 78: 49–59. 10.1016/j.ssci.2015.04.004 [DOI] [Google Scholar]
- 41.Bardossy A, Duckstein L, Bogardi I. Combination of fuzzy numbers representing expert opinions. Fuzzy Sets and Systems. 1993; 57(2): 173–181. 10.1016/0165-0114(93)90157-D [DOI] [Google Scholar]
- 42.Hsu HM, Chen CT. Aggregation of fuzzy opinions under group decision making. Fuzzy Sets and Systems. 1996; 79: 279–285. 10.1016/0165-0114(95)00185-9 [DOI] [Google Scholar]
- 43.Lavasani SM, Ramzali N, Sabzalipour F, Akyuz E. Utilisation of fuzzy fault tree analysis (FFTA) for quantified risk analysis of leakage in abandoned oil and natural-gas wells. Ocean Engineering. 2015; 108: 729–737. 10.1016/j.oceaneng.2015.09.008 [DOI] [Google Scholar]
- 44.Lin CT, Wang MJ. Hybrid fault tree analysis using fuzzy sets. Reliability Engineering and System Safety. 1997; 58(3): 205–213. 10.1016/S0951-8320(97)00072-0 [DOI] [Google Scholar]
- 45.Liang DC, Liu D, Witold P, Hu P. Triangular fuzzy decision-theoretic rough sets. International Journal of Approximate Reasoning. 2013; 54(8): 1087–1106. 10.1016/j.ijar.2013.03.014 [DOI] [Google Scholar]
- 46.Mahapatra GS. Intuitionistic fuzzy fault tree analysis using intuitionistic fuzzy numbers. International Mathematical Forum. 2010; 5: 1015–1024. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data are available from the Offshore Reliability Data Handbook. 4th ed. whose authors may be contacted at oreda@sintef.no.