Duality quantum algorithm efficiently simulates open quantum systems

Abstract

Because of inevitable coupling with the environment, nearly all practical quantum systems are open system, where the evolution is not necessarily unitary. In this paper, we propose a duality quantum algorithm for simulating Hamiltonian evolution of an open quantum system. In contrast to unitary evolution in a usual quantum computer, the evolution operator in a duality quantum computer is a linear combination of unitary operators. In this duality quantum algorithm, the time evolution of the open quantum system is realized by using Kraus operators which is naturally implemented in duality quantum computer. This duality quantum algorithm has two distinct advantages compared to existing quantum simulation algorithms with unitary evolution operations. Firstly, the query complexity of the algorithm is O(d³) in contrast to O(d⁴) in existing unitary simulation algorithm, where d is the dimension of the open quantum system. Secondly, By using a truncated Taylor series of the evolution operators, this duality quantum algorithm provides an exponential improvement in precision compared with previous unitary simulation algorithm.

Quantum computer works quantum mechanically¹,², and can efficiently factorize large numbers³ and search in an unsorted database⁴,⁵. Simulation of quantum systems is one of the most important original motivations of coming up with the idea of quantum computers¹, and the progress of quantum simulation study is developing fast⁶,⁷,⁸,⁹,¹⁰,¹¹,¹²,¹³,¹⁴,¹⁵,¹⁶. The dynamic evolutions of a closed system are described by unitary transform, which can be simulated in quantum computer directly. However, in the real world, quantum systems interact with their surrounding environment inevitably, hence most systems are open systems. The dynamic evolution of an open quantum system is usually non-unitary because of decoherence and dissipation. It is natural to describe the dynamics of an open quantum system by including the interaction between the principal system and an environment⁶. The principal system and the environment coupled together form a closed quantum system, which is denoted as total system. Assume that the Hilbert space of principal system is 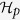with dimensions d_p and the Hilbert space of environment is with dimensions d_e, then the Hilbert space for the total quantum system consisting of principal system and environment is 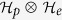⁷. We assume that the system-environment state is the product state in the beginning, and the joint density matrix is described as ρ ⊗ ρ_env. Considering the dynamics of the principal system is what we interested, the evolution of the density matrix after performing a partial trace over environment is⁶

where ρ′ is the density matrix of the final state of principal system and U is time evolution operator imposed on the total system. The corresponding Hamiltonian H of U is in the space . For convenience, we assume that the dimensions of principal system and environment are the same, namely, d = d_p = d_e. The dimension of total Hamiltonian H is d². Lloyd firstly proposed a quantum algorithm to simulate open quantum system efficiently⁷. In this algorithm, by enlarging the system to include the environment, the total system Hamiltonian is decomposed in the form where each is Hermitian and satisfies 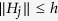for a given constant h. The query complexity of simulating time evolution of the open quantum system in an accuracy ε over time t is approximated to O(ld⁴ht²/ε). By regarding the total system as a bigger closed quantum system, this algorithm performs unitary transformation as same as in the closed system.

The concept of duality quantum computers is first proposed by Long in 2002 based on the general principle of quantum interference¹⁷,¹⁸, which draw many attentions¹⁸,¹⁹,²⁰,²¹,²²,²³,²⁴,²⁵,²⁶,²⁷,²⁸,²⁹,³⁰,³¹,³²,³³,³⁴,³⁵,³⁶,³⁷,³⁸,³⁹,⁴⁰,⁴¹,⁴²,⁴³,⁴⁴,⁴⁵. It is shown that any bounded linear operator can be expressed as a linear combinations of unitary operators in a duality quantum computer²¹. Thus, duality quantum computers can perform non-unitary transformation and provide novel way to design quantum algorithms, which can adapt the techniques in classical algorithm design to quantum algorithms, already showing flexibility and good performance in precision for closed quantum systems. Recently, several duality quantum algorithms have been proposed, which simulate Hamiltonian dynamics by linear combinations of unitary operations in a closed quantum system⁴⁶,⁴⁷,⁴⁸,⁴⁹. In the algorithms in refs ^{47, 48, 49}, the performance has exponential improvement in the dependence on precision.

Alternatively, in an open quantum system coupled with surrounding environment, the dynamics can also be described by a completely positive linear map ε(ρ). The quantum operations can be represented in operator-sum representation by Kraus operators. Suppose the initial state of environment is a pure state, denoted as ρ_env = |e₀〉 〈e₀|. Equation (1) can be rewritten as⁶

where E_k ≡ 〈e_k|U|e₀〉 is an Kraus operator and satisfies completeness relation . The complete set of 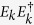is known as a “Positive Operator-Valued Measure”. It should be noted that the operator E_k is only acted on the principle system. So, if we can realize the Kraus operator, the complexity of evolution simulation that is dependent on dimensions will be decreased. Generally speaking, Kraus operator E_k is non-unitary and can not be realized in quantum computer directly. However, the Kraus operator can be realized in a duality quantum computer⁴⁰,⁴¹. In our method, the query complexity is , which exponentially improved the performance of quantum algorithm in ref. 7.

In this paper, we present a duality quantum algorithm to simulate Hamiltonian evolution for an open quantum system. There are two stages in our method. The first stage realizes Kraus operators in the duality quantum computer. The second stage of the algorithm is based upon a truncated Taylor series to approximate the evolution operators. The query complexity of the algorithm is significant decreased compared with Lloyd’s algorithm⁷. We demonstrate this algorithm by a single quibit open quantum system as an example.

Results

Realization of Kraus operators in duality quantum computer

A duality quantum computer is a moving quantum computer passing through a d-slit which exploits the wave-particle duality of quantum systems¹⁷. The physic picture is : a quantum system passing through a d-slits with its wave function being divided into d sub-waves, the dividing operation denoted as the quantum wave divider (QWD) operation. Different unitary operations are performed simultaneously on the sub-waves at different slits. This is called the duality parallelism, and it enables the duality quantum computer to perform non-unitary gate operations. Conversely, the quantum wave combiner (QWC) operation adds up all the sub-waves into one wave function. Compared to ordinary quantum computers in which only unitary operators are allowed, One can perform different gate operations on the sub-wave functions at different slits in the duality quantum computer¹⁷. Generally, we only measure the final wave functions on 0-slit to realize a duality quantum gate, which is called single output duality quantum computing. Furthermore, we make measurements of the final wave functions on all d-slits, which is called complete measurements. After detecting, through QWD operation and QWC operation, every path on each-slit realized a duality quantum gate. It means that d duality quantum gates are performed in one process. The process is denoted as multi-output duality quantum computing. Duality quantum gates are generally non-unitary and naturally suitable to perform non-unitary evolutions. A three-slits duality quantum computer is shown in Fig. 1. The input is from the 0-th slit, and it is divided into three sub-waves by the middle screen with three slits. After the middle screen, different operations are performed on the different sub-waves, and three outputs of duality quantum computing are collected from three-slits on the right wall¹⁸.

Figure 1. An illustrator for a three-slits duality quantum computer.

It has been proven that a moving n-qubit duality computer passing through a d-slit can be perfectly simulated by an ordinary quantum computer with n-qubit and an extra qudit resource¹⁸,¹⁹,²⁰, which is called duality quantum computing mode. For the convenience, we use the expressions from duality quantum computing mode¹⁹,²⁰,³²,³³ in this article.

The n-qubit ordinary quantum computer is represented by n work qubit and an auxiliary qudit represents a d-slits. The QWD operation can be represented by a general unitary operation V and the QWC operation can be represented by a general unitary operation W. The two unitary operations act on an auxiliary qudit. There are d controlled unitary operations act on ordinary quantum computer between the operations V and W. The quantum circuit of duality quantum computer is given in Fig. 2.

Figure 2. The multi-output duality quantum computing circuit in a quantum computer.

|Ψ〉 denotes the initial state of work qubit, and |0〉 is the initial state of the controlling auxiliary qudit. The circles represent the state of the controlling qudit and the squares represent unitary operations. Unitary operations U₀, U₁ , U_d−1 are activated only when the qudit holds the respective values indicated in circles¹⁸. The “readout” part marked by yellow rectangle means that: When the auxiliary qudit in the |j〉 state, where j ∈ {0, 1 , d}, the corresponding output (final state) of the work qubit will be redout by corresponding detector.

It is convenient to divide the whole process into four steps to illustrate the multi-output duality computing in a quantum computer.

Step one

The quantum system is prepared with initial state |Ψ〉|0〉 firstly. The QWD operation is implemented by performing the operator V on the auxiliary qudit |0〉, and this operation transforms the initial state into

where V_i0 = p_i is a complex number and satisfies the condition , |V_i0| ≤ 1. V_i0 represents the divider structure and is the first column element of the unitary matrix V representing the coefficient in each slit. The closure condition ∑ |i〉〈i| = I in quantum mechanics has been used in the deviation. The final state |Ψ〉|i〉 represents the sub-wave at the i-th slit.

Step two

Performing the auxiliary qudit controlled operations U₀, U₁ , U_d−1 on the work qubits with initial state |Ψ〉 which leads to the following transformation,

The corresponding physical picture is that unitary operations are implemented simultaneously on the sub-waves at different slits.

Step three

Performing the unitary operation W on the auxiliary qudit |i〉. Then the following state is obtained,

where L_k = ∑_iW_kiV_i0U_i is the duality quantum gate. In previous paper¹⁷,¹⁸, only L₀ is studied as a duality quantum gate. In this article, we discuss all the k number duality quantum gates.

Step four

After step three, the auxiliary qudit is in a superposition state. Making the complete measurements, namely, measuring the final wave function when the qudit is in state |j〉 by placing j detectors at j different slits. which described as “readout” in Fig. 2. The complete measurements are also clearly visualized by the detectors in Fig. 1.

The duality quantum gate, or generalized quantum gate is defined as follows

where U_i is unitary and c_i is the complex coefficient and satisfies

When c_i is restricted to positive real, c_i is denoted by r_i, and satisfies the constrained condition of ∑_ir_i ≤ 1. In this scenario, the duality quantum gate is called real duality gate which is denoted as L_r. So, the form of real duality quantum gate can be expressed as

This corresponds to a physical picture of an asymmetric d-slit, and r_i is the probability that the duality computer system passes through the i-th slit.

Because unitary operators have the unclosed property under addition, the duality quantum gates are generally non-unitary. Moreover, Gudder has proved that all linear bounded operators in a finite dimensional Hilbert space can be expressed as an element in the positive cone of generalized quantum gates²¹. Many recent studies about the mathematical theory of duality quantum computer have been made¹⁹,²⁰,²¹,²²,²³,²⁴,²⁵,²⁶,²⁷,²⁸,²⁹,³⁰,³¹,³⁴,³⁶.

Theorem. The duality quantum gate L_k = ∑_iW_kiV_i0U_i is a trace preserving Kraus operator, namely, .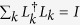

Proof. Defining L_k = ∑_iW_kiV_i0U_i firstly, then we have, . Then a straightforward derivation gives

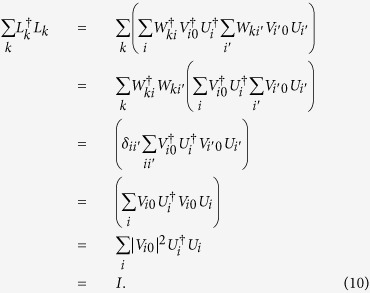The conditions that matrices W, V and operator U_i are unitary are used in the proof. So, the duality quantum gate L_k can be applied to realize Kraus operator E_k. Actually, E_k is a bounded linear operator in a finite dimensional Hilbert space which can be decomposed into a sum of unitary operators. By extending the Hilbert space, any Kraus operator E_k can be realized by duality quantum gate L_k. The effect of environment on the principal system can be explained as the combination effects of different operators performed on the system. In the expression of completely positive linear map form, we can get the dynamic evolution result of the open system directly without coupled with environment.

Simulating the time evolution of open quantum system

We have realized the Kraus operator E_k in the previous section. To perform the whole duality quantum algorithm, we only need to realize the unitary operator U_i in the Kraus operator in next step. U_i in Eq. 6 is regarded as a time evolution operator and it is approximated by a truncated Taylor series. It can be realized in a duality quantum computer just as in the BCCKS algorithm³⁵,⁴⁸.

In the algorithm, consider a quantum system with Hamiltonian where each is unitary. Dividing the finite length evolution time t into n segments, with each segment of length t/n. The time evolution operator of each segment is approximated as

where K is the order of Taylor series.

Without loss of generality, let each . The approximation is a linear combinations of unitary operations because of the assumption that is unitary. It leads to the approximated expression of U_r has a quantum duality gate form. The truncated Taylor series index is denoted as⁴⁸

Then, the expression of 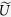can be simplified as

where , and .

According to Eq. (10), is a quantum duality gate and s is the normalization constant.

We give the quantum circuit for realizing the approximation is given in Fig. 3, which is the same as that in ref. 35. The part A of Fig. 3 is the implementation of . The controlled unitary operation U₀ which illustrated in part B corresponds to the linear combination form of the Hamiltonians, . The quantum circuit realizes the evolution in a segment,

Figure 3. Quantum circuit for the BCCKS algorithm in single output duality quantum computing.

In Part A of Fig. 3, |Ψ〉 is the initial state of work qubit and there are K numbers of |0〉 auxiliary controlling qubits and Knumbers of L level |0〉_L auxiliary controlling qudits in the auxiliary system. K numbers of |0〉 auxiliary controlling qubits control the Knumbers of L level |0〉_L auxiliary controlling qudits and the unitary operations U₀ are activated only when the L level |0〉_L auxiliary controlling qudits hold the respective values indicated in circles. Part B of Fig. 3 is to illustrate that each unitary operation U₀ is composed of H₁, H₂, …, H_L−1, H_L. We only “readout” the result with the auxiliary system in state .

The implementation of operation needs an auxiliary system and a work system(target state). The auxiliary system is composed by K auxiliary qubits |0〉^K and K numbers of L level auxiliary qudits |0〉_L, for the implementations of two QWD operations and two QWC operations. We denote the initial state of the whole system as 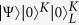, where |Ψ〉 is the work qubit state and 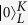means K numbers of L level auxiliary qudits all in state |0〉_L³⁵.

The first QWD can be expressed as a 2^K × 2^K matrix, denoted as V^F. Defining , the elements of the matrix is

where

Similarly, we denote the second QWD operation as V^S, which can be viewed as a L × L matrix. The elements of the matrix satisfy

Corresponding to K auxiliary qubits |0〉^K, K numbers of L level |0〉_L auxiliary controlling qudits should be transformed into K numbers of state by the same QWD operation V^S. They can be denoted as

Applying the two QWD operations V^Fand V^S to the state produces the state of total auxiliary system

where s = ∑_j∈Jβ_j is the normalization constant. We perform the auxiliary system controlled operation U_j on the work system. The state of the whole system is transformed into

Then, we need to perform two QWC operations to combine the wave functions, denoted as W^F = (V^F)^† and W^S = (V^S)^†, respectively. Physically, the two QWC operations are the counterparts of the two QWD operations.

We denote the state orthogonal to as |Φ〉, the total process can be described as:

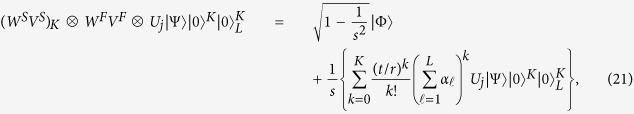where(W^SV^S)_K means K numbers of W^SV^S operations and U_j corresponds to some and j ∈ J.

The results of the duality quantum computing are in the terms with the auxiliary system in state . Therefore, we only need to readout the output of the work system with auxiliary system in state , which corresponds to the single-output duality quantum computing. Namely, the initial state goes through the transformation we interested is

Thus, we obtain

Consequently, we have successfully realized the following process,

If we make measurement directly, the probability of detecting the auxiliary state is P_s, where . Namely the probability of implementing U on the target state |Ψ〉 successfully is P_s. Amplifying the amplitude of the desired term before the measurement by applying the robust obvious amplitude amplification given in Res.⁴⁸ enables us to nearly deterministically implement . The accuracy of approximation of can be quantified by approximation error . Consider the case that all equal to m corresponding Hamiltonian is approximately decomposed into equal-sized parts. To ensure the total error of simulating time evolution under , m should be in the order . The terms of Hamiltonian decomposition are . The number of segments is in the order . According to the Chernoff bound⁴⁷, the query complexity in each segment is

The query complexity for the full simulation algorithm is r times K. Consider all the operations performed on auxiliary system and work system, the total number of gates in the simulation for time t/r in each segment is⁴⁸

where T = (α₁ +  + α_L)t.

In last section, we have realized Kraus operator by the duality quantum gate E_k = L_k = ∑_iW_kiV_i0U_i. In this section, unitary operator U_i is realised by BCCKS algorithm in duality quantum computing form with precision . So, we have successfully simulated the total evolution of an open quantum system,

The complexity of performing U_i with precision is Kr. Consider the fact that the coefficients satisfy ∑_i|W_kiV_i0| ≤ 1, the complexity of performing E_k is as the same as the complexity of performing U_i. The total complexity of the whole algorithm with d numbers of E_k is

Compared with the complexity of Llyod ‘s algorithm O(ld⁴ht²/), the dependence on dimension of principal system is decreased from O(d⁴) to O(d³) and the performance is exponential improved on precision . An example to show the implementation of this simulation algorithm is given in next section.

Application to a single quibit open quantum system

Suppose we have a principal system with single qubit, interacting with a single qubit environment. U is time evolution operator imposed on the total system⁶. The expression of U is

where X represents the usual Pauli matrix acting on the environment, and P₀ = |0〉〈0|, P₁ = |1〉〈1| are projectors acting on system. The initial state of environment is |0〉. In this special case, the number of state k is 2. Equation (1) is simplified to

where E₀ = P₀, E₁ = P₁, and satisfies completeness relation . E₀ and E₁ can be realised by duality quantum gate L₀ = ∑_iW_0iV_i0U_i and L₁ = ∑_iW_1iV_i0U_i respectively. Assume that

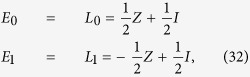where Z is the usual Pauli matrix and U₀ = Z, U₁ = I. So, the QWD operator V and the QWC operator W are chosen as

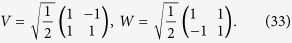Measuring the final wave functions when the qudit is in state |0〉 and |1〉 by placing two detectors as shown by “readout” in Fig. 4. We have realized the trace preserving Kraus operator E_k. Then, regarding U_i as a time evolution operator, it can be realized by BCCKS algorithm in a duality quantum computer. Ignoring the global phase factor, U₀ can be regarded as . Similarly, U₁ can be expressed as . Regarding the evolution time as t = 1, the corresponding Hamiltonian of U₀ and U₁ are H⁰ and H¹. They can be expressed as

Figure 4. Quantum circuit of realisation of Kraus operator in duality quantum computing when d = 2.

|Ψ〉 denotes the initial state of principal system, and environment is in the |0〉 state. The squares represent unitary operations and the circles represent the state of the controlling qubit. Unitary operations U₀, U₁ are activated only when the auxiliary qubit is |0〉 and |1〉 respectively.

After obtaining the expression of U₀ and U₁ and finding the corresponding Hamiltonian, we are able to simulate the Hamiltonian by approximating the truncated Taylor series of the evolution operator in duality quantum computer. The process of realizing U₀ or U₁ has given in the last section.

Discussion

In the present paper, we have briefly described the dynamics of an open quantum system and the quantum operations can be elegantly represented in operator-sum representation. The dynamics in the principal system can be described by trace preserving Kraus operators. The duality quantum computing is a suitable way to realise Kraus operators with non-unitary feature. Duality quantum computer provides the capability to perform linear combinations of unitary operations in the computation, which is called the duality quantum gates or the generalized quantum gates. The duality quantum computer can be perfectly simulated by an ordinary quantum computer with n-qubit and an additional qudit resource. By realizing Kraus operators through duality quantum computing, and approximating Hamiltonian simulation by the truncated Taylor series of the evolution operator in duality quantum computer, we present an efficient quantum algorithm for simulating Hamiltonian in open quantum system. Consider the fact that all quantum system is inevitable coupled with its environment in the real world, our method can be applied in a class of general physical systems. By realizing Kraus operators, the query complexity is decrease from O(d⁴) dimension dependence to O(d³) of the open quantum system. Moreover, through the use of truncated Taylor series in duality computing, our algorithm can provide an exponential improvement in precision.

Additional Information

How to cite this article: Wei, S.-J. et al. Duality quantum algorithm efficiently simulates open quantum systems. Sci. Rep. 6, 30727; doi: 10.1038/srep30727 (2016).