Quantitative, 3D Visualization of the Initiation and Progression of Vertebral Fractures Under Compression and Anterior Flexion

Abstract

The biomechanical mechanisms leading to vertebral fractures are not well understood. Clinical and laboratory evidence suggests that the vertebral endplate plays a key role in failure of the vertebra as a whole, but how this role differs for different types of vertebral loading is not known. Mechanical testing of human thoracic spine segments, in conjunction with time-lapsed micro–computed tomography, enabled quantitative assessment of deformations occurring throughout the entire vertebral body under axial compression combined with anterior flexion (“combined loading”) and under axial compression only (“compression loading”). The resulting deformation maps indicated that endplate deflection was a principal feature of vertebral failure for both loading modes. Specifically, the onset of endplate deflection was temporally coincident with a pronounced drop in the vertebra’s ability to support loads. The location of endplate deflection, and also vertebral strength, were associated with the porosity of the endplate and the microstructure of the underlying trabecular bone. However, the location of endplate deflection and the involvement of the cortex differed between the two types of loading. Under the combined loading, deflection initiated, and remained the largest, at the anterior central endplate or the anterior ring apophysis, depending in part on health of the adjacent intervertebral disc. This deflection was accompanied by outward bulging of the anterior cortex. In contrast, the location of endplate deflection was more varied in compression loading. For both loading types, the earliest progression to a mild fracture according to a quantitative morphometric criterion occurred only after much of the failure process had occurred. The outcomes of this work indicate that for two physiological loading modes, the vertebral endplate and underlying trabecular bone are critically involved in vertebral fracture. These outcomes provide a strong biomechanical rationale for clinical methods, such as algorithm-based qualitative (ABQ) assessment, that diagnose vertebral fracture on the basis of endplate depression.

Introduction

Vertebral fractures represent nearly one-half of the approximately 1.2 million osteoporotic fractures reported in the United States each year.⁽¹⁾ Despite their prevalence and high associated morbidity and mortality,^(2,3) the biomechanical mechanisms leading to vertebral fractures are not well understood. Little is known about the events or activities associated with vertebral fractures,⁽⁴⁾ in large part because only 25% to 30% of vertebral fractures come to clinical attention.^(5,6) This “silent” nature of many vertebral fractures also compounds the difficulty in identifying morphological features of the vertebra that predispose to fracture. Radiographic assessments of fractured vertebrae, whether from clinical evaluation^(7–9) or laboratory tests,^(10–13) can identify fracture patterns a posteriori but are limited in revealing how the failure process initiated and propagated. Visualization of the evolution of the failure process and its relationship to the applied loading and vertebral morphology would provide deeper understanding of the etiology of vertebral fractures, for the benefit of fracture prevention, management and treatment.

How vertebral loading and morphology contribute to the failure processes leading to vertebral fracture is still an open question. Biconcave fractures and wedge fractures are the most common types of clinical vertebral fracture⁽¹⁴⁾ and have been associated with axial compression^(15,16) and a combination of compression and forward bending,^(17–20) respectively. However, because the risk of a particular type of fracture depends on the ability of the vertebra to withstand the particular type of loading, studies have also examined microstructural features of the vertebra, such as endplate thickness and regional variations in density and trabecular microstructure. Trabecular density is lower in the anterior versus posterior regions of the vertebral centrum.⁽²¹⁾ This difference, which increases with degeneration of the adjacent intervertebral disc^(22,23) and with aging,⁽²⁴⁾ is consistent with evidence that the strength of the vertebra is lower in anterior flexion than axial compression.⁽²⁵⁾ Endplate porosity as well as the microstructure of the underlying trabecular bone have been associated with initiation and progression of endplate collapse in lumbar vertebrae loaded in axial compression.⁽²⁶⁾ Evidence also exists that failure of the endplate, and not the anterior cortex, is an early event in vertebral fracture under anterior flexion.^(27,28) Although the results of these studies and others^(10,29,30) implicate the endplate as a key structure in failure of the vertebra as a whole, they also suggest that further work is needed to identify whether and how failure processes in the vertebra differ between compression and flexion loading.

Image-guided failure analysis using micro–computed tomography (μCT) offers a means to identify these failure processes. This method involves acquiring μCT images as the bone is loaded to failure and was initially developed for qualitative visualization of failure processes in specimens of trabecular bone.^(31–33) This method has been extended in two ways: first, by accommodating the entire vertebral body rather than excised specimens of bone tissue⁽³⁴⁾; and second, by using an image-analysis technique, digital volume correlation (DVC), to produce quantitative maps of how the vertebra deforms as a fracture develops.^(34,35)

The overall goal of this study was to define how vertebral fractures initiate and progress under anterior flexion and axial compression. Deformations occurring throughout the entire vertebral body under axial compression and anterior flexion were quantified using time-lapsed μCT and DVC. These quantitative maps of deformation were used to examine the involvement of the endplate and cortex in the initiation of vertebral failure, and to identify associations between the failure processes and vertebral microstructure.

Materials and Methods

Specimen preparation

Segments of the mid-thoracic spine were used because of the high prevalence of fractures in this region.⁽³⁶⁾ Twenty-eight T₇–T₉ spine segments were dissected from fresh-frozen human spines (age: 35 to 91 years, mean ± SD: 71.2 ± 14.2 years; 16 male, 12 female). The anterior and posterior longitudinal ligaments and ligamentum flavum were left intact. The trabecular centrum in the T₇ and T₉ vertebral bodies was partially hollowed out using a dental tool (Komet USA, Rock Hill, SC, USA) and was filled with polymethylmethacrylate (PMMA), leaving intact at least 5 mm of trabecular bone adjacent to the endplate abutting the T₇/T₈ or T₈/T₉ intervertebral discs. The exposed endplates of the T₇ and T₉ vertebral bodies were potted in circular trays filled with PMMA such that the T₈ vertebra would be oriented in the axial direction of the loading device and the T₇ and T₉ vertebrae would be angled according to the natural curvature presented by the spine segment. The posterior elements were not potted, such that during mechanical testing, no loading would be applied to the posterior elements directly by the operator, and yet load transfer across the T₇/T₈ and T₈/T₉ zygapophysial joints would still be permitted (Supporting Information, S1). The posterior ends of the spinous processes were trimmed to accommodate the space constraints of the μCT scanner; as such, the ligaments associated with the spinous processes (interspinous and supraspinous ligaments) were at least partially removed. A quantitative computed tomography (QCT) scan (GE Lightspeed VCT; GE Healthcare, Milwaukee, WI, USA; 0.3125 × 0.3125 × 0.625 mm/voxel) was performed on each segment⁽³⁷⁾ to compute integral (ie, combining both trabecular and cortical compartments of the vertebral body) volumetric bone mineral density (vBMD) (Table 1). The spine segments were kept hydrated at all times and, when not in use, wrapped in saline-soaked gauze, sealed in plastic bags, and stored at −20°C.

Table 1.

Integral Volumetric BMD (in g/cm³) for All 28 Specimens According to Loading Mode, and Also Separated According to Two Different Scoring Systems for Intervertebral Disc Health

	Combined loading (g/cm3) mean ± SD (n)	Compression loading (g/cm3) mean ± SD (n)
All samples	203 ± 45 (14)	207 ± 48 (14)
Thompson score
1	–	–
2	285 (1)	260 (1)
	208 (1)
3	212 ± 32 (8)	198 ± 61 (7)
4	158 ± 52 (3)	204 ± 35 (4)
5	189 (1)	212 (1)
		224 (1)
ALDI score
0	180 ± 51 (6)	194 ± 58 (4)
1	225 ± 40 (4)	197 ± 54 (4)
2	231 ± 16 (4)	222 ± 42 (6)

Values presented are mean ± SD, followed by the number of specimens in parentheses, for any category with three or more specimens. For categories with only two specimens, both values of vBMD are given. For categories with only one specimen, the vBMD of the specimen is given.

ALDI = apparent loss of disc integrity.

Mechanical testing and μCT imaging

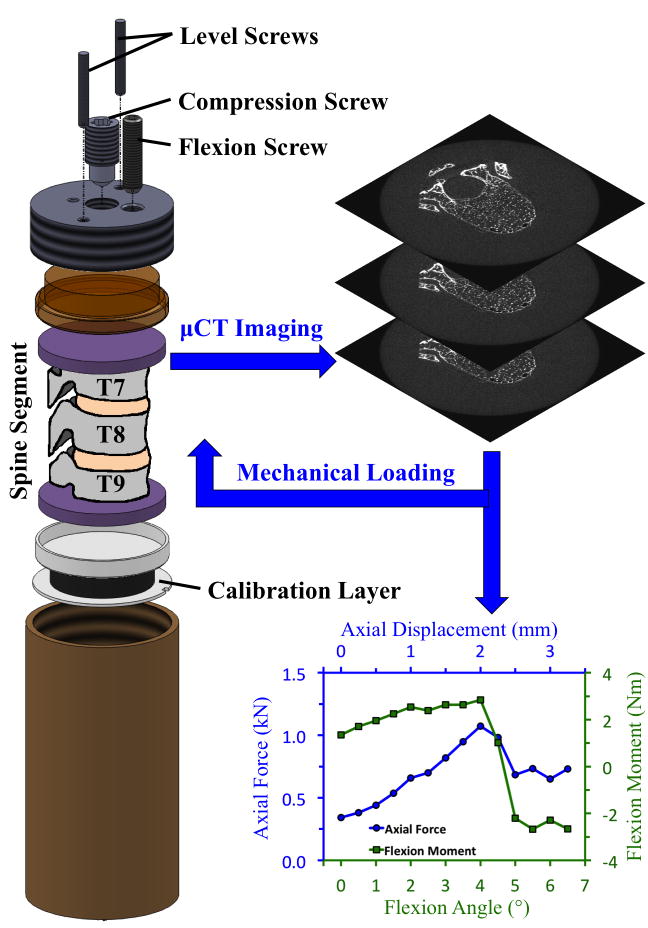
The spine segments were randomly assigned into a set for testing under axial compression (“compression,” n = 14) and a set for testing under axial compression with anterior flexion (“combined loading,” n = 14). At the time of testing, each spine segment was placed in a custom-built, radiolucent device for mechanical testing (Fig. 1) that had been filled with 60% saline and 40% of 50-proof ethanol.⁽³⁴⁾ Ten cycles of preconditioning to ~300 N (compression) or to 0.25 mm and 0.5 degrees (combined loading) were applied, after which the spine segments were imaged with μCT (μCT 80; Scanco Medical, Brüttisellen, Switzerland) at a nominal resolution of 37 μm/voxel. The settings for voltage, current, and integration time were 70 kVp, 114 mA, and 300 ms, respectively. The specimen was then loaded in a stepwise manner (0.5 mm per increment for compression; 0.25 mm and 0.5 degrees per increment for combined loading).^(26,34) The compression screw and flexion screw applied the axial compression and angle, respectively, of each loading increment, while the level screws ensured that the angle was only applied in the sagittal plane. For combined loading, the compression and flexion screws were turned in succession: the compression screw was turned to impose 0.125 mm, then the flexion screw was turned to impose 0.25 degrees, and then this process was repeated to achieve the full 0.25 mm of compression and 0.5 degrees for the loading increment. For both loading modes, after a 20-min relaxation period, the loaded specimen underwent another μCT scan with the same scan settings.

Fig. 1.

Schematic of radiolucent device for mechanical testing of spine segments under combined loading: The compression screw and flexion screw applied the axial compression and anterior flexion, respectively, at each loading step. The level screws ensured that the flexion angle was only applied in the sagittal plane. For compression loading, the flexion screw was not used, and the calibration layer was replaced with a load cell to measure the axial force. Details on the use of the calibration layer to measure the axial force and flexion moment during the combined-loading tests are provided in the Supporting Information (S2).

For the compression tests, the axial load was recorded for each load increment using a 22-kN load cell (LLB450; Futek Advanced Sensor Technology, Irvine, CA, USA) near the bottom of the mechanical testing device. For the combined loading, the axial force and flexion moment experienced by the spine segment were obtained for each load increment using a polyurethane “calibration layer” that functioned as a low-profile multiaxial load cell (Supporting Information, S2). Anteriorly and posteriorly directed moments were denoted as positive and negative, respectively.

The stepwise loading plus μCT continued until deformation of the T₈ vertebral body was visible in the lateral scout views. Subsequent examination of the force-displacement curves and moment-angle curves confirmed that the onset of visible deformation in the lateral scout view occurred one or more loading increments after a pronounced drop in the flexion moment (combined loading) or axial force (compression loading) occurred. Visible deformation in the scout view was used as the minimum criterion for stopping the loading sequence, because the values of flexion moment and axial force in the combined-loading tests were not available until after the test was complete (Supporting Information, S2). The loading increment at the “peak of loading” was defined as the loading increment immediately before the drop in flexion moment or axial force. The values of flexion moment and compressive axial force (combined loading) or compressive axial force alone (compression loading) at this increment were used as the measures of vertebral strength. After failure, the specimen was unloaded completely and imaged with μCT to quantify any post-loading recovery.

Clinical classification of vertebral fracture

A quantitative morphometric (QM) technique⁽³⁸⁾ was used to assess whether the T₈ vertebra had reached the minimum standard (grade 1) for a clinical vertebral fracture at a given load increment. The posterior, central, and anterior heights of T₈ were measured from the lateral scout view at each loading increment. Wedge and biconcave fractures were defined as a difference in posterior height to anterior and central height, respectively, of at least 20%.^(38,39) Crush fractures were defined as a difference in posterior height of at least 20% between the initial and current increment. Vertebrae that had not yet met the minimum standard for grade 1 were classified as grade 0.

Quantitative deformation maps via DVC

The methods for using DVC with time-lapsed μCT images of human vertebrae to quantify deformations throughout the entire vertebral body have been reported.⁽³⁴⁾ Briefly, image registration (IPL; Scanco Medical) was used to align the series of images of the T₈ vertebral body, and then the T₈ vertebral body was virtually subdivided into hexahedral regions with ~1.9-mm side lengths (Supporting Information, S3). The displacement of each corner of each region was estimated at a given loading increment using a custom optimization approach.^(40,41) The size of the regions (1.9 mm) was selected as the smallest size that still produced acceptably low errors in the deformation maps (mean ± SD of the displacement and strain errors = 0.021 ± 0.055 mm and 740 ± 630 microstrain, determined according to published methods⁽³⁴⁾). Larger sizes correspond to lower spatial resolution in the deformation maps and poorer ability to detect large localized displacements. Up until the peak of loading, the displacements obtained from the previous increment were used as the initial guess for the displacement field at the current increment. However, following the peak of loading, the change in displacement from one increment to the next increased substantially, particularly near either the superior or inferior endplate. Thus, the initial guess for the DVC algorithm at the increment just following the peak of loading was refined by incorporating measurement of the endplate deflection (described in “Endplate deflection, endplate volume fraction, and trabecular microstructure”) made at that increment. For subsequent increments, the change in displacement was too large to achieve convergence in the DVC analyses; these increments were not analyzed to produce deformation maps and instead were only used for QM analysis.

Endplate deflection, endplate volume fraction, and trabecular microstructure

Endplate deflection, defined as the axial displacement of each point along the surface of the calcified endplate, was quantified according to published methods.⁽²⁶⁾ These displacements were used as input into the DVC analyses as described in “Quantitative deformation maps via DVC” and, based on prior observations of the link between endplate deflection and vertebral fracture in the lumbar spine,⁽²⁶⁾ to probe further the behavior of the endplate specifically in vertebral failure. For the latter purpose, the endplate deflection was tracked over the series of loading increments. The endplate volume fraction (Ep.BV/TV) was quantified in 5-mm × 5-mm × 2-mm regions across the endplate, and the microstructure of the underlying trabecular bone (bone volume fraction [BV/TV], apparent density [ρ_app], trabecular separation [Tb.Sp*], trabecular number [Tb.N*], structure model index [SMI], degree of anisotropy [DA], and connectivity density [ConnD]) was quantified in 5-mm × 5-mm × 5-mm regions immediately adjacent to the endplate (Supporting Information, S4).⁽²⁶⁾ Measurement of Ep. BV/TV was used in lieu of measuring endplate thickness, because the ambiguity in the exact location of the boundary between endplate and trabecular bone (particularly, but not only, in vertebrae with double endplates, endplate sclerosis, or endplate defects^(30,42)) made regional measurements of endplate thickness less repeatable and standardized.^(30,43) Repeated-measures analyses of variance (ANOVA) were used to test for associations between these morphological parameters and endplate deflection (JMP 9.0; SAS Institute, Inc., Cary, NC, USA). Linear regression analyses were carried out to test for dependence of vertebral strength (compressive force or flexion moment at the peak of loading) on Ep.BV/TV averaged over all 5-mm × 5-mm × 2-mm regions, and on trabecular BV/TV averaged over all 5-mm × 5-mm × 5-mm regions. These regressions were also carried out with integral vBMD as a second independent variable to examine the dependence of vertebral strength on Ep.BV/TV or sub-endplate BV/TV after adjustment for vBMD of the entire vertebra. A significance level of 0.05 was used for all statistical analyses.

Assessment of intervertebral disc degeneration

Degeneration of the intervertebral discs adjacent to the T₈ vertebra was assessed by two ordinal grading systems (Table 1): apparent loss of disc integrity (ALDI)⁽⁴⁴⁾ grading as determined from the QCT images; and Thompson⁽⁴⁵⁾ grading as determined from gross examination of mid-sagittal sections cut after completion of mechanical testing. The ALDI grade, which ranges from 0 (healthy) to 2 (degenerated), is based primarily on the clarity of the demarcation between nucleus pulposus and annulus fibrosus in the mid-transverse QCT image and secondarily on the presence of osteophytes. Each disc was graded by two observers for each scoring system. Standard ANOVAs were carried out to test for associations between vertebral strength and Thompson grade, and between vertebral strength and ALDI grade. Pearson chi square analysis was carried out to test for associations between the location of the maximum endplate deflection at the peak of loading (central endplate or ring apophysis) and the Thompson (or ALDI) grade.

Results

Endplate deflection was a principal feature of vertebral failure in both loading modes. Although the DVC analyses detected deformation in multiple locations across the endplate, at the cortex, and also within the trabecular centrum as the peak of loading neared, the deformation was most concentrated at a single location at the endplate, and this deformation largely consisted of deflection in the axial direction (Fig. 2). Further, a sudden increase in deflection at this location always coincided with a drop in the anterior flexion moment (combined loading; Fig. 2i, Table 2) or axial force (compression loading; Fig. 2ii, Table 3). For combined loading, the axial force simultaneously decreased in six of the 14 specimens (Fig. 3). The average (±standard deviation) maximum endplate deflection under combined loading was 0.38 (±0.25) mm prior to the drop in moment and/or force and then increased 0.98 mm on average (Table 2, Fig. 4). The corresponding values for compression loading were 0.46 ± 0.26 mm and 1.04 mm (Table 3, Fig. 5). The superior endplate was the site of endplate deflection in all specimens subjected to combined loading and in ten specimens subjected to compression loading. The remaining four specimens exhibited large axial deflection of the inferior endplate. In all specimens, the opposite endplate experienced minimal deflection (<0.20 mm). Following the drop in moment and/or force, collapse of the endplate propagated outward in the transverse plane and inward into the centrum in both loading modes; however, deformations within the vertebra remained restricted to the superior or inferior half of the vertebral body, depending on which endplate had collapsed. No disc herniation was observed at any point during the loading sequence.

Fig. 2.

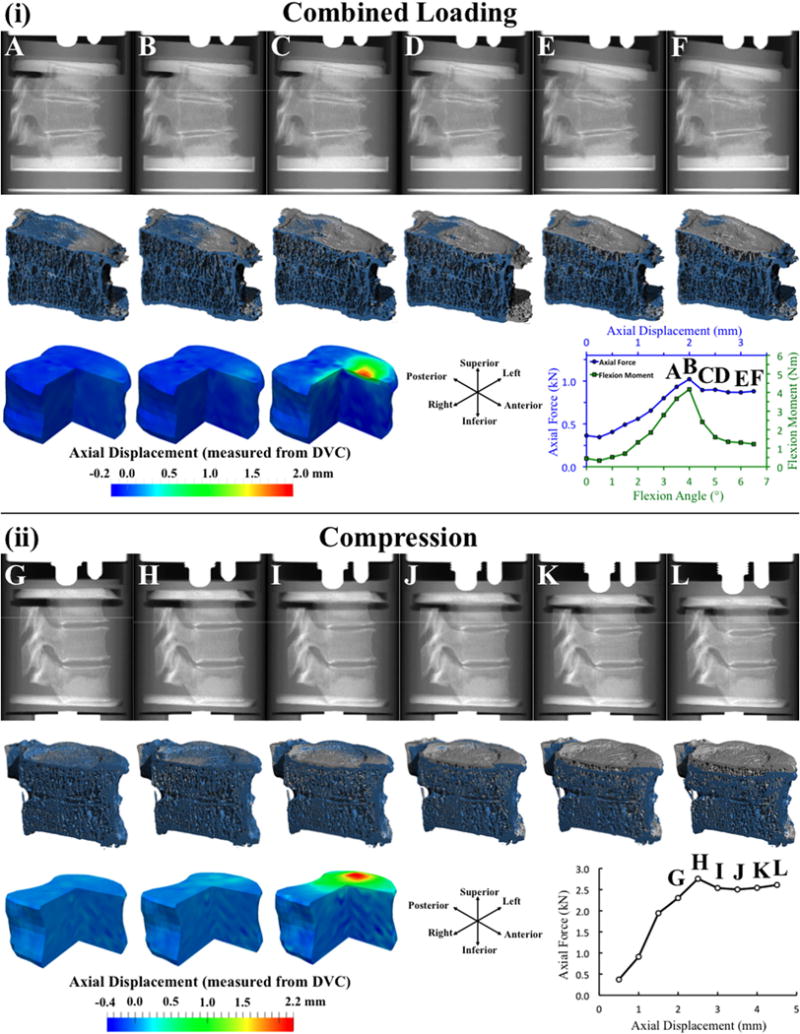
(i) For combined loading: (top row) Lateral radiographic views (created from the μCT scans) at six consecutive loading increments labeled with letters A–F on the force-displacement curve at the bottom right; (middle row) 3D rendering of a sagittal half-section of the T₈ vertebral body at the current load increment (blue; the increment corresponds to the lateral radiographic view above) registered against the rendering prior to loading (gray); (bottom row) For increments A–C, three-quarter section views of the displacement map showing displacement in the axial direction (positive values indicate downward displacement); (ii) Same presentation as in (i), but for compression loading. The force-displacement curves in (i) and (ii), and the moment-angle curve in (i) depict the values of axial force, flexion moment, axial displacement and angular displacement applied to the entire T₇–T₉ spine segment, as opposed to those applied or experienced only in T₈. The specimens shown in (i) and (ii) are each representative for the loading mode.

Table 2.

Force, Moment, and Displacement Data for the Combined-Loading Specimens

	Unit of measure	Mean ± SD	Minimum	Maximum
Compressive force and anterior flexion moment
Compressive axial force at peak of loading	kN	1.22 ± 0.56	0.22	2.32
Moment at peak of loading	Nm	6.77 ± 7.13	0.50	28.81
Drop in force immediately after peak of loading	kN	0.11 ± 0.17	−0.03	0.58
	%	11.0 ± 17.4	−3.0	58.3
Drop in force at the onset of grade 1 fracture (n = 11a)	kN	0.04 ± 0.26	−0.43	0.34
	%	12.2 ± 34.3	−34.1	89.3
Drop in moment immediately after peak of loading	Nm	1.78 ± 0.71	0.39	2.75
	%	47.1 ± 33.4	5.2	255.0
Drop in moment at the onset of grade 1 fracture (n = 11a)	Nm	3.42 ± 1.62	1.86	7.48
	%	71.5 ± 33.3	30.5	122.7
Endplate deflection
Maximum deflection at peak of loading	mm	0.38 ± 0.25	0.19	1.00
	%	1.9 ± 1.3	0.9	5.5
Maximum deflection immediately after peak of loading	mm	1.36 ± 0.66	0.37	2.78
	%	6.9 ± 3.5	1.8	15.2
Increase in deflection	mm	0.98 ± 0.50	0.15	1.78
	%	5.0 ± 2.6	0.7	9.8
Anterior displacement
Maximum anterior displacement at peak of loading	mm	0.063 ± 0.062	0.001	0.204
	%	15.8 ± 12.7	0.5	47.3
Maximum anterior displacement immediately after peak of loading	mm	0.256 ± 0.131	0.075	0.565
	%	19.9 ± 7.2	10.3	33.2
Increase in anterior displacement	mm	0.192 ± 0.134	0.045	0.548
	%	22.9 ± 12.9	4.6	40.0

Values presented are mean ± standard deviation (SD), minimum, and maximum (n = 14 except where noted). Compressive force and flexion moment at the peak of loading, and the drop in force (in kN and as a percentage of the ultimate force) and moment (in Nm and as a percentage of the ultimate moment) immediately after the peak of loading. Maximum endplate deflection measured at and immediately after the peak of loading, and the increase in deflection between these two load increments (in mm and as a percentage of the height of the vertebral body). Maximum outward displacement in the anterior cortex measured at and immediately after the peak of loading, and the increase between these two load increments (in mm and as a percentage of the maximum endplate deflection for the same specimen at the same increment).

^aThree specimens remained at grade 0.

Table 3.

Force and Endplate Deflection for the Compression Specimens

	Unit of measure	Mean ± SD	Minimum	Maximum
Compressive force
Compressive axial force at peak of loading	kN	2.37 ± 0.94	0.76	3.88
Drop in force immediately after peak of loading	kN	0.16 ± 0.15	0.02	0.57
	%	6.8 ± 6.6	1.3	21.8
Drop in force at the onset of grade 1 fracture (n = 9)a	kN	0.28 ± 0.22	0.05	0.57
	%	12.3 ± 8.4	2.1	26.5
Endplate deflection
Maximum deflection at peak of loading	mm	0.46 ± 0.26	0.11	1.04
	%	2.4 ± 1.3	0.6	5.0
Maximum deflection immediately after peak of loading	mm	1.49 ± 0.54	0.56	2.78
	%	7.7 ± 2.8	2.8	14.4
Increase in deflection	mm	1.04 ± 0.53	0.26	2.22
	%	5.4 ± 2.8	1.3	11.5

Values presented are mean ± SD, minimum, and maximum (n = 14 except where noted). Experimentally measured ultimate force and the drop in force occurring immediately after the ultimate point (in kN and as a percentage of the ultimate force). Maximum endplate deflection measured before and immediately after the drop in force, and the increase in deflection between these two load increments (in mm and as a percentage of the height of the vertebral body).

^aFive specimens remained at grade 0.

Fig. 3.

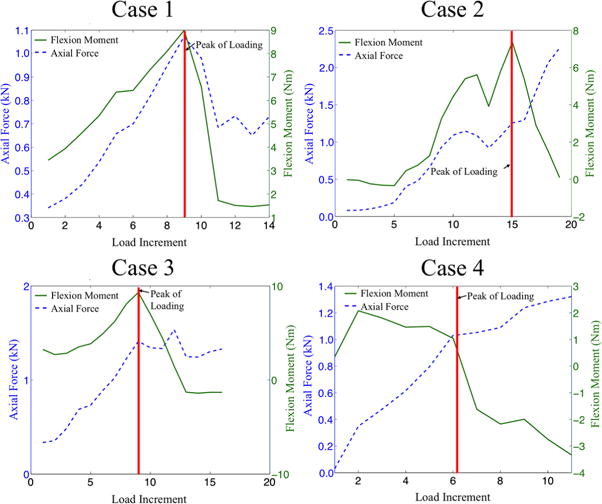
Four cases, or categories, of force-displacement (blue dashed line) and moment-angle (solid green line) curves were observed among the 14 combined-loading specimens: (1) six specimens exhibited the maximum anterior flexion moment and maximum axial force at the peak of loading (defined as the load increment immediately before the onset of visible deformation in the T₈ vertebra, and denoted by the vertical red line); (2) two specimens exhibited the maximum anterior flexion moment but not the maximum axial force at the peak of loading and also exhibited an increase in axial force immediately after the peak of loading; (3) two specimens exhibited the maximum anterior flexion moment but not the maximum axial force at the peak of loading and then exhibited a decrease in moment but not a marked decrease in force immediately after the peak of loading; and (4) four specimens exhibited neither the maximum flexion moment nor the maximum axial force at the peak of loading and then exhibited a decrease in moment but an increase in the axial force immediately after the peak of loading.

Fig. 4.

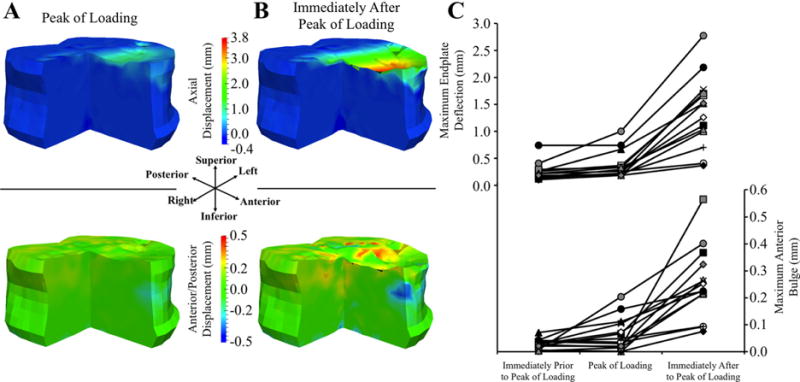
(A, B) Three-quarter section views of displacement maps showing DVC-measured displacement in the axial (top row) and anterior/posterior (bottom row) directions at and immediately after the peak of loading for a representative, combined-loading specimen: positive values in the axial direction indicate downward displacement and negative values in the anterior/posterior direction indicate anterior displacement. (C) Maximum endplate deflection and maximum anterior bulge (defined as the absolute value of the anterior displacement) prior to, at, and after the peak of loading for all combined-loading specimens: each specimen has a unique marker. Endplate deflection and anterior bulge were correlated with each other (R = 0.620; p = 0.018; Supporting Information, S5).

Fig. 5.

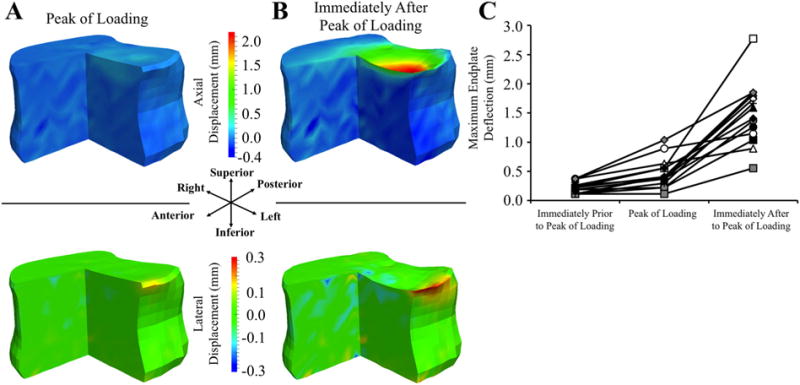
(A, B) Three-quarter section views of displacement maps showing DVC-measured displacement in the in axial (top row) and lateral (bottom row) directions at and immediately after the peak of loading for a representative specimen loaded under axial compression: Positive values in the axial direction indicate downward displacement and positive values in the lateral direction indicate displacement towards the left. (C) Maximum deflection in the superior endplate prior to, at, and after the ultimate point for all specimens loaded under axial compression; each specimen has a unique marker.

Much of the failure process occurred prior to meeting the QM definition of a clinical vertebral fracture. In both loading modes, the earliest progression from no (grade 0) to mild (grade 1) fracture occurred one load increment after the peak of loading. By the last increment for which data were available for all specimens (fourth and third increments following the peak of loading for combined loading and compression, respectively), three combined-loading specimens and five compression specimens remained grade 0, and the others were grade 1. The distribution of type of these grade 1 fractures by loading mode (combined-loading/compression) were as follows: wedge only (4/0), biconcave only (2/6), wedge and biconcave (5/3), and crush (0/0). At the onset of grade 1 fracture in combined loading, the flexion moment and compressive force had decreased 71.5% ± 33.3% (mean ± SD) and 12.2% ± 34.3%, respectively, compared to their peak values (Table 2). For compression loading, this decrease was 12.3% ± 8.4% (Table 3).

Despite the role of the endplates in the failure process in all specimens, the location of endplate deflection, the involvement of the cortex, and the association between endplate deflection and disc health differed between loading modes. For combined loading, deflection initiated, and remained the largest, at either the anterior central endplate (n = 8) or the anterior ring apophysis (n = 6), whereas the location across the endplate was more varied among the compression specimens (Fig. 6). For combined loading, the anterior cortex bulged anteriorly upon or just after the peak of loading (Fig. 4, Table 2). For compression loading, when outward bulging of the cortex occurred, the location was instead in the cortical rim, just inferior to the ring apophysis (Fig. 5). In compression specimens that featured deformation observed only in the central endplate, no bulge was observed in the cortex. The location of the site of maximum, initial endplate deflection (Fig. 6) was associated with ALDI grade in the combined-loading specimens (p = 0.007): failure at the anterior ring apophysis was predominant (6 out of 6 specimens) for ALDI grade of 1 (moderate degeneration), whereas failure at the central endplate was predominant (4 out of 4 specimens) for ALDI grade of 0 (mild degeneration). For ALDI grade of 2, two specimens failed in the ring apophysis and the remaining two failed in the central endplate. No association was found between failure location and Thompson grade for combined loading (p = 0.193) or between failure location and either disc grading system for compression loading (p > 0.553).

Fig. 6.

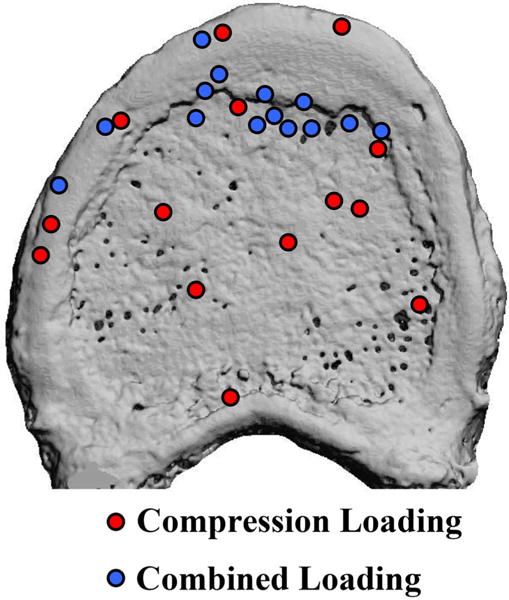
Location of the site of maximum, initial endplate deflection for spine segments experiencing compression loading (red circles) and combined loading (blue circles).

Endplate deflection was correlated with endplate volume fraction and many microstructural properties of the underlying trabecular bone, for both compression and combined loading. Endplate deflection was higher in regions with high Tb.Sp*, SMI, and DA (p < 0.025) and lower in regions with high ρ_app, BV/TV, Tb.N*, and ConnD (Fig. 7; p < 0.001), though substantial variations were observed among specimens. For compression loading, the associations with microstructure differed among load increments (p < 0.001) in that the associations with ρ_app, and BV/TV tended to strengthen as loading progressed. Under combined loading, endplate deflection was lower in regions with high Ep.BV/TV (p < 0.001), and this association weakened as loading progressed (p < 0.001). Under compression loading, endplate deflection was lower in regions with high Ep.BV/TV at the increment immediately after the peak of loading (p < 0.001) but not at any subsequent increments (p > 0.160).

Fig. 7.

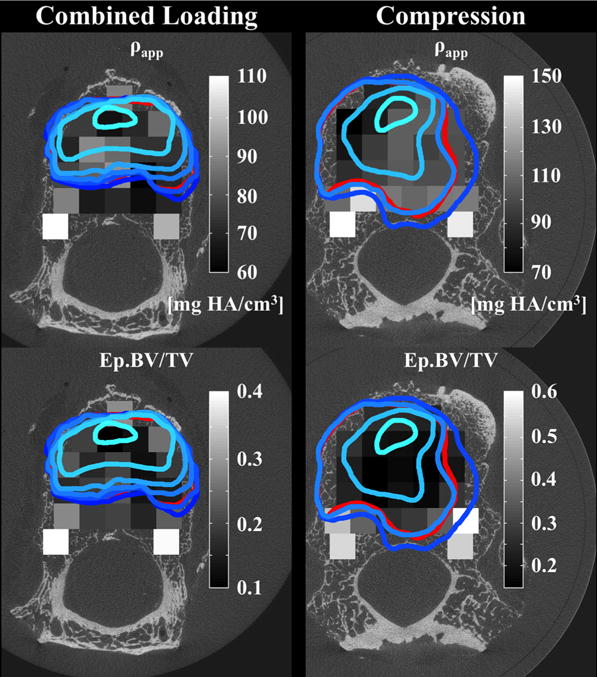
Regions of large endplate deflection (outlined in blue and red), defined as axial deflection exceeding 0.5 mm, superimposed on the distribution of apparent density (ρ_app, grayscale) of the underlying trabecular bone and on the distribution of endplate volume fraction (Ep.BV/TV, grayscale): The lightest blue outline corresponds to the loading increment just prior to or at the peak of loading. The boundaries at subsequent increments are represented with progressively darker shades of blue. The red outline corresponds to the endplate deflection remaining after the test was complete and all applied loads were removed.

Measures of vertebral strength were associated with average endplate volume fraction and the average volume fraction of the underlying trabecular bone. For combined loading, the compressive force at the peak of loading was associated with the average endplate volume fraction before (p = 0.001) and after (p = 0.024) adjustment for integral vBMD. This measure of strength was also associated with the average volume fraction of the underlying trabecular bone (p = 0.004) though this association weakened after adjustment for integral vBMD (p = 0.084). The flexion moment at the peak of loading was not associated with either the average endplate volume fraction or the average volume fraction of the underlying trabecular bone (p > 0.648). For compression loading, the magnitude of the force at the peak of loading was associated with the average volume fraction of the underlying trabecular bone (p = 0.008) even after adjustment for integral vBMD (p = 0.016). A trend toward an association between compressive strength and average endplate volume fraction was found before (p = 0.062) but not after adjustment for integral vBMD (p = 0.155). Measures of vertebral strength were not associated with either measure of disc health (p > 0.130).

Discussion

In light of the high prevalence and poorly defined pathogenesis of vertebral fractures, the goal of this study was to define mechanisms of vertebral fracture under two physiologically relevant loading modes: axial compression, and axial compression combined with anterior flexion. We found that endplate deflection and subsequent collapse was a hallmark of vertebral failure in both loading modes. Although deformation occurred in several regions of the vertebra as the peak of loading drew near, deformations were most concentrated, and increased most rapidly, at or very near the endplate as loading continued. A marked increase in deflection coincided with a sudden loss in the ability of the vertebra to support forward flexion and/or axial compression. Endplate deflection subsequently spread outward in the transverse plane, and the locations of both the site of initial depression and the sites to which the depression spread were associated with the microarchitecture of the immediately underlying trabecular bone and the volume fraction of the endplate. As such, the results of this study indicate that for the two loading modes investigated, the vertebral endplate and adjacent trabecular bone are critically and mechanistically involved in mechanical failure of the vertebra.

An important aspect of this study was that the time-lapsed assessments of deformation were paired with measurement of force and flexion moment sustained by the vertebra at each loading increment. Most prior studies noting endplate deflection^{(10,12,27,28,46,47)} have not synchronized measurements of deflection and applied loads. However, it was this synchronization in the present study that revealed that the onset of endplate deflection signals the point during the failure process at which the vertebra suffers a pronounced decrease in load-carrying capacity. This temporal coincidence indicates that endplate deflection is not merely one feature of vertebral fracture; rather, it is the principal feature from a mechanistic standpoint. This finding together with a similar result from a study on lumbar vertebrae tested in axial compression⁽²⁶⁾ suggests that endplate deflection is a principal biomechanical failure mechanism that spans multiple spine levels and types of loading.

Additional similarities were observed between the two loading modes. Endplate deflection was commonly observed at the central endplate (ie, the region of the endplate bounded by the ring apophysis; Fig. 6), the superior endplate was much more often affected than the inferior endplate, and the progression of failure involved appreciable deformation in only the half of the vertebral body exhibiting endplate collapse. These similarities are consistent with prior evidence that fractures occur more often in the superior versus inferior endplate⁽⁴⁸⁾ and that the former is thinner and is supported by less robust trabecular bone.⁽³⁰⁾ The role of the central endplate in vertebral failure due to anterior flexion has been controversial, in part because the majority of prior studies of endplate deflection have used only compressive loading. Although some prior investigations using experiment or simulation indicate that failure of the central endplate also occurs in the presence of anterior flexion, there is disagreement over the relative contributions of the central endplate versus anterior regions of the centrum and cortex.⁽²⁷⁾ The present data from the combined-loading tests demonstrated that both endplate deflection and deformation of the anterior cortex occurred, and that biconcave fractures (as opposed to wedge fractures) did occur in some combined-loading specimens. Taken together, this evidence strongly indicates that depression of the central endplate is a common feature of vertebral fracture even in the presence of forward flexion.

Nevertheless, some failure processes did differ between the two loading modes. For example, in contrast to compressive loading, endplate deflection under combined loading was more consistently located in the anterior half of the endplate, and the deformations involved the anterior cortex as opposed to the cortical rim. Although prior studies that have examined fracture patterns following the completion of loading^(30,49) or in prevalent vertebral fractures⁽⁵⁰⁾ have noted damage to the anterior cortex and/or cortical rim, the present data show that this damage occurs early in the failure process. Under combined loading, the mechanical indicator that failure had occurred was a drop in the flexion moment that was not always accompanied by a drop in compressive force, even though a marked increase in endplate deflection and anterior bulging had occurred. In contrast, the marked increase in endplate deflection under compressive loading was always coincident with a drop in axial force. This contrast implies that some vertebrae can continue to support appreciable compressive force even after their ability to support anterior flexion is compromised. This result in turn underscores how the risk of fracture, or worsening of fracture, can depend on the type of vertebral loading.

This study has several limitations. First, the temporal resolution of the deformation maps was coarse, providing only 15 load increments on average, and as few as three increments after the peak of loading. The number of increments was limited because of long scan times and the perishable tissue. Ancillary experiments of five L₃ vertebrae scanned repeatedly over 72 hours showed no change in attenuation of the bone tissue (p > 0.08), although marrow attenuation decreased 27% on average over 72 hours in four of the specimens (p < 0.01). Thus, the current protocol is sufficient for quantifying bone parameters over several days, but the prospect of increasing the duration must be evaluated with caution. For this reason, dual-energy X-ray absorptiometry (DXA) scans were not included as part of the experimental design, and thus the donors could not be classified as osteoporotic, osteopenic, or normal. With the present temporal resolution, we can conclude that endplate deflection and anterior bulging of the cortex occurred in close sequence to one another, but not that they occurred simultaneously. Second, failure mechanisms may differ between the stepwise, quasi-static loading used in this study and the dynamic loading conditions that often occur in vivo.⁽⁴⁷⁾ Sustained loading exudates fluid from the intervertebral disc, shifting a greater fraction of the load to the periphery of the endplate.⁽⁵¹⁾ However, static or “creep” loading of the vertebra has been hypothesized as a mechanism of vertebral fractures.⁽⁵²⁾ Moreover, the ultimate forces recorded in this study agree with values obtained from continuous loading of mid-thoracic segments,⁽⁵³⁾ and good correlations exists between the mechanical properties of trabecular bone under continuous versus stepwise loading.⁽³²⁾ Third, failure mechanisms are also likely to differ between the vertebrae from the elderly cohort used in this study and those from younger individuals, due to age-related changes in vertebral density and structure as well as disc properties.^(29,54,55) Fourth, in order to focus the study on failure in T₈, T₇, and T₉ were bolstered by partially filling them with PMMA, and no loading was applied directly to the T₇ and T₉ posterior elements so as to reduce the possibility of failure occurring in the T₇ superior articular process or T₉ inferior articular process. As determined by visual assessment, failure did occur in or adjacent to the inferior endplate of T₇ in five combined-loading specimens; however, perhaps due to the PMMA infill, no significant drop in flexion moment occurred until a marked increase in endplate deflection happened in T₈.

In spite of these limitations, the results of this study highlight the interplay among endplate, supporting trabecular bone, and adjacent intervertebral disc. In combined loading, depression of the central endplate versus anterior ring apophysis occurred more often when the adjacent disc was only mildly degenerated versus moderately degenerated. With disc degeneration, depressurization of the nucleus pulposus occurs, and high anterior “stress” peaks in the annulus develop under anterior flexion.^(56,57)

These changes would lead to larger amounts of force transferred to the anterior ring apophysis as compared to the central endplate, and hence a greater propensity for failure to occur in the former region. Although this association between failure location and disc health was found only for the ALDI grade, it is possible that the Thompson grades are less reliable when the gross examination of the discs is performed after a long sequence of mechanical testing. The ALDI scoring was performed on the QCT images acquired before the testing sequence commenced. The failure location was also associated with the volume fraction of the endplate and neighboring trabecular bone, as was the compressive force at the peak of loading in both loading modes. Importantly, the association between this measure of vertebral strength and the volume fraction of either the endplate or neighboring trabecular bone persisted after adjustment for integral vBMD. These findings are consistent with high-resolution finite element analyses that predict vertebral failure to initiate in the endplate and underlying trabeculae.^(27,29,58) Moreover, age-related losses in volume fraction have been found to be greater in the regions of the centrum adjacent to the endplates as compared to in the middle of the centrum.^(59,60) Taken together, these data suggest that, in the elderly spine, disc degeneration and regional changes in bone density can influence how easily the vertebra fails and the locations of failure.

The results of this study also have bearing on radiological definition of vertebral fracture. A loss of load-carrying capacity was observed in all specimens prior to meeting the minimum standard for any type of QM-based, grade 1 fracture. Further, the average loss in strength sustained upon onset of a grade 1 deformity was moderate (12.3%) in compression and very large (71.5%) in flexion. The present data did not identify any cases in which incident fracture was diagnosed based on QM assessment and yet no mechanical failure had occurred. However, due to natural variations in vertebra shape,⁽⁷⁾ such cases may exist in the population, particularly when assessing prevalent fracture. In comparison, the algorithm-based qualitative (ABQ) criterion for diagnosing osteoporotic vertebral fracture is based on detection of endplate depression.⁽⁸⁾ Our results indicate that endplate depression arises from non-recoverable endplate deflection, and that this deflection occurs when the load-carrying capacity of the vertebra is lost. Thus, our results suggest that the ABQ criterion classifies a structural feature (endplate depression) that is strongly indicative of vertebral fracture (loss of strength). As such, these results provide strong biomechanical rationale for the ABQ method of assessing vertebral fracture.