Comparison of Eight Equations That Predict Percent Body Fat Using Skinfolds in American Youth

Abstract

Background: Skinfolds are often used in equations to predict percent body fat (PBF) in youth. Although there are numerous such equations published, there is limited information to help researchers determine which equation to use for their sample.

Methods: Using data from the 1999–2006 National Health and Nutrition Examination Surveys (NHANES), we compared eight published equations for prediction of PBF. These published equations all included triceps and/or subscapular skinfold measurements. We examined the PBF equations in a nationally representative sample of American youth that was matched by age, sex, and race/ethnicity to the original equation development population and a full sample of 8- to 18-year-olds. We compared the equation-predicted PBF to the dual-emission X-ray absorptiometry (DXA)-measured PBF. The adjusted R², root mean square error (RMSE), and mean signed difference (MSD) were compared. The MSDs were used to examine accuracy and differential bias by age, sex, and race/ethnicity.

Results: When applied to the full range of 8- 18-year-old youth, the R² values ranged from 0.495 to 0.738. The MSD between predicted and DXA-measured PBF indicated high average accuracy (MSD between −1.0 and 1.0) for only three equations (Bray subscapular equation and Dezenberg equations [with and without race/ethnicity]). The majority of the equations showed differential bias by sex, race/ethnicity, weight status, or age.

Conclusions: These findings indicate that investigators should use caution in the selection of an equation to predict PBF in youth given that results may vary systematically in important subgroups.

Introduction

Percent body fat (PBF) can be accurately assessed by methods such as dual-emission X-ray absorptiometry (DXA)^1,2; however, DXA is not feasible in many field settings and can be more difficult to conduct in youth than adults because of the protocols that must be followed by participants. As an alternative, investigators have used demographic and anthropometric measures in prediction equations to estimate PBF. The variables included in prediction equations for youth vary, but it has been shown that skinfolds are feasible to measure in youth^3,4 and that equations that include skinfolds perform better than equations without skinfolds.^5–9

The majority of equations that predict PBF in youth were developed in small or moderately sized samples (n < 400) that lacked wide diversity in age, BMI, and race/ethnicity. Given that these factors influence patterns of growth, it is important to use a prediction equation that has been shown to be valid in populations similar to the group under study. The National Health and Nutrition Examination Survey (NHANES) provides a unique opportunity to explore the generalizability of published equations that predict PBF using skinfold measurements. During the 1999–2006 surveys, both anthropometric and DXA measurements were collected in a diverse, nationally representative sample of American youth. The aim of this study was to use the NHANES data to compare the accuracy and precision of published equations for the prediction of PBF in youth and examine bias by sex, race/ethnicity, BMI status, and age. We restricted our analyses to eight equations that included skinfold measurements. Our goal is to help researchers evaluate the validity and generalizability of available equations and aid in selection of an appropriate equation for use in their study sample.

Methods

Equation Selection

Published equations that predict PBF using skinfold measurements in youth were identified by searching PubMed, Google Scholar, and Web of Science for the terms “Percent Body Fat” and “Prediction Equation.” We limited our analysis to: (1) child (6–12 years) or adolescent (13–18 years); (2) equations that predicted PBF; (3) were published between 1985 and 2014; (4) developed for an American population; and (5) contained anthropometric measurements that were available in NHANES. Included studies had to include participants between the ages of 8 and 18, but could also have younger (<8) or older (>18) participants. NHANES only collected triceps and subscapaular skinfold measurements; therefore, equations that required skinfolds from other regions were excluded.

Five publications met our inclusion criteria^10–14 with one publication¹⁰ providing three equations and another publication¹¹ providing two equations for a total of 8 equations (Table 1). Slaughter and colleagues¹⁴ presented a set of equations for nine subgroups that we classified as a single, albeit complex, equation because all nine subgroup equations included both triceps and subscapular skinfolds, with only the coefficient and constants changing by subgroup. DXA was used as the criterion measure for all published equations examined except the Slaughter equations.

Table 1.

Selected Equations to Predict Percent Body Fat Using Triceps and/or Subscapular Skinfold Measurements and Demographics of the Population with Which Equations Were Originally Developed

	Study populationa
First author, year	N	Age range (years)	Sex	Race/ethnicity	Published prediction equationsb
Bray, 20018	129	10–12	Boys and girls	White and African American	= 13.26 + (1.17 * subscapular)
					= 6.77 + (1.26 * triceps)
					= 8.15 + (0.73 * subscapular) + (0.38 * triceps)
Dezenberg, 19999,c	202	4–10	Boys and girls	White and African American	= (0.342 * weight) + (0.256 * triceps) + (0.837 * sex) − 7.388
					Where male = 1, female = 2
					= (0.332 * weight) + (0.263 * triceps) + (0.760 * sex) + (0.704 * ethnicity) − 8.004
					Where male = 1, female = 2; 1 = white, 2 = African American
Goran, 199610,c	98	4–9	Boys and girls	White	= (0.23 * subscapular) + (0.18 * weight) + (0.13 * triceps) − 3.0
Loftin, 200711	166	10–15	Girls	White, African American, Hispanic, and multiethnic	= −23.39 + (2.27 * BMI) + (1.94 * triceps) − (2.95 * race) − (0.52 * age) − (0.06 * (BMI * triceps))
					Where black = 1, other = 0
Slaughter, 198812,d	310	8–18	Boys and girls	White and African American	If boy and skinfold sum ≤35 mm, then:
					= 1.21 * (triceps + subscapular) − 0.008 * (triceps + subscapular)2 − C, where C = 1.7 if prepubescent white boy; 3.2 if prepubescent black boy; 3.4 if pubescent white boy; 5.2 if pubescent black boy; 5.5 if postpubescent white boy; 6.8 if postpubescent black boy
					If girl and skinfold sum ≤35 mm, then:
					= 1.33 * (triceps + subscapular) − 0.013 * (triceps + subscapular)2 − 2.4
					If boy and skinfold sum >35 mm, then:
					= 0.783 * (triceps + subscapular) + 1.6
					If girl and skinfold sum >35 mm, then:
					= 0.546 * (triceps + subscapular) + 9.7

^aSample size, age range, sex, and race/ethnicity of the population with which equation was originally developed.

^bIn the prediction equations, weight is in kilograms, triceps and subscapular skinfolds are in millimeters, BMI is in kg/m², and age is in years.

^cThe Dezenberg and Goran equations calculate fat mass. Percent body fat was calculated from FM before comparing the DXA results.

^dSlaughter equation is considered one equation in the analysis. Appropriate subgroup equations were applied when calculating percent body fat.

FM, fat mass; DXA, dual-emission X-ray absorptiometry.

National Health and Nutrition Examination Survey Data

We used data from the 1999–2006 NHANES, which was designed to provide a representative sample of US noninstitutionalized youth and adults. Whole-body DXA scans were administered during these survey years in participants 8 years or older using the Hologic QDR-4500A fan-beam densitometer (Hologic, Inc., Bedford, MA), and results were adjusted as previously described.¹⁵ Eleven body regions were included in the DXA measurements. Participants were excluded from DXA measurement if they were pregnant, weighed over 300 pounds, were over 6 feet 5 inches tall, or if they self-reported a history of radiographical contrast material (barium) use in the past 7 days or nuclear medicine studies in the past 3 days. Girls 8–17 years old were not measured during the 1999–2000 survey period because of unresolved institutional review board (IRB) issues; however, DXA data are available for this population for the 2001–2006 surveys. As previously described,^16,17 the National Center for Health Statistics investigators imputed missing DXA values using sequential multivariate imputation.

Anthropometrics and questionnaires were collected using standardized procedures by trained research staff in mobile examination centers.¹⁸ Weight was measured to the nearest 0.1 kg in an examination gown without shoes, and standing height without shoes was measured to the nearest 0.1 cm using a stadiometer with fixed vertical backboard and adjustable head piece. BMI was calculated as weight in kilograms divided by height in meters squared (kg/m²). Triceps and subscapular skinfolds were measured using a Holtain skinfold caliper to the nearest 0.1 mm. Weight status was determined according to the CDC BMI percentile cutpoints for youth (underweight, <5th; normal weight, ≥5th–<85th; overweight, ≥85th–<95th; obese, ≥95th).¹⁹

Exclusions

There are 41,474 participants in the NHANES 1999–2006 data set, of which 11,029 (∼27%) are 8–18 years of age with a positive sampling weight. The unresolved IRB issue in 1999–2000 resulted in no DXA data available for 1232 girls. Of the 9797 youth eligible for DXA measurement, we excluded youth with missing and no imputed DXA data or implausible DXA data (n = 199), implausible or missing height or weight (n = 256), missing triceps skinfolds (n = 270), or subscapular skinfolds (n = 383). The full analytical data set included 8679 participants (5046 boys and 3633 girls) 8–18 year of age. Because more than 10% of the eligible sample was excluded, we recalculated the sampling weights.

Statistical Analysis

We calculated the PBF for each participant using the eight previously published equations. Puberty status in boys was needed to calculate PBF using the Slaughter equation,¹⁴ but was not collected in the NHANES 1999–2006 data sets. Therefore, we used published results on Tanner Stage from NHANES III²⁰ to estimate mutually exclusively age ranges for prepubertal (8–10 years of age), pubertal (11–14 years of age), and postpubertal (15–18 years of age) and used these age ranges to calculate the Slaughter equation-predicted PBF. The Dezenberg¹¹ and the Goran¹² equations calculated fat mass (FM), and we converted it to PBF by dividing by body weight (kg).

Each equation was tested in a NHANES sample that was matched to age, sex, and race/ethnicity of the original equation study population. We will refer to this as the development population. The purpose of the matched analysis was to test the equation in a nationally representative sample that was similar to the development population. We also tested equations in the full NHANES sample of 8- to 18-year-old youth and four stratified samples (by sex, race/ethnicity, weight status, and age).

Univariate regression models were performed for each published equation (PROC SURVERYREG) using the predicted PBF from equation- (explanatory variable) and DXA-measured PBF (dependent variable). We compared the adjusted R² and root mean square error (RMSE) from the regression models in the matched sample, full sample, and sex-stratified samples. The equations with lower RMSE values are more precise. For each published equation, the difference between the equation-predicted and DXA-measured PBF were calculated (equation − DXA) for each participant. The mean signed difference (MSD) was calculated (PROC SURVEYMEANS) for each equation. Negative MSD indicated that the equation, on average, underestimated the actual (DXA) PBF, whereas positive MSD, on average, an overestimation by the equation. We set a priori criteria that a strong prediction equation should have a high adjusted R² (≥0.80), high accuracy (MSD within 1 percentage point), and nondifferential bias within subgroups (within 2 percentage points).²¹ Because the full NHANES population is not used in these subgroup analyses, domain analysis was applied to obtain estimates in subgroups. We followed the standard protocol for using NHANES DXA data¹⁷ by repeating all analyses in the five different imputation data sets using 8-year sampling weights and the mean results (R², RMSE, and MSD) from the five data sets calculated (version 9.3; SAS Institute Inc., Cary, NC). All of the analyses were repeated in a data set excluding imputed DXA values, and similar results were found (data not shown).

Results

Table 2 presents characteristics of our sample. The mean DXA measured PBF was different between boys (25.3%) and girls (32.5%). The PBF predicted from equations using skinfold measurements varied from 19.7% to 27.1% in boys and 22.1% to 31.4% in girls.

Table 2.

Demographic Characteristics of Youth 8–18 Years in NHANES 1999–2006 and Anthropometric Measurements Used by the Selected Prediction Equations

	Boys (n = 5046)			Girls (n = 3633)
	Mean or %	Median	SE	Mean or %	Median	SE
Age	13.0	12.4	0.1	13.1	12.6	0.1
Ethnicity (%)
Non-Hispanic white	61.4		1.9	62.9		2.0
Non-Hispanic black	14.4		1.3	13.8		1.3
Mexican American	11.7		1.1	10.7		1.0
Other Hispanic	5.8		1.0	5.9		1.0
Other	6.8		0.8	6.7		0.8
Height (m)	1.6	1.6	0.0	1.5	1.6	0.0
Weight (kg)	55.5	54.1	0.5	52.2	51.5	0.5
Triceps skinfold (mm)	13.3	11.1	0.2	17.7	16.7	0.2
Subscapular skinfold (mm)	11.3	8.8	0.1	14.0	12.0	0.2
BMI (kg/m2)	21.2	20.4	0.1	21.6	20.8	0.1
BMI percentile	62.2	67.5	0.7	63.0	69.3	0.9
DXA % body fat	25.3	23.7	0.2	32.5	32.0	0.2
Equation predicted % body fat
BraySubscapular	26.4	23.5	0.2	29.7	27.2	0.2
BrayTriceps	23.6	20.8	0.2	29.1	27.8	0.3
BraySubscapular + Triceps	22.2	19.5	0.2	26.4	25.1	0.2
Dezenberg	27.1	27.3	0.1	30.8	31.4	0.1
DezenbergWithRace	26.5	26.7	0.1	30.1	30.6	0.1
Goran	19.7	18.8	0.1	22.1	21.9	0.1
Loftin	25.0	23.4	0.2	28.0	28.1	0.2
Slaughter	20.4	16.9	0.2	26.0	25.1	0.2

NHANES, National Health and Nutrition Examination Survey; DXA, dual-emission X-ray absorptiometry; SE, standard error.

For each equation, Table 3 presents the published R² compared to our calculated adjusted R² and RMSE in the NHANES matched sample, full sample, and stratified by sex. In the NHANES matched sample, the adjusted R² in the matched sample ranged from 0.680 to 0.808. As expected, the adjusted R² values were lower when examining the full sample compared to the matched sample. Though none of the equations in the full sample had an adjusted R² ≥0.80, there were three equations that had an adjusted R² ≥0.7 (Slaughter [0.738], Bray triceps [0.724], and Bray subscapular and triceps [0.712]). Two of these equations also had the highest R² (≥0.7) in boys (Slaughter adjusted R² = 0.727, RMSE = 0.391; Bray triceps adjusted R² = 0.717, RMSE = 4.02). In girls, four equations had adjusted R² ≥0.7 (Loftin: adjusted R² = 0.755, RMSE = 3.90; Slaughter: adjusted R² = 0.739, RMSE = 3.54: Bray subscapular and triceps: adjusted R² = 0.732, RMSE = 3.62; Bray triceps: adjusted R² = 0.701, RMSE = 3.75).

Table 3.

Comparison of Adjusted R² and RMSE From Regression Comparing the Predicted Percent Body Fat from Each Equation and DXA-Measured Percent Body Fat

	Bray, 2001			Dezenberg, 1999
	Subscapular	Triceps	Subscapular + triceps	No race	With race	Goran, 1996	Loftin, 2007	Slaughter, 1988
Publisheda	0.77	0.81	0.45	0.95	0.95	0.88	0.88	0.78
Adjusted R2
Matched sampleb	0.680	0.793	0.808	0.736	0.704	0.747	0.777	0.742
Full samplec	0.530	0.724	0.712	0.495	0.491	0.674	0.633	0.738
By sexd
Boys	0.487	0.717	0.693	0.471	0.343	0.643	0.618	0.727
Girls	0.620	0.701	0.732	0.612	0.587	0.673	0.755	0.739
RMSE
Matched sample	4.463	3.589	3.453	3.775	3.995	3.375	3.252	4.110
Full sample	5.567	4.269	4.358	5.770	5.789	4.639	4.922	4.156
By sex
Boys	5.258	4.020	4.121	5.235	6.273	4.459	4.758	3.913
Girls	4.404	3.746	3.625	4.563	4.292	3.988	3.904	3.542

^aR² extracted from the published equation article.

^bNHANES population matched on race/ethnicity, sex, and age to the original development population for each equation. Sample sizes varied for each equation. Bray, n = 1242; Dezenberg, n = 1050; Goran, n = 303; Loftin, n = 2011; Slaughter, n = 5100.

^cFull NHANES data set for youth of all race/ethnicities, and sexes who are between 8 and 18 years old (n = 8679).

^dBoys, n = 5046; girls, n = 3633.

RMSE, root mean square error; DXA, dual-emission X-ray absorptiometry; NHANES, National Health and Nutrition Examination Survey.

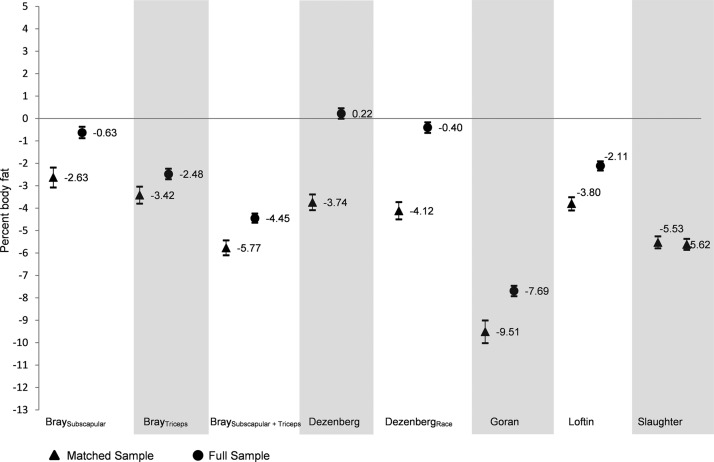
Figure 1 shows the MSD in the NHANES matched and full sample for the eight prediction equations. On average, the prediction equations underestimated PBF with the exception of the Dezenberg equation without race in the full sample. In general, the matched sample underestimated PBF to a greater extent than the full sample. However, the Slaughter equation had similar MSD in both the matched and full samples. In the full sample, the MSD was ±1.0 percentage point for both Dezenberg equations (MSD = 0.22 without race and MSD = −0.40 with race) and the Bray subscapular equation (MSD = −0.63). The other five equations had less accuracy in the full samples with the MSD ranging from −2.11 (Loftin equation) to −7.69 (Goran equation).

Figure 1.

Mean signed difference (MSD) between the predicted percent body fat and measured percent body fat in the matched sample and full sample in 8- to 18-year-old youth from NHANES 1999–2006. A negative MSD indicated that, on average, the skinfold equation underestimated percent body fat measured by DXA, and a positive MSD indicated that, on average, the equation overestimated percent body fat. The sample was matched on age, sex, and race/ethnicity. DXA, dual-emission X-ray absorptiometry; NHANES, National Health and Nutrition Examination Survey.

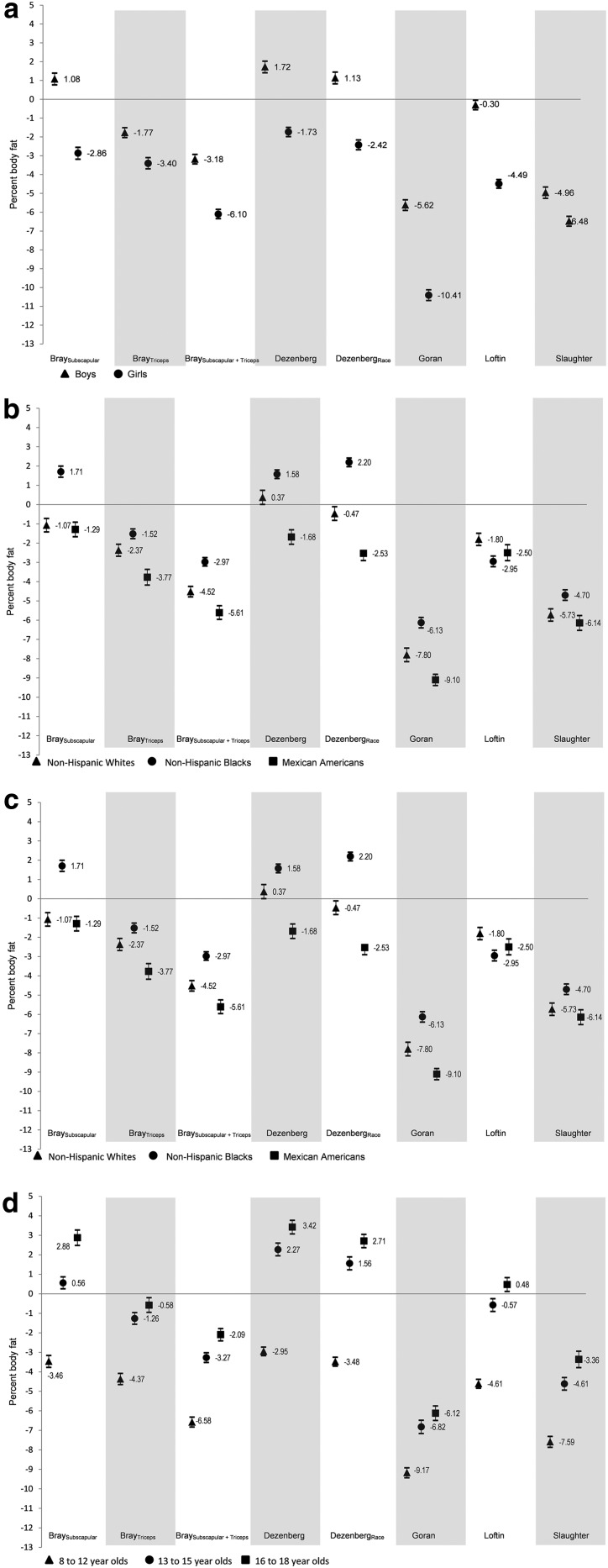
Figure 2A–D shows the MSD for the eight equations stratified by sex (Fig. 2A), race/ethnicity (Fig. 2B), weight status (Fig. 2C), and age categories (Fig. 2D). None of the equations had high accuracy (MSD within 1 percentage point) for all subgroups. After stratifying by sex (Fig. 2A), the Loftin equation in boys had small MSD (−0.30); however, the equation, on average, underestimated PBF by −4.49 percentage points in girls. The Dezenberg equation with and without race performed better than the other equations after stratifying by sex; however, PBF was, on average, overestimated in boys (1.72 without race and 1.13 with race), but, on average, underestimated in girls (−1.73 without race and −2.42 with race). The Bray subscapular equation also had differential bias by sex. The Slaughter equation (MSD = −4.96 in boys and −6.48 in girls) and the Bray triceps equations (MSD = −1.77 in boys and −3.40 in girls) were the only equations of the eight equations examined that did not exhibit differential bias by sex.

Figure 2.

(A) Mean signed difference (MSD) by sex in 8- to 18-year-old youth from NHANES 1999–2006. A negative MSD indicates that, on average, the skinfold equation underestimated percent body fat measured by DXA, and a positive MSD indicates that, on average, the equation overestimated percent body fat. (B) MSD by race/ethnicity in 8- to 18-year-old youth from NHANES 1999–2006. A negative MSD indicates that, on average, the skinfold equation underestimated percent body fat measured by DXA, and a positive MSD indicates that, on average, the equation overestimated percent body fat. (C) MSD by weight status in 8- to 18-year old youth from NHANES 1999–2006. A negative MSD indicates that, on average, the skinfold equation underestimated percent body fat measured by DXA, and a positive MSD indicates that, on average, the equation overestimated percent body fat. (D) MSD by age categories in 8- to 18-year-old youth from NHANES 1999–2006. A negative MSD indicates that, on average, the skinfold equation underestimated percent body fat measured by DXA, and a positive MSD indicates that, on average, the equation overestimated percent body fat. DXA, dual-emission X-ray absorptiometry; NHANES, National Health and Nutrition Examination Survey.

The Dezenberg equation with race performed well (as measured by MSD) in non-Hispanic whites (MSD = −0.47) but, on average, overestimated PBF in non-Hispanic blacks (MSD = 2.20) and underestimated PBF in Mexican Americans (MSD = −2.53; Fig. 2B). A similar pattern was observed in the Dezenberg equation without race. The Bray subscapular equation also had moderate accuracy and was not biased between non-Hispanic whites (MSD = −1.07) and Mexican Americans (MSD = −1.29). However, we did find differential bias with the Bray subscapular equation when comparing non-Hispanic whites or Mexican Americans to non-Hispanic blacks (MSD = 1.71). In contrast, the Loftin equation, on average, underestimated PBF more than the Bray subscapular or Dezenberg equations, but the bias was not differential by race/ethnic groups (MSD, −1.80 to −2.95). The Slaughter equation also was not biased across the race/ethnicity subgroups, but had an even lower overall accuracy (MSD, −4.70 to −6.14).

Whereas two equations had good accuracy in specific weight status subgroups (e.g., Bray triceps in obese youth MSD = −0.02 and Loftin equation in overweight youth MSD = 0.05), all of the equations except Bray subscapular plus triceps had differential bias for at least one weight status group comparison (Fig. 2C). Similar differential bias patterns were observed when examining equations across age categories (Fig. 2D). All equations except Bray subscapular did not have differential bias between 13- to 15-year-olds and 16- to 18-year-olds.

Discussion and Conclusions

Our evaluation of eight equations to predict PBF using skinfold measurements found none to have an adjusted R² ≥0.80 in a nationally representative sample of youth 8–18 years old. The published R² ranged from 0.45 from the Bray subscapular and triceps equation to 0.95 in the Dezenberg equations (Table 3). All equations except Bray subscapular plus triceps had lower adjusted R² values in the matched NHANES sample than the published value. Three equations (Bray subscapular equation and both Dezenberg equations) had low bias overall (MSD < ±1.0). However, it was concerning that we found some differential bias by sex, race/ethnicity, weight status, and age categories in those equations. It is important to use several metrics (if possible) when determining which prediction equation to use. An equation that might perform very well overall could have differential bias across an important subgroup.

Body fat distribution can vary by sex, race/ethnicity, and age. In general, girls have a higher PBF than boys at the same BMI. Trunk versus limb fat distribution between African Americans and whites differs as early as 3 years of age.²² African Americans with the same subscapular skinfold as white youth have smaller triceps skinfold. Published prediction equations have low accuracy for estimating PBF in different ethnic groups.^13,22–26 The relationship between BMI, PBF, and age is even more complex in youth than in adults. In youth 6 months to 8 years of age, both BMI and PBF change in nonlinear patterns over time. During puberty, PBF increases in girls and declines in boys. However, these relative changes are not detected by BMI.²⁷

The variables included in the eight prediction equations we examined varied (Table 1). Only three equations (both Dezenberg equations¹¹ and Slaughter equation¹⁴) included sex and only three equations (Dezenberg race equation,¹¹ Loftin equation,¹³ and Slaughter equation²⁴) included race. We only found bias by sex in the Dezenberg equations. We found differential bias between whites and African Americans in the Dezenberg equation that include race, but not in the equation that did not include race. The Dezenberg equation was developed in 10- to 12-year-olds and evaluating the equation in 8- to 18-year-olds might be one of the reasons for the differential bias. The differential bias found in the other equations that did not include sex or race/ethnicity suggest that it may be important for PBF equations to include sex and race/ethnicity and perhaps interaction with those variables if used in a diverse population.

The Dezenberg¹¹ and Goran¹² equations were created in youth from 4 years of age to 9 (Goran) or 10 (Dezenberg) years of age; however, because DXA measurements were not collected in NHANES on youth younger than 8 years of age, we were unable to validate those equations in the full age range. In addition, these equations calculated FM and were converted to PBF. The conversion from FM to PBF and/or inability to include youth 4–7 years of age might explain why the Goran equation performed poorly in the NHANES sample of 8- to 18-year-olds. The Dezenberg equation was also created in younger youth, and, despite the age restriction in our analysis, it performed relatively well. Although developed in females only, the Loftin equation¹³ was more accurate in boys (MSD = −0.34) than girls (MSD = −4.59). However, the adjusted R² was higher in girls than boys (0.759 and 0.611, respectively).

In the present study, we compared PBF prediction equations that included triceps and/or subscapular skinfolds. However, many researchers and clinicians find skinfolds to be challenging to measure accurately, particularly in young youth and obese individuals. With proper training of research staff, it is possible to collect reliable skinfold measurements. A large multinational study conducted in six countries found that intraobserver reliability of triceps skinfolds was 99.42%, and the technical error of measurement (TEM) was 0.24 mm.⁴ Waist circumference had similar intraobserver reliability of 99.02% and TEM of 0.60 cm.⁴ Several studies have shown that including skinfold measurements in equations to predict PBF improves the predictability of the equations.^{5,7–9,28,29}

PBF is an important variable that can produce different results than BMI. Unfortunately, gold-standard measures (e.g., DXA) are not feasible in most studies, so researchers need reliable equations to use. Investigators for the Pathways Trial³⁰ found that PBF calculated using an equation containing skinfolds produced different results compared to BMI. In post-hoc longitudinal analyses of Pathways data, Stevens and colleagues found that normal weight youth with higher levels of physical activity (measured by accelerometry) had lower levels of PBF, but there was no association with BMI.⁸ Similarly, in the Trial of Activity for Adolescent Girls (TAAG) study,^3,9 Stevens and colleagues found that between grades 6 and 8, a 10-minute increase in moderate-to-vigorous physical activity was associated with a 0.28-percentage-point decrease in predicted PBF in the adolescent girls (p < 0.05), but there was no statistically significant association with BMI. Puder and colleagues³¹ examined the impact of a school-based intervention in predominantly migrant preschool youth living in Switzerland. They found no difference in BMI between the control and intervention groups (−0.07 kg/m²; −0.19–0.06; p = 0.31), but the intervention group had a lower PBF (−1.1%; −2.0 to −0.2; p = 0.02). Thus, important associations missed by BMI may detected by PBF prediction equations that use measurements that can be collected in the field.

To our knowledge, this is the first study to compare skinfold equations developed for youth to a nationally representative sample. Our research group previously used the 1999–2004 NHANES data to examine 26 equations to predict PBF in adults.²¹ Similar to our findings in youth, the adjusted R² was <0.80 for all equations examined. The adjusted R² ranged from 0.59 to 0.68 in males and from 0.51 to 0.61 in females in the four equations for adults that included triceps and/or subscapular skinfold measurements. The equations underestimated PBF by 1.1–5.2 percentage points in males and 3.3–5.3 percentage points in females²¹ and also showed differential bias across age, weight status, and race/ethnicity.

Our research group used 1999–2004 NHANES data to create a new sex-specific PBF prediction equations in youth 8–18 years of age.²⁸ In the independent, but internal, validation data sample, the adjusted R² was 0.818 in girls and 0.893 in boys. The calculated PBF assessments had high accuracy (MSD = −0.078 in girls and boys) and were not biased across race/ethnicity or weight status groups. Compared to the eight published equations we examined, these equations included more variables (e.g., waist circumference), quadratic terms for anthropometric, and interactions between demographic and anthropometric variables. It is not surprising that these equations would have superior performance in the 1999–2004 NHANES data given that they were developed in those data. For a more independent evaluation, we applied those equations²⁸ to the 2005–2006 NHANES data using 2-year sampling weights and found the overall adjusted R² was 0.787 in girls and 0.870 in boys and the accuracy remained high for both girls (MSD = −0.030) and boys (MSD = −0.292; unpublished data).

Our analysis has several limitations. NHANES collected only triceps and subscapular skinfolds. As a result, equations using other skinfold measurements could not be evaluated in this analysis. The sample sizes for the matched analysis ranged from 303 youth (Goran equation) to 5100 youth (Slaughter equation; Table 2). These differences should be considered when examining the results from the matched analysis. The full sample analysis had the same sample size for all of the equations, allowing direct comparison of the equations in a national representative sample. NHANES does not collect puberty status. This variable is needed to calculate PBF using the Slaughter equation in boys with a combined subscapular and triceps skinfold less than 35 mm. In the present study, we assigned puberty status (prepuberty, puberty, and postpuberty) based on age, which most likely resulted in some misclassification. If boys were misclassified, then their estimated PBF could vary by as much as ±3.8 percentage points in white boys and ±3.6 percentage points in black boys.

A strength of our analysis is that we examined bias in informative subgroups in addition to adjusted R² and RMSE. Low random error in a prediction equation is, of course, desirable, as is lack of systematically low or high values across the entire study sample. However, it can be argued that even more important to the validity of a study is that there is not differential bias across subgroups being compared. Our subgroup analyses of MSD allowed us to detect that type of bias. Our work highlights the need for more research in the development of valid equations to predict PBF in youth of all ages, as well as racial and ethnic backgrounds. We suggest that researchers use caution when selecting equations to predict PBF given that the ability of the published equations to predict PBF might be biased in your sample population.

Author Disclosure Statement

No competing financial interests exist.