Multi-State modelling of repeated hospitalisation and death in patients with Heart Failure: the use of large administrative databases in clinical epidemiology

Abstract

In chronic diseases like Heart Failure (HF), the disease course and associated clinical event histories for the patient population vary widely. To improve understanding of the prognosis of patients and enable health-care providers to assess and manage resources, we wish to jointly model disease progression, mortality and their relation with patient characteristics. We show how episodes of hospitalisation for disease-related events, obtained from administrative data, can be used as a surrogate for disease status. We propose flexible multi-state models for serial hospital admissions and death in HF patients, that are able to accommodate important features of disease progression, such as multiple ordered events and competing risks. Fully-parametric and semi-parametric semi-Markov models are implemented using freely available software in R. The models were applied to a dataset from the administrative data bank of the Lombardia region in Northern Italy, which included 15,298 patients who had a first hospitalisation ending in 2006 and 4 years of follow up thereafter. This provided estimates of the associations of age and gender with rates of hospital admission and length of stay in hospital, and estimates of the expected total time spent in hospital over five years. For example, older patients and men were readmitted more frequently, though the total time in hospital was roughly constant with age. We also discuss the relative merits of parametric and semi-parametric multi-state models, and model assessment and comparison.

1. Introduction

Aging of the population and improved survival of cardiac patients due to modern therapeutic innovations has led to an increasing prevalence of heart failure (HF). Despite improvements in therapy, the mortality rate in patients with HF remains high.¹ The magnitude of the problem of HF is difficult to assess with precision since there is no gold standard for the diagnosis of heart failure, and there has been wide variation in the diagnostic criteria used in different studies.² At least six HF scoring systems based upon symptoms and signs have been developed to assess the presence or severity of heart failure. Clinical diagnostic criteria for heart failure have generally included history, physical examination, and chest radiographs (see Mosterd et al.,³ Roger⁴ and references therein). Regardless of the definition used, the prevalence of HF and left ventricular dysfunction increases steeply with age (see, for example, Bleumink et al.⁵). In general HF is a chronic disease (Chronic Heart Failure — CHF), caused by many conditions that damage the heart muscle, including coronary artery disease, heart attack, cardiomyopathy and conditions that overwork the heart (high blood pressure, valve disease, thyroid disease, kidney disease, diabetes, or heart defects present at birth). In addition, HF can occur in the presence of a combination of these diseases. It is the leading cause of hospitalisation in people older than 65 years. A 2010 update from the American Heart Association (AHA) estimated that there were 5.8 million people with HF in the United States in 2006 (see McMurray et al.⁶ and Lloyd-Jones et al.,⁷ among others). There are an estimated 23 million people with HF worldwide. In the Lombardia district of Italy, which provides our motivating example, the HF incidence over the last decade ranged between 25, 000 and 30, 000 cases per year in a population of 9.7 million inhabitants.⁸

In chronic diseases like CHF, clinical interest lies in both the final outcome (death or survival time) and the dynamics of the process itself. To improve understanding of prognosis, and for healthcare providers to assess the impact and costs of the disease, a comprehensive model should include both death and non-fatal clinical events. There are several methodological approaches to the modelling of times to multiple events per subject. Castaneda and Bart⁹ provide an appraisal of several methods, highlighting that the standard Cox model is not appropriate since observations are not independent. In order to overcome this, they propose the use of marginal and multi-state models using a counting process approach for the joint analysis of survival and time to disease-related hospitalisations, allowing for population average estimates of treatment effects. Several marginal models are adapted in order to account for intra-subject correlation and competing risks. The models differ in the way they define the “at-risk” population at each time. However in these marginal models it is assumed that all events are identical and can be revisited at any time, with no recognition of the serial nature of consecutive HF-hospitalisations. In their multi-state models, the serial nature of the events is allowed, but hospitalisation and death are treated as the same type of event, which, given their nature and severity, is unacceptable clinically. Thus, a multi-state model that represents multiple ordered events per subject, accounts for competing risks, and distinguishes between death and hospitalisation, is required.

A multi-state model is a stochastic process in which subjects occupy one of a set of discrete states at any time. Multi-state models are convenient for describing longitudinal data and/or repeated events. In Andersen and Keiding¹⁰ a counting process representation is stressed. In medical applications, the states may represent healthy, different severities of disease, or periods in hospital, and transition rates between states may be modelled in terms of covariates. See, for example, Hougaard¹¹ for a review, and Commenges,¹² Cook,¹³ Putter et al.,¹⁴ Sommen et al.,¹⁵ Titman and Sharples,¹⁶ Duffy et al.,¹⁷ Kay,¹⁸ Chen et al.,¹⁹ Commenges and Joly²⁰ for applications to many different diseases. In Sutradhar et al.,²¹ multi-state models are developed, in order to compare trends in hospitalisations among cancer survivors. Despite the importance of CHF both in terms of incidence and related human and monetary costs (WHO²² defines the rising incidence and prevalence of chronic diseases as one of the major global concerns), there are few examples in the literature of the application of multi-state models to hospitalisation and death from CHF. Postmus et al.²³ used a three-state model representing in hospital, out of hospital or death for 1023 patients from a randomized controlled trial with heart failure.

In this study, the impact of CHF is assessed using data from administrative databases, which provide information on the number and times of hospital admissions and time to death (or administrative censoring). Administrative databases play a central role in the evaluation of health-care systems, due to their widespread diffusion and low cost of information. There is increasing agreement among clinical epidemiologists on the validity of disease and intervention registries based on administrative databases (see, for example, Barbieri et al.,²⁴ Wirhenetal²⁵ and references therein). A key issue is the selection criteria of the observation units: different criteria may result in different estimates of prevalence or incidence of diseases (Saczynski et al.²⁶). The use of prospective patient management databases is of current interest (see, for example, Macchia et al.,²⁷ Au et al.,²⁸ Aylin et al.,²⁹ Philbin and DiSalvo³⁰). The benefits of using these data for health system planning and evaluation are many: they are population based, often combine information from multiple centres, capture real health system use, are longitudinal and are relatively inexpensive to construct and use. In addition, individual health administrative records can be linked to other data (clinical registry, public health, socioeconomic etc.). The validity of this approach is critically dependent on the reliability of the data and the accuracy of disease coding in the administrative records, as shown, for example, by Lee et al.³¹ and Saczynski et al.²⁶ If search and data linkage strategies are not carried out rigorously, administrative data on hospital admissions can be less complete and exhaustive than data from epidemiological cohort studies and clinical trials. Despite issues surrounding data reliability, and the on-going debate regarding their use in clinical research (see, for example, Quach et al.³² and Ieva et al.³³), significant improvements have been achieved in this area in the last decade, and the use of administrative databases in clinical biostatistics has become an accepted practice (see, among others, Schultz et al.,³⁴ Muggah et al.,³⁵ Iron et al.³⁶ and references therein).

We propose a multi-state modelling strategy for the joint analysis of outcomes and hospital admissions in CHF patients, whose data come from the administrative database of an Italian regional district (Lombardia). Our aim is to demonstrate a flexible approach that is able to capture important features of disease progression, such as multiple ordered events and the competing risks of death and hospitalisation, in a novel application. We go further than Postmus et al.²³ by using multiple states representing subsequent periods spent in and out of hospital, in order to model how the risk of death and further hospitalisation changes through time and with disease progression. Analyses are carried out using freely-available statistical software R.³⁷ Specifically, the survival,³⁸ mstate¹⁴ and flexsurv³⁹ packages are used to fit the multi-state models to the data. This work will provide healthcare providers with an effective modelling tool, using hospital admissions to gain insights into the burden of heart failure, how it relates to patient characteristics and how it changes over time.

We describe the data extraction and inclusion criteria in Section 2, and explain the multi-state modelling methods in Section 3. Key results from applying these methods to the Lombardia HF admissions data are presented in Section 4. In Section 5 we end with a discussion of the strengths and challenges of modelling disease progression through administrative data.

2. Study Cohort and Extraction Criteria

Within the Italian health-care regulation system, every hospital admission produces a record in the administrative database. These records are then collected in an data warehouse called SDO (Scheda di Dimissione Ospedaliera, i.e., hospital discharge paper) database. The SDO database has been interrogated to identify heart failure episodes and subsequent hospitalisations. In addition, information both on patient (sex, date and place of birth, residence, …) and on hospitalisations (date of admission and discharge, diagnoses and procedures, type of admission, type of discharge, vital status at discharge, …) over time can be retrieved.

For the current study we used data extracted from the administrative data warehouse of Regione Lombardia (the region in the northern part of Italy with capital Milan) within a project on Chronic Heart Failures.⁴⁰ The project aims to describe the epidemiology and natural history of HF patients at regional levels, to profile health service utilisation (e.g. hospitalisations, cardiac rehabilitation, diagnostic tests, outpatient visits, etc.) over time, and investigate variation in patient care according to geographic area, socio-demographic characteristics and other clinical variables.

In order to include the vast majority of HF cases, any admission of patients resident in the Northern Italy regional district of Lombardia and coded as Major Diagnostic Category (MDC) 01 (Nervous System), 04 (Respiratory System), and 05 (Circulatory System) between 2000 and 2010 was considered. Hospital admissions elsewhere in the country for patients resident in Lombardia were included and recovered. For people who died by the end of the study, the date of death was obtained through database linkage with the Italian National Registry of deaths. Starting from this population, we selected only incident cases, defined as those patients who experienced no HF-related events during 2000–2005, and whose first admission due to HF ended during 2006. HF-related events were defined as hospitalisations containing HF-related codes from AHRQ-IQI⁴¹ or CMS-HCC^{42, 43} in any of the six diagnosis fields of the SDO. The number of hospital admissions for HF and the corresponding dates of admission and discharge were recorded over a 4-year follow up (up to December 31th, 2010).

The eligible cohort consisted of 15, 856 patients (corresponding to 36, 949 records). Among these, patients who were younger than 18 years at the first hospitalisation time were excluded (62 pts., corresponding to 182 rows). Among the remaining cohort, we also removed patients admitted and discharged on the same day, i.e., patients whose length of stay (LOS) in hospital was zero (477 pts., corresponding to 2476 rows), or those having long-stay recovery (LOS greater than 180 days, 19 pts., corresponding to 67 rows). Some other pre-processing and cleaning operations were carried out, for example to check coherence in patients’ time-line progressions and test for agreement in event indicators. There were no missing data. We assumed that loss to follow-up was ignorable, since the 1.9% of the population who were lost to follow up at the end of the study had similar characteristics to those with complete follow-up. The final dataset contained records from 15, 298 patients (corresponding to 35, 224 records),

3. Multi-state Models for HF data

3.1. Definitions

To characterise the association between hospital admissions, mortality and patient characteristics, we adopt a multi-state model describing how an individual moves between a series of discrete states in continuous time. Suppose an individual is in state S(t) at time t. The next state to which the individual moves, and the time of the change, are governed by a set of transition intensities q_rs(t), r, s = 1, …, R. The intensity, or hazard, represents the instantaneous risk of moving from state r to state s. This may depend on the time t since the start of the process, patient characteristics z(t), and possibly also the “history” of the process up to that time, ℋ_t: the previous states visited by the individual and the times spent in them. Therefore, for this patient,

$$q_{rs}(t)=\underset{\delta t\to 0}{\lim }\mathbb{P}(S(t+\delta t)=s|S(t)=r)/\delta t$$

are then elements of a R × R matrix Q(t) whose rows sum to zero, so that the diagonal entries are defined by $q_{rr}(t)=-{\displaystyle \sum _{r\ne s}{q}_{rs}(t)}$, and q_rs(t) = 0 if a transition from state r to state s is not allowed.

In our application we use semi-Markov models, so that q_rs(t) only depends on ℋ_t through the time spent in the current state. This is also known as a “clock-reset” model (see e.g. Putter at al.¹⁴), that is, the time-scale returns to zero at every transition, so that the hazard is represented as q_rs(u, z(t)), where u is the time of entry to the current state. This represents how the hazard changes after discharge from hospital, or during a single hospital stay. Any additional dependence on patient age and the time t since the first hospitalisation is investigated through time-dependent covariates z(t).

3.2. Model structure for HF hospitalisation

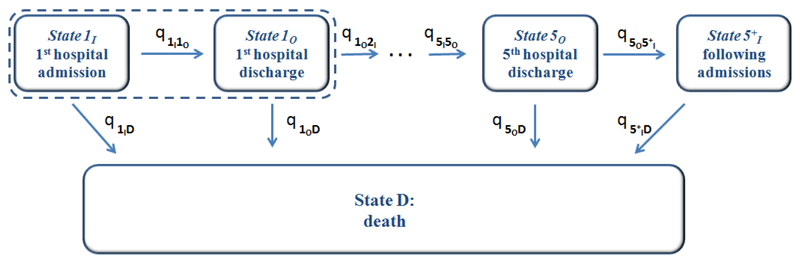
The 11 states and the 19 permitted transitions in our application are illustrated in Figure 1. Each patient starts in state 1_I, representing the first hospital admission. From there they can either be discharged from hospital, or die in hospital. Once a patient is out of hospital, they can either be admitted again or die, and once in hospital they can either be discharged or die. Death from any cause is included. A maximum of 6 hospital admissions are modelled, and subsequent admissions (but not deaths) are ignored, due to the sparsity of data from individuals with more than 6 admissions (Table 1). Thus “greater than 5 admissions” is considered as a clinically-important “severe” disease state.

Figure 1:

The multi state model, describing jointly the length of stay in hospital, risk of subsequent hospitalisation, mortality rates in and out of hospital, and how these change with increasing numbers of hospital admissions.

Table 1:

Distribution of number of admissions to hospital for chronic HF between HF patients and percentage of patients who entered each stage during the 5-year follow up.

	Hospitalisations during follow up
	≥ 1	≥ 2	≥ 3	≥ 4	≥ 5	≥ 6
Number of pts. %	15,298	8,891	4,836	2,604	1,492	855
	100%	58.12%	31.61%	17.02%	9.75%	5.59%
	≥ 6	≥ 7	≥ 8	≥ 9	≥ 10	≥ 11
Number of pts. %	855	514	302	175	97	56
	5.59%	3.36%	1.97%	1.14%	0.63%	0.37%

Simplifications of this structure are possible. For example, we could have only two living states, representing “in hospital” and “out of hospital”, with transitions allowed between them in either direction. This would allow estimation of the in-hospital and out-of-hospital mortality rate, and the average length of stay in hospital, but it would then be awkward to model how these quantities, or the probability of readmission, vary with the previous number of hospital admissions. Alternatively, if length of hospital stay is not of interest, we could omit the “discharge” states, and simply model the times between successive hospital admission dates, jointly with mortality. This would assume, however, that the risk of death does not change when a patient is in hospital. Both of these simplifications were investigated in exploratory work before deciding to use the most flexible structure of Figure 1.

3.3. Data structure and time-to-event representation

In our application, the state S(t) is known at all times for each patient, since all dates of admission to, or discharge from, hospital, and all dates of death, are known. We label these times t₁, …, t_n, where t₁ is the date of the first hospital admission. If the patient died, t_n is the date of death, otherwise it is the end of follow-up. Any intermediate times t₂, …, t_n−1 represent discharges and subsequent admissions, if they occur.

For each permitted r → s transition in the multi-state model (19 in our case) there is a corresponding time-to-event model, with cause-specific hazard rates defined by q_rs(u). To enable estimation of these hazards, the data are expressed as a series of times to events which are potentially censored: u_j = t_j+1 − t_j : j = 1, …, n − 1. For a patient who moves into state s at time t_j, their next event at t_j+1 is defined by the model structure (Figure 1) to be one of a set of competing events $s_1^{*}$,…, $s_{n_s}^{*}$.

For example, in state s = 1_I (first hospital admission), the next state must either be $s_1^{*}=1_O$ (first discharge), or death $(s_2^{*}=D)$ so n_s = 2. The time of the event which actually occurs at t_j+1 is observed, and the times of the competing events from this set (which have not occurred by this time) are censored. Each u_j contributes an observed time to one of the 19 transition-specific models, and a censored time to each of the models for the competing events. Therefore, standard tools for survival analysis can be used to estimate the q_rs(u, z(t)), independently for each r → s transition, from this form of data. Additional software is required to deal with the multi-state structure when processing the data, making predictions (Section 3.4) and presenting results.

We employ both semi-parametric (§3.3.1) and fully-parametric (§3.3.2) multi-state models. In all models,

$$q_{rs}(u,\mathbf{\text{z}}(t))=q_{rs}^{(0)}(u)\exp ({\mathit{\beta }}_{rs}^{\prime }\mathbf{\text{z}}(t))$$ (1)

thus the hazards are proportional between patient groups or covariate values, in other words the covariate value has a constant time-independent multiplicative association with the hazard. Age (at the time of transition) and sex are included as covariates in all models, with different hazard ratios exp(β_rs) for each r → s transition. Age-sex interactions were considered and judged not significant.

Age is assumed to be a step function which remains constant between each t_j and t_j+1, although this is a convenient approximation to a more realistic model in which it would vary smoothly and deterministically. Closer approximations could be achieved by inserting arbitrarily many extra rows in the data corresponding to times when the covariate changes, or (in theory) by numerically integrating the hazard over age to compute the exact likelihood. Note however that our semi-Markov models allow the hazard to change (nonparametrically or through a parametric model) as time elapes between t_j and t_j+1. Time since first hospitalisation is also investigated as a covariate using the same method as for age.

3.3.1. Semi-parametric models

In the semi-parametric case, the β_rs are estimated by maximum partial likelihood, a standard Cox regression implemented using the survival package for R.³⁸ The baseline hazard $q_{rs}^{(0)}(u)$ is left unspecified and estimated nonparametrically using the Breslow estimator,⁴⁴ via the mstate package,⁴⁴ which subsequently computes covariate-specific cumulative hazards for each of the transition-specific Cox models.

For transitions r → s representing readmission and mortality, semi-parametric models with patient-level frailties were also fitted. The corresponding baseline hazard for patient i is then $q_{rsi}^{(0)}(u)=q_{rs}^{(0)}(u){\gamma }_i$, where γ_i is a frailty or random effect, representing the hazard ratio of readmission or mortality for patient i, compared to an average patient, after adjusting for observed covariates. We assume either γ_i has a Gamma distribution with mean 1, or log(γ_i) has a normal distribution with mean 0, in each case with an unknown variance. The frailty models are fitted using maximum integrated partial likelihood⁴⁵ and the survival (function coxph) and coxme packages.⁴⁶

3.3.2. Fully-parametric models

In these cases, the baseline hazard is given by a fully-parametric function of time $q_{rs}^{(0)}(u)=g(u,{\mathit{\theta }}_{rs})$, so that each transition-specific model is a standard parametric survival model. That is, for a person in state s at t_j, with covariate values z, the time u_j to their next event at t_j+1 contributes $f(u_j|{\mathit{\theta }}_{s,s_k^{*}})$ to the likelihood if a transition to $s_k^{*}$ is observed, or $1-F(u_j|{\mathit{\theta }}_{s,s_k^{*}})$ if this is censored, where f () and F () are the density and cumulative distribution functions of the parametric model. θ_rs is a function of covariate values z and effects β_r,s, giving a proportional hazards model. The full likelihood is the product of such terms over all potential destination states (indexed by k), times j and individuals.

As a base case we use the Weibull distribution with θ_rs = (α_rs, λ_rs), hazard $q_{rs}(u,\mathbf{\text{z}}(t))={\alpha }_{rs}{\lambda }_{rs}(t)u^{{\alpha }_{rs}-1}$, and $\text{log}({\lambda }_{rs}(t))={\mathit{\beta }}_{rs}^{\prime }\mathbf{\text{z}}(t)$, giving proportional hazards again. An important special case, which we also consider, is α_rs = 1, for all r, s, where the hazard is constant conditionally on the values of any time-dependent covariates. Since these covariates are assumed constant between event times, the hazard is a step function of time, and the sojourn time in each state r has a piecewise exponential distribution, with a piecewise-constant rate q_rr(t). This is a Markov model, since future evolution only depends on the current state and covariates.

The parameters are estimated by maximum likelihood, and standard errors are obtained by standard asymptotic theory. These models can be fitted using any survival modelling software. Here the flexsurv package is used,³⁹ which also has utilities for prediction from multi-state models, as explained in the next section. This software also supports left-truncated survival times, which would have been required if we had used the clock-forward time scale.¹⁴ The Markov model can also be fitted with the msm package for R,⁴⁷ although that package is more suited to data where the exact times of transition are unknown (Kalbfleisch and Lawless,⁴⁸ Kay¹⁸). Alternatively, since the number of transitions between a particular pair of states, for given covariate values, has a Poisson distribution with rate proportional to the corresponding time at risk, standard generalized linear modelling software might be used.

Since our dataset is large, we can estimate different baseline hazards $q_{rs}^{(0)}$ and covariate effects β_rs for each r → s transition. Therefore the joint likelihood factorises into independent terms for each transition, and each transition-specific model can be fitted independently, which is more efficient than maximising the joint likelihood over all parameters simultaneously. Fiocco et al.⁴⁹ discuss techniques to obtain more parsimonious multi-state models with smaller datasets.

3.4. Prediction from multi-state models

To predict the probability of occupying a particular state at a fixed time in the future, we calculate the transition probability matrix P(u, t + u), where the (r, s) entry of P(u, t + u), p_rs(u, t + u), is the probability of being in state s at a time t + u, given the state at time u is r. Under all models, this is calculated by simulating a large number of individual state histories from the multi-state model given the covariate-specific hazards or cumulative hazards for each transition. The mstate and flexsurv packages have utilities to do this for the semi-parametric and parametric models respectively.

During prediction, time-dependent covariates (age and time since first hospitalisation) are assumed to be piecewise-constant, just as during model fitting — the covariate is set to x₀ at time t = 0, changes to x₀ + u if a transition takes place at u, and is held constant between transitions. Relaxing the piecewise-constant assumption would make prediction more difficult. For the Weibull model, for example, the next event time is only Weibull conditionally on a fixed age, and the hazard integrated over a continuously-varying age would represent a non-standard distribution.

Under the Markov (piecewise-exponential) model, an alternative method of prediction is to solve the Kolmogorov differential equations (Cox and Miller⁵⁰). In the parametric model, if the transition intensity matrix Q is constant, given the values of covariates, over the interval (u, t + u), then P(u, t + u) = P(t). In this case, the transition probability matrix can be calculated directly using a matrix exponential: P(t) = Exp(tQ). The transition probability matrix over intervals where Q is piecewise-constant is then calculated as a matrix product of terms like these. Deterministic time-dependent covariates could be assumed in advance to change only at small time intervals, such as a year or a month.

P(t) can be used to predict the expected total time spent in a state s over a given period of time (0, T), as $E_s(T)={\int }_0^T{p}_{rs}(t)dt$, given that a patient is in state r at time 0. In this study we predict the total time spent in hospital from the first admission until death, a quantity of interest to healthcare providers.

For the parametric models, we can calculate standard errors or confidence intervals for quantities such as these, which are functions of $q_{rs}^{(0)}$ and β_rs, by simulating from the assumed asymptotic normal distribution of the estimators of $q_{rs}^{(0)}$ and β_rs, and recalculating the quantities of interest.⁵¹ Under the semi-parametric model, however, the simulation to obtain P(t) assumes a piecewise-constant hazard that changes at each observed event time,⁴⁹ which is expensive.Therefore a second level of simulation to obtain an accurate confidence interval would be unfeasible.

4. Analysis and Results

4.1. Descriptives

The study cohort consists of 15, 298 patients whose first HF admission ended in 2006. Patients were followed up to December 31st, 2010. Among these individuals, 6, 646 (43.44%) died (from any cause) by the end of the study. The proportion of patients who died during a hospital admission was 8.26%.

Patient age at the time of the first hospitalisation ranged from 18 to 103 years, with mean age (SD) 75.6 (12.6) years. The age of patients at the time of the final discharge ranged from 19 and 105 years, with mean (SD) 76.7 (12.5) years. In the cohort there are 7, 184 (46.96%) males and 8, 114 (53.04%) females. Women were older than men: mean (SD) ages are 79.6 (11.4) and 71.5 (12.88), respectively.

The number of admissions to hospital per patient (Table 1) ranged between 1 and 24 (mean = 2.31, median = 2, quantiles 1 and 3). There was no significant difference between men and women in the number of hospitalisations.

Table 2 shows summary statistics for time from the previous discharge to each subsequent admission, for those patients experiencing them. The mean (and median) time to the next hospitalisation decreases as the number of readmissions increases.

Table 2:

Summary statistics for times from discharge to each successive readmission to hospital, for HF patients who experienced each corresponding number of readmissions.

	pts.	mean (sd)	median	1Q	3Q	min	max
(1st adm)	15298	—	—	—	—	—	—
to 2nd adm	8891	369.5 (422.4)	180	57.9	558.5	3	1820
to 3rd adm	4836	308.7 (348.81)	160	55	443.3	3	1738
to 4th adm	2604	279.4 (313.13)	154	59	384	4	1691
to 5th adm	1492	238.5 (266.54)	140	50	331	3	1499
to > 5th adm	855	197.5 (216.52)	118	46.5	266	4	1284

The overall mean (standard deviation) LOS in hospital is 13.2 (13.9) days (min = 1, median = 9, first and third quantiles respectively equal to 5 and 16, max = 180 days). There is a slight difference between mean LOS of male and female patients (12.9 male vs 13.5 female) and there is no significant variation in LOS across hospitalisations.

4.2. Multi-state models

The multi-state models described in Section 3 are fitted to the HF data. Table 3 shows the total number of observed transitions for each state. In-hospital mortality increases from 7.16% (first admission in-hospital death rate) up to 9.99% (fifth admission in-hospital death rate), probably due to the aging population and the increasing severity of the HF.

Table 3:

Transitions for the multi-state model in (1) fitted to HF data.

		to r − th discharge	to death			to (r + 1) − th admission	to death
From r − th admission	r = 1	14,203	1,095	From r − th discharge	r = 1	8,891	1,750
	r = 2	8,145	746		r = 2	4,836	980
	r = 3	4,383	453		r = 3	2,604	488
	r = 4	2,378	226		r = 4	1,492	236
	r = 5	1,343	149		r = 5	855	132
	r = 5+	-	394

4.2.1. Associations with covariates

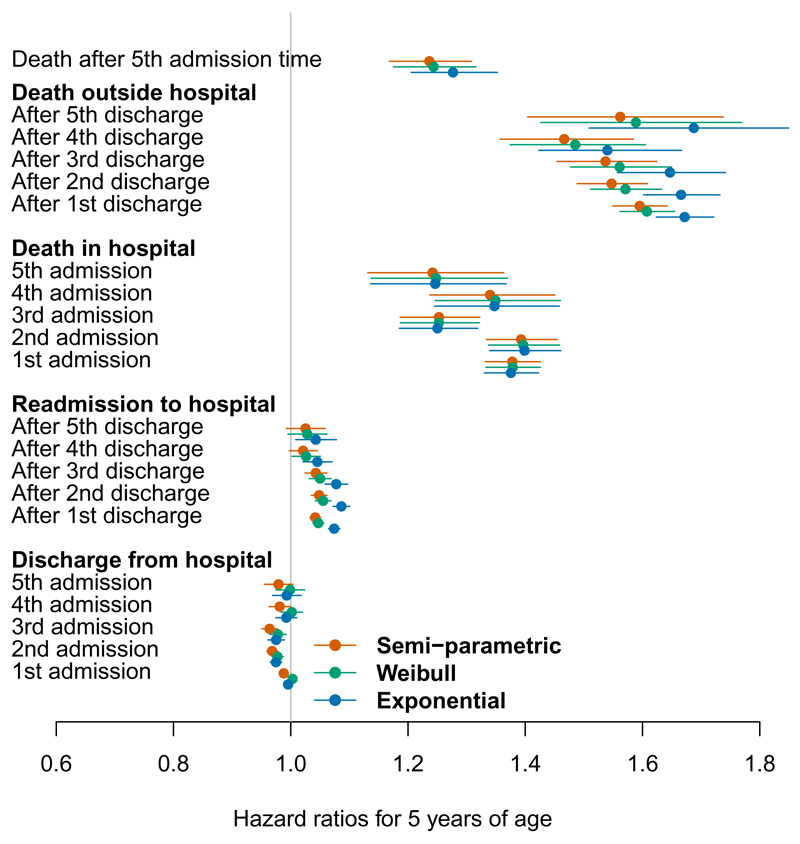
Figures 2 and 3 show maximum likelihood estimates of the hazard ratios for the effects of age and sex, under the semi-parametric models without frailties (red), and the parametric Weibull (green) and parametric exponential (blue) models, each with these as the only two covariates. An increase of 5 years in age has only a very small effect on readmission and discharge times, decreasing the chance of discharge and increasing the risk of readmission slightly. These estimates are very precise due to the large sample, though are unlikely to hold clinical significance. There is evidence, as expected, that increasing patient age increases the death hazard from all the states. This effect appears to slightly decrease with the number of hospitalisations. This may be because as the the number of admissions increases, the population becomes more homogeneous in mortality or readmission risk between ages (and between men and women), since the highest-risk patients will have died earlier. This might be modelled using frailties, as discussed in the next section.

Figure 2:

Hazard ratios for a five year increase in age, on each of 21 hospital admission, discharge or death events.

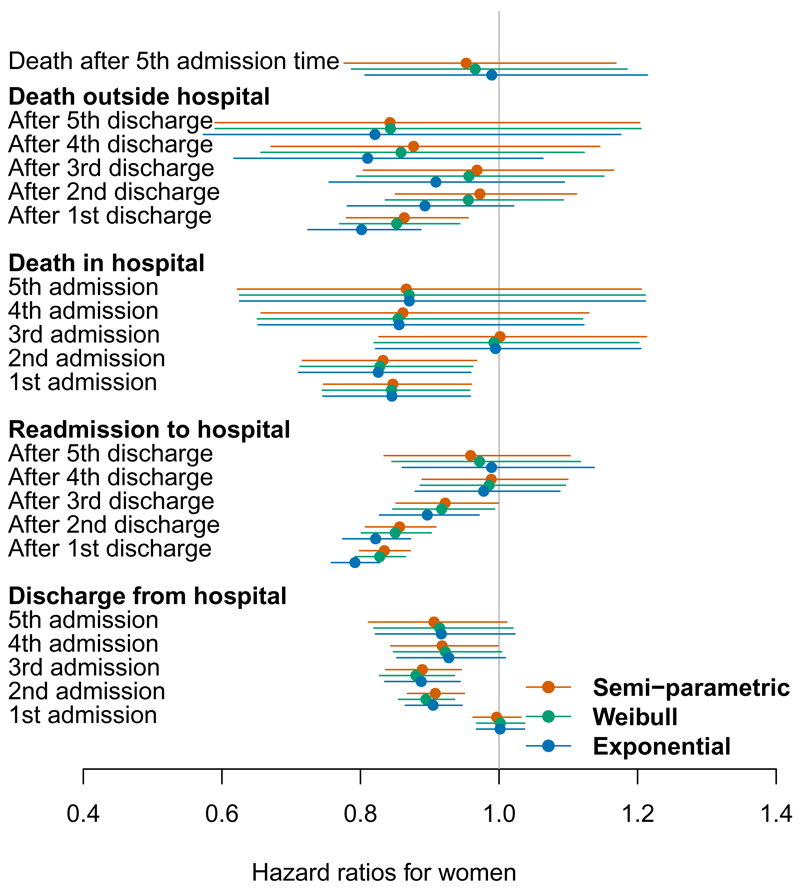
Figure 3:

Hazard ratios for a female patient relative to male, on each of 21 hospital admission, discharge or death events.

Note that age enters the models as a step function, defined as age at the previous event. Thus in Figure 2, the effects of age are interpreted as the hazard ratios between two people five years apart in age, and where the same time u has elapsed since the previous event for these two people.

In general the gender effect is smaller than the age effect, with few significant hazard ratios. In the earlier stages, women are less likely to change state (die, be admitted or discharged from hospital) than are men. The lower hazard for transitions to death may reflect the longer life-expectancy for women, which the age effect in the model may not have fully adjusted for. These data suggest that there may be a reluctance to admit to hospital women with symptoms of HF in the early stages. Once admitted, women in the early stages of HF were less likely to be discharged early. However once disease severity has reached the later stages, reflected by several admissions, progression through stages and survival is the same for both sexes.

The semi-parametric and Weibull models give similar estimates. The exponential / Markov model gives slightly different estimates from those models, although the patterns through the process were similar, and estimates of precision are comparable. The exponential model resulted in an increased effect of age on death out of hospital, and a slightly bigger effect of age on readmission rates, particularly in the early stages of disease. Note the hazards for the exponential model are assumed to be constant within each state. The disagreement is greatest for the transitions which take place over long periods of time (discharge to readmission or death) for which the hazard may not be constant and there is heavy censoring. The estimates agree between all models for the transitions from admission to discharge or death in hospital, since the hazard is more likely to be constant over the relatively short times spent in hospital, and there is minimal censoring.

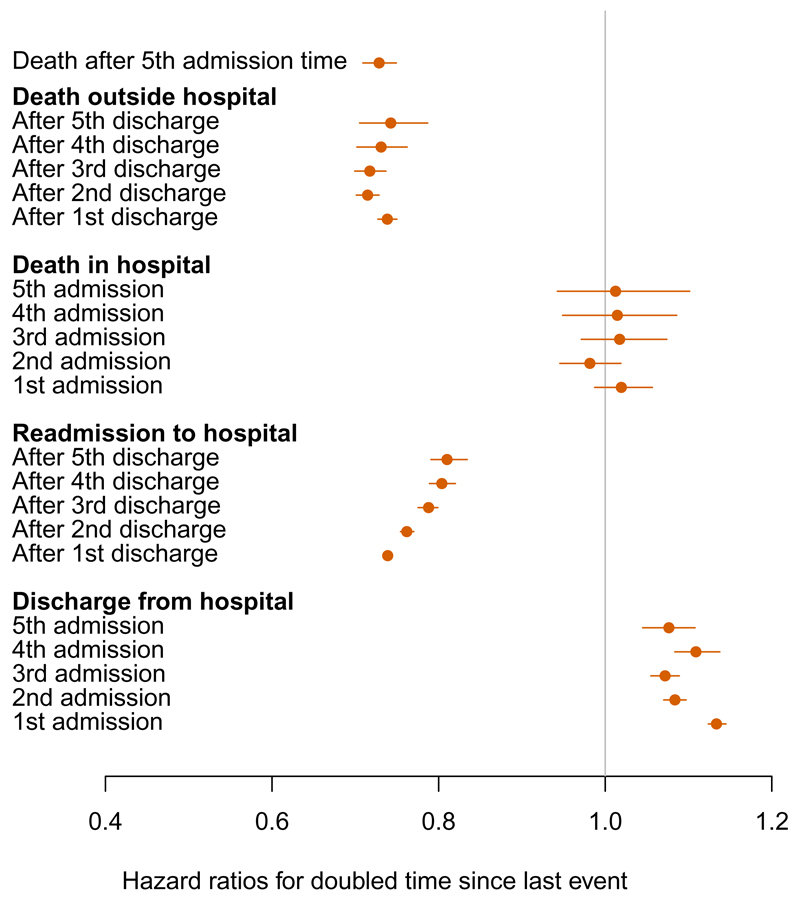
Figure 4 illustrates the estimated shape parameters from the Weibull model, transformed as 2^α_rs−1 to represent the ratio of hazards q_rs(u, z(t)) for a doubled time u since the previous event. This indicates that hazards of death and readmission are decreasing after discharge from hospital, hazards of death in hospital are constant, and hazards of hospital discharge are increasing.

Figure 4:

Hazard ratios for a doubled time since the previous event from the Weibull model, defined as 2^αrs−1, where αrs is the Weibull shape parameter for the r → s transition.

An additional Weibull model was fitted with time since first hospitalisation also included as a predictor. There was no substantive difference to the hazard ratios for age and sex when this was added (0.01 or less). This covariate had no apparent relation with mortality, though it was associated with hospital admission and discharge. Stable estimates of its effect were only available for the 2nd admission onwards, after which, one year since the first admission is associated with around a 5% decrease in expected length of hospital stay, and a 10-20% increase in the expected time to the next admission.

4.2.2. Frailties

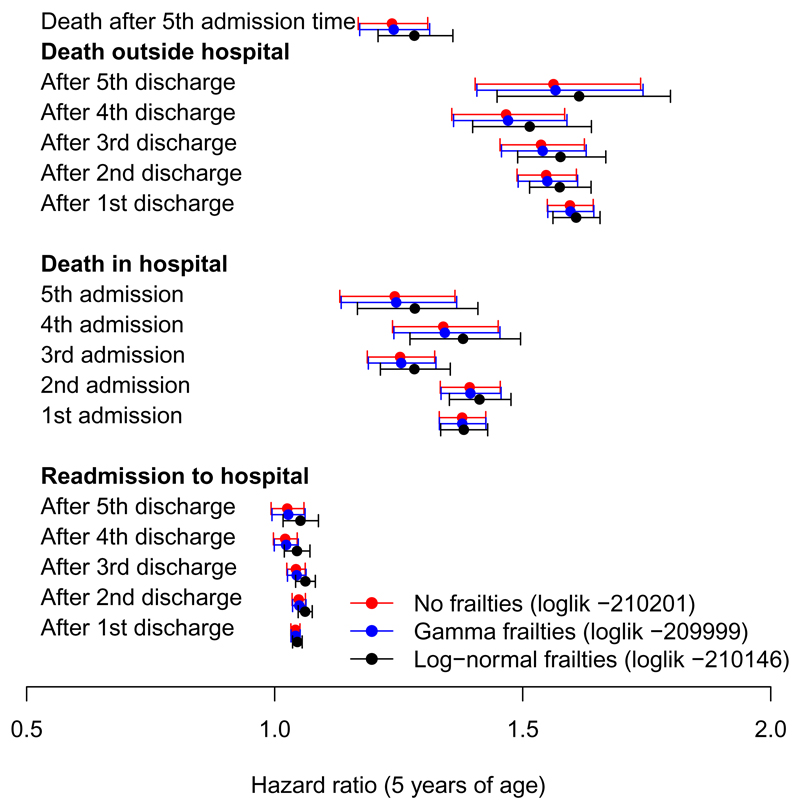
Selected covariate effects under two semi-parametric frailty models and a model without frailties are compared in Figure 5. Both frailty models had higher (integrated partial) log likelihoods than the model without frailties. Under the better-fitting gamma frailty model, the estimated frailty was negligible and the covariate effects were unchanged (Figure 5). Under the log-normal frailty model, the hazard ratios for age on death outside hospital were slightly more similar between earlier and later discharges (Figure 5). Similar patterns were seen for effects on death in hospital and readmission rates. This might be explained by the observed population becoming more homogeneous in risk between age groups as time elapses, as the people who were both older and of greater frailty are the most likely to die before a third or fourth period in hospital. Estimating the age effect conditional on frailty moderates this difference, although even after conditioning on frailty, there was still strong support for hazard ratios that are different between admission numbers.

Figure 5:

Hazard ratios for years since first hospital admission, on each of 21 hospital admission, discharge or death events (LL: maximised (integrated) partial log likelihood of model)

Under the log-normal model, the estimated standard deviation of the frailty term is 0.34, thus a person with frailty of one standard deviation above the mean has an exp(0.34) or 40% higher risk of readmission to hospital or death, indicating some unexplained heterogeneity. The extent of frailty was much less under the gamma model, with one standard deviation corresponding to about a 9% higher risk.

4.2.3. Expected survival, time in hospital, and event rates

Using the methods described in Section 3.4, we estimated the restricted mean survival, and total time spent in any of the five hospital states, over 5 years from the first HF admission. These are shown in Table 4. The mean times spent in hospital for HF treatment, up to the 6th admission, are consistent with just over 2 admissions per patient. A small proportion of patients, 5.6%, will have more than 5 admissions. An advantage of the parametric models is that measures of uncertainty for these estimates are easily available. Under the frailty models, the predictions of survival and time in hospital, for corresponding patients of average frailty, were not substantively different.

Table 4:

Expected survival over five years, and time spent in hospital over five years, by age and sex, under parametric and semi-parametric multi-state models, with 95% confidence intervals where available.

		Weibull	Exponential	Semi-parametric
Survival [years]
Men:	65	4.36 (4.24, 4.44)	4.43 (4.36, 4.51)	4.31
	70	4.21 (3.97, 4.17)	4.11 (4.07, 4.29)	4.07
	75	3.68 (3.57, 3.80)	3.86 (3.73, 3.91)	3.7
	80	3.07 (3.10, 3.37)	3.24 (3.19, 3.44)	3.21
	85	2.58 (2.49, 2.77)	2.78 (2.62, 2.85)	2.62
Women:	65	4.52 (4.34, 4.53)	4.54 (4.46, 4.61)	4.42
	70	4.20 (4.10, 4.32)	4.31 (4.22, 4.41)	4.21
	75	3.72 (3.79, 3.98)	4.02 (3.91, 4.12)	3.87
	80	3.35 (3.33, 3.54)	3.60 (3.49, 3.73)	3.41
	85	2.98 (2.74, 3.01)	2.97 (2.89, 3.17)	2.87
Time spent in hospital [days]
Men:	65	32.64 (31.46, 35.24)	33.51 (32.12, 35.43)	31.3
	70	32.81 (31.32, 34.90)	34.37 (32.08, 35.70)	30.78
	75	32.10 (30.66, 33.89)	33.93 (31.51, 35.13)	30.72
	80	28.91 (28.74, 31.93)	31.85 (30.38, 34.03)	29.8
	85	27.49 (26.45, 29.39)	29.69 (27.07, 30.41)	26.73
Women:	65	32.44 (30.53, 33.89)	33.38 (30.48, 34.08)	30.42
	70	32.24 (30.21, 33.74)	32.61 (31.08, 34.39)	31.39
	75	31.16 (29.95, 32.99)	33.56 (31.33, 34.56)	30.16
	80	28.63 (28.76, 31.77)	30.45 (29.78, 33.76)	29.75
	85	28.76 (26.68, 29.69)	29.47 (27.83, 31.30)	27.17

Another advantage of the parametric models is that the mean sojourn times in each state may be estimated. These are the expected times from state entry until transition to another state. Estimates are reported in Table 5 for men and women aged 76 years (the mean population value at first hospitalisation). Under the semi-parametric model, the hazards are only estimated within the five-year follow-up period of the data, therefore to estimate the mean sojourn times we would need additional parametric assumptions for the hazards beyond that period. The corresponding medians, however, are available for all models from Figures 6 and 7, as the time when the estimated survival in the state reaches 0.5.

Table 5:

Estimated mean sojourn times, in days, for each transient state of the parametric multi-state models (Weibull and Exponential), with 95% confidence intervals. Age on state entry is set to the mean population value (76 years).

		Days in hospital		Days until next admission
		Weibull	Exponential	Weibull	Exponential
Men:	1st	13.7 (13.5, 14.0)	13.6 (13.3, 14.0)	1224 (1156, 1297)	814 (791, 837)
	2nd	12.4 (12.1, 12.7)	12.3 (12.0, 12.7)	969 (903, 1038)	669 (645, 695)
	3rd	12.3 (11.9, 12.8)	12.3 (11.8, 12.8)	784 (720, 856)	579 (550, 609)
	4th	12.3 (11.8, 12.9)	12.3 (11.6, 12.9)	570 (511, 636)	450 (420, 480)
	5th	12.8 (12.1, 13.7)	12.8 (11.9, 13.7)	438 (384, 502)	362 (331, 395)
Women:	1st	13.8 (13.6, 14.1)	13.8 (13.4, 14.1)	1702 (1608, 1799)	1026 (998, 1054)
	2nd	13.8 (13.4, 14.2)	13.7 (13.3, 14.2)	1244 (1156, 1337)	806 (774, 837)
	3rd	13.7 (13.2, 14.3)	13.7 (13.1, 14.3)	891 (811, 977)	645 (610, 680)
	4th	13.3 (12.6, 14.0)	13.3 (12.5, 14.1)	594 (530, 667)	470 (436, 504)
	5th	14.0 (13.0, 15.0)	14.0 (12.9, 15.1)	466 (402, 543)	373 (338, 411)

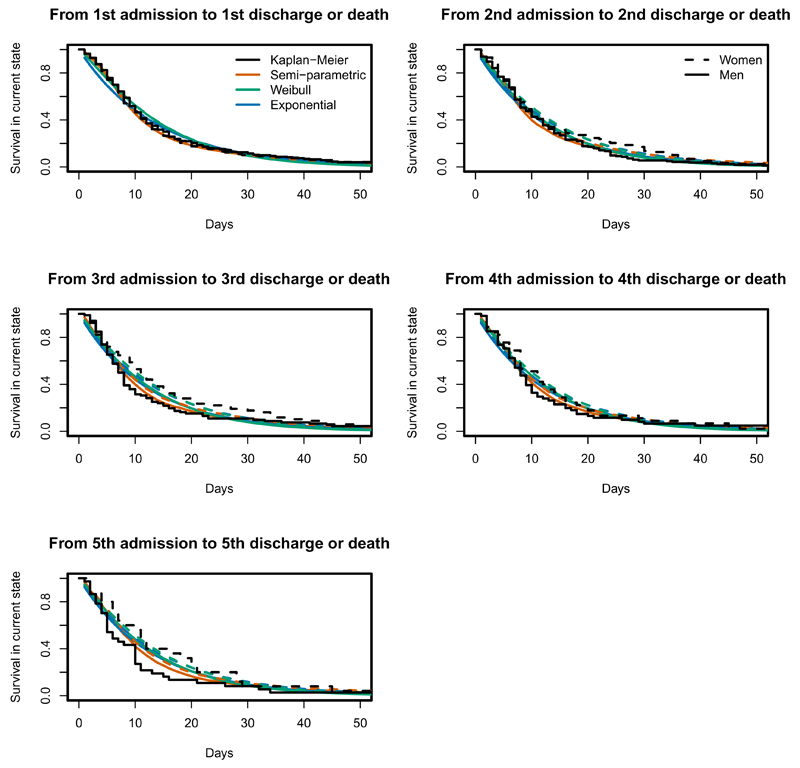
Figure 6:

Kaplan-Meier (black) curves of time to discharge or death, from each in-hospital starting state, and estimated probabilities of remaining in that state from semi-parametric (orange), parametric Exponential (blue) and parametric Weibull (forest green) models, for women and men aged 76 years at day 0.

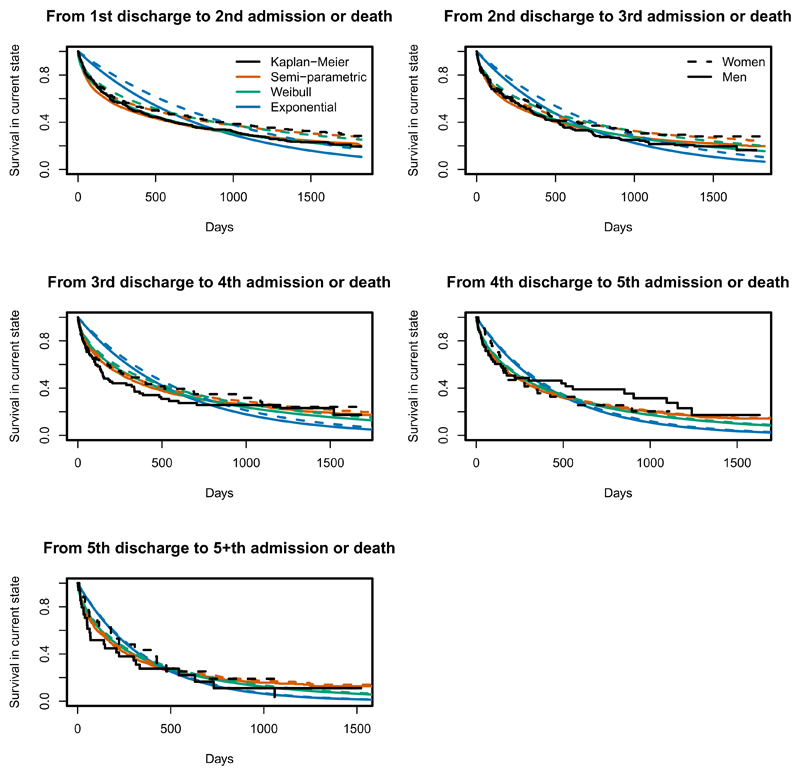
Figure 7:

Kaplan-Meier (black) curves of time to readmission or death, from each out-of-hospital starting state, and estimated probabilities of remaining in that state from semi-parametric (orange), parametric Exponential (blue) and parametric Weibull (forest green) models, for women and men aged 76 years at day 0.

Table 5 shows that mean stay in hospital does not change substantially as the number of admissions increases. However the times between admissions do decrease, reflecting an acceleration in the disease process once it has been diagnosed and has resulted in an initial admission. Mean sojourn times for women were longer, consistent with the hazard ratios which showed that women were less likely to change states than men. We could hypothesise that women are more likely to have carer commitments at home and so may only be admitted for more severe HF episodes, resulting in slightly longer stay. This and other hypotheses could be examined in future clinical studies. The exponential model appears to underestimate the sojourn times — as discussed in the following section, this fits poorly compared to the Weibull.

4.2.4. Model assessment

Since every transition time is known, we can calculate Kaplan-Meier estimates of the time from state entry until the next transition for particular age-sex subgroups as an informal diagnostic procedure. Estimates from the fitted models for the corresponding covariate category (using the methods described in Section 3.4) can be compared with these to assess model fit (as discussed by Titman and Sharples¹⁶). For patients in hospital, all models give good predictions of the probability of remaining in hospital for a 76 year old patient (Figure 6). This is consistent with the agreement of the corresponding covariate effects between the models in Figure 2. Figure 7 shows that the Weibull and semi-parametric models account better for the decrease in the hazard of readmission (or death) since the time of last discharge. This is because the assumption of constant hazard until the next transition is likely to be reasonable over the short times spent in hospital, but not over longer periods. The exponential model assumes the hazards vary only with age, whereas the Weibull and semi-parametric models relax the Markov assumption by also modelling the hazards as functions of the time spent in the current state. The Weibull distribution appears to be adequate to represent the decreasing hazards observed within five years of the first admission. Over longer time horizons, we would probably observe subsequent hazard increases with age, which we could model with a more flexible parametric model within the same software.

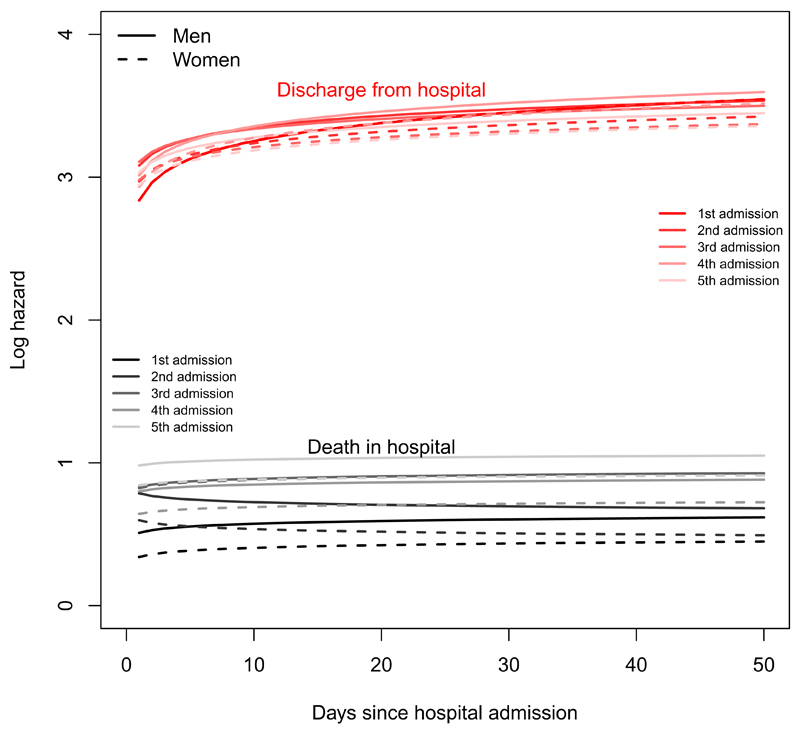
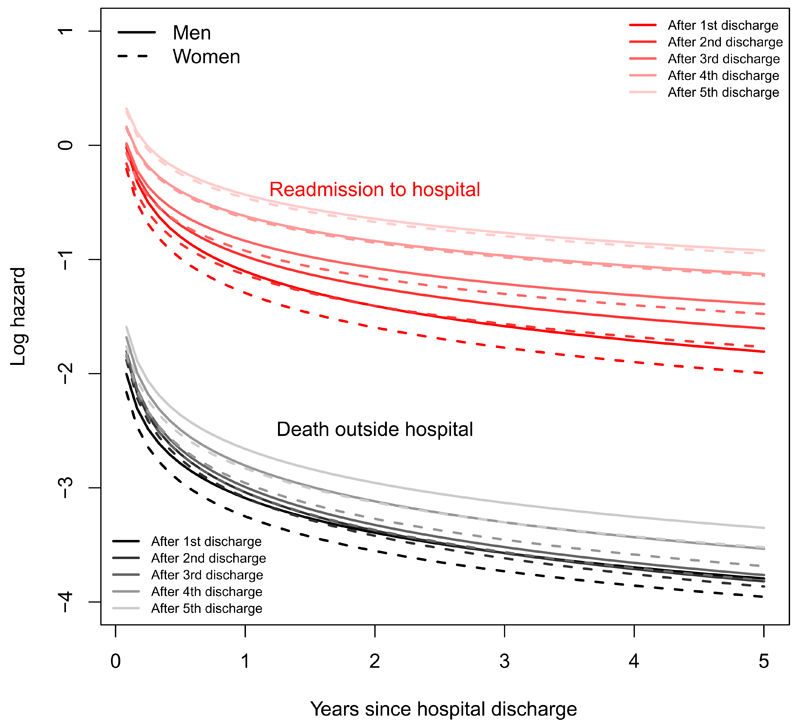
Figures 8 and 9 illustrate the transition-specific log hazards from the Weibull model for 76 year old men and women as functions of time. The death rate in hospital is roughly constant but increases with the number of previous admissions. The rate of discharge increases with length of stay, with no clear relation to admission number. For a person discharged from hospital, the risk of readmission and death decreases through the five years since admission, with higher risks for a person who has been admitted more often in the past.

Figure 8:

Log hazards of next event (discharge or death) for a person aged 76 currently in hospital, under the Weibull semi-Markov model.

Figure 9:

Log hazards of next event (readmission or death) for a person aged 76 currently out of hospital, under the Weibull semi-Markov model.

The Weibull models also give improvements in AIC (between 23 and about 5000), compared to the exponential, for all transition-specific models except for admission to discharge. Since the dataset is large, further improvements in AIC could be achieved with more elaborate parametric models, but exploratory analyses suggested these would yield diminishing returns, in that there would be no practically-significant difference in the hazard ratios and model predictions, at least for the variables we studied.

For out-of-hospital starting states, the extent of censoring and the sparsity of data at later times increases with the number of admissions, therefore any visible discrepancy between the Kaplan-Meier and fitted curves at these times is less likely to be significant. Any remaining lack of fit of the semi-parametric model may result from non-proportional hazards. A test of the correlation of the Schoenfeld residuals with the Kaplan-Meier estimates at the corresponding time showed that hazards were only significantly non-proportional for two out of the 19 transition-specific Cox models, and then only for the age effect. Since the sizes of these effects (discharge after 1st admission, and readmission after 1st discharge in Figure 2) are not clinically significant, this is not a concern. Similar results were found from fitting Weibull models with shape parameters varying by age or sex.

5. Conclusions

Contemporary administrative health care databases allow for a new kind of epidemiological research, based on real-time availability and low-cost data. Despite the issues surrounding the reliability of such data, in the last decade significant improvements have been obtained in this area, and the use of administrative databases in clinical biostatistics has become an accepted practice. The benefits of using these data for health system planning and evaluation go far beyond the fact that they are cheap and quickly available: they are population based, comprehensive, capture real health system use, longitudinal, and can be linked to other data. Even if it can be difficult to properly define a population of interest starting from these databanks, administrative databases represent a valuable clinical research resource. At the same time, they represent a great challenge for statistics and statistical models.

In this work we focused on the use of administrative data for gaining insights into the impact of heart failure. We used multi-state models to simultaneously predict survival, time to the next hospitalisation and total time spent in hospital, and how these depend on age, gender and hospitalisation history. The hazards of death and (to a lesser extent) hospital discharge were roughly constant over the short periods of time spent in hospital. However the longer times spent out of hospital, until readmission, are determined by a range of influences, including the underlying progression of the disease, comorbidities and the ageing of the population. These factors are not adequately modelled using constant hazards, although the bias in estimates of the hazard ratios was not large in this population. Thus if the focus is on estimation of covariate effects, constant hazards may be an adequate approximation, but for studies that focus on assessment of time to readmission, and associated health care consumption, it is not a reliable approach.

The effect of time in a multi-state model can operate on multiple scales: patient age, time since the last transition, and time since the start of the process (first hospitalisation in our case).⁵² Age and time since the start of the process were handled as time-dependent covariates, which were assumed to be constant between transitions. However, if the hazard is assumed to be a smooth parametric function of the time since the previous transition, as in our Weibull model, and this is conditioned on the covariate values at the start of the transition, this effectively achieves a hazard that increases smoothly with age.

We were able to show that times between hospital admissions decreased as the number of admissions increased, reflecting HF progression, and to quantify expected times between admissions. As might be expected, patients who were older at first admission were readmitted more frequently, as were men (compared with women) in the earlier stages of HF. However, the number of admissions and associated time spent in hospital, over this 5 year period was roughly constant with age, decreasing only for age of onset of around 85 years. For example, as a proportion of the restricted mean survival time over 5 years, time in hospital ranged from about 1.9% for 65 year old patients to 2.5% for 85 year old women. In this example results did not change when patient specific random effects were included.

We modelled only the first five admissions, which represented a large majority of the population (Table1), and the later admission counts were relatively small. A parsimonious model for later admissions might have been achieved by smoothing the transition rates across numbers of transitions, for example by using $q_{s_0,D}=f(s)q_{5_0,D}$ for s > 5. This could be implemented in software by treating the admission number as a covariate.

Due to the size of the Lombardia administrative databases it is possible to study a range of factors influencing health care consumption, through jointly modelling hospital admissions and death. This has resulted in precise estimates of expected survival times, times spent in hospital and covariate effects. Additionally there is sufficient power to investigate interactions between covariates, which has not been possible with smaller data registries. In this study there were no significant interaction effects between age and sex on model parameters, and the size of the dataset ensures that we can be confident in this assertion.

Multi-state models are effective in describing clinical processes as discrete states. Nevertheless, due to the difficulty in inference for some types of data, strong assumptions on the process dynamics and on covariate effects are often applied, such as the Markov assumption, constant hazards through time, or proportional hazards between individuals. As pointed out in Titman and Sharples,¹⁶ it is difficult to make universally valid recommendations on model checking as often the model assumptions depend on the particular application. In applications where all the transition times are available, as here, we can simply compare the likelihoods of fitted fully-parametric models (e.g. exponential Markov and Weibull semi-Markov), and compare parametric to semi-parametric models through informal diagnostic plots.

The flexsurv package makes flexible fully-parametric multi-state models straightforward to implement, likewise mstate for semi-parametric models. Flexible parametric models combine the advantages of having a fully-specified model, such as the ability to extrapolate and (computational and statistical) efficiency, with the goodness-of-fit of semi-parametric models. Though any extrapolation beyond the data relies on untestable assumptions. In our example the Weibull was adequate, but more flexible hazard shapes might be implemented in the same software using distributions which have more than two parameters, for example based on splines.⁵³ With intermittently-observed processes, where the exact times of transition are unknown, the msm package in R has made Markov models accessible for a wide range of model structures. Relaxing the Markov assumption with such data is more difficult, though some solutions have been proposed.^{54, 55}