Borrowing of strength and study weights in multivariate and network meta-analysis

Abstract

Multivariate and network meta-analysis have the potential for the estimated mean of one effect to borrow strength from the data on other effects of interest. The extent of this borrowing of strength is usually assessed informally. We present new mathematical definitions of ‘borrowing of strength’. Our main proposal is based on a decomposition of the score statistic, which we show can be interpreted as comparing the precision of estimates from the multivariate and univariate models. Our definition of borrowing of strength therefore emulates the usual informal assessment. We also derive a method for calculating study weights, which we embed into the same framework as our borrowing of strength statistics, so that percentage study weights can accompany the results from multivariate and network meta-analyses as they do in conventional univariate meta-analyses. Our proposals are illustrated using three meta-analyses involving correlated effects for multiple outcomes, multiple risk factor associations and multiple treatments (network meta-analysis).

1. Introduction

Meta-analysis is the synthesis of results from multiple studies that address the same research question. Multivariate meta-analysis^1,2 can be used when multiple correlated effect estimates, of more than one quantity of interest, are available. The multivariate approach is gaining popularity as, in contrast to standard univariate meta-analyses, the utilisation of correlation can lead to more precise estimation.³ This has been referred to as borrowing of strength (BoS): conditional on the modelling assumptions we can utilise additional information for each effect of interest by using related (or indirect) information from other correlated effects in the same analysis. This is especially important when some of the available studies do not report all the effects included in the multivariate meta-analysis. This type of indirect information has been found to be useful in reducing the impact of reporting bias,⁴ but here we focus on its capacity to provide more precise inference.

Network meta-analysis^5–8 has been proposed in order to perform a single meta-analysis involving more than two treatment groups. This type of analysis allows the use of both direct and indirect evidence when estimating the treatment effects, where the strength is borrowed from indirect information. Network meta-analyses can be fitted as multivariate meta-analyses⁹ and so our methods, although developed in the context of multivariate meta-analysis, can also be used for network meta-analyses. We illustrate this particular application in section 5.

The extent of BoS has frequently been assessed informally and claimed to be small, because multivariate meta-analyses have been found to provide similar numerical results to multiple univariate meta-analyses.^10–12 However, examples do exist where the BoS appears to be larger, and where there is an important statistical (and sometimes, clinical) impact of using a multivariate, rather than a univariate, meta-analysis.^4,13,14 We will show that our method is equivalent to comparing the results from multivariate and univariate meta-analyses and so is closely related to these informal assessments of BoS. This differs from the I² statistics that have been developed for multivariate meta-analysis^15–17 which instead describe the impact of the between-study heterogeneity by comparing the results from multivariate fixed-effect and random-effects models.

A related issue is the quantification of study weights in multivariate and network meta-analysis. Study weights in classical univariate meta-analysis are well-known: in a fixed-effect model they are inversely proportional to the within-study variances, and in a random-effects model they are inversely proportional to the sum of the within-study variance and the estimated between-study variance. How to define study weights in a multivariate or network meta-analysis is less obvious. A second aim of this paper is to provide formulae for the weighting of each study in these types of meta-analyses. This enables researchers to report the contribution of each study to the analysis. Our definition of weights follows naturally from our measure of BoS, and reduces to the usual weights univariately. Alternative measures of multivariate weights based on the hat matrix have also been suggested in the context of network meta-analysis⁶ and based on data-point coefficients in the context of multivariate meta-analysis of multiple outcomes.¹⁴ We prefer our method for calculating study weights because we are able to embed both study weights and BoS statistics into a single framework, where the weights can be separated into direct information and BoS. Hence, our framework enables us to clearly identify the studies that contribute the most weight to the analysis, and also to explain the way in which they provide this weight. We return to the possibility of using data point coefficients and the hat matrix to define study weights in section 3.2.

We begin by examining the fixed-effect (common true effect for all studies) model because this greatly simplifies the mathematics. This is because there is then no need to estimate the between-study covariance matrix. A wide variety of methods for estimating the between-study variance are available in the usually more plausible random-effects model.¹⁸ As we explain in section 4, this is now also the case multivariately. In the context of the multivariate random-effects model it is most natural to estimate the between-study covariance matrix using likelihood based methods when applying our proposed methods. This is because our proposals are based on a score decomposition and so are based on the likelihood function. In section 5 we estimate the between-study covariance matrix using restricted maximum likelihood estimation. However non-likelihood based methods for estimating the between-study variance structure are very popular in meta-analysis.¹⁹ Upon making the usual meta-analytic approximation of taking the between-study covariance matrix as known and equal to its estimate when making inferences about the average effects, our methods can be applied regardless of the estimation method used for the between-study covariance matrix. Our methods for calculating BoS statistics and study weights can therefore be used whenever the standard procedure for making inferences about the average effects² is used. Hence our proposals are very widely applicable.

The paper is set out as follows. In section 2 we present our proposed definition of BoS for the multivariate fixed-effect model and in section 3 we describe our proposed definition of weights for this model. In section 4 we explain how to extend our methods to the multivariate random-effects model. In section 5 we apply our methods to three example datasets, where the last example is a network meta-analysis. We conclude with a discussion in section 6.

2. BoS in the fixed-effect model

2.1. Notation and model

Suppose the data from study i = 1, …, n are the estimate y_i (a p-dimensional column vector containing the estimates of the parameters of interest, where p is the dimension of the multivariate meta-analysis) and its within-study covariance matrix S_i (a p × p matrix containing the within-study variances and covariances). The entries of these within-study covariance matrices are typically obtained from information contained in the study publications or from individual patient data. Within-study correlation occurs because different effects are calculated using correlated data from the same sets of patients. For example, if the effects of interest relate to time-to-event outcomes such as overall survival and disease-free survival, then they will almost necessarily be positively correlated within studies. Wei and Higgins²⁰ and Riley et al.²¹ describe strategies for calculating the within-study correlations. We follow the convention of taking the S_i as fixed and known but they are estimated in practice. This can be quite a crude approximation in practice, especially when the studies are small or the dimension of the multivariate meta-analysis is high.

The multivariate fixed-effect meta-analysis model is then

$${\mathbf{y}}_i\sim N(\mathit{\beta },{\mathbf{V}}_i)$$ (1)

where β is the vector containing the average effects, which are the parameters of primary interest, and we take V_i = S_i. We show how to extend our methods to the multivariate random-effects model in section 4.

The score equation for β from the multivariate fixed-effect model is

$${\mathbf{U}}^{mv}={\displaystyle \sum _{i=1}^n{\mathbf{U}}_i^{mv}}={\displaystyle \sum _{i=1}^n{\mathbf{V}}_i^{-1}({\mathbf{y}}_i-\mathit{\beta })=0.}$$ (2)

so that U^mv is obtained by summing over the independent ${\mathbf{U}}_i^{mv}$. The maximum likelihood point estimate of β from the multivariate meta-analysis is then

$${\widehat{\mathit{\beta }}}_{mv}={\left({\displaystyle \sum _{i=1}^n{\mathbf{V}}_i^{-1}}\right)}^{-1}{\displaystyle \sum _{i=1}^n{\mathbf{V}}_i^{-1}{\mathbf{y}}_i={\displaystyle \sum _{i=1}^n{\mathbf{W}}_i{\mathbf{y}}_{i\hspace{0.17em}}}}$$ (3)

where

$${\mathbf{W}}_i={\left({\displaystyle \sum _{i=1}^n{\mathbf{V}}_i^{-1}}\right)}^{-1}{\mathbf{V}}_i^{-1}$$

with variance

$$\text{var}({\widehat{\mathit{\beta }}}_{mv})={\left({\displaystyle \sum _{i=1}^n{\mathbf{V}}_i^{-1}}\right)}^{-1}.$$

Missing outcome data can be conveniently handled in all equations by allocating the missing data inordinately large variances and correlations of zero, and imputing an arbitrary value for the missing estimates (such as zero or a sample average). Hence, it is not necessary that all studies provide all p estimates; this is important because some missing outcome data are very common in application. We focus on BoS in the estimation of β_r, the rth component of β, where r takes integer values from 1 to p.

We obtain the univariate fixed-effect model for the rth effect by taking the corresponding marginal model from model (1) as

$$y_{ir}\sim N({\beta }_r,V_{irr})$$

where V_irr = S_irr. The resulting score equation for β_r is

$$U_r^{uv}={\displaystyle \sum _{i=1}^n{U}_{ir}^{uv}={\displaystyle \sum _{i=1}^n{V}_{irr}^{-1}(y_{ir}-{\beta }_r)=0}}$$ (4)

which gives the usual univariate fixed-effect inferences, ${\widehat{\beta }}_{uv,r}={\displaystyle {\sum }_{i=1}^n{w}_{ir}{y}_{ir}}$ and $\text{var}({\widehat{\beta }}_{uv,r})=1/{\displaystyle {\sum }_{i=1}^n{V}_{irr}^{-1}}$, where $w_{ir}=V_{irr}^{-1}/{\displaystyle {\sum }_{i=1}^n{V}_{irr}^{-1}}$.

2.2. BoS by comparing variances

The simplest way to study BoS is to compare the variances of the estimated rth component of β under the univariate and multivariate models. We define

$$Bo{S}_r^{RV}=1-\frac{\text{var}({\widehat{\beta }}_{mv,r})}{\text{var}({\widehat{\beta }}_{uv,r})}$$ (5)

where $\text{var}({\widehat{\beta }}_{mv,r})$ and $\text{var}({\widehat{\beta }}_{uv,r})$ are the variances of ${\widehat{\beta }}_r$ under the multivariate and univariate fixed-effect models, respectively. RV refers to ‘Relative Variance’; if $Bo{S}_r^{RV}=0$ then the variance of ${\widehat{\beta }}_r$ is the same under these two models and the additional effects included in the multivariate meta-analysis have lent no strength to ${\widehat{\beta }}_{mv,r}$. As $Bo{S}_r^{RV}$ increases the variance of ${\widehat{\beta }}_r$ from the multivariate meta-analysis decreases, relative to its variance from the univariate meta-analysis, and the additional effects lend more strength.

Riley et al.³ establish, if the variance structure is treated as fixed and known, that the precisions of the point estimates from a multivariate meta-analysis are always greater than or equal to those from separate univariate meta-analyses. Thus, under a fixed-effect model, equation (5) cannot be negative.

2.2.1. Calculations for a simple case

In order to further examine how the $Bo{S}_r^{RV}$ statistic describes the BoS in a multivariate meta-analysis, it is helpful to consider a simple special case. Suppose p = 2 and there are two groups of studies, G = A, B, where the within-study correlation is assumed common for all studies in each group. This means that there are only two values of within-study correlation in the studies that comprise the meta-analysis. Thus, we have

$${\mathbf{\text{V}}}_i^{-1}=\frac{1}{1-{\rho }_G^2}\left(\begin{array}{cc}{S}_{i11}^{-1}& -{\rho }_G{S}_{i11}^{-1/2}{S}_{i22}^{-1/2}\\ -{\rho }_G{S}_{i11}^{-1/2}{S}_{i22}^{-1/2}& S_{i22}^{-1}\end{array}\right)\hspace{0.17em}\text{for}\hspace{0.17em}i\in \hspace{0.17em}\text{group}\hspace{0.17em}G.$$

where ρ_G denotes the within-study correlation in group G. So the sum of the inverse variances over all studies in both groups is given by

$${\displaystyle \sum _{i=1}^n{\mathbf{\text{V}}}_i^{-1}}=\left(\begin{array}{ll}\frac{w_{A11}}{1-{\rho }_A^2}+\frac{w_{B11}}{1-{\rho }_B^2}& -\left(\frac{{\rho }_A{w}_{A12}}{1-{\rho }_A^2}+\frac{{\rho }_B{w}_{B12}}{1-{\rho }_B^2}\right)\\ -\left(\frac{{\rho }_A{w}_{A12}}{1-{\rho }_A^2}+\frac{{\rho }_B{w}_{B12}}{1-{\rho }_B^2}\right)& \frac{w_{A22}}{1-{\rho }_A^2}+\frac{w_{B22}}{1-{\rho }_B^2}\end{array}\right)$$ (6)

where we write

$$w_{Grs}={\displaystyle \sum _{i\in G}{S}_{irr}^{-1/2}{S}_{iss}^{-1/2}}$$

for r, s = 1, 2. We focus on estimating β₁. Under multivariate analysis $\text{var}({\widehat{\beta }}_{mv,1})$ is

$${\left\{{\left({\displaystyle \sum _{i=1}^n{\mathbf{\text{V}}}_i^{\text{−1}}}\right)}^{-1}\right\}}_{11}={\left\{\left(\frac{w_{A11}}{1-{\rho }_A^2}+\frac{w_{B11}}{1-{\rho }_B^2}\right)(1-{\rho }^{*2})\right\}}^{-1}$$

where ρ* is the correlation in the covariance structure in equation (6), so that

$${\rho }^{\text{*2}}=\frac{{\left(\frac{{\rho }_A{w}_{A12}}{1-{\rho }_A^2}+\frac{{\rho }_B{w}_{B12}}{1-{\rho }_B^2}\right)}^2}{\left(\frac{w_{A11}}{1-{\rho }_A^2}+\frac{w_{B11}}{1-{\rho }_B^2}\right)\left(\frac{w_{A22}}{1-{\rho }_A^2}+\frac{w_{B22}}{1-{\rho }_B^2}\right)}$$

Under univariate analysis, $\text{var}({\widehat{\beta }}_{uv,1})$ is

$${\left\{{\displaystyle \sum _{i=1}^n{V}_{i11}^{-1}}\right\}}^{-1}={\{w_{A11}+w_{B11}\}}^{-1}$$

so, using the definition of ρ^*2 given above, the BoS is

$$Bo{S}_1^{RV}=1-\frac{\left(w_{A11}+w_{B11}\right)\left(\frac{w_{A22}}{1-{\rho }_A^2}+\frac{w_{B22}}{1-{\rho }_B^2}\right)}{\left(\frac{w_{A11}}{1-{\rho }_A^2}+\frac{w_{B11}}{1-{\rho }_B^2}\right)\left(\frac{w_{A22}}{1-{\rho }_A^2}+\frac{w_{B22}}{1-{\rho }_B^2}\right)-{\left(\frac{{\rho }_A{w}_{A12}}{1-{\rho }_A^2}+\frac{{\rho }_B{w}_{B12}}{1-{\rho }_B^2}\right)}^2}.$$

In order to interpret this result, we consider three even more special cases. Firstly, if ρ_A = ρ_B = 0 then $Bo{S}_1^{RV}=0$. This means that if there is no within-study correlation between the two estimated effects then no BoS is possible. Secondly, if all within-study covariance matrices are proportional to each other, so that S_i = k_iS, we then have ρ_A = ρ_B = ρ and (w_A12 + w_B12)² = (w_A11 + w_B11)(w_A22 + w_B22). This means that $Bo{S}_1^{RV}=0$ when all S_i are proportional; Riley et al.³ previously noted that BoS is zero when all within-study covariance matrices are identical.

Finally, if the first effect of interest is missing in group B (represented as ${\mathbf{\text{S}}}_{i11}^{-1}=0$), then we have w_B11 = w_B12 = ρ_B = 0 and after some algebra we can derive

$$Bo{S}_1^{RV}=\frac{{\rho }_A^2\left\{1-c^2+(1-{\rho }_A^2)\lambda \right\}}{\left\{1-{\rho }_A^2{c}^2+(1-{\rho }_A^2)\lambda \right\}}$$

where $c^2=w_{A12}^2/w_{A11}{w}_{A22}$ and $\lambda =w_{B22}/w_{A22}.$ Thus, in this setting, $0<Bo{S}_1^{RV}<{\rho }_A^2.$ This means that, when within-study correlations are non-zero, some BoS by the first effect is inevitable when its data are missing in this way but also that this BoS is bounded by the magnitude of the correlation ρ_A in the complete (no missing data) studies.

These observations show that our $Bo{S}_r^{RV}$ statistic corresponds to our intuitive understanding of the nature of BoS in these simple situations: no BoS is possible when the two types of estimated effects are independent and, when there is missing data, some BoS is inevitable but the available within-study correlations constrain the extent to which this is possible. It is obvious that no BoS is possible when all within-study covariance matrices are identical, because then the data are independently and identically normally distributed so that the point estimate of β is the sample mean. However, this result establishes a stronger statement that no BoS is possible when the within-study covariance matrices are proportional to each other.

2.3. Decomposing the score function for β

We now derive an alternative BoS statistic which we will see is in fact the same as $Bo{S}_r^{RV}.$ The alternative derivation presented in this subsection is more opaque than the one presented previously, but has the advantage that it leads to a definition of study weights, as explained in section 3.

Using the standard property of score equations for normally distributed outcomes with known variance structure, we have that

$$\text{var}\left({\mathbf{\text{U}}}^{mv}\right)={\left\{\text{var}\left({\widehat{\mathit{\beta }}}_{mv}\right)\right\}}^{-1}$$

This is the usual approximation used in the asymptotic theory of maximum likelihood but this is exact for normally distributed data with known variance structure because then the log-likelihood is perfectly quadratic. We define $\mathbf{\text{M}}={\left\{{\sum }_i{\mathbf{V}}_i^{-1}\right\}}^{-1}$ where, because the V_i = S_i are treated as constants, M is also regarded as a constant. Hence

$$\mathbf{\text{M}}=\text{var}({\widehat{\mathit{\beta }}}_{mv})={\left\{\text{var}({\mathbf{\text{U}}}^{mv})\right\}}^{-1}$$ (7)

and note that

$${\mathbf{\text{MU}}}^{mv}=\left(\mathbf{\text{M}}{\displaystyle \sum _{i=1}^n{\mathbf{\text{V}}}_i^{-1}{\mathbf{\text{y}}}_i}\right)-\mathit{\beta }$$

where the right hand side is a multiple of the usual estimating equation and so an estimating equation for β_r from the multivariate model is

$${\left({\mathbf{\text{MU}}}^{mv}\right)}_r=0.$$

Appendix 1 shows that

$$\text{E}\left[{\text{U}}_i^{mv}|y_{ir}\right]=U_{ir}^{uv}{\mathbf{\text{e}}}_r$$ (8)

where e_r is the unit vector with 1 in the rth position. Hence, we can write

$${\mathbf{\text{U}}}^{mv}={\displaystyle \sum _{i=1}^n{\mathbf{\text{U}}}_i^{mv}={\displaystyle \sum _{i=1}^n{U}_{ir}^{uv}{\mathbf{\text{e}}}_r+{\displaystyle \sum _{i=1}^n\left({\mathbf{\text{U}}}_i^{mv}-U_{ir}^{uv}{\mathbf{\text{e}}}_r\right)}}}$$ (9)

where all 2n terms in the final expression in equation (9) are independent. We prove this independence in Appendix 2.

2.4. Defining BoS statistics using the score decomposition

Premultiplying equation (9) by M, and taking the rth component, gives a decomposition of the estimating equation for β_r into independent terms:

$${\left({\mathbf{\text{MU}}}^{mv}\right)}_r={\displaystyle \sum _{i=1}^n{M}_{rr}{U}_{ir}^{uv}+{\displaystyle \sum _{i=1}^n\left\{{\left({\mathbf{\text{MU}}}_i^{mv}\right)}_r-M_{rr}{U}_{ir}^{uv}\right\}}}$$ (10)

where M_rr is the entry in the rth row and column of M. We take the variances of the terms in equation (10) to express the information contributed to the estimation of β_r. The variance of the term on the left hand side of equation (10) defines the total information contribution of all estimates from all studies included in the multivariate meta-analysis to the estimation of β_r. The variance of the first term on the right hand side of equation (10) defines the direct information contribution of estimates from all studies (i.e. the estimates that would be included in a univariate meta-analysis that estimates β_r). This is because this term results from the estimating equation from a univariate meta-analysis. Finally, the variance of the second term on the right hand side of equation (10) defines the indirect information contribution of the other estimates (i.e. the estimates that would not be included in a univariate meta-analysis, and so provide indirect evidence about this parameter). As we explain above, the terms that are used to express the direct and indirect evidence are independent; this independence ensures that we can clearly distinguish between the two types of evidence in this way.

Furthermore, because the summations in equation (10) run across all studies, we further define the study specific total, direct and indirect information contributions to the estimation of β_r. Specifically, we define the total information contribution of study i to estimation of β_r as

$${\mathit{I}}_{ir}^{total}=\text{var}({({\mathbf{\text{MU}}}_i^{mv})}_r)$$

We define the direct information contribution of study i to the estimation to β_r as

$${\mathit{I}}_{ir}^{direct}=\text{var}(M_{rr}{U}_{ir}^{uv}).$$

The indirect information contribution of study i to the estimation to β_r can then be taken as ${\mathit{I}}_{ir}^{indirect}={\mathit{I}}_{ir}^{total}-{\mathit{I}}_{ir}^{direct}.$ We define the BoS for effect r (from all studies) as

$$Bo{S}_r^{SD}=1-\frac{{\mathit{I}}_r^{direct}}{{\mathit{I}}_r^{total}}=\frac{{\mathit{I}}_r^{indirect}}{{\mathit{I}}_r^{total}}$$ (11)

where SD refers to ‘Score Decomposition’; ${\mathit{I}}_r^{direct}={\displaystyle {\sum }_i{\mathit{I}}_{ir}^{direct}\hspace{0.17em}\text{and}\hspace{0.17em}{\mathit{I}}_r^{total}=}{\displaystyle {\sum }_i{\mathit{I}}_{ir}^{total}}.$ We also define the BoS for effect r that is due to the ith study as

$$Bo{S}_{ir}^{SD}=\frac{{\mathit{I}}_{ir}^{indirect}}{{\mathit{I}}_r^{total}}$$ (12)

2.5. Equality of the two BoS expressions

Although $Bo{S}_r^{RV}\hspace{0.17em}$ and $Bo{S}_r^{SD}$ are motivated in entirely different ways, it is straightforward to show that they are equivalent. From equation (7), var(MU^mv) = M so ${\mathit{I}}_r^{total}=\mathrm{var}\left({\left(\mathbf{\text{M}}{\mathbf{\text{U}}}^{mv}\right)}_r\right)=M_{rr}.$ Similarly, ${\mathit{I}}_r^{direct}=\text{var}(M_{rr}{U}_r^{uv})=M_{rr}^2{\{\mathrm{var}({\widehat{\mathit{\beta }}}_{uv})\}}^{-1}$

Again using equation (7), $M_{rr=}\text{var}({\widehat{\mathit{\beta }}}_{mv,r})$, so ${\mathit{I}}_r^{direct}/{\mathit{I}}_r^{total}=\text{var}({\widehat{\mathit{\beta }}}_{mv,r})/\text{var}({\widehat{\mathit{\beta }}}_{uv,r})$. Hence $Bo{S}_r^{RV}=Bo{S}_r^{SD}$, as stated.

3. Weights

The derivation of our BoS statistic using the score decomposition (sections 2.3 and 2.4) is much less intuitive than the derivation from comparing variances (section 2.2), but the advantage of the score decomposition derivation is that it immediately leads to a definition of study weights. The weights of studies in fixed-effect univariate meta-analyses (p = 1) are inversely proportional to the within-study variances and are usually rescaled to add up to 100%. These weights are typically displayed in standard output and forest plots and convey important information about which studies contribute the most to the estimated average effect.

We can also use the variance of the terms that result from the decomposition (10) to define the weight of study i for effect r as

$$w_{ir}=\frac{{\mathit{I}}_{ir}^{total}}{{\mathit{I}}_r^{total}}.$$ (13)

We call these “study weights” which reduce to the usual weights univariately. This definition of weights motivates us to further define the direct information for effect r that is due to the ith study as

$$\mathit{D}{\mathit{I}}_{ir}^{SD}=\frac{{\mathit{I}}_{ir}^{direct}}{{\mathit{I}}_r^{total}}$$ (14)

so that

$$w_{ir}=D{I}_{ir}^{SD}+Bo{S}_{ir}^{SD}$$ (15)

This means that the study weights for the rth outcome are equal to the sum of the studies’ direct information and their BoS for the rth outcome. Since $I_{ir}^{direct}=\text{var}(M_{rr}{U}_{ir}^{uv})$, equation (14) means that a study that does not provide the rth effect provides no direct evidence to the estimation of β_r so that $w_{ir}=Bo{S}_{ir}^{SD}.$ Study weights and BoS statistics can be displayed in tabular and graphical forms, and this is illustrated in the examples in section 5.

3.1. Invariance to scaling

It is straightforward to show that our BoS statistics and our study weights are invariant to scaling, where each effect in the meta-analysis is multiplied by an effect specific fixed constant. We will use the notation ${\mathbf{y}}_i^{*}={\mathbf{Cy}}_i$ to denote the scaling transformation, where C is a diagonal matrix containing effect specific scaling factors. Then ${\mathbf{\text{V}}}_i^{*-1}={\mathbf{\text{C}}}^{-1}{\mathbf{V}}_i^{-1}{\mathbf{\text{C}}}^{-1}$ and β* = Cβ, so that U^mv* = C⁻¹U^mv and M* = CMC. This means that M*U^mv* = CMU^mv, so that ${\mathbf{\text{M}}}^{*}{\mathbf{\text{U}}}_r^{mv*}=C_{rr}{\mathbf{\text{MU}}}_r^{mv}.$ Upon dividing both sides of the resulting score decomposition for the scaled data by C_rr we recover the score decomposition for the original data (10). Hence, our BoS statistics and study weights that are based on this decomposition apply to both the scaled and original data and so are invariant to scaling.

3.2. Data-point coefficients

It follows from equation (3) that the rth component of ${\widehat{\mathbf{\beta }}}_{mv}$, like its univariate counterpart, is a weighted sum of all the observations y_is, where the weight for the sth effect in the ith study is W_irs, the (r, s) element of W_i. We call these “data-point coefficients” and these values have previously been proposed as weights.¹⁴ These coeffcients also give an indication of the weight that each estimate y_is contributes to ${\widehat{\mathbf{\beta }}}_{mv,r}$ and so we suggest that these might be worth reporting. The data-point coefficients also reduce to the usual weights univariately but are not invariant to scaling. The data-point coefficients provide p weights per outcome and study, because each individual estimate provides a data-point coefficient, whereas the proposed weights w_ir give one weight per outcome and study.

The use of the hat matrix has also been proposed to define weights in the context of network meta-analysis.⁶ For a multivariate meta-analysis (after imputing any missing data as explained in section 2.1) the design matrix is obtained by stacking identity matrices, so that the main block diagonal of the hat matrix contains the W_i matrices. This means that using the diagonal entries of the hat matrix as weights is equivalent to using the data-point coefficients W_irr for this purpose.

4. The random-effects model

The previous sections have assumed a fixed-effect model; in other words that there is no between-study heterogeneity in any of the effects of interest. This is a strong assumption that greatly simplified the development of our methods because all variance components are treated as known under the fixed-effect model. Using a multivariate random-effects model is in general more plausible than assuming an absence of between-study heterogeneity. However, the between-study covariance matrix must also be estimated in a multivariate random-effects meta-analysis.

Upon relaxing the fixed-effect assumption, the multivariate random-effects model is given by equation (1) where V_i = S_i + Σ so that

$${\mathbf{\text{y}}}_i\sim N\left(\mathit{\beta },{\mathbf{\text{S}}}_i+\mathit{\Sigma }\right)$$

where Σ is the between-study covariance matrix. The main diagonal of Σ therefore contains the between-study variances and the other entries of Σ are between-study covariances. A variety of approaches for estimating Σ have been suggested.^22–26 Once Σ has been estimated, however, the standard procedure for making inferences about the average treatment effects approximates the true between-study variance with $\widehat{\mathit{\Sigma }}$.² We suggest also making this approximation, so that all the previous methods in sections 2 and 3 can still be used but V_i = S_i now becomes ${\mathbf{\text{V}}}_i={\mathbf{\text{S}}}_i+\widehat{\mathit{\Sigma }}$. However, since our new methods are based on a decomposition of the score function, using this standard approximation in conjunction with our proposals is most natural when the estimation of Σ is also based on the likelihood function.

There is one caveat here, however: using $\widehat{\mathit{\Sigma }}$ when calculating the $Bo{S}_r^{RV}$ statistic under the random-effects model in this way might be thought to give more credence to the multivariate model fit. This is because $\widehat{\mathit{\Sigma }}$ is forced to be as estimated from the multivariate analysis, but univariate and multivariate random-effect meta-analyses will in general provide different estimates of the between-study variances (the diagonal entries of $\widehat{\mathit{\Sigma }}$). Thus, when calculating BoS statistics for the random-effects model we are faced with a dilemma: when calculating $\text{var}\left({\widehat{\beta }}_{uv,r}\right)$ in equation (5), is it really appropriate to use the rth diagonal entry of $\widehat{\mathit{\Sigma }}$ from the multivariate analysis? If we instead use the univariate estimate of the between-study variance when calculating $\text{var}\left({\widehat{\beta }}_{uv,r}\right)$ we obtain an alternative or modified BoS statistic

$$Bo{S}_r^{\prime RV}=1-\frac{\text{var}\left({\widehat{\beta }}_{mv,r}\right)}{\text{var}\left(\widehat{\beta }{({\widehat{\tau }}_{uv,r}^2)}_{uv,r}\right)}$$ (16)

The notation $\widehat{\beta }{({\widehat{\tau }}_{uv,r}^2)}_{uv,r}$ emphasises that the univariate estimate of between-study variance is used when calculating the variance of the univariate estimate of the average effect, because τ² is conventionally used to denote the between-study variance in univariate analyses; the multivariate estimates of the between-study variance components continue to be used when calculating $\text{var}\left({\widehat{\beta }}_{mv,r}\right)$ in equation (16). However, this modified $Bo{S}_r^{\prime RV}$ presents further issues. First of all, the equivalence between $Bo{S}_r^{RV}$ and $Bo{S}_r^{SD}$ is lost when using this alternative approach. Secondly, because of the differences between the univariate and multivariate estimates of the between-study variances, $Bo{S}_r^{\prime RV}$ can be negative. From a theoretical viewpoint it would seem clear that for BoS in the multivariate random-effects model it is preferable to use equation (5) with both variances derived using $\widehat{\mathit{\Sigma }}$ from the multivariate random-effects model. Some meta-analysts may however prefer to use equation (16) in application.

When the modified BoS statistic (16) differs substantially from its counterpart then we suggest presenting both types of BoS statistics and we do this for the first two examples in section 5 (Table 2). In large samples we can anticipate little difference between the univariate and multivariate estimates of the between-study variances but their estimation is less robust in meta-analyses with small numbers of studies. If the multivariate estimates of the between-study variances are larger than the univariate estimates then equation (16) could be very considerably less than zero. This tells us that the use of a multivariate, rather than a more conventional univariate, meta-analysis has important implications (resulting in markedly different point estimates) for the estimation of the between-study variance components. This is the case for our first two examples and is especially so for the final effect (stroke) in our first example. Our methods based on the score decomposition do not describe the implications of using a multivariate meta-analysis for the estimated variance components when using random effect models, rather they measure the BoS afforded by the multivariate approach using the estimated variance components from the fitted multivariate model. Some may prefer the convention of truncating negative modified BoS statistics to zero but we present negative values in order to clarify the extent to which the fitted multivariate model results in wider confidence intervals than the fitted univariate model.

Table 2.

Meta-analysis results for the first two examples.

Example	Model	Measure	Effect type	Estimate	95% CI	$\widehat{\tau }$	BoS % (equation (12))	$Bo{S}_r^{\prime RV}\hspace{0.17em}\%$ (equation (16))
Hypertension	Uni	SBP	MD	−10.16	(−12.06, −8.27)	2.68	–	–
(section 5.1)	Uni	DBP	MD	−4.58	(−5.59, −3.57)	1.47	–	–
	Uni	CVD	HR	0.78	(0.69, 0.89)	0.00	–	–
	Uni	Stroke	HR	0.68	(0.59, 0.79)	0.00	–	–
	Multi	SBP	MD	−10.22	(−12.14, −8.30)	2.73	0.9%	−2.4%
	Multi	DBP	MD	−4.63	(−5.67, −3.60)	1.51	0.5%	−5.1%
	Multi	CVD	HR	0.79	(0.69, 0.91)	0.05	4.2%	−8.3%
	Multi	Stroke	HR	0.73	(0.61, 0.87)	0.14	20.8%	−57.2%
Fibrinogen	Uni	Part	HR	1.41	(1.33, 1.49)	0.10	–	–
(section 5.2)	Uni	Full	HR	1.31	(1.22, 1.42)	0.07	–	–
	Multi	Part	HR	1.41	(1.33, 1.50)	0.11	1.9%	−8.4%
	Multi	Full	HR	1.31	(1.25, 1.38)	0.07	53.3%	53.1%

‘Uni’ indicates that the results are obtained from univariate meta-analyses and ‘Multi’ indicates that the results are obtained from multivariate meta-analyses. ‘MD’ denotes mean difference and ‘HR’ denotes hazard ratio. Analyses were performed on the mean difference and log hazard ratios scales; $\widehat{\tau }$ is the estimated between-study standard deviation on the mean difference and log hazard ratio scales and the BoS statistics are also on these scales. The estimated between study correlations in the multivariate meta-analysis for example one are (SBP, DBP): 0.79, (SBP, CVD): −0.31 (SBP, Stroke): −0.53 (DBP, CVD): −0.83 (DBP, Stroke): −0.94, (CVD, Stroke): 0.97. The estimated between-study correlation in the multivariate meta-analysis for example two is 1.

SBP:systolic blood pressure; SBP: systolic blood pressure; CVD: cardiovascular disease; Part: partially adjusted effect of fibrinogen level; Full: fully adjusted effect of fibrinogen level.

5. Examples

In this section, we apply our methods to some contrasting real examples that have appeared in the literature. For all our examples we fit random-effects models using restricted maximum likelihood (REML) to estimate the between-study covariance matrix. We use the Stata mvmeta package²⁶ with its defaults throughout, so that the entire observed Fisher information matrix (including the variance components) is used to compute the covariance matrix of the treatment effect parameters. Hence the uncertainty in the between-study covariance matrix is reflected in the results that follow. By using methods based on the score decomposition, the BoS statistics are unchanged by acknowledging the uncertainty in the between-study variance components in this way. However methods based directly on either equation (5) or (16) would be changed by this. The Stata mvmeta package has now been updated to calculate BoS statistics and study weights using the wt option. This updated package is available at the second author’s website.

5.1. Meta-analysis of randomised trials with multiple outcomes

Riley et al.²¹ use individual participant data (IPD) for a total of 28581 patients from 10 randomised controlled trials to evaluate whether hypertension treatments lower systolic blood pressure (SBP) and diastolic blood pressure (DBP), and also whether these treatments reduce the risks of a subsequent diagnosis of cardiovascular disease (CVD) or stroke. Each trial randomised patients to either an active anti-hypertensive drug or placebo, and all four outcomes were recorded in every trial. For SBP and DBP, analysis of covariance models were used in each study to calculate adjusted (for baseline blood pressure scores) treatment effect estimates and their standard errors, in terms of mean differences (treatment minus placebo), where negative values indicate a greater blood pressure reduction in the treatment group. For CVD and stroke, Cox regression models were used in each study to calculate the treatment effect estimates (and their standard errors) in terms of log hazard ratios, with a hazard ratio of less than one indicating lower outcome risk in the treatment group. Nonparametric bootstrapping was used to obtain the within-study correlations between each pair of treatment effect estimates, as described elsewhere.²¹ These correlations are small, except for those between the estimated treatment effects on SBP and DBP. Table 1 summarises the data required for multivariate meta-analysis, and the results from univariate and multivariate random-effects meta-analysis are shown in the top part of Table 2. The meta-analyses were performed on the log hazard ratio scales for CVD and stroke but the estimates and confidence intervals in Table 2 have been converted to the hazard ratio scale. The multivariate and univariate meta-analysis results are in reasonable agreement, and suggest that anti-hypertensive drugs are effective at reducing blood pressure and the risk of CVD and stroke.

Table 1.

Data required for a multivariate meta-analysis of the 10 hypertension trials.

	Treatment effect estimates (within-study variances)				Within-study correlations
Trial	SBP (1)	DBP (2)	CVD (3)	Stroke (4)	(1)&(2)	(1)&(3)	(1)&(4)	(2)&(3)	(2)&(4)	(3)&(4)
1	−6.66 (0.72)	−2.99 (0.27)	−0.09 (0.17)	−1.91 (1.17)	0.79	0.01	−0.01	−0.02	−0.02	0.16
2	−14.17 (4.73)	−7.87 (1.44)	0.06 (0.13)	−0.15 (0.17)	0.50	0.11	0.10	0.09	0.10	0.64
3	−12.88 (10.31)	−6.01 (1.77)	−0.17 (0.20)	0.75 (0.35)	0.59	−0.21	−0.05	−0.04	−0.04	0.10
4	−8.71 (0.30)	−5.11 (0.10)	−0.24 (0.03)	−0.29 (0.07)	0.77	0.09	0.02	0.13	0.04	0.52
5	−8.70 (0.14)	−4.64 (0.05)	−0.18 (0.03)	−0.41 (0.11)	0.64	0.04	0.04	0.04	0.04	0.42
6	−10.60 (0.58)	−5.56 (0.18)	−0.23 (0.02)	−0.20 (0.03)	0.50	0.00	0.03	−0.02	0.00	0.62
7	−11.36 (0.30)	−3.98 (0.075)	−0.32 (0.02)	−0.45 (0.02)	0.48	−0.01	−0.02	−0.03	−0.03	0.69
8	−17.93 (5.82)	−6.54 (1.31)	−1.87 (1.17)	0.32 (0.83)	0.59	−0.02	−0.07	−0.03	0.00	0.35
9	−6.55 (0.41)	−2.08 (0.11)	−0.33 (0.09)	−0.48 (0.04)	0.45	0.11	0.08	0.03	0.03	0.78
10	−10.26 (0.20)	−3.49 (0.04)	−0.26 (0.03)	−0.55 (0.03)	0.48	0.05	0.04	0.04	0.05	0.62

SBP:systolic blood pressure; SBP: systolic blood pressure; CVD: cardiovascular disease.

Table 2 also shows the BoS statistics from equation (11) and the alternative BoS statistics from equation (16). The first set of BoS statistics show that, with the exception of the treatment effect for stroke, very little BoS occurs. This should be anticipated because all studies provide data on all four treatment effects. The estimated between study standard deviations are larger in the multivariate than in the univariate meta-analyses and so the $Bo{S}_r^{\prime RV}$ statistics (16) can be negative, and are so for all four effects. However, the variance components are imprecisely estimated in a relatively high dimension example with just 10 studies such as this one and so we should not be too surprised by this finding.

Table 3 shows how we can tabulate the study weights and BoS statistics from the multivariate meta-analysis, where the weights are broken down into direct information and BoS as shown in equation (15). The direct information desrcibes the contribution of data from the same outcome, whereas the BoS describes the contribution of data for all other outcomes. Each study has four weights, one for each outcome, where the weights for each outcome sum to 1 (or 100% when expressed as a percentage). Table 3 confirms that the majority of the information in this analysis comes from direct information. This table also shows that the three smaller (larger within-study variances in Table 1) trials 2, 3 and 8 contribute less weight to the analysis.

Table 3.

Study weights (%) and BoS (%) for each outcome, expressed as percentages, in the multivariate meta-analysis of the 10 hypertension trials.

	Direct information % (equation (14))				BoS % (equation (12))				Weight % (equation (13))
Trial	SBP	DBP	CVD	Stroke	SBP	DBP	CVD	Stroke	SBP	DBP	CVD	Stroke
1	10.94	10.49	2.69	0.6	0.04	0.00	0.35	3.29	10.98	10.49	3.03	3.88
2	7.34	7.21	3.55	3.7	0.17	0.40	0.23	1.07	7.51	7.62	3.77	4.77
3	5.04	6.62	2.24	1.91	0.47	0.05	0.76	1.80	5.50	6.67	2.99	3.71
4	11.54	11.23	14.37	8.3	0.04	0.01	0.20	1.08	11.57	11.24	14.57	9.38
5	11.77	11.48	13.78	5.37	0.03	0.01	0.15	2.69	11.80	11.49	13.92	8.06
6	11.12	10.87	17.04	13.74	0.01	0.01	0.30	0.30	11.13	10.88	17.34	14.04
7	11.53	11.37	23.63	19.82	0.01	0.02	1.05	5.07	11.55	11.39	24.68	24.89
8	6.74	7.46	0.39	0.83	0.14	0.03	0.44	1.79	6.88	7.49	0.83	2.62
9	11.36	11.21	4.73	11.84	0.01	0.00	0.72	3.52	11.37	11.21	5.45	15.36
10	11.69	11.52	13.37	13.11	0.01	0.01	0.03	0.17	11.70	11.54	13.4	13.28
Total	99.07	99.46	95.78	79.22	0.93	0.54	4.22	20.78	100	100	100	100

SBP: systolic blood pressure; SBP: systolic blood pressure; CVD: cardiovascular disease.

To summarise, the proposed BoS statistics and study weights add further insight to the previous analysis of these data.²¹ For example, we can see that the study weights differ very considerably for the two survival outcomes but the weights are much more similar for the blood pressure outcomes.

5.2. Meta-analysis of partially and fully adjusted results

The Fibrinogen Studies Collaboration¹³ used a bivariate meta-analysis to account for the correlation between partially adjusted and fully adjusted risk factor effects. Specifically, they examine whether fibrinogen is a risk factor for CVD using individual patient data from 31 studies. Log hazard ratios were estimated from a Cox regression, indicating the effect associated with a one unit increase in fibrinogen on the rate of CVD. All studies allowed a partially adjusted hazard ratio to be obtained, where the hazard ratio for fibrinogen was adjusted for the same core set of known risk factors, including age, smoking, BMI and blood pressure. However, a fully adjusted hazard ratio was only calculable in 14 studies, which additionally adjusted for cholesterol, alcohol consumption, triglycerides and diabetes. The data required for bivariate meta-analysis is provided in the supplementary material, where the within-study correlations are derived using nonparametric bootstrapping. The fully and partially adjusted effects of fibrinogen are modelled in a bivariate meta-analysis. We assume that the 17 missing fully adjusted hazard ratios are missing at random: this assumption is perfectly reasonable because the additional covariates that are included in the fully adjusted analyses are systematically missing in this meta-analysis.¹³

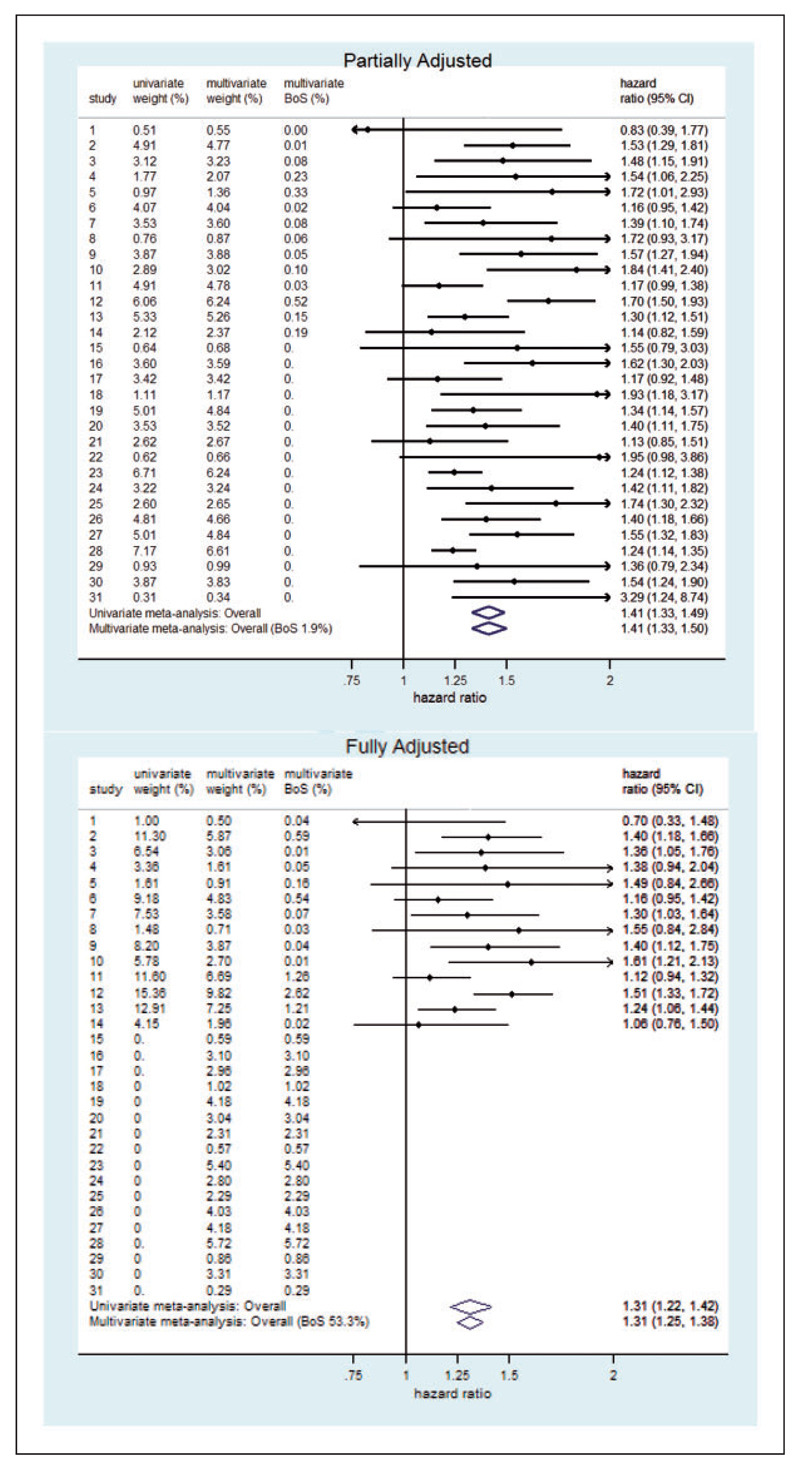
The bivariate and univariate random-effects meta-analysis results are shown in the bottom part of Table 2. Here the estimated between-study correlation in the random-effects meta-analysis is one.¹³ These analyses give almost identical estimates for the summary hazard ratios and the between-study standard deviations for both partially and fully adjusted effects. However, by utilising the large within-study and between-study correlations (all close to one), the bivariate meta-analysis has increased precision for the fully adjusted summary result: the standard error of the pooled log hazard ratio is about 30% smaller in the bivariate (0.27) compared to univariate (0.39) analysis. This is due to the bivariate analysis borrowing strength from the partially adjusted estimates, especially in those 17 studies where only partially adjusted estimates were available. This is reflected by a large BoS statistic of 53%, indicating that 53% of the information in the fully adjusted pooled result is due to the partially adjusted estimates. In contrast, BoS is just 1.9% for the partially adjusted summary result, as partially adjusted estimates are available in all 31 studies and so it gains little from the fully adjusted results. If BoS is instead calculated using equation (16), then it is again 53% for the fully adjusted result but negative (−8%) for the partially adjusted result. Figure 1 shows augmented forest plots for the partially and fully adjusted effects. These plots show the univariate random-effects models’ overall summary results in the usual way. However the bottom of the forest plots are augmented with the bivariate meta-analysis estimates and confidence intervals and the BoS statistic from equation (11). Furthermore, the bivariate weights from equation (13) and the study specific BoS statistics (12) are also shown as percentages with the univariate weights. Figure 1 illustrates how additional information from the partially adjusted estimates is being borrowed in the bivariate meta-analysis. Our new results presented here provide much more insight into how the partially adjusted estimates contribute to the estimate of the fully adjusted effect of fibrinogen than was hitherto possible. For example, from Figure 1 we can see that the partially adjusted results contribute heavily in the bivariate analysis; indeed they contribute almost half of the total information toward the fully adjusted summary result despite providing no direct evidence about this quantity. Furthermore, some studies that do not provide fully adjusted estimates provide more weight to the estimation of the fully adjusted estimate than some studies that provide both types of estimate.

Figure 1.

Forest plots for the bivariate random effects meta-analysis of the partially and fully adjusted effects of fibrinogen. The modified BoS statistic (16) for the partially adjusted effect is negative which means that the corresponding multivariate confidence interval is wider than the univariate one in the first forest plot.

5.3. Network meta-analysis: Thrombolytic treatments after acute myocardial infarction

Lu and Ades⁷ present a network meta-analysis of 28 trials that compare eight thrombolytic treatments after acute myocardial infarction: for brevity we refer to these treatments as A to H. Of interest is a comparison of the odds of mortality by 30–35 days for each pair of treatments. The supplementary material provides the raw data in terms of the number of deaths and the total patients for all studies. Here we use these data to estimate log odds ratios, and their variances and within-study correlations, for each pair of treatments in each study. As there are eight treatments, there are 28 comparisons of interest overall. However, only 13 of these comparisons are directly compared in the same trial. Further, the maximum number of trials providing direct evidence for a particular comparison is only eight (C versus A). Thus, there is an opportunity to borrow strength in this example because each treatment comparison can utilise correlated (indirect) information from other pairs of treatment in the network.

To model the data we choose a common reference group in all studies (here, we chose treatment A) and express all available treatment comparison estimates in relation to this reference group. We then fit a multivariate meta-analysis model, using the estimated log odds ratios as outcome data, in seven dimensions that describes the treatment effects of B, C, D, E, F, G, and H versus A. As the reference treatment A was unavailable in many studies, a data augmentation approach was used.⁹ Then for example, under the consistency assumption, the log odds ratio of C versus B can be expressed as the difference between the log odds ratio estimate of C versus A and the log odds ratio for B versus A. For further details, including how the within-study correlations were obtained, see White et al.⁹ and White.²⁶ The multivariate model was fitted with a common between-study variance assumed for all treatment comparisons, and all between-study correlations forced to be 0.5: this form of between-study variance structure is justified under the assumption that the heterogeneity variance is the same for all treatment comparisons for every study.⁸

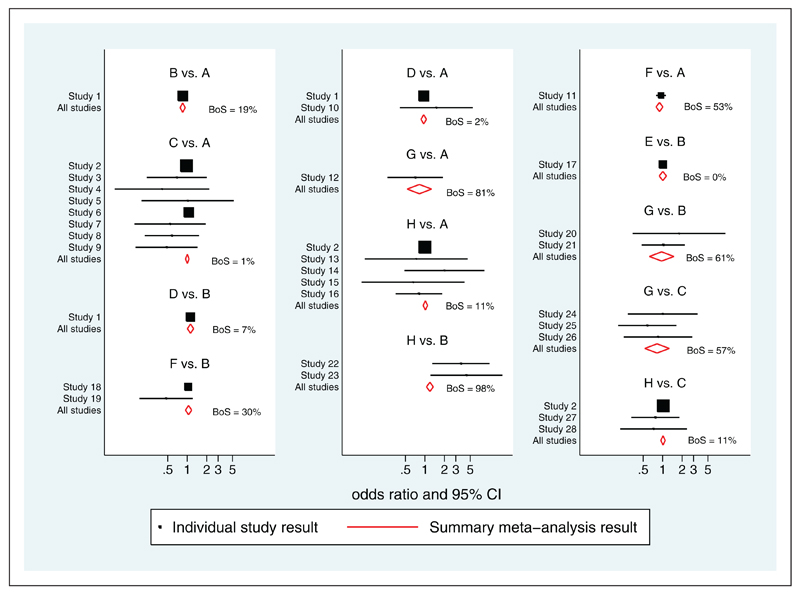
The study estimates and multivariate meta-analysis results are displayed in Figure 2 for all those comparisons where direct evidence was available in at least one trial. In order to conveniently evaluate BoS for all pairwise comparisons, and not just those involving A, the model was repeatedly refitted using the other seven treatments B–H as the reference group. This refitting was for computational convenience only; the model fit does not depend on the choice of reference group. An equivalent approach would be to perform a single model fit and instead calculate the quantities required for pairwise comparisons not involving A as contrasts of pairwise estimates that do involve A. BoS for each pairwise comparison is presented in Table 4 and the values are often large, due to the large amount of ‘indirect’ information available in the network. From Table 4 we can see that symmetrical results are obtained by this process so that the BoS statistics are the same regardless of which treatment is used as the reference. The weights for the contrasts with treatment A as the reference treatment are provided in the supplementary materials.

Figure 2.

Forest plots for the network meta-analysis of thrombolytic treatments after acute myocardial infarction.

Table 4.

BoS (%) for each pairwise comparison in the thrombolytics network meta-analysis.

Pairwise comparison	A	B	C	D	E	F	G	H
A	–	18.86	1.12	2.11	100	53.46	80.63	11.45
B	18.86	–	100	6.82	0	30.02	60.58	97.81
C	1.12	100	–	100	100	100	57.24	11.44
D	2.11	6.82	100	–	100	100	100	100
E	100	0	100	100	–	100	100	100
F	53.46	30.02	100	100	100	–	100	100
G	80.63	60.58	57.24	100	100	100	–	100
H	11.45	97.81	11.44	100	100	100	100	–

Table 4 shows clearly how the indirect information contributes to the analysis. For example, the comparison of H versus B has a BoS of 97.8%, as there are only 2 trials with direct evidence and neither of these two trials are large. This BoS is reflected by a substantial difference in the pooled estimates from multivariate (summary OR = 1.19, 95% CI: 1.06 to 1.35) and univariate (summary OR = 3.87; 95% CI: 1.74 to 8.58) analyses, with the former much closer to one. BoS is 100% for some comparisons, such as D versus A, that have no direct evidence. In contrast, BoS is 0% for E versus B, as no indirect evidence contributes to this effect.

This example illustrates how BoS can be derived for any network meta-analysis model that can be expressed in the multivariate meta-analysis framework. Extensions might consider assuming different between-study variances for some comparisons or an inconsistency model. However, a global test for inconsistency is non-significant in this example.⁹

6. Discussion

We have proposed a framework for calculating BoS statistics and study weights in multivariate meta-analysis. Whilst recognising the potential usefulness of alternative ideas, we find our approach especially attractive because we are able to incorporate BoS statistics and weights into the same framework. Our weights are equal to BoS statistics when studies do not estimate the corresponding effect. We have shown how our proposed statistics can be displayed in both tabular form and in forest plots and have explained how they are a useful aid to inference.

The strategy of comparing the variance of estimates from the multivariate and univariate models in section 2.2 is highly reminiscent of comparing the variance of estimates from the random-effects and fixed-effect models in order to calculate I² statistics that quantify the impact of between-study heterogeneity.¹⁵ I² statistics however have a completely different interpretation to the BoS statistics and weights that we develop here. It is perfectly reasonable to obtain large BoS statistics and small I² statistics, and vice versa.

Since our methodology takes the variance components as fixed and known when calculating BoS statistics and weights, it may be used with alternative random effects models, such as a reduced model where all between-study variances are assumed to be the same as in our third example. Our ideas are therefore broadly applicable. We have however assumed a ‘two-stage’ approach to estimation. In the first stage we obtain estimates and within-study covariance matrices which we combine at the second stage. One-stage approaches allow us to relax the within-study normality assumption and so we do not in general use a multivariate normal model when using this type of approach. Extending our methods to handle non-normal data in the context of a one-stage approach is perhaps the most obvious avenue for further work. We are currently investigating how to best extend the methodology to include study level covariates, so that our methods may be used in the context of multivariate meta-regression analyses. The equivalence of the use of data-point coefficients and entries of the hat matrix to define weights does not extend to multivariate meta-regression models.

To summarise, we have proposed a method for calculating BoS statistics and study weights for conventional multivariate meta-analyses, which we have embedded into a single framework. We suggest that these new statistics are a useful aid to inference and should routinely accompany multivariate and network meta-analyses just as weights are conventionally shown on forest plots and in standard output from meta-analysis computer programs and packages. All our proposals are easily computed and so add very little to the computational demands of performing multivariate meta-analyses.

Appendix 1. Proof of equation (8)

Equation (8) asserts that $\text{E}\left[{\mathbf{\text{U}}}_i^{mv}|y_{ir}\right]=U_{ir}^{uv}{\mathbf{\text{e}}}_r$ , where ${\mathbf{\text{U}}}_i^{mv}={\mathbf{\text{V}}}_i^{-1}({\mathbf{\text{y}}}_i-\mathit{\beta }),U_{ir}^{uv}=V_{irr}^{-1}(y_{ir}-{\beta }_r),$ and e_r is the unit column vector with 1 in the rth position. We use the standard result about the multivariate normal distribution that

$$\begin{array}{l}\text{E}\left[{\mathbf{y}}_i-\mathit{\beta }|y_{ir}\right]=\mathrm{cov}\left({\mathbf{y}}_i,y_{ir}\right){\left\{\mathrm{var}\left(y_{ir}\right)\right\}}^{-1}\left(y_{ir}-{\beta }_r\right)\\ ={\mathbf{V}}_i{\mathbf{e}}_r{V}_{irr}^{-1}\left(y_{ir}-{\beta }_r\right)\end{array}$$

Hence

$$\begin{array}{l}\text{E}[{\mathbf{\text{U}}}_i^{mv}|y_{ir}]=\text{E}[{\mathbf{\text{V}}}_i^{-1}({\mathbf{\text{y}}}_i-\mathit{\beta })|y_{ir}]\\ ={\mathbf{\text{V}}}_i^{-1}\text{E}[{\mathbf{\text{y}}}_i-\mathit{\beta }|y_{ir}]\\ ={\mathbf{\text{V}}}_i^{-1}{\mathbf{\text{V}}}_i{\mathbf{\text{e}}}_r{V}_{irr}^{-1}(y_{ir}-{\beta }_r)\\ ={\mathbf{\text{e}}}_r{V}_{irr}^{-1}(y_{ir}-{\beta }_r)\\ =U_{ir}^{uv}{\mathbf{\text{e}}}_r\end{array}$$

as stated in equation (8).

Appendix 2. Proof of the independence of all 2n terms in equation (9)

This independence of all 2n terms is established because the estimates from separate studies are assumed to be independent, so that the only dependence between these 2n terms could occur when $U_{ir}^{uv}{\mathbf{e}}_r\hspace{0.17em}\text{and}\hspace{0.17em}({\mathbf{U}}_i^{mv}-U_{ir}^{uv}{\mathbf{e}}_r)$ are from the same study. From equations (2) and (4), these expressions involving scores for the ith study are jointly multivariate normal, so establishing that there is no correlation between these terms proves their independence. Then $\text{cov}(U_{ir}^{uv}{\mathbf{e}}_r,{\mathbf{U}}_i^{mv}-U_{ir}^{uv}{\mathbf{e}}_r)=\text{cov}(U_{ir}^{uv}{\mathbf{e}}_r,{\mathbf{U}}_i^{mv})-\text{Var}(U_{ir}^{uv}{\mathbf{e}}_r)$. The law of total covariance, cov(X, Y) = E[cov(X, Y|Z)]+cov(E[X|Z], E[Y|Z]), with $X=U_{ir}^{uv}{\mathbf{e}}_r,Y={\mathbf{U}}_i^{mv}\hspace{0.17em}\text{and}\hspace{0.17em}Z=y_{ir}$, noting that $U_{ir}^{uv}{\mathbf{e}}_r$ given y_ir is a constant and making use of equation (8), shows that $\text{cov}(U_{ir}^{uv}{\mathbf{e}}_r,{\mathbf{U}}_i^{mv})=\text{var}(U_{ir}^{uv}{\mathbf{e}}_r)$ so that $\text{cov}(U_{ir}^{uv}{\mathbf{e}}_r,{\mathbf{U}}_i^{mv}-U_{ir}^{uv}{\mathbf{e}}_r)=0$ and hence all 2n terms are independent, as stated.