Deep Independence Network Analysis of Structural Brain Imaging: Application to Schizophrenia

Abstract

Linear independent component analysis (ICA) is a standard signal processing technique that has been extensively used on neuroimaging data to detect brain networks with coherent brain activity (functional MRI) or covarying structural patterns (structural MRI). However, its formulation assumes that the measured brain signals are generated by a linear mixture of the underlying brain networks and this assumption limits its ability to detect the inherent nonlinear nature of brain interactions. In this paper, we introduce nonlinear independent component estimation (NICE) to structural MRI data to detect abnormal patterns of gray matter concentration in schizophrenia patients. For this biomedical application, we further addressed the issue of model regularization of nonlinear ICA by performing dimensionality reduction prior to NICE, together with an appropriate control of the complexity of the model and the usage of a proper approximation of the probability distribution functions of the estimated components. We show that our results are consistent with previous findings in the literature, but we also demonstrate that the incorporation of nonlinear associations in the data enables the detection of spatial patterns that are not identified by linear ICA. Specifically, we show networks including basal ganglia, cerebellum and thalamus that show significant differences in patients versus controls, some of which show distinct nonlinear patterns.

I. Introduction

LINEAR independent component analysis (ICA) is a statistical method used to discover maximally independent underlying data sources from their observed (and approximately) linear mixture. While ICA has been able to achieve remarkable results in a wide variety of applications including brain imaging analysis, the linear mixture assumption heavily limits ICA in its ability to identify the inherent nonlinear nature of the data, such as the asynchronous dynamics of brain function [1] or the nonlinear association between brain structure and demographic factors such as age [2]. By relaxing the linear mixture restriction of ICA to a more general nonlinear hierarchical transformation, we can incorporate additional information in the data-driven unmixing process, potentially yielding components that could not be otherwise estimated by ICA from MRI data. This is the motivation behind our exploration of nonlinear ICA methods on MRI.

Preliminary work on methods to accomplish nonlinear ICA has been extensive [3]–[7]. These approaches range from the application of post-nonlinear transformations using multilayer perceptrons (MLPs) right after ICA or the use of back-propagation to minimize the mutual information of the components in MLP architectures, to the application of kernel-based methods to detect components in feature space. All of these approaches have in common that they were only validated on preliminary experiments, arguably due to issues to impose a proper regularization that may have prevented them from obtaining stable solutions on more challenging applications [8]. Another reason why these methods may have been tested on preliminary data only could have been their prohibitive computational complexity, preventing them from achieving reasonable execution time in real applications.

To date, there has not been enough progress on nonlinear ICA to suggest that it can actually replace ICA for certain applications. Nonetheless, this trend may change with the advent of deep learning, which has achieved improved scalability for unsupervised learning algorithms with high computational complexity [9]. Recent work by Dinh et al., nonlinear independent component estimation (NICE) [10], proposes a deep architecture that addresses the regularization issues of previous approaches. This is done by i) estimating an easily invertible nonlinear unmixing transformation with a trivial evaluation of the determinant of the Jacobian of this transformation, and ii) by using predefined families of probability distribution functions (pdf) to estimate the independent components via maximum likelihood.

The work presented in [10] showed that NICE could be successfully used to sample input images from the latent variables estimated by the trained model, among other tasks. In this work, we demonstrate that NICE can indeed be used to detect spatially independent components from linear and nonlinear mixtures of simulated data [11]. In addition to this, we provide novel results testing the application of NICE to a large structural MRI dataset to detect aberrant patterns of gray matter concentration in schizophrenia, its results being compared to those obtained by ICA. To accomplish this task, we further regularized the proposed model by performing dimensionality reduction of the tissue concentration volumes and controlling the complexity of NICE to reasonably capture nonlinear interactions in the data. To the best of our knowledge, this is the first work to date to extend ICA using a deep architecture applied to structural MRI data.

II. NICE Formulation

A. ICA through maximum likelihood estimation

To better understand the challenges of developing nonlinear ICA approaches, we first provide a brief introduction to the estimation of independent components under the assumption that the observed data x is a linear combination of the components h. In this case, the components are estimated as h = f(x) = Wx, where W is the so-called unmixing matrix.

One way to solve this problem in its classical setting (i.e., the number of inputs equals the number of components) is to do a maximum likelihood estimation of the parameters W that provide the best fit of the data given an assumed joint probability density function (pdf) that is as similar as possible to the actual joint pdf p_H of the unknown components h.

If the aforementioned assumptions hold and the function h = Wx is invertible, then

$$p_X\left(\mathbf{x}\right)=p_H\left(\mathbf{Wx}\right)\mid \det \mathbf{J}\mid ,$$ (1)

where J = W. Given the assumption of independence between the components, the log likelihood function can be derived from (1) as:

$$\log L=\sum _{d=1}^D\left[\log p_{H_d}\right(w_d^{⊺}\mathbf{x}\left)\right]+\log \mid \det \mathbf{W}\mid ,$$ (2)

where D is the number of estimated components.

This problem provides reasonable results even with rough estimations of prior distributions p_Hd of the components as the Jacobian (second term in (2)) is solely defined by the unmixing matrix. In addition, the transformation h = Wx meets the requirement of invertibility as long as W is nonsingular. Both the estimation of the Jacobian and the invertibility requirement are more challenging on deep neural networks as the transformation is defined by a cascade of multiple nonlinear transformations, which may render this problem intractable.

The direct estimation of the Jacobian for deep neural networks is inefficient as it would differ across implementations with different layers. An alternative approach would be to incorporate the estimation of the Jacobian in the model itself as proposed by [6]. Nonetheless, this approach can induce additional estimation errors and increase the model complexity. Moreover, this would not address the requisite of generating an invertible unmixing transformation.

In order to address these problems, NICE proposes a transformation that is the composition of simple building blocks that are trivially invertible and have ∣det J∣ = 1. By virtue of the chain rule, the composite transformation would also have unitary Jacobian determinant. As a consequence, the log likelihood would only be defined by the first term in (2), thus resolving the issue of the estimation of the Jacobian.

B. NICE architecture

Within the NICE architecture, each building block (also referred to as coupling layer) works on a partition x₁, x₂ of the input data through the following transformation:

$$\begin{array}{cc}\hfill {\mathrm{y}}_1& ={\mathrm{x}}_1\hfill \\ \hfill {\mathrm{y}}_2& =m\left({\mathrm{x}}_1\right)+{\mathrm{x}}_2\hfill \end{array}$$ (3)

where m, the coupling function, is an arbitrarily complicated function implemented with a multi-layer perceptron (MLP). This building block is trivially invertible since:

$$\begin{array}{cc}\hfill {\mathrm{x}}_1& ={\mathrm{y}}_1\hfill \\ \hfill {\mathrm{x}}_2& ={\mathrm{y}}_2-m\left({\mathrm{y}}_1\right).\hfill \end{array}$$ (4)

Therefore, a transformation generated by the concatenation of these blocks is also invertible. In addition, it has a unit Jacobian determinant (for details see [10]).

It is evident from (3) that the direct composition of coupling layers would simply propagate a subset of the observed signals directly to the outputs. To avoid this situation, these blocks need to be transposed alternatively at each layer as shown on Fig. 1. Furthermore, at least three coupling layers are necessary to fully mix the data.

Fig. 1.

Alternate transposition of three coupling layers in NICE.

C. Prior distributions parametrization

The prior distributions p_Hd are assumed to be equivalent across components, following a predefined univariate standard pdf (location=0, scale=1). However, it would be more realistic for the estimated components to follow distributions with different spread. To address this issue, a diagonal scaling matrix S is included at the top layer of the architecture such that the i-th output of the basic NICE module is multiplied by S_ii. By incorporating these parameters, the Jacobian determinant is no longer unitary, being fully characterized by the elements of S. Therefore, the log likelihood function of the NICE model is defined by the following expression:

$$\log L=\sum _{d=1}^D[\log p_{H_d}\left(f_d\left(\mathrm{x}\right)\right)+\log \mid S_{\mathit{dd}}\mid ].$$ (5)

III. Simulated Dataset

Prior to applying NICE to sMRI data, we experimentally validated that NICE could in fact estimate spatially independent components on imaging data. To do so, we needed to generate a dataset that resembled sMRI tissue concentration images for which the ground truth (the set of underlying spatial components) was known. For that purpose, we generated 2D synthetic data by combining 16 spatial components available in the simulation toolbox for fMRI data (SimTB) [12], which are shown in Fig. 2(a).

Fig. 2.

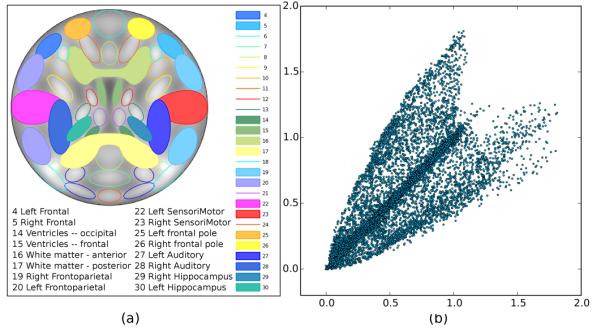
Graphical representation of (a) the spatial location of the components (separated from each other via a color code) and (b) the relationship between two randomly selected nonlinear mixtures.

The simulated data were generated from two different mixture models: a linear and a quadratic mixture. This setting allowed us to evaluate the performance of NICE not only on a nonlinear mixture for which it has been designed, but also on data that complies with the ICA linear mixture assumption, allowing for a fair comparison of both methods.

The quadratic mixture of the components, depicted in Fig. 2(b), was generated by following the method proposed in [6] as follows. Let x_i and s_j denote the i-th mixture and the j-th component, respectively. The quadratic mixture is of the form:

$$x_i=s_i+\sum _{j\ne i}\left[s_i{s}_j+{\left(s_j\right)}^2\right].$$ (6)

On the other hand, the linear mixture was obtained as follows. First, we recombined the components such that we obtained a final set of 8 symmetric and bilateral components with positively and negatively weighted regions. This yielded components that followed a symmetric pdf. Then, these were multiplied by a matrix with values sampled from the uniform distribution in the [0, 1] range: $\mathcal{U}\left(0,1\right)$.

IV. Schizophrenia Study

A. Data acquisition and preprocessing

We use data from four imaging studies conducted at Johns Hopkins University, the Maryland Psychiatric Research Center, the Institute of Psychiatry (London, UK) and the Western Psychiatric Research Institute and Clinic at the University of Pittsburgh. The sample is composed of 191 healthy controls (97 males; age = 40.26±15.02, range 16–79) and 198 schizophrenia patients (121 males; age = 39.68±12.12, range 17–81), both groups being matched for age and gender at each scanner location. MRI volumes were obtained on a 1.5 T Signa GE scanner on all sites using identical acquisition parameters [13].

The obtained T₁-weighted images were normalized to the MNI space and segmented into gray matter, white matter and cerebrospinal fluid images, using the SPM unified segmentation model [14]. The resulting gray matter concentration (GMC) images were then smoothed with an isotropic 8 mm full width at half maximum Gaussian filter. Finally, we evaluated the correlations of the images with the mean GMC image to detect noisy ones. Those images with correlation values being more than two standard deviations away from the mean correlation were discarded, yielding a final set of images composed of 334 GMC volumes.

B. Data representation

As discussed in Section II, NICE is formulated such that the number of inputs equals the number of outputs. If no dimensionality reduction were applied on the data, the number of estimated components in our study would be the same as the number of subjects. However, there is evidence that shows that the intrinsic dimensionality of brain imaging data is significantly smaller than the number of available volumes [15]. In fact, overestimation of components could convey spurious patterns and compromise the replicability of the results. Moreover, we would be unable to contrast our findings with those achieved by ICA, making it difficult to explain their novelty. For these reasons, we followed the same pipeline used by ICA, i.e., the use of principal component analysis (PCA) to perform dimensionality reduction prior to the estimation of independent components. The number of principal components was set to 30, as has been done in earlier work [16], [17]. However, we wanted to evaluate if choosing a reduced set of components would have an impact on NICE and ICA. For this reason, we also evaluated both algorithms when the number of components was set to 20, as it has been done in other studies [18], [19]. Finally, we wanted to evaluate if the usage of a nonlinear method for dimensionality reduction would somehow favor a linear method like ICA, so we also applied ICA and NICE to data that was processed by a restricted Boltzmann machine (RBM) [20] with the initial setting of the number of variables in a reduced dimension, i.e., the RBM was composed of 30 hidden units.

V. Experimental Setup

In order to properly account for both linear and nonlinear associations in the data and to achieve a suitable regularization of the trained models, we restricted the complexity of NICE by using a small number of coupling layers and a single hidden layer for each of them. This was complemented by the incorporation of reasonable estimates of the pdf of the estimated components.

The set of parameters to be tuned was the number of hidden units for each hidden layer and the number of coupling layers. We performed a grid search to obtain the optimal parameters by evaluating the mean correlation and the mean squared error (MSE) of each of the estimated components against their associated ground truth maps. The number of hidden units n_h was selected from {2, 3, 5, 10}, while the number of coupling layers n_C was pooled from {1, 2, 3, 4}. We deliberately included less than 3 coupling layers in the validation procedure to prove numerically that this setting does not perform an optimal mixture of the inputs, as discussed in section II-B. This procedure was performed for the quadratic mixture of simulated spatial components, the optimal parameters being used for the rest of the experiments in simulated and real data.

The same architecture was used by NICE in the validation and the test procedures, though for the latter ones the optimal parameters were used. Without loss of generality, the model used a composition of n_C coupling layers together with the layer of prior scaling factors, which were parameterized exponentially such that S_dd = e^a_dd. For each of these building blocks, the coupling function was a deep rectified network with 1 hidden layer (n_h hidden units) and linear output units. Since the components estimated by linear ICA on functional and structural MRI have been shown to be super-Gaussian and skewed, we used Gumbel priors to estimate them, the exception being the linearly mixed data since the components are symmetric as specified in Section III. That is the reason why a symmetric pdf such as the Laplacian was used for the linear mixture.

Each signal x_i was added Gaussian noise (μ = 0, σ² = 0.01 × V ar(x_i)) before being input to NICE. The generated models were trained with RMSProp [21] with early stopping and an initial learning rate of 10⁻³, decreasing to 10⁻⁴ with exponential decay of 1.0005 (i.e., η(t) = max (10⁻³ × 1.0005^−t, 10⁻⁴)). This was complemented with momentum, which was initially 0 and switched to 0.9 at the fifth epoch to prevent the model from overfitting.

As it has been previously discussed, for experiments using sMRI data both NICE and ICA were preceded by a dimensionality reduction method. NICE experiments were run using its implementation in Pylearn2 (a machine learning library), available at https://github.com/laurent-dinh/nice. For ICA, we used the Group ICA of fMRI (GIFT) toolbox (http://mialab.mrn.org/software/gift/).

VI. Comparison with other approaches

In addition to comparing NICE against linear ICA, we evaluated the performance of another nonlinear ICA algorithm: MISEP [6] (code available at http://www.lx.it.pt/~lbalmeida/ica/mitoolbox.html). This algorithm, which relies on a reasonable estimation of the Jacobian of the transformation it learns to be properly trained, was unable to run with the whole dataset of simulated nonlinear mixtures due to the degeneracy of the estimated Jacobian matrix. MISEP was only able to work on a mixture of 4 components (namely the bilateral sensorimotor and the frontoparietal components shown in Fig. 2), which is consistent with the results reported in [6]. This prevented us from testing MISEP on real data. Nonetheless, we present results of this algorithm when trained on the aforementioned data subset.

We also compared the performance of NICE to that achieved by another approach that estimates latent variables and is used on deep learning architectures, though the method is not designed to find independent components. The algorithm of choice was a variational autoencoder (VAE) since it learns a reduced dimensionality representation of the data by modeling the distribution of the computed latent variables, being similar to NICE in that sense. We trained the VAE in two different ways. The first one extracted components from sMRI data without prior dimensionality reduction. Even though this is the standard setup for VAE, we are aware that NICE works with a reduced set of variables. To guarantee a fair comparison between them, we applied dimensionality reduction to the data prior to applying VAE in the second experimental setup.

The VAE models in this paper were trained assuming the conventional isotropic Gaussian pdf for the prior, conditional and posterior distributions. The number of hidden units of the hidden layer of the MLPs used for both the encoder and the decoder were the same and were set to 1/3 of the input space dimension. In [22] the number of hidden units was approximately set to half the data dimensionality to process the Frey face dataset in order to avoid overfitting due to its small size. Since the signal to noise ratio of our data is very small, we used an even more conservative fraction to define the number of hidden units. Finally, the number of latent variables was set to either 20 or 30.

VII. Assessment of NICE model on sMRI

An important goal of this study is to achieve an improved interpretation of spatial patterns of GMC through the inclusion of a nonlinear analysis for the extraction of components. To do so, we need to be able to quantify the nonlinearities induced by the model, as well as the contribution of the linear and nonlinear elements of this transformation to detect differences between controls and patients.

One way to look at component-specific group differences in ICA applied to sMRI is to evaluate the contribution of each component to the GMC volumes of the subjects in both groups. In ICA, the GMC volumes are decomposed into spatial maps and loading coefficients, as shown in Fig. 3(a). These linear loading coefficients provide a numeric estimation of the contribution of the components to each subject, thus enabling comparisons between controls and patients. The contribution of the linear domain of the NICE transformation to group separability for each component was evaluated in this fashion by estimating a matrix of linear loading coefficients A such that A = XS^†, where X and S are the matrix representations of GMC volumes and estimated components and S^† is the pseudoinverse of S.

Fig. 3.

Estimation of (a) linear and (b) back-reconstructed loading coefficients.

We also wanted to evaluate the influence of NICE embedded nonlinearities to differentiate controls and patients. To this purpose, we estimated a proxy of loading coefficients from NICE by back-reconstructing the information associated with each component to the input space. These back-reconstructed loading coefficients were generated by sampling N data points (N being equal to the number of subjects) from the pdf of a given component and subtracting the mean activity of the other components. After doing so, the group mean values associated to each of these data points were estimated, yielding component-specific loadings for each group. This approach is depicted in Fig. 3(b).

To determine the nonlinearities induced by NICE for the estimation of components, we evaluated the pairwise mutual information between the components and the inputs after removing linear effects, a metric that we call adjusted mutual information. Similarly, the linear dependencies between inputs and outputs were evaluated by means of pairwise correlations.

VIII. Results

A. Simulated dataset

Table I shows the mean correlation and MSE estimates obtained by NICE on the nonlinear mixture dataset using different architectures. It can be seen that NICE performs suboptimally with less than three coupling layers, as expected. This table shows that the best configurations are those in which three coupling layers (n_C = 3) are used, achieving maximum correlation and minimum error. The different values of n_h do not have a significant impact in the accuracy of the estimated components in this case. Even so, the best results (strictly speaking) are obtained for n_C = 3 and n_h ∊ {2, 3}, so we chose the least complex architecture among them, i.e., n_h = 2.

TABLE I.

Component accuracy estimates on the quadratic mixture for different NICE configurations. We show mean correlation and MSE estimates (the latter in parentheses) for different values of n_h (rows) and n_C (columns)

	1	2	3	4
2	0.70 (0.42)	0.79 (0.33)	0.85 (0.24)	0.84 (0.26)
3	0.70 (0.42)	0.79 (0.31)	0.85 (0.24)	0.81 (0.29)
5	0.69 (0.42)	0.81 (0.29)	0.84 (0.25)	0.84 (0.25)
10	0.69 (0.43)	0.81 (0.25)	0.84 (0.26)	0.83 (0.26)

Fig. 4 shows a subset of the spatial maps used to generate the nonlinear mixture dataset and the components estimated by ICA, MISEP and NICE with the optimal parameters. As it was explained in section VI, MISEP was trained on a smaller subset of only 4 mixture maps. Even with this advantage, MISEP was unable to recover the components as accurately as NICE did, so we did not test MISEP on the remaining experiments. In contrast, NICE correctly captured their spatial extent even though it did not achieve a perfect reconstruction of the intensities at each spatial location. This performance level was not achieved by linear ICA on the same dataset.

Fig. 4.

Ground truth (GT) and estimated components by ICA, MISEP and NICE for quadratic mixtures. The correlation coefficients of these estimates with the GT are shown below them.

Fig. 5 shows a subset of the spatial maps estimated by NICE and ICA for the linear mixture of components. It can be seen that NICE achieves a reasonable performance based on visual inspection and the correlation of its estimated components to the ground truth in spite of being designed with embedded nonlinearities.

Fig. 5.

Ground truth (GT) and estimated components by NICE and ICA for linear mixtures. The correlation coefficients of these estimates with the GT are shown below them.

B. PCA dimensionality reduction

We first evaluated NICE after reducing the sMRI dataset to 30 dimensions. Fig. 6 illustrates the set of components estimated by NICE that show significant group differences between controls and patients according to a two-sample t-test on the linear loading coefficients. Statistically significant differences were tested at p < 0.05 after Bonferroni correction for multiple comparisons. Furthermore, we selected components that showed at least moderate linear effect sizes based on a Cohen’s d threshold of 0.45 as suggested in [23]. The same criteria was used to identify differential spatial patterns found by other methods using other dimensionality reduction approaches for consistency purposes, unless otherwise stated. In addition, Table II shows the effect sizes of the differences between these groups and estimates of the induced nonlinearities for each component, as well as the directionality of these differences. Linear and nonlinear group differences are estimated via the effect sizes achieved by the linear and back-reconstructed loading coefficients, respectively.

Fig. 6.

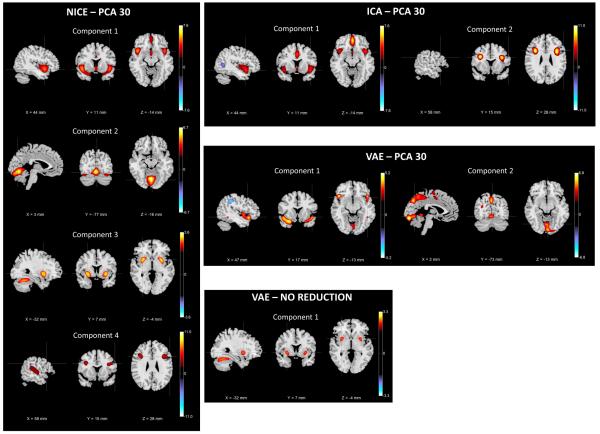
Set of the components estimated by NICE, ICA and VAE that show significant GMC differences between controls and patients after reducing the data dimensionality to 30 through PCA. This figure also shows the results obtained by VAE without prior dimensionality reduction.

TABLE II.

Spatial extent and estimates of group effect sizes and embedded nonlinearities of NICE components with differential GMC with PCA reduction to 30 dimensions. Components 1 and 4 are partially consistent with ICA, so the additional brain regions covered by NICE are shown in italics.

Comp Number	Loadings Directionality	Brain Regions	Input-Output Dependence Metrics			Effect size of loadings (Cohen’s d)
			Max. Corr.	Max. Adj. MI	Linear fit (R2)	Linear	Back- reconstructed
1	Ct > Sz	Superior Temporal Gyrus Insula Temporal Pole: Superior Temporal Gyrus Anterior Cingulum Superior Medial Frontal Gyrus Parahippocampus	0.72	0.12	0.92	0.46	0.53
2	Sz > Ct	Cerebellum Crus Vermis	0.63	0.12	0.86	−0.50	−0.34
3	Ct > Sz	Putamen Simple Lobule of the Cerebellum	0.94	0.08	0.96	0.48	0.07
4	Ct > Sz	Inferior Frontal Gyrus Superior Temporal Gyrus Middle Temporal Gyrus	0.60	0.10	0.82	0.47	0.37

We also show the components that present differential spatial patterns between controls and patients estimated by ICA and VAE in Fig. 6. In addition, we show the only component identified by VAE when trained without prior dimensionality reduction (it was replicated across all components), which resembles NICE component 3. This component did not meet the effect size threshold suggested in [23] (its value was 0.40), but we included it in our results regardless. The brain regions spanned by each of the components estimated by ICA and VAE and their group difference estimates are displayed in Table III, the exception being VAE without prior dimensionality reduction.

TABLE III.

Spatial extent and estimates of group effect sizes of ICA and VAE components with differential GMC with PCA reduction to 20 dimensions.

Method	Comp Number	Loadings Directionality	Brain Regions	Effect size of loadings
ICA	1	Ct > Sz	Superior Temporal Gyrus Insula Temporal Pole: Superior Temporal Gyrus Anterior Cingulum Superior Medial Frontal Gyrus	0.57
	2	Ct > Sz	Inferior Frontal Gyrus	0.52
VAE	1	Ct > Sz	Superior Temporal Gyrus Insula Temporal Pole: Superior Temporal Gyrus Vermis	0.48
	2	Sz > Ct	Vermis Precuneus	−0.45

There is evidence that schizophrenia patients show gray matter loss in the superior temporal gyrus, a pattern that is detected by NICE in component 1. This pattern has been consistently found in multiple studies, including those based on linear ICA [16], [17]. Furthermore, NICE detects two components (2 and 3) that span subcortical regions and the cerebellum and were not found by ICA on this dataset. In addition, components 4 in NICE and 2 in ICA are partially consistent, but the component estimated by NICE covers additional regions in the temporal gyrus. Component 1 detected by VAE is similar to component 1 detected by NICE and ICA, but it spans an additional region (vermis). This finding is inconsistent with the second component estimated by VAE, as the directionality of the latter one suggests that this region’s GMC increases on patients.

Table II also analyzes the linear and nonlinear nature of the input-output dependencies for each of these components. For example, it can be seen that components 1 and 3 have a high correlation with the inputs, in addition to high values of linear fit. However, component 3 exhibits a low adjusted mutual information and effect size corresponding to back-reconstructed loadings, as opposed to component 1. This suggests that both of these components have a high linear dependence with the inputs, but component 3 has a reduced nonlinear dependence with them. On the other hand, components 2 and 4 seem to follow the opposite pattern detected for component 3, i.e., they show a smaller linear dependence with the inputs but follow a more pronounced nonlinear transformation. This is further validated by the depiction provided on Fig. 7. Moreover, Table II shows that the nonlinearities induced by NICE do improve the differentiation of controls and patients as evidenced by the moderate effect sizes associated to the back-reconstructed loading coefficients of components 1, 2 and 4.

Fig. 7.

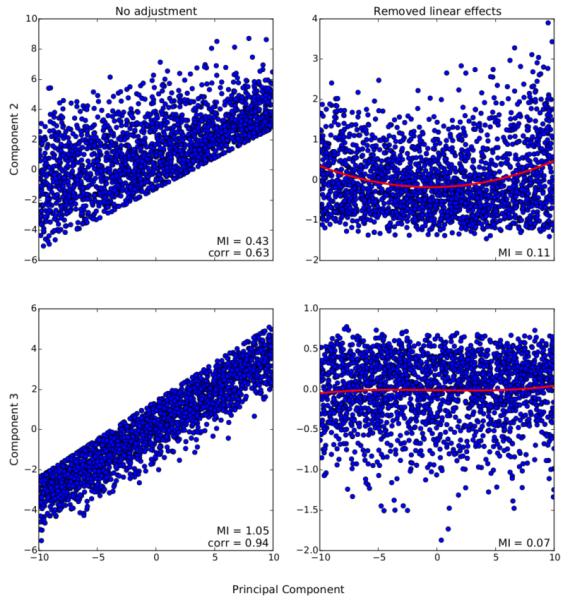
Association between components 2 and 3 and candidate principal components. The left panel shows the overall dependence pattern between them, while the right panel shows their association after removing linear effects along with a polynomial fit of order 3. Their dependence is quantified in terms of correlation and mutual information.

We repeated this analysis again when the data dimensionality was further reduced to 20 components. Fig. 8 displays the components estimated by NICE, ICA and VAE that showed differential GMC between groups. In addition, we provide extra information regarding the spatial extent, directionality and other statistics for NICE (Table IV), ICA and VAE (Table V).

Fig. 8.

Set of the components estimated by NICE, ICA and VAE that show significant GMC differences between controls and patients after reducing the data dimensionality to 20 through PCA.

TABLE IV.

Spatial extent and estimates of group effect sizes and embedded nonlinearities of NICE components with differential GMC with PCA reduction to 20 dimensions.

Comp Number	Loadings Directionality	Brain Regions	Input-Output Dependence Metrics			Effect size of loadings (Cohen’s d)
			Max. Corr.	Max. Adj. MI	Linear fit (R2)	Linear	Back- reconstructed
1	Ct > Sz	Superior Temporal Gyrus Insula Temporal Pole: Superior Temporal Gyrus Anterior Cingulum Superior Medial Frontal Gyrus	0.78	0.12	0.88	0.51	0.42
2	Sz > Ct	Cerebellum Crus Vermis	0.70	0.11	0.90	−0.47	−0.36
3	Ct > Sz	Putamen Simple Lobule of the Cerebellum	0.93	0.08	0.97	0.48	0.06
4	Ct > Sz	Left Inferior Frontal Gyrus Right Superior Temporal Gyrus Right Postcentral Gyrus	0.90	0.09	0.94	0.63	0.21

TABLE V.

Spatial extent and estimates of group effect sizes of ICA and VAE components with differential GMC with PCA reduction to 20 dimensions.

Method	Comp Number	Loadings Directionality	Brain Regions	Effect size of loadings
ICA	1	Ct > Sz	Superior Temporal Gyrus Insula Temporal Pole: Superior Temporal Gyrus Anterior Cingulum Superior Medial Frontal Gyrus	0.53
	2	Ct > Sz	Left Middle Frontal Gyrus Precentral Gyrus	0.49
VAE	1	Ct > Sz	Left Temporal Pole: Superior Temporal Gyrus	0.45

The first three components estimated by NICE when the data was reduced to 30 dimensions are very consistent with those obtained by NICE when the data was further reduced to 20 dimensions. In fact, NICE component 4 for both decompositions share some regions in common, such as the superior temporal and the inferior frontal gyri. However, component 4 for the 20-dimension data reduction seems not to be driven as strongly as the other one by embedded nonlinearities. For the new data reduction scheme, ICA still estimates a component spanning the superior temporal gyrus and another one that covers the frontal gyrus, though not on the same location. When compared to NICE, it can be seen that NICE component 4 and ICA component 2 both cover the inferior frontal gyrus. Therefore, it can be argued that NICE detects more components associated to disease than ICA for either setting of dimensionality reduction. VAE detects a component that spans the left superior temporal pole, which is consistent with component 1 detected by ICA and NICE. However, this finding provides less information about regions with abnormal tissue concentration in schizophrenia than either of the other methods.

C. RBM dimensionality reduction

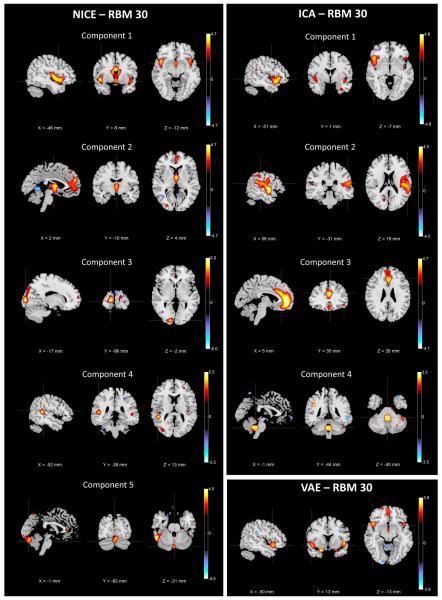
We also evaluated NICE and the other methods after reducing the data to 30 dimensions through a nonlinear approach such as an RBM. The spatial extent of the components that show differential GMC is depicted in Fig. 9, while additional information about these components is provided in Table VI for NICE and Table VII for ICA and VAE.

Fig. 9.

Set of the components estimated by NICE, ICA and VAE that show significant GMC differences between controls and patients after RBM dimensionality reduction to 30 components.

TABLE VI.

Spatial extent and estimates of group effect sizes and embedded nonlinearities of NICE components with differential GMC with RBM reduction to 30 dimensions. Underlined brain regions are those with negative component coefficients (reversed loadings directionality).

Comp Number	Loadings Directionality	Brain Regions	Input-Output Dependence Metrics			Effect size of loadings (Cohen’s d)
			Max. Corr.	Max. Adj. MI	Linear fit (R2)	Linear	Back- reconstructed
1	Ct > Sz	Superior Temporal Gyrus Insula Caudate Nucleus Anterior Cingulum Thalamus	0.93	0.10	0.90	0.50	0.19
2	Ct > Sz	Superior Medial Frontal Gyrus Thalamus Vermis	0.92	0.12	0.84	0.53	0.50
3	Ct > Sz	Superior Occipital Gyrus Middle Occipital Gyrus Calcarine Sulcus	0.87	0.13	0.84	0.53	0.55
4	Ct > Sz	Superior Temporal Gyrus Middle Temporal Gyrus Left Middle Occipital Gyrus	0.98	0.08	0.97	0.51	0.02
5	Sz > Ct	Cerebellum Crus Vermis	0.96	0.12	0.92	−0.66	−0.52

TABLE VII.

Spatial extent and estimates of group effect sizes of ICA and VAE components with differential GMC with RBM reduction to 30 dimensions.

Method	Comp Number	Loadings Directionality	Brain Regions	Effect size of loadings
ICA	1	Ct > Sz	Left Superior Temporal Gyrus Left Insula	0.45
	2	Ct > Sz	Right Superior Temporal Gyrus Temporal Pole: Superior Temporal Gyrus	0.61
	3	Sz > Ct	Cerebellum Crus Vermis	−0.47
VAE	1	Ct > Sz	Temporal Pole: Superior Temporal Gyrus Insula	0.40

The results obtained by NICE with RBM dimensionality reduction are consistent in general with the results obtained with PCA since the obtained components still cover the superior temporal gyrus, medial frontal, cerebellum and subcortical regions. However, it seems like by using a different dimensionality reduction method the overall results are slightly different. In this case, new brain regions are included in NICE components, covering the thalamus and the caudate nucleus, which have been reported to have reduced GMC in patients in [24], [25] and [26], respectively. After RBM data reduction ICA is able to capture abnormal tissue concentration in the cerebellum, which is consistent with NICE findings. In addition, ICA is still capable of detecting the regions covered by ICA component 1 with PCA reduction. Nonetheless, these regions are split into different components and ICA is unable to identify aberrant structure in the subcortical regions detected by NICE. On the other hand, VAE detected components that were non-unique (highly correlated to each other), spanning several regions that matched some of those of component 1 in NICE. It can be seen from Table VII that this component did not meet the effect size threshold suggested in [23], but we still reported it to be able to compare VAE against NICE and ICA. As it is the case with other dimensionality reduction approaches, VAE is unable to detect as many regions with aberrant structure as either NICE or ICA.

IX. Discussion

The components estimated by NICE span regions that have been reported to have aberrant GMC in schizophrenia. Component 1 (irrespective of the applied dimensionality reduction approach) detects loss of cortical gray matter in different regions, including the superior temporal gyrus, insula and the anterior cingulum, as well as the parahippocampus for reduction to 30 principal components. This finding is consistent with the patterns of decreased GMC reported in different meta-analysis of MRI studies of schizophrenia [24], [25], [27]. It is also interesting to note that while this component has been replicated in other ICA studies of sMRI [16], [17], NICE also incorporates the parahipoccampal gyrus when the data is reduced to 30 dimensions via PCA. This is congruent with the results in [25], which provided evidence that the GMC deficits in the parahippocampus and the insula were linked to common aspects of the pathophysiology of schizophrenia.

One of the regions that has been shown to have reduced GMC is the basal ganglia, which is rich in dopamine receptors and it is the target of antipsychotic treatment [28]. When applying data reduction using PCA, NICE detects reduced gray matter on the putamen in component 3, which is a subregion of the basal ganglia that has also been shown to have GMC deficits compared to healthy controls [16], [29]. This component also covers the simple lobule of the cerebellum, which has been shown to have more pronounced gray matter loss with longer duration of illness [30]. On the other hand, when PCA reduction is applied to the data component 2 shows increased GMC in schizophrenia patients in other regions of the cerebellum as reported in [31]. Deficits were also found on the inferior frontal and temporal gyri on component 4, corroborating the findings in [32].

Another important aspect of this study was the impact of the embedded nonlinearities in NICE in the estimation of components. As it was discussed in Section VIII, components 2 and 4 seem to be strongly influenced by the nonlinearities induced by NICE for PCA reduction to 30 dimensions, an argument that seems to be reinforced by the fact that these components were not detected by ICA. Nonetheless, NICE component 4 after reduction to 20 principal components seems to be less influenced by the nonlinearities embedded in the model. Similarly, it can be argued that component 2 (after PCA reduction) was detected due to the nonlinearities induced by NICE as spatial independence between all of the components is enforced. Alternatively, it may be possible that this component has not been found as consistently as others such as the one spanning the superior temporal gyrus in ICA-based studies, as the basal ganglia was shown to estimate group differences in [16]. Equally important is the finding of another subcortical region such as the thalamus when the data is reduced by means of an RBM. In this case, components 1 and 2 suggest a reduction of GMC in this region. Given that the thalamus plays a crucial role in the coordination of information between brain regions, abnormal structural patterns in the thalamus would explain some of the symptoms of schizophrenia [33]. Overall, it seems like nonlinear dependencies between inputs and outputs are present in all components, but some are influenced by stronger nonlinearities. In addition, we provide evidence that the back-reconstructed loading coefficients seem to be consistent with the differential nonlinear patterns between groups and the embedded nonlinearities of the components, as evidenced by their estimated effect sizes in the different analyses presented in this work.

Our study also shows that while the components estimated by either NICE or ICA are overall consistent for different dimensionality reduction approaches, there are slight changes among them, especially when switching from PCA to RBM. Differences are almost unnoticeable when different number of principal components are used prior to estimating the ICs. This may be related to potential overfitting of the data by RBM, even though early stopping was used to train it. This problem could be solved by further regularizing RBM training through unit dropout or weight decay. In any case, neither a reduction of the number of components nor the inclusion of a nonlinear approach for dimensionality reduction improved the performance of ICA compared to NICE.

Of equal importance is the issue of regularization of nonlinear ICA approaches. In this study we evaluated the performance of a low complexity model after dimensionality reduction that would slightly deviate from the assumption of linear mixing of underlying sources, but this is by no means the only way to address its regularization. Other ways to regularize the problem are to incorporate prior knowledge of the domain being analyzed. Regarding the specific case of sMRI data, the regularization could impose a lower bound on the size of connected clusters in each component or enforce a certain degree of correlation between neighboring pixels for the estimated components. By taking into account these considerations, it would be possible to use alternative approaches for dimensionality reduction based on deep learning architectures.

X. Conclusions

This paper demonstrates the benefits of the incorporation of nonlinear associations for the estimation of independent components on neuroimaging data, and represents the first work to demonstrate the feasibility of nonlinear ICA for biomedical data analysis. The obtained results are consistent with previous findings of aberrant volumetric changes of GMC in schizophrenia and significantly extend preceding results obtained by ICA on this field by identifying several components showing group differences that were not identified with linear ICA. These additional components contain regions that are known to be implicated in schizophrenia and provide a more comprehensive picture of the underlying anatomic changes associated with this chronic mental illness.