Abstract
Adaptive, model-based, dose-finding methods, such as the continual reassessment method, have been shown to have good operating characteristics. One school of thought argues in favour of the use of parsimonious models, not modelling all aspects of the problem, and using a strict minimum number of parameters. In particular, for the standard situation of a single homogeneous group, it is common to appeal to a one-parameter model. Other authors argue for a more classical approach that models all aspects of the problem. Here, we show that increasing the dimension of the parameter space, in the context of adaptive dose-finding studies, is usually counter-productive and, rather than leading to improvements in operating characteristics, the added dimensionality is likely to result in di culties. Among these are inconsistency of parameter estimates, lack of coherence in escalation or de-escalation, erratic behaviour, getting stuck at the wrong level and, in almost all cases, poorer performance in terms of correct identification of the targeted dose. Our conclusions are based on both theoretical results and simulations.
Keywords: parameters, Continual Reassessment Method, Dose escalation, Dose finding studies, Phase I trials, parsimony, Toxicity
1 Introduction
1.1 Background
Model based Phase I designs guide dose escalation and de-escalation by appealing to some simple model structure. The aim is twofold: first, to locate the maximum tolerated dose (MTD) as accurately as we can and, second, to concentrate as many patients as possible at doses close and at the MTD itself. Many of these designs come under the heading of the Continual Reassessment method (CRM) [1]. The CRM, leaning on an assumption of a strictly monotonic relationship between dose and the probability of observing a DLT (dose limiting toxicity), postulates a particularly simple 1-parameter model. In the long run, the fit of this model at the MTD itself should be perfect (almost sure convergence) but, at other dose levels the fit will typically only provide an approximation to the truth that worsens as we move away from the MTD. In the light of the sequential, adaptive nature of the trial, we can see that at doses other than the MTD the accumulating information, relative to that at the MTD, diminishes with sample size.
The crucial point to keep in mind is that the purpose of these studies is not to provide any kind of estimate of the overall dose-toxicity curve but, instead, to sensibly guide dose escalation and deescalation, to identify the MTD with the greatest possible accuracy and to treat as many patients as we can at and close to the MTD. This di ers from the more general aim of estimating the dose-response curve itself as is the case in some studies; examples include comparative studies involving randomization to dose levels or pharmaco- kinetics/dynamic studies. In practice, sample sizes of Phase I studies are quite small, in many cases no more than 20 observations. It is still necessary to consider both large and small sample behaviour. Large sample theory helps us to anticipate the finite sample behavior of estimators but can be difficult in view of models being misspecified, while small sample theory is yet more complex and is typically addressed via simulations for plausible situations.
We first recall the statistical structure to dose-finding problems. We have available k doses labeled as d1, . . . , dk, and these can be multidimensional. The doses are ordered in terms of the probabilities, R(di), for toxicity at each of the levels, i.e. R(di) ≤ R(dj) whenever i < j. The most appropriate dose, the ‘target’ dose in any study and the dose defined to be the “maximum tolerated dose (MTD)”, denoted d0 ∈ {d1, . . . , dk} is that dose having an associated probability of toxicity, R(d0), as close as we can get to some target “acceptable” toxicity rate θ. Specifically we define d0 ∈ {d1, . . . , dk} such that
| (1) |
The binary indicator Yj takes the value 1 in the case of a toxic response for the j th entered subject (j = 1, . . . , n) and 0 otherwise. The dose for the j th entered subject, Xj is viewed as random, taking values xj ∈ {d1, . . . , dk}; j = 1, . . . , n. Thus Pr (Yj = 1|Xj = xj) = R(xj). We write and to be any general model based estimate of the MTD using the available data. We then have two statistical goals; (1) estimate d0 consistently and efficiently and, (2) during the course of the study, concentrate as many patients as possible around d0, specifically we treat the j th included patient at the same level we would have estimated as being d0 had the study ended after the inclusion of j − 1 patients.
1.2 Local modeling of the dose-toxicity curve
We can choose a specific model to represent R(xj), the true probability of toxic response at Xj = xj ; xj ∈ {d1, . . . dk} by
where ψ(xj, a) is a working model. The parameter a could be multidimensional although, in the standard setting, it is usually taken to be of dimension one. Dose allocation follows the algorithm as [1], where given the visited dose levels and toxicity outcomes, we estimate a sequentially and the predicted toxicity rates given by ψ(xj,â) provide a sequential estimate of the MTD. For every a, the working model ψ(x, a) should be monotone increasing in x and, for any x, in the one dimensional case, ψ(x, a) should be monotone in a. For every di there exists some such that R(di) = ψ(di, ai), i.e. the model is rich enough, at each dose, to exactly reproduce the true probability of toxicity at that dose. We have a lot of flexibility in our choice for the working model ψ(x, a), the simple choice:
| (2) |
where 0 < α1 < . . . < αk < 1 and −∞ < a < ∞, being a common one. In the Bayesian setting, the αi are often viewed as our prior best guesses of the probability of DLT at level i. In the pure likelihood setting it is difficult to interpret the αi since, at every step, for any w > 0, a model based on αi and a model based on produce identical results. For any model , an important theorem known as the impossibility theorem is the following;
Theorem 1
Suppose the current estimator of the MTD, satisfies where is the sigma-algebra generated by the sample. There exists a scenario satisfying the monotonicity constraint such that:
The theorem and a proof is given by Azriel et al.[2] Essentially it says, for general models with the above property, then, only for specific restricted situations can we claim to obtain large sample almost sure convergence when allocation corresponds to the current estimator for the MTD. Suppose however that we eventually settle on level di that is not the MTD. We still have,
Theorem 2
If as n → ∞ then, for ϵ > 0,
| (3) |
The theorem is almost immediate and follows from the Glivenko-Cantelli theorem and its extension to smooth functionals (see [3], Chapter 3). Almost sure convergence of the 1-parameter model used in CRM, under certain conditions, has been shown [4]. However, under very general conditions, Theorem 2 continues to apply and, in particular, shows that at whatever level we finally settle, we correctly estimate the probability of toxicity at that level. This provides a lot of information. If, for instance, the estimated probability is 0.19, and the target is 0.20, then although the MTD may not be at the level corresponding to 0.19 (eg, the MTD corresponds to 0.199), we can still make accurate statement about the rate of toxicity at the estimated MTD. However, for over parameterized models, not only does Theorem 1 apply, Theorem 2 will generally fail to apply as seen below.
If we were allowed to randomly experiment at all available dose levels then, clearly, a more flexible model is going to be generally rewarded by more accurate inference. There is also value in fitting parsimonious models when there are only likely to be a few dozen observations. However, once we rule out randomization and experimentation at all available levels, then much of our intuitive thinking is put to the test. For instance, let us suppose that some simple 1-parameter model really does generate the observations. We would often guess that, in this situation, the best model for our purposes would be one belonging to this same 1-parameter class. Perhaps surprisingly, this is not the case and it can be confirmed by simulation studies.
How important is overall fit? In almost any non-sequential, non-adaptive situation, fit is crucial; the better the fit the better the performance. In our adaptive situation that is no longer so. Only local fit matters. Overall fit is not important since it only relates very indirectly to measures of performance. We need to assess, directly, the relevant measures of performance. Indicators of performance refer to both asymptotic and finite sample behaviour. Almost sure convergence is an asymptotic property and while getting to the right place after an infinite effort may seem to have limited value, in fact, the almost sure convergence gives us more in that it indicates that increasing sample size is rewarded appropriately by more accurate inference. We might also view this as a very minimal attribute in as much as any method failing to show large sample convergence, whether in probability or almost surely, would fail to inspire confidence for finite samples. Finite sample behaviour on its own is of course very important and is typically investigated via broad collections of simulations. For a wide range of possibilities we would like to know how often any method locates the MTD, how concentrated at and around the MTD are those patients included in the study and, all else being equal, how many patients are needed for some given level of accuracy.
In this paper, we present several motivating examples, where a model that is not parsimonious and that may otherwise appear to be a reasonable choice, will show very poor operating characteristics as well as undesirable mathematical properties in the specific setting of adaptive sequential dose-finding designs. Although the performance of these models has been previously shown to be poor via simulated trials ([5, 6]) these models are being increasingly used in practice [7] raising concerns about safety and accuracy. In this work we describe, via both theoretical arguments and simulations, the potential negative consequences of using over parameterized models in dose finding studies.
2 Motivating example
Neuenschwander et al. [8] report on a 1-parameter CRM trial. The initial design indicated a total of 15 possible levels ranging from 1-250mg with the prior distribution indicating dose level 10 (50 mg) to be the likely MTD before seeing any data (Table 1). This example is referred to as a demonstration that CRM is aggressive in escalation since, having observed two DLTs out of two patients at dose level 7, the subsequent recommendation is to treat at dose level 9. The authors conclude that this undesirable behaviour can be attributed to the lack of flexibility of the 1-parameter model. Such a conclusion is erroneous.
Table 1.
Patient sequence and dose levels for Neuenschwander et al. 2008 study for the first 10 dose levels (no data were provided for dose levels 11-15). Probability mass at each level for prior and posterior shown in bold
| Doses (mg) | 1.0 | 2.5 | 5 | 10 | 15 | 20 | 25 | 30 | 40 | 50 |
| No. of patients | 3 | 4 | 5 | 4 | 0 | 0 | 2 | - | - | - |
| No. of DLTs | 0 | 0 | 0 | 0 | - | - | 2 | - | - | - |
| prior | .17 | .02 | .01 | .01 | .01 | .02 | .04 | .07 | .09 | .56 |
| posterior | .01 | .01 | .01 | .01 | .02 | .03 | .10 | .28 | .37 | .19 |
Details of the trial parameters and data are given in Table 1 for the first 10 dose levels. The trial design was constructed in such a way to make the most likely MTD to be dose level 10 and this was reflected by a large probability weight at level 10. If we were to allow the prior to guide our experimentation then we will treat the first patient or cohort of patients at dose level 10. This would correspond to a correct implementation of the CRM as described in O'Quigley et al (1990). However, clinical investigators often want to be cautious and start experimentation at dose level 1. This can be readily achieved although, if we wish to implement the CRM correctly, then we need to either match the planned experimentation to the design or match the design to the planned experimentation. In the former case, we must treat the first entered patient at dose level 10. In the latter case we need to choose an appropriate prior, one centered at level 1 and not at level 10. Level 10, at more than 50 times the dose, is very far removed from level 1 at which experimentation began (Table 1). The early observed non-toxicities have the effect of very slowly moving the prior from being centered at level 10 to being centered at level 11. Thus, when, as a result of observing 2 out of 2 toxicities at level 7, the model recommends level 9, this is a shift from level 11 to level 9. The recommendation to “escalate” was not a result of using a simple, under-parameterized model. Had the CRM design been correctly implemented, this would have been a de-escalation. [9] If we correctly follow CRM, then coherence, i.e., no escalation after observing a DLT, is guaranteed mathematically [12]. We return to this in Section 2.1 and relate the definitions to specific models. Section 5 describes the solution to the problem within the context of Bayes inference. In the next section, we show that the 2-parameter logistic model while generally behaving poorly also fails consistency.
2.1 Operating characteristics
Several authors ([10],[11]) have identified large and small sample operating characteristics that are desirable, even necessary, for any dose-finding design to be used in practice. Cheung [12] showed that both Bayesian and likelihood based 1-parameter CRM designs enjoy the property of coherence, which means that the method cannot recommend escalation from any level following an observed dose limiting toxicity at that level or de-escalation following a non toxicity. This property ensures safety and e ciency. It has been argued that failing to use the more flexible 2-parameter model could result in CRM getting stuck at a level or aggressive escalations may follow a toxicity. This is not true. The definition of rigidity was given by Cheung (2011) [13] to describe the case when a design gets stuck at a dose level or when the parameter estimation remains at a particular location in the parameter space, regardless of the updated data (refer to [13] for details). We describe these properties below and give examples in Section 4:
Consistency of estimators. By consistent we mean the usual convergence with probability one (almost sure convergence) to the population value. In particular we would like, under certain conditions, to be able to claim that the recommended dose converges almost surely to the true MTD.
Coherence of design. Given that the current level at which the patient is treated has been recommended by the model, then a toxicity should result in recommending either the same level or a lower one and a non-toxicity should result in a recommendation for the same level or a higher one [12].
Rigidity. Informally, the accumulating information should guide us in the right direction. In particular, we should be able to move away from a level when the data do not support that level being the MTD. [13].
Efficiency. Any design should make e cient use of the data, in particular performance should be satisfactory when contrasted with the non-parametric optimal design. [5]
2.2 Statistical properties
Suppose that Pr(Y = 1|di) = ψ(di; a, b), is a two parameter-model, specifically let,
| (4) |
i.e., the usual logistic model. Let us also suppose that g(a, b) is a two-dimensional prior distribution for the pair (a, b). This set up was first studied in the context of dose finding by O'Quigley, Pepe, Fisher 1990 [1], described here as 2 parameter CRM. Elsewhere this set-up has been called ADEPT [14, 15], LDRS [16], BLR [8].
Lemma 1
Let ψ(a) = ∂ψ(a, b)/∂a and ψ(b) = ∂ψ(a, b)/∂b and the symbol → to denote almost sure convergence, then
| (5) |
where
PROOF: See Appendix
Lemma 2
Let πn(di) ∈ [0, 1] be the frequency that the level di has been used by the first n experiments, and an, ãn, bn, b̃n are defined by In(an, bn) = Jn(an, bn) = 0, Ĩn(ã, b̃) = J̃n(ã, b̃) = 0, we have that
and that |an − ãn| → 0, |bn − b̃n| → 0 where, as before, → indicates almost sure convergence.
PROOF: See Appendix
Lemmas 1 and 2 establish the connection between the law of large numbers for the observations and theoretical properties of the chosen model. These lemmas provide the support to the following theorem. The corollary to the theorem below shows that, under adaptive sequential sampling, the two parameter logistic model is inconsistent. The theorem shows that the determinant of the Fisher Information, instead of increasing without bound as is required for consistency, will in fact converge almost surely to zero. Bringing these results together we have the main theoretical result:
Theorem 3
Suppose that ψ = exp(a + bdi)/(1 + exp(a + bdi)), then
Proof of the theorem
Let us assume that the working model ψ(a, b|di = xj) = exp (a + bxj)/1 + exp (a + bxj).
Then the likelihood after n patients have been treated is log where Lj = (a+bxj)I(yj = 1)−log[1+exp (a + bxj)] is the contribution from the j th patient. Let us calculate the first and second derivatives of Lj so that we can calculate the Fisher Information matrix for this likelihood function. We have, ∂Lj/∂a = yj − 1/[1 + exp (a + bxj)], ∂Lj/∂b = xjyj − xj/[1 + exp (a + bxj)] = xj∂Lj/∂a, ∂2Lj/∂a2 = exp (a + bxj)/[1 + exp (a + bxj)]2, , ∂2Lj/∂a∂b = xj∂2Lj/∂a2 and ∂2Lj/∂b∂a = xj∂2Lj/∂a2. Using the above components we can see that the observed Fisher Information can be written,
| (6) |
As n → ∞ then all patients are being treated at the MTD thus xj → dm where dm is the MTD. It was shown that contributions to the likelihood function from patients being treated at levels different than the MTD, i.e. at xj ≠ dm are negligible asymptotically [4]. Under the conditions listed in Appendix specific to the logistic model and Lemma 2, we have . Note, from the above, that all of the partial derivatives can be expressed in terms of partial derivatives with respect to a alone, from which we have,
where the terms i11, ... , i22 are all O(n−1) and where nm denotes the number of patients treated at dm. The determinant of since nm/n is bounded by 1 and the terms i11, ... , i22 are all O(n−1). Assuming that the prior g(a, b) is a non degenerate prior, then g(a, b) is bounded so that, as n → ∞, then n−1 log g(a, b) → 0. It follows that
Corollary 1
The 2-parameter logistic model is not consistent.
By not consistent we mean that the parameter estimates fail to converge almost surely to their population counterparts. This is true whether or not the model is misspecified. It may be true that we have almost sure convergence to the MTD or possibly the weaker result, convergence in probability to the MTD (where we would not settle at the MTD but the probability of sampling there would go to one) but it is not at all clear how either of these could be shown. Our view is that a failure to obtain consistency for the parameter estimates is a serious shortcoming and a hint of things to come for finite samples.
3 Small sample impact of over-parameterization
It may be thought that failing to achieve large sample convergence is not important in this setting and that, in practice, with small samples the structure of the model should be su ciently solid to enable reliable results. The main complication caused by the 2-parameter logistic model occurs because the design points, xi's, are not sufficiently spread out. Thus, in this sense, the problem of dose-finding differs from that of the classical bioassay problem, which can lead to such problems as being confined indefinitely to suboptimal doses (rigidity). When dose allocation is guided by the 2-parameter model other issues may arise. These difficulties include a negative or a near zero slope being estimated and/or incoherence. Before illustrating these problems, we recall the conditions in which the MLE's of a and b exist. Silvapulle [17] shows that, assuming there are at least two distinct xj's, the MLE's â and b̂ exist and are unique if and only if any of the following conditions hold:
| (1) |
where ,, , and . Recall that, in the case of the 1-parameter CRM, the MLE of a in model (2) exists as soon as there is heterogeneity in the responses (i.e. at least one DLT and one non-DLT). Since Condition (1) is a stronger condition than that of response heterogeneity, it requires more observations before the MLE's, and the model-recommended dose, can be obtained using the 2-parameter model. A simulated trial based on the NeuSTART design (Neuroprotection with Statin Therapy for Acute Recovery Trial; [18]) illustrates that the MLE's for a and b do not exist until after observing the response of the 21st patient in a 33 patient trial [13]. Therefore, approximately two-thirds of the final sample size is used before the MLE's exist, so Condition (1) may not allow for effective use of the 2-parameter model given the sample size constraints of a dose-finding trial.
3.1 Problems resulting from estimation at the boundary of the parameter space
Single stage trials follow the model from the beginning and employ a Bayesian prior, as opposed to two stage trials where the first stage is not guided by a model. The model is fit after the conditions for the existence of MLE's are met. Using initial DLT rates as (0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7) and initial values as a0 = 3, b0 = 1, we obtain standardized dose units as (−5.197, −4.386, −3.847, −3.405, −3.0, −2.594, −2.153) using model (4). Suppose we are conducting a two-stage design using an initial escalation scheme which replicates the traditional 3+3 design. Let us assume the first three patients have been treated at dose level 1, and 1/3 experienced DLT. At this point, although we do have heterogeneity in the response data, the MLE's for the 2-parameter model do not exist because Condition (1) has not been satisfied. Therefore, investigators decide to continue following the 3+3 design and enroll 3 more patients on dose level 1. None of these next three patients experience DLT, so the trial escalates to a higher dose level. The next patient is treated at dose level 2, and does not experience a DLT. With 1/6 DLT's on level 1, and 0/1 DLT's on level 2, the conditions for the existence of â and b̂ exist. The predicted DLT rates are 1.67 × 10−1, 8.65 × 10−9, 1.10 × 10−11, 1.07 × 10−17, 2.23 × 10−21, 4.63 × 10−25, 4.50 × 10−29 with â = −110.28 and b̂ = −20.91 showing the models’ instability as this curve is decreasing and higher levels have lower DLT rates. If we restrict b > 0, which is almost always done in practice, then b̂ = 1.05 × 10−7, â = −1.609 resulting in ties in the predicted rates at all levels (0.17), since b is estimated at the boundary of the parameter space. Given these same data, the 1-parameter power model with the same initial rates (skeleton) would result in exp(â) = 0.873, where a corresponds to Equation 2 and predicted rates as (0.13, 0.25, 0.35, 0.45, 0.55, 0.64, 0.73) for the 7 levels respectively. This is an example where the 2-parameter model breaks down.
The following example also shows problems with estimation at the boundary of the parameter space. The data are in the form shown in Table 2, (Example 1). Given the data from the first 20 patients from stage 1, the model is fit and the recommendation is level 3 based on â = −1.89, b̂ = −0.20, and predicted rates equal to 0.30, 0.27, 0.25, 0.23, 0.22, 0.20, 0.19. At level 3 one patient is treated with non DLT and the estimated parameters are b̂ = −0.21, â = −1.99 leading to estimated DLT rates of 0.257 and 0.236 at d2 and d3. The fact that d2 is recommended, ie de-escalation, after a non DLT is not acceptable. In all these recommendations b can take any value, i.e. it is not restricted to be positive. Negative values for b result in decreasing rates with dose, which means the condition that the probability of toxicity strictly increases with dose fails. Restricting b > 0, results in b being estimated close to 0, b̂ = 4.42 × 10−8 again indicating estimation problems at the boundary of the parameter space.
Table 2.
Example 1 is described in Section 3.1; (*) indicates that model estimation initiates after the 20th patient has been treated at level 6. Examples 2 and 3 illustrate rigidity (Section 3.2); the trial is confined to d2 and d5 respectively, no matter how many consecutive non-DLT's occur at that level.
| Example 1 | Example 2 | Example 3 | ||||||
|---|---|---|---|---|---|---|---|---|
| Dose | No of DLTs | No of patients treated | Patient | No of DLTs | Dose | Dose | No of DLTs | No of patients treated |
| 1 | 1 | 4 | 1 | 0 | 1 | 1 | 0 | 1 |
| 2 | 1 | 3 | 2 | 0 | 2 | 3 | 0 | 1 |
| 3 | 1 | 4 | 3 | 1 | 3 | 5 | 1 | 3 |
| 4 | 1 | 4 | 4 | 0 | 1 | 6 | 1 | 1 |
| 5 | 1 | 3 | 5 | 0 | 2 | |||
| 6 | 0 | 2* | 6 | 1 | 2 | |||
| 3 | 0 | 1 | ||||||
3.2 Rigidity
The instability associated with 2-parameter estimation may confine the trial to suboptimal doses, known as rigidity. In this section we present such examples and show that even with weakly informative prior information, rigidity still exists in the Bayesian context. For an illustration of rigidity, we return to the NeuSTART example. The study investigated high-dose lovastatin given to patients for 3 days after stroke, followed by a standard dose for 27 days. There were five escalating dose levels 1, 3, 6, 8, 10 mg/kg/day under consideration, and the primary objective of the trial was to identify a dose with DLT rate closest to θ = 10%. The first cohort of three patients were treated at dose level 1, and 0 out of 3 experienced DLT. The trial escalated to dose level 2, and 1 DLT was observed in the second cohort of 3 patients. At this point in the trial, Condition (1) is satisfied, and the MLE's of the 2-parameter logistic model exist. Using skeleton values (0.02, 0.06, 0.10, 0.18, 0.3) and initial values as a0 = 3, b0 = 1, we obtain standardized dose units as (−6.892, −5.751, −5.197, −4.516, −3.84) using model (4). The estimated DLT rates are (0.00, 0.33, 1.00, 1.00, 1.00) with â = 94.50 and b̂ = 16.55. As a result, the recommendation is level 1 for the next entered patient (closest to θ = 0.10). It is straightforward to confirm, using standard logistic regression software (such as R function glm) that the 2-parameter model will recommend level 1 from this point on in the trial, regardless of what outcomes are observed at this dose. In other words, no amount of non-DLT's will result in an escalation back to dose level 2. In the presence of non-DLT's, the predicted DLT rate for level 1 will remain close to zero, whereas a lack of experimentation at level 2 will result in it's predicted rate remaining at 0.33. Therefore, level 2 will never have an estimated DLT closer to 0.10 than dose level 1, no matter what sequence of outcomes are observed at level 1. Similar arguments can be made to illustrate rigidity if 0/2 and 1/2 DLT's are observed at the lowest two levels, respectively, in a trial targeting θ = 0.20. The 2-parameter model was heavily influenced by the single DLT that occurred early in the trial at level 2. Rigidity is still present when incorporating a weakly informative prior distribution such as that recommended for logistic regression models by [19]. Using the default priors a ~ Cauchy(0, 10) for the intercept and b ~ Cauchy(0, 2.5) for the slope, the 2-parameter logistic will be confined to level 1 based on the data observed from the first six entered patients. This can easily be confirmed using the function bayesglm in R package arm. In contrast, a 1-parameter logistic model with the intercept fixed at a0 = 3 would result in more stable probability estimates of (0.03, 0.09, 0.14, 0.23, 0.36), thus recommending level 2 for the 7th patient.
A further illustration of the restrictive nature of the 2-parameter model can be seen using the initial data from a study by Dougherty et al.[20]. The trial aimed to find the dose with DLT rate closest to θ = 20%, among four doses 0.25, 0.50, 0.75, 1.00 μg/kg of nalmefene. Patients were treated in cohorts of 1, and a 1-parameter logistic model with the intercept fixed at a0 = 3 was used to predict DLT rates. The study used skeleton values (0.10, 0.20, 0.40, 0.80) and initial values a0 = 3, b0 = 1 to obtain the standardized dose units (−5.197, −4.386, −3.405, −1.614). The first two patients were treated on the first two dose levels, respectively, and neither had DLT. The third patient was entered onto dose level 3, and experienced a DLT. Heterogeneity in the observed data now exists, so we are able to fit a 1-parameter model, which recommends de-escalation back to level 1. After a non-DLT for the 4th patient, the 1-parameter model recommends escalation to level 2, at which level the next patient does not have a DLT. The 6th patient suffers DLT on level 2 (Table 2, Example 2, data from first 6 patients). The authors used the 1-parameter logistic model where the intercept is held constant, and correctly identified d2 as the MTD with an observed DLT rate of 3/18 and a target rate of 20%. However, for the purposes of illustration here we use the 2-parameter logistic model. After 6 patients, Condition (1) is satisfied, and we would be able to fit a 2-parameter model. In doing so, the estimated DLT rates are (0.00, 0.33, 1.00, 1.00) with â = 98.68 and b̂ = 22.66, from which level 2 has predicted rate closest to 0.20 and is recommended. It can again be confirmed via R function glm that, based on this early data, the trial will be confined to dose 2, no matter how many consecutive non-DLT's happened to be observed at this level. Of course, a DLT at level 2 could result in de-escalation to level 1, but the 2-parameter model will never allow escalation to return to level 3. A potential solution to the amount of patients required for Condition (1) to be satisfied is o ered by Piantadosi et al. [21], which is that of including pseudo-data into the model fitting so as to establish the existence of MLE's. Although this approach o ers a practical solution from a computational standpoint, it is still possible for the 2-parameter model to overfit based on few observation early in the study. Consequently, care should be taken in using pseudo-data prior approaches.
Example 3 (Table 2) also shows the rigidity of the 2-parameter model under a scenario that is very plausible in real trials. A DLT at level 6 among 8 possible levels (k = 8, θ = 0.25, skeleton= (0.05,0.1,0.2,0.3,0.4,0.5,0.6,0.7)) leads to de-escalation to level 5, and no matter how many non-DLTs are observed at d5, the method stays at level 5 indefinitely. The predicted rates are (0, 0, 0, 0, 0.0097, 1, 1, 1) at the 8 levels respectively after 100 non-DLTs are observed at d5, showing that a single DLT at d6, although it might be an isolated clinical adverse event, it is an influential observation. The estimated dose-toxicity curve is so steep that escalation to d6 is no longer permitted.
3.3 Simulations
Table 3 shows the performance of the 1-parameter power model, the 2-parameter logistic model and the theoretical benchmark optimal design defined in [5]. The skeleton values used for this simulation were (0.06, 0.11, 0.20, 0.30), k = 4, N = 25, B = 2000, θ = 0.20, where B is the number of simulations, along with pseudo-data given as DLT rates of (0.20,0,0,0.33) with 2 patients in total. Dose allocation started at the lowest dose and dose jumps were not allowed. The true DLT rates shown in Table 3 are close to the 1 parameter model and Table 5 describes a situation in which the actual observed data are generated by a 2-parameter logistic model and 1 versus 2 parameter models are fit to the data. We present percent of correct selection, dose-patient alloccation, and summarize the results using an accuracy index summarizing the entire distribution of selected doses levels. Higher values of accuracy index are desirable. The accuracy index is given by
where Δl measures the distance of the true DLT rate at dose l from the target rate.
Table 3.
Percent of trials that selected each dose for 5 scenarios and accuracy index (γ). The first row in each scenario shows the true DLT rates. The true MTD is the dose closest to θ = 0.20.
| Scenario 1 | 0.10 | 0.20 | 0.30 | 0.45 | γ |
| 1-parm | 0.24 | 0.51 | 0.23 | 0.02 | 0.53 |
| 2-parm | 0.25 | 0.49 | 0.21 | 0.06 | 0.47 |
| optimal | 0.20 | 0.52 | 0.26 | 0.02 | 0.54 |
| Scenario 2 | 0.02 | 0.11 | 0.20 | 0.35 | |
| 1-parm | 0.01 | 0.29 | 0.52 | 0.17 | 0.48 |
| 2-parm | 0.03 | 0.35 | 0.51 | 0.11 | 0.49 |
| optimal | 0 | 0.23 | 0.56 | 0.2 | 0.51 |
| Scenario 3 | 0.01 | 0.07 | 0.10 | 0.20 | |
| 1-parm | 0 | 0.05 | 0.28 | 0.67 | 0.68 |
| 2-parm | 0.04 | 0.09 | 0.41 | 0.46 | 0.42 |
| optimal | 0 | 0.05 | 0.18 | 0.76 | 0.76 |
| Scenario 4 | 0.20 | 0.29 | 0.36 | 0.44 | |
| 1-parm | 0.65 | 0.27 | 0.07 | 0.01 | 0.70 |
| 2-parm | 0.55 | 0.26 | 0.08 | 0.11 | 0.48 |
| optimal | 0.66 | 0.24 | 0.09 | 0.02 | 0.68 |
| Scenario 5 | 0.01 | 0.07 | 0.20 | 0.40 | |
| 1-parm | 0 | 0.23 | 0.64 | 0.13 | 0.57 |
| 2-parm | 0.01 | 0.28 | 0.64 | 0.08 | 0.59 |
| optimal | 0 | 0.13 | 0.75 | 0.12 | 0.6812 |
Table 5.
Performance 2-parameter logistic (2-parm CRM) versus 1-parameter power model (1-parm CRM) when the true underlying model is the 2-parameter logistic; entries represent proportion of trials recommending each dose (as shown in O'Quigley, Pepe, Fisher 1990). R(di) denotes the true DLT rates at each dose level; the target was 0.2, and true MTD was level 4.
| Dose | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| R(di) | .06 | .08 | .12 | .18 | .40 | .71 |
| 1-parm CRM | .00 | .04 | .23 | .57 | .15 | .00 |
| 2-parm CRM | .01 | .11 | .16 | .48 | .19 | .05 |
Across all scenarios we see higher performance with 1-parameter power model with average percent correct selection at the MTD given by : 0.58, 0.52, and 0.65 for the 1-parameter model, 2-parameter model and optimal design respectively, and average index across levels given by 0.57, 0.49, and 0.63 for the 1-parameter, 2-parameter and optimal design respectively. Table 4 shows the number of patients treated per dose level, and the overall observed DLT rate.
Table 4.
Number of patients treated at each dose level out of 25 patients and overall % of patients with dose-limiting toxicities (DLT). The first row in each scenario shows the true DLT rates; θ = 0.20.
| Scenario 1 | 0.10 | 0.20 | 0.30 | 0.45 | % of patients with DLT |
| 1-parm | 7.80 | 9.50 | 6.06 | 1.64 | 0.213 |
| 2-parm | 7.05 | 9.79 | 5.43 | 2.72 | 0.223 |
| Scenario 2 | 0.02 | 0.11 | 0.20 | 0.35 | |
| 1-parm | 2.64 | 7.18 | 10.37 | 4.81 | 0.187 |
| 2-parm | 2.81 | 8.21 | 9.72 | 4.26 | 0.179 |
| Scenario 3 | 0.01 | 0.07 | 0.10 | 0.20 | |
| 1-parm | 1.65 | 3.14 | 7.79 | 12.42 | 0.142 |
| 2-parm | 2.95 | 3.97 | 8.31 | 9.77 | 0.128 |
| Scenario 4 | 0.20 | 0.29 | 0.36 | 0.44 | |
| 1-parm | 14.62 | 6.24 | 3.17 | 0.97 | 0.256 |
| 2-parm | 11.69 | 6.54 | 3.10 | 3.67 | 0.282 |
| Scenario 5 | 0.01 | 0.07 | 0.20 | 0.40 | |
| 1-parm | 2.06 | 7.68 | 11.63 | 3.64 | 0.176 |
| 2-parm | 1.92 | 7.44 | 12.03 | 3.61 | 0.175 |
Several authors have previously examined the behavior of 1 versus 2-parameter models within dose escalation designs. Over a large number of simulations, accuracy of recommendation was clearly superior for the misspecified 1-parameter CRM against the 2-parameter CRM even though the data were generated by 2-parameter CRM (0.57 versus 0.48; Table 5).
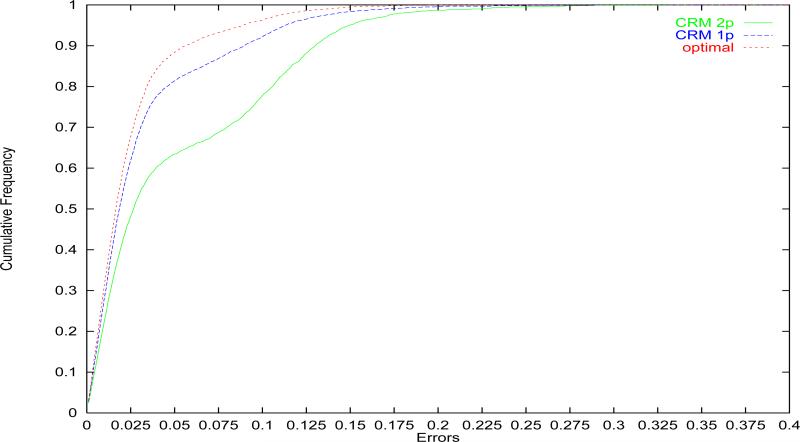
Over a much wider class of situations, O'Quigley et al. [5] compared the performance in terms of accuracy of recommendation of the correct MTD of the optimal design, 1-parameter CRM and 2-parameter CRM and confirmed the superior performance of 1-parameter CRM as illustrated in Figure 1. Paoletti and Kramar [6] also found that the performance of 2-parameter model is inferior consistently to the 1-parameter model within the Bayesian and Likelihood framework regardless of the choice of other design parameters. They examined cases where the number of levels and sample size varies, and illustrated examples where the behavior of 2-parameter logistic model is unstable. They also described the performance of each model relative to the optimal method when performance is measured via the errors on the probability scale.
Figure 1.
Cumulative distribution of errors. Optimal design, 1-parameter CRM and 2-parameter CRM as shown in O'Quigley, Paoletti and Maccario, 2002.
A question that often comes up in this context is the following: does the current estimate of the MTD contain all of the useful information needed for efficient estimation? In terms of the goals of the study, i.e. accurate estimation of the MTD and experimentation at and around the MTD, does the distribution of the estimated MTD, rather than just the summary statistic alone, e.g. the estimated mean, provide any way to improve performance? The answer is that it does not [22]. Taking into account the uncertainty in the estimation of the MTD in terms of identifying when to stop the trial or which levels to take into the expansion phase can be useful [23] but this uncertainty does not help in terms of dose allocation and the recommended MTD at the end of the trial [24]. Although designs such as EWOC are conceptually interesting, controlling the risk of overdosing can be achieved without the addition of extra parameters and this was shown by Chu et al. [24].
4 Dimensionality in more complex models
In this paper we have mostly focused on the relatively simple situation of a single agent and no additional complicating features. However, one of the main attractions of model based designs when compared to the old standard 3+3 design is that they can readily address more involved problems. Such problems include patient heterogeneity, making use of information on grades, partially ordered combination studies, finding the most successful dose (MSD) that makes use of efficacy as well as toxicity outcomes and many other more complex situations. What is the impact of model dimensionality in these yet more involved studies? Our intuition, based on the results of this paper and others looking at the 1-parameter versus 2-parameter CRM models [6], would suggest that not only are richly parameterized models not going to be rewarded with improved performance but the opposite is likely to be true.
Consider for example the case of partial ordering when studying the safety of drug combinations. The results of Wages et al,[25] are generally superior to those obtained from models that try to model all marginal and secondary effects. The reason for this is due to the ethical necessity of treating patients at the currently best estimate of the MTD. Richer models with more parameters require more sources of information, including experimentation at various levels, than can be provided by algorithms that tend to concentrate at and around the MTD. As a result, the parameter estimates can be highly correlated resulting in unstable information matrices (non-invertible matrices). Strong Bayesian priors can help overcome this weakness but have their own weakness in that when prior assumptions are not correct the resulting biases can be large [26].
Another interesting illustration can be seen when we attempt to deal with simultaneous binary information on both toxicity and efficacy. Correlation or dependency between these two binary outcomes can be expressed via the odds-ratio which quantifies the difference between two conditional probabilities; that of efficacy given non-toxicity and that of efficacy given toxicity. The problem is fully specified via 3 rates; that of toxicity and those of efficacy given toxicity or no toxicity. O'Quigley et al [27] argued that the probability of efficacy given toxicity is not very relevant in terms of locating the most successful dose (MSD) and that overall success hinges on only 2 rates; that of toxicity and that of efficacy given no toxicity. Bypassing the need to model the rate of efficacy given toxicity reduces the dimension of the parameter space from 3 to 2. The results were very good and allowed accurate and reliable estimation of the MSD based only on two rates, both of which can be viewed as marginal rates if, in addition, we assume that the probability of efficacy and the probability of toxicity are independent given dose. Such an assumption may well be wrong but, as shown in Iasonos and O'Quigley [28] the algorithm is completely insensitive to different odds-ratios and so, in particular, why not simply fix the odds-ratio at the value 1 (conditional independence given dose). This parallels the situation we have for elementary dose-finding with, say, a two-parameter logistic model reduced to a one-parameter model by fixing the intercept at some arbitrary value. Regardless of the value, we know that this works very well when the goal is to locate the MTD. If the goal is to estimate the whole curve then, unless we experiment away from the MTD, we will not obtain good results.
Including an association parameter into a dose-finding study can present a considerable challenge and the performance of the resulting method can depend upon unknown quantities. An example is given in the simulations by Thall and Cook [29], where the percentage of selecting a specific dose decreases from 82% to 14% on the basis of differences in the value of the association parameter. This case again illustrates that when modeling additional parameters such as the association parameter in a bivariate endpoint setting, correct specification of the additional parameter is crucial for the design's performance . In the clinical setting such exact information is not usually available and methods that avoid the inclusion of such association parameters into the model seem to be preferable. [26]
5 Recommendations
In this paper we showed that the 2-parameter model is not consistent and will behave erratically when compared to the 1-parameter model. The solution to ensure safety and e ciency is not to be found by adding more parameters to the model. We suggest several possible solutions as follows:
If we use the Bayesian CRM then we need to choose an appropriate prior so that the dose at which we carry out the experiment (eg. dose level 1) is a dose indicated by the prior. A CRM design requirement is to experiment at the level indicated by the model and, while a gap of one or two levels between the dose actually being used and the one indicated by the prior/posterior is not problematic, a gap of too many levels, such as 9 levels as in the motivating example will be problematic [9].
Keep the prior chosen by the investigators but then make sure to actually evaluate the sensitivity of the dose-allocation algorithm to the choice of model and prior. This was emphasized by Gatsonis and Greenhouse in 1992 [30] who showed that the marginal posterior distribution of the MTD was not sensitive to the form of the model but it was sensitive to the choice of the prior distribution. Simulations above showed that the 2-parameter model cannot override the prior in certain cases even as the sample size increased (inconsistent). We suggest the use of a non-informative prior making each dose equally likely to be the MTD, when reliable data cannot be the basis of an informative prior.
When available, relevant historical data can be used to form an informative prior then this is a viable option in certain clinical scenarios. The data can be from another Phase I study in a similar patient population or it can be from a study evaluating a different schedule. These ideas have been studied under bridging and different models have been used depending on the clinical scenario [25, 31]. The weight of the prior data needs to be examined via simulations and the operating characteristics will determine how informative a prior can be. It is important that the design remains robust and various levels can be reached as the final MTD even when the trial data are at odds with the historical data. [32, 33]
Abandon the use of any prior and use a two-stage likelihood based design, the first stage being necessarily a non model based design since, until heterogeneity in the responses is observed, we do not have parameter estimates in the interior of the parameter space. This requires that the first entered patients be treated according some scheme decided by the clinical investigators. This approach can be very attractive and allows the investigators to make use of great flexibility. For instance, we can use intermediary grades to guide initial escalation whereby only one or two patients are included at any level in the presence of low-grade toxicities and more, three say, in the presence of intermediary toxicities. [34] As soon as the first DLT is observed then we switch to the second stage of the 2-stage design and base escalation or de-escalation on the 1-parameter working model. Two stage designs are very useful when we have many dose levels such as > 10, so that we can eliminate levels far away from the MTD. Paoletti and Kramar [6] used the 1 parameter model with a strongly informative prior at the lower levels, and observed that there was difficulty reaching levels beyond level 8. This is very interesting since it would appear to show very conservative behavior as opposed to the aggressive behavior described by Neunschwander et al. In fact both examples illustrate the same error; that of supposing that a very strong prior can be easily overwritten by the data. In the Paoletti and Kramar example the prior corresponded to approximately 7.7 DLTs out of 8.7 patients, on the basis of exponential prior and skeleton value of 0.88 at level 9 (or > 0.75 to levels above 6) . Given such information, any method would require to observe many non-toxicities at level 8 before taking the risk of returning to level 9.
6 Conclusion
The essential difficulty for over-parameterized models is that they can be too flexible. In this paper we have presented examples where just a few observations, sometimes a single observation, will exercise an undue influence on the 2-parameter logistic model. This influence can even last indefinitely and not be overwritten by any amount of data. In practice, this means poor performance when compared with an efficient parsimoniously parameterized model, and, in some cases, the algorithm becomes completely stuck at an obviously incorrect dose level. In contrast, the 1-parameter model, although rigid in shape is not rigid in nature and is able to escalate and de-escalate appropriately in response to the observations and quickly homing in on the vicinity of the MTD.
While more complex clinical problems call for more complex models such as the 2-group heterogeneity problem where an additional parameter is needed - the principle of parsimony is always a good guide. Include only as many parameters as are necessary in order to characterize those key aspects of the problem that our interest is focused on. We can often avoid estimating secondary or nuisance parameters. If the purpose is to estimate the whole dose-toxicity curve and not just locate the MTD, as is often the case in PK studies, then more parameters will be needed. In order to estimate these additional parameters in any satisfactory way, we will need to spread the observations and follow a different allocation rule. Randomization may or may not be used to do this and, only if we obtain information across a broader spectrum of levels can we hope to tackle the more difficult problem of estimating the whole dose-toxicity curve rather than locating a single point. Other problems include evaluation of efficacy in the dose expansion setting or Phase I/II trials.
Lastly, particular care is needed when using Bayesian methods in the Phase I setting. Unlike later phase clinical trials, Phase I trials will rarely have the opportunity to fully overcome the prior influence due to the small sample size. Priors that amount to high rates of toxicities or zero rates of toxicities will affect how conservatively or aggressively the method escalates respectively. Prudence in choosing an appropriate prior is required and the choice of a suitable model still requires careful consideration. Priors and model parameters are not always easily interpreted and it can be of great value to transform these, if only approximately, to more concrete quantities such as the equivalent number of toxicities and the total number of patients in terms of pseudo observations at given levels. As described in this paper, such information allows us to understand and avoid model behavior that is clinically unacceptable.
Acknowledgment
We would like to thank the Editors for their helpful comments. This work was partially funded by National Institute of Health (Grant Numbers 1R01CA142859, P30 CA008748, K25CA181638).
Appendix
Proof of Lemma 1
Let us assume ψ = exp(a + bxj)/(1 + exp(a + bxj)) is the usual logistic model and that g(a, b) is a two-dimensional prior distribution that is non degenerate for the pair (a, b).
| (A.1) |
| (A.2) |
| (A.3) |
| (A.4) |
| (A.5) |
| (A.6) |
Observe that for each dose level xj, and are uniformly continuous in a and b over the finite interval [A1, A2], [B1, B2]. Then for any ϵ > 0 and for each xj there must exist a partition A1 = t0 < t1 < ... < tk = A2 and B1 = r0 < r1 < ... < rk = B2 such that for any a ∈ [A1, A2], b ∈ [B1, B2], there is a tk0 ∈ [A1, A2] and rk0 ∈ [B1, B2] such that
It follows that supa∈[A,B] |In(a, b)| ≤ ϵ and supa∈[A,B] |În(a, b)| ≤ ϵ since . Define
In2(a, b) converges to 0 almost surely because of the limit theorem of martingales (Shiryayev, A. N. (1984), Probability. (Trans. R. P. Boas). New York: Springer-Verlag) and since for fixed (tk0, rk0), {nIn2 : n ≥ 1} forms a martingale. Since there is a finite number of partition points it follows that
The same arguments can be used to show supa∈[A,B] |Jn(a) − J̃n(a)| → 0, since
Proof of Lemma 2
Condition 1: ψ is strictly increasing,; it is continuous and strictly monotone in a, b in the same direction for all x. Condition 2: , and , are continuous and strictly monotone in a, b. Condition 3: The parameters a, b belong to a finite interval [A1, A2], [B1, B2] respectively. Let
| (A.7) |
| (A.8) |
Let us assume the conditions 1- 3 hold. It follows from conditions 1-3 and the monotonicity assumption that unique solutions exist for Ĩn(a, b) = 0 and J̃n(a, b) = 0. Since an, bn solve In(an, bn) = Jn(an, bn) = 0, Lemma 1 ensures that almost surely for n large enough, the solution of In(an, bn) = Jn(an, bn) = 0 is close to the solution of Ĩn(an, bn) = J̃n(an, bn) = 0. Since ãn, b̃n solve Ĩn(an, bn) = J̃n(an, bn) = 0 for each 1 ≤ i ≤ k the definition of ãn, b̃n, and condition 2 imply that ãn, b̃n are the unique solution of
| (A.9) |
| (A.10) |
As n tends to infinity, all the πn(di) → 0 for di ≠ dm in A.7 and A.8 and πn(di) → 1 for di = dm. Thus if ãn, b̃n are the solution of Equations A.9 and A.10, will be close to the solution of:
The solution of the above equation is ãn, b̃n and Lemma 1 ensures the consistency of an, bn.
References
- 1.O'Quigley J, Pepe M, Fisher L. Continual reassessment method: a practical design for phase 1 clinical trials in cancer. Biometrics. 1990;46:33–48. [PubMed] [Google Scholar]
- 2.Azriel D, Mandel M, Rinott Y. The treatment versus experimentation dilemma in dose finding studies. Journal of Statistical Planning and Inference. 2011 Aug;141(8):2759–2768. 2011. [Google Scholar]
- 3.Serfling RJ. U-Statistics, in Approximation Theorems of Mathematical Statistics. John Wiley Sons, Inc.; Hoboken, NJ, USA: 1980. [Google Scholar]
- 4.Shen LZ, O'Quigley J. Consistency of continual reassessment method in dose finding studies. Biometrika. 1996;83:395–406. [Google Scholar]
- 5.O'Quigley J, Paoletti X, Maccario J. Non-parametric optimal design in dose finding studies. Biostatistics. 2002 Mar;3(1):51–6. doi: 10.1093/biostatistics/3.1.51. [DOI] [PubMed] [Google Scholar]
- 6.Paoletti X, Kramar A. A comparison of model choices for the continual reassessment method in phase I cancer trials. Statistics in Medicine. 2009;28(24):301228. doi: 10.1002/sim.3682. [DOI] [PubMed] [Google Scholar]
- 7.Liao O, Dragalin V. JSM. Boston, MA: 2014. Bayesian Two-Parameter Logistic Regression Model–Based Method for Single Dose-Finding Trial. Abstract No 636. [Google Scholar]
- 8.Neuenschwander B, Branson M, Gsponer T. Critical aspects of the Bayesian approach to phase I cancer trials. Stat Med. 2008;27(13):2420–39. doi: 10.1002/sim.3230. [DOI] [PubMed] [Google Scholar]
- 9.Iasonos A, O'Quigley J. Adaptive Dose-Finding Studies: A Review of Model-Guided Phase I Clinical Trials. Journal of Clinical Oncology. 2014 Aug 10;32(23):2505–2511. doi: 10.1200/JCO.2013.54.6051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.O'Quigley J, Shen LZ. Continual reassessment method: a likelihood approach. Biometrics. 1996;52:673–84. [PubMed] [Google Scholar]
- 11.Cheung YK, Chappell R. A simple technique to evaluate model sensitivity in the continual reassessment method. Biometrics. 2002;58(3):671–4. doi: 10.1111/j.0006-341x.2002.00671.x. [DOI] [PubMed] [Google Scholar]
- 12.Cheung YK. Coherence principles in dose-finding studies. Biometrika. 2005;92:863–873. [Google Scholar]
- 13.Cheung YK. Dose finding by the continual reassessment method. Chapman and Hall/CRC Biostatistics Series; New York: 2011. [Google Scholar]
- 14.Whitehead J, Brunier H. Bayesian decision procedures for dose determining experiments. Stat Med. 1995 May 15-30;14(9-10):885–93. doi: 10.1002/sim.4780140904. discussion 895-9. [DOI] [PubMed] [Google Scholar]
- 15.Gerke O, Siedentop H. Optimal Phase I dose-escalation trial designs in oncologyA simulation study. Stat Med. 2008;27:53295344. doi: 10.1002/sim.3037. [PubMed] [DOI] [PubMed] [Google Scholar]
- 16.Murphy JR, Hall DL. A logistic dose-ranging method for Phase I clinical investigations trial. J of Biopharmaceutial Statistics. 1997;7(4):635–647. doi: 10.1080/10543409708835213. [DOI] [PubMed] [Google Scholar]
- 17.Silvapulle M. On the Existence of Maximum Likelihood Estimators for the Binomial Response Models. Journal of the Royal Statistical Society. Series B (Methodological) 1981;43(3):310–313. [Google Scholar]
- 18.Elkind MSV, Sacco RL, MacArthur RB, Fink DJ, Peerschke E, Andrews H, Neils G, Stillman J, Corporan T, Leifer D, Cheung K. The Neuroprotection with Statin Therapy for Acute Recovery Trial (NeuSTART): an adaptive design phase I dose-escalation study of high-dose lovastatin in acute ischemic stroke. International Journal of Stroke. 2008;3:210218. doi: 10.1111/j.1747-4949.2008.00200.x. doi: 10.1111/j.1747-4949.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gelman A, Jakulin A, Pittau M, Su Y. A Weakly Informative Default Prior Distribution for Logistic and Other Regression Models. The Annals of Applied Statistics. 2008 Dec.2(4):1360–1383. [Google Scholar]
- 20.Dougherty TB, Porche VH, Thall PF. Maximum Tolerated Dose of Nalmefene in Patients Receiving Epidural Fentanyl and Dilute Bupivacaine for Postoperative Analgesia. Anesthesiology. 2000;92(4):1010–6. doi: 10.1097/00000542-200004000-00018. [DOI] [PubMed] [Google Scholar]
- 21.Piantadosi S, Fisher JD, Grossman S. Practical implementation of a modified continual reassessment method for dose-finding trials. Cancer Chemother Pharmaco. 1998;41(6):429–36. doi: 10.1007/s002800050763. [DOI] [PubMed] [Google Scholar]
- 22.Clertant M, O'Quigley J. Abstract. Symposium Phase I methodology. Paris, France: 2015. [Google Scholar]
- 23.Iasonos A, O'Quigley J. Sequential Monitoring of Phase I Dose expansion cohorts. Stats Med. 2016 doi: 10.1002/sim.6894. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chu P, Ling Y, Shih WJ. Unifying CRM and EWOC designs for phase I cancer clinical trials. Journal of Statistical Planning and Inference (Impact Factor: 0.68) 2009;139(3):1146–1163. 03 DOI: 10.1016/j.jspi.2008.07.005. [Google Scholar]
- 25.Wages NA, Conaway MR, O'Quigley J. Continual reassessment method for partial ordering. Biometrics. 2011 Dec;67(4):1555–63. doi: 10.1111/j.1541-0420.2011.01560.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Cunanan K, Koopmeiners JS. Evaluating the Performance of Copula Models in Phase I-II Clinical Trials Under Model Misspecication.”. BMC Medical Research Methodology. 2014;14 doi: 10.1186/1471-2288-14-51. Article 51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.O'Quigley J, Hughes MD, Fenton T. Dose-finding designs for HIV studies. Biometrics. 2001 Dec;57(4):1018–29. doi: 10.1111/j.0006-341x.2001.01018.x. [DOI] [PubMed] [Google Scholar]
- 28.Iasonos A, O'Quigley J. Dose expansion cohorts in Phase I trials. Stats Biopharmaceutical Research. 2016 doi: 10.1080/19466315.2015.1135185. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Thall PF, Cook JD. Dose-finding based on efficacy-toxicity trade-offs. Biometrics. 2004 Sep;60(3):684–93. doi: 10.1111/j.0006-341X.2004.00218.x. [DOI] [PubMed] [Google Scholar]
- 30.Gatsonis C, Greenhouse JE. Bayesian methods for phase I clinical trials. Stats Med. 1992;11:1377–1389. doi: 10.1002/sim.4780111011. [DOI] [PubMed] [Google Scholar]
- 31.O'Quigley J, Shen L, Gamst A. Journal of Biopharmaceutical Statistics. 1999;9(1) doi: 10.1081/BIP-100100998. [DOI] [PubMed] [Google Scholar]
- 32.Iasonos A, Gnen M, Bosl GJ. Scientific Review of Phase I Protocols With Novel Dose-Escalation Designs: How Much Information Is Needed? J Clin Oncol. 2015 Jul 1;33(19):2221–5. doi: 10.1200/JCO.2014.59.8466. doi: 10.1200/JCO.2014.59.8466. Epub 2015 May 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Petroni GR, Wages NA, Paux G, Dubois F. Implementation of adaptive methods in early-phase clinical trials. Statistics in Medicine. 2016 doi: 10.1002/sim.6910. to appear. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Iasonos A, Zohar S, O'Quigley J. Incorporating lower grade toxicity information into dose finding designs. Clin Trials. 2011 Aug;8(4):370–9. doi: 10.1177/1740774511410732. [DOI] [PMC free article] [PubMed] [Google Scholar]