INVESTIGATING SHAPE REPRESENTATION USING SENSITIVITY TO PART- AND AXIS-BASED TRANSFORMATIONS

Abstract

Part -and axis-based approaches organize shape representations in terms of simple parts and their spatial relationships. Shape transformations that alter qualitative part structure have been shown to be more detectable than those that preserve it. We compared sensitivity to various transformations that change quantitative properties of parts and their spatial relationships, while preserving qualitative part structure. Shape transformations involving changes in length, width, curvature, orientation and location were applied to a small part attached to a larger base of a two-part shape. Increment thresholds were estimated for each transformation using a 2IFC procedure. Thresholds were converted into common units of shape difference to enable comparisons across transformations. Higher sensitivity was consistently found for transformations involving a parameter of a single part (length, width, curvature) than those involving spatial relations between two parts (relative orientation and location), suggesting a single-part superiority effect. Moreover, sensitivity to shifts in part location—a biomechanically implausible shape transformation—was consistently poorest. The influence of region-based geometry was investigated via stereoscopic manipulation of figure and ground. Sensitivity was compared across positive parts (protrusions) and negative parts (indentations) for transformations involving a change in orientation or location. For changes in part orientation (biomechanically plausible), sensitivity was better for positive than negative parts; whereas for changes in part location (biomechanically implausible), no systematic difference was observed.

Introduction

A fundamental question in visual perception is how the human visual system represents object shape. Part of the difficulty in addressing this question is that the notion of shape itself is not as clear-cut as many other visual attributes. One definition of shape, originating in geometry and mathematics, is that it refers to geometric properties that are unaffected by rigid transformations (transformations that preserve inter-point distances) and uniform scaling. This is consistent with intuition: moving a statue to a different location, making it face in a different direction, or even having a replica made that is half the original size, does not alter what we consider to be “its shape”. Under this view, two shapes are equivalent if they can be brought into alignment by applying one or more of these transformations (e.g. Ullman, 1989). As a result, the mathematical “distance” between two shapes can be defined in terms of how much they still differ once they have been brought into maximal alignment using these transformations (e.g. Kendall, 1989; Mardia & Dryden, 1998).

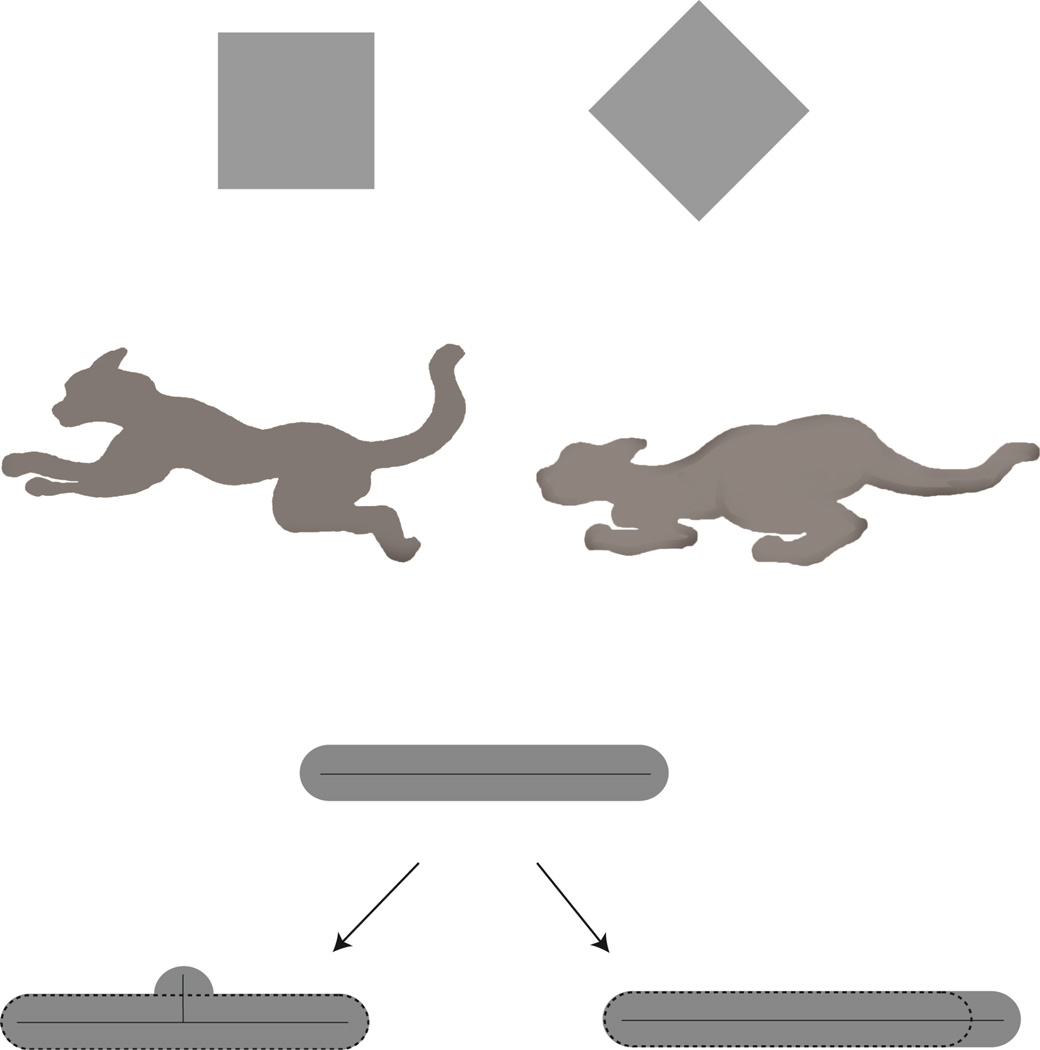
Psychologically speaking things are more complicated, however, and the above definition fails to capture the notion of “perceived shape”—i.e. as far as representation by the human visual system is concerned. First, two forms that are geometrically equivalent can look different. Figure 1A shows an example due to Mach (Mach, 1914/1959) in which the two shapes look different ("square" versus "diamond") despite the fact that they differ only by a rigid rotation in the image plane through 45° degrees. Indeed, there is a great deal of work demonstrating large effects of orientation on shape perception (e.g., Rock, 1973; Tarr & Pinker, 1989). Second, geometrically distinct shapes (i.e. shapes not related by rigid transformations and uniform scaling, or even by affine transformations) are often perceived to be the same. Consider a cat viewed in a crouching position versus one in a pouncing pose (Figure 1B). Technically, the two shapes are of course different: no rigid template could possibly work for both shapes. Yet there is a sense in which the two shapes are in fact equivalent, namely, the two differ only in the articulation of the limbs of the same biological form. Such part articulations are in fact extremely common in animate objects, and define an important class of shape transformations that the visual system must deal with successfully.

Figure 1.

Clarifying the inadequacy of geometric equivalence in capturing shape perception. (A) Two geometrically equivalent shapes that look different: “square” vs. “diamond” (Figure adapted from Mach 1914/1959). (B) Two geometrically distinct shapes (i.e., they cannot be related by rigid transformations and uniform scalings) that look perceptually similar. These two are naturally perceived as arising from actions of the same biological organism. The cat is shown in two different poses, each with different configurations of its limbs. (C) Shape transformations that alter qualitative part structure are perceived as larger changes (“bump” on the bottom left) than those that preserve part structure (“extension” on the bottom right). Note that the transformation on the right actually involves a larger physical change to the original (top) shape.

Part-based representation of shape

The non-rigid movements of biological forms have been an important source of motivation for the part-based approach to shape representation. According the part-based approach, the visual system represents the shape of complex objects in terms of simpler parts, and the spatial relationships between these parts. In other words, it proceeds by segmenting complex shapes into parts, and organizing the shape representation as a hierarchy of parts. An important feature of this “structural” approach to shape is that it separates the representation of the shape of the individual parts from the representation of the spatial relationships between these parts. As a result, an object can be readily identified as composed of the same parts as another object, though in slightly different (but still “valid”) spatial relationships. This property allows part-based representations to be more robust to changes in the articulated pose of an object: the cat can be recognized as being essentially the same “form,” irrespective of whether it is sleeping or running.

An important cue for segmenting a shape into parts is the presence of negative minima of curvature along its bounding contour (Hoffman & Richards, 1984). Negative minima of curvature are points with locally maximal magnitude of curvature that lie in concave regions of shape (i.e. regions with negative curvature). The minima rule is motivated by a regularity of nature known as transversality: the process of joining two separate objects to form a single composite object generically produces negative minima—in this case, tangent discontinuities—at their locus of intersection (Hoffman & Richards, 1984). Similarly, the sprouting of a new part (say, from a seed or embryo) similarly produces negative minima of curvature (Leyton, 1989). Thus, given only a composite shape, points of negative minima provide natural candidate points for segmenting the shape into parts. This is not to say that negative minima are sufficient by themselves to divide shapes into parts. First, they do not specify how candidate boundary points should be paired to form cuts that divide the shape. Second, negative minima can fail to be part boundaries (e.g. negative minima along a bending snake), and part boundaries can fail to be negative minima (see Barenholtz & Feldman, 2003; Siddiqi, Tresness & Kimia, 1996; Singh & Hoffman, 2001; Singh, Seyranian, Hoffman, 1999; Singh 2014; Winter & Wagemans, 2006). Negative minima do, however, provide an important cue for part segmentation.

A great deal of psychophysical work has shown that the visual system represents shapes in terms of parts (Biederman, 1987; Biederman & Cooper, 1991; Cave & Kosslyn, 1993; Hayworth & Biederman, 2006; Hoffman & Richards, 1984; Hoffman & Singh, 1997; Lamberts & Freeman, 1999; Lamote & Wagemans, 1999), and that this has important implications for a number of perceptual phenomena, including figure/ground assignment (e.g. Barenholtz & Feldman, 2006; Baylis & Driver, 1995; Hoffman & Singh, 1997; Kim & Feldman, 2009; Stevens & Brookes, 1988), change detection (Barenholtz, Cohen, Feldman, & Singh, 2003; Bertamini & Croucher, 2003; Bertamini & Farrant, 2005; Cohen, Barenholtz, Singh & Feldman, 2005), contour completion (e.g. Liu, Jacobs, & Basri, 1999; Fulvio & Singh, 2006), perception of transparency (Singh & Hoffman, 1998), visual search (e.g., Hulleman, te Winkel, & Boselie, 2000; Wolfe & Bennet, 1997; Xu & Singh, 2002), visual attention (Vecera, Behrmann, & Filapek, 2001; Vecera, Behrmann, & McGoldrick, 2000; Watson & Kramer, 1999), and the perceptual organization of 3D surfaces (Phillips, Todd, Koenderink & Kappers, 2003).

In a large-scale study, de Winter & Wagemans (2006) examined partsegmentation performance by having subjects draw cuts on a large set of line drawings of objects, in order to decompose them into natural parts. They found that the vast majority of cuts drawn by subjects passed near negative minima of curvature. Psychophysical evidence has also shown that part segmentation is an automatic process, whose implications can be demonstrated using indirect “objective” tasks, even when the instructions to subjects do not involve explicit reference to “parts”. For example, Baylis & Driver (1994) showed that observers' higher sensitivity to symmetry than to repetition (or parallelism) within a shape can be explained in terms of “obligatory” part segmentation. Symmetric shapes have corresponding parts on the two sides, whereas shapes with parallel sides have non-corresponding parts. By creating novel displays that teased apart these two factors, they were able to demonstrate that the original symmetry benefit derives from the presence of corresponding parts, and not from symmetry per se. Barenholtz & Feldman (2003) showed that observers are faster at discriminating two probes in a same/different task when they lie on a single part, than when they lie on two different parts (i.e. across a part boundary). Importantly, this part-based effect was obtained despite the fact that the curvature profile of the intervening contour was carefully controlled to be identical in the two cases. Cohen & Singh (2006) employed a segment-identification task in which observers indicated whether a given contour segment matched some portion of a (whole) test shape. They found that observers were more accurate at identifying segments whose part boundaries are defined by negative minima of curvature, than segments of comparable (or even greater) length segmented at other qualitative types of points (e.g. positive maxima of curvature, or inflection points). Perceptual organization of shape in terms of parts has also been shown to influence global judgments on shapes, such as the visual estimation of an object’s center of mass (Denisova et al., 2006) and perceived orientation (Cohen & Singh, 2007) of two-part shapes.

Skeleton or axis-based approaches to shape

A complementary approach to shape representation is in terms of axes or shape skeletons. A shape skeleton (or "stick-figure") provides a compact and efficient representation of complex shape that emphasizes its structural aspects (see Figure 2). Figure 2A shows some examples of pipe-cleaner objects from a well-known paper by Marr & Nishihara (1978). These objects are readily recognizable as specific animals, despite the absence of any information about surface color and texture, or even surface geometry—thereby suggesting that skeletal structure carries a great deal of information about shape for human vision.¹ Psychophysical studies (Burbeck & Pizer, 1995; Kovacs et al., 1998) and a recent imaging study (Lescroart & Biederman, 2012) have provided evidence for the representation of shape axes by the human visual system. The results of Kovacs and colleagues, for example, showed an enhanced contrast sensitivity for Gabor patches located along a shape's medial axis (Kovacs & Julesz, 1994; Kovacs et al., 1998).

Figure 2.

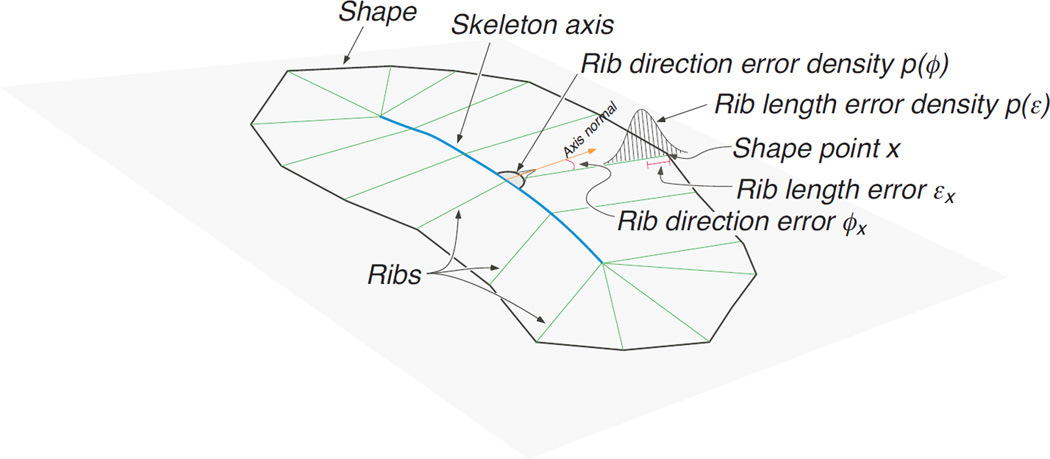
The concept of skeletal representation. (A) Marr & Nishihara’s models made out of pipe cleaners are easily recognized as specific animals despite the absence of surface color or texture, or even surface geometry. This points to the importance of skeletal representations in shape perception (Figure adapted from Marr & Nishihara, 1978) (B) Illustration of the probabilistic generative model (i.e., the likelihood function) that models how shapes are generated or “grow” from skeletons along “ribs” that are roughly orthogonal to the skeleton (Figure adapted from Feldman & Singh, 2006) (C) The Bayesian or MAP skeleton provides a compact “stick-figure” representation that captures the qualitative branching structure of its parts, shown here for different animals (Figure adapted from Feldman & Singh, 2006).

It is natural to conceive of part-based and axis-based representations as two complementary ways of capturing the structural aspects of a complex shape. Indeed, the shape skeleton was originally proposed by Blum as a compact means of capturing the morphological aspects of biological form—i.e. a representation that makes explicit the internal structure of a biological form, such as the branching structure of its parts)—by having an axial branch devoted to each structural part (see Blum, 1973). In practice, however, this one-to-one correspondence between parts and axial branches was not achieved by Blum’s medial-axis transform (as noted by Blum & Nagel, 1978), or its modern descendants. A more recent probabilistic approach to computing the shape skeleton does establish this one-to-one correspondence, however (Feldman & Singh, 2006).

In Feldman & Singh’s (2006) Bayesian approach to skeleton computation, a shape is treated as a combination of generative factors and noise. The skeletal representation seeks to model the generative factors, which ignoring noise. Their approach begins with a probabilistic generative model (or likelihood function) that captures how shapes “grow” from skeletons along “ribs” that are roughly orthogonal to the skeleton (see Figure 2B). The generative model thus provides the probability of generating different shapes from a given skeleton. Given any shape, the model then uses Bayes to “invert” probabilities and estimate the skeleton that best “explains” that shape—under the assumptions embodied in the generative model and the prior. The prior here simply favors skeletons with fewer branches, and with straighter (i.e. less curved) branches. Skeletons with more branches and/or more curved axes can always fit a shape better (i.e. yield a higher likelihood); however they are penalized for their added complexity (lower prior probability). Thus the “best” skeletal estimate—i.e. the maximum-a-posteriori (MAP) skeleton—is the result of a Bayesian tradeoff between fit to the shape and skeletal complexity. One implication of this tradeoff is that an axial branch is included in the skeleton only if it improves the fit to the shape sufficiently to warrant the added complexity of the skeleton. The Bayesian approach thus effectively “prunes” spurious branches (they are effectively treated as noise), and is able to establish a one-to-one correspondence between parts and axial branches (see Figure 2C for examples).

Recent empirical work has demonstrated the importance of the shape skeleton in superordinate shape classification—specifically, it has shown that the classification of shapes into broad natural categories (such as animals vs. leaves) can be understood in terms of simple statistical classification of the Bayesian shape skeleton that is tuned to the natural statistics of shape (Wilder, Feldman & Singh, 2011). This suggests both that the visual system employs a skeleton-based representation of shape, and that it has internalized the statistics of skeletal parameters for various shape categories, presumably over the course of evolution.

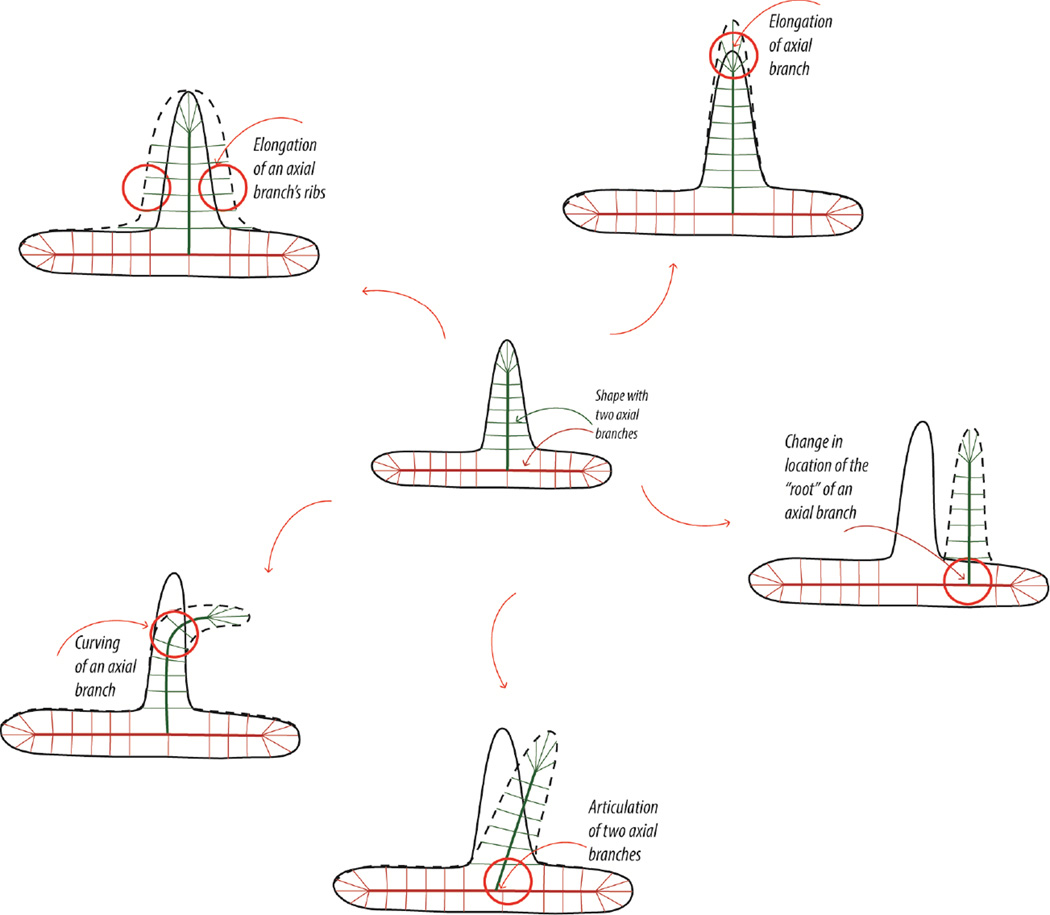
It is worth noting that key parameters of a skeletal representation of shape include: the length of an axial branch, the length of its “ribs” (which determine the width of that branch), its curvature, the orientation of the axial branch relative to its parent branch (the one that it protrudes from), and the locus of attachment to the parent branch. The shape transformations we will use in our experiments will involve precisely these five parameters.

Our Experimental Approach

In the current study, we investigate observers' visual sensitivity to different shape transformations that involve basic parameters in a part or axis-based representation. Measuring the relative visual sensitivity to different shape transformations provides a natural means of investigating visual shape representation. Sensitivity to shape change links fairly directly to shape similarity. For instance: If the visual system is highly sensitive to a particular type of shape transformation, a transformed shape will start to look different (i.e. highly dissimilar) with even a small magnitude of change. Conversely, if the visual system is fairly insensitive to some other type of transformation, then even large changes of that type may still result in very similar looking shape. Starting with the shape depicted in Figure 1C (top), for example, the transformed shape at the bottom left looks clearly different, whereas the one on the right looks quite similar. This is so despite the fact that the bottom-right shape in Figure 1C actually involves a larger physical difference from the original. Thus the relative visual sensitivity to different types of shape transformations is likely to be highly informative about the underlying shape representations—e.g. telling us something about the relative "distances" between shape pairs in the mental space of shapes (cf. Feldman & Richards, 1998).

Previous work has employed this general rationale in conjunction with the change-detection methodology to examine the role of parts and curvature polarity (convexity vs. concavity) in the visual representation of shape (e.g. Barenholtz et al., 2003; Cohen et al., 2005; Bertamini & Farrant, 2005; Vandekerckhove, Panis & Wagemans, 2008). This research has shown that: (i) changes to a shape that alter its qualitative part structure are easier to detect that those of comparable magnitude that preserve part structure; and (ii) shape changes at concave vertices are easier to detect than comparable changes at convex vertices. These results point to the fundamental importance of parts and of concavities (negative-curvature regions that tend to define part boundaries) in the visual representation of shape.

In contrast to this previous work, the current study investigates relative sensitivity to different shape transformations, all of which preserve qualitative part and axis structure, while manipulating specific quantitative parameters in a part- or axis-based representation. Our stimulus shapes are comprised of a narrow part protruding out of a larger “base” part. The shape transformations we use are motivated directly by parameters of the skeleton-based model summarized above (Feldman & Singh, 2006). If we consider the small protruding part, its axial representation is defined by the following skeleton-based parameters: the length of its axis, the curvature of its axis, the length of its “ribs” (which determine the width of the part), the location where its axis connects to the larger base part, and the orientation of its axis relative to that of the base part. Either of these five parameters may thus be perturbed in order to introduce a shape change (see Figure 3 for a schematic depiction). It should be noted that some of these shape transformations (namely, changes to part length, width, and curvature) involve only the protruding part in isolation, whereas others (namely, changes to part orientation and location) involve the spatial relationship between the two parts. Moreover, not all of these transformations are equally plausible biomechanically. The length and width of a limb or branch tend to change during growth, part orientation changes during articulation of the limbs, and certain types of biological parts or bodies can curve (e.g. tails or snakes). By contrast, a shape transformation involving a change in the part’s location is not biomechanically plausible.

Figure 3.

Transformations within the skeletal (axial) framework. The shape in the center is a “base” shape with two skeletal branches or parts. Counter-clockwise, five transformations are illustrated based on an axial framework with two skeletal branches: length (elongation of the axial branch), width (lengthening of the axial branch’s ribs), curvature, orientation (articulation), and location (change in locus of attachment of one of the axial branches).

There is some evidence to suggest that the visual system is sensitive to whether or not a shape transformation or movement is biomechanically plausible. This evidence is consistent with the general idea that, over the course of the evolution, the visual system has internalized constraints that reflect regularities in the natural environment (e.g. Shepard, 2001). The role of biomechanical plausibility has been demonstrated in the interpretation of apparent motion, for example (e.g. Chatterjee, Freyd, & Shiffrar, 1996; Shiffrar & Freyd, 1990; 1993). In estimating the trajectory of a moving object in apparent motion, it is well known that the visual system has a default preference for the shortest path (generally a straight line). However, it has been shown that this preference is easily overridden by biomechanical constraints. Specifically, in apparent-motion sequences showing two frames of the human body in slightly different poses, observers tend to perceive longer, curved motion trajectories of the limbs that are consistent with biomechanical (and physical) plausibility. This violation of the shortest-path principle occurs whenever sufficient time is available (i.e. with relatively long SOAs), and suggests that the visual system is incorporating constraints involving biomechanical plausibility in inferring motion trajectories (see Chatterjee, Freyd, & Shiffrar, 1996; Shiffrar & Freyd, 1990; 1993).

Similarly, in the context of figure-ground assignment, Barenholtz & Feldman (2006) showed subjects apparent-motion sequences in which the two frames differed in the location of point or segment along a polygonal contour. Subjects indicated whether they perceived one or the other side as figural (“which side moved?”). They found that figure and ground tends to be assigned in such a way that hinging vertices have negative curvature (i.e. correspond to part boundaries)—so that the motion is perceived as an articulating part or limb. Therefore implicit knowledge about how biological objects tend to move (e.g. in a part-wise articulated manner) affects the basic—and often considered low-level—process of figure-ground assignment.

Our experiments here measure increment thresholds for a number of shape transformations—involving changes in a part’s length, width, curvature, orientation, and location—in order to estimate the visual system’s relative sensitivity to these different types of shape changes. We use the method of constant stimuli with a 2IFC paradigm to derive psychometric curves and estimate the increment threshold for each transformation. We then convert these thresholds into common units of shape difference in order to allow direct comparison of the visual sensitivities to these different shape transformations.

Experiment 1: Two-part shapes

The goal of this experiment was to measure the differential sensitivity of human observers to several types of transformations to a shape with a simple two-part structure: a small narrow part protruding out of a larger base. The general experimental strategy used in this experiment is similar in spirit to the change-detection paradigm summarized above (e.g. Barenholtz et al., 2003; Cohen et al., 2005; Bertamini & Farrant, 2005; Vandekerckhove, Panis & Wagemans, 2008). However, the current experiment measures increment thresholds for different types of shape transformations by deriving full psychometric curves using the method of constant stimuli with a 2IFC task. A total of five transformations to the attached part were tested. We compared perceptual sensitivity to changes in part length, width, curvature, and orientation, and location (i.e. locus of attachment to the base shape).

Methods

Observers

Six observers affiliated with Rutgers University participated in the study. Five of the observers were naïve about the experimental goals and were paid volunteers; one was author KD. All had normal or corrected-to-normal vision. This research study has been approved by the Rutgers University Institutional Review Board. Informed consent from all participants was obtained prior to beginning the experimental procedures. The work was carried out in accordance with the Code of Ethics of the World Medical Association (Declaration of Helsinki).

Apparatus

Stimuli were generated using MATLAB and the Psychophysics Toolbox extensions (Brainard, 1997; Pelli, 1997). They were presented on a high-resolution (1280 × 960) 19-inch monitor (Mitsubishi DiamondPro) with a 120 Hz refresh rate, connected to a dual-core G5 Macintosh computer.

Stimuli

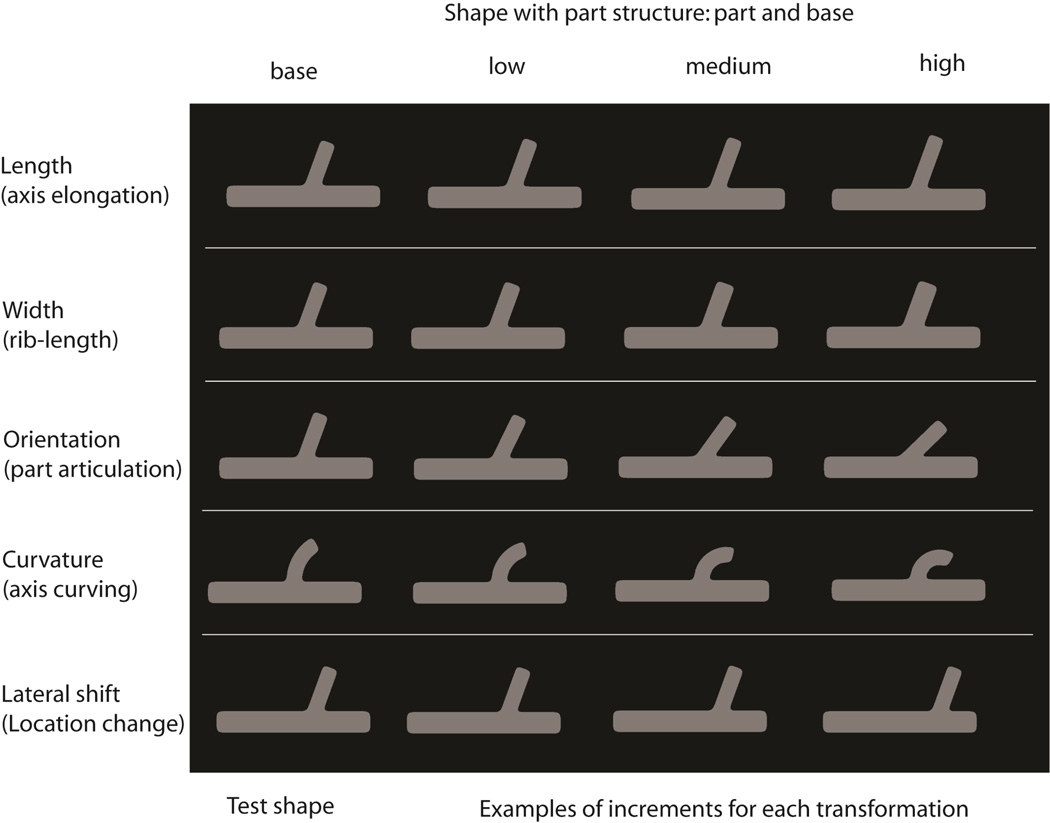
Two-part shapes were used in this experiment, composed of a narrow part protruding out of a larger base part (see Figure 4). When the axis of the attached part was straight, the part shape was rectangular (2.58 × 0.86 dva) with rounded corners. The base part of the shape was also rectangular (8.6 × 1.2 dva) with rounded corners. The boundaries between the two parts were also rounded (using a 1-D Gaussian smoothing operation along the contour).

Figure 4.

Stimuli used in Experiment 1. Five different shape transformations were used involving changes to the length, width, curvature, orientation, and locus of attachment of the small part in a two-part shape. Each row shows a different transformation, with the baseline shape followed by three different magnitudes of shape change for that transformation. Note that, in the actual experiment, each of these shapes was presented at a much larger size: the base part had dimensions of 8.6 dva×1.2 dva. These rounded corners were thus clearly visible as rounded, and therefore as intrinsic to the shape itself (rather than, say, as belonging to an invisible occluding surface, such as that of an aperture).

The small part was attached to the larger one near its horizontal center—in most conditions drawn from a uniform distribution on the range of +/− 1.55 dva from the center (this range corresponds to roughly one-third of the length of the base part). The attached part was, in most conditions, oriented either + 20° or − 20° from the vertical (i.e. orthogonal to the orientation of the base part). The combination of these two factors results effectively provided inter-trial jitter of the spatial position of the shapes. Any deviations from these default values are explicitly noted in the description of individual conditions below.

On each trial, observers were shown three versions of a shape: a “test” or “standard” shape followed by two “alternatives”. One of the two alternatives resulted from applying a particular transformation to the test shape, while the other alternative was identical to the test shape. The parameters of the test shape for length, width, and orientation transformations were exactly as described above. In the location condition, the location of the attached part in the test shape was either +1.20 or −1.20 dva from the center of the base part. In the curvature condition, the test shape was different in two respects: first, it had a standard orientation of 0° (it had a vertical tangent at its lower end, where it connected to the base shape; see Figure 4, 1^st column, 4^th row). Second, its standard curvature value was set to 0.41 dva⁻¹. (In other words, the axis of the curved part was a circular arc with the radius equal to 1/0.41 = 2.44 dva, and it could curve either to the right or to the left).

In the length condition, the comparison shape differed from the test shape in the elongation of the attached part. The part’s length was manipulated by applying one of seven increments to the standard length value of 2.58 dva: .09, .17, .27, .34, .43, .52, & .60 dva. In the width condition, the width of the attached part of the comparison shape was manipulated by applying one of seven increments to the standard width value of .86 dva: .03, .05, .09, .12, .15, .19, & .22 dva. The width variable corresponds to approximately twice the rib length in an axis-based representation (see Feldman & Singh, 2006). The orientation transformation manipulated the part’s tilt away from the vertical. Seven increments were applied to the standard orientation value of 20°: 2°, 6°, 10°, 14°, 18°, 22° and 26°. The curvature transformation altered the curvature of the part’s axis. One of seven increments was applied to the base curvature parameter of 0.41 dva⁻¹: .06, .12, .17, .23, .29, .35, .41 dva⁻¹ (for subjects KD, SK, & CC) and .04, .08, .12, .16, .2, .24, .28 dva⁻¹ (for subjects SC, SS, SHK). These different ranges were selected for different observers, based on their performance in pilot studies. The location condition shifted the locus of attachment of the small part relative to the base shape. One of seven increments was applied to the initial location of the part of +/− 1.20 dva (measure from the horizontal center of the base shape): .14, .28, .42, .55, .69, .83, or .96 dva. Since stimulus presentation was masked (see below), no jitter was applied within a single trial. Pilot testing showed that observers found the task somewhat difficult (given that every stimulus was masked). So as to avoid increasing the difficulty of the task further (and also avoid increasing stimulus presentation time further), we did not apply intra-trial jitter (i.e. all 3 shapes appeared in the same spatial location on a particular trial).

Procedure

Observers viewed the displays binocularly with head position fixed using a chinrest. They were instructed to look at the fixation cross which was presented at the center of the monitor at the beginning of each trial. Each of the three shapes (the test shape and the two alternatives) was shown for 200 ms and was followed by a mask. The test shape and its mask were followed by a longer delay of 900 ms; the two alternative shapes were separated by a delay of 300 ms. The final frame of each trial was a mask, which remained on the screen until the observer responded using the keyboard. The 2IFC task of the observer was to indicate which interval, first or second, contained the shape that matched the test shape. No feedback was provided. After the response was given, the fixation cross re-appeared to signal the onset of the next trial.

Design

Each observer participated in 2 experimental sessions for each of the 5 transformations (length, width, orientation, curvature and location) for a total of 10 experimental sessions per observer. A total of 350 trials were run for each transformation. This resulted in a total of 50 repetitions for each of the seven increment values, for each transformation. The order of the transformation conditions was counterbalanced across observers. Observers completed a brief practice session prior to each experimental session.

Results

Weibull psychometric curves were fit to individual observers’ data for each transformation condition using the psignifit software for MATLAB (Wichmann & Hill, 2001a,b). Based on these fits, increment thresholds and corresponding 95% confidence intervals were computed. The data (proportion correct for each increment level) and the psychometric fits for one representative observer are shown in Supplemental Figure 1. Table 1 provides a summary of the thresholds for all observers.

Table 1.

Results of Experiment 1: Raw thresholds (T), and thresholds converted to the Area-based shape metric (A), and Distance-based shape metric (D), with corresponding 95% CIs, for shape transformations involving part length, width, curvature, orientation and location.

	Raw threshold			Area difference			Distance (avg)
KD	T	CI (low)	CI (high)	A	CI (low)	CI (high)	D	CI (low)	CI (high)
length	0.3032	0.2487	0.3297	5.48	4.56	6.05	0.0392	0.0323	0.0421
width	0.1137	0.0987	0.1254	6.19	5.51	6.82	0.0457	0.0399	0.0507
curv	0.1629	0.1454	0.1803	19.84	17.83	21.67	0.1382	0.1238	0.1509
ori	10.7000	9.4660	11.9997	27.32	24.15	30.55	0.1911	0.1690	0.2142
loc	0.5898	0.4639	0.6334	65.29	51.67	69.96	0.3945	0.3709	0.4015
SS	T	CI (low)	CI (high)	A	CI (low)	CI (high)	D	CI (low)	CI (high)
length	0.2205	0.1580	0.2490	4.20	3.10	4.56	0.0301	0.0206	0.0323
width	0.0711	0.0564	0.0790	4.09	3.29	4.60	0.0290	0.0227	0.0329
curv	0.1222	0.1047	0.1338	15.28	13.26	16.61	0.1060	0.0919	0.1149
ori	6.0800	4.8939	6.9570	15.50	12.62	17.78	0.1088	0.0880	0.1244
loc	0.6190	0.5779	0.6881	68.34	64.11	75.77	0.3979	0.3938	0.4088
SC	T	CI (low)	CI (high)	A	CI (low)	CI (high)	D	CI (low)	CI (high)
length	0.2140	0.1663	0.2435	4.12	3.24	4.51	0.0271	0.0237	0.0323
width	0.0601	0.0484	0.0681	3.44	2.86	3.81	0.0240	0.0200	0.0271
curv	0.0931	0.0814	0.1047	11.83	10.50	13.26	0.0816	0.0722	0.0919
ori	9.4500	8.1884	10.4195	24.11	20.87	26.58	0.1687	0.1463	0.1860
loc	0.3741	0.3097	0.4218	41.95	34.78	47.05	0.3037	0.2501	0.3400
SK	T	CI (low)	CI (high)	A	CI (low)	CI (high)	D	CI (low)	CI (high)
length	0.3011	0.2774	0.3585	5.44	5.16	6.39	0.0392	0.0362	0.0449
width	0.0593	0.0468	0.0672	3.40	2.76	3.79	0.0237	0.0194	0.0268
curv	0.0989	0.0873	0.1163	12.52	11.15	14.68	0.0864	0.0769	0.1014
ori	6.7616	5.6154	7.5901	17.22	14.42	19.37	0.1209	0.1010	0.1356
loc	0.2353	0.1348	0.2730	26.65	15.38	30.77	0.1915	0.1096	0.2216
SHK	T	CI (low)	CI (high)	A	CI (low)	CI (high)	D	CI (low)	CI (high)
length	0.2342	0.1935	0.2554	4.39	3.62	4.67	0.0323	0.0260	0.0333
width	0.0526	0.0400	0.0600	3.04	2.32	3.44	0.0214	0.0159	0.0240
curv	0.0989	0.0873	0.1105	12.52	11.15	14.02	0.0864	0.0769	0.0969
ori	10.4321	9.2330	11.2178	26.60	23.52	28.61	0.1862	0.1648	0.2005
loc	0.2416	0.1719	0.2751	27.30	19.55	31.05	0.1962	0.1393	0.2232
CC	T	CI (low)	CI (high)	A	CI (low)	CI (high)	D	CI (low)	CI (high)
length	0.3922	0.3407	0.4198	7.11	6.22	7.64	0.0496	0.0441	0.0504
width	0.0932	0.0808	0.1107	5.23	4.66	6.05	0.0380	0.0336	0.0445
curv	0.1047	0.0814	0.1163	13.26	10.50	14.68	0.0919	0.0722	0.1014
ori	10.1415	8.6745	11.1635	25.84	22.13	28.47	0.1809	0.1549	0.1996
loc	0.3474	0.3021	0.4088	39.01	34.00	45.66	0.2817	0.2446	0.3306

These raw increment thresholds for different transformations cannot of course be used to directly compare the visual sensitivity to different transformations, because they are in different units, e.g. degrees of visual angle (dva) for length, degrees for orientation, dva⁻¹ for curvature, etc. A standard way of comparing sensitivities across different dimensions (or even modalities) is to use Weber fractions, ΔI/I, where I is the standard intensity and ΔI is the difference threshold. However, computation of Weber fractions is only possible for dimensions with a well-defined ratio scale—i.e. with a canonical zero—which is not the case for orientation. (For example, the same angular deviation from the vertical could be coded either as −30° or +60°, depending on whether the vertical or the horizontal axis is taken as the “zero”.) Thus, in order to directly compare the thresholds across all transformations, the thresholds were converted into a common measure of shape difference in the next step of data analysis. Moreover, in order to ensure the robustness of the ordering in sensitivity to different transformations, we used two distinct measures of shape difference: one based on area differences, the other based on average distance.²

Area-based difference measure

The area-based difference is defined in terms of the area of the non-overlapping regions of two shapes, once they have been aligned maximally (see Supplemental Figure 2A). Given any two shapes Sh₁ and Sh₂, the area-based difference is thus Area(Sh₁ − Sh₂) + Area(Sh₂ − Sh₁), where Sh₁ − Sh₂ refers to points of Sh₁ that are not in Sh₂, and similarly Sh₂ − Sh₁ refers to points of Sh₂ that are not in Sh₁. In the context of our two-part shapes, we normalize this non-overlapping area by the sum of areas of the two attached parts, i.e., Area(Part _ Sh₁) + Area(Part _ Sh₂).³

$$A(S{h}_1,S{h}_2)=\frac{\mathit{\text{Area}}(S{h}_1-S{h}_2)+\mathit{\text{Area}}(S{h}_2-S{h}_1)}{\mathit{\text{Area}}(\mathit{\text{Part}}\_S{h}_1)+\mathit{\text{Area}}(\mathit{\text{Part}}\_S{h}_2)}$$ (1)

The raw increment thresholds estimated from the psychometric fits were converted to this area-based measure by taking the standard (“test”) shape as Sh₁ and the “threshold shape” (i.e., the shape corresponding to a particular observer’s threshold value added to the standard value) as Sh₂. The formula above produces a proportion or percentage (of the part area), which corresponds to the area difference by which the threshold shape differs from the test shape.

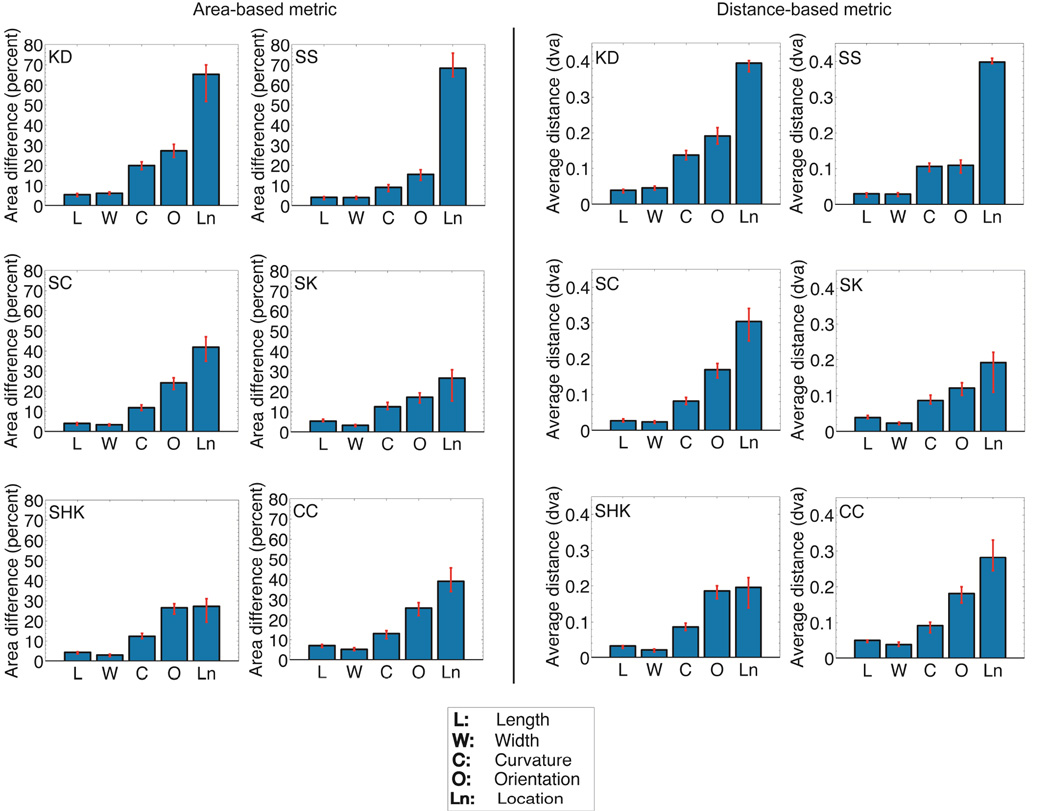
Figure 5A shows bar plots of each observer’s thresholds converted to the common area-based shape metric. From these plots, it is evident that observers are most sensitive to the transformations of part width and length, then to axis curvature, and are least sensitive to the transformation involving part location. The average thresholds across observers, in terms of this area-based metric, were 5.12% for length, 4.23% for width, 14.21% for curvature, 22.77% for orientation, and 44.76% for location.

Figure 5.

Differential perceptual sensitivity of human observers to five shape transformations, based on the skeletal model (Experiment 1). (A) Raw increment thresholds for all observers converted into the common area-based metric. Observers are most sensitive to the width and length transformations, followed by curvature, and then by orientation and location. Observers are least sensitive to the location transformation. (B) Raw increment thresholds for all observers converted into the common distance-based metric. Consistent with the ordering obtained with the area-based metric, observers are most sensitive to the width and length transformations, followed by curvature, and then by orientation and location. Observers are least sensitive to the location transformation.

All six observers were significantly more sensitive to length and width change than to curvature change. All six observers were more sensitive to curvature than to orientation change; this difference was statistically significant for four of the six observers. All six observers were more sensitive to orientation than location change; this difference was statistically significant for four of the six observers.

Distance-based difference measure

A natural question is whether the ordering of sensitivities of different transformations observed above might somehow be due to the specific measure we used to provide a common scale. In order to obtain a greater degree of confidence in this ordering, we used a second, distinct, measure—based on average distance rather than non-overlapping area. This measure is related to the Hausdroff distance in mathematics (e.g. Edgar, 2007), except that we use mean distance rather than maximal distance between two shapes.⁴ For each point on a given shape (Sh₁), the distance to the closest point on the second shape (Sh₂) is determined (see Supplemental Figure 2B). This is done for all points on Sh₁, and the average value of these distances is computed. We denote this d(Sh₁ → Sh₂). This process is then repeated by starting with Sh₂ (i.e. for each point on Sh₂, computing the distance to the closest point on Sh₁, and then averaging these distances). In general, d(Sh₁ → Sh₂) will not be equal to d(Sh₂ → Sh₁). The average of these two values is then taken to be the final (symmetric) distance between the two shapes.

$$D(S{h}_1,S{h}_2)=\frac{d(S{h}_1\to S{h}_2)+d(S{h}_2\to Sh1)}{2}$$ (2)

As before, the raw increment thresholds were converted to this metric by taking, for each observer and each shape transformation, the standard shape as Sh₁ and the threshold shape as Sh₂.

Figure 5B shows bar plots of each observer’s thresholds converted to the distance-based shape metric. The ordering of thresholds for the different transformations is essentially the same as the one obtained with the area-based measure: observers are most sensitive to transformations of length and width, followed by curvature, and are least sensitive to part location. The average thresholds across observers converted to this common distance metric were 0.0362 dva for length, 0.0303 dva for width, 0.0984 dva for curvature, 0.1594 dva for orientation, and 0.2943 dva for location.

All six observers were significantly more sensitive to changes in the length and width of the attached part than to its curvature. All six observers were more sensitive to curvature change than to orientation change; this difference was statistically significant for four of the six observers. All six observers were more sensitive to orientation change than location change; this difference was statistically significant for four of the six observers.

Discussion

Observers are consistently most sensitive to changes in part width and length, followed by part axis curvature, then part orientation, and finally part location. Sensitivity is consistently worst for changes to the part’s location. This ordering is identical for both the area-based and the distance-based metric (Table 1) as well as for the corresponding Weber fractions, whenever these can be defined (see Supplementary Table 1). This consistency across the various metrics indicates that this ordering in perceptual sensitivities is a function of the shape transformations themselves, and not simply an artifact of any particular measure of shape difference.

How should we understand this ordering in sensitivities to different shape transformations? One relevant factor is that some of these transformations involve a change to a single part (namely, length, width, and curvature of the attached part), whereas others involve a change in the spatial relations between two parts (namely, orientation and location of the small part relative to the large base part). The results are therefore consistent with a part-superiority effect, i.e. observers are more sensitive to judgments involving a single part than to those involving two parts (Watson & Kramer, 1999; Vecera, Behrmann, & Filapek, 2001; Barenholtz & Feldman, 2003).

Furthermore, when we compare the two transformations that involve spatial relationships between the two parts, we find that sensitivity to changes in the locus of part attachment is consistently worse than sensitivity to changes in part orientation. As noted earlier, changes in part orientation are biomechanically plausible shape transformations that are in fact quite common in biological shapes. This is a natural consequence of the biological skeletal structure of most animal species. On the other hand, changes in locus of part attachment are extremely rare, almost never occurring in biological shapes and, unlike our other transformations, have no meaningful interpretation either in terms of growth or articulation of biological forms. It is therefore likely that the differential sensitivity to these two types of shape transformations reflects this difference in biomechanical plausibility and/or probability of occurrence in the natural environment. Such an interpretation is consistent with previous findings that show the influence of biomechanical plausibility on various aspects of visual perception, including shape similarity (Barenholtz & Tarr, 2008), figure-ground perception (Barenholtz & Feldman, 2006) and apparent motion (Chatterjee, Freyd, & Shiffrar, 1996; Shiffrar & Freyd, 1990; 1993).

Experiment 2: Positive vs. negative part transformations

The goal of Experiment 2 is to investigate how surface (or region-based) geometry influences sensitivity to shape transformations, beyond the contributions of contour geometry. A natural way to separate contour and region-based geometry⁵ is by manipulating figure and ground: By keeping the contour between two regions fixed, but making one or the other side figural, one can alter the geometry of the perceived surface. Among other things, this manipulation turns convex protrusions into concave indentations, thereby altering the perceived part structure of the object (see e.g. Hoffman & Richards, 1984; Hoffman & Singh, 1997; Cohen et al., 2005; Kim & Feldman, 2009). Previous work has revealed the contributions of region-based geometry in such diverse contexts as the detection of symmetry and parallelism (Baylis & Driver 1994), shape memory (Baylis & Driver 1994), perceived transparency (Singh & Hoffman, 1999), object grouping behind an occluder (Liu et al., 1999), localization of vertex height (Bertamini, 2001), change detection (Barenholtz et al., 2003; Cohen et al., 2005; Bertamini & Farrant, 2005), amodal completion (Fantoni & Gerbino, 2005), and illusory contour shape (Fulvio & Singh, 2006). The direction of the benefit seems to depend on the precise task, however, with some tasks eliciting a convexity advantage (e.g., Baylis & Driver 1994, 1995; Bertamini, 2001), and others eliciting a concavity advantage (e.g., Barenholtz et al., 2003; Bertamini & Farrant, 2005; Cohen et al., 2005).

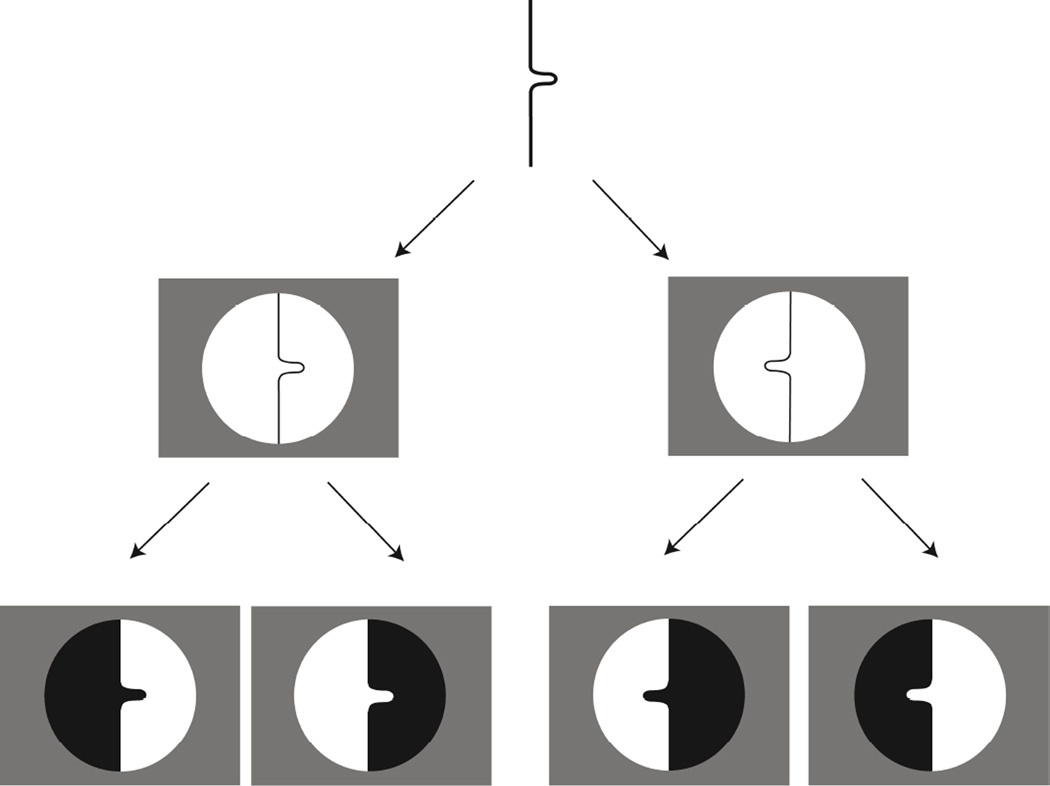
In the current experiment, the contour geometry of the displays was kept fixed, while the region-based geometry was manipulated by reversing figure and ground using binocular disparity. This is demonstrated schematically in the bottom row of Figure 6 (left-most example). As illustrated, the two regions (black and white) share the same central undulating contour. When the black region is designated as figure, it appears as a part protruding out of a shape (i.e. a positive part). On the other hand, when the white region is designated as figure, it appears as a shape with a cavity (i.e. a negative part). Thus the same contour geometry can result in different surface geometries—and hence different axial structures—as the result of a figure-ground reversal.

Figure 6.

Stimulus design illustration for Experiment 2. The same contour with a protrusion facing left or right (middle row). Either side of the contour can be assigned to be figure (depicted here by the black region in the panels at the bottom). This yields different region-based geometries for the same contour: a positive part (protrusion) or negative part (cavity).

Unlike Experiment 1 in which the entire bounding contour of the stimulus shape was visible, in Experiment 2, only the critical portion of the shape was visible through a circular aperture. This choice was motivated by the results of a pilot study in which the shapes with positive and negative parts were similar to Experiment 1 (i.e. closed shapes shown in their entirety; see Supplemental Figure 3). The results of this pilot study showed a higher sensitivity for shape transformations involving a negative part relative to a positive part. However, one potential concern was that observers might be making their judgments based on the negative part’s proximity to the nearest edge on the opposite side of the base part. For example, in detecting changes in the length of a negative part, observers can make their judgments based on the size of the gap between the bottom of the indentation and the lower edge of the base shape—e.g. between points A and B in Supplemental Figure 3—rather than on the length of the negative part per se. The current experiment addresses this concern by showing the critical contour segment through a circular window. Observers thus never see the entire bounding contour on either side.

In this experiment, we focused on the two shape transformations that involve changes in spatial relationships between parts, namely, part orientation and part location (or locus of attachment). As noted earlier, the orientation transformation represents a shape change that is common in biological forms, e.g. corresponding to the articulation of animal limbs. By contrast, a shift in the part’s locus of attachment is not biomechanically plausible. Both transformations were applied to positive as well as negative parts. This was done using binocular disparity to manipulate figure-ground relationships along the same set of contours.

The objective of the experiment was to examine whether there are systematic differences in visual sensitivity to shape transformations involving positive vs. negative parts. More specifically, we wondered if the existence of such an effect depends on the type of shape transformation under consideration. In the case of change in part orientation, for example, the positive-part transformation corresponds to part articulations and is biomechanically plausible, whereas the negative-part transformation is not (see also Barenholtz & Feldman, 2006). Therefore, for shape transformations involving a change in part orientation, one might expect a difference between positive and negative part transformations. In the case of a change in part location, however, the positive-part and negative-part transformations are both biomechanically implausible. Therefore, for shape transformations involving a change in locus of part attachment, there is no reason to expect a difference in visual sensitivity to positive and negative part transformations.

Methods

Observers

Six observers participated in this experiment: three of these had previously participated in Experiment 1, whereas the other three were new. All observers had normal or corrected-to-normal vision, and were screened for binocular vision. Informed consent from all participants was obtained prior to beginning the experimental procedures.

Apparatus

Stimuli were generated using MATLAB and the Psychophysics Toolbox extensions (Brainard, 1997; Pelli, 1997). Stimuli were presented on a high-resolution (1280 × 1024) 19-inch monitor (Mitsubishi DiamondPro) connected to a dual-core G5 Macintosh computer with a 120 Hz refresh rate. The stereo images were presented using an infrared emitter and stereoscopic shutter glasses system StereoGraphics CrystalEyes.

Stimuli

Random Dot Stereograms (Julesz, 1971) were used to present the stimulus shapes. Each “dot” was a square of 4 × 4 pixels (4.2 × 4.2 arc min) with equal probability of black and white dots. The entire stereo display was presented within a square measuring 900 by 900 pixels (15.47 × 15.47 dva) against a black background. The trial sequence is shown schematically in Supplemental Figure 4.

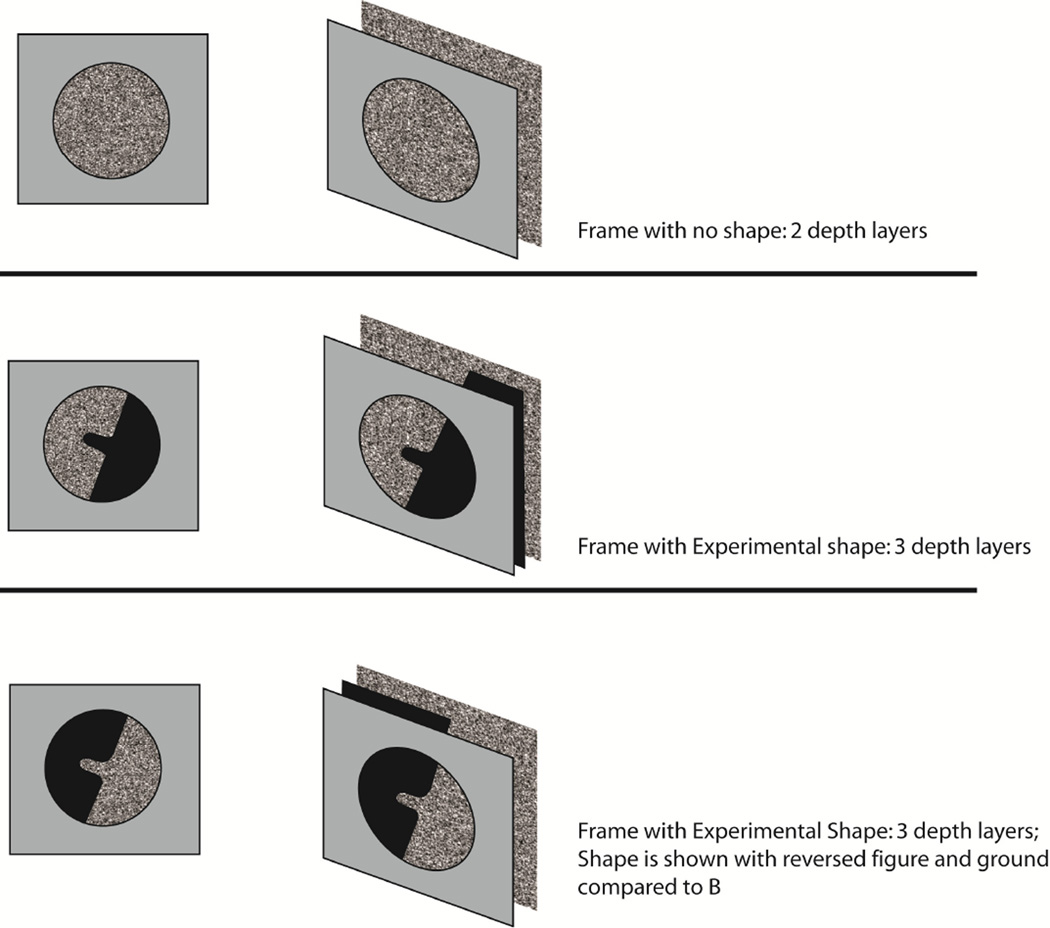
The first frame displayed a circular window through which only the background surface was visible (no shape was shown). The random-dot texture outside the circular window was generated independently on every trial, but remained the same throughout the trial, while the background texture within the circular window was randomly drawn from 16 different (previously generated) randomly generated texture patterns that changed on every display frame within a trial. The disparity between the circular window and the background surface was 15.7 min arc. The next few frames showed, sequentially, the three experimental shapes (shown through the circular window): a test shape followed by two alternatives. All three were masked. The random-dot texture for the shape itself was generated at random for every display frame within the trial. The experimental shape was positioned in depth between the circular window and the background: the disparity between the circular window and the shape was 5.4 min arc, while the disparity between the shape and the background surface was 10.3 min arc. The mask frame consisted of a circular window and a background, and changed on every frame. A schematic of depth relationships between the different depth layers is shown in Figure 7.

Figure 7.

Illustration of the binocular depth layering in the stimuli in Experiment 2. Note that the figural shapes are shown schematically here in black. In the actual experiment, all stimuli surfaces were presented as random-dot textures.

Four types of stimuli were used. They were defined by two contours: one whose bulge faced left, and one whose bulge faced right. Since the same contour can yield two differently shaped surfaces depending on figure-ground relationships, two different shapes resulted from each of these contours (see Figure 6). Thus, there were a total of 4 possible combinations: part type (positive vs. negative) X bulge direction (facing left vs. facing right). The bounding contour of the attached part used in this experiment was identical to that used in Experiment 2. The “base” contour (on which the part was attached) was oriented at either +20° or −20° from the vertical meridian.

The transformations of orientation and location change were applied to the part (positive or negative). The parameters of the part shape, as well as of the transformed versions, were identical to those used in Experiment 1.

Procedure

The 2IFC procedure was identical to Experiment 1. The only difference was that the presentation time for each (binocularly presented) shape was increased to 600 ms. This increase was necessary because the shape in each stereoscopic display could only be seen once binocular fusion had taken place.

Design

Each observer participated in 10 experimental sessions: 5 sessions for each of the two transformations of orientation and location change. Each transformation had a total of 700 trials (350 for positive and 350 for negative part transformations). This resulted in a total of 50 repetitions for each of the seven increment values for negative and positive transformations. Positive and negative part transformations were interleaved within each single experimental session. Each observer completed a brief practice session prior to the experimental sessions.

Results

The data were analyzed in the same manner as Experiment 1. The raw data and the psychometric fits are shown in Figure 8A (part orientation change) and Figure 8B (part location change). Table 2 provides a summary of the thresholds, reported in degrees of visual angle (dva) for the location condition, and in degrees for orientation condition. Since the primary interest in this experiment was to compare sensitivity to negative vs. positive part conditions within each transformation, conversion to a common metric was not necessary.

Figure 8.

Perceptual sensitivity to shape transformations involving region-based in addition to contour-based geometry (Experiment 2). Raw data and psychometric fits for positive-part vs. negative-part transformations for all observers: (A) for the orientation transformation, and (B) for the location transformation. The increment thresholds derived from these fits are summarized in Table 2.

Table 2.

Results of Experiment 2: Raw thresholds (T) and 95% CIs for transformations involving part orientation and location, shown for both positive-part (P) and negative-part (N) transformations.

	Raw thresholds
MZ	T	CI (low)	CI (high)
ori (N)	10.1005	8.8652	11.7178
ori (P)	7.2044	5.9273	8.1742
location(N)	0.2731	0.2226	0.3277
location(P)	0.3458	0.2955	0.3890
AK	T	CI (low)	CI (high)
ori (N)	4.1841	3.0128	5.3398
ori (P)	7.0300	5.6390	8.2133
location(N)	0.4136	0.3740	0.4707
location(P)	0.4609	0.4238	0.5218
HH	T	CI (low)	CI (high)
ori (N)	6.9313	5.5827	8.0779
ori (P)	4.8807	3.8695	5.5198
location(N)	0.2964	0.2546	0.3273
location(P)	0.2137	0.1617	0.2520
SK	T	CI (low)	CI (high)
ori (N)	3.8886	2.6600	4.5601
ori (P)	3.6330	2.4923	4.3307
location(N)	0.2967	0.2487	0.3318
location(P)	0.3492	0.2935	0.3842
SHK	T	CI (low)	CI (high)
ori (N)	5.1453	3.5916	5.9541
ori (P)	5.3072	4.2386	6.0962
location(N)	0.3451	0.2918	0.4049
location(P)	0.3249	0.2708	0.3589
CC	T	CI (low)	CI (high)
ori (N)	14.6469	11.2913	21.0889
ori (P)	6.1055	4.8988	8.5340
location(N)	0.1765	0.0270	0.2742
location(P)	0.2437	0.1425	0.2917

Orientation change: positive vs. negative parts

The mean threshold was 5.69 degrees for positive part transformations (95% C.I.: [4.51, 6.81]), and 7.48 degrees for negative part transformations (95% C.I.: [5.83, 9.46]). Thus, on average, observers were more sensitive to the positive-part transformation than to the negative-part transformation. At the level of group data, each of the two means lies outside of the 95% confidence interval around the other. At the level of individual observers, 5 of the 6 observers exhibited the positive-part advantage, i.e. had a lower threshold for the positive-part transformation (it was statistically significant for 3 observers).

Location change: positive vs. negative parts

The mean threshold was 0.32 dva for positive-part transformations (95% C.I.: [0.26, 0.37]), and 0.30 dva for negative part transformations (95% C.I.: [0.24, 0.36]). Three observers had a lower threshold for positive-part transformation, and three had a lower threshold for the negative-part transformation. In the case of location change, therefore, we see no evidence of a systematic difference in the sensitivity to negative vs. positive part transformations.

Overall, the results show some evidence for greater sensitivity to positive-part transformations in the case of orientation change; but no such difference is evident in the case of location change.

Discussion

The goal of Experiment 2 was to investigate the role of region-based geometry in determining observers’ sensitivity to shape transformations, beyond any contribution of contour geometry. Region-based geometry was manipulated using binocular disparity to define one side of the contour as “figure”, the other as “ground”. Observers’ sensitivity in detecting changes in the orientation and location of a positive vs. a negative part was measured.

For the orientation transformation, we found evidence for higher sensitivity to positive-part over negative part transformations, but no such difference was evident for the location transformation. One reason for this difference may be that orientation change is a common and naturally occurring, biomechanically plausible transformation for positive parts (i.e. articulating limbs)—but not so for negative parts (these would correspond to “articulating indentations”; see also Barenholtz, 2010). Hence there is good reason to expect a difference in sensitivity between positive vs. negative parts in the case of orientation changes. On the other hand, a location change is biomechanically implausible for both positive and negative parts and, therefore, there is no reason to expect a difference in this case. This interpretation is consistent with a study by Barenholtz & Tarr (2008) who found that observers’ judgments of shape similarity were strongly affected by whether the shape transformation was a “biologically valid” articulation of a limb, or a “biologically invalid” part rotation (where the point of rotation was located outside of the shape). In addition, as previously noted, biomechanical plausibility has also been shown to influence figure-ground perception (Barenholtz & Feldman, 2006) and perceived trajectory in apparent motion (Shiffrar & Freyd, 1990; 1993).

General Discussion

Part-based approaches to shape representation segment complex shape into simpler parts, and organize them as spatial arrangements of these parts. A great deal of psychophysical evidence has shown that the visual system segments shapes automatically into parts (“obligatorily” to use Baylis & Driver’s term). Axis-based approaches provide compact stick-figure descriptions of shape, and can provide a one-to-one correspondence between parts and axial branches (Feldman & Singh, 2006). The branching structure of a shape’s skeleton and the relative positions and orientations of the different branches provide a compact summary of the shape’s overall structure. The shape of each individual part is represented in terms of the length and curvature of each axial branch, and the width (or rib-length) function along it. Parts and axes are thus naturally viewed as complementary aspects of a structural approach to shape representation.

An important advantage of shape representations based on parts and axes is that they readily capture the shape of biological objects, as well as naturally occurring transformations of biological forms. This is probably no coincidence since the evolution of shape representations employed by the visual system is likely to have been guided by the statistics of natural shapes (cf. Wilder et al., 2011). The shape of animal and plant bodies are readily represented as spatial arrangements of simpler parts, and the shape transformations they typically undergo as involving simple parameters of either individual parts, or of the spatial relationships between these parts. Changes in the length or width of a part are generally associated with growth processes, changes in the curvature of a part are associated with bending action (e.g. a curving tail), whereas changes in the relative orientations of parts are associated with articulation of the limbs.

Several earlier studies have involved global shape transformations, that is, transformations that are applied uniformly to an entire object. D'Arcy Thompson (1942) famously illustrated how some variations in biological forms can be understood as simple affine transformations. More recently Wagemans et al. have studied perceptual effects of affine transformations (Wagemans, van Gool, Lamote, and Foster, 2000) as well as projective and perspective transformations (Wagemans, Lamote, and van Gool, 1997). Certain global shape transformations are known to have distinct perceptual interpretations; a well-studied example is cardiodal strain, which gives an impression of growth or aging (Pittenger & Shaw, 1975; Mark, Todd, and Shaw, 1980; Todd, Mark, Shaw & Pittenger, 1980), at least when applied to shapes that appear biological in nature (Mark, Shapiro & Shaw, 1986). The transformations studied in our experiments are distinct from these in that they are applied locally in a part-wise manner, that is, in a way that respects the perceptual segmentation of shapes into parts.

Previous work on local shape transformations has shown that changes that alter qualitative part structure are more easily detected than those that preserve part structure (e.g. Barenholtz, Cohen, Feldman & Singh, 2003; Cohen, Barenholtz, Singh & Feldman, 2005; Bertamini & Farrant, 2005). By contrast, the current study compared observers’ visual sensitivity to a number of shape transformations, all of which preserved qualitative part structure. In other words, the number of parts and the branching topology of the shape never changed as a result of our transformations. Each transformation involved a change to a single parameter in a part/axis-based representation: part length, part width, part curvature, part orientation relative to the base shape, and part location along the base shape.

We found clear and systematic differences in visual sensitivity across the different types of shape transformations, even after thresholds were carefully converted into common units of shape difference, in order to allow a meaningful comparison between different transformations. Indeed, common units based on different metrics yielded essentially the same ordering of visual sensitivity. The results suggest that two part-based factors contribute to determining visual sensitivity to shape transformations: (i) whether a transformation affects a single part in isolation, or the spatial relationship between two parts; and (ii) whether the transformation is biomechanically plausible or not. Overall, the results highlight the fact that measures of shape similarity based simply on physical differences—such as the ones based on non-overlapping areas, or average distances—are clearly inadequate to capture perceived shape similarity.

Experiment 1 compared visual sensitivities to shape transformations involving a small, protruding, part on a simple two-part shape. These included changes to the length, width, curvature, orientation and location of the small protruding part. The results showed a clear differential sensitivity to these transformations, with observers being most sensitive to transformations involving changes in the length and width of the part, followed by the curvature of the part’s axis, then the relative orientation of the part, and finally the locus of attachment of the part. This ordering was highly consistent both across observers, as well as across the different metrics used to compare these thresholds along a common scale—area-based metric, distance-based metric, and Weber fractions (wherever these could be meaningfully defined).

This ordering may be understood in terms of two basic factors. First, visual sensitivity is consistently better for shape transformations involving a single axis or part (length, width, curvature) than those involving the spatial relationship between two parts (part orientation, part location). This result may thus be viewed as a form of the single-part superiority effect (e.g. Watson & Kramer, 1999; Vecera, Behrmann, & Filapek, 2001; Barenholtz & Feldman, 2003). Second, within the transformations involving spatial relations between parts, sensitivity is consistently worse for changes in part location than to part orientation. This difference likely reflects the fact that changes in part orientation correspond to a common and naturally occurring, biomechanically plausible transformation in biological shapes (namely, articulation of the limbs), whereas the changes in the locus of attachment of a part almost never occur, at least in biological forms. As noted above, the first four of our transformations (changes to part length, width, curvature, and orientation) are not only common in biological shapes, but also have natural interpretations in terms of growth or locomotion of biological forms. Hence change in part location is the only one of our transformations that is both rare in biological forms (if it occurs at all), and has no meaningful interpretation in terms of growth or locomotion. This interpretation is consistent with previous findings showing the influence of biomechanical plausibility on perceived shape similarity (Barenholtz & Tarr, 2008), figure-ground assignment (Barenholtz & Feldman, 2006) and perceived trajectory in apparent motion (Chatterjee, Freyd, & Shiffrar, 1996; Shiffrar & Freyd, 1990; 1993).

It is possible that some of the observed differences in visual sensitivity reflect more basic sensitivities to properties such as length or curvature. It should also be noted, however, that some of the comparisons in sensitivity we examined are meaningful only in the context of shape. For example, it is not clear what it would mean to ask whether observers are more sensitive to changes in line length or in line orientation. The increment thresholds in the two cases are in different units. Moreover, there is no canonical way to define a Weber fraction in the case of line orientation—because of the lack of a canonical origin (e.g. should 0° correspond to the vertical or the horizontal orientation?). Indeed this is what necessitated the use of the area-based and distance-based metrics of shape overlap in the current study.

Experiment 2 used binocular disparity to manipulate figure-ground assignment on the same set of contours, thereby altering the region-based geometry of the figural surface—positive part (protrusion) vs. negative part (cavity or indentation). Sensitivity was compared across positive vs. negative part transformations involving (i) orientation change (articulation), and (ii) location change. The results provided evidence for higher sensitivity to positive-part transformations in the case of orientation change, but not in the case of location change. One way to understand this result is that, because orientation change (i.e. part articulation) is a naturally occurring transformation for biological shapes for positive parts—but not for negative parts—the difference in sensitivity between positive and negative parts makes sense for this transformation. However, shape transformations involving a change in the locus of part attachment are biomechanically implausible —for both positive and negative parts—hence there is no principled reason to expect a difference between the two. The results of Experiment 2 thus point to the role of surface or region-based geometry in the visual representation of shape (since the geometry of the contour of course remains unchanged when figure and ground are reversed). Contour geometry is thus not sufficient to explain these results.

Overall, along with previous work involving change detection on shapes (e.g. Barenholtz et al., 1993; Cohen et al., 1995; Bertamini & Farrant, 2005; Vandekerckhove, Panis & Wagemans, 2008), our results point to the role of parts and axes in organizing the visual representation of shape. The visual system estimates shape differences (and shape similarity) based not simply on notions of “average distance” between two shapes, or the extent of their non-overlapping areas (both of which are essentially “blind” to part and axis structure), but in a way that specifically respects part and axial structure. One reason why part- and axis-based representations are so relevant to visual processing is that they easily capture the natural transformations that biological forms tend to undergo—e.g. in processes of growth, and of locomotion (such as articulation of the limbs). Consistent with the idea of naturalscene statistics, the visual representation of shape is likely to have evolved to reflect regularities in how objects—especially animate objects—in the world tend to move and transform. This would explain why biomechanical plausibility plays an important role in detecting shape transformations, and also why the visual system does not rely on contour geometry alone.

Highlights.

• Visual sensitivity to shape transformations is influenced by region-based geometry

• Physical metrics of shape difference are insufficient to predict human sensitivity

• Biomechanical plausibility of part-based transformations plays an important role