cit: hypothesis testing software for mediation analysis in genomic applications

Abstract

Motivation: The challenges of successfully applying causal inference methods include: (i) satisfying underlying assumptions, (ii) limitations in data/models accommodated by the software and (iii) low power of common multiple testing approaches.

Results: The causal inference test (CIT) is based on hypothesis testing rather than estimation, allowing the testable assumptions to be evaluated in the determination of statistical significance. A user-friendly software package provides P-values and optionally permutation-based FDR estimates (q-values) for potential mediators. It can handle single and multiple binary and continuous instrumental variables, binary or continuous outcome variables and adjustment covariates. Also, the permutation-based FDR option provides a non-parametric implementation.

Conclusion: Simulation studies demonstrate the validity of the cit package and show a substantial advantage of permutation-based FDR over other common multiple testing strategies.

Availability and implementation: The cit open-source R package is freely available from the CRAN website (https://cran.r-project.org/web/packages/cit/index.html) with embedded C ++ code that utilizes the GNU Scientific Library, also freely available (http://www.gnu.org/software/gsl/).

Contact: joshua.millstein@usc.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

The causal inference test (CIT) (Millstein et al., 2009), can play an important role in ‘post GWAS’ analyses that seek to identify molecular mediators of the effects of genetic variation on disease phenotypes. A growing number of groups have used the CIT to identify mediators such as methylation (Hong et al., 2015; Liu et al., 2013; Yuan et al., 2014) and gene expression (Hong et al., 2015; Liu et al., 2013; Millstein et al., 2011; Tang et al., 2014).

The previously published CIT function was limited in scope, accommodating a single discrete SNP-like variable, a continuous mediator and a continuous outcome. We have developed the ‘cit’ R package to extend software capabilities in a number of important ways: (i) binary as well as continuous outcomes, (ii) continuous as well as binary instrumental variables, (iii) multiple instrumental variables simultaneously and (iv) an approach for generating permutation-based q-values (the false discovery rate (FDR) analog to P-values) with confidence intervals.

2 Implementation

The CIT simultaneously evaluates multiple conditions known to be consistent with causal mediation (Millstein et al., 2009). Consider a locus (L), a gene expression feature (G) as a potential mediator of an effect of L on T, and a disease trait (T), then the conditions are: (i) L is associated with T, (ii) L is associated with G conditional on T, (iii) T is associated with G conditional on L and (iv) T is independent of L conditional on G. A P-value is computed for each condition using a general linear modeling framework, and the maximum P-value is interpreted as an omnibus hypothesis test (the CIT) for the intersection of the component rejection regions, an ‘intersection/union test’ (IUT). The omnibus null hypothesis is that at least one component null hypothesis is true.

In genomic settings where thousands of mediation tests may be performed, a separate test would be conducted for each (L,G,T) set, and a multiple testing approach applied for the family of tests. FDR makes sense as a multiple testing strategy due to its sensitivity, which increases as the number of false null hypotheses increase. Thus, even though tests are conducted independently, there is still information exchange across tests. In contrast, the Bonferroni approach is much more conservative, with each test independent of other tests. However, achieving adequate power is a challenge even with an FDR approach. We have implemented the Millstein and Volfson FDR approach (Millstein and Volfson, 2013), which is permutation-based thus non-parametric, and less conservative than the popular Benjamini and Hochberg (BH) approach. For a given mediation test, the q-value can be thought of as representing the probability of a false discovery at a significance threshold defined by the P-value, therefore an FDR analogue to the IUT could be constructed as, P[any component test is a false discovery] = 1 – P[all component tests are true discoveries] = 1 – (1 – q₁) * (1 – q₂) * (1 – q₃) * (1 – q₄), where q_j represents the q-value for the jth component test. Note that this expression is related to the conventional IUT in that it is greater than or equal to the maximum of the component test q-values. The enhanced cit software has implemented this concept with the permutation-based FDR approach, which is computationally efficient because relatively few permutations are required (Millstein and Volfson, 2013). Although the approach is nonparametric, the assumption of exchangeability must be considered when conducting any permutation test. (See supplemental material for discussion of exchangeability and computational efficiency.)

3 Results

In simulated data, we compared the permutation-based FDR approach implemented in the new software as described above to its parametric equivalent as described by Millstein and Volfson (2013) (Supplemental Eq. S2), computed on the omnibus CIT P-values. 2000 replicate datasets were simulated for each scenario, binary versus continuous outcome, and multiple testing corrections were based on the corresponding 2000 P-values. Because parametric assumptions were satisfied in the simulated data, and the theory behind both FDR estimators is the same, we would expect close agreement between the two approaches. Very close agreement was observed (Fig. 1), which demonstrates the validity of the permutation-based IUT approach. Also apparent in the results is the substantial gain in power of the Millstein and Volfson FDR approach over the Bonferroni and BH methods, which is consistent with theoretical properties of the respective tests (Millstein and Volfson, 2013). The unadjusted P-value curve for simulations conducted under reverse causality shows that fewer tests are called significant than would be expected under the null. Thus, the results demonstrate the robustness of the method to reverse causality confusion, and that the test is actually conservative under these conditions. Other simulation results also demonstrated similar properties when multiple instrumental variables with and without statistical interactions were involved (Supplemental Figs S1 and S2).

Fig. 1.

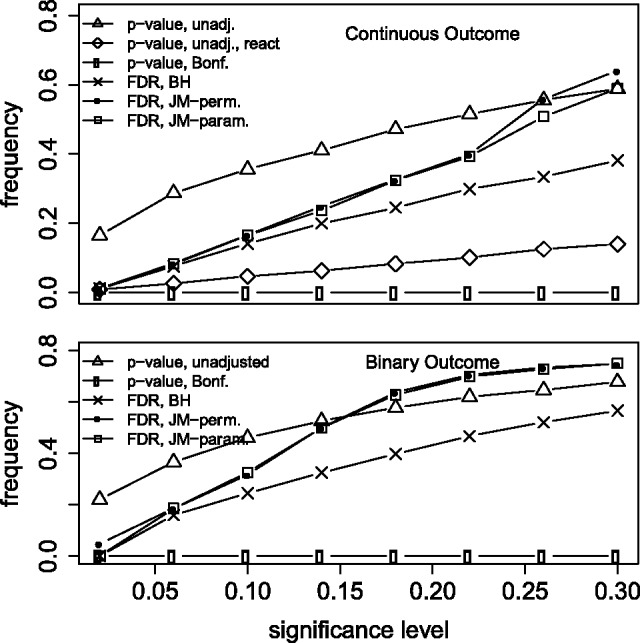
Power of the CIT function under the causal model (true mediator), with the exception that the ‘react’ curve in the upper plot demonstrates low type I error in the presence of reverse causation. The y-axis represents the proportion of tests called significant at a significance threshold specified on the x-axis. ‘FDR, JM-perm’ and ‘param’ denote the permutation-based and parametric omnibus CIT FDR, respectively. The proposed FDR approach is consistently more powerful than the Benjamini and Hochberg (BH) and much more powerful than the Bonferroni correction (Bonf.). (See supplemental material for additional simulation details.)

4 Conclusion

The cit package provides a general and powerful tool for identifying the most likely molecular mediators of genetic effects. The permutation-based q-value method makes the CIT fully non-parametric. The ability to apply a permutation based FDR approach with confidence intervals has the potential to substantially increase the utility of the method by uncoupling statistical significance with the conventional .05 level. Results that do not achieve this threshold may nevertheless be biologically important, and the q-value estimate along with confidence intervals provides a quantitative measure of uncertainty in the results.

Funding

This work was supported by the National Institutes of Health [grant number R01ES022216].

Conflict of Interest: none declared.