Multiscale Modeling of Cell Shape from the Actin Cytoskeleton

Abstract

The actin cytoskeleton is a dynamic structure that constantly undergoes complex reorganization events during many cellular processes. Mathematical models and simulations are powerful tools that can provide insight into the physical mechanisms underlying these processes and make predictions that can be experimentally tested. Representation of the interactions of the actin filaments with the plasma membrane and the movement of the plasma membrane for computation remains a challenge. Here, we provide an overview of the different modeling approaches used to study cytoskeletal dynamics and highlight the differential geometry approach that we have used to implement the interactions between the plasma membrane and the cytoskeleton. Using cell spreading as an example, we demonstrate how this approach is able to successfully capture in simulations, experimentally observed behavior. We provide a perspective on how the differential geometry approach can be used for other biological processes.

1. INTRODUCTION

Cell shape and structure are controlled by the actin cytoskeleton, a self-assembled polymeric system that is dynamic. In addition to maintaining or changing cell shape, the actin cytoskeleton is also required for sensing environmental cues, aiding processes such as exo- and endocytosis, cell motility, and cell division. The actin cytoskeleton is a structural polymeric system that is dynamic: monomers of actin assemble into filaments and disassemble on a continuing basis. The energy for this process is provided by ATP hydrolysis. The actin cytoskeleton can exist in different structural configurations: lamellipodium, filopodium, and stress fibers. The actin cytoskeleton structure is used in different cell types for different purposes. In neurons, the varied uses include driving axon growth at the growth cone¹ and changing size of the spine upon synaptic transmission.² The subcellular mechanisms that are operational in neurons are largely the same as in other cell types. The modeling approaches described here can be used to model cellular behaviors as varied as differentiation and shape changes in neurons, movement of fibroblasts, and regulation of foot process interactions in kidney podocytes. The different structural configurations of the actin cytoskeleton result from different biochemical and mechanical cues that control a range of actin-associated regulatory proteins. Mathematical modeling of the actin cytoskeleton has provided unique insights into the regulation, growth, and dynamics of these structures. In this chapter, we consider the reorganization of the actin cytoskeleton as a multiscale process in both time and space and outline the different computational modeling approaches that can be used in understanding each step of the process. We focus specifically on a stochastic approach combining both discrete biochemical kinetics and evolving differential geometry that we used to computationally model the interaction between the actin cytoskeleton and the plasma membrane.

2. CELL SPREADING

The ability to move and migrate is very important for the various cell types to perform different physiological functions. White blood cells move freely in the blood stream, neutrophils migrate to sites of injury in response to cytokines, and fibroblasts migrate within connective tissue to wound sites. Furthermore, cell migration is fundamental to embryonic development.³ The motile behavior of cells is made possible by the dynamic reorganization of the underlying cytoskeleton. The coupling of actin filament reorganization with the movement of the membrane has been studied extensively.^4–9 It was shown that the filament reorganization events alone can generate sufficient force to push the leading edge of the membrane forward.^5,10,11

Cell motility is a complex process, dependent on the reorganization of the underlying actin cytoskeleton. There are three main steps in motility: protrusion, attachment, and traction.^12–14 Each of these steps recruits different sets of coordinated signaling molecules that in concert with the actin cytoskeleton reorganization events allow the cell to change shape and move forward. This multistep-integrated process of motility is observed in embryonic development, tissue repair and wound healing, immune response, and growth cones in neurons.

The steps involved in cell motility have been studied in depth experimentally.^15–17 Cell adhesion to a substrate or an extracellular matrix plays a critical role in the regulation of downstream signaling pathways via connections to the cytoskeleton.^14–23 Once the cell forms adhesive contacts with the substrate, it starts spreading on the surface. These contacts, termed focal contacts, are the signaling centers that connect the signaling pathways to the actin cytoskeleton. Cell spreading is dependent on actin filament dynamics and force generation by the focal contacts on the surface.¹⁴

Plasma membrane protrusion is driven by actin filament reorganization; the protrusion can take on different forms such as filopodia, lamellipodia, and pseudopodia.²⁴ While all three structures are made of the core actin cytoskeleton, different arrangements of the actin polymers result in different shapes. In a filopodium, the filaments are long and bundled to form fingerlike protrusions. Lamellipodia on the other hand are characterized by sheet-like structures and contain a cross-linked meshwork of actin filaments. Pseudopodia have been observed in ameobae and neutrophils. Among these three structures, lamellipodia are best understood.

The lamellipodium contains all the machinery necessary for cell motility. In order to understand how the protrusion of the lamellipodium occurs and aids cell motility, it is important to understand the dynamics of the underlying actin cytoskeleton.

3. ACTIN CYTOSKELETON

Actin cytoskeletal reorganization occurs during cell membrane protrusion and retraction.^16,25,26 Actin is a globular protein that exists in the monomeric form (G-actin) and polymeric filamentous form (F-actin). G-actin is an ATPase, containing a deep cleft where the adenosine nucleotide binds in the presence of divalent magnesium. F-actin is polarized with preferred monomer addition occurring at the barbed end and monomer depolymerization occurring at the pointed end. ATP-bound G-actin rather than ADP-bound G-actin is favorable for filament elongation and branching reactions.²⁷ F-actin is spatially organized into a variety of structures, such as stress fibers, cortical actin networks, surface protrusions, and the contractile ring formed during cell division.^28,29 Precise temporal and spatial control of the actin cytoskeleton is required for these activities, but it is not clear how the changes are mediated. The biochemistry of actin reorganization in response to external cues includes filament elongation, branching, capping, and depolymerization.

4. BIOCHEMICAL SIGNALING TO THE ACTIN CYTOSKELETON

Actin cytoskeleton reorganization is mediated by four major proteins: (i) profilin, (ii) cofilin, (iii) Arp2/3, and (iv) gelsolin. The dendritic nucleation model outlines the sequence of events that take place during actin reorganization at the leading edge.³⁰ Profilin mediates the fast exchange of ATP for ADP in G-actin molecules, favoring filament elongation.^29,31,32 The exchange product, profilin–ATP–actin complex, leads to filament elongation at the barbed or growing end of the filament. Cofilin is a depolymerization factor which mediates actin depolymerization by sequestering ADP-bound G-actin tightly, thereby regulating the amount of free monomer available for filament elongation.^29,33–35 Arp2/3 is important for filament branching at the leading edge of the cell and acts by nucleating new filaments from existing filaments by binding to seven actin molecules on an existing filament and initiating a new branch formation at a 70° angle.^28,36–38 The concentration of Arp2/3 is regulated by WASP in response to extracellular signals.³⁸ The capping protein gelsolin negatively regulates filament growth by binding to the barbed end of a growing filament, thereby preventing further monomer addition.^39,40 Actin filaments are thus regulated by multiple proteins, each of which separately and collectively modulates cytoskeletal reorganization. Recently, Urban et al. showed using electron tomography that the actin filaments at the leading edge may be predominantly unbranched.⁴¹ This suggests that there may be multiple mechanisms of actin polymerization at the leading edge, resulting in different configurations of actin filaments.

4.1. Regulatory proteins for actin filament reorganization

4.1.1 Arp2/3

Arp2/3 is responsible for actin filament branching. Arp2/3 is a seven-protein complex containing Arp2, Arp3, and five unique polypeptides.^42,43 Arp2/3 is activated by WASP (Wisckott–Aldrich syndrome protein), which exists in an autoinhibited conformation. Binding of Cdc42 (GTP bound) and PI(4,5) P₂ relieves the inhibitory conformation of WASP and allows Arp2/3 complex formation and subsequently actin filament branching. WASP is phosphorylated by Src, and this phosphorylation event leads to WASP ubiquitination and degradation.^44–46 WAVE is another protein that activates Arp2/3. Unlike WASP, WAVE is not autoinhibited and is activated by Rac and PI(3,4,5)P₃ binding.⁴² Thus, WASP and WAVE are important signal transducers that convert signals from protein–protein and protein–membrane interactions to actin polymerization.

4.1.2 Profilin

Profilin binds to ATP-bound G-actin and promotes filament elongation. Binding of VASP to profilin facilitates actin polymerization.⁴⁷ Ligand-bound activated integrin receptors form a complex with α-actinin, zyxin, and VASP that is responsible for profilin activation. PI(4,5)P₂ on the other hand, binds profilin and sequesters it. PI(4,5)P₂-bound profilin is incapable of promoting actin filament elongation.⁴⁸ Phosphorylation of VASP reduces its actin-binding capability. VASP and profilin interaction promotes actin elongation by interacting with barbed ends, shielding them from capping protein.⁴⁹ This effect is also modulated by PI(4,5)P₂. PI(4,5)P₂ binding to gelsolin inactivates it, and profilin and gelsolin compete to bind with PI(4,5)P₂, antagonizing each other.

4.1.3 Capping protein/gelsolin

Capping protein binds to the barbed ends of actin filaments and caps them, thus preventing filament elongation. Capping can be considered to be a terminal event in filament dynamics because the off-rate constant for capping protein to fall off a barbed end is slow, predicting the half-life of a capped filament to be at least 30 min.⁵⁰ PI(4,5)P₂ and PI(4)P cause rapid and efficient dissociation of capping protein from capped filaments.⁴⁸ Binding of phosphoinositides to the capping protein gelsolin prevents it from capping actin filaments.^50,51

4.1.4 Cofilin

Cofilin depolymerizes the pointed, slow-growing ends of actin filaments. Cofilin phosphorylation by LIM kinase renders it incapable of depolymerization activity. LIM kinase is activated by p65PAK and p160ROCK, downstream of cdc42, Rac, and Rho, respectively.^52,53 PI(4,5)P₂ can sequester cofilin and prevent phosphorylation by LIMK.⁴⁸ Cofilin is the only known substrate of LIM kinase.^52,53

Cell motility is a process governed by both spatial and temporal variations in the various regulators of the actin cytoskeleton.²¹ Processes involved in cell migration and morphology depend on the spatial regulation of both cytoskeletal activity and the upstream signaling network. This spatial regulation controls the appropriate polar response of the cell to extracellular signals, and the control of membrane extension and retraction. Spatial regulation is controlled mainly by the polarized nature of F-actin and the binding properties of the intermediary proteins to F-actin.⁵⁴ Temporal regulation controls when the cell responds to the extracellular signals and is determined by the kinetic parameters of the biochemical reactions.

5. DIFFERENT APPROACHES FOR COMPUTATIONALLY MODELING THE ACTIN CYTOSKELETON

Many informative computational models of actin polymerization–depolymerization cycles have been developed.^{5,6,8,9,55–57} Often these models are in one spatial dimension and analyze the cytoskeletal reorganization process in an abstracted cytoskeletal structure at steady state. These models have yielded substantial insight into the dynamics of the underlying actin cytoskeleton and enable the development of models that explore the relationship between actin cytoskeleton dynamics and whole cell behavior such as cell spreading. Brownian ratchet models provide mechanisms by which actin polymerization can drive the motility of a load, in this case, the plasma membrane.^4,6 The Brownian ratchet model⁴ posits that if the membrane undergoes Brownian motion, then occasionally the distance between the barbed end of the actin filament and the membrane is large enough to allow the addition of a new monomer. The elastic Brownian ratchet model is a modification of the original model where the random bending of the filament provides space for the addition of new monomer.⁶ The membrane is then pushed forward because of the elastic energy stored in the filament. Recently, Schaus et al. developed a computational model of actin filament orientation in the dendritic nucleation model.⁵⁸ This model provides insight into how the steady-state actin filament patterns emerge using stochastic simulations. Using these observations, other groups have developed models of populations of actin filaments and analyzed the work required to push a flexible membrane forward.^10,59

5.1. Kinetic modeling of the cytoskeleton

A large number of experimental studies of the cytoskeleton focus on purification of the cytoskeletal components and studying their interactions and effects in cell-free systems. These experiments provide us with kinetic rate constants and have identified the important components required for the cytoskeletal reorganization events to occur. These experiments can be used to build kinetic models of the actin cytoskeleton. The premise here is that in a well-mixed system of actin, reactions can be treated as occurring spatially uniformly, and the concentrations of the different biochemical species are changing only in time and not in space. The mathematical modeling effort gives us the concentrations of the different actin species in time and the equilibrium concentrations. We demonstrate this with an example. Consider the actin reactions required for filament growing, branching, and capping. The rate of filament elongation depends on the concentration of monomeric actin (G-ATP–actin) and the concentration of filamentous actin (F-actin). The addition of a monomer to an “n-mer” of filamentous actin results in a filament that is of length “n+1-mer.” The rate of filament branching depends on the concentration of Arp2/3 and the amount of filamentous actin, and the rate of capping of filaments depends on the amount of capping protein and filamentous actin available. As in Refs. 27,60, we assume that this set of reactions is sufficient to capture the fundamental dynamics of growing actin filaments. Further complexity can be added by adding filament depolymerization and severing, but the fundamental events of the reorganization can be captured by these three reactions of growing, branching, and capping.

In a well-mixed system, the rate of polymerization is a direct measure of F-actin concentration in the system and an indirect measure of spread cell area and therefore size. In this model, the actin reactions are treated as irreversible and the reaction rates are written as mass–action laws.

The elongation reaction and the corresponding reaction rate are given by

$$\begin{array}{c}\hfill \text{G-ATP}-\text{actin}+{\text{F-actin}}_n\stackrel{k_{\text{elongation}}}{\to }{\text{F-actin}}_{n+1}\hfill \\ \hfill R_{\text{elongation}}=k_{\text{elongation}}\left[{\text{F-actin}}_n\right]\left[\text{G-ATP}-\text{actin}\right]\hfill \end{array}$$ (7.1)

The branching reaction results in the addition of a new filament along the side of an existing filament. Two G-ATP–actin monomers and one Arp2/3 molecule participate in this reaction:

$$\begin{array}{cc}\hfill & \text{Arp2/3}+\text{2G-ATP}-\text{actin}+{\text{F-actin}}_n\stackrel{k_{\text{branching}}}{\to }{\text{F-actin}}_n+{\text{F-actin}}_2\hfill \\ \hfill & R_{\text{branching}}=k_{\text{branching}}\left[{\text{F-actin}}_n\right]{\left[\text{G-ATP}-\text{actin}\right]}^2\left[\text{Arp2/3}\right]\hfill \end{array}$$ (7.2)

The capping reaction results in the capping of a filament; only existing filaments and the capping protein participate in this reaction:

$$\begin{array}{cc}\hfill & \text{Gelsolin}+{\text{F-actin}}_n\stackrel{k_{\text{capping}}}{\to }{\text{F-actin}}_n-\text{capped}\hfill \\ \hfill & R_{\text{capping}}=k_{\text{capping}}\left[{\text{F-actin}}_n\right]\left[\text{gelsolin}\right]\hfill \end{array}$$ (7.3)

The net rate of polymerization is now given by

$$\begin{array}{cc}\hfill R_{\text{polymerization}}& =\frac{\mathrm{d}\left[\text{F-actin}\right]}{\mathrm{d}t}=R_{\text{elongation}}+R_{\text{branching}}-R_{\text{capping}}\hfill \\ \hfill \frac{\mathrm{d}\left[\text{F-actin}\right]}{\mathrm{d}t}=& k_{\text{elongation}}\left[\text{G-ATP}-\text{actin}\right]\left[{\text{F-actin}}_n\right]\hfill \\ \hfill & +k_{\text{branching}}\left[{\text{F-actin}}_n\right]{\left[\text{G-ATP}-\text{actin}\right]}^2\left[\text{Arp2/3}\right]\hfill \\ \hfill & -k_{\text{capping}}\left[{\text{F-actin}}_n\right]\left[\text{gelsolin}\right]\hfill \end{array}$$ (7.4)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}\left(\ln \left[\text{F-actin}\right]\right)}{\mathrm{d}t}=& k_{\text{elongation}}\left[\text{G-ATP}-\text{actin}\right]\hfill \\ \hfill & +k_{\text{branching}}{\left[\text{G-ATP}-\text{actin}\right]}^2\left[\text{Arp2/3}\right]\hfill \\ \hfill & -k_{\text{capping}}\left[\text{gelsolin}\right]=R_{\text{free}}\hfill \end{array}$$ (7.5)

Therefore, the net rate of filament growth can be written as a function of the actin-regulating proteins alone. This type of calculation can allow us to generate time plots of F- and G-actin concentrations in the system as observed in cell-free experiments.^33,57,61 This approach has been used to explain the role of actin in endocytosis.⁶² Including diffusion of reacting species in addition to reaction rates alone has allowed researchers to model the spatial distribution of actin components. An elegant example of this is seen in the modeling studies of keratocyte movement.^63,64

In cellular systems, such as endocytosis and spreading, the regulation of the actin proteins is not controlled by experimentally adding Arp2/3 or WASP to the system but by an upstream signaling system in response to an extracellular signal. In that case, a model of the biochemical signaling network is required to capture the dynamics of the system. We developed a model of the key signaling events for actin in Ref. 65. These reactions then provide additional equations to the set of differential equations shown above and can be integrated simultaneously to obtain the time courses of the concentrations of the signaling proteins.

5.2. Interaction of actin filaments with the plasma membrane

5.2.1 Local membrane regulation of cell spreading

While the deterministic models described above provide insight into the dynamics of the actin reorganization events, within cells, the actin cytoskeleton reactions take place in the vicinity of the plasma membrane. The actin filament reorganization reactions are modulated by the interaction of the cytoskeleton with the plasma membrane. The membrane has been studied as a smooth surface, allowing continuum mechanics approaches to develop partial differential equations for the shape of the membrane.⁶⁶ The actin filament network can be treated as a viscous gel, also a continuum formulation.⁶⁷ However, the interface between the membrane and the actin filaments is based on the elastic Brownian ratchet, a principle based on thermal fluctuations.^4–6

The elastic Brownian ratchet model proposed by Mogilner and Oster^4–6 is adapted in three dimensions to model the filament–membrane interactions. The actual reaction velocity in the presence of a load is less than the reaction velocity for a freely growing filament without any resistance and is dependent on the probability that a gap of width (δ) is created between the filament tip and the load (in this case, the membrane). The modified rate constant is given by

$$k_{\text{on}}^{\prime }=k_{\text{on}}{\mathrm{e}}^{-\Delta E∕k_{\mathrm{B}}T}$$ (7.6)

where ΔE is the energy change required to push the membrane forward by a distance δ. ΔE is a local parameter and depends on the location of the growing filament and the area of the membrane it is pushing. ΔE is computed as follows.

There are three main contributions to the energy change—membrane surface energy, filament flexibility, and membrane bending.^5,68 Here, we treat the actin filaments as rigid filaments based on the assumption that filament bending undulations are much faster than the polymerization kinetics.^6–8 We include two major contributions to the membrane energy change—the membrane surface energy and the membrane-bending energy.

The membrane surface energy characterizes the work required by the filament to push an area ΔA (nm²) of the membrane forward to accommodate an actin monomer of length (δ=0.275 nm). We characterize the membrane surface resistance by a pressure p (pN/nm²). This is the load offered by the plasma membrane, similar to the definitions in Refs. 6,69. The energy contribution from the membrane surface term is given by

$$\Delta E_{\text{surface}}=p\mathrm{d}A\delta$$ (7.7)

The other important contribution comes from membrane bending. The membrane-bending coefficient is a physical property that characterizes the flexibility of the membrane K_b (pN nm). By incorporating this term, we are accounting for a bendable rather than rigid membrane. The bending energy contribution is then given by⁶⁶

$$\Delta E_{\text{bending}}=K_{\mathrm{b}}\int H^2\mathrm{d}A$$ (7.8)

where H is the local membrane curvature (μm⁻¹). Therefore, the net change in energy that affects the biochemical rates is

$$\Delta E=\Delta E_{\text{bending}}+\Delta E_{\text{surface}}$$ (7.9)

In the presence of the membrane, each reaction experiences resistance offered by the membrane by a combination of surface load and bending rigidity (Eq. 7.13). Then, the observed average rate of polymerization is now given by

$$\begin{array}{cc}\hfill & \frac{d\left(\ln \left[F\text{-actin}\right]\right)}{\mathit{dt}}=(k_{\text{elongation}}\left[G\text{-ATP}-\text{actin}\right]+k_{\text{branching}}\phantom{)}\hfill \\ \hfill & \phantom{(}{\left[G\text{-ATP}-\text{actin}\right]}^2\left[\text{Arp2/3}\right]-k_{\text{capping}}\left[\text{gelsolin}\right])e^{\left(-\Delta E∕k_{B}T\right)}=R_{\text{observed}}\hfill \end{array}$$ (7.10)

The first observation is that the concentration of F-actin is influenced mainly by the amount of G-ATP–actin present. Sensitivity of the time evolution of F-actin to Arp2/3 concentration (F-actin/Arp2/3=d (ln[F-actin])/d[Arp2/3]) is independent of Arp2/3 concentration and depends on G-actin concentration alone.

$$\frac{\mathrm{d}{\Phi }_{\text{F-actin/Arp2/3}}}{\mathrm{d}t}=k_{\text{branching}}{\left[\text{G-ATP}-\text{actin}\right]}^2{\mathrm{e}}^{-\Delta E∕k_{\mathrm{B}}T}$$ (7.11)

Similarly, the sensitivity of temporal evolution of F-actin to gelsolin concentration (Φ_{F-actin/gelsolin} =d(ln[F-actin])/d[gelsolin]) is a constant.

$$\frac{\mathrm{d}{\Phi }_{\text{F-actin/gelsolin}}}{\mathrm{d}t}=-k_{\text{capping}}{\mathrm{e}}^{-\Delta E∕k_{\mathrm{B}}T}$$ (7.12)

These relationships highlight the fact that while Arp2/3 and gelsolin are required for the maintenance of filament branching and polymerization, within a reasonable concentration range, the actual value of Arp2/3 and gelsolin is less important than the amount of monomeric actin present for polymerization to proceed.

In the foregoing discussion, we have assumed that each point along the membrane exerts the same energy penalty on the growing actin filaments. However, actin filament reactions are stochastic in time and space. How do we implement the growth of the actin filament network in the presence of the membrane along with the spatial and temporal stochasticity? As we noted above, the membrane alone can be characterized by the bending energy and surface tension, and continuum models including the Helfrich model⁶⁶ can capture the change of membrane shape. On the other hand, the actin filament network can be treated as a viscous gel and treated as a continuum. However, putting the two pieces together and capturing the dynamics of cytoskeletal reorganization is something that requires more than a continuum approach. In Section 6, we outline a computational geometry method for implementing the actin cytoskeleton reorganization events and its interaction with the cytoskeleton.

6. COMPUTATIONAL GEOMETRY APPROACH FOR MODELING CELL SPREADING

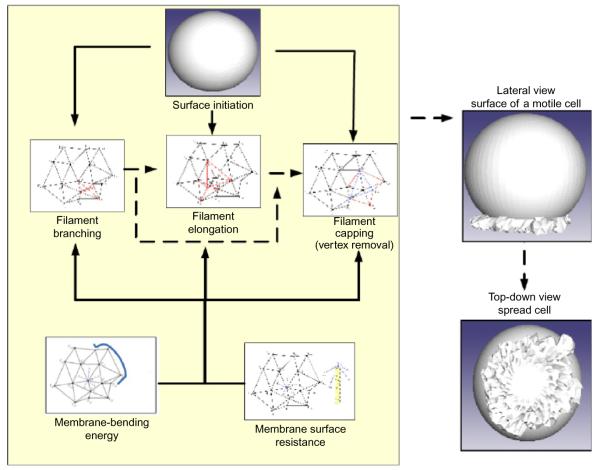
How can we model the interaction of the membrane with the growing actin filaments and track the change in cell shape during active motile events? Here, we elaborate on a computational geometry approach to develop an interface between the ends of the actin filament and the membrane. The concept behind this model is simple: rather than represent the membrane as a smooth manifold, we represent the membrane as a triangulated mesh (Fig. 7.1). Each vertex on this mesh represents the end of an uncapped actin filament. When a filament grows by the addition of an actin monomer, then the vertex moves forward by the length of the monomer. When a filament is capped, the vertex is fixed in space and may be removed from further calculations as described below, and when a new filament branches from an existing filament, a new vertex is added to the mesh surface. As a result, we have a realistic, three-dimensional model of the actin cytoskeleton and the plasma membrane.

Figure 7.1.

Differential geometry approach for interfacing the membrane with the cytoskeleton. A differential geometry approach is used to represent the membrane and its interaction with the actin filament. Each vertex on the triangulated surface represents an end of one actin filament. The vertices move according to the underlying growth of actin filaments in response to biochemical reactions modulated by the energy penalty imposed by membrane bending and surface resistance. As these events proceed in space and time, we are able to simulate cell spreading behavior.

During cell spreading, the absolute area of the membrane surface at the leading edge increases as the leading edge protrudes outward. Such area increase is realized by the removal of invaginations in the plasma membrane or fusion of inner membrane reservoir to cell surface to meet the need of cell spreading. When uncapped filaments elongate and push the cell membrane, the mechanical energy associated with the change of surface geometry is represented as a change in surface curvature. This energy change regulates filament growth negatively and is incorporated as a feedback feature in our model, where change in energy becomes the negative regulator of reactions underlying filament growth. This energy change of the cell membrane is estimated by the work that actin filaments have to do in order to break and reform the surface. These concepts are implemented in the model using computational geometry methods linking the actin filament biochemistry to membrane biophysics.

7. COMPUTATIONAL IMPLEMENTATION

This computational core of the model is composed of four parts: dynamic filament network, dynamic cell surface, membrane energy feedback, and stochastic reaction machinery. Each part describes one aspect of the model: dynamic filament network is modified in response to individual actin filament reactions, dynamic cell surface represents the changing cell geometry, membrane energy-based filament growth reflects the interaction between biochemical actin filament reactions and biophysical cell membrane mechanics, and stochastic reaction machinery determines the temporal dynamics of the system. These parts are integrated into autonomous and functional machinery that drives cell motility. The computational program, written in C++, contains about 10,000 lines of code.

7.1. Dynamic filament network

This module forms the basis of the actin filament network structure at the leading edge. The actin filament network is initialized as a set of seeding filaments (composed of one Arp2/3 and two prepolymerized actin monomers) evenly distributed in the leading edge beneath the spherical cell surface (molecule reservoir). The filaments in this module are initiated and connected with other filaments by branches originating from Arp2/3 binding sites on the actin filament. The dynamics growth of this network is modulated by the iterative occurrences of the three actin biochemical reactions as specified by a modified Gillespie’s algorithm.⁷⁰

The barbed ends point radially outward toward the cell membrane. The occurrence of the elongation, branching, and capping reactions leads to filament growth and branching. One challenge in validating this model is that the actual number of filaments at the leading edge of a cell is not known. We conducted parameter variation for initial values of actin filament density.⁷¹ Setting values too low causes the rate of filament polymerization to be slow and prevents branching reactions from occurring within the timescale of the observed experimental effect. High initial densities resulted in reaction rates that caused clashes of filaments and terminated cell spreading in the simulations. Based on these observations, we selected an initial condition of 4000 actin filaments distributed evenly around the periphery of the leading edge.

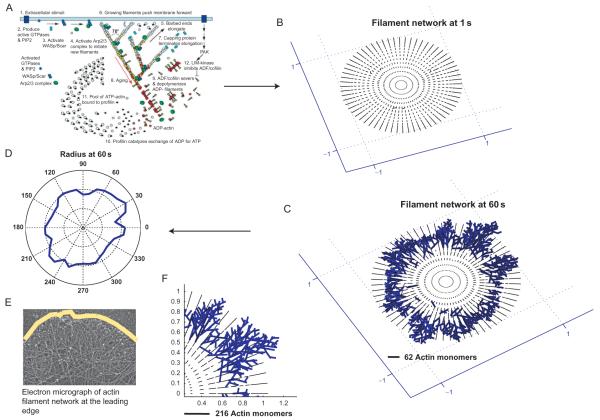
From the simulation program, we collect the barbed and pointed end location of every filament in the cytoskeleton in the x, y, and z dimensions. We then plot the filament network as shown in Fig. 7.2 as x–y projection for 0.2-μm thick slices. Over the duration of the simulation, the filament network shows an increase in elongation and branch density. We also show an electron micrograph provided by Dr. Tatyana Svitkina (University of Pennsylvania) and trace the outermost edge of the filament network in a representation of the membrane. The comparison between the micrograph and the simulation filament network shows that the model assumptions are reasonable and the stochastic spatiotemporal reactions are able to qualitatively capture the filament reorganization events. A sequence of steps on the growth of the actin cytoskeleton in our spreading model is shown in Fig. 7.2A.

Figure 7.2.

Growth of the actin cytoskeleton from the spreading model. The filament network in the model is initiated as a number of seed filaments, which can elongate, branch or cap, based on the actin reactions (A). The resulting actin network (B and F) looks similar to the cross-linked actin network at the leading edge (E). Tracing the periphery of the filaments (C) allows us to construct the shape of cell (D) as a function of time. Figure S2 from Xiong et al., ⁷¹.

7.2. Dynamic cell surface

The dynamic cell surface keeps track of the exact location of the leading edge. Based on the nature of actin-based motility machinery used by the model, the surface of a motile cell is constructed from the underlying actin filament network. Changes in the biochemical reactions lead to the change of cell surface and consequently lead to cell spreading. The cell surface is constructed by a series of adjacent triangular polyhedrons enclosed by a triangulated surface embedded in a three-dimensional space, resulting in a triangularized sphere (Fig. 7.1). This is similar to the experimentally observed round fibroblast cell as its starts to spread on a fibronectin-coated glass surface.¹⁴ As the underlying filament reactions progress, the cell surface is actively updated, such that the dynamics of the filament network directly changes the location of the cell surface, therefore, representing the experimentally observed movement of the leading edge.

Surface construction using triangulation algorithms and computational geometry is not new.⁷² However, using these methods to simulate changes in cell shape has not been done before. In this representation, each vertex of the cell surface corresponds to the barbed end of an actin filament beneath the cell surface, and the edges connecting all vertices define the triangulation of the surface. Thus, the membrane surface results from the underlying actin cytoskeleton. Because we are not simulating the membrane independent of the cytoskeleton, we do not consider situations where there are no filaments (similar to lipid vesicles). As a result, the cell surface is a direct consequence of the underlying actin filament structure.

The large number of filament reactions requires each step of the Monte Carlo simulation to be extremely efficient. Furthermore, the surface triangulation must be extremely efficient in order to be included in the stochastic framework. These requirements led to the development of the original computational method to reconstruct dynamic cell surface based on filament network growth used in the model.⁷¹

7.2.1 Initial cell surface

The geometry of cell surface at the leading edge is initialized to a triangulated surface. As mentioned before, the vertex of surface triangles represents the barbed end of underlying actin filaments. Each initial actin filament is composed of one Arp2/3 and two polymerized actin monomers, and the direction of filament growth is initialized to the radial orientation of the sphere.

7.2.2 Update of cell surface

The occurrence of a filament polymerization reaction increases the length of the existing filament by one actin monomer. Thus, the vertex on the cell surface corresponding to this barbed end moves its location along the direction of filament growth by the length of one actin monomer. Since the vertex of a filament is always connected with the vertex of its neighboring filaments, this connectivity must be updated once the vertex moves to a new location in order to maintain surface smoothness. The model searches for the closest vertices to the moving vertex and connects them together. Previously, connected vertices that are not included in the new set of closest vertices are removed from the connection with the moving vertex. All facets containing removed connection edges are deleted and new facets containing added connection edges are created. During the addition and removal of surface facets, the topology of cell surface is carefully maintained such that the entire cell surface remains closed in three dimensions.

The update method when a filament capping reaction occurs is similar to the case of filament polymerization reaction except that the molecule added to the barbed end of a filament is a capping protein. The only difference is that the current filament is now capped and is not able to grow anymore. Thus, the vertex corresponding to the capped filament is now incapable of moving.

The filament branching reaction creates a new actin filament from an existing filament by the binding of Arp2/3 to the side of the existing filament. Therefore, a new vertex representing the barbed end of the new filament must be created and added into the cell surface (Fig. 7.1). The spatial location of the new filament is determined by the binding site of Arp2/3 on the existing filament, the branching orientation, and the initial length of the new filament. Because Arp2/3 is activated by the upstream signaling molecules that are attached to the cell membrane, the model assumes that Arp2/3 binds to the membrane facing side of the existing filament, usually three to four actin monomers away from the barbed end of the existing filament. The angle between the new filament and the existing filament is 70°, and the number of initially polymerized actin monomers is 2. Based on these constraints, the new filament can be created from the Arp2/3 binding site on the existing filament and its possible orientations form a conic surface around the existing filament. The resulting cytoskeletal structure from these simulations is shown in Fig. 7.2 and compared against electron micrographs of the actin network at the leading edge of cells.

7.3. Membrane energy-based feedback to the biochemical reaction rate

The filament network has to overcome the change in the mechanical energy associated with the forward movement of the membrane. This results in a reduction of the rate of the reaction as shown in Eq. (7.10). The concept of the elastic Brownian ratchet is explained in Ref. 5. In our model, we consider two contributions to the change in membrane energy—the surface-resistance pressure p and the membrane-bending stiffness K_b.

The energy computation in the simulation characterizes the resistance imposed on the growing filaments. In our model, we use the energy–velocity dependence defined in Eq. (7.6) to compute the effective rate constants for all three biochemical reactions. The main challenge here lies in the computation of dA and H for the triangular facets while keeping a closed smooth surface. We turn to discrete differential geometry framework for computing dA and H. The geometrical framework for calculating the area and the curvature integral for a given filament is shown in Fig. 7.3.

Figure 7.3.

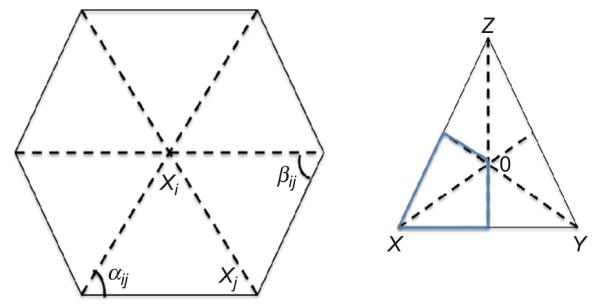
Computation of area element to obtain membrane resistance. In order to calculate the Voronoi area of the vertex X in the triangle XYZ, we find the circumcenter O. The Voronoi area associated with the vertex X lies within the triangle (marked by the blue lines) for nonobtuse angles and is (1/8)(∣XY∣² cot∠Z+∣XZ∣² cot ∠ Y). Using this method, we then sum these areas for a vertex x_i as a function of the neighbors x_j and obtain the area associated with each filament. Xiong et al., ⁷¹ supplemental figure 7.

The calculation of local area of a facet and local curvature is well established for triangular meshes in discrete differential geometry. We use the method proposed in Ref. 72 to calculate the area of a facet and to obtain the mean curvature integral of the surface. The complete mathematical framework for this is presented in Ref. 72.

Using the triangulations shown in Fig. 7.3, for a vertex x_i on the surface, the area as a function of its neighbors x_j is given by

$$\mathrm{d}{A}_{\mathit{ij}}=\frac{1}{8}\sum \left(\cot \left({\alpha }_{\mathit{ij}}\right)+\cot \left({\beta }_{\mathit{ij}}\right)\right){\Vert x_i-x_j\Vert }^2$$ (7.13)

The pressure term is used to compute the vectorial force acting on each filament during the motion of the surface. In order to compute the curvature integral, we use the following equation:

$$U=\int H^2\mathrm{d}A=\frac{1}{2A_{\text{mixed}}}\sum \left(\cot \left({\alpha }_{\mathit{ij}}\right)+\cot \left({\beta }_{\mathit{ij}}\right)\right)\left(x_i-x_j\right)$$ (7.14)

The vertices and angles in Eqs. (7.13) and (7.14) also correspond to Fig. 7.3. A_mixed is the cumulative area of the individual triangles on the surface. The complete derivation of this relationship between the curvature integral U and the individual angles can be found in Ref. 72.

7.4. Membrane surface resistance

The membrane surface resistance is characterized by a pressure term p (pN/nm²). The energy change associated with moving a membrane facet of area dA by a length (one actin monomer) is given by ΔE_surface =pdAδ. The force associated with this energy change is pdA. The resistance force f imposed on growing filaments gets updated as soon as the local membrane geometry changes throughout the simulation process. The resistance force f imposed on a growing filament is calculated by the following formula:

$$f=\widehat{n}\cdot \sum _{i=1}^5\overrightarrow{f_i}$$ (7.15)

where $\widehat{n}$ is a unit vector pointing to the inverse direction of filament growth, $\overrightarrow{f_i}$ is the resistance force generated by the neighboring triangular facet O–V_1,i–1–V_1,i, and its magnitude is calculated by

$$f_i=p\cdot \mathrm{d}{A}_{O-V_{1,i-1}-V_{1,i}}$$ (7.16)

where p is the resistance pressure of membrane surface and dA_O–V1,i–1–V_1,i is the area of the triangular facet O–V_1,i–1–V_1,i. The direction of $\overrightarrow{f_i}$ points from the vertex O to the center of the triangular facet O–V_1,i–1–V_1,i. Therefore, using the cotangents calculated for the Voronoi area, the integral can be computed directly for the surface. For further details, please see Ref. 71. Based on these two membrane energy contributions, we compute the energy change associated with moving the membrane forward and suitably modify the reaction rate of the actin filament reactions.

7.5. Surface clashes

The model only selects the orientation that makes the new filament intersect with the cell surface in order to avoid the formation of a concave surface around the newly added vertex. For filaments that have been capped, no filament reactions can occur on them and they cannot grow any more. Then as the neighboring filaments keep growing, the local surface around the barbed ends of these filaments becomes concave or even invaginated. Such concave surface may cause the clash of local surfaces. In order to avoid this, once the spatial location of the new filament is determined, the vertex corresponding to the barbed end of new vertex is added into the cell surface and the vertex connectivity in this local surface area is updated by following the same principle as that used in filament polymerization reaction.

In order to determine when to remove the attachment of a capped filament from the cell surface, we have used the resistance force imposed on this filament by the cell membrane as the criterion: if the resistance force on the capped filament disappeared based on the geometry of the local surface around this filament, then the barbed end of this capped filament should be removed from cell surface by removing the corresponding vertex from cell surface. As the removal of a vertex leaves a three-dimensional polygon hole on the cell surface, the surface area within this region must be retriangulated to maintain the closed topology of cell surface. A straightforward method is used to triangulate this polygon hole by connecting neighboring edges of the polygon to form new triangular facets.

The mechanism of alternating branching and capping reactions keeps filaments short during filament network growth, and the filament network remains rigid enough to be able to push the cell membrane forward. On the other hand, this mechanism causes the cross growth of uncapped filaments which leads to the clash of cell surface. Surface clash not only causes a jagged cell surface but also makes the filament network have equal chance to grow both forward and backward such that there is no net forward growth for the leading edge for a spreading cell. This problem is avoided by the nature of the membrane: rigidity (such as membrane elasticity and membrane-bending resistance) and merging intracellular membranes into the cell surface membrane during the spreading process. The computational model uses the concept of protrusion guidance to direct the branching direction of filament branching reaction based on the experimental observations of fibroblast cell spreading. Protrusion guidance posits that the branching direction that deviates the least from the protrusion direction of the leading edge is preferred. Together with the intersection requirement of creating new filaments, the branching reaction that creates a new filament that intersects with the cell surface and has the least deviation angle from the protrusion direction of the leading edge is preferred.

7.6. Dynamic dependency graph

A dynamic dependency graph is built on the graph data structure. Each node of the dependency graph contains three dependency lists: the list of other nodes that this node can modify, the list of other nodes that this node can destroy, and the list of other nodes that can modify or destroy this node. At the beginning of the spreading simulation, this dependency graph is initialized to reflect the interaction relationships among the initial filament reactions. At each step of simulation: (1) when a filament polymerization reaction occurs, the filament reactions affected by the current reaction are updated based on their interaction relationships in the dependency graph; (2) when a filament branching reaction occurs, three associated filament reactions are created and their interaction relationships are added into the dependency graph; and (3) when a filament capping reaction occurs, the filament reactions associated with the capped filament are destroyed and their dependency relationships are removed from the graph.

The dynamic dependency graph is then integrated with Gillespie’s stochastic framework, specifically the first reaction method, by introducing the sorted list of the waiting time of all filament reactions into the model. This waiting time list updates the waiting time of a filament reaction if this reaction is changed indicated by the dynamic dependency graph and uses a dichotomy sorting algorithm to move the updated waiting time to a new position to keep the list sorted. Since this waiting list is always sorted from the minimum to the maximum, the filament reaction to occur at the next simulation step is always at the front of this list.

8. COMPARISON OF EXPERIMENTS AND SIMULATED CELL SPREADING

One application of our model has been to understand how cell spreading during the isotropic phase is regulated. Using this spreading model, we were able to capture key aspects of cell spreading during the isotropic phase. Our model also identified that the shape of the spreading cell is maintained primarily by the membrane properties and the interaction of the growing cytoskeleton with the plasma membrane.^65,71 While signaling and the concentrations of actin-regulating proteins are required for initiation of cell spreading, they do not control the shape evolution of the spreading cell. These observations were validated experimentally using fibroblasts spreading on fibronectin-coated surfaces. Thus, a simple model of three actin reactions, coupled with a unique representation of membrane geometry was sufficient to model the spreading behavior of fibroblasts during the isotropic phase. Our approach of including the membrane interactions with the actin not just allowed us to capture experimentally observed behavior in a complex cellular system but also provided some fundamental insights into how membrane properties regulate actin reactions.

9. CONCLUSIONS AND PERSPECTIVES

In this chapter, we describe a distinctive approach to modeling the cytoskeletal changes during cell spreading. Borrowing from techniques for chemical reactions, mechanics of actin filaments and the plasma membrane, and implementation techniques from computational geometry allowed us to build a three-dimensional model of cell spreading. This approach can be extended to study contractile processes in cells, neurite outgrowth, and reorganization during synaptic transmission, with suitable modifications.

Mathematical and computational modeling compliment experimental studies in biology. This is particularly true in complex biological systems where multiple variables may be affected by a single change in an experimental setting. Modeling tools allow us to distill complex processes into a set of equations that explicitly describe multiple relationships. Solutions to these equations can provide deep insight into the mechanisms that regulate the process of interest. Since most biological models are solved numerically, the simulations often provide explicit predictions that can be tested experimentally. There is the ever-present danger of the urge to oversimplify biological processes in modeling; however, the ability of such models to predict the role of regulatory molecules in controlling the dynamics of the process and comparison of the simulations with experimental results as a gold standard can help us build models with the correct level of detail that provide deep mechanistic insight not obtained solely from experiments.