Air-coupled acoustic radiation force for non-contact generation of broadband mechanical waves in soft media

Abstract

A non-contact method for efficient, non-invasive excitation of mechanical waves in soft media is proposed, in which we focus an ultrasound (US) signal through air onto the surface of a medium under study. The US wave reflected from the air/medium interface provides radiation force to the medium surface that launches a transient mechanical wave in the transverse (lateral) direction. The type of mechanical wave is determined by boundary conditions. To prove this concept, a home-made 1 MHz piezo-ceramic transducer with a matching layer to air sends a chirped US signal centered at 1 MHz to a 1.6 mm thick gelatin phantom mimicking soft biological tissue. A phase-sensitive (PhS)-optical coherence tomography system is used to track/image the mechanical wave. The reconstructed transient displacement of the mechanical wave in space and time demonstrates highly efficient generation, thus offering great promise for non-contact, non-invasive characterization of soft media, in general, and for elasticity measurements in delicate soft tissues and organs in bio-medicine, in particular.

Acoustic radiation force (ARF) is commonly used in ultrasound (US)-based elastography to remotely generate shear waves deep within tissue.^1–3 Detection of shear waves can be performed with a conventional ultrasound (US) imaging probe or with another imaging method, e.g., optical coherence tomography (OCT). The combination of ARF with high frame rate OCT can produce quantitative cross-sectional maps of the shear modulus in soft tissues.⁴ For many clinical applications, however, a totally non-contact system for generation/detection of mechanical waves is desirable and, in some cases (for instance, the eye), is necessary. OCT is an ideal approach for these applications if an efficient and robust non-contact generation technology can be developed.

Generation of mechanical waves with an air puff was used in Ref. 5 to produce very narrow bandwidth displacements in the cornea, which may not be able to characterize corneal elasticity at the spatial resolution required for clinical decision making. Our group has recently demonstrated non-contact generation using absorption of pulsed UV laser light.⁶ Although UV generation can provide the bandwidth required for high spatial resolution maps of corneal elasticity, it is not clear at this point whether the required UV energy levels will meet the safety requirement for routine clinical use.

Here we propose a fully non-contact and non-invasive US technique to create efficient localized wideband mechanical waves in soft tissue. The method utilizes US launched with an air-coupled transducer (i.e., through air) to the air/medium interface. The US wave reflected from this interface provides radiation force to the medium surface, which induces a transient displacement at that surface, ultimately generating a propagating shear/guided/interface/Lamb wave (wave type determined by boundary conditions). We will call this the mechanical wave to maintain generality.

Previous ARF methods in elastography used loss and scattering mechanisms to convert acoustic energy into displacements.² In contrast, the method presented here uses reflection-based ARF for highly efficient displacement generation. Acoustic radiation force is determined by the spatial shape of the pump beam and duration of the ultrasound pulse.^1–3,7 For pulsed insonification, it acts like a “hammer” on the surface. Relaxation of the induced displacement generates the mechanical wave.

In reflection mode, the radiation pressure P (force per unit area) is

$$P=\frac{(1+R^2)I}{c_{\mathit{a}\mathit{i}\mathit{r}}},$$ (1)

where R is the reflection coefficient at the air/medium interface, I is the acoustic intensity [Watts/m²], and $c_{\mathit{a}\mathit{i}\mathit{r}}$ is the sound speed. For air-coupled ultrasound, the reflection coefficient at the air-tissue boundary is nearly one ($R\cong 1$) so that the radiation force can be approximated as $P=2I/c_{\mathit{a}\mathit{i}\mathit{r}}$. Since the sound speed in air is low (about $c_{\mathit{a}\mathit{i}\mathit{r}}$ = 340 m/s) and nearly all acoustic intensity is converted into radiation pressure, significant force can be produced at modest acoustic pressures.

Interestingly, ARF delivered through air was previously used to produce a mechanical impact on a fluid.⁸ Non-localized, low frequency sound waves were generated in air by a vibrating plate located near the surface and used for fluid leveling. This approach, however, cannot be used to excite localized, wideband mechanical waves to probe soft material elasticity at mm and sub-mm scales. In contrast, ARF by reflection at the air/medium interface can produce highly localized surface transient displacements using acoustic frequencies in the ultrasound range (i.e.,  >20 kHz and up to several MHz) to generate wideband propagating mechanical waves in soft materials such as biological tissue.

By shaping the pump ultrasound field launched with a focused air-coupled transducer, and also with acoustic masks, focusing mirrors,^9–11 and Fresnel plates^11–13), the radiation pattern (i.e., spatial distribution of I) can be manipulated at the air/medium interface. In addition, ultrasound arrays can electronically scan the pump field across the interface.

As noted above, the more localized the radiation force, the higher the bandwidth of the generated mechanical wave. Signal bandwidth ultimately determines spatial resolution. Thus, for diagnostic needs, highly localized ARF is desirable. As is well known, localization of a field is limited by diffraction, so a high US frequency is desired. Increasing the pump US frequency, however, is limited by strong US attenuation in air (proportional to frequency squared^14,15). Thus, relatively short US propagation paths must be used for air delivery.

To prove this concept, a home-made, unfocused, 1 MHz air-coupled transducer was used for ARF-based generation of mechanical waves in a tissue mimicking phantom. US attenuation in air is about 2 dB/cm at 1 MHz,¹⁴ quite reasonable for a few cm propagation path. A 91.2 kHz A-line rate optical coherence elastography (OCE) imaging system¹⁶ was operated in M-B mode to image the induced mechanical waves, as discussed below. Thus, both mechanical wave generation and detection are non-contact, which enables remote and non-invasive characterization of soft tissue.

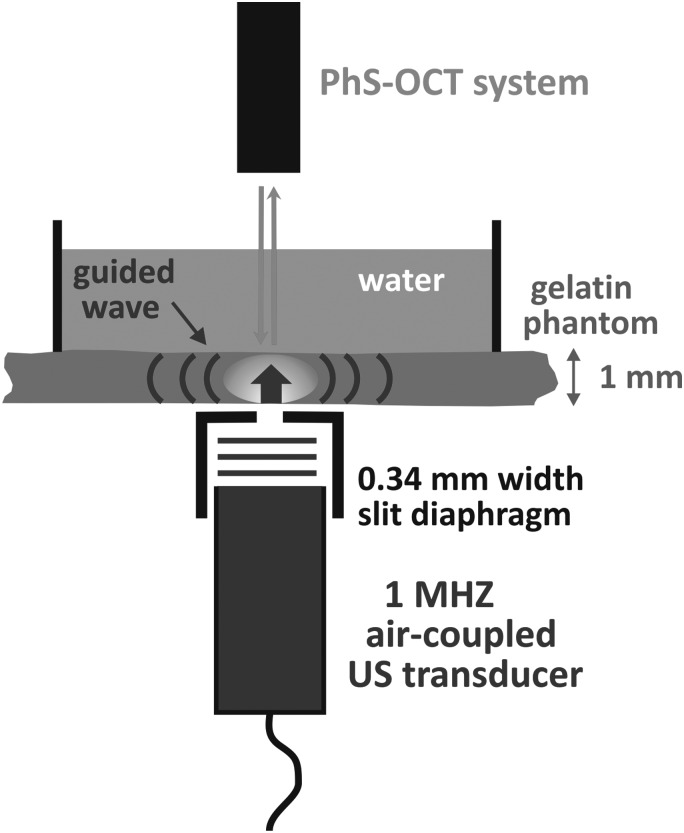
Figure 1 shows the experimental setup used to prove the concept described above. A tissue mimicking phantom was made of an 8% w/w gelatin (Sigma-Aldrich, G2500) and 0.02% w/w titanium dioxide (TiO₂) powder as optical scatterers for OCT imaging. The thickness of the phantom is 1.6 mm. A 5 mm water layer was above the gelatin phantom to mimic mechanical loading of the phantom similar to that for the cornea at the front of the eye.

FIG. 1.

Proof of concept demonstration of air-coupled ultrasound stimulation of transient mechanical waves in soft media. A 1 MHz air-coupled ultrasound transducer launches a beam from the bottom of a tissue-equivalent gelatin phantom through a slit to shape the excitation beam. The narrow slit, 0.34 mm wide by 15 mm long, was used to shape the mechanical wave source at the air/phantom interface. Detection of generated mechanical waves was performed from the opposite side of the phantom with a PhS-OCT system described in Ref. 16.

A home-made air-coupled PZT-based transducer with a matching layer (a 0.45 μm pore size nylon membrane filter, Cat. No. 7404-004, GE Healthcare UK Limited, Little Chalfont, UK) bounded to the transducer surface with a silicon adhesive coupled US into air. The transducer resonance frequency is 1 MHz and the emitting aperture is 12.2 mm in diameter. The transducer was located 1 cm away from the medium surface. It was excited using a burst signal with repetition frequency of 20 Hz. The burst was a linear chirp 400 V peak to peak in amplitude and 400 μs in duration, where a chirp was used to minimize potential US standing wave effects between the transducer and the phantom surface. The bandwidth of the driving voltage signal ranged from 0.9 MHz to 1.1 MHz (i.e., chirp has a time-bandwidth product of approximately 80).

The pressure amplitude in the generated US beam was measured with a home-made 28 μm thick polyvinylidene difluoride (PVDF) transducer calibrated in the frequency band 50 kHz–30 MHz, as described in Refs. ¹⁷ and ¹⁸. The measured acoustic pressure amplitude in the generated beam was about 1 kPa at 1 cm from the air-coupled transducer surface.

A narrow slit was made from two glass cover plates (170 μm thick) separated by 0.34 mm from each other and placed in the air 0.5 mm below the phantom surface to localize the ARF-based excitation. Note that there are many different ways to generate focused US beam, e.g., with a focused air-coupled transducer, lensing, zone plates, and properly shaped reflecting mirrors. The slit here is just a simple way to mimic the focused US beam for the proof of concept. The width of the slit was chosen to be close to the US wavelength in air, the typical diffraction limit for shaping. Thus, the pump US beam at the phantom surface represented a strip about 12 mm long by 0.34 mm wide. Unlike a round shape, the slit maximizes the bandwidth of the generated mechanical wave, induces directional (i.e., one-dimensional) propagation, minimizes diffraction loss, and approximates a one-dimensional propagation model. Again, the bandwidth of the mechanical wave directly determines the ultimate spatial resolution of tissue elasticity properties imaged in the lateral direction.

A phase-sensitive (PhS)-OCT system¹⁶ was used to detect the guided mechanical wave generated in the gelatin phantom from the opposite side of the phantom. The PhS-OCT system operated in M-mode at a 91.2 kHz A-scan rate, enabling mechanical wave tracking in time and space frame by frame, with a displacement sensitivity of ∼3 nm.⁶ OCT M-mode is analogous to motion-mode, or M-mode, in medical ultrasonography. The OCT detection beam is fixed at one position, and repeated A-scans are acquired so that motion at any position along the beam line can be detected. After acquiring motion information over a fixed dwell time (5.6 ms, representing 512 A-scans, in this case), the position of the OCT bean is moved to another point. Multiple points form the entire M-B scan.

The phase difference in PhS-OCT is linearly proportional to displacement, measured to be more than 1 μm at the excitation point, which can easily be detected by OCT (see below). With a 3 nm detection sensitivity, at least 40 dB signal-to-noise ratio (SNR) was achieved in this phantom study, demonstrating practical applicability of the proposed ARF-based approach under conditions close to real biomedical measurements.

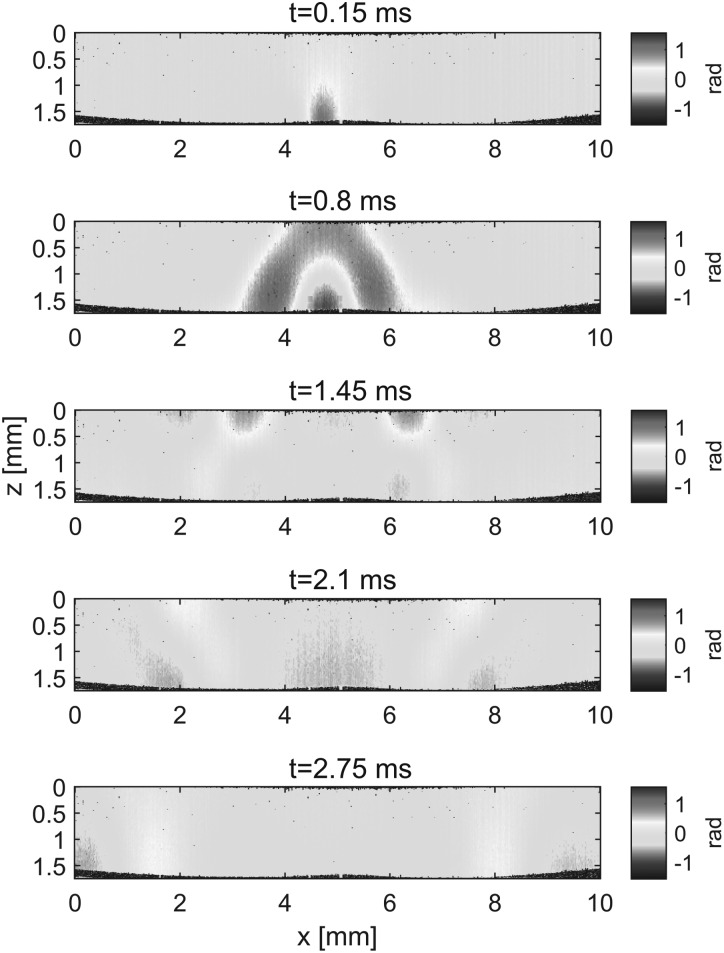
Five sequential instants stepped by 0.65 ms in mechanical wave propagation recorded with OCT are shown in Fig. 2 (see Multimedia view for complete set of frames). In the near field of the source, the wave diverges in both Z (depth) and X (lateral) directions (Fig. 2, first two panels (t = 0.15 ms and t = 0.8 ms)) until it reaches the interface of the gelatin phantom with water (Fig. 2, second panel (t = 0.8 ms)). Beyond that instant, the wave is guided in the X direction with opposite phases at the interfaces with water (Z = 0) and air (Z = 1.6 mm). Note that wave propagation images are free from sample surface ripple artifacts commonly observed in OCT mechanical wave imaging, due to the layer of water acting as an optical coupling media.¹⁹

FIG. 2.

Propagating transient mechanical waves launched in a tissue-mimicking gelatin phantom by an ARF-based, air-coupled ultrasound source and captured by a PhS-OCT system¹⁶ with time instants shown at the top of each panel. See for complete set of frames. (Multimedia view) [URL: http://dx.doi.org/10.1063/1.4959827.1] Download video file ^{(2MB, mov)} DOI: 10.1063/1.4959827.1

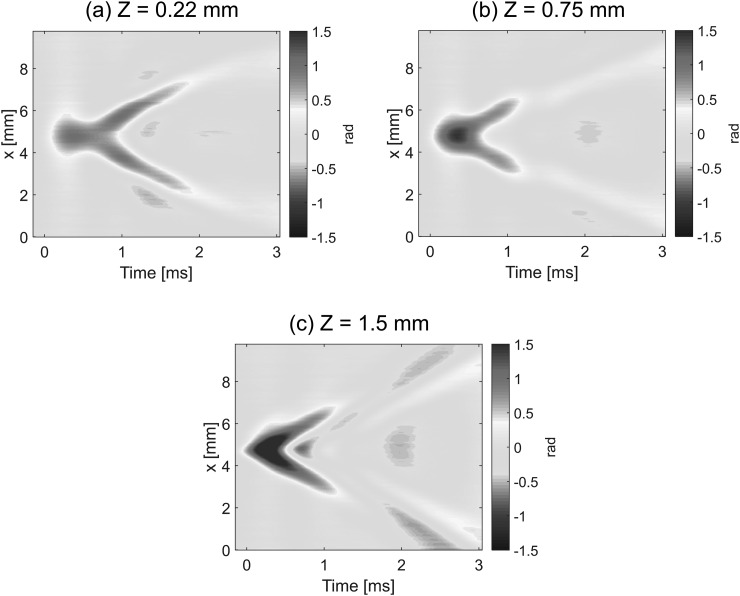
Figure 3 shows how the temporal shape of the mechanical wave changes during propagation from the center of the excitation to the side in the X (lateral) direction for three different Z (depth) positions: close to the water interface (a), the phantom center (b), and air interface (c). It is clear that the waveform is not conserved even in the near field and even when the line source was used for excitation, i.e., wave propagation is strongly dispersive. The dispersion is depth dependent, showing opposite sign in displacement at water and air interfaces at the same time instant.

FIG. 3.

Two-dimensional maps of the temporal profiles (lateral coordinate, X, versus time, t) for the mechanical wave propagating in the gelatin phantom illustrated in Fig. 1. The maps correspond to depths from the phantom/water interface: (a) Z = 0.22 mm, (b) Z = 0.75 mm, and (c) Z = 1.5 mm.

The speed of the mechanical wave can be determined in each point of the medium under study with the method demonstrated above. However, the speed depends on frequency, as is clear from Fig. 3. The wave speed also depends on excitation geometry and the type of mode generated. Indeed, we used a 1.6 mm thick gelatin phantom with a water layer on one side to mimic the cornea in the anterior segment of the eye. The phantom has two different interfaces and, therefore, the generated mode is not purely shear and, moreover, is not purely symmetric or asymmetric.⁵ Thus, mechanical wave dispersion cannot be ignored in most real situations, and tissue elasticity μ cannot be determined directly at each image point using the simple mechanical relationship $\mu =\rho c^2$ (where ρ and c are the density and speed of the mechanical wave in tissue). The solution of an eigenvalue problem must be considered, which, in general, can be a complicated mathematical problem. However, for one-dimensional propagation of a broad bandwidth mechanical wave, the situation can be greatly simplified and the solution can be found numerically.^20,21 The mechanical wave dispersion curve determined experimentally can be fit with that found theoretically to determine tissue elasticity, as discussed previously in Ref. 5. Thus, the proposed non-contact method can be directly used for soft tissue elasticity mapping, which will be the goal of our forthcoming studies.

To summarize, ARF excitation of shear/guided/interface/Lamb waves based on the reflection of an US beam from an air/tissue interface has been shown very efficient even for a relatively high frequency (1 MHz) acoustic excitation beam propagating through air. This method shows much higher efficiency in terms of amplitude and bandwidth than other non-contact laser and air-puff methods demonstrated before.^5,6 We used a narrow slit in the screen to shape the area of mechanical wave excitation, which allows careful tracking of wave dispersion during propagation. In the future, the slit will be replaced with a diffraction limited focusing approach.

The PhS-OCT system¹⁶ was used to detect the generated mechanical wave from the opposite side of a phantom, mimicking the cornea, to avoid any artifacts related with the excitation itself. The sensitivity of the OCT system has been shown to be sufficient to detect ARF-based generated mechanical waves. Thus, the combination of air-coupled US to generate mechanical waves and OCT-based detection creates a fully non-contact and non-invasive method to characterize the elastic properties of soft tissue. The method can be easily adopted for many medical applications, such as characterization of tissues in intestinal walls, characterization of skin, etc. The method can also easily meet all safety requirements, is painless for patients, and is convenient to use because it is absolutely non-contact. Medical applications of the proposed method are the primary focus, but many non-medical applications are also possible. For example, the elasticity of any soft substance, especially fragile or delicate samples, can be characterized because no contact is made with the sample.

A double-sided approach was used as a proof of concept in this paper; it will be replaced in our next studies with a single-sided one, i.e., generation and detection of mechanical waves at the same surface. In this case, mechanical waves induced by ultrasound can interfere with OCT imaging. The amplitude of the transient displacement is small, however, typically below one wavelength of the OCT light source with minimal effect on conventional OCT imaging. Due to the optical refractive index mismatch at the air-tissue interface, mechanical motion of the sample surface can induce some lens effect, modulating the OCT motion detection signal below the sample surface. Nevertheless, this effect can be compensated using a map of the surface contour acquired by OCT, as described in Ref. 19. Hence, a single-sided approach is quite feasible and is currently under investigation in our lab and will be tested using both ex vivo and in vivo experiments.