Morphological dependency of cutaneous blood flow and sweating during compensable heat stress when heat-loss requirements are matched across participants

In this experiment, individuals of widely variable body size exercised in thermally compensable conditions under work loads that elicited equivalent heat-loss requirements and body temperature changes. This novel design yielded the first comprehensive evaluation of the morphological dependency of the resulting cutaneous vascular and sudomotor responses, explaining up to half of the interindividual, thermoeffector variability. This relationship provides a mechanism through which to explain thermoregulatory differences among men and women, and children and adults.

Abstract

Human heat loss is thought, in part, to be morphologically related. It was therefore hypothesized that when heat-loss requirements and body temperatures were matched, that the mass-specific surface area alone could significantly explain both cutaneous vascular and sudomotor responses during compensable exercise. These thermoeffector responses were examined in 36 men with widely varying mass-specific surface areas (range, 232.3-292.7 cm²/kg), but of similar age, aerobic fitness, and adiposity. Subjects completed two trials under compensable conditions (28.1°C, 36.8% relative humidity), each involving rest (20 min) and steady-state cycling (45 min) at two matched metabolic heat-production rates (light, ∼135 W/m²; moderate, ∼200 W/m²). Following equivalent mean body temperature changes, forearm blood flow and vascular conductance (r = 0.63 and r = 0.65) shared significant, positive associations with the mass-specific surface area during light work (P < 0.05), explaining ∼45% of the vasomotor variation. Conversely, during light and moderate work, whole body sweat rate, as well as local sweat rate and sudomotor sensitivity at three of four measured sites, revealed moderate, negative relationships with the mass-specific surface area (correlation coefficient range −0.37 to −0.73, P < 0.05). Moreover, those relationships could uniquely account for between 10 and 53% of those sweating responses (P < 0.05). Therefore, both thermoeffector responses displayed a significant morphological dependency in the presence of equivalent thermoafferent drive. Indeed, up to half of the interindividual variation in these effector responses could now be explained through morphological differences and the first principles governing heat transfer.

NEW & NOTEWORTHY

In this experiment, individuals of widely variable body size exercised in thermally compensable conditions under work loads that elicited equivalent heat-loss requirements and body temperature changes. This novel design yielded the first comprehensive evaluation of the morphological dependency of the resulting cutaneous vascular and sudomotor responses, explaining up to half of the interindividual, thermoeffector variability. This relationship provides a mechanism through which to explain thermoregulatory differences among men and women, and children and adults.

the capacity to store heat is size dependent, with larger objects being more thermally stable, and resisting rapid and significant temperature changes. On the other hand, the avenues for physical heat exchange are surface-area dependent. Therefore, for geometrically dissimilar objects of identical composition, heat exchange and storage are tightly linked to the ratio of surface area to mass (mass-specific or specific surface area). These principles also relate to allometric structures, including humans. However, few researchers have considered the possibility that the autonomically driven avenues for heat exchange (vasomotor and sudomotor function) might also share a morphological dependence. Indeed, although our ability to explain interindividual variations in thermoeffector responses is comprehensive (25, 39), we know relatively little about the contribution of body morphology to that modulation. Although this information must represent a cornerstone for interpreting group comparisons (e.g., gender and age), as well as providing a foundation upon which physiological adaptations develop, systematic research of this fundamental relationship remains surprisingly sparse and often incomplete (7, 8, 20, 21). Therefore, the focus of this project was to provide a detailed evaluation of the body-size dependency of cutaneous vascular and sweating responses within individuals of widely varying size.

Although the suggestion that thermal homoeostasis may be linked with body morphology is not novel (36, 47), previous studies have primarily focused on body temperature regulation (10, 19, 23). While some investigators have compared forearm blood flow (16, 20, 21) and whole body sweating (14, 34) in people of varying size, participants in those investigations performed exercise at either the same absolute or relative work rates. Unfortunately, such workloads frequently represent unequal requirements for heat loss in those who differ significantly in size (7, 8). Furthermore, those investigations typically involved individuals who differed not only in body size, but also in secondary factors that may independently influence thermoeffector function (e.g., age and aerobic fitness). Although one group of researchers recently compared sweating responses in smaller and larger individuals matched for some of those secondary factors (7), that project did not consider cutaneous vasomotor function, nor did it involve the examination of individuals spanning the body size range required to fully elucidate the morphological dependency. Moreover, neither that study (7), nor its recent iteration (8), were designed to provide an unequivocal assessment of the relationship between body morphology and the autonomically mediated heat-loss responses. To achieve that, thermal clamping is required so that both thermoeffector functions can be simultaneously assessed in the presence of equivalent thermoafferent drive across participants; Cramer and Jay (8) reported a fivefold variation in deep-body temperature across subjects. To our knowledge, no one has attempted such an experiment using individuals evenly distributed across adult body sizes, and under steady-state conditions that evoked equivalent heat-loss requirements.

Because mass-specific surface area increases as body size decreases, smaller individuals possess a morphological configuration that is suited to dry-heat dissipation under compensable thermal conditions, and perhaps may be less reliant upon sweating. In this circumstance, cutaneous vascular responses may be preferentially recruited, resulting in fluid conservation (10, 33, 47). Conversely, larger individuals who have a lower mass-specific surface area, but more fluid per unit area (44), may be forced to rely more heavily on the sweating mechanism. Such an hypothesis has teleological appeal from ecological (1) and thermal-adaptation perspectives (38).

Accordingly, the purpose of this investigation was to identify the extent to which differences in morphology may help to explain the relative contributions of the vasomotor and sudomotor heat-loss responses within morphologically different individuals. It was hypothesized that participants with a greater mass-specific surface area would depend more upon the vascular mechanism (convective heat delivery) while concurrently displaying a reduced sudomotor contribution. To test this hypothesis, both thermoeffector responses were simultaneously examined in thermally clamped individuals of widely variable size during two levels of compensable, steady-state cycling, but with similar phenotypic characteristics for other factors known to influence heat production and heat storage.

METHODS

Subjects

Thirty-six young, physically active and healthy, but not heat-adapted, adult men of similar adiposity, but varying body size, participated in this study (Table 1). This was a single-gender study because of the size of the project and the need to standardize hormonal influences on thermoregulatory function. Subjects were first recruited from a large university student sample, and then selected on the basis of their morphological configuration, so that they represented a broad range and even distribution of mass-specific surface areas (Fig. 1A). The first selection criterion was aimed at reducing variations in adiposity, with an inclusion threshold for the height-adjusted sum of six skinfold thicknesses being <88 mm (27, 31). This represented the 60th percentile for the corresponding age- and gender-specific Caucasian population (2), with participants having an adiposity range between the 40th and 60th percentiles (Table 1). To minimize aging and endurance-training influences, selection was restricted to individuals <30 yr who routinely performed aerobic exercise >3 h/wk. Furthermore, subjects were nonsmokers, took no medications, and had no history of cardiovascular or thermal illness. The procedures for this research were approved by the Human Research Ethics Committee (University of Wollongong) in accordance with the regulations of the National Health and Medical Research Council (Australia). All participants provided written, informed consent.

Table 1.

Physical characteristics of participants

Characteristic	Mean ± SD	Range
Age, yr	21 ± 3	18–30
Mass, kg	75.0 ± 10.3	56.3–94.2
Height, cm	179.4 ± 8.2	157.2–192.8
Surface area, m2	1.94 ± 0.17	1.56–2.25
Mass-specific surface area, cm2/kg	259.9 ± 15.2	232.3–292.7
Sum of six skinfolds thicknesses, mm	58.1 ± 15.4	42.0–90.0
Height-adjusted sum of skinfolds, mm	55.2 ± 14.5	39.7–88.0
Absolute peak oxygen consumption, liter/min	3.43 ± 0.60	2.03–4.62
Normalized peak oxygen consumption, ml·kg−0.87·min−1	80.3 ± 11.1	57.9–105.8

Sample size = 36. The sums of six skinfold thicknesses (triceps, subscapular, supraspinale, abdominal, thigh, and calf) were scaled to a common stature (170.18 cm) to derive height-adjusted measures of skinfold thickness and to approximate adiposity (27, 32). Peak oxygen consumption scores were scaled per unit of body mass raised to the exponent of 0.87 (after, 45; see text).

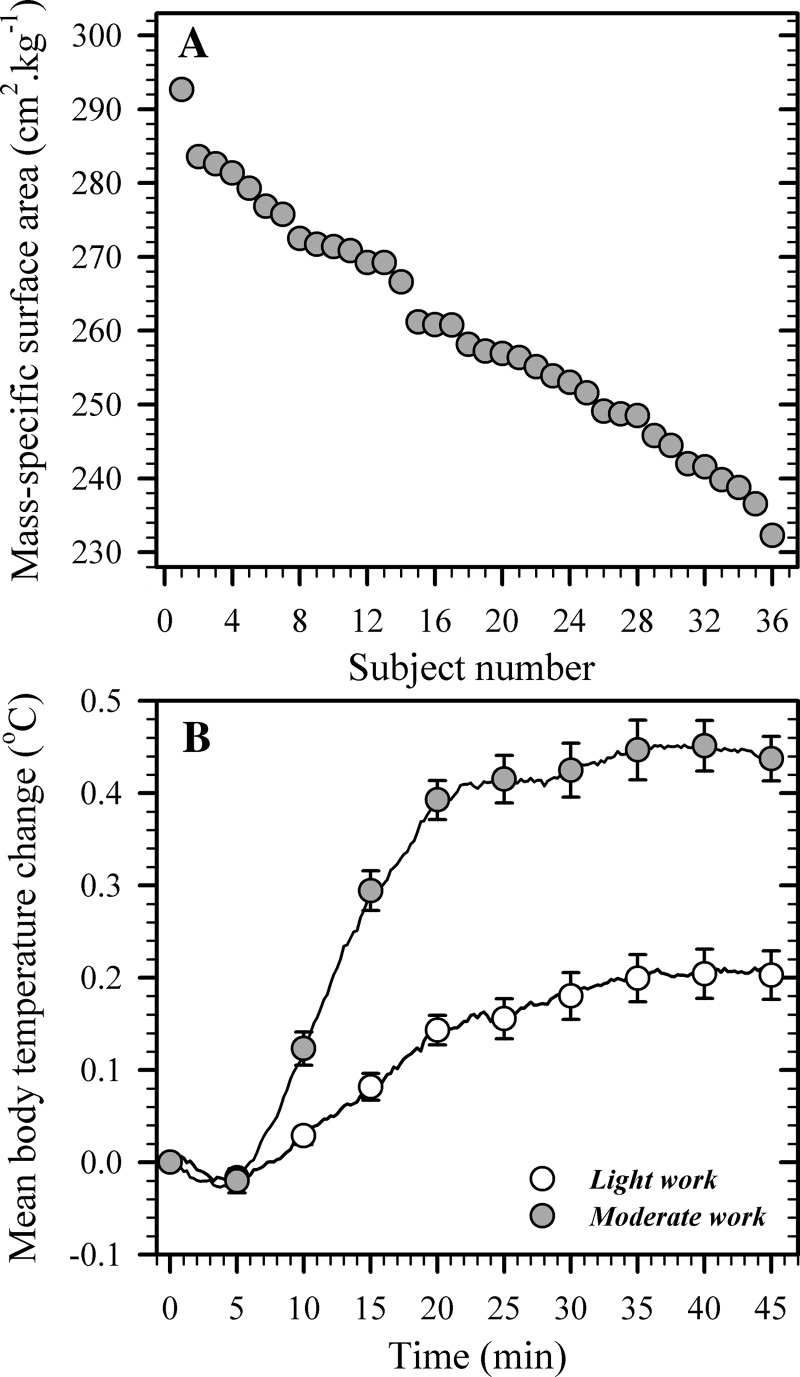
Fig. 1.

A: variations in mass-specific surface area (cm²/kg) of participants within this experiment (n = 36), arranged in descending order. B: mean body temperature changes during exercise (45 min) performed at fixed, area-specific metabolic heat-production rates of either ∼135 W/m² (n = 36, light work) or ∼200 W/m² (n = 35, moderate work) following a resting, thermal equilibration period in a warm-dry environment (28°C, 37% relative humidity). Data are presented as average response curves with means ± SE provided at 5-min intervals.

Procedures

On separate days, fully hydrated subjects completed two exercise trials (cycling) dressed in minimal clothing (cotton shorts, socks, and sports shoes). Non-weight-bearing exercise was used to minimize differences in heat production associated with variations in body mass. Following a preparatory period, subjects entered a climate chamber (28°C, 37% relative humidity) with limited air movement (<0.5 m/s). These conditions were chosen to ensure that thermal and water-vapor pressure gradients existed between the skin surface and ambient air that permitted both dry- and evaporative-heat dissipation. This was critical because it ensured thermoeffector recruitment was not dictated by environmental, but by physiological influences.

Each trial commenced with seated rest (mesh-lined chair; 20 min) in a semirecumbent position behind an electronically braked cycle ergometer (Excalibur Sport; Lode, Groningen, The Netherlands). Subjects then cycled at a constant frequency (60 revolutions/min) for 45 min at equivalent, normalized external work rates. These were referenced to the body surface area of each participant (area-specific work rate), because mass-specific work rates (W/kg) did not yield equivalent changes in mean body temperature within larger and smaller individuals (pilot research). This standardization was determined during a familiarization session. It ensured that each participant was required to dissipate heat in proportion to his skin surface area, and that mean body temperature was equivalently elevated, and then clamped. In a balanced order, subjects exercised at ∼135 W/m² and ∼200 W/m² at the same time on different days. These work rates are hereafter described as light and moderate work (respectively) because they averaged 25.5% (standard deviation [SD] 4.2) and 48.6% (SD 6.9) of the peak oxygen consumption of the current sample. This provided three experimental conditions (rest within each trial plus two exercise intensities), with all 36 individuals completing trial one (light work) and 35 successfully completing trial two.

These work intensities were determined through pilot testing, with the lighter work rate chosen in combination with the ambient conditions to elicit a state in which dry-heat loss could largely satisfy the total heat-loss requirement. Conversely, the moderate intensity was aimed at replicating conditions in which evaporative cooling would be dominant. Thus if either thermoeffector response was morphologically related, this design would allow for the expression of that association to be identified. Nevertheless, observations arising from this experiment relate only to physiologically compensable and load-supported exercise (cycling) undertaken in warm and somewhat dry conditions.

Preliminary session.

Each participant completed a laboratory familiarization session, an incremental exercise test to volitional fatigue, and an anthropometric assessment prior to the experiment. For incremental, semirecumbent exercise, subjects cycled at 75 revolutions/min (Excalibur Sport; Lode), commencing with a warm-up (2 min), followed by a ramp increase in work rate (36 W/min) until volitional fatigue. Expired respiratory gases and volumes were used to derive peak oxygen consumption (TrueOne 2400; ParvoMedics, Sandy, UT). Because those values have an allometric relationship with body mass (28, 37), data were expressed per unit body mass raised to the exponent of 0.87 (ml·kg^−0.87·min⁻¹) (45) to avoid the size bias introduced with arithmetic normalization (28).

Measurements of height (Harpenden Stadiometer; Holtain, Crymych, UK) and body mass (fw-150k; A&D scale, San Jose, CA) were used to approximate body surface area (12). Skinfold thicknesses were measured in triplicate (Eiken skinfold caliper; Meikosha, Tokyo, Japan) at six locations (triceps, subscapular, supraspinale, abdominal, thigh, and calf), with median scores recorded and summed. Because taller and shorter individuals with identical total skinfold thicknesses will have a different relative adiposity, then it follows that such indices must be adjusted for stature to remove the size bias when applied across individuals (31). Therefore, the sum of skinfolds (mm) was adjusted to a common stature (170.18 cm), yielding height-adjusted data (170.18/height ∗ [sum of six skinfolds]) (27, 32). Such standardization procedures are used for undertaking proportional growth assessments and for comparing the anthropometric characteristics of elite athletes who differ significantly in body size. Both raw and height-adjusted data are presented (Table 1), with the latter used as a surrogate of relative adiposity (31). Because total body water varies inversely with adiposity, this procedure was adopted to reduce variability in the body-fluid reserve.

Standardization.

Participants acted as their own controls, and the ambient conditions were stable within and between trials. Subjects were instructed to refrain from strenuous exercise and the consumption of alcohol during the 12-h period before each trial. For the night preceding, they were instructed to drink 15 ml/kg of additional water and to eat an evening meal and breakfast high in carbohydrate and low in fat. Dietary recommendations were provided. In the morning, subjects were required to drink 500 ml of fluid with breakfast, and to refrain from caffeine consumption for 2 h before presentation. Given the preparatory, equilibration, and exercise periods, this ensured caffeine abstinence for >5 h prior to data collection.

On presentation, participants were given an isotonic drink (10 ml/kg, sodium-chloride concentration 40–45 mmol/l) and their urine specific gravity was measured (Clinical Refractometer 140; Shibuya Optical, Tokyo, Japan) to confirm adequate hydration. Across subjects, the mean preexposure urine specific gravity was 1.019 (SD 0.01) on both test days. To maintain a standardized hydration state, subjects consumed 4 ml/kg of isotonic drink at the mid point of each trial, served at chamber temperature (28°C).

Measurements

Ambient conditions.

A climate-controlled chamber with limited air movement (<0.5 m/s) was used to regulate air temperature (28.1°C [SD 0.2]), and relative humidity (36.8% [SD 2.4], water vapor pressure 1.4 kPa). Radiant (black globe) temperature was monitored at the level of the subject (Type EU; Yellow Springs Instruments, Yellow Springs, OH), and was within 0.5°C of air temperature throughout all trials (28.5°C [SD 0.4]).

Deep-body and skin temperatures.

Deep-body temperature was monitored using an ear-molded plug with a thermistor protruding 1 cm (Edale Instruments, Cambridge, UK), positioned within the external auditory meatus (auditory canal temperature) and insulated with cotton wool secured to, and covering, the pinna. These procedures isolate the auditory canal from the ambient environment and minimize cutaneous thermal artifacts (41), and have been shown to permit this index to closely track esophageal temperature within temperate conditions (25°C) (42), with a baseline offset of approximately 0.05°C. Skin temperatures were measured from eight skin sites (forehead, chest, scapula, upper arm, dorsal forearm, dorsal hand, anterior thigh, and calf; Type EU; Yellow Springs Instruments). These data were collected at 15-s intervals (1206 Series Squirrel; Grant Instruments, Cambridge, UK). All thermistors were calibrated against a certified reference thermometer in a stirred water bath (Dobros total immersion; Dobbie Instruments, Sydney, NSW, Australia). Mean skin temperature was derived from the weighted summation of these eight local temperatures (24), with mean body temperature taken as 80% of the deep-body, plus 20% of the mean skin temperature (22). In the absence of evidence to the contrary, it was assumed that this weighting would accurately reflect changes in the heat content of a morphologically diverse sample. Mean body temperature change was calculated as the temperature difference between the final 5 min of exercise and the preexercise rest periods.

Cutaneous blood flow.

Limb segment and local cutaneous blood flows were measured simultaneously. Forearm blood flow was determined using a mercury-in-silastic strain gauge placed at the widest girth of the right forearm (EC6 Plethysmograph; D.E. Hokanson, Bellevue, WA). These data were used to represent skin blood flow within the nonapical regions. Venous return was occluded proximal to the elbow by inflating a blood-pressure cuff to 50 mmHg (SC12D cuff; D.E. Hokanson). This was automatically controlled (AG 101 Cuff inflator air source and E20 rapid cuff inflator; D.E. Hokanson) and followed a cycle of 8 s inflated and 12 s deflated, with 3 cycles/min. Data were collected for ∼2.5 min during the final 5 min of each rest and exercise period. A wrist cuff was simultaneously inflated to 20 mmHg above systolic blood pressure prior to data collection to remove artifacts introduced by variations in hand blood flow. This was deflated after each measurement. It was implicitly assumed that, while venous-occlusion plethysmography detects blood flow changes within all vascular beds, those measurements would primarily reflect cutaneous flows in both resting (9, 13) and exercising individuals (26), providing the limb remained inactive. To minimize movement artifacts and to position the limb above heart level, the arm was supported and stabilized at the wrist and upper arm using mesh slings anchored and tensioned at four points to optimize comfort and minimize local-pressure effects.

Laser-Doppler flowmetry (TSI Laserflo BPM2 with a P-435 fiber-optic probe; Vasamedics, St. Paul, MN) was used to estimate local cutaneous (nonapical) blood flow, but within a very small skin volume. The probe was secured (double-sided tape) at the mid point of the left ventral forearm. This location was found to best represent forearm cutaneous blood flow (5), and it was marked to ensure the probe placement was identical between trials. The forearm was stabilized at heart level throughout experimentation. Data were recorded for ∼2.5 min during the final 5 min of rest and exercise. Exercising measurements were expressed as a percentage of the resting (baseline) values. Due to technical difficulties, these measurements were not always recorded (trial 1, n = 33; trial 2, n = 29).

Although blood flow determines the rate of convective heat transfer (mass flow), that flow is a function of both mean arterial pressure and total peripheral resistance. Therefore, to account for flow changes that accompany variations in blood pressure, both forearm and local cutaneous blood flow measurements were also expressed in conductance units, with mean arterial pressure measured immediately prior to the blood flow measurement (MD 777 dual head stethoscope and MDF 808 Calibra pro sphygmomanometer; MDF Instruments, Los Angeles, CA).

Whole-body sweat rate.

Gross mass changes (before and after rest and exercise) were used to approximate whole-body sweat losses (±20 g, fw-150k; A&D Weighing). Data were corrected for fluid replacement and urine production, with respiratory and metabolic mass losses approximated using standard derivations (17). Whole-body sweat rate is often normalized to the body surface area to minimize interindividual variability. However, this can introduce a bias when that relationship varies significantly from linearity, or it does not pass through zero (28, 35). Because the relationship between whole body sweat rate and surface area did not satisfy those criteria, individual sweat rates were normalized using the adjusted regression analysis technique (after 45). This first involved determining the group regression slope between the whole-body sweat rate and body surface area. Normalized sweat rates were then calculated by subtracting individual rates from the product of this regression slope and the difference between each person's surface area and the group mean body surface area (after 43). This practice is critical when one's research objective is to explore realistic associations between physiological and morphological phenomena, for not to do so could lead to impossible physiological circumstances, such as sweat production from beings without mass.

Because the unadjusted sweat losses were also used to derive the rate of evaporative-heat dissipation (17), those data were similarly adjusted. However, all remaining heat exchanges shared an approximate linear relationship with body surface area that passed through, or near to, the origin when expressed in absolute terms (watts, W).

Local sweat rate.

Ventilated sweat capsules (3.16 cm²) were used to simultaneously measure local sweat rates from four sites (dorsal hand, dorsal forearm, upper back [scapula], and forehead) throughout each trial. These were glued to the skin to prevent pressure artifacts (Collodion U.S.P.; Mavidon Medical Products, Lake Worth, FL). Low-humidity air was created by passing room air over an enclosed, saturated, lithium chloride solution housed outside the chamber, with the local air temperature independently measured. Air collected from above this solution will remain at 12% relative humidity over a broad range of temperatures (46) and was pumped through each sweat capsule at flows that ensured the complete evaporation of sweat (600 ml/min), and through tubes long enough to guarantee thermal equilibration with chamber air temperature. Postcapsular (exhaust) air temperatures (thermistors) and humidities (capacitance hygrometers) were continuously sampled downstream (1 m) as part of an integrated sweat monitor system (Clinical Engineering Solutions, NSW, Sydney, Australia). Temperature and humidity sensors were equilibrated prior to experimentation, with sensor calibration preceding experimentation. Data were recorded at 1-s intervals (DAS1602; Keithley Instruments, Cleveland, OH) and used to derive local sweat rates (40).

Sudomotor sensitivity (gain) was calculated for each participant within the 5-min period after sweating first exceeded basal levels, and remained so for at least 5 min. This was determined as the slope of the linear regression relationship between auditory canal temperature and the postthreshold sweating data (6).

Oxygen consumption and carbon dioxide production.

Expired gases and air flows were analyzed continuously (TrueOne 2400; Parvo Medics) and used to derive oxygen consumption, carbon dioxide production, and minute ventilation as 15-s averages. The analyzers were calibrated before each trial using alpha gas standards (15.97% oxygen, 4.03% carbon dioxide, balance nitrogen). Data collection was briefly interrupted (∼2 min) to obtain whole-body mass measurements prior to commencing (20 min) and at the completion (65 min) of exercise.

Indirectly derived heat production and heat exchanges.

Heat production and exchanges were approximated using partitional calorimetry and normalized to each individual's body surface area, unless stated otherwise (W). The exercise duration was set to satisfy the steady-state requirements essential for these calculations to be valid. The first derivation was metabolic rate (M, Eq. 1), expressed in W/m² (29):

$$M=\frac{\left(\dot{\text{V}}{\text{O}}_2\cdot \left[\frac{\left(\text{R}-0.7\right)}{0.3}\cdot 21130+\frac{\left(\text{1}-\text{R}\right)}{0.3}\cdot 19620\right]\right)}{60\cdot A_D}$$ (1)

where: V̇o₂ = rate of oxygen consumption (liter/min STPD), R = respiratory exchange ratio (nondimensional), 21,130 = caloric equivalent of carbohydrate oxidation (J/liter), 19,620 = caloric equivalent of lipid oxidation (J/liter), and A_D = body surface area (after, 12) (m²).

External work rate (W) was controlled to maintain metabolic heat production (H_prod, [M − W]) at ∼135 W/m² or ∼200 W/m² for each participant. This was determined during familiarization and was fine-tuned during every trial from calculations performed at 2-min intervals (Eq. 1). Dry-heat exchanges (H_dry) were calculated as the sum of the radiative and convective exchanges (Eq. 2), expressed in W/m² (29):

$$H_{dry}=h_r\cdot \left({\stackrel{}{\overline{T}}}_{sk}-T_g\right)+h_c\cdot \left({\overline{T}}_{sk}-{\stackrel{}{\overline{T}}}_a\right)$$ (2)

where: T_sk = mean skin temperature (°C), T_g = mean radiant (black globe) temperature (°C), T_a = air temperature (°C), h_c = convective heat-transfer coefficient (taken as 5.476 W·m⁻²·K⁻¹) (17) (W·m⁻²·K⁻¹), and h_r = radiative heat-transfer coefficient (Eq. 3), expressed as W·m⁻²·K⁻¹ (17):

$$h_r=4\epsilon \sigma \cdot \left(A_r/A_D\right)\cdot \left(273.2+{\left(\left({\overline{T}}_{sk}-{\stackrel{}{T}}_g\right)/2\right)}^3\right)$$ (3)

where: ε = emissivity of the body surface (assumed to be 0.95) (nondimensional), σ = Stefan-Boltzmann constant (5.67 × 10⁻⁸) (W·m⁻²·K⁻⁴), and A_r/A_D = ratio of the effective radiative area of the body (A_r) and body surface area (assumed to be 0.73) (15) (nondimensional).

Convective (C_res) and evaporative (E_res) heat exchanges within the respiratory tract were derived from metabolic heat production rate, the air temperature, and absolute ambient air humidity (P_a [kPa]) (Eq. 4), expressed as W/m² (17):

$$C_{res}+E_{res}=\left(0.0014\cdot H_{prod}\right)\cdot \left(34-T_a\right)+\left(0.00173\cdot H_{prod}\right)\cdot \left(5.87-P_a\right)$$ (4)

Measurements of whole-body mass loss (in grams, g), corrected for fluid intake, urine production, and respiratory (Eq. 5; expressed in grams) and metabolic (Eq. 6; expressed in grams) mass losses (17), were used to determine evaporative-heat loss (latent heat of evaporation, 2,426 J/g) normalized to the body surface area (W/m²). It was assumed all mass changes reflected fluid losses. It was also assumed that the thermal energy for this phase change was taken wholly from the skin, although this assumption is less valid in hotter states.

$$\text{Evaporative mass loss from respiration}=E_{res}\cdot \left(t/2426\right)$$ (5)

where: E_res = evaporative-heat loss through respiration (W/m²), t = time period of each measurement (s), and 2,426 = latent heat of sweat vaporization (J/g).

$$\text{Metabolic mass loss}=t\cdot \left(\left(\dot{V}{O}_2\cdot \left(44\cdot R-32\right)/22.4\right)\right)$$ (6)

The evaporative requirement for heat balance [E_req; Eq. 7; expressed in W/m² (17)] was determined by subtracting the metabolic heat-production rate from the sum of the dry, and convective and evaporative respiratory heat exchanges

$$E_{req}=H_{prod}-\left(H_{dry}+C_{res}+E_{res}\right)$$ (7)

Design and Analysis

This study was based on a single-factor, repeated-measures design (metabolic heat production: rest and two exercise intensities). With the exception of whole-body sweat secretion, data were collected throughout and averaged over the final 5 min of each steady-state period. Differences in resting physiological responses were evaluated using paired t-tests. Relationships between the physiological responses and variations in the mass-specific surface area were assessed using Pearson's correlation coefficient and classified as being of a weak, moderate, or strong effect size (r ≤ 0.10, r = 0.3, and r ≥ 0.5, respectively) (4).

Hierarchical, multiple-linear regression analyses were also performed on the thermoeffector responses that shared significant relationships with mass-specific surface area. Two predictive models were used. Model 1 incorporated the mean body temperature change, peak oxygen consumption, and the height-adjusted sum of skinfolds. These were the design-controlled variables. For model 2, these three variables were combined with the mass-specific surface area. Changes in the coefficients of determination (r²) between these two models represented the proportion of thermoeffector variance that could be independently explained by differences in mass-specific surface area, after first accounting for individual variations in the three design-controlled variables. This was another critical design feature that allowed for isolating the influence of morphological variations on the modulation of these thermoeffector functions, and these two models were compared using ANOVA. An a priori power analysis indicated that the minimum sample size required to detect a change in the coefficient of determination between models of large effect size (Cohen's f², 0.35), and with at least 80% statistical power, was 28 subjects (4). Therefore, with the current sample (n = 36), these regression analyses were adequately powered (>80%) at the large-effect-size level. Test assumptions of normality, linearity, and homoscedasticity were determined by inspecting quantile-comparison, scatter, and residual plots. Collinearity, as assessed using the variance inflation factor, was minimal between independent variables (range, 1.024–1.710). For all statistical comparisons, α was set at 0.05 with data reported as means ± SE, unless stated otherwise (SD).

RESULTS

Subject characteristics.

To enable a thorough evaluation of the morphological dependence of thermoeffector function, it was essential that subjects spanned a sufficiently wide range of body sizes. Subjects differed by almost 40 kg in mass and ∼0.7 m² in surface area, with pronounced variations in the mass-specific surface area (Table 1), with an even distribution across that range (Fig. 1). The height-adjusted sums of skinfolds, however, were similar among participants (Table 1), placing subjects between the 40th to 60th percentiles of the age- and gender-specific normative distribution for relative adiposity (2).

Indirectly derived heat production and heat exchanges.

By design, metabolic heat production was fixed at an equivalent surface area-dependent intensity for all participants (light work, 139 W/m² [SD 7]; moderate work, 207 W/m² [SD 11]). Accordingly, neither external work (21 [±0, light] and 61 W/m² [±1, moderate]) nor metabolic heat production differed significantly with variations in mass-specific surface area during light (P = 0.26 and P = 0.28, respectively) or moderate work (P = 0.51 and P = 0.76, respectively). This meant that each individual had the same relative heat-loss requirement, despite large variations in body size. To the best of our knowledge, this is the first investigation in which this has been achieved.

The dry- and evaporative-heat losses (Eqs. 2 and 7), as well as the evaporative requirement for heat loss, were also similar among individuals (Table 2) and were not significantly correlated with mass-specific surface area during light (P = 0.84, P = 0.72, and P = 0.45, respectively) or moderate work (P = 0.28, P = 0.28, and P = 0.35, respectively). That outcome verified the size-independent nature of these variables across subjects. When these heat exchanges were expressed in absolute terms (W), however, each displayed a strong, negative relationship with the specific surface area (Table 3, all P < 0.01). Because the metabolic heat-production rate was a function of body surface area, then the absolute heat production was greater in those with a lower specific surface area. It was therefore expected that the absolute rates of dry- and evaporative-heat loss, as well as the rate of evaporative-heat loss required to maintain heat balance, would also be greater in those larger individuals.

Table 2.

Heat exchanges, body temperatures, cutaneous blood flows and sudomotor responses during light and moderate exercise

	Light Work	Moderate Work
Heat exchange, W/m2
Dry-heat loss, Eq. 2	50 ± 1	56 ± 3
Evaporative-heat loss, mass change	63 ± 3	162 ± 8
Evaporative heat-loss requirement, Eq. 7	83 ± 1	142 ± 2
Body temperature, °C
Auditory canal temperature	37.0 ± 0.0	37.2 ± 0.1
Mean skin temperature	33.3 ± 0.1	33.9 ± 0.1
Mean body temperature	36.3 ± 0.0	36.6 ± 0.0
Cutaneous blood flow
Forearm, ml·100 ml−1·min−1	5.29 ± 0.15	8.46 ± 0.38
Local, % of initial resting value*	145.7 ± 13.4	293.1 ± 18.1
Cutaneous vascular conductance
Forearm, ml·100 ml−1·min−1·mmHg−1	0.06 ± 0.00	0.08 ± 0.00
Local, % of initial resting value*	134.4 ± 13.0	345.3 ± 21.3
Local sweat rate, mg·cm−2·min−1
Dorsal hand	0.60 ± 0.06	2.02 ± 0.09
Dorsal forearm	0.27 ± 0.03	1.27 ± 0.07
Upper back	0.32 ± 0.04	1.38 ± 0.10
Forehead	0.56 ± 0.06	2.55 ± 0.17
Sudomotor sensitivity, mg·cm−2·min−1·°C−1
Dorsal hand	2.74 ± 0.26	3.22 ± 0.18
Dorsal forearm	1.73 ± 0.16	2.32 ± 0.16
Upper back	1.79 ± 0.24	2.35 ± 0.18
Forehead	2.71 ± 0.28	4.12 ± 0.26

Values are given as means ± SE. Light work consisted of exercise at approximately 135 W/m² (n = 36); moderate work occurred at approximately 200 W/m² (n = 35). Subjects performed two trials (28°C, 37% relative humidity), each commencing with seated rest (20 min) followed by either light or moderate (45 min) exercise.

^*Local cutaneous blood flows (laser-Doppler flowmetry) and vascular conductances were not determined in all participants (light work n= 33 and moderate work n = 28).

Table 3.

Correlation coefficients between mass-specific surface area and indirectly derived heat exchanges, and sudomotor sensitivity during light and moderate exercise

	Light Work	Moderate Work
Heat production and exchange, W
Metabolic heat production, metabolic − external work rate	−0.64	−0.67
Dry-heat loss, Eq. 2	−0.51	−0.55
Evaporative-heat loss, mass loss	−0.55	−0.73
Evaporative heat-loss requirement, Eq. 7	−0.48	−0.56
Sudomotor sensitivity, mg·cm−2·min−1·°C−1
Dorsal hand	−0.46	−0.42
Dorsal forearm	−0.33	−0.37
Dorsal forehead	−0.47	−0.51

Only correlations that were statistically significant are included (P < 0.01). Negative correlations between heat exchanges expressed in absolute terms and mass-specific surface area were expected, and reflect the increases in body surface area that accompany decreases in mass-specific surface area. Correlations between heat exchanges normalized to body surface area and the mass-specific surface area did not approach significance (P > 0.05).

Body temperature.

Resting deep-body, mean skin, and mean body temperatures (including standard errors) were identical across both trials: 36.8 ± 0.1, 33.2 ± 0.1, and 36.1 ± 0.1°C (P = 0.85, P = 0.63, and P = 0.90, respectively). Body temperatures were also similar among individuals during both light and moderate work (Table 2) and exceeded air and radiant temperatures. This permitted dry-heat transfer to the ambient medium, thereby satisfying the first experimental design criterion. While deep-body temperature shared significant relationships with the mass-specific surface area during light work (r = 0.36, P = 0.03), mean skin and mean body temperatures did not (P = 0.82 and P = 0.09, respectively). During moderate work, none of those temperatures was significantly related to the mass-specific surface area (P = 0.33, deep body; P = 0.22, mean skin; and P = 0.77, mean body). As a consequence of the experimental design, the exercise-induced changes in mean body temperature (0.2°C ± 0.0 [light] and 0.4°C ± 0.0 [moderate]) were similar across individuals within each state, and remained clamped throughout (Fig. 1B), and unrelated to specific surface area (P = 0.33 and P = 0.65, respectively). Thus interindividual differences in thermoeffector function could now be uniquely evaluated against a background of matched thermoafferent flow across participants.

Cutaneous blood flow.

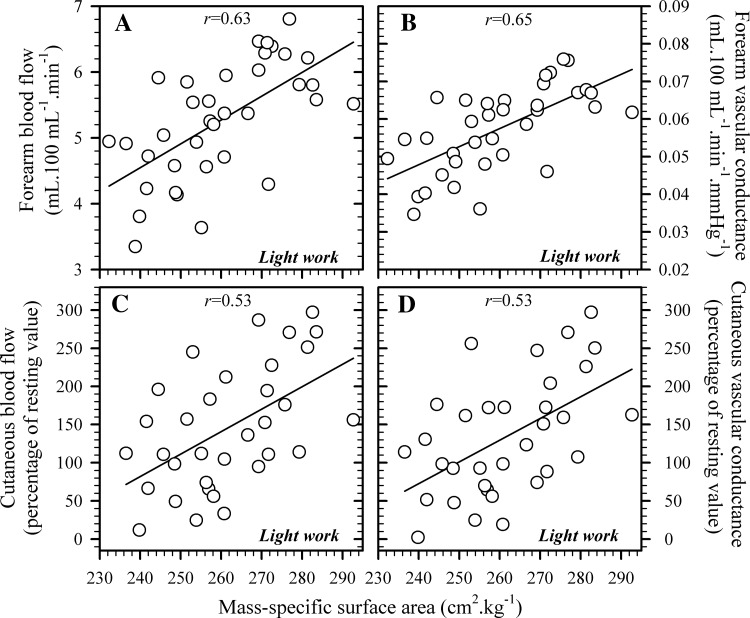
Resting forearm blood flows (3.68 ± 0.18 [light work] and 3.89 ± 0.18 ml·100 ml⁻¹·min⁻¹ [moderate work]) and forearm vascular conductances (0.04 ± 0.00 [light work] and 0.04 ± 0.00 ml·100 ml⁻¹·min⁻¹·mmHg⁻¹ [moderate work]) did not differ significantly between trials (P = 0.25 and P = 0.31, respectively), but varied widely during exercise (Table 2). During light work, both forearm blood flow and vascular conductance, as well as local cutaneous blood flow and cutaneous vascular conductance, displayed strong, positive associations with the mass-specific surface area (all P < 0.01, Fig. 2). However, none of those relationships was significant during moderate work (all P > 0.05).

Fig. 2.

Relationships between mass-specific surface area and forearm blood flow (A: strain-gauge plethysmography, n = 36) and forearm vascular conductance (B), as well as local cutaneous blood flow (C) (laser-Doppler flowmetry, n = 33) and local cutaneous vascular conductance (D) during light work. Data were collected during steady-state exercise (45 min at ∼135 W/m²) following 20 min of resting, thermal equilibration (28°C, 37% relative humidity), and are presented as means for each subject over the final 5 min of exercise. Solid lines are least-squares, best-fit, linear regressions, with all correlations being significant (P < 0.05).

Hierarchical regression analysis was used to identify variations in cutaneous blood flow that could be explained by the design-controlled variables alone (model 1: mean body temperature change, peak oxygen consumption, and the height-adjusted sum of skinfolds), as well as the additional variance that could be accounted for solely on the basis of variations in the mass-specific surface area (model 2, Table 4). Model 1 was not a significant predictor of the cutaneous vascular responses (Table 4). Model 2, however, provided a significant prediction of those responses during light work. Indeed, the specific surface area alone could respectively account for 43% and 46% of the individual variations within forearm blood flow and vascular conductance (both P < 0.01) and for 24% and 27% of the local cutaneous blood flow and vascular conductance variability (Table 4, P = 0.02 and P = 0.03, respectively). Although during moderate work, which was aimed at forcing evaporative-heat loss to dominate, neither model significantly predicted those vascular responses (Table 4).

Table 4.

Coefficients of determination and their changes for two regression models used to predict forearm and local cutaneous blood flow and vascular conductance during light and moderate exercise

			Slope Coefficients
Dependent Variable	Model	Intercept, Constant	ΔT̄b	∑skf	V̇o2peak	Specific AD	r2	Δr2
Light work
Forearm blood flow	1	4.81	0.90	0	0.01		0.03
	2	−9.44	0.13	0.02	0.02	0.05	0.46*	0.43†
Local cutaneous blood flow	1	223.57	133.73	−0.85	−0.75		0.08
	2	−770.40	90.62	0.77	0.40	3.14	0.32*	0.24†
Forearm vascular conductance	1	0.04	0.02	0	0		0.05
	2	−0.15	<0.01	0	0	<0.01	0.51*	0.46†
Local cutaneous vascular conductance	1	223.49	86.45	−0.65	−0.90		0.05
	2	−782.49	48.82	0.99	0.26	3.181	0.31*	0.27†
Moderate work
Forearm blood flow	1	11.44	−4.03	0.01	−0.02		0.07
	2	−6.24	−3.73	0.04	<−0.01	0.06	0.18	0.11
Local cutaneous blood flow	1	448.31	−55.00	−0.80	−1.09		0.02
	2	−428.60	−51.16	0.84	0.13	2.64	0.13	0.11
Forearm vascular conductance	1	0.10	−0.05	0	0		0.10
	2	−0.11	−0.05	0	0	<0.01	0.24	0.14†
Local cutaneous vascular conductance	1	551.15	−8.41	−1.28	−1.66		0.02
	2	−512.93	−3.75	0.72	−0.18	3.20	0.14	0.12

r², coefficient of determination; Δr², change in the coefficient of determination. Model 1 included the change in mean body temperature (ΔT̄_b), height-adjusted sum of skinfolds (∑skf), and peak oxygen consumption (V̇o_2peak); model 2 included those variables and the mass-specific surface area (specific A_D).

^*Significant predictors of thermoeffector responses; † significant changes in r² between the two models (P < 0.05). Local cutaneous blood flows and vascular conductances were not determined in all participants (see methods). Light work n = 33; moderate work n = 28.

Whole-body and local sweat secretion.

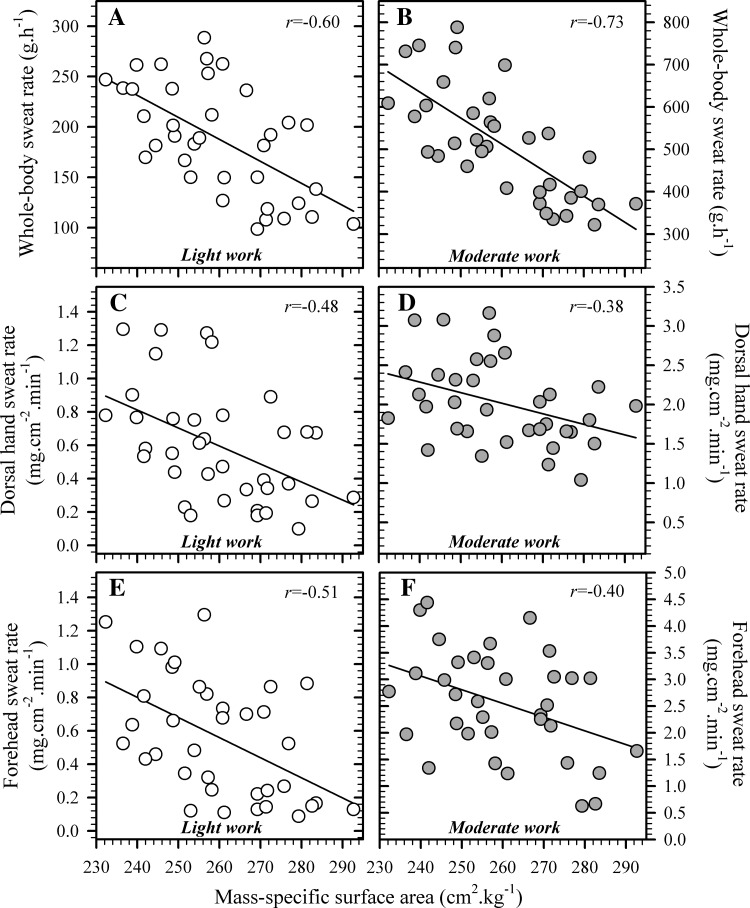
Steady-state sweating responses are shown in Table 2, with the whole-body sweat rate during light work (188 ± 9 g/h) and moderate work (513 ± 22 g/h) sharing strong, negative associations with mass-specific surface area (Fig. 3, both P < 0.01). Those outcomes were predictable because heat production rates were set as a function of the body surface area, and this caused systematic increases in absolute heat production in individuals with a lower specific surface area, and increased the absolute evaporative heat-loss requirement for larger subjects. However, when the whole-body sweat rate was normalized to body surface area, it was not significantly associated with the mass-specific surface area during either light (P = 0.12) or moderate work (P = 0.31).

Fig. 3.

Relationships between mass-specific surface area and whole-body sweat rate (A and B), local sweat rate at the dorsal hand (C and D) and forehead (E and F) during light (∼135 W/m², n = 36) and moderate work (∼200 W/m², n = 35). Data were collected during steady-state exercise (45 min) that proceeded 20 min of resting, thermal equilibration (28°C, 37% relative humidity), and are means for each individual over the final 5 min of exercise. Solid lines are least-squares, best-fit, linear regressions, with all correlations being significant (P < 0.05).

Local sweat rates at the dorsal hand and forehead shared moderate, negative relationships with mass-specific surface area during both light and moderate work (Fig. 3, all P < 0.05). Sweat rate at the dorsal forearm, however, demonstrated this association only during light work (r = −0.56, P < 0.01), whereas upper-back sweating was not significantly related to this morphological description in either state (light, P = 0.25; moderate, P = 0.71). Sudomotor sensitivities at the dorsal hand, dorsal forearm, and forehead, but not the upper back, were also negatively associated with specific surface area during both work rates (Table 3, all P < 0.05).

When the same prediction models were evaluated with regard to sweat secretion, the controlled variables (model 1) significantly predicted the whole-body sweat rate and local sweating from the dorsal forearm during light work (P = 0.01 and P = 0.02, respectively), as well as sudomotor sensitivity at the dorsal hand during moderate work (Table 5, P = 0.03). Model 2 significantly predicted sweat secretion and sudomotor thermosensitivity at three of the four local sites during light work (Table 5, all P < 0.05), with the mass-specific surface area alone accounting for between 17 and 24% of that variation (Table 5, all P < 0.05). During moderate work, model 2 predicted whole-body sweat rate and sudomotor sensitivity at the dorsal hand and forehead only (Table 5; P < 0.01, P < 0.01, and P = 0.03, respectively). Moreover, between 10 and 53% of the interindividual variations in those responses, and 13% of the variations in local sweat secretion at the forehead, could be explained independently by variations in the mass-specific surface area (Table 5, all P < 0.05).

Table 5.

Coefficients of determination and their changes for two regression models used to predict sudomotor responses during light and moderate exercise

			Slope Coefficients
Dependent Variable	Model	Intercept, Constant	ΔT̄b	∑skf	V̇o2peak	Specific AD	r2	Δr2
Light work
Whole-body sweat rate	1	61.97	−166.48	1.23	1.17		0.28*
	2	669.97	−133.66	0.10	0.57	−1.95	0.51*	0.23†
Dorsal hand sweat rate	1	−0.65	−0.49	0.01	0.01		0.24*
	2	1.60	−0.37	0.01	0.01	−0.01	0.31*	0.07
Dorsal forearm sweat rate	1	−0.21	−0.48	<0.01	<0.01		0.26*
	2	1.54	−0.39	<0.01	<0.01	−0.01	0.43*	0.17†
Forehead sweat rate	1	0.07	−0.55	0.01	<0.01		0.09
	2	3.88	−0.35	<−0.01	0	−0.01	0.28*	0.19†
Dorsal hand thermosensitivity	1	4.08	−2.50	<−0.01	−0.01		0.05
	2	22.38	−1.51	−0.03	−0.03	−0.06	0.29*	0.24†
Dorsal forearm thermosensitivity	1	1.84	−2.36	0.01	<0.01		0.11
	2	8.74	−2.01	−0.01	−0.01	−0.02	0.19	0.09
Forehead thermosensitivity	1	−0.29	−1.16	0.03	0.02		0.06
	2	16.29	−0.26	<−0.01	<0.01	−0.05	0.24	0.18†
Moderate work
Whole-body sweat rate	1	228.51	33.77	2.02	1.97		0.04
	2	2,514.69	−5.16	−2.15	−0.59	−7.05	0.57*	0.53†
Dorsal hand sweat rate	1	−0.06	0.35	0.01	0.03		0.12
	2	3.33	0.30	0.01	0.01	−0.01	0.19	0.07
Dorsal forearm sweat rate	1	0.04	−0.14	0.01	0.01		0.09
	2	2.17	−0.18	0.01	0.01	−0.01	0.13	0.04
Forehead sweat rate	1	1.20	−0.49	0.01	0.01		0.04
	2	9.98	−0.64	<−0.01	0	−0.03	0.17	0.13†
Dorsal hand thermosensitivity	1	1.65	−2.69	0.03	0.02		0.25*
	2	9.73	−2.83	0.01	0.01	−0.03	0.35*	0.10†
Dorsal forearm thermosensitivity	1	−0.10	0.15	0.02	0.01		0.11
	2	5.53	0.05	0.01	0.01	−0.02	0.16	0.04
Forehead thermosensitivity	1	−0.44	0.40	0.02	0.04		0.06
	2	17.16	0.10	−0.01	0.02	−0.05	0.29*	0.23†

r², coefficient of determination; Δr², change in coefficient of determination. Model 1 included the change in mean body temperature (ΔT̄_b), height-adjusted sum of skinfolds (∑skf), and peak oxygen consumption (V̇o_2peak), whereas model 2 included those variables as well as the mass-specific surface area (specific A_D).

^*Significant predictors of thermoeffector responses; † significant changes in r² between the two models (P < 0.05).

DISCUSSION

This study is believed to be the first that was designed to provide a comprehensive evaluation of the morphological dependency of human heat-loss responses, while controlling for other factors known to modulate those mechanisms. Thus, thermoeffector responses were simultaneously assessed in individuals with similar endurance exercise habits and whole-body relative adiposity, but with considerably different body sizes, during standardized heat-production rates and equivalent surface-area specific, heat-loss requirements. This level of control produced almost identical mean body temperature changes that were also independent of body size. This was essential to test the hypothesis that cutaneous vasomotor function would be positively linked to the mass-specific surface area, whereas sudomotor responses would be inversely related to that ratio. As hypothesized, individuals with a greater specific surface area were able to rely more heavily on changes in cutaneous blood flow during light work. Conversely, those with a lower mass-specific surface area, but greater body mass, were more reliant upon sweating, and this was most evident during moderate work. Indeed, both sweat secretion and sudomotor sensitivity at three of the four measured sites were significantly linked to the specific surface area. Moreover, that morphological characteristic alone accounted for a significant, albeit modest, proportion of the interindividual variation in these responses.

These observations are important because the extent to which these effector responses were a simple function of morphology, and the first principles governing heat exchange, has remained uncertain. Others have identified the ratio between body surface area and mass as a key determinant of deep-body temperature change during exercise at matched absolute work rates (10, 14, 34). Those findings can be ascribed to the use of the same absolute work rates, which elicited a greater heat-loss requirement in people with a lower mass-specific surface area (7). Although work intensities set relative to the maximal aerobic power (11, 21, 16) or body mass (7) of participants reduces that variability, the former standardization increases the area-specific heat production in those with greater aerobic fitness, whereas the latter elevates the area-specific heat production in individuals with a lower specific surface area. In the current study, exercise was completed at heat-production rates normalized to the body surface area. With this design, equal heat-loss requirements were induced across all individuals while variations in the secondary factors that independently influence thermoeffector function were minimized. These strategies resulted in approximately equal mean body temperature changes across all participants (Table 2, Fig. 1B) despite large variations in body mass (Table 1). This unique approach permitted an independent evaluation of the effect of body morphology in determining which thermoeffector function might provide more effective heat loss.

Under most thermal states, objects with a greater mass-specific surface area exchange dry heat more readily, and this supports thermoregulation during light work when the ambient temperature is below skin temperature (10, 33, 47). It was therefore expected that smaller individuals would be less reliant on evaporative cooling and more dependent on the vasomotor-mediated, dry-heat exchanges to regulate body temperature. That prediction was realized during light work, with cutaneous blood flow possessing a positive relationship with the specific surface area, and accounting for up to 46% of the interindividual variation (Fig. 2, Table 4). That outcome may have a significant occupational relevance. Since workers are expected to operate with minimal physiological and psychological impediments within warm-humid conditions, then those with a larger mass-specific surface area may have superior tolerance.

While cutaneous blood flow increases in smaller individuals should have been accompanied by greater radiative and convective heat dissipation, the dry-heat losses derived using partitional calorimetry were surprisingly similar among individuals when normalized to body surface area (Table 2) and were unrelated to the mass-specific surface area. That outcome was most likely due to those approximations lacking the necessary sensitivity and precision to detect individual differences in the autonomically mediated dry-heat losses, even though steady-state requirements were satisfied. To test this, whole-body calorimetric evaluations of heat exchange are required.

It was also hypothesized that larger individuals (smaller mass-specific surface area) would be forced to rely more heavily on evaporative cooling. That hypothesis was also accepted (Fig. 3, Table 5). Moreover, specific surface area was a principal determinant of whole-body sweating during moderate work, explaining more than half of the interindividual variation (Table 5). Nevertheless, that association was caused by an elevated absolute evaporative requirement in those with a lower specific surface area (Table 3), which increases whole-body sweating (18). Therefore, when the effects of body surface area were removed, whole-body sweat rate was not significantly related to the mass-specific surface area.

Despite those similarities, local sweat rate and sudomotor thermosensitivity at the dorsal hand, dorsal forearm, and forehead shared moderate negative relationships with the mass-specific surface area (Fig. 3, Table 3). Furthermore, that ratio explained 10–24% of the interindividual variation in those responses (Table 5). Consequently, individuals with a lower specific surface area needed to maintain higher local sweat rates to meet their total heat-loss requirements. Indeed, it is quite possible that, under similar environmental and exercise conditions, gender-related differences in thermoeffector responses can be partially explained on the basis of these morphological attributes, and that possibility is currently being investigated. Although such individuals possess a larger fluid reservoir (44), they may be disadvantaged during prolonged exercise unless fluid consumption matches sweat losses.

It has been suggested that size-dependent variations in local sweat rates might be reduced by prescribing work intensities on the basis of the area-standardized evaporative cooling required to balance metabolic heat production (3, 7, 8); a partitional calorimetric derivation (Eq. 7). The current authors were conceptually supportive of that, perhaps overly complex, solution. Nevertheless, in our hands, that method did not fully remove the affect of body size, with sweating at three of the four sites measured being significantly related to the mass-specific surface area (Table 3, Fig. 3), despite similarities in the area-specific evaporative requirement (Table 2). That discrepancy may be explained by the well known limitations of using local sweating to approximated whole-body sudomotor function (39). For instance, Cramer and Jay (7) measured local sweating at just two sites (upper back and forearm), with Cramer and Jay (8) reporting just one site (forearm), even though the intersite sudomotor variability is extensive before (39) and after heat adaptation (30). Thus those selections may have introduced a bias because, in the current study, the relationship between mass-specific surface area and upper-back sweat secretion did not approach significance, whereas the only significant association with forearm sweating was evident during light work. Indeed, the strongest associations with specific surface area were observed at the dorsal hand and forehead (Fig. 3). Therefore, apparent size-independent local sweat rates may not be representative of the interaction between whole-body sweating and morphology. Instead, such responses may actually represent an atypical phenomenon, depending upon where the sweat capsules are located.

Finally, the aim of this project was to minimize extraneous influences on the autonomic control of heat loss by uncovering biophysical factors that independently modulate both the passive and active heat-loss mechanisms. It was anticipated that a thermoeffector recruitment cascade might exist, with the transition from one mechanism to the next being determined by the effectiveness of each step, such that progressive heat storage might precipitate a sequential activation of these effectors, with larger individuals progressing rapidly and more fully from vasomotor to sudomotor pathways. To explore that possibility, thermally compensable conditions were required. While the strength of this morphological explanation was only moderate (46% for vasomotor and 10–24% for local sudomotor functions), it represents the foundation upon which layers of genetic and phenotypic variations exist (e.g., exercise, heat adaptation), thereby further increasing the explained variance.

Conclusions.

When challenged through matched increments in mean body temperature, participants with a broad range of body sizes revealed a morphological dependency in the activation of dry (vasomotor) and evaporative (sudomotor) heat-loss mechanisms. To maintain heat balance under these compensable conditions, smaller individuals (higher mass-specific surface area) were more dependent on the vasomotor pathway, with forearm and cutaneous blood flows and vascular conductances sharing positive associations with mass-specific surface area during light work. Indeed, ∼45% of the variation in forearm blood flow and conductance could be explained on the basis of interindividual differences in specific surface area. On the other hand, a moderate negative association was observed with sweat secretion, indicating that larger individuals were obliged to be more reliant on the sweating mechanism, with 10–53% of that variance being morphologically dependent. This outcome may provide mechanistic explanations for thermoregulatory differences observed between men and women, as well as children and adults, under thermally compensable conditions. Finally, it appears that the best way to elicit isothermal work rates in diverse population samples is to standardize work rates to the body surface area.

GRANTS

S. Notley was supported by a University of Wollongong Postgraduate Award.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

S.R.N., N.O., and N.A.S.T. conception and design of research; S.R.N., J.P., K.T., and N.O. performed experiments; S.R.N. analyzed data; S.R.N., N.O., and N.A.S.T. interpreted results of experiments; S.R.N. prepared figures; S.R.N. and N.A.S.T. drafted manuscript; S.R.N., J.P., K.T., N.O., and N.A.S.T. edited and revised manuscript; S.R.N., J.P., K.T., N.O., and N.A.S.T. approved final version of manuscript.