Tissue-specific regulatory circuits reveal variable modular perturbations across complex diseases

Abstract

Mapping the molecular circuits that are perturbed by genetic variants underlying complex traits and diseases remains a great challenge. We present a comprehensive resource of 394 cell type and tissue-specific gene regulatory networks for human, each specifying the genome-wide connectivity between transcription factors, enhancers, promoters and genes. Integration with 37 genome-wide association studies (GWASs) shows that disease-associated genetic variants — including variants that do not reach genome-wide significance — often perturb regulatory modules that are highly specific to disease-relevant cell types or tissues. Our resource opens the door to systematic analysis of regulatory programs across hundreds of human cell types and tissues.

Introduction

Genome-wide association studies (GWASs) have successfully identified thousands of genetic loci associated with complex traits and diseases. However, translating these findings into a functional understanding of disease processes remains a major challenge, notably because the effect of individual trait-associated variants is typically minute, underlying mechanisms are generally cell type-specific^1–3, and most variants lie in poorly understood noncoding regions of the genome⁴.

Integration of regulatory genomics data is emerging as a promising strategy to address these challenges: it has been shown that GWAS variants enrich in regulatory regions of cell types that are relevant to the pathophysiological basis of a given trait^5,6, and regulatory annotations have been used to prioritize and fine-map GWAS loci^7–9. However, these studies do not consider the inter-play between variants at the pathway and network level. Pathway- and network-based approaches, on the other hand, have been successful at identifying relevant pathways or modules based on the connectivity between trait-associated genes, but current studies typically rely on protein-protein interaction^10,11, co-expression¹² or functional association networks¹³ lacking fine-grained regulatory and, with few exceptions^14–16, tissue-specific information. Indeed, a suitable compendium of tissue-specific regulatory circuits was previously not available, as most studies focused on building gene regulatory networks either globally^17–19 or for a single tissue or condition of in terest^20–22.

Here we introduce a unique resource of 394 cell type and tissue-specific gene regulatory networks for human. We infer networks by integrating transcription factor (TF) sequence motifs with promoter and enhancer activity data from the FANTOM5 project^23,24 (Fig. 1a,b) and validate edges using ChIP-seq, eQTL and RNA-seq data. We find that GWAS variants often perturb genes that are clustered within specialized regulatory circuits of trait-relevant tissues (Fig. 1c). While previous studies have established the value of disease-specific gene networks²⁵, the present resource of 394 regulatory circuits enables systematic analysis of the fine-scale mechanism of driver genes across cell types and tissues. All networks and tools are freely available at: http://regulatorycircuits.org.

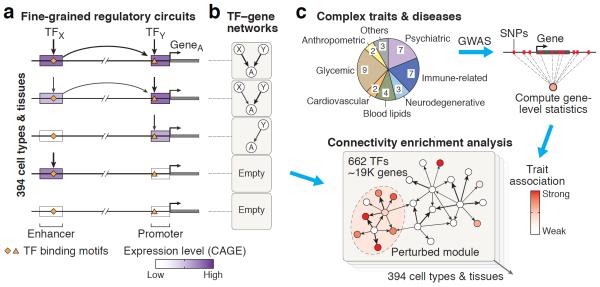
Figure 1. Inference of regulatory circuits and connectivity between trait-associated genes.

(a) The resource of 394 cell type and tissue-specific regulatory circuits is based on expression profiles of CAGE-defined enhancers and promoters from the FANTOM5 project^23,24. Weighted, tissue-specific links between TFs and regulatory elements (enhancers and promoters) are inferred using TF binding motifs and tissue-specific expression of target elements. Links between regulatory elements and target genes are inferred based on genomic distance and joint expression in the given tissue. Different circuit configurations are shown schematically for five tissues. For clarity only one enhancer and promoter are shown, but genes typically have multiple tissue-specific enhancers and promoters. (b) In order to summarize which TFs regulate which genes, we also define coarse-grained TF–gene networks that encapsulate the fine-grained circuitry of enhancers and promoters. (c) We systematically assess the interconnectivity of genes that are perturbed by trait-associated variants within our networks for a large panel of 37 GWASs. Our pipeline first integrates GWAS summary statistics at the level of genes using Pascal⁴¹, a tool that accurately corrects for confounders such as linkage disequilibrium, and then evaluates whether top ranked genes tend to cluster in network modules based on a random-walk graph kernel (connectivity enrichment analysis, Methods and Supplementary Figs. 27–30). Importantly, this approach does not use a cutoff for the GWAS p-values and thus also assesses the contribution of weakly associated variants. We apply this pipeline to pinpoint cell type or tissue-specific regulatory networks where modules are perturbed for different traits and diseases.

Results

Cell type and tissue-specific gene regulatory circuits

Our pipeline to reconstruct transcriptional regulatory circuits involves: (1) genome-wide mapping of promoters and enhancers, (2) linking TFs to promoters and enhancers, and (3) linking enhancers and promoters to target genes (Fig. 1a, Methods). Here, we applied this approach to data from the FANTOM5 consortium^23,24, which has performed cap analysis of gene expression (CAGE) for ~1000 human primary cell, tissue and cell line samples. CAGE maps regions of transcription initiation with high resolution and sensitivity, enabling the identification of both active promoters and enhancers (active enhancers are transcribed at low levels, resulting in a CAGE signature of bidirectional transcription initiation²⁴). In order to identify regulatory inputs of promoters and enhancers, we used a curated collection of sequence binding motifs for 662 TFs^26,27. We found >10-fold enrichment of these TF motifs within CAGE-defined promoters and distal enhancers, supporting the FANTOM5 data (Methods, Supplementary Figs. 1–3).

We used this pipeline to infer 394 weighted, transcriptional regulatory circuits, including 146 different cell types, 111 tissues, and 137 cell lines (Supplementary Table 1, Supplementary Figs. 4–5). Each circuit has up to 662 TFs, 41K enhancers, 59K promoters, and 43K gene isoforms from 19K protein-coding genes. Enhancers and promoters are regulated by a median number of 16 TFs, and on average gene isoforms receive inputs from two distinct promoters and five enhancers (Supplementary Figs. 6–8).

Validation of regulatory circuits using independent ChIP-seq, eQTL and RNA-seq data

While systematic validation of our regulatory circuits is difficult because the ground truth is not known²⁸, independent datasets that support regulatory edges are available for a subset of cell lines and tissues. First, we assessed the inferred TF–enhancer and TF–promoter edges using TF binding data (ChIP-seq) for 59 TFs in five cell lines from ENCODE (Supplementary Table 2). Overall, about half of the TF edges were confirmed by a corresponding ChIP-seq peak, which is not far off the reproducibility of the ChIP-seq data themselves (Fig. 2a, Supplementary Figs. 9–10).

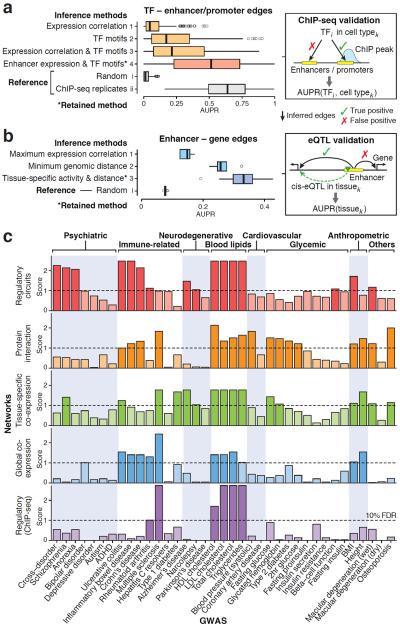
Figure 2. Assessment of regulatory circuits.

(a) Evaluation of different approaches to infer edges between TFs and regulatory elements (enhancers and promoters): (1) standard network inference based on expression correlation between TFs and regulatory elements across samples; (2) presence of TF motifs within regulatory elements; (3) presence of TF motifs, weighted by expression correlation; and (4) presence of TF motifs, weighted by target element expression in the given cell type (the retained method to reconstruct regulatory circuits). For each TF and cell type where ChIP-seq data was available (159 samples, including 59 TFs and five cell lines), the area under the precision-recall curve (AUPR) was computed. As reference, AUPR values were also computed for (i) random data and (ii) replicates of ChIP-seq experiments. Boxplots show the distribution of AUPR values for each method. The retained method (*) achieves a median AUPR of 0.51, which is significantly better than alternative methods (p < 10⁻¹⁵, one-sided Wilcoxon rank-sum test) and the performance is close to that of of ChIP-seq replicates (median AUPR=0.64). (b) Assessment of different approaches to link enhancers to target genes: (1) maximum expression correlation across tissues (assign enhancer to most strongly correlated gene within 500kb); (2) minimum genomic distance (assign enhancer to closest gene); and (3) joint tissue-specific activity (defined as geometric mean of enhancer and gene expression) weighted by genomic distance (the retained method to construct regulatory circuits). AUPR was evaluated for each method as well as random predictions in 13 tissues where eQTL data were available. The retained method (*) has a median AUPR of 0.33, which is significantly better than alternative methods (p < 0.05, one-sided Wilcoxon rank-sum test). Of note, AUPR values are only comparable within each panel, not across panels (a) and (b) because the underlying gold standards are different (Methods). (c) Evaluation of whether trait-associated genes tend to cluster within modules for different types of networks and GWAS traits. Five types of networks are compared: (1) cell type and tissue-specific regulatory networks (the 32 high-level networks defined in Supplementary Fig. 14), (2) four protein-protein interaction networks, (3) 35 tissue-specific co-expression networks¹⁵, (4) a global co-expression network inferred from the FANTOM5 data, and (5) a global regulatory network based on ChIP-seq¹⁷ (Methods). In addition, tissue-specific regulatory networks based on DNaseI footprints⁴² were assessed, but did not show any significant enrichment. The plot summarizes whether trait-associated genes are more densely interconnected than expected (maximum connectivity enrichment score) for each network type (row) and trait (column). The scores correspond to the negative log of the q-values. (False discovery rate (FDR) correction was performed separately for each network type to allow for a fair comparison). Rows are ordered based on the overall enrichment (Supplementary Fig. 31a): tissue-specific regulatory networks show the strongest connectivity enrichment. Some traits did not show significant connectivity enrichment, which may be either because the signal was too weak, the relevant tissues were not profiled (e.g., our library does not include pancreatic islet cells relevant for type 2 diabetes⁹), or other types of networks (e.g., post-transcriptional) may be more relevant for these traits.

Second, we assessed enhancer–gene edges of our circuits in 13 tissues where eQTL data were available from GTEx²⁹ (Supplementary Table 3, Methods). Overall, about one third of the enhancer–gene edges in our circuits were confirmed by a cis-eQTL, outperforming alternative approaches such as assigning enhancers to the closest or most strongly correlated target gene (Fig. 2b, Supplementary Figs. 11–12).

Lastly, we sought to evaluate whether the regulatory circuits are predictive of gene expression levels. To this end, we obtained RNA-seq data for 40 matching tissues from the Roadmap Epigenomics project³⁰ (Supplementary Table 4). We indeed found a strong correlation between the TF input of a gene (defined as the sum of its incoming edge weights) and its expression level in a given tissue (Methods, Supplementary Fig. 13).

Network architecture reflects developmental and functional relationships among cell types and tissues

Having evaluated the accuracy of our circuits, we next sought to compare regulatory programs of genes across lineages. To this end, we defined for each regulatory circuit a corresponding coarse-grained network, summarizing TF inputs at the level of genes (Fig. 1b, Methods). We hierarchically clustered these networks based on edge overlap (Methods). As expected, developmentally and functionally related lineages were consistently grouped together, indicating that they share regulatory components (Supplementary Figs. 14–24). Analysis of network architecture showed that immune cells, followed by cells and tissues of the nervous system, have the highest number of TFs per gene, while other network properties are comparable across lineages (Supplementary Figs. 25–26).

GWAS variants perturb regulatory modules in disease-relevant cell types and tissues

In order to systematically evaluate the relevance of tissue-specific regulatory networks for a broad range of traits and diseases, we compiled a large panel of 37 GWASs (Supplementary Table 5) and assessed whether trait-associated variants perturb genes that cluster in network modules (connectivity enrichment analysis, Fig. 1c and Methods). To reduce the burden of multiple testing (394 networks × 37 GWASs), we first considered 32 high-level networks derived from the hierarchical clustering described above. (Networks in the same cluster were merged). We found that the majority of GWAS traits show stronger connectivity enrichment in tissue-specific regulatory networks than in protein interaction, co-expression and ChIP-based networks (Fig. 2c). Moreover, connectivity enrichment often extended to weakly associated genes that did not pass the GWAS significance threshold (Supplementary Fig. 31b).

Next, we asked whether the observed clustering of perturbed genes was specific to regulatory networks of trait-relevant tissues. We examined all GWAS traits that showed connectivity enrichment in at least one network (score > 1.0 in Fig. 2c) and ranked the 32 high-level networks by their enrichment score. Networks of disease-relevant cell types and tissues consistently ranked at the top, thus showing the strongest evidence for perturbed modules. For example, the psychiatric, cross-disorder study showed the strongest clustering of associated genes precisely in the three high-level networks of nervous system and brain, schizophrenia in the two networks specific to adult brain, and anorexia nervosa in networks of the endocrine system followed by nervous system and hindbrain, suggesting that endocrine dysregulation, a hallmark of chronic starvation in anorexia nervosa³¹, may be implicated (Fig. 3a).

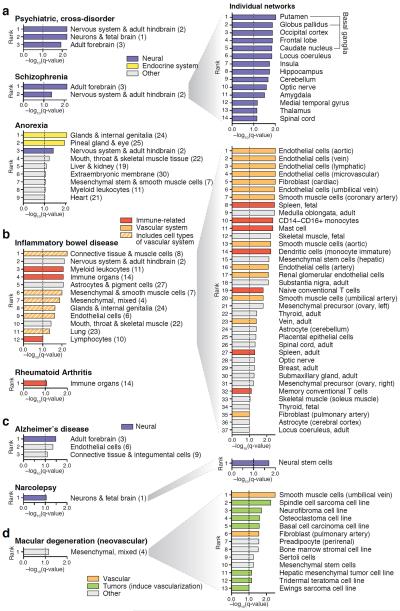
Figure 3. Network connectivity enrichment reveals disease-relevant cell types and tissues.

Connectivity enrichment scores across the 32 high-level networks (left; numbers in parenthesis correspond to cluster indexes in Supplementary Fig. 14) and corresponding individual networks (right) for selected GWAS traits. (Similar results were obtained for the remaining traits, see main text and Supplementary Figs. 32–43). Networks of trait-relevant cell types and tissues consistently rank at the top, i.e., show strongest clustering of perturbed genes. All networks with enrichment scores > 1.0 are shown. (a) Psychiatric disorders show strongest clustering of associated genes in regulatory networks of neural tissues, with the exception of anorexia nervosa, where we further observe strong signal for tissues of the endocrine system (hormonal glands, Supplementary Fig. 14c). For schizophrenia, connectivity enrichment is shown both for the high-level networks (left) and the corresponding individual networks (right), illustrating how perturbed regulatory modules pinpoint specific, disease-relevant brain structures. (b) Inflammatory bowel disease (IBD) and rheumatoid arthritis are examples of immune disorders, which display connectivity enrichment in immune-related networks. IBD also shows enrichment in other high-level networks, most of which include vascular cells that are involved in the inflammatory response and are driving the signal, as shown to the right. (c) Alzheimer's disease and narcolepsy, two neurodegenerative disorders, show strongest network connectivity enrichment in adult brain and neurons, respectively. (d) Age-related macular degeneration (AMD) of neovascular type shows the strongest connectivity enrichment in regulatory networks of vascular smooth muscle cells followed by diverse tumors, which induce vascularization to achieve growth. As a control, we further confirmed that the dry form of AMD, which does not involve neovascularization, does not show any connectivity enrichment in these networks.

Going one step further, for all high-level networks that showed connectivity enrichment, we also assessed the individual cell type and tissue-specific networks pertaining to the corresponding clusters. For example, within the two adult brain clusters that showed signal for schizophrenia, we found the strongest clustering of perturbed genes in components of the basal ganglia, which modulate motor, cognitive and emotional behavior (Fig. 3a). The dopaminergic system of the basal ganglia manifests pathological anomalies in schizophrenia patients and is the primary target of current antipsychotic drugs³². This example demonstrates that perturbed regulatory modules can pinpoint disease-relevant tissues with remarkable precision.

We made similar observations for the remaining traits (Supplementary Figs. 32–43). The psychiatric cross-disorder study showed strong clustering of perturbed genes in regulatory networks of the caudate nucleus, thalamus, locus coeruleus, and other core structures underlying cognitive and emotional functions that are impaired in psychiatric disorders (Supplementary Fig. 33). For bipolar disorder, the amygdala, a group of brain nuclei key to memory, experienced emotions, and mood that has been consistently implicated in etiological models of bipolar disorder³³, ranked first (Supplementary Fig. 34). Inflammatory bowel disease showed strong connectivity enrichment in endothelial cells, which are gatekeepers of inflammatory processes targeted by current drugs³⁴, as well as immune cells and tissues involved in pathogenesis (spleen, monocytes and mast cells^35,36; Fig. 3b). For rheumatoid arthritis, the strongest clustering of perturbed genes was found in neutrophils, which have an activated phenotype in patients and contribute to pathogenesis³⁷ (Supplementary Fig. 37). For Alzheimer's disease, the strongest clustering of associated genes occurred in regulatory networks of adult forebrain followed by endothelial cells, suggesting that neurovascular dysregulation may be implicated³⁸ (Fig. 3c, Supplementary Fig. 38). Narcolepsy, a rare sleep disorder caused by autoimmune targeting of hypocretin-producing neurons³⁹, shows connectivity enrichment in neural stem cells (Supplementary Fig. 39). Body mass index (BMI) shows the strongest clustering of perturbed genes in regulatory networks of the intestinal tract and immune system, thus suggesting a potential link with the gut microbiome, which has recently been proposed to have a heritable component that impacts BMI⁴⁰ (Supplementary Fig. 42). Finally, of the two subtypes of age-related macular degeneration, only the neovascular type caused by abnormal blood vessel growth showed network connectivity enrichment in vascular smooth muscle cells, consistent with their function in neovascularization (Fig. 3d).

Discussion

Lately, there has been growing interest in tissue-specific gene networks for understanding human physiology and disease^14–16. The present resource of 394 regulatory circuits dramatically expands the number of cell types and tissues for which networks are available, and it is the first collection of fine-grained regulatory circuits connecting TFs, enhancers, promoters, and gene isoforms in human.

The FANTOM5 enhancers and promoters underlying our networks have been previously validated^23,24 and the observed enrichment for the independently curated TF motifs provides further support. In addition, we validated the inferred tissue-specific edges using indpendent ChIP-seq, eQTL and RNA-seq data, in each case finding good support. Of note, TF motifs alone are known to have low specificity for predicting TF binding, as we confirmed. Key to our approach is that we require both a TF motif and activity of the corresponding regulatory element to infer an edge in a given tissue. Implicitly, this approach also accounts for co-factors on which the TF may be dependent for binding at a specific regulatory element: if co-factors or other conditions to activate the TF are not present, the regulatory element is not active and thus no edge would be added in this tissue, explaining the high specificity of our circuits.

Genetic association data provide an orthogonal means of validation: our systematic analysis across 37 GWASs showed that perturbed regulatory modules often pinpoint cell types and tissues that are known to be involved in pathophysiological processes, and in some cases are targets of current medications, with remarkable precision. For most traits, evidence of increased connectivity between perturbed genes extended to variants that did not pass the genome-wide significance threshold, indicating that regulatory network information will be useful for prioritizing candidate variants.

Our analysis of network architecture showed that similarity between regulatory networks closely reflects developmental or functional relationships between respective cell types and tissues, suggesting that phenotypic relatedness results from shared circuit components. Identifying and functionally characterizing these components is an important avenue for future work. We also found variability in network architecture across different lineages, with regulatory networks of the immune and nervous system having by far the most TF inputs per gene. Both immune cells and neurons perform highly adaptive functions. Our networks suggest that the orchestration of transcriptional responses in these cells involves intricate regulatory programs. Interestingly, the high number of TF inputs (i.e., binding sites) also makes these genes more likely to be perturbed by regulatory variants, which suggests that immune and neural processes may be particularly prone to genetic dysregulation. This proposition is further supported by the strong network connectivity enrichment that we observed for immune-related, psychiatric, and neurodegenerative disorders. Tissue-specific regulatory networks may thus be key to understanding the etiology of these disorders.

We did not yet attempt to infer causal variants in the context of our circuits. This is a difficult task because a given GWAS locus often spans multiple genes and regulatory regions, harboring many potentially causal variants. To this end, a probabilistic graphical model applied to 127 reference epigenomes recently showed promising results (Quon et al., in preparation). Another challenge is to characterize perturbed pathways and their role in disease processes, which will be extremely valuable for biomarker and drug discovery. We make our networks along with user-friendly software tools freely available and hope that this resource will spur the development of additional methods capable of integrating large collections of networks to identify disease-relevant tissues and dissect the regulatory architecture of complex traits.

Methods

Inference of cell type and tissue-specific regulatory networks

We represent transcriptional regulatory networks as graphs, which include four different types of nodes: TFs, enhancers, promoters, and gene isoforms. Directed, weighted edges connect TFs to enhancers and promoters, and enhancers and promotes to gene isoforms. Regulatory circuit inference involves defining the nodes and the edges for each of these layers. To this end, we developed a pipeline consisting of four steps.

The first step is to map regulatory elements (promoters and enhancers) and their tissue-specific activity. Both chromatin-state and CAGE-defined maps can be used for this purpose. Here, we used the CAGE-defined maps from the FANTOM5 project because they currently cover the largest number of human cell and tissue types (~1000 samples compared to 127 epigenomes available from the ENCODE⁴³ and Roadmap Epigenomics³⁰ projects). First, we obtained the FANTOM5 set of 184,827 robust CAGE peaks and their activity levels across all samples (RLE normalized expression profiles)²³. These CAGE peaks represent high-confidence regions of transcription initiation; we refer to them as CAGE-defined promoters (note that the full promoter region where TFs bind extends beyond these peaks, as described below). Second, we obtained the FANTOM5 set of 43,012 CAGE-defined enhancers and their activity levels across all samples (RLE normalized expression profiles)²⁴. These enhancers have been identified based on enhancer RNAs (eRNAs) that are detectable through a robust signature of weak, bi-directional transcription in CAGE data^24,44. After discarding samples that were not present in either the promoter or expression data, we were left with 808 cell and tissue samples, which formed the basis for regulatory circuit reconstruction (Supplementary Table 1).

The second step is to link TFs to promoters and enhancers. To this end, we used a curated collection of sequence binding motifs (position weight matrices) for 662 TFs provided by Kheradpour et al., where each motif occurrence in the genome (referred to as a motif instance) was further assigned a confidence score based on it's evolutionary conservation across mammals^26,27,45. Based on our positional enrichment analysis (described in the next section), we determined that motif instances are >10-fold enriched in a window 400bp upstream to 50bp downstream of CAGE-defined promoters (Supplementary Fig. 1). We thus linked TFs to CAGE-defined promoters based on the occurrence of TF motif instances within these windows (of note, since the bulk of the motif instances are located around the TSS (see distribution in Supplementary Fig. 1a), the cutoff at 10-fold enrichment is not a critical parameter: using a less stringent cutoff expands the windows but adds only a small fraction of edges to the networks). The weight of TF–promoter edges was defined as the confidence score of the corresponding TF motif instance (if multiple motif instances of the same TF were found in a given window, the maximum confidence score was taken). The exact same approach was used to link TFs to enhancers, the only difference being that the window where motif instances were >10-fold enriched coincided with the CAGE-defined enhancers, i.e., it did not extend up or downstream. Edge weights were defined in the same way as for TF–promoter links.

The third step is to link CAGE-defined promoters to known gene isoforms. We used the Ensembl genome annotation, comprising 53,449 isoforms from 19,125 protein-coding genes (accessed May 31st, 2014). Note that the isoforms, not the genes, constitute nodes of our circuits. This is because different isoforms of the same gene often have distinct transcription start sites (TSSs) that are under control of independent promoters, which may have different regulatory inputs and tissue-specific activity. We linked CAGE-defined promoters to TSSs of gene isoforms using the exact same approach as described above: we determined that CAGE-defined promoters enrich >10-fold in a window 250bp upstream to 500bp downstream around TSSs and linked promoters within these windows to the corresponding gene isoforms. The weight of promoter–gene edges was defined as the normalized activity level of the promoter across all samples (normalization was done per regulatory element because expression levels of diverse enhancers and promoters may not be on the same scale). Thus, if the promoter is not active in a given cell type, the edge weight is zero (i.e., the edge is not present), and if the promoter is maximally active, the edge weight equals one.

The fourth step is to link enhancers to their target gene isoforms, which is more challenging because enhancers are often distal and their targets may be cell type-specific^1,3. We opted for a parsimonious approach weighting potential enhancer–isoform links based on just two factors: their genomic distance and activity level in the given tissue. The weighting function for the distance was derived directly from the distance distribution of known cis-eQTLs from their target genes. To this end, we obtained 38,935 high-confidence cis-eQTLs from RegulomeDB⁴⁶, computed their distance from the TSS of their target genes, and defined the weighting function as a smooth fit of the resulting distance distribution (we used local polynomial regression fitting). The weighting function was defined for the range [1kb, 500kb] and scaled to give a maximum weight of one; enhancers at a distance of <1kb and >500kb were assigned weights of one and zero, respectively (Supplementary Fig. 1d). This implies that enhancer–isoform interactions over more than 500kb were not included in our networks. However, the cis-eQTL distribution shows that this is only a minor fraction of all interactions (Supplementary Fig. 1d, less than 6% of cis-eQTLs are located over 500kb away from their target gene) and our correlation analysis suggests that these long-range interactions would be difficult to identify from CAGE data alone (Supplementary Figs. 2, 3). Given the distance-based weight d_ij for a given enhancer i and gene isoform j, we defined the weight of the corresponding edge in cell type k as:

$$w_{ij}\left(k\right)=d_{ij}\cdot \sqrt{x_i\left(k\right)y_j\left(k\right)}$$

where the second term is the geometric mean of the normalized activity levels of the enhancer and the gene isoform. The activity level of isoforms was defined as the maximum activity level of their promoters (which are usually few — the majority of isoforms have only one or two alternative promoters, Supplementary Fig. 6). Accordingly, our confidence that an enhancer regulates a gene isoform increases as they are located more closely together and have higher joint activity in the given cell type.

Application of this pipeline to the FANTOM5 panel of samples gave rise to 808 regulatory circuits. Next, we merged regulatory circuits of closely related samples (Supplementary Table 1), such as samples of the same cell or tissue type from different donors and cell lines from the same cancer subtype, by taking the graph union (this amounts to taking the union of the node and edge sets, while retaining the maximum weight for each edge). The resulting 394 cell type and tissue-specific regulatory circuits constitute the basis of our analysis (corresponding sample annotations are provided in Supplementary Table 1). Note that the samples being merged were typically very similar to each other: if one of them was left out, on average 94% of edges in the final network remained the same (Supplementary Figs. 4, 5).

We kept our approach to reconstruct regulatory circuits deliberately simple, making it generally applicable: here we used CAGE-defined enhancers and promoters from FANTOM, but the same approach could directly be applied to chromatin-defined enhancers and promoters, for instance. Future work will show if performance can be improved by implementing more sophisticated inference algorithms^28,47 for specific steps, e.g., to infer the target regulatory elements of TFs or to infer the target genes of enhancers.

Positional enrichment of motif instances and regulatory elements

Positional enrichment of TF motif instances near CAGE-defined promoters (Supplementary Fig. 1a) was computed as follows. First, a window of 10kb was defined around each promoter, and the distance of each motif instance within this window to the promoter was evaluated. Distance was defined as the number of base pairs separating the motif from the promoter, with the sign indicating whether the motif was located up or downstream from the promoter (negative: upstream; positive: downstream; zero: the two elements overlap). The empirical distribution of motif–promoter distances was computed using a bin size of 50bp. Note that only promoters of genes with a single TSS were considered (to avoid potential bias due to nearby TSSs of isoforms). Second, a background distribution was computed by shuffling motif instances within the region defined by the union of all promoter-centric windows. The resulting motif–promoter distances and corresponding distance distribution were evaluated as described. This procedure was repeated 100 times, leading to a very precise estimate of the background distribution due to the large number of motif instances and promoters. Finally, positional enrichment of motifs was defined as the ratio of the actual distance distribution to the background distance distribution. The entire analysis was performed independently for motif instances of distinct confidence scores (0.1, 0.2, …, 1.0). All operations on genomic elements (overlap, distance, union, shuffling, etc.) were performed using the BEDOPS toolkit⁴⁸.

The same approach was used to compute positional enrichment of TF motif instances near CAGE-defined enhancers (Supplementary Fig. 1b) and of CAGE-defined promoters near TSSs (Supplementary Fig. 1c). For the former, there is a slight difference because enhancers have no orientation (i.e., no negative distance values for upstream location). Note that only enhancers located over 10kb away from any known TSS in Ensembl were considered to avoid potential bias due to nearby promoters.

Validation of TF–enhancer and TF–promoter edges using ChIP-seq data

Edges between TFs and regulatory elements (enhancers and promoters) were assessed using ChIP-seq data from ENCODE⁴³ in five cell lines that are also present in our library (Supplementary Table 2). Besides from our method to infer edges described above, which weights edges based on motif confidence and regulatory element expression, we also assessed three alternative inference approaches: (1) standard network inference based on expression correlation²⁸ (edges are weighted using Spearman correlation between TF expression and regulatory element expression across samples), (2) TF motifs alone (edges are weighted based on motif confidence), and (3) both TF motifs and expression correlation (edges are weighted based on correlation and filtered for those containing at least one motif instance of the given TF at the target regulatory element).

For each TF and cell line where ChIP-seq data was available, we assessed inferred TF–target edges using the area under the precision–recall curve^28,47 (AUPR, see discussion of this choice below). Edges were considered positives if they were supported by TF binding (i.e., there is a ChIP-seq peak of the TF overlapping the target regulatory element) and negatives otherwise. It should be kept in mind that ChIP-seq is an imperfect gold standard and some edges may thus be incorrectly labeled as negatives (binding was not detected) or positives (non-specific or non-functional binding). The AUPR was computed separately for TF–enhancer and TF–promoter edges.

As a reference, we further computed the AUPR for: (i) random data, obtained by shuffling the ChIP peaks of a given TF within the bound regions (the union of ChIP peaks from all TFs) and (ii) ChIP-seq replicates (edges defined by the first replicate were assessed using the second replicate and vice-versa). The AUPR values for random data and ChIP-seq replicates represent lower and upper bounds for the expected performance of inference methods.

We chose to report the AUPR for TF–target edges (and also enhancer–gene edges, see next section) in the main text because it is a standard metric in the field of network inference, e.g., it is used in the DREAM network inference challenges to assess predictions^28,47. Note that because of class imbalance — there are few positives (true edges) compared to negatives (absent edges) — the AUPR is better suited as performance metric than the area under the receiver operator characteristic (ROC) curve⁴⁹. Similar results were obtained using the F-score as performance metric (Supplementary Fig. 12).

Validation of enhancer–gene edges using eQTL data

Edges between enhancers and genes were assessed using cis-eQTLs from GTEx²⁹ in 13 tissues that are also present in our library (Supplementary Table 3; GTEx data was not used to construct the regulatory circuits, see discussion below). In addition to our method described above, which links enhancers to target genes based on their genomic distance and joint activity in the given tissue, we also assessed two alternative approaches: (1) link enhancers to the closest gene (minimum genomic distance) and (2) link enhancers to the most strongly correlated gene (maximum Spearman correlation of enhancer and gene expression across samples). For each of these methods, only genes within 500kb from the enhancer were considered. As a reference, we further assessed the performance for random predictions (linking enhancers to randomly selected genes within the given window of 500kb).

For each tissue where eQTLs were available, we assessed the inferred enhancer–gene edges using the AUPR and F-score (same approach as for TF edges, see previous section). Only enhancers that contain at least one eQTL were considered. We defined edges as positives if they were confirmed by an eQTL (i.e., the enhancer contains an eQTL for this target gene) and negatives otherwise. As mentioned above, both ChIP-seq and eQTLs are imperfect gold standards and may thus contain incorrectly labeled edges. In particular, the eQTLs from GTEx are known to be largely incomplete as they were called using only ~100 samples per tissue²⁹.

Of note, the tissue-specific eQTLs from GTEx used for validation are independent from our regulatory circuits, where enhancers were linked to target genes solely based on their distance and joint tissue-specific activity (possible eQTLs of a given enhancer were never used to determine its targets). The weighting function used for the distance (Supplementary Fig. 1d) is the same for all enhancers and tissues and was derived from a different eQTL dataset (RegulomeDB⁴⁶), which does not include GTEx tissues.

Correlation between regulatory edge strength and target gene expression level

We assessed whether incoming regulatory edges of a gene are predictive of its expression level using RNA-seq data from the Roadmap Epigenomics project³⁰ in 40 cell types and tissues that are also present in our library (Supplementary Table 4). First, we defined the gross TF input of a gene as its weighted indegree in the given tissue, i.e., the sum of the weights of all incoming TF edges (TF–gene edges are given by the coarse-grained networks defined in the next section). For each gene, the correlation coefficient between its TF input and expression level (RPKM value) was computed across the 40 tissues (Supplementary Fig. 13).

Hierarchical clustering of regulatory networks

First, we derived a coarse-grained TF–gene network from each cell type or tissue-specific regulatory circuit. TF–gene networks are useful for high-level analyses where we are most interested in the TFs regulating each gene, and not the detailed and often redundant wiring of these interactions at the level of enhancers, promoters, and isoforms. They also have the advantage of being smaller, and thus computationally more amenable, than the fine-grained circuits. TF–gene networks were defined as follows. First, we created a network encapsulating all regulatory interactions via promoters. For each pair of edges forming a chain that connects a TF to a promoter to an isoform, i.e., edges (TF_i, promoter_j) and (promoter_j, isoform_k) with weights w_ij and w_jk, a corresponding edge (TF_i, gene_l) with weight w_il = w_ij w_jk was added to the TF–gene network (where isoform_k belongs to gene_l). If several redundant edges between the same TF and gene were found (via different promoters or isoforms), they were merged and the maximum edge weight was retained. A separate TF–gene network encapsulating all regulatory interactions via enhancers was created using the same approach. Both TF–gene networks thus have edge weights ranging from zero (absent edge) to one (highest confidence), which were added to form a combined TF–gene network including evidence from both promoters and enhancers.

Pairwise similarity of regulatory networks was defined based on similarity of the two edge sets. For unweighted networks, the Jaccard index can be used for this purpose (size of the intersection divided by size of the union). Here, we used an extension of the Jaccard index defined as:

$$f(\mathbf{a},\mathbf{b})=\frac{\mathbf{a}\cdot \mathbf{b}}{{\mid \mathbf{a}\mid }^2+{\mid \mathbf{b}\mid }^2-\mathbf{a}\cdot \mathbf{b}}$$

where a and b are the edge weight vectors of the two networks (elements a_i and b_i giving the weights of corresponding edges [connecting the same TF and gene] in the two networks; if the edge is not present in one of the networks, the weight is zero). Note that for unweighted networks (edge weights equal zero or one), this definition is equivalent to the Jaccard index. We used the difference function 1 − f for the hierarchical clustering of the 394 regulatory networks because we empirically found that it resulted in more homogeneous clusters than Eucledian distance, for instance. We also systematically tested clusters of networks defined by a given dendrogram cutoff for enriched sample annotations (Supplementary Figs. 14–24). To this end, FANTOM5 sample annotations from the Cell Ontology (CL), Anatomical Ontology (UBERON), and Disease Ontology (DOID) were propagated to the corresponding networks and each cluster was tested for enriched terms (hypergeometric test, FDR was controlled using Benjamini–Hochberg procedure).

The high-level networks corresponding to the 32 clusters defined in Supplementary Fig. 14 were formed by taking the union of the individual networks within each cluster, retaining always the maximum edge weights (i.e., same approach as described above for merging regulatory circuits of closely related samples). The same approach was also used to create a global regulatory network by taking the union of all 394 cell type and tissue-specific networks.

GWAS summary statistics and computation of gene-level p-values

We obtained SNP-phenotype association summary statistics for a comprehensive collection of 37 GWASs including psychiatric^50–53, neurodegenerative^39,54,55, immune-related^56–60, cardiovascular^61,62, blood lipid^63,64, glycemic^65–70, anthropometric^71,72 and other traits^73,74 (Supplementary Table 5). Most of these studies are well-powered meta-analyses: the average sample size is over 50,000 individuals with about a third having over 100,000 individuals. The average number of SNPs is over 2,2 million.

Since we did not have access to genotype data for most studies, we used LD information from a reference population (the European panel of the 1000 genomes project⁷⁵ [1KG]) to summarize SNP association p-values at the level of genes using a similar approach as implemented by the popular VEGAS tool⁷⁶. (We used the summary statistics as provided by the original studies, i.e., some studies are not 1KG-imputed, which is not critical to summarize the signal at the level of genes). Briefly, SNPs in the vicinity of a gene were aggregated using either the maximum or sum of chi-square statistics, which measure the strongest and the average association signal per gene, respectively. (Multiple isoforms of the same gene were merged because, due to LD, the resolution of GWAS is typically too low to differentiate between individual isoforms of a gene). We found that VEGAS, which relies on costly Monte Carlo simulations to estimate p-values for these statistics, was not well suited for the high-powered GWASs in our collection (266 hours run time to estimate genome-wide p-values down to 10⁻⁶ for a 1KG-imputed study). We thus developed a novel approach called Pascal (Pathway scoring algorithm), which leverages analytic solutions offering dramatic increase in both speed and precision (1.7 hours run time to estimate genome-wide p-values down to 10⁻¹⁵). The Pascal tool is described in detail elsewhere⁴¹. Here, we applied Pascal to define gene-level p-values for all 37 GWASs using default parameters. Results reported in this paper are based on the maximum of chi-square statistic; similar results were obtained using the sum of chi-square statistic.

Network connectivity enrichment analysis

Given a network and summary statistics from a GWAS, our aim is to evaluate whether genes perturbed by trait-associated variants are more densely interconnected than expected. We refer to such groups of densely interconnected nodes as network modules. (Here we only evaluate the degree to which trait-associated genes cluster in modules — we do not identify discrete modules or pathways). An overview of the four steps of the approach is given in Supplementary Fig. 27.

The first step is to aggregate GWAS summary statistics at the level of genes, as described in the previous section.

The second step is to define how “close” any two genes are in the network. The directionality of links is not considered for this purpose: for example, two genes that are co-regulated by a TF gene may be considered “close” because they are connected through this TF, and two TF genes that regulate the same target gene could be considered “close” because they are connected through this target gene. Shortest path length is sometimes used to define “closeness”, but is not very informative for biological networks because the shortest path between any two nodes is typically short due to the presence of hubs. An alternative approach is to use diffusion kernels on graphs⁷⁷, where “closeness” (hereafter referred to as connectivity) between two genes is defined based on the probability that a random walk on the graph leads from one gene to the other. This approach naturally captures the hierarchical modular structure of biological networks (genes in the same module have higher probability to be connected by a random walk). Here, we used a weighted p-step random-walk kernel⁷⁸ to define the pairwise connectivity between nodes:

$$K={(I+\tilde{W})}^p,\text{with}\tilde{W}=D^{-\frac{1}{2}}W{D}^{-\frac{1}{2}}$$

where I is the identity matrix, W is the weighted adjacency matrix of the graph (entry w_ij is the weight of the edge between nodes i and j, entries on the diagonal are set to zero), D is the degree matrix of the graph (a diagonal matrix where entry d_ii is the degree of node i), and p is the number of steps in the random walk (we used p=4 because biological networks are typically shallow and we expect few meaningful interactions over paths longer than four). Note that K can be computed cheaply because W is sparse. As mentioned above, the directionality of links was not considered for the purpose of defining pairwise connectivity, i.e., W and K are both symmetric (thus, co-regulated genes are connected trough their shared regulators and tend to have high pairwise connectivity, in particular if they are part of a regulatory module with multiple shared regulators [i.e, many possible random walks connecting them]).

The third step is to compute connectivity enrichment curves. To this end, genes were ranked by their GWAS p-value, from most to least significant. For each position n in the ranked list (n = 1, 2, …, N, where N is the number of genes), the connectivity between the top n genes was defined as the mean of their pairwise connectivity values k_ij (gene pairs in LD were excluded, see below). Next, the connectivity between the top n genes was computed in the same way for 10,000 permutations of the ranked gene list. Importantly, only labels of genes with similar network centrality were permuted among each other (the centrality of a gene was defined as its mean pairwise connectivity with all other genes). Specifically, genes were separated into 100 bins based on their centrality, and only labels within the same bin were shuffled (a similar approach, within-degree gene label permutation, is commonly used in network-based GWAS analysis^11,79; Supplementary Fig. 30). Finally, the connectivity enrichment curve was computed as the ratio of the observed connectivity between the top n genes to the median connectivity between the top n genes across the 10,000 permutations, for each position n in the ranked list.

The fourth step is to summarize the connectivity enrichment curves by the signed area under the curve. This is done both for the original data and the 10,000 permutations, enabling the computation of a corresponding empirical p-value. Finally, the connectivity enrichment score for the given GWAS and network is defined as the negative log₁₀ of the empirical p-value.

Note that the connectivity between neighboring genes on the genome was excluded from this analysis (Supplementary Fig. 29). This is important because, on the one hand, the GWAS association signal of neighboring genes is often correlated due to LD, and on the other hand, neighboring genes are often also functionally related or co-regulated (i.e., they may also be neighbors at the network level). To ensure that such groups of correlated and functionally related genes did not inflate connectivity enrichment, we took a conservative approach and completely excluded the connectivity between all neighboring genes (distance < 1mb) from the network connectivity enrichment analysis (the corresponding entries in the connectivity matrix K were set to NA (not available), i.e., they were ignored in all calculations). Since the human leukocyte antigen (HLA) genes form an exceptionally large cluster that also shows strong association with many immune-related traits, we further completely excluded all genes in the HLA region. Taken together, this ensures that the observed network connectivity enrichment is not driven by the HLA genes or similar gene clusters.

We confirmed using phenotype-label permutations that our method corrects for LD structure and other potential confounders (Supplementary Fig. 30).

Assessment of other network types

Besides from our cell type and tissue-specific regulatory networks, we also assessed connectivity enrichment for five other types of networks. We only considered molecular networks derived from experimental data, not functional networks that were mined from the literature (e.g., co-citation networks).

First, we generated a global co-expression network from the FANTOM5 data²³ (i.e., the same dataset that was used to construct the regulatory circuits). To this end, gene expression levels were defined as the sum of the corresponding promoter expression levels. TF–gene edge weights were computed using Spearman correlation and the top 100k edges were retained.

Second, we obtained 35 tissue-specific co-expression networks from Piersen et al.¹⁵ These networks were inferred from GTEx data²⁹ using an algorithm that shares information between related tissues.

Third, we collected four well-established protein-protein interaction networks: (1) the InWeb protein interaction database developed by Lage et al.⁸⁰ and used by the popular DAPPLE tool¹¹ probabilistically integrates evidence from diverse sources, including MINT, BIND, IntAct, KEGG annotated protein-protein interactions (PPrel), KEGG Enzymes involved in neighboring steps (ECrel), Reactome and others; (2) Entrez GeneRIF (gene reference into function) includes protein interactions from BIND, BioGRID, HPRD and other sources⁸¹; (3) the BioGRID database provides literature-curated protein interactions⁸²; and (4) the Human Interactome project is systematically screening the human proteome for interactions using yeast two-hybrid and other assays⁸³.

Fourth, we obtained a global regulatory network from Gerstein et al.¹⁷ The network is based on ChIP-seq data from ENCODE.

Fifth, we considered 41 tissue-specific regulatory networks based on DNaseI footprints from Neph et al.⁴² Of note, these networks only comprise TF–TF edges, i.e., edges between TFs and target genes that are not TFs themselves have not been included.

Identification of trait-relevant regulatory networks

A possible approach to identify trait-relevant cell type and tissue-specific networks would be to perform connectivity enrichment analysis exhaustively for all 37 traits and 394 regulatory networks in our library (i.e, ~15,000 trait–network combinations). However, this is not practical because of the resulting multiple testing burden and compute time (a single run with 10,000 permutations takes about 15 minutes, depending on the network size). Thus, we leveraged the fact that related networks are often very similar and exhaustively tested connectivity enrichment only for the 32 high-level networks across all traits (FDR was controlled using Benjamini–Hochberg procedure). Subsequently, for each trait, we only tested connectivity enrichment for individual cell type and tissue-specific networks belonging to high-level networks that had shown connectivity enrichment with score > 1.0 for this trait (i.e., 10% FDR). We deliberately chose a permissive threshold because cell-type-specific modules may be “diluted” in the high-level networks by links from other cell types or tissues, which could weaken the observed connectivity enrichment in high-level networks.

Availability of networks, data, tools and source code

We provide all networks, supplementary data, and code along with a user-friendly desktop app on our website: http://regulatorycircuits.org. In addition, the networks and supplementary data have been deposited on an external repository for biomedical data (Synapse⁸⁴) and code has been deposited on GitHub. Links to these resources are available on our website and in Supplementary Table 6.