Abstract
Key points
In the majority of species, including humans, increased heart rate increases cardiac contractility. This change is known as the force–frequency response (FFR). The majority of mammals have a positive force–frequency relationship (FFR). In rat the FFR is controversial.
We derive a species‐ and temperature‐specific data‐driven model of the rat ventricular myocyte.
As a measure of the FFR, we test the effects of changes in frequency and extracellular calcium on the calcium–frequency response (CFR) in our model and three altered models.
The results show a biphasic peak calcium–frequency response, due to biphasic behaviour of the ryanodine receptor and the combined effect of the rapid calmodulin buffer and the frequency‐dependent increase in diastolic calcium.
Alterations to the model reveal that inclusion of Ca2+/calmodulin‐dependent protein kinase II (CAMKII)‐mediated L‐type channel and transient outward K+ current activity enhances the positive magnitude calcium–frequency response, and the absence of CAMKII‐mediated increase in activity of the sarco/endoplasmic reticulum Ca2+‐ATPase induces a negative magnitude calcium–frequency response.
Abstract
An increase in heart rate affects the strength of cardiac contraction by altering the Ca2+ transient as a response to physiological demands. This is described by the force–frequency response (FFR), a change in developed force with pacing frequency. The majority of mammals, including humans, have a positive FFR, and cardiac contraction strength increases with heart rate. However, the rat and mouse are exceptions, with the majority of studies reporting a negative FFR, while others report either a biphasic or a positive FFR. Understanding the differences in the FFR between humans and rats is fundamental to interpreting rat‐based experimental findings in the context of human physiology. We have developed a novel model of rat ventricular electrophysiology and calcium dynamics, derived predominantly from experimental data recorded under physiological conditions. As a measure of FFR, we tested the effects of changes in stimulation frequency and extracellular calcium concentration on the simulated Ca2+ transient characteristics and showed a biphasic peak calcium–frequency relationship, consistent with recent observations of a shift from negative to positive FFR when approaching the rat physiological frequency range. We tested the hypotheses that (1) inhibition of Ca2+/calmodulin‐dependent protein kinase II (CAMKII)‐mediated increase in sarco/endoplasmic reticulum Ca2+‐ATPase (SERCA) activity, (2) CAMKII modulation of SERCA, L‐type channel and transient outward K+ current activity and (3) Na+/K+ pump dynamics play a significant role in the rat FFR. The results reveal a major role for CAMKII modulation of SERCA in the peak Ca2+–frequency response, driven most significantly by the cytosolic calcium buffering system and changes in diastolic Ca2+.
Key points
In the majority of species, including humans, increased heart rate increases cardiac contractility. This change is known as the force–frequency response (FFR). The majority of mammals have a positive force–frequency relationship (FFR). In rat the FFR is controversial.
We derive a species‐ and temperature‐specific data‐driven model of the rat ventricular myocyte.
As a measure of the FFR, we test the effects of changes in frequency and extracellular calcium on the calcium–frequency response (CFR) in our model and three altered models.
The results show a biphasic peak calcium–frequency response, due to biphasic behaviour of the ryanodine receptor and the combined effect of the rapid calmodulin buffer and the frequency‐dependent increase in diastolic calcium.
Alterations to the model reveal that inclusion of Ca2+/calmodulin‐dependent protein kinase II (CAMKII)‐mediated L‐type channel and transient outward K+ current activity enhances the positive magnitude calcium–frequency response, and the absence of CAMKII‐mediated increase in activity of the sarco/endoplasmic reticulum Ca2+‐ATPase induces a negative magnitude calcium–frequency response.
Abbreviations
- AP
action potential
- CaB
background Ca2+
- CAMKII
Ca2+/calmodulin‐dependent protein kinase II
- CFR
calcium frequency response
- DCFR
diastolic calcium frequency response
- Ito
transient outward K+ current
- LCC
L‐type Ca2+ channel
- LV
left ventricle
- FFR
force–frequency response
- MCFR
magnitude calcium–frequency response
- NCX
Na+/Ca2+ exchanger
- PCFR
peak calcium–frequency response
- RyR
ryanodine receptor
- PMCa
plasma membrane Ca2+‐ATPase
- SERCA
sarco/endoplasmic reticulum Ca2+‐ATPase
- SRl
SR leak
- TRPN
troponin buffer
Introduction
In the majority of species, including humans, increased heart rate increases cardiac contractility and the rate of relaxation (Pieske et al. 1999). This change in response to changes in pacing frequency, known as the force–frequency response (FFR), is described as either positive or negative with increasing or decreasing myocyte contraction strength, respectively, with increasing pacing frequencies. As an essential self‐regulatory mechanism, FFR allows the cardiac output to respond to systemic requirements through coordinated changes in heart rate and contraction strength.
Key to understanding the cardiac FFR are the physiological mechanisms that regulate calcium handling in the heart. With each heartbeat, cardiomyocytes are depolarized, activating the voltage‐dependent L‐type Ca2+ channels (LCCs) that, in turn, induce an influx of Ca2+ (Hobai & Levi, 1999). The Ca2+ entering the cell signals the opening of the intracellular Ca2+ release channels known as ryanodine receptors (RyRs) in the sarcoplasmic reticulum (SR) (Fabiato & Fabiato, 1979), allowing rapid Ca2+‐induced Ca2+‐release to occur (Sham et al. 1995). The release of Ca2+ from the intracellular calcium stores results in a rapid increase in the cytosolic Ca2+ concentration, which is sufficient to generate contraction at the level of the myofilaments. During the relaxation phase, Ca2+ ions are sequestered back into the SR by the sarco/endoplasmic reticulum Ca2+‐ATPase (SERCA) or driven out the cell by the Na+/Ca2+ exchanger (NCX) and the sarcolemma Ca2+‐ATPase (PMCa), returning Ca2+ concentration to low diastolic levels. FFR manifests at the cellular scale where contraction, Ca2+ transients and action potentials (APs) in isolated myocytes adapt in response to changes in pacing frequency (Endoh, 2004; Dibb et al. 2007; Monasky & Janssen, 2009). Specifically changes in the intracellular Ca2+ ([Ca2+]i) handling mechanism are the primary cellular responses that, in turn, produce the FFR (Endoh, 2004). Humans have a positive FFR (Pieske et al. 1999), while in the rat, the majority of murine studies have reported a negative FFR (Bers, 1989; Bouchard & Bose, 1989) and only a few studies have described a biphasic or positive FFR (Frampton et al. 1991 b; Layland & Kentish, 1999). Central to this controversy are the physiological conditions under which the rat heart operates, specifically the heart rate, the temperature and the extracellular calcium concentration ([Ca2+]o).
The relative importance of the mechanisms regulating the FFR has been debated for more than a century and remains a source of controversy. Early works in the rat found a negative FFR at physiological frequencies in ventricular strips maintained at 38°C (Benforado, 1958). These responses were attributed to changes in intracellular sodium concentration ([Na+]i) with pacing frequency. With the discovery of the Na+/Ca2+ exchanger (NCX), Langer et al. (1975) suggested that, following a [Na+]i increase with frequency, increases in force may be generated by the coupled gain of intracellular calcium via NCX, thus shifting attention to the Ca2+–frequency relationship (CFR) as a measure of FFR. Later experiments by Stemmer & Akera (1986) rejected this hypothesis and proposed that frequency‐dependent [Ca2+]i changes could be caused by a decrease in intracellular Ca2+ resulting from a reduction in Ca2+ available for release from the SR ([Ca2+]SR). This hypothesis was further tested in rats by Bers (1989) who attributed a negative FFR to a decrease in [Ca2+]SR with increasing frequency.
In conflict with these results, Frampton et al. (1991 b) showed a positive FFR, positive CFR and an increase in [Ca2+]SR with frequency in isolated rat ventricle myocytes at room temperature. A frequency‐dependent loading of the SR was also reported by Layland & Kentish (1999) in isolated rat ventricular trabeculae and Dibb et al. (2007) in isolated rat ventricular myocytes. In particular, Layland's results support the hypothesis that a shift from negative to positive FFR occurs as the pacing frequency approaches physiological rates, first noted by Koch‐Weser & Blinks (1963).
Recent studies have suggested that the Ca2+/calmodulin‐dependent protein kinase II (CaMKII) contributes to enhanced activity of the target proteins that control the FFR (Sossalla et al. 2010; Wu et al. 2012) such as the sarco/endoplasmic reticulum Ca2+‐ATPase, the L‐type channel and the transient outward K+ current I to, although other studies contradict this hypothesis (Lokuta et al. 1995; Dibb et al. 2007). What is now widely accepted and validated through experiments is that CAMKII indirectly enhances SR uptake of Ca2+ through SERCA by phosphorylation of the endogenous inhibitor of SERCA, phospolambam, inducing a frequency‐dependent acceleration of relaxation (Picht et al. 2007; Dibb et al. 2007). Other experiments have also revealed CAMKII‐mediated facilitation of the L‐type Ca2+ current (Xiao et al. 1994) and the transient outward potassium current (Colinas et al. 2006). The effects of CaMKII phosphorylation of the RyRs, however, remain controversial as CAMKII has been reported to both increase (Wehrens et al. 2004) and decrease (Lokuta et al. 1995) the channel open probability.
This evidence collectively confirms that FFR regulation in rats still remains controversial and the mechanisms are not clear. Ca2+ dynamics are directly responsible for changes in FFR (Endoh, 2004) and in rats they appear to be different from canine, guinea pig and human as their rate relies more on intracellular calcium cycling than the other species. Thus, to be able to unravel the causes of positive and negative FFR we need to consider the rat‐specific Ca2+ physiology. In this context, the development of a species‐ and temperature‐specific model of Ca2+ dynamics in the cardiac myocyte, which integrates multiple data sources and can operate at physiological frequencies, provides a novel and promising methodology for quantitatively interpreting experimental data and quantifying the principal regulators of FFR in rats.
This study adopts this approach to focus on understanding FFR in rats. Firstly, we derive a species‐ and temperature‐specific model of the rat ventricular myocyte electrophysiology that captures the change in Ca2+ response to pacing. Secondly, to study the FFR, we test the effects of changes in pacing frequency and [Ca2+]o on the Ca2+ transient characteristics in a model with (1) CAMKII SERCA inhibition, (2) CAMKII modulation of SERCA, LCC and transient outward K+ current (I to) activity and (3) reduced Na+/K+ activity to quantify the relative role of those mechanisms in the response.
Methods
Ethical approval
Experiments were performed in healthy Wistar rats at physiological temperature (37°C). Ten‐week‐old Wistar rats were anaesthetized by inhalation of 2% isoflurane–98% oxygen in a chamber, and then killed by cervical dislocation. Animal experiments were approved by the Norwegian National Animal Research Committee and conformed to the Guide for the Care and Use of Laboratory Animals (National Institutes of Health, USA, publication no. 85‐23, revised 1996) and the principles of UK regulations, as described in Drummond (2009).
Isolation of myocytes
Left ventricle (LV) myocytes were isolated using a standard enzymatic dispersion technique (Louch et al. 2011). The heart was perfused with a Ca2+‐free solution (mm: 130 NaCl, 25 Hepes, 5.4 KCl, 0.5 MgCl2, 0.4 NaH2PO4, 5.5 d‐glucose; pH 7.4) followed by 15 min with an enzyme‐containing solution (collagenase, 1 mg ml−1, Worthington Biochemical Corp., Lakewood, NJ, USA; Ca2+: 0.05 mm). The LV free wall was isolated, cut into small pieces and gently minced. Isolated cardiomyocytes were allowed to sediment several times while Ca2+ concentration was gradually increased (0.1, 0.2, 0.5 mm). The myocyte suspension was stored at room temperature, and cells were used within 8h of isolation.
Ca2+ measurements
LV myocytes were plated on laminin‐coated coverslips, and placed in a perfusion chamber on the stage of an inverted microscope. [Ca2+]i transients were recorded in fluo‐4 AM‐loaded (Molecular Probes; Thermo Fisher Scientific, Waltham, MA, USA) myocytes during field stimulation at 1 and 6 Hz during superfusion with Hepes–Tyrode solution containing (in mm): 140 NaCl, 1.8 CaCl2, 0.5 MgCl2, 5.0 Hepes, 5.5 glucose, 0.4 NaH2PO4 and 5.4 HCl (pH 7.4, 37°C). The fluorescence measurements were converted to free [Ca2+]i prior to their use. The conversion was developed using the following equation proposed by Cheng et al. (1993):
| (1) |
where [Ca2+]i is the free Ca2+ concentration in the cytosol, [Ca2+]d is the diastolic Ca2+ concentration at 1 Hz, K d is the dissociation constant, and R is the fluorescence divided by diastolic fluorescence at 1 Hz (F/F 0). K d was set to 1100 nm and [Ca2+]d to 100 nm.
Patch‐clamp experiments
Whole‐cell patch‐clamp experiments were performed with patch pipettes (1–2 MΩ) connected to an Axoclamp‐2B amplifier (Axon Instruments/Molecular Devices, Sunnyvale, CA, USA). Action potential recordings were performed as described in Mørk et al. (2009), with a pipette solution containing (in mm): 120 potassium aspartate, 0.5 MgCl2, 6 NaCl, 0.06 EGTA, 10 Hepes, 10 glucose, 25 KCl and 4 K2‐ATP (pH 7.2), and an identical extracellular solution as described for field stimulation experiments. Action potentials were triggered by a 3 ms suprathreshold current.
For recordings of L‐type Ca2+ current, the fast transient outward K+ currents were blocked by the presence of aminopyridine and Cs+ (Frisk et al. 2014). The intracellular solution contained (in mm): 133 CsCl, 0.33 MgCl2, 4 Mg‐ATP, 10 Hepes and 20 TEA, while the extracellular solution contained (in mm): 20 CsCl, 1 MgCl2, 135 NaCl, 10 Hepes, 10 d‐glucose, 4‐aminopyridine and 1 CaCl2. The additional presence of 0.06 mm of EGTA in the intracellular solution implies some Ca2+ buffering. Current was recorded during discontinuous voltage clamp (sample rate ∼8 Hz), with a train of 10 conditioning pulses (50 ms) from –70 to 0 mV, followed by a 210 ms depolarizing voltage step to a range of potentials (–40 to +40 mV in 10 mV increments). The peak inward current for each test potential was measured relative to steady‐state current, and normalized to cellular capacitance. Cell capacitance was measured by integrating the capacitive current elicited by a voltage step from −70 mV to −80 mV.
Computational methods
Model structure
The importance of species and temperature specificity in heart modelling has recently been highlighted in a number of published studies (Li et al. 2010). Starting with the Pandit model of rat ventricular myocyte electrophysiology (Pandit et al. 2001), we created a phylogenetic tree to analyse the dependence of model parameters on experimental data (Fig. 1 A). Specifically, the tree shows the link between model components and the modelling and experimental studies used to determine the parameters involved in that component's formulation. This approach identifies the Ca2+ handling system and Na+/K+ model as being derived predominantly from canine and guinea pig data. Based on this analysis and due to the lack in graded Ca2+ release of the Pandit model, we replaced the Ca2+ dynamics system with the Hinch model (Hinch et al. 2004) and we updated the Na+/K+ model by replacing it with the more recent Lewalle model (Lewalle et al. 2014), fitted to rat data at 37°C. The Hinch model phylogenetic tree is presented in Fig. 1 B, highlighting data from species other than rat and rat data at temperatures lower than physiological. Based on this analysis we thus refitted the Ca2+ dynamics parameters and channel densities using MATLAB (The MathWorks, Natick, MA, USA) fitting tools (nonlinear least squares method with Trust‐Region algorithm) to update data dependencies. In particular, we simulated and constrained six key proteins in the Ca2+ regulation system: the Na+/Ca2+ exchanger current (I NCX), the Ca2+ pump current (I PMCa), the sarco/endoplasmic reticulum Ca2+‐ATPase current (I SERCA), the L‐type Ca2+ current (I LCC), the ryanodine receptor current (I RYR) and the leak from the SR current (I SRl). We introduced equations for CAMKII‐mediated increase in SERCA activity from the model of Li et al. (2010). To account for the presence of EGTA in the patched pipettes generating our experimental data, we included a model of EGTA buffering. Hence, the Ca2+ transient simulations were conducted using [EGTA] = 0 mm, while the AP simulations were performed with [EGTA] = 0.06 mm, consistent with the experimental methods.
Figure 1. Phylogenetic trees .
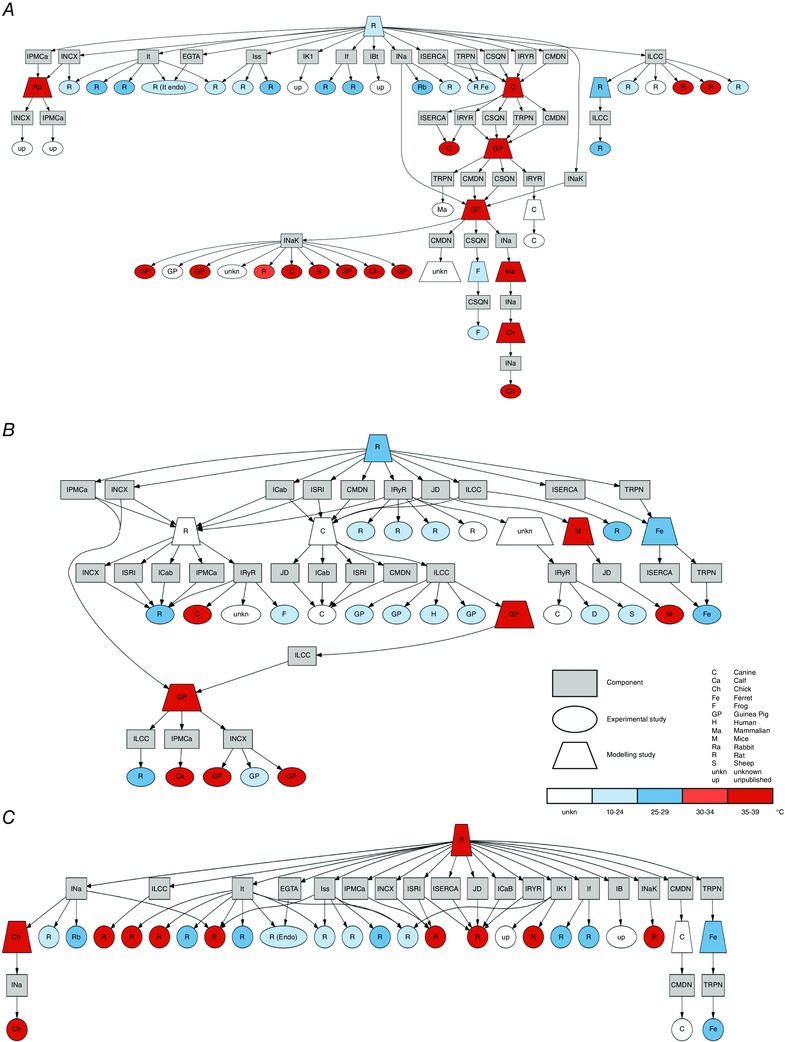
The figures show an analysis conducted on the transmembrane currents and the Ca2+ dynamics system showing the inheritance of data as links between modelling studies (trapezium) and experimental studies (ellipses). Modelling studies components (boxes) are connected (arrows) to published studies. Models and experiments within the trees are classified by species (label) and temperature (colour). The observed model's components are: L‐type Ca2+ channel current (I LCC), SR Ca2+‐ATPase current (I SERCA), troponin buffer (TRPN), calsequestrin buffer (CSQN), flux from the dyadic space to the cytosol (J D), ryanodine receptor current (I RYR), calmodulin buffer (CMDN), Ca2+ pump current (I PMCa), Na+/Ca2+ exchanger current (I NCX), EGTA buffer (EGTA), steady‐state outward K+ current (I ss), inwardly rectifying K+ current (I K1), hyperpolarization‐activated current (I f), background Na+, K+ and Ca2+ currents (I Bt, in A), background Na+ and K currents (I B in B and C), background Ca2+ current (I CaB in B and C), SR leak current (I SRl), Na+ current (I Na), Na+/K+ pump (I NaK). A: Pandit phylogenetic tree. B: Hinch phylogenetic tree. C: new model phylogenetic tree.
Model parameter fitting
The fluxes through NCX and PMCa were evaluated using caffeine‐induced Ca2+ transients at 1 and 6 Hz. NCX parameters were fitted in order for the pump to extrude 90% of the measured Ca2+ flux during a caffeine transient, while the remaining 10% was used to fit PMCa parameters. Those results were then combined with Ca2+ transient measurements at 1 and 6 Hz to study the Ca2+ flux of SERCA and its changes with frequency. The Ca2+ influx from the LCCs was fitted using the peak I LCC current–voltage relationship curve, where peak I LCC is the maximum value of I LCC. The flux through the RyR was modulated to match the time to peak of the field simulated Ca2+ transients. The leak from the SR was fitted to constrain the [Ca2+]SR to fall within the maximum value defined by the integral of NCX during a caffeine transient and the minimum value defined by the integral of SERCA during a field simulated Ca2+ transient. The background Ca2+ current was modified to reproduce the peak of the Ca2+ transients at 1 and 6 Hz. The remaining Na+ and K+ currents were modified using rat data recorded at physiological temperatures. The resulting coupled rat ventricular myocyte calcium dynamics and electrophysiology model's data dependences are shown in Fig. 1 C, whereas the fitted parameters’ values are shown in section 1.2.7 of Appendix. The model's coupling and refitting procedure is also described in detail in section 1 of Appendix.
Generation of model variants to simulate specific mechanisms
Using this data‐driven species‐ and temperature‐specific rat electrophysiology model (the DD model), we developed three model variants to analyse how CAMKII‐mediated SERCA, L‐type channel and I to alterations (CAMK model), inhibition of CAMKII increase in SERCA activity (NO CAMK model) and altered Na+/K+ (RNaK model) affect the Ca2+ transient at different frequencies and [Ca2+]o (see Fig. 3).
Figure 3. The calcium frequency response (CFR) .
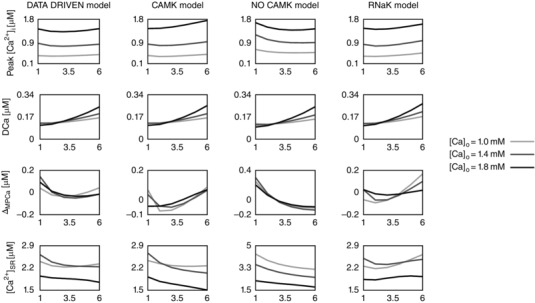
Rate‐dependent changes in peak [Ca2+]i, diastolic [Ca2+]i (DCa), magnitude of peak [Ca2+]i relative variation (ΔMPCa), and Ca2+ in the sarcoplasmic reticulum ([Ca2+]SR) due to changes in the extracellular Ca2+ concentration ([Ca2+]o). Each column represents a different model: the baseline model (DD), a model with inclusion of the CAMKII mediation of LCC and I to activity (CAMK), a model with inhibition of the CAMKII‐mediated increase in SERCA activity (NO CAMK) and a model with reduced Na+/K+ affinity to Na+ (RNaK). Different colours represent different [Ca2+]o: 1.0 mm (light grey), 1.4 mm (dark grey) and 1.8 mm (black).
In the DD model, CAMKII modulation of SERCA was already included, as it was required to allow the model to fit the distinct Ca2+ relaxation rates at 1 and 6 Hz due to changes in SERCA flux. It must be noted that L‐type measurements were not performed at different frequencies and so do not provide a frequency‐dependent response and no measurements of I to were performed in our study.
As previous studies in the literature have reported CAMKII‐mediated facilitation of the L‐type Ca2+ (Xiao et al. 1994) and I to (Colinas et al. 2006) currents, in the CAMK model we included CAMKII modulation of the L‐type channel and I to. The LCC and I to models were fitted using CAMKII data in the literature, collected in rats and mice (for further details see section 5 of Appendix).
In the NO CAMK model we inhibited CAMKII activation of SERCA, by fixing the SERCA conductivity parameter value at 6 Hz for all the frequencies, to test the effect of increased SERCA activity on the CFR. This choice was forced by the development of alternans for frequencies > 4 Hz when fitting the SERCA conductivity at 1 Hz and is discussed in section 6.2 of Appendix.
In the RNaK model we reduced Na+/K+ affinity to Na+. Results in Lewalle et al. (2014) have showed an increase in the Na+/K+ pump affinity to Na+ in rats relative to the affinity in guinea pigs. To test the effect of this increase on the CFR we reduced the Na+/K+ affinity to Na+ and we altered the maximum I NaK current parameter, I NaK,max = 0.0002 μA, to obtain an intracellular Na+ concentration of around 10 mm, comparable to results at 37°C performed by Harrison et al. (1992) in rats at 1 Hz (for further details see section 1.1.4 of Appendix).
Simulated phenotypes for comparison to experimental data
Previous studies tested the CFR response in rats by observing the peak systolic [Ca2+]i (peak [Ca2+]i), diastolic [Ca2+]i (DCa) and magnitude of peak [Ca2+]i (MPCa = peak [Ca2+]i – DCa) fluorescence ratios (Frampton et al. 1991 b; Layland & Kentish, 1999). In our work, we simulated the peak [Ca2+]i frequency response (PCFR), the diastolic [Ca2+]i frequency response (DCFR), the magnitude of peak [Ca2+]i frequency response (MCFR) and the [Ca2+]SR frequency response, due to changes in [Ca2+]o. [Ca2+]o was varied from 1 to 2 mm with 0.2 mm steps. An extracellular concentration of 2 mm did not allow AP repolarization, generating alternans at all frequencies, and so was not considered for analysis. Measurements were conducted at steady state, varying frequency from 1 to 6 Hz with 1 Hz steps. Results of the peak [Ca2+]i, DCa, relative change of the magnitude (ΔMPCa) and [Ca2+]SR frequency‐dependent changes with [Ca2+]o are shown in Fig. 3. Here, the relative change of the magnitude, for each frequency i, is defined as:
| (2) |
where and N is the number of tested frequencies.
Results
Comparison between model results and experimental data
The final DD model shows close agreement between simulations and experimental data (see Fig. 2). The simulated Ca2+ transients, fitted to representative traces at 1 and 6 Hz, were in close agreement with the experimental data in rat ventricular myocytes at 37°C as shown in Fig. 2 G and H. Comparisons of modelling simulations against experimental measurements of peak [Ca2+]i, DCa, time to 50% relaxation of the [Ca2+]i transient (RT50) and time to peak [Ca2+]i (T peak) at both 1 and 6 Hz are summarized in Table 1.
Figure 2. Parameter fitting and model validation .
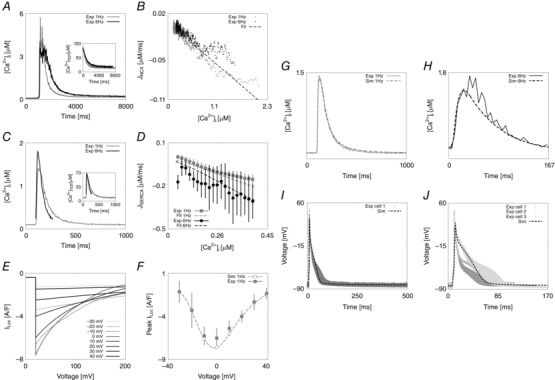
A, NCX fitting procedure. Experimentally measured caffeine‐induced transients recorded at 1 Hz (grey) and 6 Hz (black) and correspondent [Ca2+]TOT transient decays used for the fitting (in small window). B, NCX fitting results. Comparison of the experimental NCX flux (I NCX) as a function of internal Ca2+ at 1 Hz (grey) and 6 Hz (black) with the line of best fit (dashed black). NCX parameters were fitted in order for the pump to extrude 90% of the measured Ca2+ flux during a caffeine transient, while the remaining 10% was used to fit PMCa parameters. C, SERCA fitting procedure. Experimentally measured representative Ca2+ transients recorded at 1 Hz (grey) and 6 Hz (black) and correspondent [Ca2+]TOT transients (in small window). D, SERCA fitting results. Comparison of the experimental SERCA flux (J SERCA), obtained by integrating the previously fitted models for NCX and PMCa with the Ca2+ traces at 1 and 6 Hz and the simulated SERCA flux (dashed lines). To characterize SERCA, the [Ca2+]i fluxes from 157 [Ca2+]i transients measured in 5 cells at 1 Hz and 217 [Ca2+]i transients measured in five different cells at 6 Hz were calculated after 110 ms (at 1 Hz) and 80 ms (at 6 Hz) had elapsed from the peak of the [Ca2+]i transient. The experimentally measured values are expressed by horizontal bars (mean ± σ) with colours representing different frequencies, 1 Hz (grey) and 6 Hz (black). The fittings at 1 and 6 Hz are represented by dashed grey and black lines, respectively, at 1 and 6 Hz. E, LCC fitting procedure. Simulated peak current–voltage protocol. A series of voltage clamps are performed between –40 and 40 mV with 10 mV steps, for 200 ms. This simulation allows recording of the dependence of peak L‐type current on voltage. F, LCC fitting result. Bell‐shaped peak I LCC–V relationship, experiments (squares) and fit (circles and interpolating dashed line). G, experimental (continuous grey line) and simulated (dashed grey line) Ca2+ transient at 1 Hz. H, experimental (continuous black line) and simulated (dashed black line) Ca2+ transient at 6 Hz. I, experimental (continuous grey line) and simulated (dashed black line) AP at 1 Hz. J, experimental (continuous grey lines, for 3 different cells) and simulated (dashed black line) AP at 6 Hz.
Table 1.
Experimental and simulated [Ca2+]i transient characteristics at 1 and 6 Hz
| [Ca2 + ]i metrics | Unit | Experimental values | Simulated values |
|---|---|---|---|
| Peak [Ca2 + ]i | |||
| 1 Hz | μm | 2.000 ± 1.000 | 1.420 |
| 6 Hz | μm | 1.900 ± 0.850 | 1.439 |
| DCa | μm | ||
| 1 Hz | μm | 0.105 ± 0.016 | 0.106 |
| 6 Hz | μm | 0.220 ± 0.090 | 0.245 |
| RT50 | |||
| 1 Hz | ms | 82 ± 15 | 111 |
| 6 Hz | ms | 66 ± 9 | 61 |
| T peak | |||
| 1 Hz | ms | 30 ± 9 | 27 |
| 6 Hz | ms | 32 ± 8 | 25 |
To validate the model, we measured the ratio of Ca2+ extrusion via SERCA, NCX and PMCa at 1 Hz and found those to be 88.9%, 9.5% and 1.6%, respectively. This compares well to measurements of 87–92%, 7.5–9% and 1–3.7% observed experimentally (Bassani et al. 1992; Negretti et al. 1993; Choi & Eisner, 1999; Mackiewicz & Lewartowski, 2006). The simulated AP is also comparable with the experimental observations at 1 and 6 Hz. Figure 2 I and J shows the modelled AP superimposed to the available experimental measurements in one cell at 1 Hz and three different cells at 6 Hz. The simulated and experimentally measured AP characteristics are summarized in Table 2 where we show values for: resting membrane voltage, peak voltage, peak dV/dt, action potential duration at 20% repolarization (APD20), 50% repolarization (APD50), 70% repolarization (APD70) and 90% repolarization (APD90). Calcium and AP characteristics at all tested frequencies from 1 to 6 Hz are shown in section 2 of Appendix.
Table 2.
Experimental and simulated AP characteristics at 1 and 6 Hz
| AP metrics | Units | Experimental values | Simulated values |
|---|---|---|---|
| Resting membrane voltage | |||
| 1 Hz | mV | −87.34 ± 1.47 | −83.06 |
| 6 Hz | mV | −85.16 ± 3.03 | −83.16 |
| Peak voltage | |||
| 1 Hz | mV | 35.26 ± 3.09 | 38.52 |
| 6 Hz | mV | 37.43 ± 8.95 | 28.82 |
| APD20 | |||
| 1 Hz | ms | 1.82 ± 0.27 | 2.6 |
| 6 Hz | ms | 1.88 ± 0.62 | 3.0 |
| APD50 | |||
| 1 Hz | ms | 10.07 ± 1.72 | 15.7 |
| 6 Hz | ms | 12.21 ± 6.24 | 20.6 |
| APD70 | |||
| 1 Hz | ms | 23.09 ± 3.01 | 33.0 |
| 6 Hz | ms | 31.01 ± 13.45 | 34.6 |
| APD90 | |||
| 1 Hz | ms | 43.41 ± 7.08 | 50.6 |
| 6 Hz | ms | 55.52 ± 14.51 | 48.9 |
| Peak | |||
| 1 Hz | mV | 256.84 ± 44.93 | 171.76 |
| 6 Hz | mV | 223.16 ± 39.31 | 132.87 |
CFR response in rats at physiological temperature
Using our species‐ and temperature‐specific rat electrophysiology model, we observed the CFR response for the DD, CAMK, NO CAMK and RNaK models. The results of our study are reported in Fig. 3 and show the simulated rate‐dependent changes in peak [Ca2+]i, DCa, ΔMPCa and [Ca2+]SR due to changes in [Ca2+]o in the four developed models. For completeness, phenotypes changes with frequency in all model variants are also reported in Table 12 (Appendix).
The PCFR in the DD model shows biphasic behaviour with frequency, with a negative staircase in the range 1 Hz to 2 or 3 Hz and a positive staircase in the range 2 or 3 Hz to 6 Hz, depending on [Ca2+]o. The same PCFR response is also visible in the RNaK model. In the CAMK model we see a positive PCFR at [Ca2+]o = 1.8 mm and the same biphasic response as the DD model at lower [Ca2+]o, while in the NO CAMK model we see a shift of the biphasic response, decreasing from 1 Hz to 4 or 5 Hz and increasing from 4 or 5 Hz to 6 Hz, depending on [Ca2+]o.
The MCFR in the DD model shows a mild biphasic staircase, negative from 1 Hz to 4 Hz and positive from 4 Hz to 6 Hz at [Ca2+]o = 1.8 mm, with a shift of the turning point to lower frequencies as we decrease [Ca2+]o. Results of the CAMK model and RNaK model show biphasic MCFR, with a shift of the turning point to lower frequencies compared with the DD model at almost all tested levels of [Ca2+]o. The case [Ca2+]o = 1.8 mm in the CAMK model shows positive MCFR. In the NO CAMK model, we report a negative MCFR staircase, at all tested levels of [Ca2+]o.
The DCFR shows a positive staircase with frequency in all the developed models. Compared with the DD model, we see a slight increase in diastolic [Ca2+]i in the NO CAMK and RNaK models at [Ca2+]o = 1.8 mm.
The [Ca2+]SR frequency response in the DD model is biphasic for [Ca2+]o = 1.0 mm and decreases with frequency for higher tested [Ca2+]o. Biphasic [Ca2+]SR frequency response is also shown in the RNaK model, negative in the range 1 Hz to 2 or 3 Hz and positive in the range 2 or 3 Hz to 6 Hz, depending on [Ca2+]o. A contrasting behaviour is reported in the CAMK and NO CAMK models where the [Ca2+]SR decreases with frequency for almost all tested levels of [Ca2+]o.
When increasing [Ca2+]o, we see a general increase in peak [Ca2+]i and [Ca2+]i transient magnitude in all the four models. Interestingly, diastolic [Ca2+]i shows a decrease at 1–2 Hz followed by an increase at 2–6 Hz.
Intracellular and extracellular fluxes
To observe how single fluxes affect the CFR, we report the changes in all Ca2+ fluxes with [Ca2+]o and frequency. The observed fluxes are the following: sarco/endoplasmic reticulum Ca2+‐ATPase (SERCA), ryanodine receptors (RyR), SR leak (SRl), troponin (TRPN), L‐type channels (LCC), Na+/Ca2+ exchanger (NCX), sarcolemma Ca2+‐ATPase (PMCa) and background Ca2+ (CaB). In these reported results, we have included the effect of the rapid calmodulin buffer on the Ca2+ fluxes.
Specifically, we have assumed a rapid Ca2+ buffering equation for the calmodulin buffer:
| (3) |
where,
| (4) |
Here, k CMDN is the half‐saturation constant and B CMDN is the total cytosolic calmodulin concentration, whose values were parameterized from the comprehensive model of the canine ventricular myocyte developed by Greenstein & Winslow (2002), [Ca2+]i is the intracellular Ca2+ concentration and [Ca2+]TOT is the total Ca2+ concentration. This means that a portion of the [Ca2+]TOT is buffered and the remaining portion is the free [Ca2+]i.
Equation (1) expands to
| (5) |
based on
| (6) |
Changes in fluxes due to changes in [Ca2+]o and frequency were observed in two different cases. In the first case (without rapid buffering), we integrated and summed the single fluxes to calculate the changes in [Ca2+]TOT with frequency and [Ca2+]o. In the second case (with rapid buffering), we integrated and summed each flux multiplied by the rapid calmodulin buffer coefficient to observe the changes in [Ca2+]i with frequency and [Ca2+]o. The currents were integrated from the time that the stimulus was applied to the time that the peak calcium transient was reached (T peak). [Ca2+]o was varied from 1 to 1.8 mm with 0.2 mm steps. Measurements were conducted at steady state and frequency was varied from 1 to 6 Hz with 1 Hz steps. The variation (ΔI) of the integral (I) as a function of frequency, in the case with and the case without buffering, is presented in Fig. 4. Here, the variation of the integral, for each frequency i, is defined as:
| (7) |
where and N is the number of tested frequencies.
Figure 4. The intracellular and extracellular fluxes behind CFR .
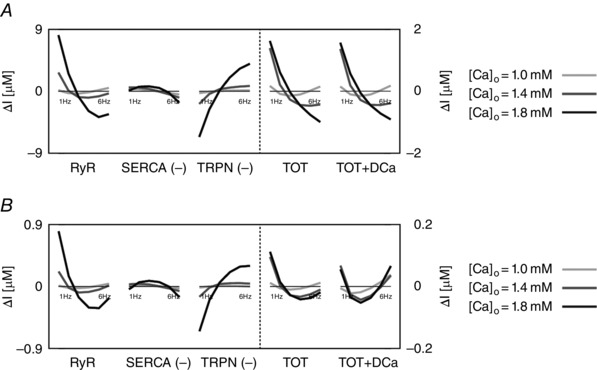
DD model intracellular and extracellular current variation of integrals (ΔI) as a function of frequency (1–6 Hz). A, DD model without rapid calmodulin buffer. B, DD model with rapid calmodulin buffer. In both cases the integrals were evaluated from time = 0 to time = T peak, where T peak is the time to peak of the correspondent simulated Ca2+ transient. Colours represent different extracellular Ca2+ concentrations: 1 mm (light grey), 1.4 mm (dark grey) and 1.8 mm (black). The most important fluxes, plotted in the figure are the following: ryanodine receptors (RyR), Ca2+‐ATPase (SERCA), troponin buffer (TRPN), total current (TOT) and total current plus diastolic Ca2+ (TOT+DCa). The other observed fluxes, L‐type Ca2+ channel (LCC), background Ca2+ current (CaB), reverse mode Na+/Ca2+ exchanger (NCXR), forward mode Na+/Ca2+ exchanger (NCXF), Ca2+ pump (PMCa) and SR leak current (SRl) were one or more orders of magnitude smaller, and therefore we did not include them in the figure.
These results identify the main currents responsible for the size and magnitude of the Ca2+ transient to be the RYR, SERCA and TRPN Ca2+ fluxes. All other currents were one or more orders of magnitude smaller than those. Figure 4 shows the variation of the integrals (ΔI) up to peak [Ca2 + ]i (time < T peak) of those currents in the DD model, the total current (TOT) and the sum of the total current plus the diastolic [Ca2+]i (TOT+DCa), for [Ca2+]o = 1.0, 1.4 and 1.8 mm. To clarify, negative fluxes (SERCA, TRPN) are labelled with (−).
At [Ca2+]o = 1.0 mm, in the case without buffering, the variation of the integral of the total flux up to the peak (TOT) is biphasic. We see an increase in SERCA and a general decrease in TRPN flux, when frequency is increased from 1 to 6 Hz. Here, the biphasic response of the RyR, is responsible for the biphasic PCFR response we have shown in Fig. 3. In fact, in the negative tract of the biphasic PCFR response, the RyR shows a decrease in flux with frequency from 1 to 2 Hz, while in the positive tract of the biphasic PCFR response the RyR shows an increase in flux with frequency from 2 to 6 Hz. These results indicate that the turning point of the RyR efflux, changing from negative to positive staircase with frequency, is consistent with the turning point of the PCFR response. We know that DCa increases with frequency, as reported in many previous studies and demonstrated in the results of our model. Changes in DCa, which are not accounted for in TOT, might thus also play a significant role in PCFR changes. Adding DCa to the total flux (TOT+DCa) we still report the biphasic trend shown in TOT. At [Ca2+]o = 1.0 mm, in the case with buffering, TOT is still biphasic and the biphasic behaviour is further amplified in the TOT+DCa flux.
At [Ca2+]o = 1.4 and 1.8 mm, in the case without buffering, TOT decreases with frequency and adding DCa to the total flux (TOT+DCa) does not change the non‐biphasic trend shown for the total flux. Here, the RyR efflux is still biphasic but flattened and the transition from a negative to a positive staircase is shifted to higher frequencies compared with the case at [Ca2+]o = 1.0 mm. In the positive tract of the RyR biphasic response (i.e. at higher frequencies), SERCA activity is enhanced, thus inducing a negative PCFR. The biphasic PCFR at [Ca2+]o = 1.4 and 1.8 mm, seen in Fig. 3, only appears when the effect of the rapid calmodulin buffer is included in the integrals evaluation, revealing the importance of the buffering system in shaping the PCFR response. This result is further amplified by the frequency‐dependent increase of DCa, as seen in TOT+DCa. Particularly, in the case [Ca2+]o = 1.8 mm, the DCa induces a shift of the PCFR biphasic turning point to lower frequencies, showing the significant role of DCa in the PCFR.
Discussion
We have developed a biophysical model of rat ventricular cardiac myocyte electrophysiology, parameterized, for the first time to our knowledge, at a physiological temperature and capable of capturing Ca2+ and AP responses to changes in pacing frequency. In the baseline DD model, we have reported a biphasic PCFR, shifting from a negative to positive staircase as the rat physiological frequency range is approached, consistent with previously reported studies (Koch‐Weser & Blinks, 1963; Borzak et al. 1991; Endoh, 2004). Using our modelling framework we have shown that (1) changes in CAMKII‐mediated SERCA activity play a major role in shaping the biphasic PCFR; (2) CAMKII‐mediated SERCA, LCC and I to activity enhance the biphasic MCFR response; and (3) a reduction of Na+/K+ affinity for Na+ induces a shift of the PCFR and MCFR biphasic staircases. We suggest that the PCFR is mainly driven by the combined effect of the rapid calmodulin buffer and the frequency‐dependent changes in DCa.
Model development
The heterogeneity in species and temperature in available measurements able to be used for model parameterization is a notable limitation in the computational physiology approach. This situation hampers model reliability and obfuscates the translation of animal results into human studies. For this reason, the first aim of our work was to develop a species‐ and temperature‐consistent rat electrophysiological model at a physiological frequency and temperature, using consistent experimental data whenever possible. Using the result of this process, our goal was to show the direct link between model parameters and experimental sources.
The main advance of our model is that it significantly reduces the dependency on data from other species and non‐physiological temperatures and introduces modified components to reflect temperature effects, as shown in the phylogenetic tree in Fig. 1 C. In our model, 14 out of 17 components were fitted using rat data and, among those, 13 components were fitted using rat data at physiological temperatures. This compares with 8 out of 16 components parameterized using rat data in previous models.
Our model of the rat ventricular cardiac myocyte electrophysiology matches the experimental measurements that we performed in rat ventricular myocytes at 37°C as seen in ‘Results, Comparison between model results and experimental data’ and it represents a robust framework to test Ca2+ responses to changes in pacing frequency and [Ca2+]o.
Validation
Using the developed framework, the second aim of our study was to observe the Ca2+ response of the model to changes in frequency and [Ca2+]o, as a measure of the FFR.
FFR and CFR measurements are not consistent across the literature. This lack of consensus means that the model cannot match all measurements. Model results at [Ca2+]o = 1.8 mm are, however, consistent with the experimental observations, showing an increase in peak [Ca2+]i and DCa and a decrease in [Ca2+]i transient magnitude when increasing frequency from 1 to 6 Hz. It should be noted that while our model was developed at 37°C, changes in temperature have been shown to induce changes in channel behaviour that could also affect the Ca2+ response to frequency. Furthermore, we used calibrated measurements, in contrast to the majority of publications in the literature, which only report ratio measurements. If calibrated, ratio measurements would be altered, thus also affecting the observations. To validate our model's predictions, we have compared the simulated PCFR, DCFR and MCFR in our model with experimental data in the literature.
The DD model in Fig. 3 shows a biphasic PCFR, negative in the range 1 Hz to 2 or 3 Hz and positive in the range 2 or 3 Hz to 6 Hz, depending on [Ca2+]o. Borzak et al. (1991) showed a biphasic FFR in rats negative in the range 0.1–1 Hz, flat in the range 1–2 Hz and positive in the range 2–6 Hz, which agrees with the biphasic changes in CFR shown in our model. In accordance with our observations, previous work in rats has shown a negative FFR at frequencies lower than 1–2 Hz (Koch‐Weser & Blinks, 1963; Capogrossi et al. 1986; Mubagwa et al. 1997; Layland & Kentish, 1999). The positive PCFR predicted by the model at high frequencies is consistent with the measurements of Dibb et al. (2007) and Monasky & Janssen (2009) that show respectively a positive PCFR in rats at 37°C for frequencies in the range 4–8 Hz and a positive PCFR in rats at 37°C when increasing frequency from 4 to 8 Hz at [Ca2+]o = 1.5 mm.
In the DD model, the MCFR shows a biphasic staircase. Our results replicate the MCFR response that we reported in the experimental data at [Ca2+]o = 1.8 mm and are in accordance with Frampton et al. (1991) and Picht et al. (2007), who showed a negative MCFR respectively in rat for frequencies in the range 0.2–2 Hz and mouse in the range 0.2–4 Hz. Other published works showed a positive MCFR response (Layland & Kentish, 1999; Dibb et al. 2007; Monasky & Janssen, 2009). Among those, experiments of Monasky & Janssen (2009) in rats at 37°C showed a positive MCFR increasing frequency from 4 to 8 Hz at [Ca2+]o = 1.5 mm, in accordance with our findings. Layland & Kentish (1999) showed a positive MCFR for all frequencies from 1 to 6 Hz at 30°C and [Ca2+]o = 1.0 mm. Interestingly, when increasing [Ca2+]o to 8 mm, they reported negative PCFR and MCFR in the range 1–2 Hz, thus demonstrating a clear dependency of their observations on the experimental conditions.
DCFR is less often reported and shows a much more consistent behaviour, increasing with frequency in many previous publications (Layland & Kentish, 1999; Dibb et al. 2007; Monasky & Janssen, 2009). Consistent with those experiments, our DD model predicts a positive DCFR across frequencies.
Increasing [Ca2+]o caused a general increase in peak [Ca2+]i and [Ca2+]i transient magnitude. This result is consistent with the findings reported by Bouchard & Bose (1989), showing an increase in peak [Ca2+]i in rats, when increasing [Ca2+]o from 0.5 to 2.5 mm. When [Ca2+]o is increased, our model shows a decrease in DCa at 1–2 Hz followed by an increase at 2–6 Hz. Layland & Kentish (1999) reported an increase in DCa with [Ca2+]o at all frequencies, in disagreement with our observations in the range 1–2 Hz. Interestingly, Frampton et al. (1991 b) reported a slight decrease in DCa when increasing [Ca2+]o from 0.5 to 1 mm at 1 Hz frequency in rat measurements at 24°C followed by an increase when further increasing [Ca2+]o to 3 and 6 mm.
The [Ca2+]SR hypothesis and analysis of the intracellular and extracellular fluxes behind CFR
Bers (1989) hypothesised that changes in [Ca2+]SR are responsible for changes in the FFR response, where an increase in [Ca2+]SR induces a positive FFR response and a decrease in [Ca2+]SR induces a negative FFR response. In the DD model at [Ca2+]o = 1.0 mm, the [Ca2+]SR has a biphasic response, negative at lower frequencies and positive at higher frequencies. The [Ca2+]SR decreases with frequency for the remaining tested values of [Ca2+]o. These DD model results contradict this hypothesis by showing positive PCFR and negative [Ca2+]SR–frequency response.
To observe the role of each of the ion channels on the CFR in the DD model and test how the fast calmodulin buffer affects the response, in Fig. 4 we analysed the variation of the integrals of each one of the Ca2+ fluxes in two cases: with and without fast calmodulin buffering. These results showed that the biphasic PCFR response is mainly driven by changes in the RyR flux with frequency at low [Ca2+]o and the effect of the rapid calmodulin buffer at high [Ca2+]o. In all cases, changes in RyR efflux modulate the frequency‐dependent increase in DCa that, along with the non‐linear behaviour of the buffering curve, induces changes in the PCFR.
In Fig. 5, we propose a schematic representation of the mechanism behind changes in the PCFR, due to the DCa and the non‐linearity of the buffering curve. Assuming that the DCai increases with frequency (DCai,1Hz < DCai,6Hz), the DCaTOT will increase with frequency (DCaTOT,1Hz < DCaTOT,6Hz). The same change in CaTOT (∆CaTOT,1Hz = ∆CaTOT,6Hz), due to the non‐linearity of the buffering curve, will translate to a greater change in the Cai (∆Cai,1Hz < ∆Cai,6Hz). In particular, even a smaller change in CaTOT (∆CaTOT,6Hz < ∆CaTOT,1Hz) can result in increased Cai change (∆Cai,1Hz < ∆Cai,6Hz). In this way the PCFR response is altered by two distinct mechanisms: the change in DCa with frequency and the buffering curve. The effects of the buffering curve on the PCFR were shown to be particularly prominent with increasing [Ca2+]o. As we have reported in our results, increased [Ca2+]o translates to increased [Ca2+]i, which, in turn, causes a shift towards a shallower area of the buffering curve, where this mechanism is more accentuated.
Figure 5. Changes in PCFR due to changes in diastolic calcium and buffering .
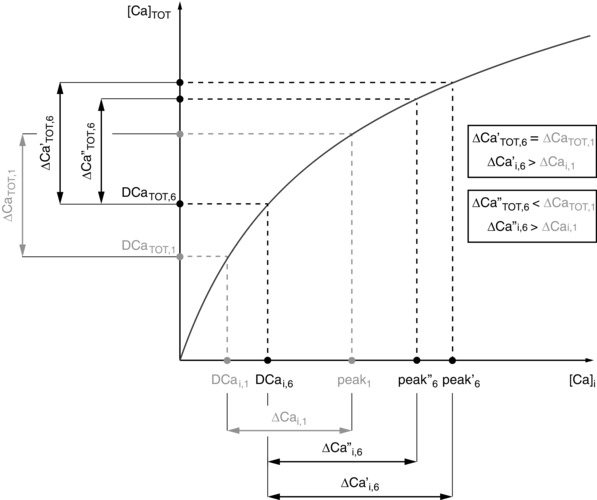
Schematic diagram showing how changes in diastolic Ca2+ (DCa) and a shift of the buffering curve (black curve in figure) affect the PCFR. Assuming that the DCai increases with frequency (DCai,1Hz < DCai,6Hz), the DCaTOT will increase with frequency (DCaTOT,1Hz < DCaTOT,6Hz). The same change in CaTOT (ΔCaTOT,1Hz = ΔCaTOT,6Hz), due to the non‐linearity of the buffering curve, will translate to a greater change in the Cai (ΔCai,1Hz < ΔCai,6Hz). In particular, even a smaller change in CaTOT (ΔCaTOT,6Hz < ΔCaTOT,1Hz) can cause an increase in the Cai change (ΔCai,1Hz < ΔCai,6Hz). In this way the PCFR response is altered by two distinct mechanisms: the change in DCa and the buffering curve.
Overall, these results show that the biphasic PCFR is caused by the biphasic staircase of the RyR efflux at [Ca2+]o = 1.0 mm. However, the flattened biphasic behaviour of the RyR release is balanced by the increase of SERCA activity with frequency and is not sufficient to generate a biphasic PCFR response at [Ca2+]o = 1.4 and 1.8 mm. In our analysis, the biphasic PCFR response is caused by the non‐linearity of the buffering curve. The RyRs and SERCA operate by modulating DCa, which further amplifies the behaviour. Notably, this mechanism is model independent, as both the increase in DCa with frequency and the non‐linearity of the buffering curve are well‐known properties of ventricular myocytes. The mechanism behind PCFR changes, shown in Fig. 5, explains how the buffering system and DCa affect the PCFR response.
Model variants still reveal the importance of the buffering system on the PCFR
As already discussed, previous works in rats proposed the hypotheses that CAMKII regulation of the L‐type channel, I to current and SERCA activity and a reduction of the Na+/K+ pump affinity to Na+ could be responsible for alterations in the FFR and CFR responses. In our work we tested these hypotheses by altering the DD model to simulate those conditions.
Results of the CAMK model in Fig. 3 show that the PCFR is qualitatively the same as that of the DD model, although we report a positive PCFR at [Ca2+]o = 1.8 mm and a clear enhancement of the MCFR positive staircase. Additional simulations revealed the same mechanism already presented for the DD model in the previous section (‘Discussion, The [Ca2+]SR hypothesis and analysis of the intracellular and extracellular fluxes behind CFR’), showing that the PCFR is mainly driven by the RyR flux, with a clear effect of the rapid calmodulin buffer and DCa on the response, especially at high levels of [Ca2+]o (for further details see section 6.1 of Appendix). Interestingly, previous studies showed positive MCFR response (Layland & Kentish, 1999; Dibb et al. 2007; Monasky & Janssen, 2009) that was not replicated in our DD model but is significantly enhanced in the CAMK model, highlighting the importance of CAMKII regulation on the MCFR. These results show that CAMKII‐mediated activity, directly acting on Ca2+ release from the RyR, enhances the positive MCFR staircase.
Analysis of the NO CAMK model reveals that CAMK inhibition mainly affects the PCFR, MCFR and [Ca2+]SR. Compared with the biphasic behaviour in the DD model, the NO CAMK model in Fig. 3 reveals a flattened PCFR staircase, negative MCFR in all cases and a notable increase in [Ca2+]SR at low frequencies compared with the DD model, which in turn activates more Ca2+ release from the RyR. Consistent with our results of the DD model, additional simulations showed that the RyR flux and the dependent increase in DCa are the main responsible for the PCFR staircase in this case (for further details see section 6.2 of Appendix). Our results are consistent with Wu et al. (2012) who showed that CAMKII inhibition flattens the FFR response in mice. These results show that CAMKII up‐regulated SERCA modulates the shift from negative to positive PCFR by altering the [Ca2+]SR, inducing changes in the RyR frequency response.
Compared with the DD model, results of the RNaK model in Fig. 3 show a shift of the turning point of the biphasic PCFR and MCFR responses to lower frequencies, reduced [Na+]i for frequencies < 2 or 3 Hz and augmented [Na+]i for frequencies > 2 or 3 Hz depending on [Ca2+]o. The biphasic PCFR response here reveals the same mechanism as demonstrated in the DD model (for further details see section 6.3 of Appendix). Decreasing the Na+/K+ pump affinity for Na+, our model shows positive PCFR and MCFR for frequencies > 2 or 3 Hz depending on [Ca2+]o, highlighting the role of [Na+]i in enhancing the positive staircase effect at physiological frequencies, as suggested by Langer et al. (1975).
Conclusions
In our work, we have concluded that a biphasic PCFR response in rats at 37°C is due to the biphasic behaviour of the RyR efflux at low [Ca2+]o and the combined effect of the Ca2+ buffering mechanism and the frequency‐dependent increase in DCa at higher levels of [Ca2+]o. This result is consistent with the observation of a shift from negative to positive FFR when approaching the rat physiological range of frequencies. We have shown that CAMKII‐mediated SERCA, LCC and I to activity, directly acting on Ca2+ release from the RyR, enhances the positive MCFR staircase. Absence of a CAMKII‐mediated increase in SERCA activity affects the CFR by altering the [Ca2+]SR frequency response, which in turn affects RyR release, flattening the PCFR and inducing negative MCFR. Reduced Na+/K+ affinity to Na+ acts on the CFR, increasing [Na+]i and [Ca2+]i at high frequencies and inducing a shift of the biphasic PCFR and MCFR turning point to lower frequencies.
Additional information
Competing interests
The authors declare there are no competing interests.
Author contributions
S.G. developed the modelling framework, performed the parameter fittings and analysis, and wrote the manuscript. A.T.R, M.F and W.L. acquired the data and assisted in the writing of the manuscript. S.A.N. and N.P.S. contributed to the conception and motivation of the analysis and to the interpretation of the results, and assisted in the writing of the manuscript. All authors approved the final version of the manuscript. All authors agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. All persons designated as authors qualify for authorship.
Funding
This work was supported by the Virtual Physiological Rat Project (NIH 1 P50 GM094503‐01). The project has also received funding from the European Union's Horizon 2020 research and innovation programme (Consolidator grant, WEL) under grant agreement No 647714, South‐Eastern Norway Regional Health Authority, Anders Jahre's Fund for the Promotion of Science, the Norwegian Institute of Public Health, Oslo University Hospital Ullevål, and the University of Oslo.
Acknowledgements
The authors acknowledge financial support from the Department of Health via the National Institute for Health Research (NIHR) comprehensive Biomedical Research Centre award to Guys & St Thomas NHS Foundation Trust in partnership with Kings College London and Kings College Hospital NHS Foundation Trust.
Development of the DD model, the parameter fitting procedure and further information about model's alterations and limitations
To achieve a model that captures rat cardiac electrophysiology and can simulate graded response, we combined the Pandit electrophysiology framework (Pandit et al. 2001) with the Hinch calcium dynamics model (Hinch et al. 2004). Figure 6 shows the components taken from the Pandit model (in black) and the Hinch model (in grey). Section 1 describes the model development and parameter refitting procedure. In this section we show how we developed the reconciliation of units between the two models, we describe choices for cell, SR volume and capacitance parameters, intracellular and extracellular Na+ and K+ concentrations, fixed ionic concentrations and buffers, and we describe the parameter fitting procedure for all the fitted channels within the model. Section 2 describes the results for all simulated Ca2+ and AP phenotypes at frequencies from 1 to 6 Hz with step 1 Hz. In sections 3 and 4 we show the effects of changes in [K+]o and AP on the PCFR, DCFR, MCFR and [Ca2+]SR frequency response. Section 5 describes how we included CAMKII alteration of L‐type channel and transient outward K+ current in the CAMK model. Sections 6 and 7 provide insight about the differences in CFR in the CAMK, NO CAMK and RNaK model compared with the DD model.
Figure 6. Inheritance of components in our model .
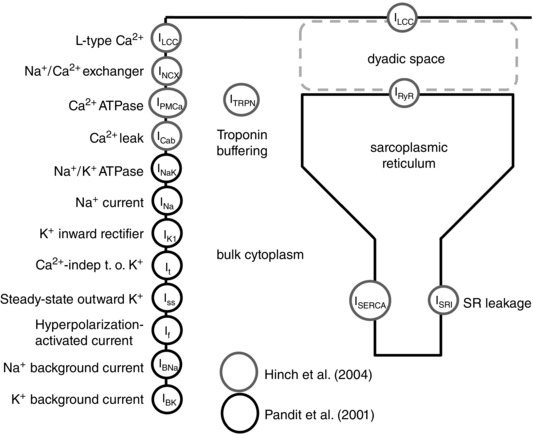
Schematic showing the coupling between Pandit and Hinch models. Components are highlighted in black when their equations were kept from Pandit, in grey when their equations were kept from Hinch.
Model development and parameter refitting
We explain in detail the coupling between the Pandit (Pandit et al. 2001) and Hinch (Hinch et al. 2004) models and the parameter fitting procedure that we adopted to reparametrize the developed electrophysiology framework.
Model development
Unit and structural consistency
The movement of ions across the cell membrane can be represented in terms of ion fluxes or whole‐cell current. In the Hinch model all the ionic transports are expressed in terms of calcium ions flux in millimolar per millisecond whereas in the Pandit model all the cell currents are represented in nanoamps. This type of inconsistency cannot be simply solved using an automated conversion between equivalent units but instead requires additional information regarding the volume of the myocyte or the valence of the species. Using the same approach developed by Terkildsen et al. (2008), we converted the Hinch calcium fluxes into compatible calcium currents using the formula:
| (A1) |
where j is the flux (in Hinch), z is the valence, F is the Faraday constant and V myo is the volume of the myocyte (see Table 3).
Table 3.
Capacitance and volumes
| Parameter | Unit | Definition | |
|---|---|---|---|
|
|
μF | Membrane capacitance | |
|
|
μm3 | Volume of the myocyte | |
|
|
μL | Volume of the myocyte | |
|
|
μL | Volume of the SR |
In general, units are expressed in ms, mV, mm, μA, μF, mS.
Cell, SR volume and capacitance
The membrane capacitance C m was kept from the original Pandit model, based on experimental measurements in rat ventricular cells (Clark et al. 1993). The cell and SR volumes were maintained from Hinch et al. (2004), based on Greenstein & Winslow (2002) (see Table 3).
Na+ and intracellular and extracellular concentrations
We assumed [Na+]i = 10 mm at 1 Hz, consistent with experiments developed in rats at 37°C (Harrison et al. 1992). Following the hypothesis by which increase in rate might produce increase in intracellular sodium ([Na+]i) (Woodbury, 1963; Cohen et al. 1982; Maier et al. 1997), we assumed [Na+]i = 14 mm at 6 Hz. Extracellular sodium ([Na+]o) was held fixed to a value of [Na+]o = 140 mm following experiments conducted in rats. Extracellular potassium ([K+]o) was set to a value of [K+]o = 5.4 mm at all frequencies. Experimentally measured intracellular and extracellular Na+ concentrations in previous works can be observed in Table 4 while intracellular and extracellular concentrations in previous works can be observed in Table 5.
Table 4.
Intracellular and extracellular concentrations NR: not reported
| Publication | Temperature (°C) | Frequency (Hz) | [Na+]i (mm) | [Na+]o (mm) |
|---|---|---|---|---|
| Polimeni (1974) | NR | NR | 21 ± 1 | 140 ± 2 |
| Polimeni & Al‐Sadir (1975) | NR | NR | NR | 134 ± 1 |
| Shattock & Bers (1989) | 30 | 1 | 16.71 ± 0.6 | NR |
| Harrison et al. (1992) | 37 | 1 | 10.26 ± 0.23 | NR |
| Borzak et al. (1992) | 37 | NR | 14 ± 2 | NR |
| Donoso et al. (1992) | 27 | 1 | 10.7 ± 1.2 | NR |
| Levi et al. (1994) | 30 | 1 | 10.9 ± 0.74 | NR |
| Baartscheer et al. (1997) | 37 | 8 | 9.6 ± 0.4 | NR |
| Despa et al. (2002) | 25 | Rest | 11.1 ± 0.7 | NR |
Table 5.
intracellular and extracellular concentrations NR: not reported
Fixed ionic concentrations and buffers
The Ca2+‐binding proteins included in our model are troponin, calmodulin and EGTA. Total cytosolic calmodulin concentration (B CMDN) and half‐saturation constant (K CMDN) values were taken from the comprehensive model of canine ventricular myocyte developed by Greenstein & Winslow (2002). Ca2+ buffering to TRPN was modelled as described by Hinch et al. (2004). All troponin parameters were obtained from the model of ferret ventricular myocytes at room temperature (Bondarenko et al. 2004). The effects of the intracellular Ca2+ buffer EGTA were also modelled as described by Pandit, following an adaptation from (Winslow et al. 1999) mimicking the experimental conditions developed in Shimoni et al. (1995). The Ca2+‐binding protein parameters are shown in Table 6.
Table 6.
Fixed ionic concentrations and buffers
| Parameter | Unit | Definition | |
|---|---|---|---|
|
|
mm | Total cytosolic calmodulin concentration | |
|
|
mm | Half‐saturation constant of calmodulin | |
|
|
mm −1 ms−1 | Binding rate of calcium to troponin | |
|
|
ms−1 | Dissociation rate of calcium to troponin | |
|
|
mm | Calcium half‐saturation constant for EGTA |
Parameter refitting procedure
Membrane Ca2+ extrusion: Na+/Ca+ exchanger (I NCX) and Ca2 + pump (I PMCa)
In single cell experiments, caffeine triggers full release of [Ca2+]SR, with subsequent increase of [Ca2+]i (Blayney et al. 1978; Klein et al. 1990; Sitsapesan & Williams, 1990; Meissner et al. 1997; Herrmann‐Frank et al. 1999). There are three main mechanisms of Ca2+ extrusion from the cytosol: I NCX, I PMCa and I SERCA. The presence of caffeine assures inhibition of the SERCA pump, which is no longer able to drive Ca2+ back to the SR allowing the assumption, exploited for the purposes of model fitting, that no Ca2+ SR reuptake occurs. This leaves only two currents actively contributing to Ca2+ extrusion: I NCX and I PMCa. During caffeine‐induced transients in rats, NCX and PMCa account for approximately 80–90% and 10–20% of the Ca2+ extrusion from the cell, respectively (Bassani et al. 1992; Choi & Eisner, 1999; Bers, 2001).
In our work, the experimental caffeine‐induced Ca2+ transients at 1 and 6 Hz were converted to the total cytosolic Ca2+ concentration ([Ca2+]TOT)using the following fast buffering approximation proposed by Trafford et al. (1999):
| (A2) |
where K buffer is the affinity of the buffer and B buffer is its concentration (the buffers used in our model are troponin, calmodulin and EGTA). This type of conversion is necessary because the calibrated fluorescence measurements describe the change in intracellular free Ca2+ ([Ca2+]i) and for our fitting purposes we are interested in the total flux of Ca2+ ions across the membrane ([Ca2+]TOT). After defining Peak[Ca2+]TOT as the maximum value of [Ca2+]TOT, each converted caffeine transient was separated into an early release phase, which occurred prior to Peak[Ca2+]TOT, and a later exponential decay, occurring after Peak[Ca2+]TOT, where the membrane calcium transporters extrude Ca2+ from the cytosol. The change in total amount of Ca2+ over time can be described as a differential equation:
| (A3) |
where and . Focusing on the later exponential decay of the caffeine‐induced [Ca2+]TOT transient and assuming that only I PMCa and I NCX are active, this reduces to:
| (A4) |
For this reason, we fitted the Ca2+‐dependent kinetics of the remaining two transporters to the later exponential decay of the curve. We assumed that the contribution of I PMCa to the decay is comparatively small and we attributed 90% of the total Ca2+ extrusion to I NCX. The flux through the NCX exchanger was modelled using the formulation from Hinch et al. (2004), developed by Luo & Rudy (1994):
| (A5) |
where g NCX is the pump rate of NCX, η is the parameter describing the dependence of NCX flux on voltage, F is the Faraday constant, V is voltage, R is the universal gas constant, T is temperature, K mNa is the Na+ half‐saturation of NCX, K mCa is the Ca2+ half‐saturation of NCX, K sat is the low potential saturation factor of NCX and [Na+]i, [Ca2+]i, [Na+]o and [Ca2+]o are the intracellular and extracellular Na+ and Ca2+ concentrations, respectively. All the parameters involved in the NCX formulation, except for g NCX, where kept from Hinch et al. (2004). Because [Na+]i is unlikely to change during the period that NCX is active, [Na+]i was assumed constant for the fitting, with a value [Na+]i = 10 mm. This implies that the equation takes the form of a first‐degree polynomial having two parameters: . As no major changes in NCX behaviour at different frequencies are reported in the literature, we fitted a linear relation along the two data sets at 1 and 6 Hz and evaluated the conductivity of the exchanger to be g NCX = 0.0515 mm ms−1.
Current through the Ca2+ pump was modelled using the formulation from Hinch et al. (2004), first published in Luo & Rudy (1994):
| (A6) |
where g PMCa is the maximal pump rate and K PMCa is the half‐saturation rate. In our simulations, I PMCa makes approximately 10% of the NCX job at both 1 and 6 Hz frequencies, which agrees with the reported percentage in the literature (Bers, 2001). Therefore, there was no need to re‐parameterize the pump. Parameter values were maintained from the Hinch model (Hinch et al. 2004): g PMCa = 5 × 10−6 mm ms−1 and K PMCa = 0.00035 mm.
Sarco/endoplasmic reticulum Ca2 + ‐ATPase (SERCA)
We assumed that during a field stimulated Ca2+ transient there are two sources of [Ca2+]i (I LCC and I RYR) and three [Ca2+]i sinks currents (I NCX, I PMCa and I SERCA). Fluorescence experiments in rats, performed under whole‐cell voltage‐clamp conditions and in the presence of EGTA to detect Ca2+ sparks (Song et al. 1998), revealed that after 80–100 ms, both I LCC and I RYR Ca2+ pathways are closed and the cell predominantly extrudes Ca2+ from the cytosol through I NCX, I PMCa and I SERCA. This implies that the effects of [Ca2+]i influx through I LCC and [Ca2+]i release through I RYR can be neglected when analysing the later part of the [Ca2+]i transient. Furthermore, using the models of I NCX and I PMCa described above, we can remove their effects on the change in Ca2+ to isolate the extrusion of Ca2+ attributed to SERCA. It must be noted that at higher pacing the pump's uptake becomes faster to facilitate frequency‐dependent acceleration of relaxation, a process mediated by Ca2+/calmodulin kinase II (CaMKII) that still remains unclear (Li et al. 1998; Hagemann et al. 2000; Huke & Bers, 2007).
In our work, the experimentally recorded Ca2+ transients were first converted to the total cytosolic Ca2+ concentration [Ca2+]TOT (see eqn (A2)) and then used for fitting purposes. The behaviour of the pump was studied taking into account the decay phase of the [Ca2+]i transients elicited by field stimulation at 1 and 6 Hz, integrated with the previously fitted models for I NCX and I PMCa. To characterize SERCA, the [Ca2+]i fluxes from 157 [Ca2+]i transients measured in five cells at 1 Hz and 217 [Ca2+]i transients measured in five different cells at 6 Hz were calculated after 110 ms (at 1 Hz) and 80 ms (at 6 Hz) had elapsed from the peak of the [Ca2+]i transient. The flux through SERCA (I SERCA) was modelled using the formulation from Hinch et al. (2004), previously published in Jafri et al. (1998):
| (A7) |
where g SERCA and K SERCA are the maximum pump rate and the half‐saturation of the SERCA pump, respectively. Plotting the change in total flux of Ca2+ across the membrane in time (d[Ca2+]TOT/dt) against the [Ca2+]free we fitted the function through our data and we evaluated the parameters a and b, respectively representing g SERCA and K SERCA. The SERCA formulation within the Hinch model (Hinch et al. 2004) did not take into account the frequency‐dependent behaviour. To approximate the lack of calmodulin up‐regulation of SERCA at different electrophysiological frequencies, we fitted the conductivity of the pump at 1 Hz (g SERCA1 = 0.47 × 10−3 μm 3 ms−1) and 6 Hz (g SERCA6 = 0.68 × 10−3 μm 3 ms−1) by assuming that the affinity parameter (K SERCA = 0.45 × 10−3 mm) did not change with frequency, consistent with the findings previously reported in the literature (Picht et al. 2007). Following the approach already used by Li et al. (2010), we included a CaMKII regulation model in the developed framework to simulate the effects of pacing frequency. The model, proposed by Hund and Rudy for canine ventricular myocytes (Hund & Rudy, 2004) and adapted from more recent finding by Li et al. (2010), includes three states representing the fractional occupancies of active CaMKII (f a), bound CaMKII (f b) and trapped CaMKII (f t):
| (A8) |
| (A9) |
| (A10) |
where α (0.05 ms−2) and β (0.0002 ms−1) are the phosphorylation and dephosphorylation rates of CaMKII, respectively, f 0 (5%) is the fraction of active CaMKII binding sites at equilibrium and K mCaM (0.7 μm) is the [Ca2+]i concentration at half‐maximum CaMKII activation. Using the experimental representative Ca2+ transients at 1 and 6 Hz, we measured the level of active CaMKII at both frequencies and we modelled the dependence of I SERCA on the kinase by defining g SERCA and K SERCA as a function of f a:
| (A11) |
| (A12) |
where ΔgCaMK is the maximum increase in g SERCA due to CaMKII and K m,CaMK is the half‐saturation coefficients. The line of best fit for g SERCA plotted against f a resulted in K m,CaMK = 2.224 and = 0.001158.
L‐type Ca2+ channels (LCCs) and Ryanodine Receptors (RyR)
The function of the LCC was investigated using the experimentally recorded peak I LCC–V relationship curve. During the peak I LCC–V experiment the membrane potential is held fixed at −40 mV and then clamped between −40 mV and 40 mV with 10 mV steps (see Fig. 2 E and F). I Na contribution is negligible, since the holding potential around −40 mV assures inactivation of the Na+ channel and the K+ currents are pharmacologically blocked. The peak transmembrane current is recorded at each membrane potential and gives an approximation of the I LCC current.
In our work, the current through the L‐type channels was modelled using the formulation from Hinch et al. (2004), a simplified Markovian model of the Jafri et al. (1998) model. The I LCC representation presents three states, I (inactivated), C (closed) and O (open), with the respective probabilities to move from one state to another:
| (A13) |
| (A14) |
| (A15) |
| (A16) |
where V L is the potential when 50% of the LCCs channels are open, ΔVL is the width of opening potentials, φL is the proportion of time the channels are still closed but in open mode, t L is the time switching between closed and open states, T L is the inactivation time, K L is the concentration when the LCCs inactivate, a and b are the biasings to make inactivation a function of V and J L is the permeability of a single channel (see Fig. 7). A Goldman–Hodgkin–Katz equation is then used to model the open channel current:
| (A17) |
where δ = zF/RT , z is the valence for Ca2+, F is the Faraday constant, R is the universal gas constant, T is temperature, J L is the permeability of the channel, V is voltage, and [Ca2+]o and [Ca2+]ds are respectively external Ca2+ and Ca2+ in the dyadic space. It must be noted that [Ca2+]ds is evaluated using the rapid equilibrium approximation:
| (A18) |
where J RyR is the current through the rynoadine receptors and g D is the Ca2+ flux permeability from the dyadic space to the cytosol. This approximation is one of the crucial steps in the Hinch model simplification (Hinch et al. 2004). This yields to the following equation for I LCC:
| (A19) |
where V myouL is the volume of the myocyte in microlitres.
Figure 7. LCC representation .
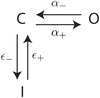
The figure is a schematic representation of the LCC model. There are three possible states, I (inactivated), C (closed) and O (open), with the respective probabilities to move from one state to another α+, α_, ε+ and ε_.
The model, despite its simplifying assumptions, still has nine parameters. We reproduced the peak I LCC–V experiment in silico and we performed a sensitivity analysis to evaluate the contribution of each of the nine parameters to the quality of the fit. The experiment was found to be primarily sensitive to the following parameters: V L, the potential when 50% of the LCC channels are open; J L, the permeability of a single channel; and φL, the proportion of time the channels are still closed but in open mode. In particular the parameters J L and φL scale the I–V curve while V L determines the slope. We then fitted the parameters to the available experimental data (Fig. 2 A).
The current through the RyR channels (I RYR) was modelled using the formulation from Hinch et al. (2004), a simplified Markovian model of Scheme 6 in Stern et al. (1999). The majority of experiments used to parameterize I RyR in Hinch were conducted in isolated SR. This means that they do not capture the process of Ca2+‐induced Ca2+‐release and are not consistent with our modelling framework (Chu et al. 1993; Sitsapesan & Williams, 1994; Mejía‐Alvarez et al. 1999). The flux through the RyR was modulated to match the experimentally measured time to peak of the Ca2+ transients at 1 and 6 Hz. In particular, the half‐concentration at activation of the RyR channel (K RyR) was increased from 0.041 to 0.065 mm. It must be noted that we increased the parameter representing the Ca2+ flux rate from the dyadic space to the cytosol (g D) from 0.065 μm 3 ms−1 to 0.099 μm 3 ms−1 to allow more Ca2+ to move between the compartments. This is reasonable as we are dealing with much bigger Ca2+ transients than those represented in Pandit et al. (2001). In fact, in the Pandit model, the peak of the simulated Ca2+ transients approximately spanned from 0.3 μm in the epicardial model to 0.6 μm in the endocardial model. The simulated results were compared with rat experimental traces in Bouchard et al. (1995) showing much higher Ca2+ transients with peak Ca2+ ≈ 1.2 μm in normal conditions. In our model, we took into account the notable increase in peak Ca2+ and amplitude by refitting the whole Ca2+ dynamic system.
The leak from the SR current I SR: evaluation of [Ca2+]SR
During a caffeine transient all Ca2+ is released from the SR and it is extruded from the cell via I NCX and I PMCa. There is no change in voltage, and therefore the L‐type channels remain in the closed state and SERCA is not pumping Ca2+ back to the SR. By integrating the flux of I NCX + I PMCa we can estimate an upper bound on the amount of Ca2+ in the SR. Furthermore, during a normal [Ca2+]i transient, Ca2+ is pumped back into the SR by SERCA. At a limit cycle the Ca2+ released by the SR must be replaced via SERCA. Integrating I SERCA over a cycle provides a lower bound estimate of the fraction of Ca2+ in the SR. With these assumptions we were able to estimate reasonable ranges for [Ca2+]SR at both 1 and 6 Hz: [Ca2+]SR ∈ [1.13 × 10−3, 2.62 × 10−3] mm at 1 Hz and [Ca2+]SR ∈ [0.97 × 10−3, 3.48 × 10−3] mm at 6 Hz. We then scaled the parameter representing the conductivity of the leak SR current, gSRL = 7.11 × 10−6 ms−1, in order to keep [Ca2+]SR within these plausible ranges.
The sodium potassium pump (I NaK)
In the Pandit model the I NaK formulation was inherited as a variant of the NKA model by Luo & Rudy (1994), developed using a spectrum of different species and temperatures (see Fig. 1 A). In our model, the current through I NaK was modelled using the formulation from Lewalle et al. (2014), directly parameterized from rat data at 37°C:
| (A20) |
where
| (A21) |
The maximum pump rate of I NaK was increased to a value I NaK = 0.00138 μA to maintain the intracellular Na+ gradients within the values found in the literature (see Table 4).
Other K+ and Na+ currents
The original Pandit electrophysiology model was fitted to Ca2+ data at room temperature and is unable to repolarize sufficiently fast at 6 Hz, causing the model to fail at faster pacing rates. A potential contributor to this particular issue is the transient outward potassium current (I to), which opens immediately after the AP has reached its upstroke and together with the inwardly rectifying K+ current (I K) plays a significant role in rat repolarization, shaping the AP (Amin et al. 2010; Chae et al. 2012). Furthermore, during systole the entrance of Ca2+ in the myocyte is driven by the electrical force influenced by I to (Sah et al. 2003). In our model, we took into account the notable increase in peak Ca2+ and amplitude by refitting the entire Ca2+ dynamic system (see Fig. 2) and this inevitably required some major changes in I to. The I to current was tuned to obtain AP repolarization at 6 Hz, maintaining the simulated Ca2+ transients. To ensure the AP recovered at higher pacing frequencies we refitted the peak current, activation and recovery rates for I to. With detailed literature research we found I to τ of inactivation values to be much lower in rat experimental data compared with the values used in Pandit (see Table 7). We reduced the values to τs ≈ 50 ms and τsslow ≈ 1100 ms consistent with values reported by Apkon & Nerbonne (1991) and Varro et al. (1993) and τr ≈ 0.01 ms. This modification significantly improved the ability of the model to repolarize at 6 Hz. The I to peak density was maintained around 2.1 nA at 1 Hz, consistent with the findings in Wickenden et al. (1997). Both the equations for I K and the steady state outward K+ current (I ss) were kept from Pandit. The I K conductivity parameter was scaled to a value of g K1 = 4 × 10−5 mS to take into account the changes in the I K current with temperature reported by McLarnon et al. (1993) (Q 10 = 1.4 from 10°C to 20°C and Q 10 = 1.6 from 20°C to 30°C). The I ss conductivity parameter was chosen to be g ss = 1.2 × 10−5 mS, to obtain a peak current value equal to the mean value between the epicardial and endocardial Pandit model's peak current measurements. The background K+ current (I BK) was unchanged. The Na+ current (I Na) conductivity parameter was fitted to achieve the peak of the AP at 1 Hz. The background Na+ current (I BNa) and the hyperpolarized activated current (I f) were unchanged.
Table 7.
Summary of I to current measurements reported in the literature
| Publication | T (°C) | F (Hz) | Amplitude (nA) |
|
|
|
|||
|---|---|---|---|---|---|---|---|---|---|
| Apkon & Nerbonne (1991) | 23 ± 1 | NR | 1.4 | 0.96 | 41.0 ± 14.5 | 1238 ± 566 | |||
| Varro et al. (1993) | 20–25 | 0.33 | 47.4 ± 4.0 | 1185 ± 102 | |||||
| Wickenden et al. (1997) | 23 ± 1 | 1 | 2.10 ± 0.18 | 31.7 ± 2.7 | |||||
| Wickenden et al. (1997) (N) | 23 ± 1 | 1 | 1.01 ± 0.15 | 64.3 ± 8.8 | 8216 ± 2396 | ||||
| Pandit et al. (2001) (endo) | 22–24 | 1 | 1.22 | 0.14 | 514 | 2985 | |||
| Pandit et al. (2001) (epi) | 22–24 | 1 | 2.44 | 0.14 | 254 | 3325 | |||
| Huang et al. (2014) | 22–24 | 0.33 | 1.67 ± 0.02 |
N, neonatal cells; epi, epicardial cells; endo, endocardial cells.
Summary of fitted parameters
A summary of all the fitted parameters within the model is shown in Tables 8 and 9.
Table 8.
Summary of all the fitted Ca2 + current parameters
| Parameter | Unit | Definition | |
|---|---|---|---|
|
|
μm 3 ms−1 | Pump rate of NCX | |
|
|
μm 3 ms−1 | Maximum pump rate of sarcolemmal pump | |
|
|
mm | Half‐saturation of sarcolemmal pump | |
|
|
μm 3 ms−1 | Maximum pump rate of SERCA at 1 Hz | |
|
|
mm | Half‐saturation of SERCA at 1 Hz | |
|
|
μm 3 ms−1 | Maximum pump rate of SERCA at 6 Hz | |
|
|
mm | Half‐saturation of SERCA at 6 Hz | |
|
|
μm 3 ms−1 | Permeability of single LCC | |
|
|
mm | Concentration at inactivation LCC | |
|
|
mV | Potential when half LCC open | |
|
|
mV | Width of opening potential | |
|
|
Unitless | Proportion of time closed in open mode LCC | |
|
|
mS | Inactivation time | |
|
|
mm | Half concentration of activation | |
|
|
μm 3 ms−1 | Permeability of the leak current from the dyadic space | |
|
|
ms−1 | Rate of leak from the SR to the cytosol | |
|
|
mm mV−1 ms−1 | Background Ca2 + current rate |
Table 9.
Summary of the Na+and K+currents parameters
| Parameter | Unit | Definition | |
|---|---|---|---|
|
|
mS | Transient outward potassium current conductivity | |
|
|
mS | Inwardly rectifying current conductivity | |
|
|
mS | Steady‐state outward K+ current conductivity | |
|
|
mS | Inward Na+ current conductivity | |
|
|
mS | Background K+ current conductivity | |
|
|
mS | Background Na+ current conductivity |
Simulated Ca2+ and AP phenotypes at all tested frequencies for data‐driven (DD) model
For the sake of completeness, in Tables 10 and 11 we report the results of all simulated Ca2+ and AP phenotypes for all tested frequencies from 1 to 6 Hz with step 1 Hz.
Table 10.
Simulated Ca2 + phenotypes at all tested frequencies
| Phenotype | Unit | 1 Hz | 2 Hz | 3 Hz | 4 Hz | 5 Hz | 6 Hz |
|---|---|---|---|---|---|---|---|
| Peak [Ca2+]i | μm | 1.420 | 1.331 | 1.314 | 1.331 | 1.372 | 1.439 |
| DCa | μm | 0.1056 | 0.1141 | 0.1369 | 0.1663 | 0.2014 | 0.2445 |
| RT50 | ms | 111 | 80 | 68 | 63 | 60 | 61 |
| T peak | ms | 27 | 26 | 25 | 24 | 24 | 25 |
Table 11.
Simulated AP phenotypes at all tested frequencies
| Phenotype | Unit | 1 Hz | 2 Hz | 3 Hz | 4 Hz | 5 Hz | 6 Hz |
|---|---|---|---|---|---|---|---|
| Resting membrane V | mV | −83.06 | −83.19 | −83.26 | −83.28 | 83.24 | −83.16 |
| Peak V | mV | 38.52 | 37.45 | 36.03 | 34.2 | 31.8 | 28.8 |
| APD20 | ms | 2.6 | 2.6 | 2.6 | 2.7 | 2.9 | 3.0 |
| APD50 | ms | 15.7 | 17 | 17.6 | 18.2 | 19.1 | 20.6 |
| APD70 | ms | 33.0 | 33.3 | 33.1 | 33.1 | 33.6 | 34.6 |
| APD90 | ms | 50.6 | 49.2 | 48.3 | 47.9 | 48 | 48.9 |
APD, action potential duration.
Changes in extracellular potassium concentration
The initial model is parameterized to experimental measurements where [K+]o was set to 5.4 mm. However, lower [K+]o values between 3.3 and 5.8 mm were reported in vivo, as reviewed by Niederer (2013). To test if changes in [K+]o could affect our CFR results we have simulated frequency‐dependent changes in PCa, DCa, ΔMPCa and [Ca2+]SR in the base model with [K+]o = 4.2 mm and [K+]o = 4.5 mm as shown in Figs 8 and 9, respectively. No major changes in the calcium–frequency behaviour have been reported in these cases.
Figure 8. PCa, DCa, ΔMPCa and [Ca2+]SR changes with [Ca2+]o when [K+]o = 4.2 mm .
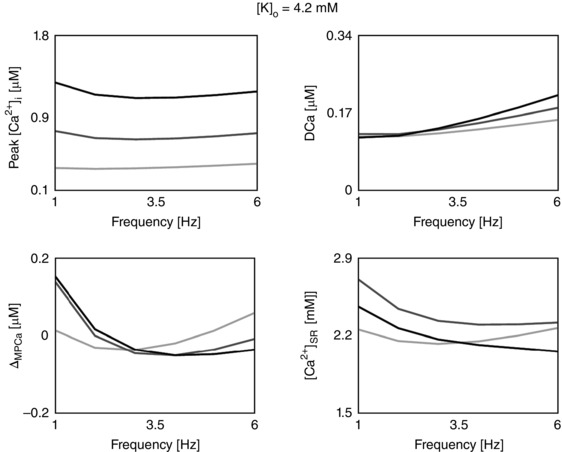
No major changes in the calcium–frequency behaviour have been reported in this case.
Figure 9. PCa, DCa, ΔMPCa and [Ca2+]SR changes with [Ca2+]o when [K+]o = 4.5 mm .
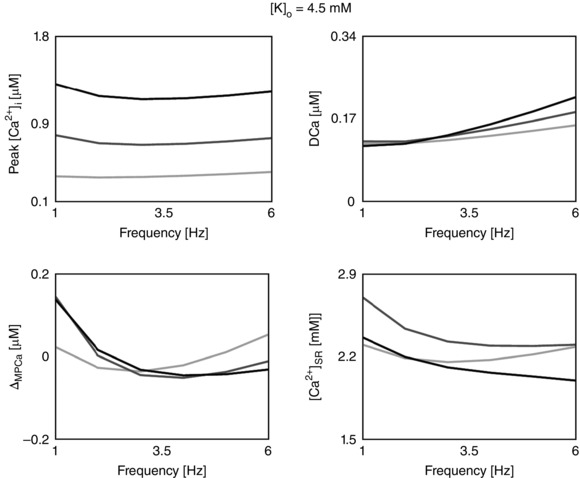
No major changes in the calcium–frequency behaviour have been reported in this case.
Fixed AP simulations
To study the effects of changes in AP on the calcium–frequency response, in Fig. 10 we have simulated frequency‐dependent changes in PCa, DCa, ΔMPCa and [Ca2+]SR when clamping the AP to 1 Hz morphology at all frequencies. Compared with the results in the DD model, no major changes in the calcium–frequency behaviour have been reported in this case.
Figure 10. PCa, DCa, ΔMPCa and [Ca2+]SR changes with [Ca2+]o when fixing the AP to 1 Hz morphology .

No major changes in the calcium–frequency behaviour have been reported in this case.
CAMKII alteration of L‐type channel and transient outward K+ current (CAMK model)
CAMKII alteration of I LCC
Previous studies in rats have shown a CAMKII‐mediated increase in I LCC magnitude of approximately 10–20% and accelerated recovery from inactivation (Xiao et al. 1994; Guo & Duff, 2006). In accordance with these findings, results in human models by O'Hara et al. (2011) have also shown an increase in peak current and faster recovery from inactivation of I LCC when phosphorylated by CAMK. Following those studies, to obtain an increased magnitude and slowed inactivation in the CAMK model, we increased the LCC permeability by 20% and we doubled the τL of inactivation. CAMKII activation of the L‐type channel was developed using the same approach we have used for CAMKII SERCA activation:
| (A22) |
| (A23) |
where f a is the fractional occupancies of active CaMKII, , K m,JL = 1.72, and K m,τ = 1.153. Results in Fig. 11 show an increase in the current magnitude and slowed inactivation comparable with results digitalized from Xiao et al. (1994). Interestingly, Dibb et al. (2007) found no evidence for frequency‐dependent facilitation of I LCC in rat experiments at 37°C and they showed that peak I LCC decreases with increasing stimulation frequency. Consistent with these studies, our DD model shows decreased peak I LCC with increasing frequency as shown in Fig. 12.
Figure 11. LCC experimental data and simulations .
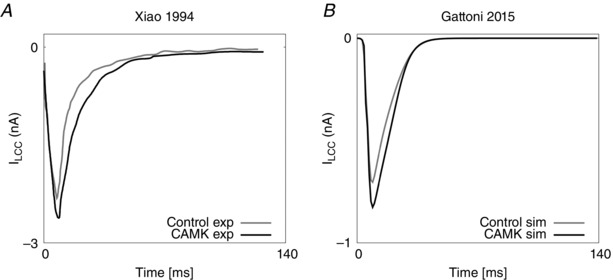
A, I LCC experimental current data in control (grey) and CAMK (black) cases, digitalized from Xiao et al. (1994). B, I LCC simulated current in control (grey) and CAMK (black) cases in our model.
Figure 12. ILCC simulations in the DD model at 1 Hz (grey) and 6 Hz (black) .
Results show decreased peak I LCC with increasing frequency.
CAMK alteration of I to
Experiments by Colinas et al. (2006) in rat cardiac myocytes have revealed a direct regulation of the fast I to component by CAMKII. Furthermore, inhibition of CAMKII with KN‐93 resulted in acceleration of I to inactivation, thought to be caused by a reduction in the I to slow component with no physiologically significant changes on the constants of inactivation. More recent experiments developed by Wagner et al. (2009) in mouse showed that CAMKII does not produce regulation of I to amplitude or activation, although it accelerates recovery from inactivation for both the fast and slow I to components.
Following these studies, in the CAMK model we altered the I to steady state inactivation with a 15 mV shift in the depolarizing direction, to reduce both the fast and the slow inactivating components, and we introduced CAMKII activation of the I to τ of inactivation, to accelerate recovery from inactivation:
| (A24) |
| (A25) |
where f a is the fractional occupancies of active CaMKII, and K a = 0.435.
| (A26) |
| (A27) |
| (A28) |
| (A29) |
| (A30) |
where 14.87, K b = 1.118, , K g = 0.8757, and K d = 1.007. Results in Fig. 13 show slowed I to inactivation compared with the DD case and no changes in I to amplitude or activation concordant with results by Colinas et al. (2006) and Wagner et al. (2009).
Figure 13. Ito current in control and CAMK cases .
I to simulated data in control (grey) and CAMK (black) cases. Results show slower inactivation of the I to current when including the effects of CAMKII compared with the control case.
Mechanisms behind the CFR in model variants
In our work we have simulated the PCFR, DCFR, MCFR and [Ca2+]SR frequency response in the DD model and three model variants: CAMK, NO CAMK and RNaK models (Fig. 3). Here for completeness, we report the frequency‐dependent changes in those phenotypes for all model variants (in Table 12) and we describe the effects of model variants on the CFR.
Table 12.
PCFR, DCFR, MCFR and [Ca2 + ]SR frequency relationship () for the DD, CAMK, NO CAMK and RNaK models
| DD MODEL | CAMK MODEL | NO CAMK MODEL | RNaK MODEL | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Phenotype | [Ca2+] (mm) | Negative | Positive | Negative | Positive | Negative | Positive | Negative | Positive |
| PCFR | 1.0 | 1–2 Hz | 2–6 Hz | 1–2 Hz | 2–6 Hz | 1–4 Hz | 4–6 Hz | 1–2 Hz | 2–6 Hz |
| 1.4 | 1–3 Hz | 3–6 Hz | 1–2 Hz | 2–6 Hz | 1–5 Hz | 5–6 Hz | 1–2 Hz | 2–6 Hz | |
| 1.8 | 1–3 Hz | 3–6 Hz | 1–6 Ηz | 1–4 Hz | 4–6 Hz | 1–2 Hz | 2–6 Hz | ||
| 1.0 | 1–6 Hz | 1–6 Ηz | 1–2 Hz | 2–6 Hz | l–6 Hz | ||||
| DCFR | 1.4 | 1–6 Hz | 1–6 Ηz | 1–6 Ηz | l–6 Hz | ||||
| 1.8 | 1–6 Hz | 1–6 Ηz | 1–6 Ηz | l–6 Hz | |||||
| 1.0 | 1–3 Hz | 3–6 Hz | 1–2 Hz | 2–6 Ηz | 1–6 Hz | 1–2 Hz | 2–6 Hz | ||
| MCFR | 1.4 | 1–4 Hz | 4–6 Hz | 1–3 Hz | 3–6 Hz | 1–6 Hz | 1–2 Hz | 2–6 Hz | |
| 1.8 | 1–4 Hz | 4–6 Hz | 1–6 Ηz | 1–6 Hz | 1–3 Hz | 3–6 Hz | |||
| 1.0 | 1–3 Hz | 3–6 Hz | l–4 Hz | 4–6 Hz | 1–6 Hz | 1–2 Hz | 2–6 Hz | ||
| [Ca2+]SRFR | 1.4 | 1–6 Hz | 1–6 Ηz | 1–6 Hz | 1–3 Hz | 3–6 Hz | |||
| 1.8 | 1–6 Hz | 1–6 Ηz | 1–6 Hz | 1–2 Hz | 2–6 Hz | ||||
CAMK model
In the CAMK model, we introduced equations for CAMKII‐mediated LCC and I to activity and tested how this mechanism affected the CFR. Note that CAMK SERCA modulation is also modelled in the CAMK model, as it is already included in the DD model. Table 12 shows that the PCFR in the CAMK model is qualitatively the same as that of the DD model, although we report a positive PCFR at [Ca2+]o = 1.8 mm. In the CAMK model the MCFR is biphasic at [Ca2+]o = 1.0 and 1.4 mm; however, compared with the DD model we see an increased positive staircase for higher frequencies and a shift of the turning point to lower frequencies. MCFR is positive at [Ca2+]o = 1.8 mm.
Following the same approach we have used for the DD model, to observe how single fluxes affect the CFR, we simulated the changes in all Ca2+ fluxes with [Ca2+]o and frequency in two cases: with and without rapid calmodulin buffering. Simulation results in Fig. 14 reveal the same mechanism already presented for the DD model in ‘Discussion, The [Ca2+]SR hypothesis and analysis of the intracellular and extracellular fluxes behind CFR’. The PCFR is mainly driven by the RyR flux, with a clear effect of the rapid calmodulin buffer and DCa on the response, especially at high levels of [Ca2+]o. We report biphasic RyR response with frequency at all values of [Ca2+]o. The biphasic RyR explains the biphasic PCFR at [Ca2+]o = 1.0 and 1.4 mm. The positive PCFR staircase at [Ca2+]o = 1.8 mm only appears when the effect of the rapid calmodulin buffer is included in the integrals evaluation, showing the clear role of the buffering system in shaping the PCFR response. These results show that CAMKII‐mediated activity, directly acting on Ca2+ release from the RyR, enhances the positive MCFR staircase.
Figure 14. Integral variations in the CAMK model .
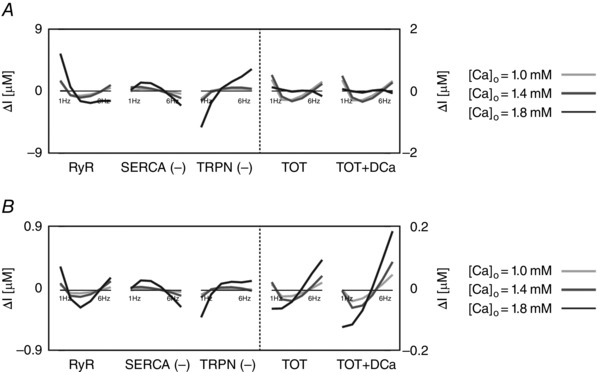
CAMK model intracellular and extracellular current variation of integrals (∆I) as a function of frequency (1 to 6 Hz). A, CAMK model without buffer. B, CAMK model with buffer. In both cases the integrals were evaluated from time = 0 to time = T peak, where T peak is the time to peak of the corresponding simulated Ca2+ transient. Colours represent different extracellular Ca2+ concentrations: 1.0 mm (light grey), 1.4 mm (dark grey) and 1.8 mm (black). The most important fluxes, plotted in the figure, are ryanodine receptors (RyR), Ca2+‐ATPase (SERCA), troponin buffer (TRPN), total current (TOT) and total current plus diastolic Ca2+ (TOT+DCa). The other observed fluxes, L‐type Ca2+ channel (LCC), background Ca2+ current (CaB), reverse mode Na+/Ca2+ exchanger (NCXR), forward mode Na+/Ca2+ exchanger (NCXF), Ca2+ pump (PMCa) and SR leak current (SRl) were one or more orders of magnitude smaller, and therefore we did not include them in the figure.
NO CAMK model
In the NO CAMK model, we inhibited CAMKII up‐regulation of SERCA with frequency to observe the effects on the CFR, by fixing the SERCA conductivity parameter to its value at 6 Hz. Fixing SERCA conductivity at 1 Hz resulted in alternans for frequencies > 4 Hz. Results of the NO CAMK model in Table 12 reveal that removal of SERCA CAMKII dependency mainly affects the PCFR and MCFR. Compared with the biphasic behaviour in the DD model, the NO CAMK model shows a flattened PCFR staircase and a negative MCFR in all cases. In Fig. 15 we observed how single fluxes affect the CFR by simulating the changes in all Ca2+ fluxes with [Ca2+]o and frequency in two cases: with and without rapid calmodulin buffering. Compared with the DD model, where we saw increased SERCA activity with frequency, in the NO CAMK model we report a decrease in SERCA flux with frequency from 1 to 5 Hz and a slight increase from 5 to 6 Hz which in turn modulates the [Ca2+]SR and the RyR flux. In the NO CAMK model the flattened RyR flux is mainly responsible for the PCFR staircase and we see the effect of the frequency‐dependent increase in DCa, inducing a shift to a positive PCFR at high frequencies. In particular, in Fig. 8 we see a notable increase in [Ca2+]SR at low frequencies in the NO CAMK model compared with the DD model, which in turn activates more Ca2+ release from the RyR. Compared with the RyR flux in the DD model, in the NO CAMK model we report more Ca2+ flux at low frequencies and less Ca2+ flux at high frequencies leading to an increase in [Ca2+]i at low frequencies and a decrease in [Ca2+]i at high frequencies, responsible for the negative MCFR. These results show that CAMK up‐regulated SERCA modulates the shift from negative to positive PCFR by altering the [Ca2+]SR, inducing changes in the RyR frequency response.
Figure 15. Integral variations in the NO CAMK model .
NO CAMK model intracellular and extracellular current variation of integrals (∆I) as a function of frequency (1 to 6 Hz). A, NO CAMK model without buffer. B, NO CAMK model with buffer. In both cases the integrals were evaluated from time = 0 to time = T peak, where T peak is the time to peak of the correspondent simulated Ca2+ transient. Colours represent different extracellular Ca2+ concentrations: 1.0 mm (light grey), 1.4 mm (dark grey) and 1.8 mm (black). The most important fluxes, plotted in figure, are ryanodine receptors (RyR), Ca2+‐ATPase (SERCA), troponin buffer (TRPN), total current (TOT) and total current plus diastolic Ca2+ (TOT+DCa). The other observed fluxes, L‐type Ca2+ channel (LCC), background Ca2+ current (CaB), reverse mode Na+/Ca2+ exchanger (NCXR), forward mode Na+/Ca2+ exchanger (NCXF), Ca2+ pump (PMCa) and SR leak current (SRl) were one or more orders of magnitude smaller, and therefore we did not include them in the figure.
It could be argued that pinning SERCA to its 6 Hz value does not appear to correspond with inhibition but rather over‐expression of CaMKII, since SERCA would presumably be less active at slower rates. Thus for the sake of completeness, we performed the same simulations in the range 1–4 Hz by fixing the SERCA conductivity parameter at 1 Hz. Results in Fig. 16 do not show relevant changes in the PCFR, DCFR and MCFR in this case.
Figure 16. Ca2+ phenotype changes with [Ca2+]o when inhibiting CAMKII up‐regulation of SERCA with frequency, by fixing the SERCA conductivity parameter to its value at 1 Hz .
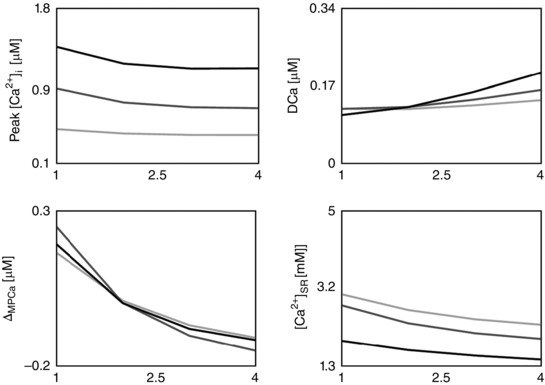
Results do not show main changes in the CFR response.
RNaK model
In the RNaK model we reduced the Na+/K+ affinity to Na+ to test the effects on the CFR. Results of the RNaK model in Table 12 show a shift of the turning point of the biphasic PCFR and MCFR responses to lower frequencies compared with the DD model. We report reduced [Na+]i for frequencies < 2 or 3 Hz and augmented [Na+]i for frequencies > 2 or 3 Hz depending on [Ca2+]o. In particular, at [Ca2+]o = 1.8 mm, we report an [Na+]i increase of ∼10% at 3 Hz and ∼30% at 6 Hz.
To observe how single fluxes affect the CFR in the RNaK model, in Fig. 17 we simulated the changes in all Ca2+ fluxes with [Ca2+]o and frequency in two cases: with and without rapid calmodulin buffering. As NCX kinetics are dependent on [Na+]i and [Ca2+]i, at lower [Na+]i levels (i.e. at lower frequencies), NCX operates less in reverse mode and more in forward mode inducing a reduction in [Ca2+]i, in the RNaK model compared with the DD model. Conversely at higher [Na+]i levels (i.e. at higher frequencies) NCX operates more in reverse mode and less in forward mode inducing an increase in [Ca2+]i in the RNaK model compared with the DD model. Changes in [Ca2+]i are sensed by the RyR. Compared with the RyR flux in the DD model, in the RNaK model at [Ca2+]o = 1.0 and 1.4 mm we report less Ca2+ flux at low frequency and more Ca2+ flux at high frequencies leading to a reduction in [Ca2+]i at low frequency and an increase in [Ca2+]i at high frequencies, responsible for the enhanced positive MCFR in this model (Fig. 17). At [Ca2+]o = 1.8 mm, we report a decrease in the RyR flux with frequency, due to the very high increase in DCa, which leads to a decrease in SERCA flux with frequency. Results at [Ca2+]o = 1.8 mm still show enhanced biphasic MCFR response due to the lower [Ca2+]i levels at low frequency in the RNaK compared with the DD model. The RNaK model biphasic PCFR response reveals the same mechanism as demonstrated in the DD model in ‘Discussion, The [Ca2+]SR hypothesis and analysis of the intracellular and extracellular fluxes behind CFR’. When [Ca2+]o < 1.8 mm, the biphasic PCFR staircase is due to the biphasic RyR flux, amplified by the rapid buffering system and DCa as shown in Fig. 17. At [Ca2+]o = 1.8 mm the RyR staircase results are negative with frequency. Here the biphasic PCFR staircase only appears when the rapid buffering coefficient is included in the simulation, revealing the importance of the buffering system in the PCFR staircase. Decreasing the Na+/K+ affinity to Na+, our model shows positive PCFR and MCFR for frequencies > 2 or 3 Hz depending on [Ca2+]o, highlighting the role of [Na+]i in enhancing the positive staircase effect at physiological frequencies.
Figure 17. Integral variations in the RNaK model .
RNaK model intracellular and extracellular current variation of integrals (∆I) as a function of frequency (1 to 6 Hz). A, RNaK model without buffer. B, RNaK model with buffer. In both cases the integrals were evaluated from time = 0 to time = T peak where T peak is the time to peak of the corresponding simulated Ca2+ transient. Colours represent different extracellular Ca2+ concentrations: 1.0 mm (light grey), 1.4 mm (dark grey) and 1.8 mm (black). The most important fluxes, plotted in the figure, are ryanodine receptors (RyR), Ca2+‐ATPase (SERCA), troponin buffer (TRPN), total current (TOT) and total current plus diastolic Ca2+ (TOT+DCa). The other observed fluxes, L‐type Ca2+ channel (LCC), background Ca2+ current (CaB), reverse mode Na+/Ca2+ exchanger (NCXR), forward mode Na+/Ca2+ exchanger (NCXF), Ca2+ pump (PMCa) and SR leak current (SRl) were one or more orders of magnitude smaller, and therefore we did not include them in the figure.
Intracellular and extracellular fluxes in the CAMK, NO CAMK and RNaK models
Changes in CFR with alterations in [Ca2+]o are due to changes in the balance of Ca2+ fluxes and the degree of buffered Ca2+. For the sake of completeness, in Figs 14, 15 and 17 we show the variation of the integrals of fluxes with changes in [Ca2+]o and frequency in the CAMK, NO CAMK and RNaK models, respectively.
Limitations
The choice of performing experiments at 37°C, although interesting from the physiological point of view, could represent a limitation in our model as previous literature studies have shown the presence of voltage clamp artifacts when performing experiments at temperatures greater than 30°C. Increasing temperature causes reactions to become faster and it is more difficult to accurately control the clamped voltage. To address this problem, we have used data that have employed low resistance pipettes and a rapid switching frequency, which enables improved voltage control. These methods are considered to be widely employed and reliable.
In our experiments we have used [Ca2+]o = 1.8 mm and [K+]o = 5.4 mm. This choice represents a limitation, as the concentration of free calcium in rat plasma remains contentious. Previous studies have measured the extracellular free calcium concentration to be between 1 and 1.3 mm in rats (Moore, 1970; Polimeni, 1974) and the plasma concentrations of potassium to be between 3.3 and 5.8 mm, as reviewed in Niederer (2013). Our simulated results are consistent with the experimental data at [Ca2+]o = 1.8 mm and [K+]o = 5.4 mm and we predicted how changes in [Ca2+]o affect the CFR response in our model. To study the effects of changes in [K+]o concentration on the calcium–frequency response, in Figs 8 and 9 we have simulated frequency‐dependent changes in PCa, DCa, ΔMPCa and [Ca2+]SR in the base model with [K+]o = 4.2 mm and [K+]o = 4.5 mm and we have shown that those do not affect the conclusions of our work.
The interplay between calcium, TnC and tension generation is not included in our analysis and represents a limitation in our model. The inclusion of a sarcomere model with tension‐dependent Ca2+ buffering feedback would address this, albeit with a significant increase in model complexity. However, due to the relative timing of the tension and the Ca2+ transient, the largest effect of tension‐dependent buffering will occur during the relaxation of the Ca2+ transient with limited impact on the peak or magnitude of the Ca2+ transient.
Another important consideration is the significant variability of data. Our computer model is deterministic and thus contrasts sharply with the high levels of intra‐ and intermyocyte variability in action potentials and Ca2+ transient measurements. The challenge of interpreting the experimental results is further compounded by the uncoupled measurement of action potential and Ca2+ transients. It is also not known which action potential pairs with which Ca2+ transient. This lack of information on covariation of data and high variability motivated us to fit the model to representative traces.
The parameters describing the SR geometry and Ca2+ buffering represent a limitation in our model. The SR geometry parameters are assumed to be temperature independent and were thus maintained unchanged from the Hinch model (Hinch et al. 2004) based on data in canine ventricular myocytes (Greenstein & Winslow, 2002). Interestingly, Page et al. found the SR volume to be 3.5% of the cell volume (Page et al. 1971; Page, 1978) in rats, slightly lower than the value used in our model. We tested how such a reduction could affect the results and we found no qualitative or quantitative change in the Ca2+ transient characteristics. Buffering remains an important but poorly experimentally characterized property of cardiac myocytes, in part due to the need to measure both voltage and calibrated free calcium to characterize the steady state properties of the system. Bers (2001) found that these parameters did not vary significantly between measurements when averaged, although buffering in individual myocytes has been reported to vary significantly (Hove‐Madsen & Bers, 1993). The current data are derived from ferret and canine measurements (Greenstein & Winslow, 2002; Bondarenko et al. 2004).
Changes in action potential duration might also contribute to FFR (Endoh, 2004), although they appear to be a consequence of changes in [Ca2+]i. To observe how changes in AP could affect the CFR, we clamped the AP to 1 Hz morphology when simulating at different frequencies. Figure 10 shows that no major changes in the CFR response were detected.
In our experimental data set, AP early repolarization, recorded at 6 Hz, is very different among different cells. Furthermore, the early repolarization phase of the AP appears to be faster in some of the experiments compared with our model's predictions. There are a number of possible reasons for this. One reason could be due to changes in the I to current in different cell types (epicardial/endocardial) that where not accounted for in the model and could explain this variation in AP early repolarization (Fedida & Giles, 1991; Clark et al. 1993). Another reason could be due to the fact that AP measurements were recorded in the presence of a small but significant EGTA calcium buffer concentration. The shape of the AP is definitely altered by changes in the intracellular calcium concentration, especially in the early repolarization phase and the presence of a calcium buffer during the experimental recording phase could alter the AP measurements. The effects of changes in EGTA concentration were included when simulating AP in our model although the EGTA model was not re‐parameterized for experiments in rats at 37°C. Furthermore, it is not known which AP pairs with which Ca2+ transient. This can be a problem, due to the very high variability of the Ca2+ experimental data.
References
- Amin AS, Tan HL & Wilde AAM (2010). Cardiac ion channels in health and disease. Heart Rhythm 7, 117–126. [DOI] [PubMed] [Google Scholar]
- Apkon M & Nerbonne JM (1991). Characterization of two distinct depolarization‐activated K+ currents in isolated adult rat ventricular myocytes. J Gen Physiol 97, 973–1011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassani RA, Bassani JW & Bers DM (1992). Mitochondrial and sarcolemmal Ca2+ transport reduce [Ca2+]i during caffeine contractures in rabbit cardiac myocytes. J Physiol 453, 591–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baartscheer A, Schumacher CA & Fiolet JW (1997). Small changes of cytosolic sodium in rat ventricular myocytes measured with SBFI in emission ratio mode. J Mol Cell Cardiol 29, 3375–3383. [DOI] [PubMed] [Google Scholar]
- Benforado JM (1958). Frequency‐dependent pharmacological and physiological effects on the rat ventricle strip. J Pharmacol Exp Ther 122, 86–100. [PubMed] [Google Scholar]
- Bers DM (1989). SR Ca loading in cardiac muscle preparations based on rapid‐cooling contractures. Am J Physiol Cell Physiol 256, C109–C120. [DOI] [PubMed] [Google Scholar]
- Bers DM (2001). Excitation‐Contraction Coupling and Cardiac Contractile Force. Springer Netherlands, Dordrecht: Available at: http://link.springer.com/10.1007/978‐94‐010‐0658‐3 (Accessed 21 April 2015). [Google Scholar]
- Blayney L, Thomas H, Muir J & Henderson A (1978). Action of caffeine on calcium transport by isolated fractions of myofibrils, mitochondria, and sarcoplasmic reticulum from rabbit heart. Circ Res 43, 520–526. [DOI] [PubMed] [Google Scholar]
- Bondarenko VE, Bett GC & Rasmusson RL (2004). A model of graded calcium release and L‐type Ca2+ channel inactivation in cardiac muscle. Am J Physiol Heart Circ Physiol 286, H1154–H1169. [DOI] [PubMed] [Google Scholar]
- Borzak S, Murphy S & Marsh JD (1991). Mechanisms of rate staircase in rat ventricular cells. Am J Physiol Heart Circ Physiol 260, H884–H892. [DOI] [PubMed] [Google Scholar]
- Borzak S, Reers M, Arruda, J , Sharma VK, Sheu SS, Smith TW & Marsh JD (1992). Na+ efflux mechanisms in ventricular myocytes: measurement of [Na+]i with Na(+)‐binding benzofuran isophthalate. Am J Physiol 263, H866–H874. [DOI] [PubMed] [Google Scholar]
- Bouchard RA & Bose D (1989). Analysis of the interval‐force relationship in rat and canine ventricular myocardium. Am J Physiol Heart Circ Physiol 257, H2036–H2047. [DOI] [PubMed] [Google Scholar]
- Bouchard RA, Clark RB & Giles WR (1995). Effects of action potential duration on excitation‐contraction coupling in rat ventricular myocytes. Action potential voltage‐clamp measurements. Circ Res 76, 790–801. [DOI] [PubMed] [Google Scholar]
- Capogrossi MC, Kort AA, Spurgeon HA & Lakatta EG (1986). Single adult rabbit and rat cardiac myocytes retain the Ca2+‐ and species‐dependent systolic and diastolic contractile properties of intact muscle. J Gen Physiol 88, 589–613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chae JE, Kim HS, Ahn DS & Park WK (2012). Ionic mechanisms of desflurane on prolongation of action potential duration in rat ventricular myocytes. Yonsei Med J 53, 204–212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng H, Lederer WJ & Cannell MB (1993). Calcium sparks: elementary events underlying excitation‐contraction coupling in heart muscle. Science 262, 740–744. [DOI] [PubMed] [Google Scholar]
- Choi HS & Eisner DA (1999). The effects of inhibition of the sarcolemmal Ca‐ATPase on systolic calcium fluxes and intracellular calcium concentration in rat ventricular myocytes. Pflugers Arch 437, 966–971. [DOI] [PubMed] [Google Scholar]
- Chu A, Fill M, Stefani E & Entman ML (1993). Cytoplasmic Ca2+ does not inhibit the cardiac muscle sarcoplasmic reticulum ryanodine receptor Ca2+ channel, although Ca2+‐induced Ca2+ inactivation of Ca2+ release is observed in native vesicles. J Membr Biol 135, 49–59. [DOI] [PubMed] [Google Scholar]
- Clark RB, Bouchard RA, Salinas‐Stefanon E, Sanchez‐Chapula J & Giles WR (1993). Heterogeneity of action potential waveforms and potassium currents in rat ventricle. Cardiovasc Res 27, 1795–1799. [DOI] [PubMed] [Google Scholar]
- Cohen CJ, Fozzard HA & Sheu SS (1982). Increase in intracellular sodium ion activity during stimulation in mammalian cardiac muscle. Circ Res 50, 651–662. [DOI] [PubMed] [Google Scholar]
- Colinas O, Gallego M, Setien R, Lopez‐Lopez JR, Perez‐Garcia MT & Casis O (2006). Differential modulation of Kv4.2 and Kv4.3 channels by calmodulin‐dependent protein kinase II in rat cardiac myocytes. Am J Physiol Hear Circ Physiol 291, H1978–H1987. [DOI] [PubMed] [Google Scholar]
- Dibb KM, Eisner DA & Trafford AW (2007). Regulation of systolic [Ca2+]i and cellular Ca2+ flux balance in rat ventricular myocytes by SR Ca2+, L‐type Ca2+ current and diastolic [Ca2+]i . J Physiol 585, 579–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donoso P, Mill JG, Oneill SC & Eisner DA (1992). Fluorescence Measurements of Cytoplasmic and Mitochondrial Sodium Concentration in Rat Ventricular Myocytes. J Physiol‐London 448, 493–509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drummond GB (2009). Reporting ethical matters in The Journal of Physiology: standards and advice. J Physiol 587, 713–719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Endoh M (2004). Force‐frequency relationship in intact mammalian ventricular myocardium: Physiological and pathophysiological relevance. Eur J Pharmacol 500, 73–86. [DOI] [PubMed] [Google Scholar]
- Fabiato A & Fabiato F (1979). Calcium and cardiac excitation‐contraction coupling. Annu Rev Physiol 41, 473–484. [DOI] [PubMed] [Google Scholar]
- Fedida D & Giles WR (1991). Regional variations in action potentials and transient outward current in myocytes isolated from rabbit left ventricle. J Physiol 442, 191–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frampton JE, Harrison SM, Boyett MR & Orchard CH (1991. a). Ca2+ and Na+ in rat myocytes showing different force‐frequency relationships. Am J Physiol Cell Physiol 261, C739–C750. [DOI] [PubMed] [Google Scholar]
- Frampton JE, Orchard CH & Boyett MR (1991. b). Diastolic, systolic and sarcoplasmic reticulum [Ca2+] during inotropic interventions in isolated rat myocytes. J Physiol 437, 351–375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frisk M, Koivumäki JT, Norseng PA, Maleckar MM, Sejersted OM & Louch WE (2014). Variable t‐tubule organization and Ca2+ homeostasis across the atria. Am J Physiol Heart Circ Physiol 307, H609–H620. [DOI] [PubMed] [Google Scholar]
- Greenstein JL & Winslow RL (2002). An integrative model of the cardiac ventricular myocyte incorporating local control of Ca2+ release. Biophys J 83, 2918–2945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo J & Duff HJ (2006). Calmodulin kinase II accelerates L‐type Ca2+ current recovery from inactivation and compensates for the direct inhibitory effect of [Ca2+]i in rat ventricular myocytes. J Physiol 574, 509–518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagemann D, Kuschel M, Kuramochi T, Zhu W, Cheng H & Xiao RP (2000). Frequency‐encoding Thr17 phospholamban phosphorylation is independent of Ser16 phosphorylation in cardiac myocytes. J Biol Chem 275, 22532–22536. [DOI] [PubMed] [Google Scholar]
- Harrison SM, McCall E & Boyett MR (1992). The relationship between contraction and intracellular sodium in rat and guinea‐pig ventricular myocytes. J Physiol 449, 517–550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrmann‐Frank A, Lüttgau HC & Stephenson DG (1999). Caffeine and excitation‐contraction coupling in skeletal muscle: a stimulating story. J Muscle Res Cell Motil 20, 223–237. [DOI] [PubMed] [Google Scholar]
- Hinch R, Greenstein JL, Tanskanen AJ, Xu L & Winslow RL (2004). A simplified local control model of calcium‐induced calcium release in cardiac ventricular myocytes. Biophys J 87, 3723–3736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hobai IA & Levi AJ (1999). Coming full circle: membrane potential, sarcolemmal calcium influx and excitation‐contraction coupling in heart muscle. Cardiovasc Res 44, 477–487. [DOI] [PubMed] [Google Scholar]
- Hove‐Madsen L & Bers DM (1993). Passive Ca buffering and SR Ca uptake in permeabilized rabbit ventricular myocytes. Am J Physiol Cell Physiol 264, C677–C686. [DOI] [PubMed] [Google Scholar]
- Huang ZB, Fang C, Lin MH, Yuan GY, Zhou SX & Wu W (2014). Effect of fosinopril on the tran‐ sient outward potassium current of hypertrophied left ventricular myocardium in the spontaneously hypertensive rat. Naunyn‐Schmiedeberg's Arch of Pharmacol 387, 419–425. URL: http://www.ncbi.nlm.nih.gov/pubmed/24441766, doi:10.1007/s00210‐014‐0956‐6. [DOI] [PubMed] [Google Scholar]
- Huke S & Bers DM (2007). Temporal dissociation of frequency‐dependent acceleration of relaxation and protein phosphorylation by CaMKII. J Mol Cell Cardiol 42, 590–599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hund TJ & Rudy Y (2004). Rate dependence and regulation of action potential and calcium transient in a canine cardiac ventricular cell model. Circulation 110, 3168–3174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jafri MS, Rice JJ & Winslow RL (1998). Cardiac Ca2+ dynamics: the roles of ryanodine receptor adaptation and sarcoplasmic reticulum load. Biophys J 74, 1149–1168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein MG, Simon BJ & Schneider MF (1990). Effects of caffeine on calcium release from the sarcoplasmic reticulum in frog skeletal muscle fibres. J Physiol 425, 599–626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koch‐Weser J & Blinks JR (1963). The influence of the interval between beats on myocardial contractility. Pharmacol Rev 15, 601–652. [PubMed] [Google Scholar]
- Langer GA, Brady AJ, Tan ST & Serena D (1975). Correlation of the glycoside response, the force staircase, and the action potential configuration in the neonatal rat heart. Circ Res 36, 744–752. [DOI] [PubMed] [Google Scholar]
- Layland J & Kentish JC (1999). Positive force‐ and [Ca2+]i‐frequency relationships in rat ventricular trabeculae at physiological frequencies. Am J Physiol Hear Circ Physiol 276, H9–H18. [DOI] [PubMed] [Google Scholar]
- Levi Aj, Lee CO & Brooksby P (1994). Properties of the fluorescent sodium indicator “SBFI” in rat and rabbit cardiac myocytes. J Cardiovasc Electrophysiol 5, 241–257. [DOI] [PubMed] [Google Scholar]
- Lewalle A, Niederer SA & Smith NP (2014). Species‐dependent adaptation of the cardiac Na+/K+ pump kinetics to the intracellular Na+ concentration. J Physiol 592, 5355–5371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li L, Chu G, Kranias EG & Bers DM (1998). Cardiac myocyte calcium transport in phospholamban knockout mouse: relaxation and endogenous CaMKII effects. Am J Physiol Heart Circ Physiol 274, H1335–H1347. [DOI] [PubMed] [Google Scholar]
- Li L, Niederer SA, Idigo W, Zhang YH, Swietach P, Casadei B & Smith NP (2010). A mathematical model of the murine ventricular myocyte: a data‐driven biophysically based approach applied to mice overexpressing the canine NCX isoform. Am J Physiol Heart Circ Physiol 299, H1045–H1063. [DOI] [PubMed] [Google Scholar]
- Lokuta AJ, Rogers TB, Lederer WJ & Valdivia HH (1995). Modulation of cardiac ryanodine receptors of swine and rabbit by a phosphorylation‐dephosphorylation mechanism. J Physiol 487, 609–622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Louch WE, Sheehan KA & Wolska BM (2011). Methods in cardiomyocyte isolation, culture, and gene transfer. J Mol Cell Cardiol 51, 288–298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo CH & Rudy Y (1994). A dynamic model of the cardiac ventricular action potential. II. Afterdepolarizations, triggered activity, and potentiation. Circ Res 74, 1097–1113. [DOI] [PubMed] [Google Scholar]
- Mackiewicz U & Lewartowski B (2006). Temperature dependent contribution of Ca2+ transporters to relaxation in cardiac myocytes: Important role of sarcolemmal Ca2+‐ATPase. J Physiol Pharmacol 57, 3–15. [PubMed] [Google Scholar]
- Maier LS, Pieske B & Allen DG (1997). Influence of stimulation frequency on [Na+]i and contractile function in Langendorff‐perfused rat heart. Am J Physiol Heart Circ Physiol 273, H1246–H1254. [DOI] [PubMed] [Google Scholar]
- McLarnon JG, Hamman BN & Tibbits GF (1993). Temperature dependence of unitary properties of an ATP‐dependent potassium channel in cardiac myocytes. Biophys J 65, 2013–2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meissner G, Rios E, Tripathy A & Pasek DA (1997). Regulation of skeletal muscle Ca2+ release channel (ryanodine receptor) by Ca2+ and monovalent cations and anions. J Biol Chem 272, 1628–1638. [DOI] [PubMed] [Google Scholar]
- Mejía‐Alvarez R, Kettlun C, Ríos E, Stern M & Fill M (1999). Unitary Ca2+ current through cardiac ryanodine receptor channels under quasi‐physiological ionic conditions. J Gen Physiol 113, 177–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monasky MM & Janssen PML (2009). The positive force‐frequency relationship is maintained in absence of sarcoplasmic reticulum function in rabbit, but not in rat myocardium. J Comp Physiol B Biochem Syst Environ Physiol 179, 469–479. [DOI] [PubMed] [Google Scholar]
- Moore EW (1970). Ionized calcium in normal serum, ultrafiltrates, and whole blood determined by ion‐exchange electrodes. J Clin Invest 49, 318–334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mørk HK, Sjaastad I, Sejersted OM & Louch WE (2009). Slowing of cardiomyocyte Ca2+ release and contraction during heart failure progression in postinfarction mice. Am J Physiol Heart Circ Physiol 296, H1069–H1079. [DOI] [PubMed] [Google Scholar]
- Mubagwa K, Lin W, Sipido K, Bosteels S & Flameng W (1997). Monensin‐induced reversal of positive force‐frequency relationship in cardiac muscle: role of intracellular sodium in rest‐dependent potentiation of contraction. J Mol Cell Cardiol 29, 977–989. [DOI] [PubMed] [Google Scholar]
- Negretti N, O'Neill SC & Eisner DA (1993). The relative contributions of different intracellular and sarcolemmal systems to relaxation in rat ventricular myocytes. Cardiovasc Res 27, 1826–1830. [DOI] [PubMed] [Google Scholar]
- Niederer S (2013). Regulation of ion gradients across myocardial ischemic border zones: a biophysical modelling analysis. PLoS One 8, e60323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Hara T, Virág L, Varró A & Rudy Y (2011). Simulation of the undiseased human cardiac ventricular action potential: model formulation and experimental validation. PLoS Comput Biol 7, e1002061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Page E & Page EG (1968). Distribution of ions and water between tissue compartments in the perfused left ventricle of the rat heart. Circ Res 22, 435–446. [DOI] [PubMed] [Google Scholar]
- Page E (1978). Quantitative ultrastructural analysis in cardiac membrane physiology. Am J Physiol Cell Physiol 235, C147–C158. [DOI] [PubMed] [Google Scholar]
- Page E, McCallister LP & Power B (1971). Stereological measurements of cardiac ultrastructures implicated in excitation‐contraction coupling. Proc Natl Acad Sci USA 68, 1465–1466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pandit SV, Clark RB, Giles WR & Demir SS (2001). A mathematical model of action potential heterogeneity in adult rat left ventricular myocytes. Biophys J 81, 3029–3051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Picht E, DeSantiago J, Huke S, Kaetzel MA, Dedman JR & Bers DM (2007). CaMKII inhibition targeted to the sarcoplasmic reticulum inhibits frequency‐dependent acceleration of relaxation and Ca2+ current facilitation. J Mol Cell Cardiol 42, 196–205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pieske B, Maier LS, Bers DM & Hasenfuss G (1999). Ca2+ handling and sarcoplasmic reticulum Ca2+ content in isolated failing and nonfailing human myocardium. Circ Res 85, 38–46. [DOI] [PubMed] [Google Scholar]
- Polimeni PI (1974). Extracellular space and ionic distribution in rat ventricle. Am J Physiol 227, 676–683. [DOI] [PubMed] [Google Scholar]
- Polimeni PI & Al‐Sadir J (1975). Expansion of extracellular space in the nonischemic zone of the infarcted heart and concomitant changes in tissue electrolyte contents in the rat. Circ Res 37, 725–732. [DOI] [PubMed] [Google Scholar]
- Powell T, Terrar DA & Twist VW (1980). Electrical properties of individual cells isolated from adult rat ventricular myocardium. J Physiol 302, 131–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sah R, Ramirez RJ, Oudit GY, Gidrewicz D, Trivieri MG, Zobel C & Backx PH (2003). Regulation of cardiac excitation‐contraction coupling by action potential repolarization: role of the transient outward potassium current (I to). J Physiol 546, 5–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sham JS, Cleemann L & Morad M (1995). Functional coupling of Ca2+ channels and ryanodine receptors in cardiac myocytes. Proc Natl Acad Sci USA 92, 121–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shattock MJ, Bers DM (1989). Rat vs. rabbit ventricle: Ca flux and intracellular Na assessed by ion‐selective micro‐ electrodes. Am J Physiol 256, C813–C822. [DOI] [PubMed] [Google Scholar]
- Shimoni Y, Severson D & Giles W (1995). Thyroid status and diabetes modulate regional differences in potassium currents in rat ventricle. J Physiol 488, 673–688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sitsapesan R & Williams AJ (1990). Mechanisms of caffeine activation of single calcium‐release channels of sheep cardiac sarcoplasmic reticulum. J Physiol 423, 425–439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sitsapesan R & Williams AJ (1994). Gating of the native and purified cardiac SR Ca2+‐release channel with monovalent cations as permeant species preparation of SR membrane vesicles. Biophys J 67, 1484–1494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song LS, Sham JSK, Stern MD, Lakatta EG & Cheng H (1998). Direct measurement of SR release flux by tracking “Ca2+ spikes” in rat cardiac myocytes. J Physiol 512, 677–691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sossalla S, Fluschnik N, Schotola H, Ort KR, Neef S, Schulte T, Wittköpper K, Renner A, Schmitto JD, Gummert J, El‐Armouche A, Hasenfuss G & Maier LS (2010). Inhibition of elevated Ca2+/calmodulin‐dependent protein kinase II improves contractility in human failing myocardium. Circ Res 107, 1150–1161. [DOI] [PubMed] [Google Scholar]
- Stemmer P & Akera T (1986). Concealed positive force‐frequency relationships in rat and mouse cardiac muscle revealed by ryanodine. Am J Physiol Heart Circ Physiol 251, H1106–H1110. [DOI] [PubMed] [Google Scholar]
- Stern MD, Song LS, Cheng H, Sham JS, Yang HT, Boheler KR & Ríos E (1999). Local control models of cardiac excitation‐contraction coupling. A possible role for allosteric interactions between ryanodine receptors. J Gen Physiol 113, 469–489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terkildsen JR, Niederer S, Crampin EJ, Hunter P & Smith NP (2008). Using Physiome standards to couple cellular functions for rat cardiac excitation‐contraction. Exp Physiol 93, 919–929. [DOI] [PubMed] [Google Scholar]
- Trafford AW, Díaz ME & Eisner DA (1999). A novel, rapid and reversible method to measure Ca buffering and time‐course of total sarcoplasmic reticulum Ca content in cardiac ventricular myocytes. Pflugers Arch 437, 501–503. [DOI] [PubMed] [Google Scholar]
- Varro A, Negretti N, Hester SB & Eisner DA (1993). An estimate of the calcium content of the sarcoplasmic reticulum in rat ventricular myocytes. Pflugers Arch 423, 158–160. [DOI] [PubMed] [Google Scholar]
- Wagner S, Hacker E, Grandi E, Weber SL, Dybkova N, Sossalla S, Sowa T, Fabritz L, Kirchhof P, Bers DM & Maier LS (2009). Ca/calmodulin kinase II differentially modulates potassium currents. Circ Arrhythm Electrophysiol 2, 285–294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wehrens XHT, Lehnart SE, Reiken SR & Marks AR (2004). Ca2+/calmodulin‐dependent protein kinase II phosphorylation regulates the cardiac ryanodine receptor. Circ Res 94, e61–e70. [DOI] [PubMed] [Google Scholar]
- Wickenden AD, Kaprielian R, Parker TG, Jones OT & Backx PH (1997). Effects of development and thyroid hormone on K+ currents and K+ channel gene expression in rat ventricle. J Physiol 504, 271–286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winslow RL, Rice J, Jafri S, Marbán E & O'Rourke B (1999). Mechanisms of altered excitation‐contraction coupling in canine tachycardia‐induced heart failure, II: model studies. Circ Res 84, 571–586. [DOI] [PubMed] [Google Scholar]
- Woodbury JW (1963). Interrelationships between ion transport mechanisms and excitatory events. Fed Proc 22, 31–35. [PubMed] [Google Scholar]
- Wu Y, Luczak ED, Lee EJ, Hidalgo C, Yang J, Gao Z, Li J, Wehrens XH, Granzier H & Anderson ME (2012). CaMKII effects on inotropic but not lusitropic force frequency responses require phospholamban. J Mol Cell Cardiol 53, 429–436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao RP, Cheng H, Lederer WJ, Suzuki T & Lakatta EG (1994). Dual regulation of Ca2+/calmodulin‐dependent kinase II activity by membrane voltage and by calcium influx. Proc Natl Acad Sci USA 91, 9659–9663. [DOI] [PMC free article] [PubMed] [Google Scholar]


