A Combined Experimental and Computational Approach to Subject-Specific Analysis of Knee Joint Laxity

Abstract

Modeling complex knee biomechanics is a continual challenge, which has resulted in many models of varying levels of quality, complexity, and validation. Beyond modeling healthy knees, accurately mimicking pathologic knee mechanics, such as after cruciate rupture or meniscectomy, is difficult. Experimental tests of knee laxity can provide important information about ligament engagement and overall contributions to knee stability for development of subject-specific models to accurately simulate knee motion and loading. Our objective was to provide combined experimental tests and finite-element (FE) models of natural knee laxity that are subject-specific, have one-to-one experiment to model calibration, simulate ligament engagement in agreement with literature, and are adaptable for a variety of biomechanical investigations (e.g., cartilage contact, ligament strain, in vivo kinematics). Calibration involved perturbing ligament stiffness, initial ligament strain, and attachment location until model-predicted kinematics and ligament engagement matched experimental reports. Errors between model-predicted and experimental kinematics averaged <2 deg during varus–valgus (VV) rotations, <6 deg during internal–external (IE) rotations, and <3 mm of translation during anterior–posterior (AP) displacements. Engagement of the individual ligaments agreed with literature descriptions. These results demonstrate the ability of our constraint models to be customized for multiple individuals and simultaneously call attention to the need to verify that ligament engagement is in good general agreement with literature. To facilitate further investigations of subject-specific or population based knee joint biomechanics, data collected during the experimental and modeling phases of this study are available for download by the research community.

Introduction

Motion of the human knee is constrained by the collective contributions of articular geometry, ligamentous tissue, and muscle forces. When damaged by injury or disease, the balance of constraints is altered, which can further degrade the integrity of the knee through degenerative processes and lead to pain and disability. Thus, quantifying the mechanical environment at the knee has long been of interest to clinicians and researchers. While direct in vivo measurement of soft-tissue loads at and surrounding the knee would be ideal, it is not practical. In vitro biomechanical testing allows greater access to and measurement of specific structures, but is often restricted by cost, equipment limitations, and access to knees with specific pathologies. Thus, many researchers utilize computer models to quantify knee motion, loads on the constraining tissues, and their response to pathology and treatment [1–4].

Modeling complex knee biomechanics is a continual challenge. As a result, the detail in published models has varied considerably, including the number and complexity of included structures, material behavior, or the use of generic versus subject-specific representations of bone and cartilage geometry [3,5–9]. Decisions regarding model complexity and behavior may be based on specific knee structures, loading profiles of interest, or computational limitations. Regardless of the level of complexity, validating model predictions is a critical step in model development and application. While some models have been presented with no validation, others demonstrate varying levels of agreement with experimental data [1,2,5,10,11]. Often, models are not calibrated with one-to-one experimental data from cadaveric specimens, which can be precarious given intersubject variability and sensitivity to different loading protocols [12]. Furthermore, even in cases presenting one-to-one experiment and model pairs, many models examine only highly limited motions, use only a single knee (thereby excluding variation among knees) or neglect to verify proper engagement of ligaments and other included structures [5,7,11]. Beyond modeling the knee in a healthy, intact state, another challenge is to accurately mimic knee mechanics in states of pathology such as after cruciate rupture or meniscectomy. For broad application, a model must be able to replicate those altered states, yet may not be able to do so reliably if validated to only the more constrained motions of an intact knee.

An effective method for measuring the timing and extent of ligament recruitment during knee motion in various degrees-of-freedom (DOF) is with experimental tests of knee laxity. Quantitative knee laxity (i.e., knee envelope) tests can provide important information about ligament engagement and overall contributions to knee stability [12–16]. When developing a computational model, knee laxity tests in multiple DOF can be used to calibrate simulated ligament material properties and ensure accurate prediction of ligament-constrained knee motion and loading.

We have previously presented validated FE models of knee mechanics after total knee arthroplasty (TKA) [10]. Those models used laxity tests of cruciate-sacrificing implanted knees to tune ligament behavior. In the current study, we present the methodology and validation results of a series of FE models of natural knees. Our objective was to provide combined experimental tests and FE models of natural knee laxity that are subject-specific, have one-to-one experiment to model validation, simulate ligament engagement in agreement with literature, and are adaptable for a variety of biomechanical investigations (e.g., cartilage contact, ligament strain, in vivo kinematics). The resulting models are also sufficiently robust to accurately predict changes in knee kinematics in whole knees, as well as knees after resection of important support structures such as the cruciate ligaments and the meniscus.

Materials and Methods

Experimental Testing.

Magnetic resonance images of the lower limb (femoral head to toes) from four fresh-frozen cadaveric specimens (three male, 26 ± 10 BMI, 51 ± 15 years old) were taken after 24 hrs of thawing at room temperature. MR images were captured with T2 weighting and true fast 3D gradient echo sequence with in-plane resolution of 0.5–0.6 mm and slice thickness of 0.5–1.0 mm. After imaging, each specimen was dissected at the midfemur and midtibia, retaining all tissue approximately 20 cm proximal and distal to the joint line and leaving the knee joint capsule intact. The femur and tibia were then potted in aluminum cylindrical fixtures. High-speed optical motion tracking arrays (collection frequency = 100 Hz) were rigidly attached to the femur, tibia, and patella (Fig. 1) and subsequent knee joint motion was then captured using the Optotrak 3020 camera system (accuracy = 0.1 mm, Northern Digital, Inc., Waterloo, ON, Canada).

Fig. 1.

Experimental setup for laxity testing. Each leg was inverted, with the femur rigidly mounted to a base and a 6DOF load cell attached to the distal tibia. Optotrak arrays tracked segment motion while torques and displacements were manually applied.

Passive laxity tests were performed at 0, 15, 30, 45, and 60 deg knee flexion by applying up to ±10 N · m VV torque, ±8 N · m IE torque, and ±80 N AP force in each direction. To begin, the knee was placed in full extension and a VV torque was manually applied. Torque magnitudes were measured with a 6DOF load cell attached to the distal tibia and synchronized with Optotrak motion capture data using a custom labview (National Instruments Corp., Austin, TX) script. labview provided live feedback of the knee flexion angle and applied torques to ensure that the knee stayed near the desired position and that torques increased through the desired range (0–10 N · m). After testing at full extension, the knee was flexed to 15 deg, and so on, with VV torques applied at each flexion angle. Finally, the knee was repositioned at full extension and the procedure was repeated, except with IE torques or AP forces applied. The order of testing (e.g., VV then IE then AP) was randomized for each knee. Laxity testing was completed for each knee with all soft-tissue intact and repeated after controlled resection of the anterior and posterior cruciate ligaments (PCLs) and the lateral and medial meniscus. The joint capsule was sutured closed after each resection.

Following experimental testing, each knee was completely dissected. Attachment site locations of the anteromedial and posterolateral bundles of the anterior cruciate ligament (amACL, plACL), anterolateral and posteromedial bundles of the PCL (alPCL, pmPCL), superficial and deep medial collateral ligament (MCL, dMCL), and lateral collateral ligament (LCL) were digitized using a handheld Optotrak motion capture array fixed to a metallic probe.

Experimental knee laxity motion and loading information were processed for all DOF using the radial basis function (RBF) technique described by Cyr and Maletsky [17]. While loads were manually applied in a single plane, knees experience an inherent multiplanar response due to articular geometry constraints and the coupled constraint of passive structures pulling in different DOF. RBF processing allowed quantification of these coupled joint motions in all DOF, and isolation of the 6DOF kinematics and loads that occurred at discrete flexion angles. For example, during a valgus loading test, where torque was ramped from 0 N · m to 10 N · m at a given flexion angle, corresponding 6DOF kinematics and off-axis loads were determined. These 6DOF kinematics and loads were available as targets for FE modeling.

FE Modeling.

Subject-specific three-dimensional reconstructions of the proximal femur, tibia, tibial cartilage, and femoral cartilage were generated for each cadaveric specimen. Specifically, the cortical bone and cartilage were segmented from the MR images using scanip software (v6.0, Simpleware, Exeter, UK). The reconstructed surfaces were discretized and meshed using hypermesh software (v11.0, Altair, Troy, MI) with triangular shell elements for the cortical bone and eight-node hexahedral elements for the femoral and tibial cartilage. As noted, ligament attachment sites were digitized on each knee after dissection. Additionally, points were digitized along the borders the articular surfaces and on the shafts and distal ends of the resected femur and tibia bones. The digitized points were aligned to the laxity experimental space by minimizing the Euclidean distance between the cloud of points on a body (e.g., femur bone) and that body's rigid body reference frame established during the experiment. Next, the surface meshes were aligned to the point clouds to position the FE model within the experimental space, resulting in root mean square distances less than 2.0 mm between the 300 and 900 digitized points collected for each knee and the nearest mesh nodes.

Kinematics was calculated using a tibiofemoral three-cylindrical open-chain coordinate system [18]. In brief, bony landmarks on the tibia (medial and lateral dwell points of the plateau, proximal tip of the medial spine of the tibial eminence, center of the distal intramedullary canal) and femur (posterior of medial and lateral condyles, distal point between condyles, hip ball center) were digitized during experimentation. These points were used to establish local coordinate systems for the femur and tibia in their respective rigid body reference frame, and allowed calculation of the relative motion of the tibia relative to the femur in an anatomically relevant coordinate system.

Ligamentous structures were represented with bundles of point-to-point, tension-only, nonlinear spring elements [19]. Placement of the amACL, plACL, alPCL, pmPCL, MCL, dMCL, and LCL was determined using the experimentally digitized attachment points with the knee in a neutral, full extension position. The following structures, important to knee stability, were added based on literature descriptions: posterior oblique ligament (POL) [20,21], popliteofibular ligament (PFL) [22–26], lateral and medial posterior capsule (mPCAP, lPCAP), and anterolateral structure (ALS) [10,27,28]. The PFL was represented as four springs in series between attachment points at the fibula and femur, which replicated the angled architecture and mechanical restraint of the PFL where it would intertwine with the popliteus tendon and attach at the lateral meniscus. The amACL, plACL, alPCL, pmPCL, and POL were each represented with two springs, while the remaining ligaments were each represented with three springs to cover the broad area of ligament anatomy (Fig. 2). Because of the broad AP dimension of the MCL, it was represented with anterior, middle, and posterior springs (MCLA, MCLM, MCLP), each with individual reference strain values. Initial ligament material properties were assigned based on the literature and a previous validation study of TKA modeling [10]. For more rapid calibration of ligament contributions to knee stability, such that experimental and computational kinematic profiles matched, bone and cartilage were represented as rigid with tibiofemoral cartilage contact defined by a pressure-overclosure relationship [4]. Analysis of knee kinematics during the laxity tests with knees intact and after resection of the meniscus found that the meniscus did not significantly affect kinematic excursions during laxity tests, and therefore was excluded from the model as is consistent with previous studies [5].

Fig. 2.

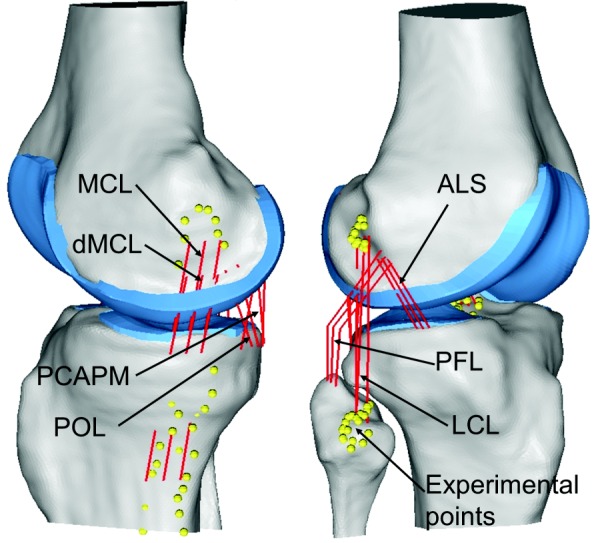
Medial (left) and lateral (right) views of FE model from one knee. Yellow dots indicate digitized points taken during the experiments to identify attachment locations for the LCL, MCL, ACL, and PCL. Other ligaments were placed based on anatomical descriptions.

Beginning with the FE model aligned in a full extension position, loads were applied in the VV, IE, or AP directions and resulting knee kinematics was determined. For example, during a valgus laxity test at 15 deg of flexion, a valgus load was applied to the tibia from 0 N · m to 10 N · m, with resulting kinematics being affected by ligament restraint and tibiofemoral contact. A nominal 20 N load was constantly applied along the long axis of the tibia during all simulations to provide a baseline amount of joint compression.

Model Calibration.

Ligament parameters, including ligament stiffness, reference strains (i.e., initial ligament strain), and attachment locations, were calibrated for each ligament in the model to reduce differences in model and experimental kinematics. Calibration was performed using Isight (v7, SIMULIA) optimization software. During calibration, an adaptive simulated annealing optimization technique was applied simultaneously to models of applied VV and IE torques at 0 deg, 15 deg, 30 deg, 45 deg, and 60 deg flexion for a given knee. When one iteration of the models completed, the root mean square errors (RMSEs) between model and experimental kinematics, calculated at 1 N · m increments, were calculated for the DOF of interest (e.g., valgus rotation of the knee when a valgus torque was applied, or internal rotation when an internal torque was applied). Ligament parameters were adjusted and the models were run for a second iteration, after which RMSE between models and experiments were again calculated. This process was repeated for a minimum of 300 iterations, during which the objective function, being the sum of squared differences between experimental targets and model results, converged and no longer differed between iterations by more than 0.01 deg.

During the calibration process, ligament attachment locations were allowed to vary up to 3 mm from the original location, keeping ligament footprints within the spread of digitized points for the collateral and cruciate ligaments. Ligament attachments were not perturbed in a direction that would place them off or inside the bone. Ligament stiffness values were allowed to vary within bounds similar to those used in our previous validation study and from literature reports [10,29–31]. Reference strain is associated with measured initial ligament length. The reference strain of ligaments for which digitized footprints were available from experimental data (i.e., MCL, LCL, ACL, PCL), was allowed to vary by only 10% during calibration. Reference strains for ligaments placed using anatomical descriptions (i.e., PFL, POL, ALS), and thereby with less certain initial lengths, were allowed to vary by up to 25% during calibration.

The objective of the calibration process was one-to-one matching of model kinematics to experimental targets for a given knee, but also assurance that the ligaments engaged in agreement with their physiological function. Thus, mediolateral and AP motion were constrained during the VV and IE tests using experimental values, and mediolateral motion only was constrained during AP tests. Furthermore, after Isight-based calibration, if ligament engagement was not qualitatively similar to literature descriptions, the ligament parameters were manually adjusted, the parameter bounds were further restricted, and the Isight calibration process was repeated.

Each knee was calibrated separately to its own experimental targets. The models were first calibrated for the fully resected state using VV and IE torques and kinematics (i.e., AP forces and displacement tests were not used to calibrate the resected models). Resulting ligament parameter values were then applied to the intact knee model, and the ACL and PCL were calibrated using torques and kinematics from VV, IE, and AP experimental tests.

Results

RMSE between experimental and model kinematics for the four knees and associated ranges of motion covered during each laxity test are presented in Table 1. RMSE during AP tests are reported for the knees in both their intact and resected states, although calibration was performed only in the intact state. For the intact knees, average RMSE was less than 2 deg during VV rotations, less than 6 deg during IE rotations, and less than 2.2 mm of translation during AP displacements. Errors did not increase appreciably between the intact and resected states for VV or IE tests, but did increase, as did the range of motion, during AP tests. Matching of torque-rotation and torque-displacement profiles between the experiments and models with the knees intact and after cruciate and meniscus resection is shown in Fig. 3.

Table 1.

RMSEs (mean ± stdev) between experimental and model-predicted kinematics for the four knees at each flexion angle and each DOF in which loads were applied. Brackets indicate the average range of motion covered by the knees during the experimental testing.

Flexion angle (deg)	Loading DOF	Resected RMSE [ROM]	Intact RMSE [ROM]
0	VV (deg)	1.2 ± 0.2 [7.0 ± 3.3]	1.2 ± 0.4 [4.6 ± 1.4]
	IE (deg)	3.6 ± 0.7 [33.0 ± 7.7]	4.9 ± 0.7 [27.8 ± 5.6]
AP (mm)	3.3 ± 0.7 [16.0 ± 11.0]	2.0 ± 1.2 [7.7 ± 3.0]
15	VV (deg)	1.1 ± 0.2 [9.0 ± 3.5]	1.8 ± 0.5 [6.6 ± 1.5]
	IE (deg)	4.0 ± 0.4 [40.0 ± 8.1]	5.8 ± 1.9 [35.7 ± 4.8]
AP (mm)	4.4 ± 1.9 [18.3 ± 10.3]	2.2 ± 1.0 [9.0 ± 3.0]
30	VV (deg)	1.3 ± 0.4 [9.9 ± 3.4]	1.5 ± 0.5 [7.7 ± 1.6]
	IE (deg)	2.1 ± 0.3 [44.5 ± 8.1]	3.5 ± 1.1 [40.9 ± 3.6]
AP (mm)	4.0 ± 1.4 [19.5 ± 8.6]	1.5 ± 0.7 [9.1 ± 2.4]
45	VV (deg)	1.2 ± 0.3 [10.6 ± 3.3]	1.2 ± 0.6 [8.6 ± 1.9]
	IE (deg)	2.1 ± 0.9 [45.6 ± 8.0]	2.1 ± 0.7 [42.9 ± 3.2]
AP (mm)	4.3 ± 1.7 [20.0 ± 7.6]	1.4 ± 0.6 [8.2 ± 2.2]
60	VV (deg)	1.5 ± 0.4 [10.2 ± 4.4]	1.7 ± 1.2 [9.3 ± 2.2]
	IE (deg)	5.5 ± 2.5 [45.1 ± 8.2]	4.1 ± 1.4 [43.0 ± 3.6]
AP (mm)	6.8 ± 2.5 [22.8 ± 5.5]	1.8 ± 0.8 [7.3 ± 2.1]

Fig. 3.

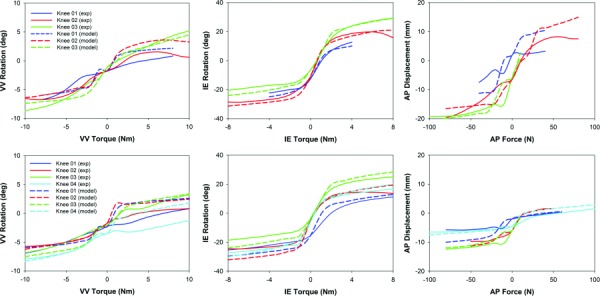
Experimental and FE model torque versus displacement curves at 30 deg flexion for the resected (top) and intact (bottom) cases. Positive torque or force values and positively directed rotation and displacement values represent valgus, external, and anterior.

During experimental testing and subsequent RBF postprocessing, load data were not available for every knee to the full ±10 N · m VV torque, ±8 N · m IE torque, and ±80 N AP force. In the cases of knee #1 and knee #4, this was due to increased VV and IE laxity, leading to instability (i.e., subluxation) after resections were made. In the cases of knee #2 and knee #3, AP loads were limited in the intact case to ensure preservation of soft-tissue for later resection experiments. In either case, the reduction of applied load was performed to ensure only controlled changes (i.e., isolated resections) were performed and to limit unintentional damage from experimental evaluations. RMSE between models and experiments reflects calibration to the available experimental data.

Final ligament stiffness and reference strain values for each calibrated knee model are shown in Table 2. The bounding values reported for ligament stiffness and reference strain were used for all knees during the first cycle of Isight-calibration and manual adjustment. For each individual knee, the bounds were incrementally decreased for each calibration cycle to determine the final values reported in Table 2. The calibration process required two to three cycles for each knee.

Table 2.

Final ligament stiffness and reference strains in the calibrated models. Reference strains were allowed to vary by up to 15% (i.e., 0.85 to 1.15) for the ACL, LCL, MCL, and PCL, and up to 25% (i.e., 0.75 to 1.25) for the ALS, PCAP, PFL, and POL. Stiffness bounds allowed for each ligament are shown in brackets.

	Reference (initial) strain
Knee	ALS	amACL	plACL	LCL	MCLA	MCLM	MCLP	dMCL	POL	PCAPL	PCAPM	alPCL	pmPCL	PFL
01	0.83	1.04	1.01	1.01	1.02	1.08	1.08	0.80	0.85	1.04	0.96	0.93	1.00	1.00
02	0.75	0.99	0.96	1.05	1.07	1.07	1.07	0.95	0.97	1.06	1.06	1.06	0.97	0.90
03	0.85	0.85	0.85	1.00	1.03	1.00	1.01	0.90	0.90	1.05	0.98	0.85	0.85	0.80
04	0.79	1.1	1.1	1.00	1.04	1.04	1.04	1.01	0.94	1.02	1.09	0.97	1.07	1.06
	Ligament stiffness (N/mm)
	[15–135]	[50–150]	[45–150]	[60–200]		[60–180]		[50–180]	[30–90]	[50–110]	[50–110]	[30–100]	[30–100]	[10–90]
01	40	100	47	163		115		50	35	110	100	35	60	35
02	36	106	108	197		149		80	50	90	90	36	42	31
03	30	50	51	153		115		70	30	90	90	50	60	20
04	43	90	90	129		110		50	80	100	85	52	74	89

The timing of engagement for each ligament in the FE model varied with flexion angle and with the DOF in which loading was applied (Fig. 4). The MCL was engaged most heavily during valgus loading. As flexion angle increased above 30 deg of flexion, the MCLM and MCLP sections of the MCL shortened and did not generate substantial force. The MCL was also heavily engaged during external rotation, with contributions from the MCLM and MCLP again diminishing rapidly beyond 30 deg flexion, but contributions from MCLA remained strong, especially for knee 04 (Fig. 5). At full extension and 15 deg flexion, the MCL was weakly engaged during internal rotation, although ligament forces were lower and drastically reduced as flexion increased. The MCLA section was also engaged during anterior and posterior loading, for knees 02 and 04 in both the intact and resected states. The dMCL was engaged during valgus loading, although it acted as a secondary support to the MCL, with lower force generation. Some engagement of the dMCL was also seen during external rotation. The POL was engaged primarily during internal rotation tests and especially at lower flexion angles for the intact knees. Relative to its engagement during internal rotation, the POL generated smaller forces during valgus rotations, particularly at 15 deg and 30 deg flexion.

Fig. 4.

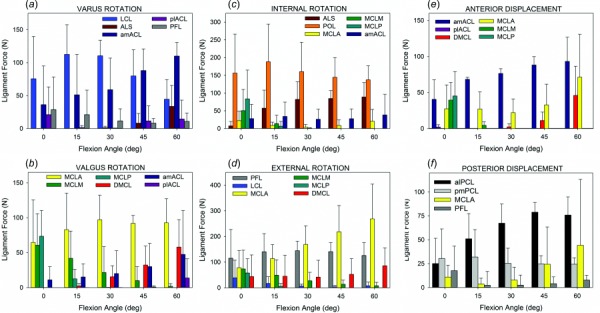
Engagement of ligaments contributing to resistance of tibia motion during (a) varus, (b) valgus, (c) internal, (d) external, (e) anterior, and (f) posterior tests for the intact state. Forces represented are the average and standard deviation forces for all knees at the end of the applied 10 N·m for VV or 8 N·m for IE torque tests. For AP tests, not all knees reached 80 N during experimental testing; shown here are averages at applied forces of 50 N for anterior and 80 N for posterior.

Fig. 5.

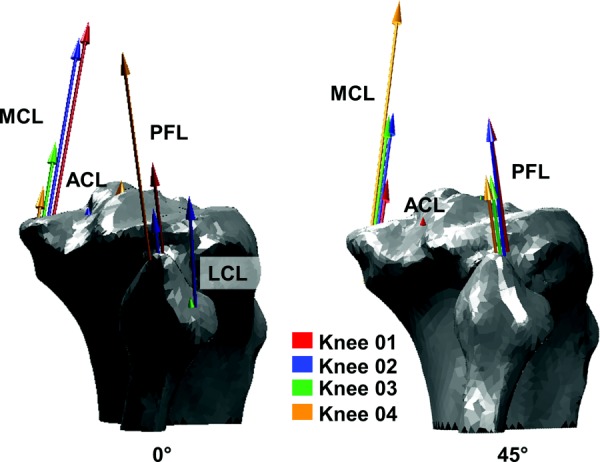
Representation of force within ligaments engaged during external rotation at 0 deg flexion (left) compared to 45 deg flexion (right). Arrow sizes indicate ligament forces in the four. Major contributors during external rotation were the PFL and MCL. The MCLA of knee 04, particularly, became increasingly engaged as flexion increased.

On the lateral side of the knee, the LCL was engaged and was the major contributor to stability during varus rotation, with far less engagement during internal and external rotation. The ALS was also engaged during varus rotation, but only at flexion angles above 30 deg to provide stability as the role of the LCL decreased. The ALS was more engaged during internal rotation, with greater contributions seen in the resected models than the intact models. The PFL was primarily engaged during external rotation with low engagement during posterior tibia displacement at full knee extension. The PCAPL and PCAPM were engaged during varus and valgus rotations, respectively, but only at full extension; at flexion angles above 0 deg, these structures were slack.

The ACL was strongly engaged during anterior displacement tests, with greater contributions from the amACL than the plACL. The ACL was also slightly engaged during internal rotation tests and was increasingly engaged during varus rotations as flexion increased in the intact knee models. The PCL was engaged during posterior displacement with contribution of the pmPCL increasing and the contribution of the alPCL decreasing with increases in flexion angle.

Discussion

The objective of this study was to present the combined experimental testing and FE modeling of natural knee joint laxity that have one-to-one experiment to model calibration in healthy and pathologic conditions, and that simulate ligament engagement in agreement with literature. The models presented herein utilized subject-specific bone and articular geometry and ligament representations based on experimental and anatomical reports. We calibrated the laxity models by using simple, one-dimensional spring bundles to represent the ligaments stabilizing the knee. The simplified spring elements allowed for rapid iteration of ligament parameters to establish the correct general constraint of knee kinematics in intact knees and after simulating loss of the cruciate ligaments. These constraint models can be adapted for various research questions by altering the complexity of the ligament representations, including additional geometry such as the patella, or incorporating the models into larger FE simulations in which the influence of the musculature is analyzed while still maintaining correct multi-DOF constraints at the knee.

Our modeling approach, including calibration of ligament parameters, was somewhat similar to the methods of previous studies [5,10,31]. However, in the present study, we have provided a more exhaustive calibration and validation than prior studies by directly validating with four natural cadaveric knees at five flexion angles using dynamic (versus quasi-static) motions, inclusion of more stabilizing structures beyond the cruciate and collateral ligaments, and calibration of the models in both a fully intact and a less stable state.

Errors between model and experimental kinematics averaged less than 2 deg during VV rotations, less than 6 deg during IE rotations, and less than 2.2 mm of translation during AP displacements for the intact knees. Errors did not increase appreciably between the intact and resected states for VV or IE tests, but did increase, as did the range of motion, during AP tests. Because of the large contribution of the cruciate ligaments to knee stability during AP loading, the knees were not calibrated to the experimental AP kinematics in the cruciate deficient state. As such, it is unsurprising that the errors during AP tests in the cruciate deficient state were much higher. The resulting error values for all tests should be interpreted in context of the range of motion covered by the knees during the experimental testing (Table 1). In this context, agreement between the experiments and models was very good.

The errors in the present study are greater than the average 2.4 deg and 0.6 deg of IE and VV errors reported by Baldwin et al. for knees subjected to similar loading profiles [10]. These differences may be attributable to Baldwin's use of knees that had been implanted with cruciate-sacrificing total knee components by a trained surgeon, who focused on reducing laxity and malalignment during implantation. The implants also provided a consistent, constrained articular geometry that resulted in more uniform motions between specimens, higher constraints to range of motion and smoother torque-rotation than those seen for natural knees. Errors in the present study are similar to those reported previously during similar experimental tests, including the 0–8 deg of error during internal rotations and 3–5 mm during AP displacement reported by Blankevoort et al. when knees were loaded with 3 N · m of internal torque or 100 N AP load, respectively [5]. Similar to results reported by Mommersteeg et al., model-predicted valgus rotations in the current study tended to be higher than experimental rotations during lower flexion angles, yet lower than experimental rotations as flexion angles increased [31]. This trend speaks to the inherent difficulty identifying and subsequently representing the distinct and interconnected structures of the medial side and posteromedial corner of the knee.

Ultimately, a model and accompanying simulations, like those presented herein, consist simply of constraints (i.e., ligament representations) meant to direct overall knee motion to match experimental targets. While anatomically based placement of the ligaments will inherently affect when they are engaged, it would be possible to have some ligaments engaged or disengaged in disagreement with true ligament behavior. In the current study, ligament engagement was part of the validation process. The result was ligaments that engaged in agreement with most literature descriptions.

Specifically, the MCL was a major resistor against valgus rotation and was also actively engaged during external rotation [13,15,16,30,32,33]. The MCL also engaged to a lesser degree during internal rotation [30]. The dMCL provided a secondary restraint to valgus rotation [15]. The POL, which is sometimes described as part of a general posteromedial corner, was represented in the current study as an obliquely aligned two-spring bundle to help stabilize the posteromedial knee [14,15]. The POL became engaged primarily to resist internal rotation of the tibia and offered a small resistance to valgus rotation at flexion angles lower than 30 deg [15,34].

The LCL, ALS, and PFL were the main lateral support structures represented in the model, and served to resist varus, external, and internal rotations. The LCL exhibited well documented engagement during varus rotations [22,32]. The ALS and PFL were included to more completely represent the knee restraint to IE rotation than can be done with the MCL and LCL alone. Anatomical and functional descriptions of the ALS are still emerging, but it has been proposed as a restraint to anterior tibial displacement [28] and internal tibial rotation [27]. As represented in the current study, the ALS did not engage during anterior tibial displacement, but did resist internal rotation. As reported previously, the PFL primarily resisted external rotation [22,23]. The PFL did offer some resistance to posterior motion, as reported by Shahane et al., but this contribution quickly decreased after 0 deg flexion [25]. This decrease was likely due to the absence of the meniscus and popliteus muscle to provide intermediary PFL attachments.

As expected, the ACL and PCL were engaged most heavily during anterior and posterior tibial displacement, respectively. Generally, the two bundles of ACL and those of the PCL did not reverse their roles or levels of contributions as flexion increased, as described in some experimental literature [35]. Because we used nonlinear springs without explicitly described interactions between bundles (i.e., bundles did not twist around each other) and approximated bundle locations from digitized points of the entire ligament footprint, the roles of each bundle did not change appreciably. However, as described by Markolf et al., the alPCL was the major contributor to posterior translation resistance beyond 30 deg of flexion, with the pmPCL playing a minor role [36]. The amACL increasingly engaged during varus rotations for most of the knees, which is not a commonly described role of the ACL. Engagement of the amACL is likely a limitation of ligament placement required to satisfy anterior displacement and IE rotation targets. At terminal range of motion, the knees were placed in up to 9.5 deg of varus rotation and coupled with small anteriorly directed displacements as varus torque increased, making it possible that the ACL would engage (also see in Fig. 4, amACL engagement with increased flexion during anterior displacement test).

Calibration of the FE models for each knee highlighted the intersubject variability and the importance of subject-specific modeling. Applying the experimental protocol to each individual knee resulted in torque-displacement and torque-rotation curves that were similar in trend, but each had subtly unique kinematics that were likely influenced by subject-specific articular geometry, ligament laxity, and ligament size and attachment. As a result, when applying a standardized set of restraining ligaments, variation in ligament properties and attachment was necessary to calibrate the model to each subject's kinematic profiles (Table 2). Consequently, force production in each ligament for a given subject and test varied to some degree compared to the other subjects (Fig. 5). These results demonstrate the ability of our constraint models to be customized for multiple individuals and simultaneously call attention to the need to verify that ligament engagement is in good general agreement with literature.

Both the experimental and computational aspects of the current study have limitations. During the experimental testing, every effort was made to maintain the structural integrity of the knee during the intact state and to only disrupt the meniscus and cruciate ligaments for the resected state. However, surgical rupturing of the cruciate ligaments and detachment of the meniscus may have disrupted tissues surrounding the knee, such as the capsule and collaterals. As a result, the mechanical environment of the knee may have been changed. Also, because of the resection of important tissues and concurrent use of the same knees for walking and squatting mechanical tests and quadriceps loading as part of separate studies [37], the knees could become unstable, as was the case for knee 04 which became too unstable to collect laxity data in the resected state.

Limitations of the FE model include the fact that simple spring mechanisms were used to represent complex 3D ligaments. Spring representations were computationally efficient which allowed for rapid iteration of ligament parameters to establish general constraint and motion of the knee to match experimental profiles. The springs were suitable for observing engagement of the ligaments but would not be appropriate for studies of ligament stress. For such investigations, continuum-level meshes would be required [3,38,39].

Also, calibration of the models was performed between full knee extension and 60 deg flexion. Previous studies have found that calibration of ligament behavior at deeper flexion angles requires a separate set of ligament parameters [11]. Indeed, posthoc testing of our calibrated models during laxity simulations at 90 deg and 120 deg found that the estimated rotation and translation matched trends of the experimental data, but RMSE was elevated, most especially for IE rotation. For example, for the intact knee models at 90 deg of knee flexion, RMSE ranged from 2.0 to 3.7 deg for VV rotations, 4.4–11.1 deg for IE rotations, and 2.3–3.2 mm for AP translations, with broadening ranges of error at 120 deg flexion. Calibration of ligamentous constraint up to 60 deg of flexion covers the most common ranges of motion during which heavy loading occurs and when ligaments make substantial contributions to knee stability [9].

The intent of the models presented here was to sufficiently represent passive tissue restraint across a range of motions and loads. In future work, models will be incorporated into more complex musculoskeletal models of the lower extremity. Finally, acquisition of in vitro data of knee biomechanics can be costly and can make it difficult for researchers to create computational models for one-to-one validation. So, as part of this work, we have made motion and loading data collected during experimental sessions freely available. We have also provided the digitized points of ligament attachment, MR images for the knees and 3D reconstructions of bone and cartilage geometry available for download. Information about the data available and instructions about how to obtain the data can be found at our website2. Other researchers may use the data to create their own models, analyze in vitro knee mechanics, or for other purposes such as statistical shape modeling.