Neuroprotective Role of Gap Junctions in a Neuron Astrocyte Network Model

Abstract

A detailed biophysical model for a neuron/astrocyte network is developed to explore mechanisms responsible for the initiation and propagation of cortical spreading depolarizations and the role of astrocytes in maintaining ion homeostasis, thereby preventing these pathological waves. Simulations of the model illustrate how properties of spreading depolarizations, such as wave speed and duration of depolarization, depend on several factors, including the neuron and astrocyte Na⁺-K⁺ ATPase pump strengths. In particular, we consider the neuroprotective role of astrocyte gap junction coupling. The model demonstrates that a syncytium of electrically coupled astrocytes can maintain a physiological membrane potential in the presence of an elevated extracellular K⁺ concentration and efficiently distribute the excess K⁺ across the syncytium. This provides an effective neuroprotective mechanism for delaying or preventing the initiation of spreading depolarizations.

Introduction

Both cortical spreading depression and spreading depolarizations correspond to slowly propagating waves of rapid, near-complete depolarization of brain cells (1, 2, 3, 4, 5, 6). Cortical spreading depression typically arises in normal tissue, as in migraine, whereas spreading depolarizations typically arise in metabolically compromised tissue, as in ischemia (1, 4, 7, 8). Both are characterized by a disruption of transmembrane ionic gradients, the collapse of ion homeostasis, cell swelling, and elevated extracellular K⁺ levels.

Cell damage and death during ischemia result from reduced oxygen and glucose supply to brain cells (1, 3, 6, 9). This decreases mitochondrial ATP production, leading to failure of the Na⁺-K⁺ ATPase pump, which, in turn, leads to the rapid accumulation of Na⁺ and chloride ions inside the cell, elevated extracellular K⁺ ions, cell swelling and, ultimately, recurrent spreading depolarizations in both neurons and astrocytes. Depolarization of excitatory neurons stimulates an excessive release of the neurotransmitter glutamate leading to excitotoxicity.

Astrocytes play a central role in brain homeostasis and, therefore, may critically affect the development and outcome of both cortical spreading depression and spreading depolarizations (10, 11, 12, 13, 14). Several studies have demonstrated that astrocytes are required for the recovery of pathologically elevated extracellular K⁺ levels, which initiate spreading depolarizations, and in reducing high extracellular glutamate (15, 16).

In this study, we develop a computational model for a neuron/astrocyte network to explore mechanisms responsible for the initiation and propagation of spreading depolarizations and the role of astrocytes in maintaining ion homeostasis, thereby preventing these waves. Although there have been numerous previous studies that have developed detailed models to address various issues related to the spreading depression (17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32), the model presented here is the first, to our knowledge, to incorporate a detailed biophysical model for the astrocytes. This allows us to explore more fully the role of specific astrocyte processes in preventing pathological wave propagation.

In particular, we consider the role of gap junction connections between astrocytes. The neuroprotective role of gap junctions during diseased states has been under considerable debate (33, 34). Numerous experimental results suggest that depending on the severity of injury, gap junction communication may either be beneficial following injury or amplify ischemic damage. In a recently published article, we demonstrated both experimentally and with a computational model that a syncytium of electrically coupled astrocytes can maintain a physiological membrane potential in the presence of an elevated extracellular increase in K⁺ concentration and efficiently distribute the excess K⁺ across the syncytium (35). Here we extend this model to a neuron/astrocyte network and demonstrate that a syncytium of electrically coupled astrocytes provides an effective mechanism for delaying or preventing spreading depression and depolarizations. However, gap junctions may also play a role in amplifying these signals, once they are initiated.

Materials and Methods

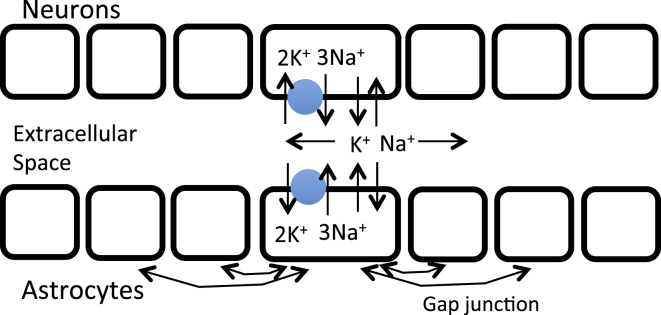
A schema of our model is shown in Fig. 1. The model consists of a one-dimensional array of astrocyte-neuron pairs sharing an extracellular space. The neuron and astrocyte models include equations for membrane potential, ionic currents, and ionic fluxes, as well as balance equations for Na⁺ and K⁺ concentrations inside the cells and in the shared extracellular space. Neurons are not coupled and communicate only through ionic diffusion in the extracellular space, whereas astrocytes may be connected to other astrocytes by gap junctions that carry ionic currents and fluxes.

Figure 1.

Schema of model. There is a one-dimensional array of neurons, astrocytes, and compartments corresponding to extracellular space. Each neuron and astrocyte has K⁺ and Na⁺ channels and a Na⁺-K⁺ ATPase pump, represented as a blue circle. K⁺ and Na⁺ ions diffuse in the extracellular space, as well as through gap junctions among the astrocytes. To see this figure in color, go online.

Neurons

Each neuron is modeled as a single compartment using the Hodgkin-Huxley formalism (36). This model is similar to that in previous modeling studies of spreading depression (17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32); however, our neuron model is minimal in the sense that it includes only those ionic currents required to generate the dynamics considered in this study.

The neuron’s membrane potential V_N satisfies an equation of the following form:

$$C_m\frac{d{V}_N}{dt}=-I_{Na}-I_{NaP}-I_K-I_L-I_{P,N},$$

where I_Na, I_NaP, I_K, and I_L correspond to fast Na⁺, persistent Na⁺, K⁺, and leak currents, respectively. These are given by the following:

$$I_{Na}=g_{Na}{m}_{\infty }^3\left(V_N\right)\left(1-n\right)\left(V_N-E_{Na,N}\right),$$

$$I_{NaP}=g_{NaP}{m}_{p\infty }\left(V_N\right)h_p\left(V_N-E_{Na,N}\right),$$

$$I_K=g_K{n}^4\left(V_N-E_{K,N}\right),$$

$$I_L=g_L\left(V_N-E_L\right).$$

Here, h_p and n are dynamic variables satisfying equations of the following form:

$$\frac{dX}{dt}={\varphi }_X\frac{X_{\infty }\left(V_N\right)-X}{{\theta }_X\left(V_N\right)},$$

where X = h_p and n.

The asymptotic functions are of the following form:

$$X_{\infty }\left(V\right)=\frac{1}{1+\text{exp}\left(-\left(V-V_X\right)/{\tau }_X\right)},$$

where $V_m$ = −34, ${\tau }_m$ = 5, $V_n$ = −55, ${\tau }_n$ = 14, $V_{m_p}$ = −40, ${\tau }_{m_p}$ = 6, $V_{h_p}$ = −48, and ${\tau }_{h_p}$ = −6. Moreover,

$${\theta }_n\left(V\right)=0.05+\frac{0.27}{1+\text{exp}\left(\left(V+40\right)/12\right)}\text{and}{\theta }_{h_p}\left(V\right)=\frac{10000}{\text{cosh}\left(\left(V+49\right)/12\right)}.$$

The reversal potentials are given by the following:

$$E_{K,N}=\frac{RT}{F}\text{ln}\left(\frac{{\left[{\text{K}}^{+}\right]}_e}{{\left[{\text{K}}^{+}\right]}_{i,N}}\right)\text{and}{E}_{Na,N}=\frac{RT}{F}\text{ln}\left(\frac{{\left[{\text{Na}}^{+}\right]}_e}{{\left[{\text{Na}}^{+}\right]}_{i,N}}\right),$$

where R, T, and F are the gas constant, temperature, and Faraday’s constant, respectively.

As in (30), the Na⁺-K⁺ATPase pump current is given by the following:

$$I_{P,N}={\rho }_N{\left(\frac{{\left[{\text{K}}^{+}\right]}_e}{K_{K,N}+{\left[{\text{K}}^{+}\right]}_e}\right)}^2{\left(\frac{{\left[{\text{Na}}^{+}\right]}_{i,N}}{K_{Na,N}+{\left[{\text{Na}}^{+}\right]}_{i,N}}\right)}^3,$$

where ${\rho }_N$ represents the maximal pump current.

Parameters corresponding to the neurons are given in Table 1.

Table 1.

Neuron Parameters

Notation	Value	Unit	Description
R	8.31	J/mol K	ideal gas constant
F	96,485	C/mol	Faraday’s constant
T	310	K	absolute temperature
$C_m$	1.00	μF/cm2	membrane capacitance per unit area
${\varphi }_n$	0.80	ms−1	maximum rate of activation of potassium channels
${\varphi }_h$	0.05	ms−1	maximum rate of activation of sodium channels
$g_{Na}$	3.0	mS/cm2	maximum fast sodium current conductance
$g_{NaP}$	0.4	mS/cm2	maximum persistent sodium current conductance
$g_K$	5.0	mS/cm2	maximum delayed rectifier potassium conductance
$g_L$	0.3	mS/cm2	nonspecific leak current conductance
$E_L$	–70.0	mV	leak current reversal potential
${\rho }_N$	parameter	μA/cm2	maximum neuron Na+-K+-ATPase pump current
$S_N$	922	μm2	neuron total membrane surface area
${\Omega }_N$	2160	μm3	neuron total volume
${\alpha }_0$	0.10		volume fraction between a neuron and astrocyte and the extracellular space
$K_{K,N}$	2	mM	half activation [K+] concentration for the neural Na+-K+ATPase
$K_{Na,N}$	7.7	mM	half activation [Na+] concentration for the neural Na+-K+ATPase

Astrocytes

The astrocytes are modeled as in (35). As with neurons, each astrocyte is modeled as a single compartment using the Hodgkin-Huxley formalism; however, following (35), the currents are modeled using the Goldman-Hodgkin-Katz (GHK) equations. We use the GHK formulation to account for strongly rectifying currents at nonphysiological ionic concentrations that occur in spreading depression/depolarization.

Each astrocyte’s membrane potential, V_A, satisfies an equation of the following form:

$$C_m^A\frac{d{V}_A}{dt}=-I_{Na,A}-I_{K,A}-I_{P,A}-I_{gap},$$

where the K⁺ and fast Na⁺ currents are now given, respectively, by the following:

$$I_{K,A}=P_{K}F\varphi \left(\frac{{\left[{\text{K}}^{+}\right]}_e{e}^{-\varphi }-{\left[{\text{K}}^{+}\right]}_{i,A}}{e^{-\varphi }-1}\right),$$

$$I_{Na,A}=P_{Na}F\varphi \left(\frac{{\left[{\text{Na}}^{+}\right]}_e{e}^{-\varphi }-{\left[{\text{Na}}^{+}\right]}_{i,A}}{e^{-\varphi }-1}\right).$$

Here P_K and P_Na are the K⁺ and Na⁺ permeability constants, ${\left[{\text{K}}^{+}\right]}_{i,A}$ and ${\left[{\text{Na}}^{+}\right]}_{i,A}$ are the K⁺ and Na⁺ concentrations in the astrocyte’s cytosol, and $\varphi =V_{A}F/RT$. Similar to the neurons, the Na⁺-K⁺ ATPase pump current is modeled as the following:

$$I_{P,A}={\rho }_A{\left(\frac{{\left[{\text{K}}^{+}\right]}_e}{K_{K,A}+{\left[{\text{K}}^{+}\right]}_e}\right)}^2{\left(\frac{{\left[{\text{Na}}^{+}\right]}_{i,A}}{K_{Na,A}+{\left[{\text{Na}}^{+}\right]}_{i,A}}\right)}^3.$$

Currents due to the gap junctions are modeled using the GHK constant field equation with the potential difference across the gap junction as the driving force. Suppose there is a gap junction between astrocytes j and k. Denote the membrane potentials and intracellular ion concentrations of these cells as $\left(V_A^j,{\left[{\text{K}}^{+}\right]}_{i,A}^j,{\left[{\text{Na}}^{+}\right]}_{i,A}^j\right)\text{and}\left(V_A^k,{\left[{\text{K}}^{+}\right]}_{i,A}^k,{\left[{\text{Na}}^{+}\right]}_{i,A}^k\right)$, respectively. Let

$${\varphi }^{jk}=\frac{F}{RT}\left(V_A^j-V_A^k\right),$$

and

$$I_{K,gap}^{jk}=P_{K,gap}F{\varphi }^{jk}\left(\frac{{\left[{\text{K}}^{+}\right]}_{i,A}^k{e}^{-{\varphi }^{jk}}-{\left[{\text{K}}^{+}\right]}_{i,A}^j}{e^{-{\varphi }^{jk}}-1}\right),$$

$$I_{Na,gap}^{jk}=P_{Na,gap}F{\varphi }^{jk}\left(\frac{{\left[{\text{Na}}^{+}\right]}_{i,A}^k{e}^{-{\varphi }^{jk}}-{\left[{\text{Na}}^{+}\right]}_{i,A}^j}{e^{-{\varphi }^{jk}}-1}\right).$$

Here, $P_{K,gap}\text{and}{P}_{Na,gap}$ are the K⁺ and Na⁺ gap junction permeabilities, averaged over the entire cell membrane. As in (35), we assume that

$$P_{K,gap}={\sigma }_{gap}{P}_K\text{and}{P}_{Na,gap}=0.8\cdot P_{K,gap},$$

for a constant ${\sigma }_{gap}$. Then, for the cell j we set

$$I_{K,gap}^j=\sum I_{K,gap}^{jk}\text{and}{I}_{Na,gap}^j=\sum I_{Na,gap}^{jk},$$

where the sums are over all indices k for which there is a gap junction between cells j and k. Finally, let

$$I_{gap}^j=I_{K,gap}^j+I_{Na,gap}^j.$$

Parameters corresponding to the astrocytes are given in Table 2.

Table 2.

Astrocyte Parameters

Notation	Value	Unit	Description
$P_K$	4.810−6	cm/s	membrane K+ permeability coefficient
$P_{Na}$	1.510−8	cm/s	membrane Na+ permeability coefficient
$S_A$	1600	μm2	astrocyte total membrane surface area
${\Omega }_A$	2000	μm3	astrocyte total volume
$C_m^a$	1.00	μF/cm2	membrane capacitance per unit area
${\rho }_A$	parameter	μA/cm2	maximum astrocyte Na+-K+-ATPase pump current
${\sigma }_{gap}$	parameter	unitless	measure of gap junction strength
$K_{K,A}$	2	mM	half activation [K+] concentration for the astrocytic Na+-K+ATPase
$K_{Na,A}$	7.7	mM	half activation [Na+] concentration for the astrocytic Na+-K+ATPase

Ion concentrations

The neurons’ intracellular K⁺ and Na⁺ concentrations satisfy the following equations:

$$\frac{d{\left[{\text{K}}^{+}\right]}_{i,N}}{dt}=-\frac{10S_N}{F{\Omega }_N}\left(I_K-2I_{P,N}\right),$$

$$\frac{d{\left[{\text{Na}}^{+}\right]}_{i,N}}{dt}=-\frac{10S_N}{F{\Omega }_N}\left(I_{Na}+I_{NaP}+3I_{P,N}\right),$$

where S_N is the neuron’s surface area and ${\Omega }_N$ is the volume of the neuron’s cytoplasm. The factor ‘10’ is needed for consistency of units. Similarly, the astrocyte’s intracellular K⁺ and Na⁺ concentrations satisfy the following equations:

$$\frac{d{\left[{\text{K}}^{+}\right]}_{i,A}}{dt}=-\frac{10S_A}{F{\Omega }_A}\left(I_{K,A}-2I_{P,A}-I_{K,gap}\right),$$

$$\frac{d{\left[{\text{Na}}^{+}\right]}_{i,A}}{dt}=-\frac{10S_A}{F{\Omega }_A}\left(I_{Na,A}+3I_{P,A}-I_{Na,gap}\right),$$

where S_A is the astrocyte’s surface area and ${\Omega }_A$ is the volume of the astrocyte’s cytoplasm.

We assume that K⁺ and Na⁺ ions diffuse in the extracellular space. In the continuum limit, where the number of cells become unbounded, these extracellular ionic concentrations satisfy equations of the following form:

$$\frac{\partial {\left[{\text{K}}^{+}\right]}_e}{\partial t}={\overline{D}}_K\frac{{\partial }^2{\left[{\text{K}}^{+}\right]}_e}{\partial x^2}+\frac{10S_N}{F{\Omega }_E}\left(I_K-2I_{P,N}\right)+\frac{10S_A}{F{\Omega }_E}\left(I_{K,A}-2I_{P,A}\right),$$

$$\frac{\partial {\left[{\text{Na}}^{+}\right]}_e}{\partial t}={\overline{D}}_{Na}\frac{{\partial }^2{\left[{\text{Na}}^{+}\right]}_e}{\partial x^2}+\frac{10S_N}{F{\Omega }_E}\left(I_{Na}+I_{NaP}+3I_{P,N}\right),$$

$$+\frac{10S_A}{F{\Omega }_E}\left(I_{Na,A}+3I_{P,A}\right),$$

where ${\Omega }_E$ is the volume of the extracellular space, assumed to be a fixed fraction of the total volume, given by ${\Omega }_E={\alpha }_0\left({\Omega }_N+{\Omega }_A\right)$.

We simulated injecting K⁺ into the extracellular space of a neuron/astrocyte pair by adding a positive constant, E, to the right-hand side of the equation for ${\left[K^{+}\right]}_e$ corresponding to those cells.

We use Dirichlet boundary conditions to simulate healthy tissue at the boundaries, with ${\left[{\text{K}}^{+}\right]}_{e,bdry}$ = 3.5 mM and ${\left[{\text{Na}}^{+}\right]}_{e,bdry}$ = 138 mM. The numerics correspond to an “ischemic insult” to the network’s center.

Numerics

Network simulations were performed in XPPAUT (37) and MATLAB (The Mathworks, Natick, MA). The model was integrated variously using XPPAUT, MATLAB’s ode15s, and an implicit 4th-order Runge-Kutta method implemented in C.

Results

Initiation of waves

We start the system at rest and then simulate the injection of K⁺ at a constant rate into the extracellular space of some subset neuron/astrocyte pairs. As the extracellular K⁺ concentration, [K⁺]_e, increases, the neuron’s resting potential also increases. There is a [K⁺]_e threshold beyond which the corresponding neurons quickly depolarize, extruding additional K⁺, and this initiates a wave of spreading depolarization. The time it takes for [K⁺]_e to reach this threshold depends on both the rate at which [K⁺]_e is increased and the rate at which [K⁺]_e is sequestered by the astrocytes and neurons. This latter rate is determined by several factors including the strength of the ATPase pumps, the maximal conductance of K⁺ channels, and the strength of astrocytic gap junction coupling, as well as diffusion of K⁺ in the extracellular medium.

Clearly, strengthening the influx of K⁺ across the membrane by ATPase pumps and K⁺ channels leads to greater uptake of extracellular K⁺ and, therefore, a longer delay before a wave is initiated. It is less clear why adding gap junctions between astrocytes results in a longer delay or even failure to initiate a wave. This will be discussed later.

Simulations

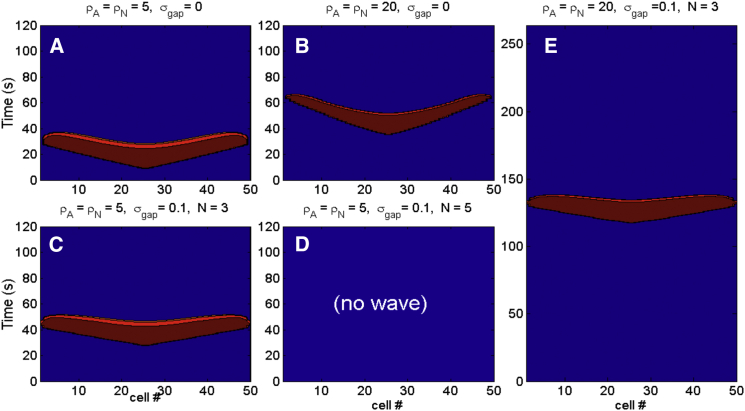
Some representative solutions of the model are shown in Fig. 2. For each simulation, we consider a network of 50 neuron/astrocyte pairs. We start the network at rest and then simulate the injection of K⁺ to the extracellular space of the middle cells 24, 25, 26, and 27 at a rate of 5 mM/s. For these simulations, we vary the following parameters: 1) ${\rho }_N$ and ${\rho }_A$, the maximal strength of the neuron and astrocyte Na⁺-K⁺ ATPase pump currents, respectively; 2) ${\sigma }_{gap}$, a measure of the maximal conductance of a gap junction that is formally defined in Materials and Methods; and 3) N, where each astrocyte has gap junction connections to its N closest neighbors on each side (for a total of 2N connections). If an astrocyte near one of the two edges of the network has fewer than N neighbors on one of its sides, then we assume that the astrocyte shares a gap junction with only those other astrocytes on that side.

Figure 2.

Solutions of the model with simulated [K⁺]_e injection at a rate of 5 mM/s until a wave is initiated. Fifty neuron-astrocyte pairs are simulated, with the middle four cells stimulated with K⁺. Pictured is V_N, with color banding corresponding to potentials greater than −30 mV. (A) A wave of spreading depolarization is generated if the pump strengths, ${\rho }_N$ and ${\rho }_A$, and strength of gap junction connections, ${\sigma }_{gap}$, are sufficiently small. The time until a wave is initiated is lengthened if we increase either: (B) the pump strengths; (C) the strength of gap junction connections and the number of neighbors on each side that each astrocyte has gap junction connections with, N; or (E) both. (D) A wave is not initiated if the pump strengths, strength of gap junction connections and number of connections are all sufficiently large. To see this figure in color, go online.

Increasing pump strengths lengthens the delay and shortens recovery time, whereas adding gap junctions causes a larger delay and increases the speed propagation, visible as the slope of the wavefront. For example, Fig. 2 C shows that if ${\rho }_N={\rho }_A=5$, ${\sigma }_{gap}=0.1$, and N = 3, then there is a significant delay until a wave is initiated. Increasing ${\sigma }_{gap}$ or the number of connections can prevent the wave entirely. This is the case in Fig. 2 D where ${\rho }_N={\rho }_A=5$, ${\sigma }_{gap}=0.1$, and N = 5.

To compute the wave speed, we note that the K⁺ and Na⁺ diffusion coefficients in the extracellular fluid are given by ${\overline{D}}_K=1.96\times {10}^{-5}$ cm²/s and ${\overline{D}}_{Na}=1.33\times {10}^{-5}$ cm²/s (28). The coefficients $D_K$ and $D_{Na}$, defined in Materials and Methods, are obtained from ${\overline{D}}_K\text{and}{\overline{D}}_{Na}$, scaled by the square of the average distance δ between neurons. In our model, $D_K$ =.002 ms^–1, $D_{Na}$ =.00133 ms^–1, and δ ≈.0313 × 10^–2 mm. The waves pictured in Fig. 2 travel ∼1–2 cells per second, from which it follows that the wave speed is ∼2–4 mm/min, consistent with published results (4).

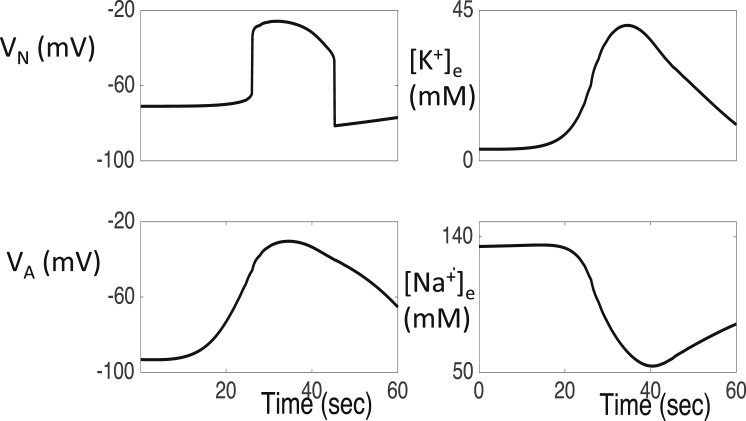
The propagation of the wave is due primarily to the diffusion of K⁺ in the extracellular space. That is, elevated extracellular K⁺ leads to an increase in a neuron’s K⁺ Nernst potential. The resulting depolarization increases Na⁺ currents, which leads to the upstroke of the neuron’s membrane potential. The neuron’s K⁺ channels then activate, K⁺ is released into the extracellular space and then diffuse to the extracellular space of nearby neurons. This may lead to a wave of spreading depolarization. This mechanism was originally proposed by Grafstein (38). Once a neuron depolarizes, its K⁺ and Na⁺ ion concentrations slowly recover. As shown in Fig. 3, once these concentrations recover sufficiently, the neuron can no longer maintain its depolarized state and returns to physiological resting levels.

Figure 3.

Time evolution of dependent variables V_N, V_A, [K⁺]_e, and [Na⁺]_e corresponding to a fixed neuron/astrocyte pair during a wave of spreading depolarization. Here, ${\rho }_N={\rho }_A=10$ and ${\sigma }_{gap}=0.$

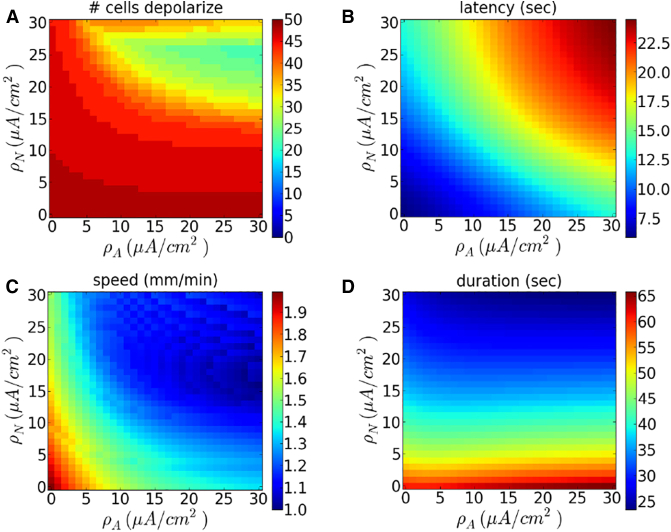
Dependence on parameters

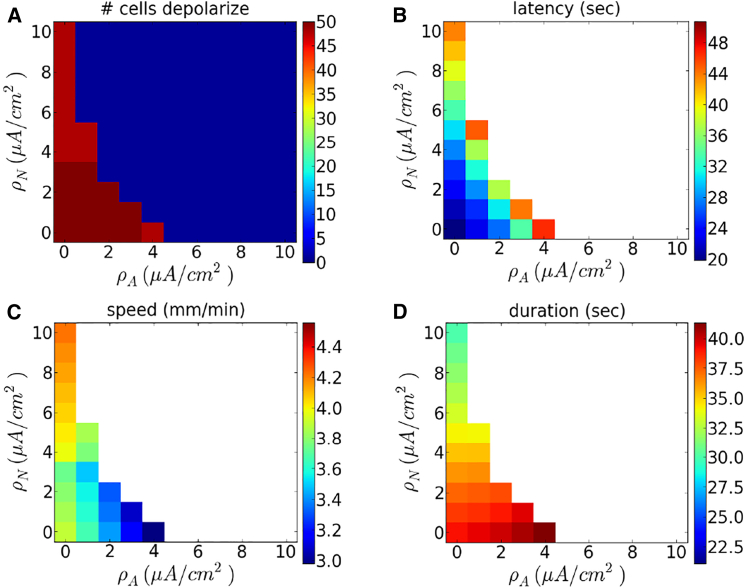
We varied the pump strengths ${\rho }_N$ and ${\rho }_A$ independently and quantified the speed and duration of waves, as well as the delay before wave initiation. Results are shown in Fig. 4. We find that wave speed decreases with ${\rho }_N$ and ${\rho }_A$, and latency increases, as expected. The duration of depolarization remains relatively constant in ${\rho }_A$, but decreases with ${\rho }_N$ (Fig. 4 D). The duration varies from roughly 20 s, for large neuron pump strengths, to more than 1 min for small neuron pump strengths. This is consistent with experimental findings and previous models for spreading depression and spreading depolarizations (4, 30). Fig. 4 A shows the number of neurons, which depolarize after a wave is initiated. This figure demonstrates that the wave may fail to propagate to the end of the one-dimensional array if the pump strengths are sufficiently large.

Figure 4.

Dependence of wave properties on pump strengths without gap junctions. Shown, as a function of ${\rho }_N$ and ${\rho }_A$, are (A) the number of cells whose voltage exceeds −40mV, (B) latency (time until one of the neuron’s membrane potential reaches −40 mV), (C) wave speed, and (D) duration of depolarization at cell V₂₄. Here ${\sigma }_{gap}=0$ and K⁺ is injected at a rate of 5 mM/s. To see this figure in color, go online.

With gap junctions, the wave may fail to propagate except for small values of the pump strengths. We demonstrate this in Fig. 5, where N = 5 and ${\sigma }_{gap}=1$. In this case, a wave does not initiate if both ${\rho }_N$ and ${\rho }_A$ are greater than 3 μA/cm². As before, the latency increases and the speed of propagation decreases with pump strengths. Furthermore, duration of depolarization remains relatively constant in ${\rho }_A$, but decreases with ${\rho }_N$.

Figure 5.

Dependence of wave properties on pump strengths with gap junctions. Shown, as a function of ${\rho }_N$ and ${\rho }_A$, are (A) the number of cells whose voltage exceeds −40 mV, (B) latency (time until one of the neuron’s membrane potential reaches −40 mV), (C) wave speed, and (D) duration of depolarization at cell V₂₄. Here ${\sigma }_{gap}$ = 1, N = 5, and K⁺ is injected at a rate of 5 mM/s. To see this figure in color, go online.

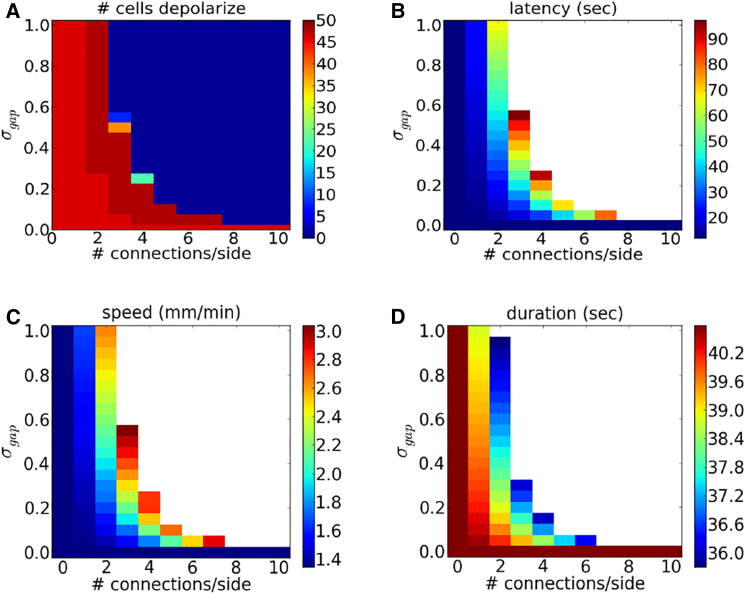
We studied the existence, speed, latency, and duration of depolarization as we varied the gap strength ${\sigma }_{gap}$ and the number of neighbors each astrocyte shares a gap junction connection with (Fig. 6). If both ${\sigma }_{gap}$ and the number of neighbors are sufficiently large, a wave is not initiated. Note that the wave speed and latency are both increasing functions of both ${\sigma }_{gap}$ and the number of connections. This suggests that whereas strengthening gap junction coupling either delays or even prevents a wave, once a wave is initiated, gap junctions promote a greater wave speed.

Figure 6.

Dependence of wave properties on gap junction coupling strength. Shown, as a function of ${\sigma }_{gap}$ and number of neighbors with gap junction connections, are (A) the number of cells whose voltage exceeds −40mV, (B) latency (time until one of the neuron’s membrane potential reaches −40 mV), (C) wave speed, and (D) duration of depolarization at cell V₂₄. Here ${\rho }_N={\rho }_A=10$ and K⁺ is injected at a rate of 5 mM/s. To see this figure in color, go online.

The role of gap junctions in buffering extracellular K⁺

We now address the role played by gap junctions in buffering extracellular K⁺, thereby delaying or even preventing the initiation of spreading depolarizations. We begin by noting that membrane K⁺ currents are typically outward; that is, K⁺ ions leave a cell through K⁺ channels. So why should elevated K⁺ enter the astrocytes and what role do gap junctions play in this?

Consider the equation for a K⁺ current written using the conductance-based Hodgkin-Huxley formalism: $I_{K,A}={\overline{g}}_K\left(V_A-E_{K,A}\right)$, where $\overline{g}$ is the total conductance. The current is outward if V_A > E_K,A and inward if V_A < E_K,A. As we shall see, the role of gap junctions is to keep V_A < E_K,A when there is elevated [K⁺]_e. This allows astrocytes to sequester extracellular K⁺ through K⁺ channels.

Consider a fixed astrocyte that is coupled through gap junctions with N other astrocytes as part of a syncytium. Moreover, suppose that there is a sudden increase in [K⁺]_e to just the fixed astrocyte. Since $E_{K,A}=\left(RT/F\right)\text{ln}\left({\left[{\text{K}}^{+}\right]}_e/{\left[{\text{K}}^{+}\right]}_{i,A}\right)$, it is clear that an increase in [K⁺]_e is accompanied with a corresponding increase in E_K,A. In isolation, the astrocyte will quickly readjust its intracellular ion concentrations to bring its membrane potential above the new E_K,A.

An important function of the astrocyte syncytium is maintaining isopotentiality. As demonstrated in (35), if N is sufficiently large and the gap junction coupling is sufficiently strong, then the membrane potential of the fixed astrocyte will remain close to that of its coupled neighbors, even when there is a sharp increase in [K⁺]_e. In other words, a local increase in [K⁺]_e to a single astrocyte leads to an increase in that cell’s E_K,A, but not its membrane potential. We may therefore have V_A < E_K,A for an extended period, causing K⁺ ions to flow into cell through membrane K⁺ channels.

To illustrate this computationally, we consider networks of 50 neuron/astrocyte pairs with different degrees of gap junction coupling. Each network begins initially at rest, except we raise the extracellular K⁺ concentration of the middle cells, $\mathcal{M}=\left\{\mathrm{24,25,26,27}\right\}$, to 15 mM. The elevated K⁺ can then spread through the network either by diffusion in the extracellular space, by uptake into neurons and astrocytes through K⁺ channels and ATP pumps, or via gap junctions. These, in turn, lead to changes in both the neuron and astrocyte membrane potentials.

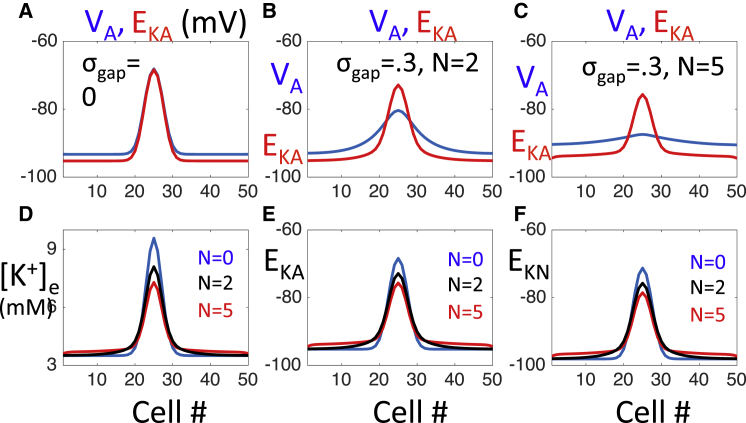
The spatial profile of V_A, [K⁺]_e and the K⁺ Nernst potentials, E_K,N and E_K,A, at t = 1 s are shown in Fig. 7. Here we consider a network with no gap junctions $\left({\sigma }_{gap}=0\right)$ and two networks with gap junctions $\left({\sigma }_{gap}=.3\right)$, with N = 2 and 5.

Figure 7.

Response to a local increase in extracellular K⁺. The network is initially at rest, except we raise the extracellular K⁺ concentration of the middle cells to 15 mM. Each panel shows a solution at time t = 1 s. (A) Without gap junction coupling, V_A follows E_K,A. (B) With gap junctions, there is a smaller gradient in V_A. (C) If gap junction coupling is sufficiently large, then V_A is nearly constant. (D) Dependence of [K⁺]_e on N, the degree of gap junction coupling. As N increases, cells near the initial disturbance have lower values of [K⁺]_e, whereas cells away from the initial disturbance have elevated levels of [K⁺]_e. (E and F) Dependence of the Nernst potentials E_K,A and E_Na,A on N. As N increases, both astrocytes and neurons near the initial disturbance become less excitable, whereas cells away from the initial disturbance become more excitable. To see this figure in color, go online.

Without gap junctions, V_A always remains above E_K,A (Fig. 7 A). In this case, the K⁺ current, I_K,A, is always outward and decreases in [K⁺]_e are due to diffusion of K⁺ in the extracellular space and the uptake of K⁺ through the ATP pumps. Note that V_A tracks E_K closely and remains depolarized at those cells in which [K⁺]_e is elevated.

With gap junctions, there is less of a gradient in V_A (Fig. 7, B and C). When N = 5, V_A is nearly constant. This causes V_A < E_K,A at those cells at which K_E is elevated. The K⁺ current is now inward and this provides a powerful mechanism for the uptake of elevated extracellular K⁺.

Whereas gap junctions lead to a lowering of V_A for those cells near $\mathcal{M}$, where K_E is initially elevated, they also result in an increase in V_A for those cells further away from $\mathcal{M}$. This depolarization strengthens I_K,A, which is outward at these cells, resulting in an increase in [K⁺]_e, as shown in Fig. 7 D. With gap junctions, the decrease in [K⁺]_e for cells near $\mathcal{M}$ results in a lowering of both the neuron and astrocyte K⁺ Nernst potentials, E_K,N and E_K,A. Moreover, the increase in [K⁺]_e for cells away from $\mathcal{M}$ results in an increase in both E_K,N and E_K,A. Hence, with gap junctions, neurons, and astrocytes near $\mathcal{M}$ are less excitable, whereas cells away from $\mathcal{M}$ are more excitable. For this reason, it is more difficult to initiate a wave near $\mathcal{M}$; but once a wave is initiated, it propagates with increased velocity.

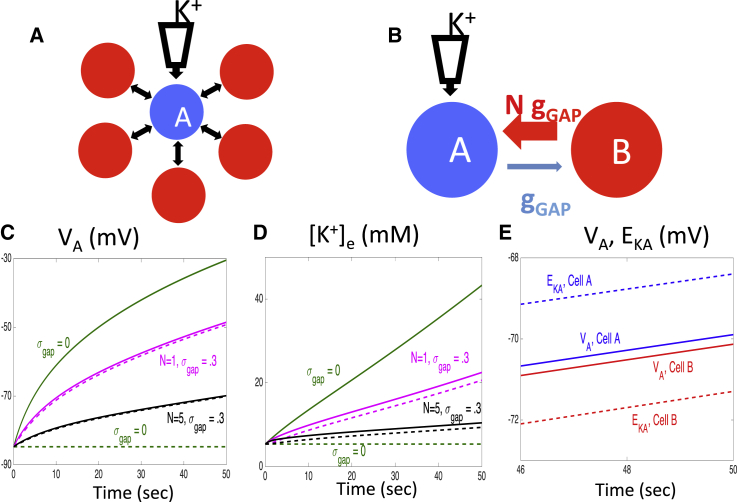
Next consider a network of just astrocytes, as pictured in Fig. 8 A. Here there is one astrocyte, which we denote as $\mathcal{A}$, that has gap junction coupling with N other cells. There is no diffusion of ions in the extracellular space. The network is started at rest and we slowly increase [K⁺]_e for $\mathcal{A}$ at a fixed rate. We then consider how changes in [K⁺]_e and V_A depend on N.

Figure 8.

Response of an astrocyte network to a constant increase in [K⁺]_e. (A) The network consists of N + 1 astrocytes. Extracellular K⁺ is slowly injected into astrocyte $\mathcal{A}$ (blue cell), which is electrically coupled with each of the other N astrocytes (red cells). (B) A two-cell astrocyte model that is equivalent to the network shown in (A). (C) Time evolution of V_A for the two astrocytes, depending on N. Solid curves correspond to astrocyte $\mathcal{A}$ and dashed curves correspond to the other equivalent astrocyte. (D) Time evolution of [K⁺]_e for the two astrocytes, depending on N. (E) The membrane potentials and K⁺ Nernst potentials of the two cells for N = 5 and ${\sigma }_{gap}$ =.3. For each panel, ${\rho }_A$ = 10 and K⁺ is injected at a rate of 1 mM/s. To see this figure in color, go online.

Except for $\mathcal{A}$, the astrocytes are all homogeneous. Therefore, we can lump these other astrocytes together to form a single cell, which we denote as $\mathcal{B}$. Thus the network in Fig. 8 A is equivalent to the two-astrocyte network pictured in Fig. 8 B. If the maximal conductance of the gap junction from $\mathcal{A}$ to $\mathcal{B}$ is $g_{gap}$, then the maximal conductance of the gap junction from $\mathcal{B}$ to $\mathcal{A}$ is $N\times g_{gap}$.

Fig. 8, C and D, show how the time evolution of the membrane potentials and extracellular K⁺ concentrations of the two cells depend on N. Each of these decreases as N increases. In particular, the very slow rise in [K⁺]_e when N = 5 demonstrates there must be a very long delay until [K⁺]_e is able to reach a threshold value, needed to trigger a wave of spreading depolarization in the neuron/astrocyte network. Fig. 8 E shows the membrane potentials and K⁺ Nernst potentials for the two cells when N = 5. We note that except for N = 0, V_A lies below E_K,A for cell $\mathcal{A}$, whereas the opposite is true for cell $\mathcal{B}$.

Discussion

This study has considered several important issues that, to our knowledge, have not been discussed in previous modeling studies of cortical spreading depression and spreading depolarizations. Namely, nearly all previous models assumed that the role of the astrocytes is to simply buffer extracellular K⁺; this was modeled by including a simple buffering term in the equation for extracellular K⁺. In our study, we incorporated a detailed biophysical model for the astrocytes. This allowed us to explore more fully the role of specific astrocyte processes in either promoting or preventing wave propagation. Furthermore, earlier modeling studies were primarily concerned in demonstrating that the models were capable of generating spreading depressions for some fixed value of the pump strengths. In our study, we identify neuroprotective processes, which may help to prevent or block wave propagation.

Our model is minimal in the sense that it includes only those processes needed to generate the dynamics under study. As noted in (30), the neuron’s ability to generate pathological spreading depolarization (SD) behavior does not necessarily depend on abnormal activity of ion channels, but rather a positive feedback based on ion currents causing ion concentration changes. To generate SD, the neuron model includes 1) a voltage dependent Na⁺ current that induces a depolarization and then release of K⁺ ions into the extracellular space; 2) a slowly inactivating Na⁺ current that maintains prolonged excitability, and 3) a fixed leak to stabilize the neuron’s resting potential.

The astrocyte model is based on experimental results in (35). Because of their high and selective membrane permeability to K⁺ ions, astrocytes act as nearly perfect potassium electrodes. The astrocyte model, therefore, includes a Kir4.1 type K⁺ current and a small Na⁺ leak current. The primary role of the astrocytes in this study is to sequester elevated levels of extracellular K⁺, thereby preventing the initiation of spreading depolarizations. As shown here and in (35), this requires that each astrocyte belongs to a syncytium consisting of a sufficiently large number of cells with sufficiently strong electrical coupling between cells.

The basic mechanism for extracellular K⁺ clearance described in this study extends the concept of K⁺ spatial buffering, which was introduced more than a half century ago (39). There have been several experimental, modeling, and analytic studies of K⁺ spatial buffering since then (40, 41, 42, 43). The basic mechanism for K⁺ spatial buffering is the following (see, for example (44)): A local increase in [K⁺]_e produces an astrocyte depolarization that spreads passively to coupled astrocytes. The difference between V_A and E_K,A drives K⁺ inward at the region where it is raised and outward at distant regions. The result is a net flux of K⁺ away from the region where it has accumulated. What we have described in this study is certainly closely related to this classic description. However, the classic description does not take into account isopotentiality of the astrocyte syncytium. With sufficiently strong and widespread gap junction coupling, astrocytes near the region of elevated K⁺ concentration do not depolarize significantly and this provides a powerful driving force, E_K,A − V_A, for K⁺ uptake through membrane K⁺ channels.

Earlier mathematical models and analysis of K⁺ spatial buffering also do not take into account isopotentiality. These studies assume the astrocyte membrane potential is passive, in the sense that they ignore the fast timescales associated with the membrane capacitance. This timescale is on the order of milliseconds, whereas earlier models and analysis consider timescales on the order of tens of seconds. Isopotentiality is achieved on the fast timescale and is critically important to account for the rapid uptake of extracellular K⁺ ions, needed to prevent the initiation of the pathological signals.

We previously demonstrated that isopotentiality depends on the number of astrocytes each astrocyte has gap junction connections with (35). These simulations predict that a syncytium consisting of cells coupled with ∼11 neighbors is sufficient to maintain a physiological membrane potential in the presence of a 20 mM extracellular increase in K⁺ concentration. In this study, we demonstrate that, except for very low gap junction coupling strengths, waves of spreading depolarization will not be generated if N is larger than 5. See Fig. 6. This corresponds to each astrocyte being connected to 10 neighboring astrocytes These results are consistent with experimental findings that demonstrate that each hippocampal astrocyte is coupled directly with, on average, 11 of its nearest neighbors (45).

The neuroprotective role of syncytial coupling during diseased states has been under considerable debate. For reviews, see (33, 34). Naus and coworkers demonstrated that reduced expression of the connexin 43 (Cx43), the most common form of gap junctions, in astrocytes significantly increased the size of ischemic infarcts and they suggested that gap junctional coupling played a critical role in the removal of ions (46, 47). Farahani et al. proposed a number of possible mechanisms by which gap junction communication may be beneficial following injury (48). For example, gap junctions may allow for the buffering of toxic metabolites, such as calcium and glutamate, from damaged cells. On the other hand, some studies indicate that gap junction communication may amplify ischemic damage by providing a conduit for the propagation of pro-apoptotic signals between dying and viable astrocytes (49).

As reviewed in (33), the response of Cx43 varies with the severity of injury. Mild to moderate injury appears to lead to increased Cx43 immunoreactivity in the lesion site, whereas sever injury seems to result in decreased Cx43 immunoreactivity.

In our study, we demonstrated with a computational model that gap junction coupling may play a neuroprotective role by preventing the initiation of propagating pathological signals. However, gap junctions may also play a role in amplifying these signals, once they are initiated. These computational modeling results are consistent with those described in (33), who suggest that permanent blockade of Cx43 may not be neuroprotective, but the transient blockade of targeting the window of initial Cx43 upregulation observed following injury is potentially therapeutic.

We have clearly not included many details and processes believed to be important in spreading depolarizations. We have, for example, ignored cell swelling, assumed a simple neuron/astrocyte geometry, and assumed the extracellular space is isopotential. Each of these assumptions needs to be reconsidered. The extracellular space may become severely restricted, especially during ischemic-induced cell swelling, in which case extracellular potential gradients may be comparable with intracellular potential gradients. Extending the model from one- to two-dimensional arrays will allow us to consider more realistic spatial arrangements of the cells, as well as connectivity patterns between cells, and the impact of complex astrocytic branching processes. In future studies, it will be important to explore the roles of such things as changes in cell volume, vasculature, extracellular signals including glutamate, Ca²⁺ dependent processes (16), more realistic geometries, etc. Our hope is that the model considered in this study will serve as a useful starting point and framework for these further studies.

Conclusions

A syncytium of electrically coupled astrocytes can maintain a physiological membrane potential in the presence of an elevated extracellular K⁺ concentration and efficiently distribute the excess K⁺ across the syncytium. This provides an effective neuroprotective mechanism for delaying or preventing the initiation of spreading depolarizations. However, gap junctions may also play a role in amplifying these signals, once they are initiated.

Author Contributions

G.H., L.M.M., R.B., and D.T. designed research and performed model development. All authors performed numerical simulations. G.H., L.M.M., and D.T. performed theoretical analysis. G.H., R.B., and D.T. wrote the manuscript. All authors discussed results and commented on the manuscript.

Editor: Richard Bertram