Quantifying Instrumental Artifacts in Folding Kinetics Measured by Single-Molecule Force Spectroscopy

Abstract

Force spectroscopy is commonly used to measure the kinetics of processes occurring in single biological molecules. These measurements involve attaching the molecule of interest to micron-sized or larger force probes via compliant linkers. Recent theoretical work has described how the properties of the probes and linkers can alter the observed kinetics from the intrinsic behavior of the molecule in isolation. We applied this theory to estimate the errors in measurements of folding made using optical tweezers. Errors in the folding rates arising from instrument artifacts were only ∼20% for constant-force measurements of DNA hairpins with typical choices of linker length and probe size. Measurements of transition paths using a constant trap position at high trap stiffness were also found to be in the low-artifact limit. These results indicate that typical optical trap measurements of kinetics reflect the dynamics of the molecule fairly well, and suggest practical limitations on experimental design to ensure reliable kinetic measurements.

Main Text

Single-molecule force spectroscopy (SMFS), in which tension is applied to individual molecules via mechanical probes (1), has been used widely to study the properties of macromolecules, in particular the conformational dynamics of proteins and nucleic acids (2). SMFS measurements involve force probes like atomic force microscopes or optical or magnetic tweezers that apply load to the molecule being studied via mechanical linkers connecting the molecule to the probe (Fig. 1 A, upper inset). Because only the probe motion is observed directly, not the motion of the molecule itself, the properties of the latter must be inferred from the former. The probe and linker dynamics may then alter the observed response from the intrinsic molecular behavior that would have been expected without this coupling, complicating the interpretation of data.

Figure 1.

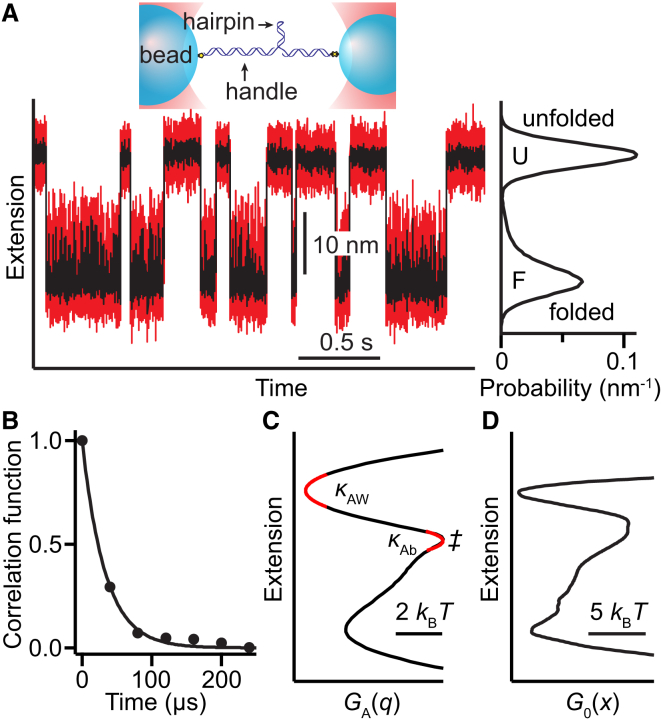
Analysis of rates. (A) Extension trajectory for hairpin 30R50/T4 at constant force. (Upper inset) Schematic of measurement showing hairpin attached to beads via DNA handles. (Right inset) Probability density from trajectory. (B) Decay of extension autocorrelation in unfolded state yields τ_A. (C) PMF from the extension trajectory, yielding κ_Ab, κ_Aw, and ΔG_A^‡. (D) Landscape obtained by deconvolution of PMF. To see this figure in color, go online.

Analysis of SMFS experiments has often assumed that the effects of the instrumental coupling can be ignored, as in the classic Bell-Evans-Zhurkov model for the force-dependent kinetics of folding and unfolding (3). However, experimental and theoretical studies of the ways that SMFS assay implementation can alter observations have provided improved frameworks for more reliable analysis of SMFS data (4, 5, 6, 7, 8, 9, 10, 11, 12). A particularly important focus has been on the effects of the probe size and linker stiffness (12, 13, 14, 15, 16, 17, 18), with recent work showing how these can alter the apparent values of properties like the conformational diffusion coefficient (15, 16, 17) or the kinetics (18). Here, we apply the framework of Cossio et al. (18) to gauge the extent to which the rates and transition path times observed in SMFS folding studies are distorted by instrumental effects under typical experimental conditions, using DNA hairpins measured in optical tweezers (19) as a model system.

DNA hairpins of specific sequences that fold as two-state systems were connected at each end to polystyrene beads (820- and 600-nm diameter) via double-stranded DNA linkers of total length ∼2000 basepairs, as described previously in Woodside et al. (19). Two kinetic properties were investigated: 1) the folding rates, measured in equilibrium at a constant force maintained by a passive force clamp (20) to avoid feedback-loop artifacts (9), with the stiffness of the two traps set at 0.3 and 0 pN/nm; and 2) the transition path times, i.e., the time required to move across the energy barrier between the two states, measured in equilibrium at a constant trap position using stiff traps (0.56–0.63 and 0.75–1.1 pN/nm). In both cases, the force was kept near the value, F_1/2, where the hairpins occupied the folded (F) and unfolded (U) states with equal probability.

The folding rates measured from extension trajectories at constant force (Fig. 1 A), denoted k_MA, are listed in Table 1. To determine how well these rates reflect the true folding rates, denoted k_M, we first estimated the rate k_A expected if the system were diffusing over the potential of mean force (PMF) along the measured extension coordinate, G_A(q), with the diffusion coefficient implied by the extension dynamics observed, D_q (18). Only if k_A is fast compared to k_MA can the latter be a good estimate of k_M (18). D_q reflects the contributions from the beads and linkers, and is defined by D_q = 〈δq²〉/τ_A, where δq is the deviation of extension from its average value within F or U and τ_A the relaxation time obtained via single-exponential fits of the extension autocorrelation function within the same state (Fig. 1 B). D_q, listed in Table 1, was the same for both F and U (Table S1 in the Supporting Material); notably, it was a bit slower than the free diffusion of a bead alone (7 × 10⁵ nm²/s). We then used G_A(q) (Fig. 1 C), found from the logarithm of the extension probability distribution (Fig. 1 A, right inset), to obtain k_A via Kramers’ equation:

$$k_{\text{A}}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2\pi $}\right.\sqrt{{\kappa }_{\text{Ab}}{\kappa }_{\text{Aw}}}\beta D_q\text{exp}\left(-\beta \Delta G_{\text{A}}^{‡}\right),$$ (1)

where ΔG_A^‡ is the barrier height in the PMF, κ_Ab is the barrier stiffness, κ_Aw is the well stiffness, and β is the inverse thermal energy. The results for hairpins 30R50/T4 and 20TS06/T4 from Woodside et al. (4) are listed in Tables 1 and S1.

Table 1.

Kinetic Parameters, Average of Folded and Unfolded

	30R50/T4	20TS06/T4
Constant Force
Dq (× 105 nm2/s)	2.4 ± 0.2	4.0 ± 0.3
kA (s−1)	105 ± 7	700 ± 100
kMA (s−1)	3.3 ± 0.2	11 ± 3
kM (s−1)	4 ± 1	15 ± 3
Dx (× 105 nm2/s) (via Kramers’)	4.6 ± 0.5	5 ± 3
Constant Trap Position
Dq (× 105 nm2/s)	6.0 ± 0.3	5.7 ± 0.3
Dx (× 105 nm2/s) (transition time)	4.4 ± 0.4	3.4 ± 0.8

Comparing k_A and k_MA (Table 1), we found that indeed k_A ≫ k_MA. Thus k_MA ≈ k_M, and the error caused by instrumental effects could be estimated from (18)

$${\left[k_{\text{MA}}\right]}^{-1}={\left[k_{\text{M}}\left(1-{\left[\beta \left|{\kappa }_{\text{b}}\right|\langle \delta q^2\rangle \right]}^{-1}\right)\right]}^{-1}+{\left[k_{\text{A}}\right]}^{-1},$$ (2)

where κ_b is the barrier stiffness in G₀(x) (Fig. 1 D), the intrinsic energy landscape, found by deconvolving the effects of instrument compliance (4, 21). From Eq. 2, k_MA was 20–30% lower than k_M (Table 1). The rate artifacts were thus small, similar in size to the experimental uncertainty in the rates. As (β〈δq²〉)⁻¹ varies with the system stiffness, small errors require the system stiffness to be less than the barrier stiffness. The errors were not force-dependent: repeating the analysis of hairpin 20TS06/T4 at a force where it was 99.7% unfolded and the rates for folding and unfolding differed greatly (respectively, k_MA = 1.4 and 290 s⁻¹ (Table S2)), we found k_M = 1.5 and 330 s⁻¹, respectively—indicating an error of ∼10–15%, similar to that near F_1/2.

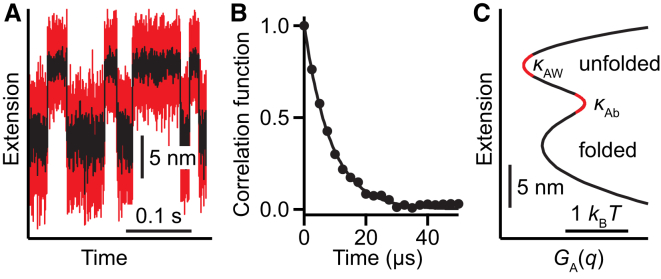
Turning next to the effects of the instrument on transition-path time measurements, we note that these are expected to be small when D_q ≳ D_x, the diffusion coefficient along the intrinsic molecular free-energy profile (18). Transition path times have recently been measured directly with SMFS for the first time (22, 23). Measuring the same hairpins but now at constant trap position (Fig. 2 A), we recalculated D_q as above from the extension fluctuations and autocorrelation function (Fig. 2 B). D_q was noticeably faster than in constant-force measurements (Table 1), because the higher trap stiffness decreased τ_A more than it did 〈δq²〉 (which depends on the well stiffness as well as the trap stiffness). D_x was found in two ways: from the constant-force kinetics, via Kramers’ equation applied to the energy profile obtained after instrument compliance effects on G_A(q) (Fig. 2 C) were removed by deconvolution (15, 21); and from the average transition-path time measured from constant-position trajectories (23) using Eq. S1 (Table S1). The two methods yielded the same result. For both hairpins, D_x < D_q in these measurements (Table 1), suggesting that the observed transition paths should not be distorted too much by instrumental artifacts.

Figure 2.

Constant trap position measurements. (A) Extension trajectory for hairpin 20TS06/T4. (B) Decay of extension autocorrelation in unfolded state yields τ_A. (C) PMF from extension trajectory yields κ_Ab, κ_Aw, and ΔG_A^‡. To see this figure in color, go online.

This work shows that for typical optical trapping assays, using 1/2–1 μm beads and 1–2 kb double-stranded DNA linkers, the rates observed are predicted to be close to the intrinsic molecular rates. Only minor artifacts arise from the linkers and beads, giving confidence that the observed behavior reflects the molecular dynamics faithfully. The 20–30% error predicted by the theory matches well with the error found empirically in previous work by Chang et al. (14). Large bead-size or linker-stiffness increases may lead to larger artifacts, however, as noted previously (15, 16, 17, 18); this is unfortunate because stiff linkers in particular allow for easier reconstruction of free-energy profiles (10, 11, 24, 25). Optimizing assay design for one purpose (e.g., landscape reconstruction) may thus degrade its suitability for others (e.g., measuring kinetic properties). Furthermore, molecules with very soft barriers (low κ_b) are especially susceptible to artifacts (17, 18) and may thus require special attention to linker design. As it turns out, however, ∼2 kb DNA linkers represent a decent compromise, allowing both reliable kinetic measurements and landscape reconstructions even for molecules with relatively soft barriers like DNA hairpins.

We can estimate the errors expected if stiffness or bead size is increased up to or beyond the practical limits for optical tweezers measurements by considering the effects on hairpin 30R50/T4. Because bead size primarily affects τ_A (increasing τ_A roughly linearly with bead size in the large bead limit), changing 〈δq²〉 and G_A(q) little, using 10-fold larger beads would decrease k_A ∼10-fold, roughly doubling the rate error from Eq. 2. Larger effects are seen from stiffness changes: if the system stiffness values were high enough to avoid the need for compliance deconvolution (higher than the stiffness of any feature in the landscape), then assuming only order-unity changes in D_q (because both τ_A and 〈δq²〉 would be smaller), k_A would be reduced ∼100-fold, because ΔG_A^‡ would increase from ∼4 to 9 k_BT (15), leading to k_A ≈ k_MA rather than k_A ≫ k_MA as above.

These examples suggest how rate artifacts may manifest in other SMFS assays. Magnetic tweezers assays usually use DNA linkers like those above, so slow τ_A arising from large bead size (usually ∼2–10 μm) is likely to be the main source of artifacts. Atomic force microscope assays are often done using short peptide linkers and much stiffer force probes (cantilevers); artifacts may thus arise primarily from reductions in k_A so that k_A ≈ k_MA. Shaping the cantilever to optimize stiffness, drag, and time response (26) may help reduce its contribution to errors, but artifacts will also arise from the significant compliance difference when varying numbers of repeats are unfolded in the tandem-repeat constructs most often used (18). Single-repeat constructs with longer, more compliant linkers may then be needed for accurate rate measurements. Finally, other artifacts not considered here, such as basculation effects in traps (27) and feedback-loop artifacts (9, 12), can also alter the observed rates.

Author Contributions

K.N. and M.T.W. designed research and wrote the article, and K.N. performed research.

Editor: Thomas Perkins.