Noise-Induced Increase of Sensitivity in Bacterial Chemotaxis

Abstract

Flagellated bacteria, like Escherichia coli, can swim toward beneficial environments by modulating the rotational direction of their flagellar motors through a chemotaxis signal transduction network. The noise of this network, the random fluctuation of the intracellular concentration of the signal protein CheY-P with time, has been identified in studies of single cell behavioral variability, and found to be important in coordination of multiple motors in a bacterium and in enhancement of bacterial drift velocity in chemical gradients. Here, by comparing the behavioral difference between motors of wild-type E. coli and mutants without signal noise, we measured the magnitude of this noise in wild-type cells, and found that the noise increases the sensitivity of the bacterial chemotaxis network downstream at the level of the flagellar motor. This provided a simple mechanism for the noise-induced enhancement of chemotactic drift, which we confirmed by simulating the E. coli chemotactic motion in various spatial profiles of chemo-attractant concentration.

Introduction

The chemotaxis signaling network allows bacteria to sense and respond to changes in concentrations of chemical attractants and repellents in the environment (1, 2). Binding of chemical ligands to the receptors modulates the activity of the associated histidine kinase CheA, thereby changing the level of phosphorylation of the response regulator CheY. Phosphorylated CheY (CheY-P) binds to the motor C-ring at the base of the flagellar motor (3), and modulates the direction of motor rotation. The chemotaxis network exhibits robust adaptation (4, 5), mediated by receptor methylation and demethylation by CheR and CheB.

Escherichia coli cells are propelled by several flagellar filaments, each driven at its base by the reversible flagellar rotary motor (6). When all motors on a cell rotate counterclockwise (CCW), the filaments form a helical bundle that pushes the cell smoothly forward (a run). When one or more motors switch to clockwise (CW), their filaments come out of the bundle and the cell moves erratically with little net displacement (a tumble) (7). At the end of a tumble, the cell randomly starts a new direction for the next run. Thus, the cell can modulate its run length by modulating the CCW interval lengths of the flagellar motors. Runs are extended (tumbles are suppressed) when cells move up spatial gradients of chemical attractants (8).

The relatively small number of molecules involved in biochemical reactions in cells makes signaling noise ubiquitous in biological signaling transduction networks. In the case of the bacterial chemotaxis signaling network, the network output (the intracellular concentration of CheY-P) fluctuates with time (9). The dynamics of the CheY-P concentration can be described using the Langevin equation (10, 11):

$$dY/dt=-\left(Y-Y_0\right)/{\tau }_Y+\eta \left(t\right),$$ (1)

where Y is the CheY-P concentration, Y₀ is its time-averaged value (or a preferred CheY-P concentration), τ_Y is the relaxation timescale, and η(t) is a Gaussian white noise, with

$$\begin{array}{c}\langle \eta \left(t\right)\rangle =0,\\ \langle \eta \left(t\right)\eta \left(t^{\prime }\right)\rangle ={\sigma }_{\eta }^{2}Y\left(t\right)\delta \left(t-t^{\prime }\right).\end{array}$$ (2)

A multiplicative noise is used to ensure Y(t) never goes negative (11). The fluctuation of CheY-P concentration described by the above equation has a Gamma distribution with variance

$${\sigma }_Y^2=Y_0{\tau }_Y{\sigma }_{\eta }^2/2.$$ (3)

Therefore, the dynamics of CheY-P concentration can be described by the Langevin equation with two parameters τ_Y and σ_Y. The relaxation of CheY concentration to its time-averaged value Y₀ is controlled by adaptation, thus τ_Y is equivalent to the adaptation timescale, which has been measured to be ∼20 s for wild-type E. coli cells (12).

The value σ_Y/Y₀ has been estimated to be ∼20% for wild-type cells to account for the experimentally observed power-law tails in the distribution of CCW intervals (9, 10), and was estimated to be in the range of 5–20% to reproduce the fluctuations measured for single motors in wild-type cells, and the coordinated response of adjacent motors on a wild-type cell (13). In a recent experimental measurement, σ_Y was measured as a function of CW bias (14), using wild-type cells and cells overexpressing CheR. However, the data was mixed with both type of cells, which would lead to an underestimation of σ_Y for wild-type cells because overexpressing CheR suppresses the fluctuation. The fluctuation of CheY-P concentration in wild-type cells was found to be important in coordination of multiple motors in a bacterium (11, 13) and in enhancement of bacterial drift velocity in chemical gradients (13, 15). Here, we found a surprising difference in the CCW-interval-versus-CW bias relationship for wild-type cells and mutant cells that lack the fluctuation of CheY-P concentration. By comparing the difference in this relationship, we provided a measurement of the values of σ_Y for wild-type cells, and discovered a large increase in the chemotaxis sensitivity at the level of the motor induced by the fluctuation of CheY-P concentration in wild-type cells.

Materials and Methods

Strains and plasmids

All strains used in this study are derivatives of E. coli K12 strain RP437 (16): JY26 [ΔfliC], HCB901 (ΔcheZ fliC, Ptrc420 cheY^13DK106YW), and JY33 (ΔcheB cheZ fliC, with the wild-type promoter of cheY on the chromosome replaced with a Ptrc promoter). The plasmid pKAF131 constitutively expresses the sticky filament FliC^st (17). The plasmid pBES38 constitutively expresses both LacI^q and FliC^st (18). JY26 carrying pKAF131, HCB901 carrying pBES38, and JY33 carrying pBES38 were used in this study.

Experimental procedure

Cells were grown at 33°C in T-broth with the appropriate antibiotics (170 μg/mL chloramphenicol, 100 μg/mL ampicillin) and various amounts of the inducer isopropyl-β-D-thiogalactoside (IPTG, 0–50 μM) to an OD₆₀₀ between 0.45 and 0.50, and were harvested by washing twice with motility medium (10 mM potassium phosphate, 0.1 mM EDTA, 10 mM lactate, and 70 mM NaCl, at pH 7.0).

For the bead assays, cells were sheared to truncate flagella by passing 1 mL of the washed-cell suspension 80 times between two syringes equipped with 23-gauge needles and connected by a 7-cm-long section of polyethylene tubing (0.58 mm i.d., no. 427411; Becton Dickinson, Franklin Lakes, NJ). Then, 1.0-mm-diameter polystyrene latex beads (no. 07310; Polysciences, Warrington, PA) were attached to the flagellar stubs, as described previously in Chen and Berg (19). The polystyrene beads were observed by phase-contrast microscopy using a Ti-E microscope (Nikon, Melville, NY). All experiments were performed at room temperature of 23°C. The motion of the polystyrene beads was recorded with a CMOS camera (DCC3240M; Thorlabs, Newton, NJ) at a frame rate of 500 Hz with a reduced region of interest that covered selected trajectories of beads. For each frame, the position of a bead was calculated as the averaged pixel position weighted by the intensity of the pixels. The bead positions were converted into angular positions by connecting them with the center of the bead motion trajectory, and further into angular velocities. CW and CCW intervals were determined using the threshold-crossing algorithm described previously in Yuan et al. (20).

Simulation of the Ising-type model with [CheY-P] fluctuation

The Ising-type model was described in the main text. The parameters used in the simulation were: ω = 10⁴ s⁻¹, E_A = 1.0 k_BT, E_J = 2.6 k_BT, and k_ligand = 10 s⁻¹. An exact stochastic Gillespie algorithm was used for the simulation, which involves the following steps: First, one of the events among all possible events is picked randomly to be processed, with weighting proportional to individual event rate. The possible events include CheY-P binding/unbinding and CW/CCW switching for each FliM unit in the motor switch. All rate formulae were taken from Duke et al. (21). Second, the time is advanced by −log(ξ)/Γ, where ξ is a random number picked from a uniform distribution of [0, 1], and Γ is the sum of the rates of all possible events. Each motor was simulated for 600 s, with the motor rotational state recorded every 0.001 s. The fluctuation of CheY-P concentration was simulated using the Langevin equation: the deviation δY of the CheY-P concentration from its steady-state value was updated using the Ornstein-Uhlenbeck formula (22, 23):

$$\delta Y\left(t+\Delta t\right)=\delta Y\left(t\right)\times e^{-\Delta t/{\tau }_Y}+{\sigma }_Y\times \sqrt{1-e^{-2\Delta t/{\tau }_Y}}\times n\left(\mathrm{0,1}\right),$$ (4)

where n(0,1) is a random number following unit normal distribution. At each value of Y₀, a temporal sequence of motor rotational states was generated using the Ising-type model, and the CW and CCW intervals were identified using the threshold-crossing algorithm described previously in Yuan et al. (20). Then the average CCW interval and CW bias were calculated. By changing Y₀ in steps of 0.002 μM, the average CCW interval as a function of the CW bias was obtained. For each trial value of σ_Y, this function was generated and compared to the experimental data to calculate the χ². Fitting of this function to the experimental data is carried out by minimizing χ².

To extract σ_Y as a function of the CW bias B, we first fit the wild-type 〈T₊〉 versus B data with a power-law function ax^b as it fits the data better than the simple inverse function used in the main text, with a = 0.194 ± 0.006 and b = −0.898 ± 0.007. Then, starting from the Ising-type model with parameters for the mutant data, and at a specific Y₀, the fluctuation of CheY-P concentration was added into the model with trial values of σ_Y. The σ_Y that resulted in a data point (B₀, 〈T₊〉) that agrees with the power-law function mentioned above leads to the data point (B₀, σ_Y) in Fig. 5. To extract σ_Y as a function of the CW bias B with varying τ_Y, we assumed a linear relationship between τ_Y and σ_Y as suggested in the previous study: τ_Y = C × σ_Y², where C = 257 s μM⁻² (14).

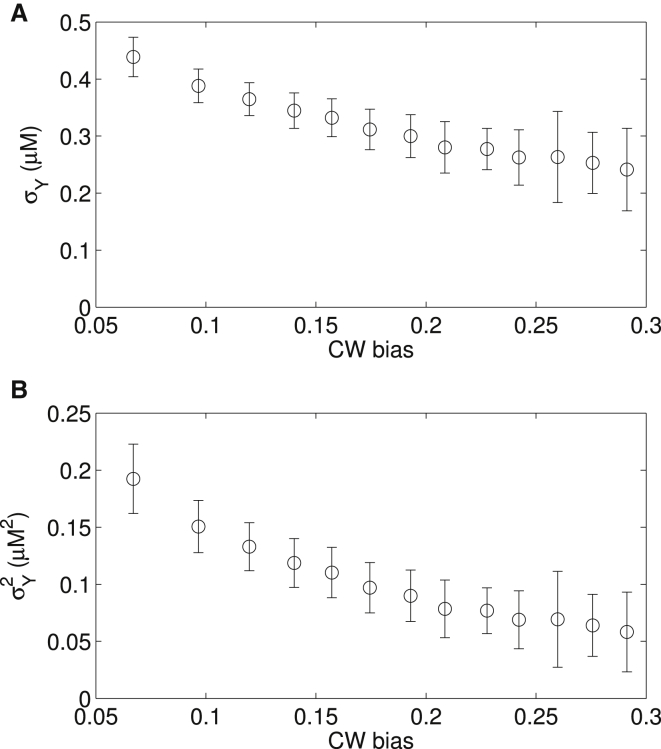
Figure 5.

σ_Y (A) and σ_Y² (B) as a function of the CW bias extracted using the 1D Ising-type model.

Simulation of chemotactic motion

Each functional chemoreceptor complex was represented with a Monod-Wyman-Changeux model in which the complex switches rapidly between active and inactive states. These states are separated by an energy difference Nε(m, [L]), where N is the number of the receptor homo-dimers in the complex. The value ε(m, [L]) can be written as a methylation level (m)-dependent term plus a ligand concentration ([L])-dependent term (12, 24, 25):

$$\epsilon \left(\text{m},\left[\text{L}\right]\right)=\alpha \left(m_0-m\right)+\text{ln}\left(\frac{1+\left[L\right]/K_I}{1+\left[L\right]/K_A}\right),$$ (5)

where K_I and K_A are the binding constants of the inactive and active receptors, respectively. Then the receptor activity is a = 1/(1 + e^Nε). Parameter values used in this model (for nonmetabolizable aspartate analog α-methyl-aspartate) were K_I = 18.2 μM, K_A = 3 mM, N = 6, α = 1.7, and m₀ = 1. The methylation kinetics values were modeled by the dynamic equation (26):

$$\frac{dm}{dt}=k_R\left(1-a\right)-k_{B}a,$$ (6)

where k_R and k_B are the rates for the methylation and demethylation processes. We take k_R = k_B/2 to fix the steady-state activity a₀ = 1/3 (k_R = 0.005 s⁻¹ was used in this article (27)). The CheY-P concentration Y is assumed to be proportional to the receptor activity: Y = 7.86 × a(t), where the proportional factor is set by the fact that the wild-type strain has a steady state Y of 2.62 μM as mentioned in the main text at the steady-state receptor activity a₀ = 1/3. A cell switches between run and tumble stochastically. The average run duration is set to the average motor CCW interval T_Run = f(B) = 0.11/B, where B = Y^10.3/(Y^10.3 + 3.1^10.3), and the rate of switching from run to tumble is 1/T_Run. The tumble duration is roughly independent of Y as shown before with an average of 0.2 s (8), so the rate of switching from tumble to run is 5 s⁻¹. Simulated cells have a constant run speed of 20 μm/s, and a rotational diffusion constant of 0.062 rad²/s (8, 28). After each tumble, the cells are oriented randomly. In the cases with signaling noise, the CheY-P concentration fluctuation is modeled using the Langevin equation with τ_Y = 20 s and σ_Y = 0.26 μM.

Results

To get information on the magnitude of the fluctuation, we compared the behavior of wild-type E. coli cells and mutant cells that lack this fluctuation. All cells were derivatives of E. coli K12 strain RP437 (16). The wild-type cells, JY26, carried a null mutation in the filament gene fliC. The plasmid pKAF131 carrying the sticky fliC allele was introduced into JY26 through transfection, so that we can use the bead assay to monitor the behavior of the flagellar motors (29). The mutant cells, HCB901, carried null mutations in cheA and the CheY-P phosphatase gene cheZ, and the cheY gene on the chromosome was replaced by a mutant allele that expresses CheY^13DK106YW (a CheY double mutant that is active without phosphorylation) under the control of the IPTG-inducible promoter Ptrc (18). The plasmid pBES38, which constitutively expresses LacI^q and sticky FliC, was transformed into HCB901 to offer tighter control of the expression of CheY (18).

We observed 227 motors of JY26 cells. Most of the CW bias fell in the range of values smaller than 0.5, with an average of ∼0.15. Each motor was observed for 2.5 min, and the averaged CCW interval was computed for each motor. We varied the IPTG concentration from 0 to 50 μM for the mutant strain HCB901, to get a population of motors with CW bias covering the range of 0–0.5. We measured 478 motors of HCB901, and compared the CCW intervals as a function of CW bias for both strains, as shown in Fig. 1 with a CW bin size of 0.02. Each data point is the averaged CCW interval for the population of motors whose CW biases fall within each bin. There is a clear difference in the CCW-interval-versus-CW bias relationships, which is attributed to the fluctuation of CheY-P concentration in JY26. This can be understood qualitatively. In the mutant strain with no fluctuation of CheY concentration (thus no fluctuation of CW bias B), the CCW interval (denoted as T₊) is a specific function of B with a convex shape, say T₊ = f(B), with d²f/dB² > 0. In the wild-type strain with temporal fluctuation of B, the ordinate in Fig. 1 is actually the time-averaged value of T₊. For each motor, B fluctuates around an average value B₀, and T₊ can be written as a Taylor expansion about B₀:

$$T_{+}\approx f\left(B_0\right)+f^{\prime }\left(B_0\right)\times \left(B-B_0\right)+\frac{f^{″}\left(B_0\right)}{2}\times {\left(B-B_0\right)}^2.$$ (7)

Thus

$$\langle T_{+}\rangle \approx f\left(B_0\right)+\frac{f^{″}\left(B_0\right)}{2}\times \langle {\left(B-B_0\right)}^2\rangle ,$$ (8)

where 〈〉 denotes time average. Thus 〈T₊〉 is always larger than f(B₀), the corresponding value for the mutant strain. Therefore, the data points for the wild-type are always above that for the mutant strain in Fig. 1. We can get quantitative information about the magnitude of the fluctuation of B (and thus the CheY-P concentration) from this difference between the wild-type and mutant data (and the difference does not depend much on the relaxation time τ_Y), as what we will do below using a model of the motor switch.

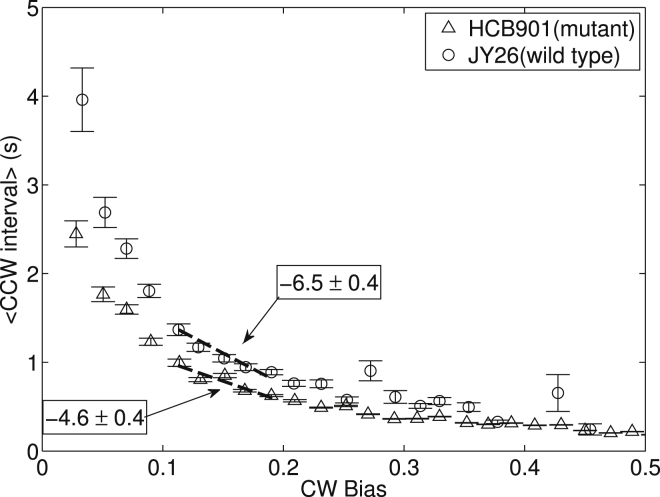
Figure 1.

Average CCW interval as a function of CW bias for 227 motors of wild-type cells (JY26) and 478 motors of mutant cells (HCB901). The data are sorted by CW bias into bins with bin size of 0.02. For each bin, the mean and the SE of the mean for the CCW interval were calculated and plotted. The dashed lines are linear fits using the five data points near the CW bias of 0.15, showing different slopes in the CCW-interval-versus-CW bias relationship.

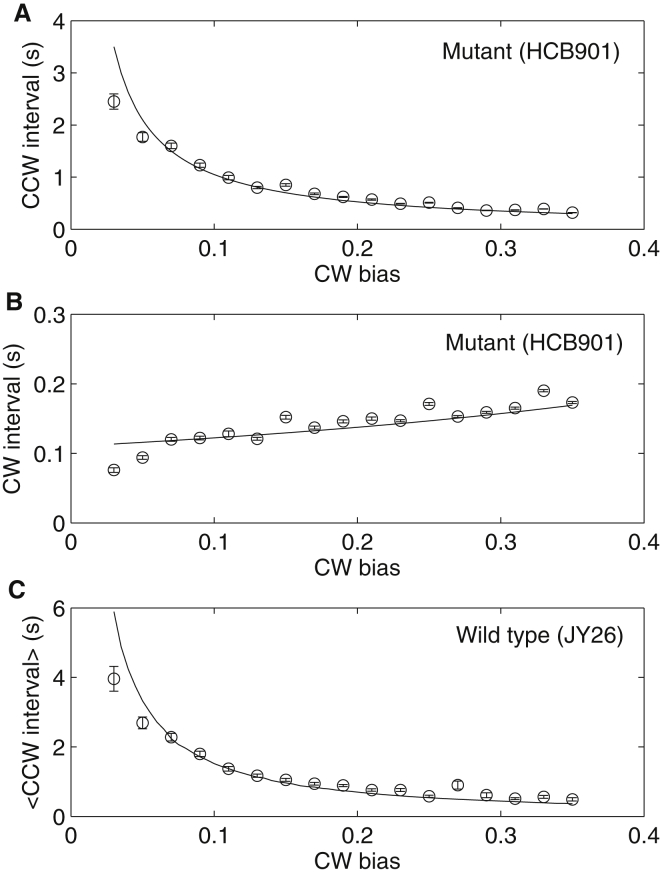
The mutant strain HCB901 expresses CheY^13DK106YW, a CheY double mutant that is active without phosphorylation, so there is no temporal fluctuation of activated CheY (30). To be certain of the mutant behavior, we used another mutant strain JY33 to compare. JY33 carries null mutations of cheB, cheZ, and fliC, and the wild-type promoter of cheY on the chromosome is replaced with a Ptrc promoter (30). The plasmid pBES38, which constitutively expresses LacI^q and sticky FliC, was transformed into JY33 to offer tighter control of the expression of CheY. In this strain, all cytoplasmic CheY is thought to be phosphorylated, so there should be no temporal fluctuation of CheY-P concentration. 538 motors of JY33 were observed. Fig. 2 shows the CCW-interval-versus-CW bias relationship for both HCB901 and JY33, and it exhibits a clear agreement.

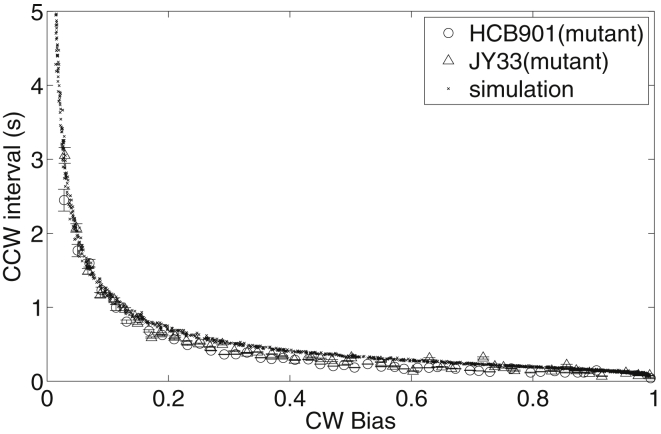
Figure 2.

CCW interval as a function of CW bias for motors of two different mutant strains, HCB901 and JY33 (number of motors: 538). (Black dots) Results of simulation using a 1D Ising-type allosteric model of the motor switch.

To explain the CCW-interval-versus-CW relationship we observed, we used the one-dimensional (1D) Ising-type allosteric model proposed by Duke et al. (21). In this model, the motor switch is modeled as a ring of subunits; each exists in either an inactive (CCW) or an active (CW) conformational state with a fundamental flipping rate of ω. Each subunit may bind a single molecule of CheY-P with a characteristic binding rate of k_ligand. The free energy of CheY-P binding to a subunit is E_L = −ln(Y/Y_0.5), where Y is the intracellular CheY-P concentration, and Y_0.5 is the CheY-P concentration at which the motor CW bias is 0.5. The affinity of CheY-P to a subunit is different, depending on its conformational state. The free energy of the active state relative to the inactive state for each subunit changes from +E_A to −E_A when CheY-P binds to the subunit, so CheY-P binding favors the active state. The coupling energy between adjacent subunits is −E_J if they are in the same states but zero otherwise, so this favors same conformations for adjacent subunits. A motor switching event is mediated by conformational changes that spread from subunit to subunit via nearest-neighbor interactions. Taking the switching from the fully inactive (CCW) state to the fully active (CW) state as an example, it occurs in two steps. First, one or more active domains are nucleated when one or more subunits undergo a conformational change; then, the domains grow until they spread throughout the entire ring.

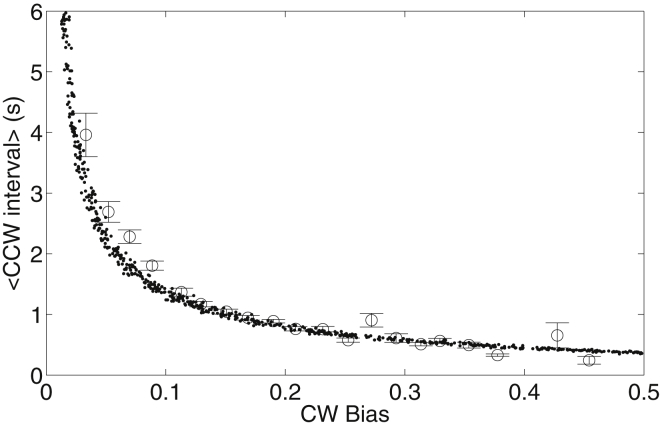
Besides a slight adjustment of the parameter E_J (we used 2.6 compared to 3.0 k_BT in Duke et al. (21)), all other parameters are the same as in Duke et al. (21). The model can reproduce the mutant data, as shown in Fig. 2. To fit the data for JY26 (wild-type), we added an ingredient to the model: the fluctuation of intracellular CheY-P concentration. We modeled it using the Langevin equation with the parameter τ_Y fixed to be 20 s, so there is only one free parameter: the standard deviation of CheY-P fluctuation σ_Y. We fit the model to the wild-type data using this single free parameter, and the result of fitting is shown in Fig. 3, with the fitted parameter σ_Y = 0.26 ± 0.05 μM. The correlation time τ_Y was shown previously to be different for cells with different CW bias (14, 31). However, changing the value of τ_Y in our model does not affect the simulated CCW-interval-versus-CW bias relationship, as long as τ_Y is much larger than the average CCW interval, as demonstrated in Fig. S1 in the Supporting Material, where we used σ_Y = 0.26 μM and tried three values of τ_Y: 5, 10, and 20 s. The CCW-interval-versus-CW bias curves collapse onto each other for the three cases. The insensitivity of the wild-type CCW-interval-versus-CW bias relationship to τ_Y is also suggested by Eq. 8. Therefore, for simplicity we fix τ_Y to be 20 s in our fitting. The average CW bias for our wild-type strain JY26 is 0.15, corresponding to Y₀ = 2.62 μM using the Hill response curve of CW-bias-versus-CheY-P concentration with a Hill coefficient of 10.3 and Y_0.5 of 3.1 μM (32). Thus the relative fluctuation (σ_Y/Y₀) of CheY-P concentration in a wild-type E. coli cell is ∼10%. Due to motor adaptation (33), the actual motor response curve (preadaptation) is much steeper with a Hill coefficient of ∼20 (34). However, our experiments were carried out for motors in a steady and full adapted state, so we used the value of 10.3 for the Hill coefficient in our calculations.

Figure 3.

Comparison of experiment (circles with error bars) and simulation (dots) results for the CCW-interval-versus-CW bias relationships for motors of wild-type cells (JY26).

We tried also to estimate the magnitude of the CheY-P fluctuation in a model-independent way. We noticed that both the CCW-interval-versus-CW bias and the CW-interval-versus-CW bias relationships for the mutant can be reasonably well fitted using two simple equations, T₊ = τ_D/B and T₋ = τ_D/(1-B), respectively, where T₋ is the CW interval, and τ_D is the characteristic dwell time (11). We fit both data sets using a single parameter τ_D = 0.11 s, as shown in Fig. 4, A and B. We then sought to calculate the T₊ versus B curve for the wild-type with a given σ_Y using this simple relation of T₊ versus B. For each value of B, the CheY-P concentration Y is calculated using the measured motor B-Y Hill function: B = Y^10.3/(Y^10.3 + 3.1^10.3), then a sequence of normally distributed random numbers with a mean of Y and a SD of σ_Y is generated, mimicking the fluctuation, which is transformed into a sequence of B values using the B-Y Hill function and then into a sequence of T₊ values using the relation T₊ = τ_D/B, and the mean value 〈T₊〉 of the last sequence is calculated. Varying B from 0.03 to 0.35, we calculated the 〈T₊〉-versus-B curve for the wild-type. Therefore, with a single parameter of σ_Y, we can fit the T₊-versus-B data for the wild-type, and the result of fitting is shown in Fig. 4 C with fitted parameter σ_Y = 0.21 ± 0.05 μM. This estimate agrees reasonably well with our extraction using the Ising-type model. The difference may be due to the imperfect fit of T₊-versus-B data for the mutant using the simple equation T₊ = τ_D/B (Fig. 4 A).

Figure 4.

Estimates of the magnitude of CheY-P fluctuation in a model-independent way. (A and B) Fits of the CCW-interval-versus-CW bias and CW-interval-versus-CW bias data for the mutant using the equations T₊ = τ_D/B and T₋ = τ_D/(1-B), respectively, with the fitted parameter τ_D = 0.11 s. (C) A fit of the mean CCW-interval-versus-CW bias data for the wild-type with the fitted parameter σ_Y = 0.21 ± 0.05 μM. (Circles) Data points; (lines) fits.

A recent measurement of σ_Y in wild-type cells and cells overexpressing CheR found a correlation between σ_Y and the CW bias B (14). Our analysis above assumed a single σ_Y for the wild-type data for B < 0.5. Hence, σ_Y obtained above is an averaged magnitude of CheY concentration fluctuation for these wild-type cells. To extract σ_Y as a function of B, we relaxed the restriction of a single σ_Y in our extraction using the Ising-type model, and the result of σ_Y plotted against B is shown in Fig. 5 A. As we were using the difference in wild-type and mutant 〈T₊〉-versus-B relationships to extract σ_Y, and this difference is too small to get a reliable extraction for B > 0.3, as seen in Fig. 1, we only extract σ_Y as a function of B for B < 0.3. To compare with Park et al. (14), we also plotted σ_Y² as a function of CW bias in Fig. 5 B. We also tried varying τ_Y when we extracted σ_Y as a function of B by assuming a linear relationship between τ_Y and σ_Y, as suggested in the previous study (14). The results are essentially the same as in Fig. 5, with the relative differences of within 1%, which are much smaller than the error bars.

E. coli cells perform chemotaxis by modulating the length of their runs, which corresponds directly to the motor CCW intervals. The motor CW bias has a one-to-one relationship with the intracellular CheY-P concentration (32). Therefore, the slope of the CCW-interval-versus-CW bias curve manifests the sensitivity downstream of the chemotaxis signaling network. We compare the slope for the wild-type and mutant strains near the wild-type CW bias of 0.15, and found that the slope dT₊/dB changed from −4.6 ± 0.4 for mutant cells to −6.5 ± 0.4 for wild-type cells, a 40% increase in the absolute value of the slope.

To investigate the implication of the noise-induced dT₊/dB increase on bacterial chemotaxis performance, we constructed a stochastic model of the chemotactic motion based on a coarse-grained description of the intracellular chemotaxis signaling network following a computational model that couples signaling and swimming proposed by Jiang et al. (27). In the simulation, the average run duration was set to the average motor CCW interval, and we utilized the simple relation between run length and the CW bias: T_Run = τ_D/B, with τ_D = 0.11 s, as fitted from our experimental data (Fig. 4 A).

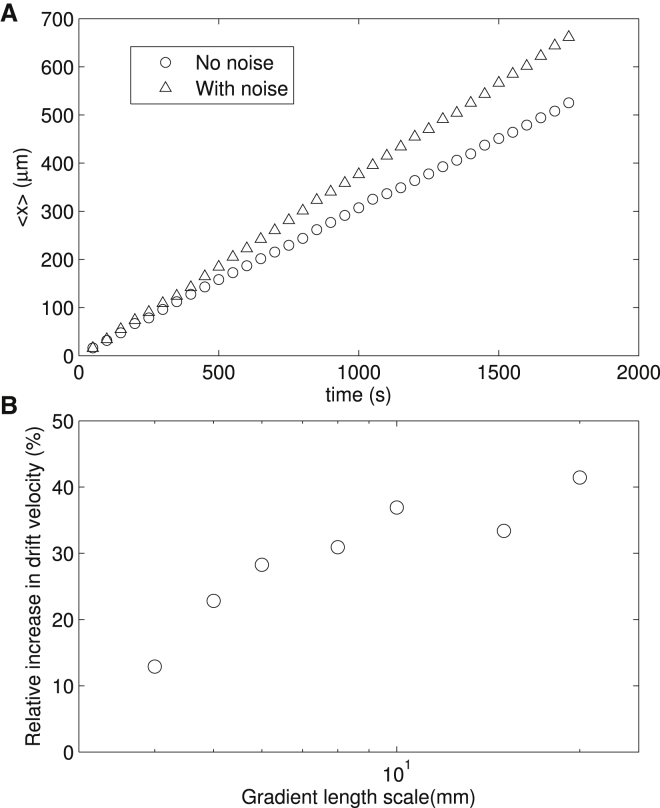
We simulated cells swimming in an exponential α-methyl-aspartate concentration profile [L] = [L]₀exp(x/d) with [L]₀ = 5K_I, which leads to a constant chemotaxis drift velocity due to logarithmic sensing in bacterial chemotaxis (35). For each gradient length d, we simulated the motion of 2000 cells, each of which swims for 30 min starting from the origin of axis in a random initial swimming direction. The averaged cell position is calculated as a function of time, as shown in Fig. 6 A for d = 10 mm. We compared the cases with and without the fluctuation of CheY-P concentration, and saw a clear difference in the drift velocities (Fig. 6 A). The percentage increment in dT₊/dB as measured above should not be directly translated into the same amount of increment in the drift velocity. In bacterial chemotactic motion, the increment of sensitivity downstream of the signaling network feeds-back via the output (modulated run lengths) into the input, altering the pattern in which the bacteria sense the environment, thereby resulting in a complex enhancing effect on the drift velocity. We calculated the effect of noise on the run lengths in the simulation. For d = 10 mm, the average run length for backward runs down the gradient was 17.50 μm, and 18.22 μm for forward runs up the gradient, resulting in a relative difference of 4.1% between the average forward and backward run lengths. With signaling noise, the average backward and forward run lengths were 18.06 and 19.26 μm, respectively, resulting in a relative difference of 6.6% between the average run lengths. Consistent with our motor studies (Fig. 1), both backward and forward run lengths increased when signaling noise was included, and the relative difference between the forward and backward run lengths was larger for cells with noise, increasing the drift velocity. We expect that the increment in drift velocity due to noise is larger in shallower gradients of attractants, where the gradient length scale is much larger than run lengths and therefore extended runs (due to noise) allow the cell to sense the gradient more efficiently. We calculated the relative increment in drift velocity for cells with signaling noise compared to cells without noise under various ligand gradient lengths d, and showed that the relative increment is larger for shallower gradients (Fig. 6 B).

Figure 6.

Comparison of chemotactic motions with or without noise in exponential ligand profiles. (A) Averaged x positions of the bacterial population with (triangles) or without (circles) noise as a function of time for gradient length d = 10 mm. (B) Relative increment in drift velocity for cells with noise compared to cells without noise in exponential ligand profiles with different gradient length scales.

Discussion

In this study, we found a surprising difference in the CCW-interval-versus-CW bias relationship for wild-type cells and mutant cells that lack the signaling noise. By comparing the difference in this relationship, we provided a measurement of the values of the signaling noise σ_Y for wild-type cells. The values of σ_Y as a function of the CW bias we measured here agrees qualitatively with the previous finding that σ_Y decreases with the CW bias, but our measured values of σ_Y are approximately twice those from the previous measurement (14). The difference may in part be due to the fact that they mixed data from wild-type cells and cells overexpressing CheR in the previous measurement (14), and overexpressing CheR suppresses the noise. Therefore, we provided an extraction of this important parameter in bacterial chemotaxis for wild-type cells. This signaling noise plays an important role in coordinating multiple motors on a cell, as shown in recent theoretical studies (11, 13). The magnitude of the noise we measured here falls in the region that is required to reproduce the coordinated response of adjacent motors on a cell, as found earlier (13, 36). Furthermore, we found that the signaling noise increases chemotaxis sensitivity by 40% at the level of the flagellar motor by increasing dT₊/dB, and a manifest of which in bacterial swimming behavior is that noise enhances the bacterial drift velocity in a chemical gradient. This is consistent with two recent theoretical reports that cells with optimal signaling noise drift more rapidly in attractant gradients (13, 15). Here, we have found a straightforward phenomenological mechanism explaining the enhancement in drift velocity, which is that the signaling noise increases chemotaxis sensitivity by increasing dT₊/dB. Our simulation of the bacterial chemotactic swimming confirmed this mechanism: when bacteria swim in an attractant gradient, both forward and backward run lengths increase for cells with signaling noise compared to those without noise, but the relative difference in the forward and backward run lengths is larger for cells with noise, consistent with our finding that both T₊ and dT₊/dB increase for cells with noise (Fig. 1). In a previous modeling study not including the effect of noise, the drift velocity was shown to also be sensitive to the steady-state CW bias, and it was maximal at low CW bias where the slope of the expected run length as a function of CheY-P concentration is largest (37).

In summary, by comparing the motor behavior of wild-type E. coli cells and mutant E. coli cells that lack the fluctuation of CheY-P concentration, we measured the SD of the fluctuation on average to be σ_Y = 0.26 ± 0.05 μM for wild-type cells, a 10% relative fluctuation. Here, we found that the noise plays a direct role in increasing the chemotaxis sensitivity: it increases dT₊/dB from −4.6 ± 0.4 for mutant cells to −6.5 ± 0.4 for wild-type cells, a 40% increment. Considering that dB/dY is the same for motors of wild-type and mutant cells, this amounts to a 40% increment in chemotaxis sensitivity. This increment in sensitivity is due to the signaling noise and the nonlinearity (convex shape) in the motor response of CCW-interval-versus-CW bias. Considering the ubiquity of noise and nonlinear response in biological networks, similar mechanisms should exist in other biological systems.

Author Contributions

J.Y. and R.Z. planned the work and wrote the article; R.H. performed the measurements and the Ising model simulation; and J.Y. performed the simulation of chemotactic motion.

Editor: Dennis Bray.