Spontaneous Formation of a Globally Connected Contractile Network in a Microtubule-Motor System

Abstract

Microtubule (MT) networks play key roles in cell division, intracellular transport, and cell motility. These functions of MT networks occur through interactions between MTs and various associated proteins, notably motor proteins that bundle and slide MTs. Our objective in this study was to address the question of how motors determine the nature of MT networks. We conducted in vitro assays using homotetrameric kinesin Eg5, a motor protein involved in the formation and maintenance of the mitotic spindle. The mixing of Eg5 and MTs produced a range of spatiotemporal dynamics depending on the motor/filament ratio. Low motor/filament ratios produced globally connected static MT networks with sparsely distributed contractile active nodes (motor-accumulating points with radially extending MTs). Increasing the motor/filament ratio facilitated the linking of contractile active nodes and led to a global contraction of the network. When the motor/filament ratio was further increased, densely distributed active nodes formed local clusters and segmented the network into pieces with their strong contractile forces. Altering the properties of the motor through the use of chimeric Eg5, which has kinesin-1 heads, resulted in the generation of many isolated asters. These results suggest that the spatial distribution of contractile active nodes determines the dynamics of MT-motor networks. We then developed a coarse-grained model of MT-motor networks and identified two essential features for reproducing the experimentally observed patterns: an accumulation of motors that form the active nodes necessary to generate contractile forces, and a nonlinear dependency of contractile force on motor densities. Our model also enabled us to characterize the mechanical properties of the contractile network. Our study provides insight into how local motor-MT interactions generate the spatiotemporal dynamics of macroscopic network structures.

Introduction

Living cells continuously change their state to adapt to external environments (1). This dynamic behavior relies on the continual reorganization of the cytoskeleton (2, 3). Microtubules (MTs) are a major component of the cytoskeleton, interacting with various associated proteins to organize hierarchical structures spanning tens of micrometers to millimeters. The structures vary dynamically during the cell cycle according to the physiological roles of the cell (4, 5, 6), including mitotic spindle assembly (7), intracellular transport (8), neural pathfinding (9, 10), plant cell morphogenesis (11, 12, 13), and regulation of protein synthesis (14).

In most of these phenomena, the centrosome plays central roles in nucleating and organizing MT structures (15, 16, 17, 18, 19). In addition to these centrosome-associated MTs, acentrosomal MTs form bundles and network structures (20) and contribute to various cellular processes, including cell migration (21), neuron morphology (22), and the formation and maintenance of plant cell shapes (23, 24). In both cases, a number of associated proteins are known to be involved in structure formation, including PRC1 in mitotic spindle assembly (25, 26, 27), and MAP2 and tau in neural morphogenesis (28).

Although many kinds of elements are required for the formation of MT-related structures in cellular contexts, previous in vitro studies have found that characteristic structures such as asters, vortices, and networks thereof can emerge from a mixture of only a few components (29, 30, 31, 32, 33). These experimental findings have sparked a wealth of theoretical research (34, 35). An important finding from these in vitro studies is that the bundling and sliding of cytoskeletal filaments play a crucial role in pattern formation. However, it is not yet understood how the bundling and sliding of MTs generate various pattern dynamics.

To address this question, we used Eg5 as a motor protein with the ability to both bundle and slide MTs. Eg5 is an evolutionarily conserved kinesin that is known to contribute to the formation and maintenance of the mitotic spindle and the morphogenesis of axons and dendrites (36, 37, 38, 39, 40). A striking feature of Eg5 is that it has two motor units (each of which has two motor heads) linked through a coiled-coil region, so that each Eg5 molecule has the defined and minimum number of motor units to bundle and slide MTs. Using this eminently suitable motor protein, we investigated the temporal evolution of the motor-MT mixture under a wide range of motor/filament ratios.

Although a previous study using native Eg5 reported that it did not form asters (32), we found that Eg5, under some conditions, can form asters and aster networks. The MTs associated with the asters have defined polarity, generating a flux of MTs toward the center of the aster that results in local contractions between two connected asters. We observed that these local contractile dynamics generated diverse spatiotemporal dynamics in macroscopic MT networks depending on the spatial distribution of the asters. These dynamics are characterized by the connectivity and contractility of the MT network, which is categorized as a static network, active network, or aggregation. The contractile dynamics of global MT networks was also observed in a recent study (published after the original submission of this work) using Xenopus egg extract (41, 42). We also found that the modulation of motor properties, such as velocity and affinity for MTs, induced a different kind of dynamics that led to the formation of uniformly sized, isolated asters.

Using these findings, we developed a coarse-grained model based on the local interactions of multiple asters to reproduce our experimentally observed patterns. This model revealed two features essential to the active patterning of the MT-motor system: an accumulation of motors that forms the active nodes needed to exert contractile forces, and a nonlinear dependency of contractile force on motor densities. With this model, we calculated the mechanical energy stored in MT networks, which enabled us to recharacterize our experimentally observed patterns in terms of the mechanical behaviors of MT-motor systems.

Our study raises the possibility that living cells may utilize diverse macroscopic MT patterns through the regulation of geometrical network hub configurations (43, 44). These configurations may be controlled by changing the local interactions, densities, and activities of a few basic cytoskeletal elements (45) in the absence of an elaborate network-organizing apparatus.

Materials and Methods

Cloning and plasmid construction

The human Eg5 construct (pcDNA3.4/HsEg5-EGFP-FLAG-8xHis) used in this work was a kind gift from Ken’ya Furuta (National Institute of Information and Communications Technology, Tokyo, Japan). To generate the chimeric KIF5B_head-Eg5_tail construct, the motor domain sequence of kinesin family member 5B (KIF5B, NM_004521.2; amino acid residues 5–333) was amplified from cDNA from HEK293 cell total RNA, which was isolated from 2 × 10⁶ cells using the SV Total RNA Isolation System (Z3101; Promega, Madison, WI). The amplified sequence was replaced with the Eg5 motor domain sequence (1–368) using the ligation-independent In-Fusion (Clontech, Palo Alto, CA) method.

Protein expression and purification

To purify the kinesin constructs, Expi293F cells (Invitrogen) were used as previously described (46). Cells were collected by centrifugation at 700 g for 10 min, washed three times with phosphate-buffered saline (pH 7.4), and stored at −80°C. The frozen cells were suspended in lysis buffer (20 mM Tris-HCl at pH 7.5, 250 mM NaCl, 1 mM MgSO₄, 100 μM ATP, 10% (w/v) sucrose, 10 mM imidazole-HCl at pH 7.5, and 0.5 mM dithiothreitol) containing 1 mM phenylmethylsulfonyl fluoride and a protease inhibitor cocktail (Nacalai Tesque, Kyoto, Japan). The resuspended cells were then disrupted by a sonicator (Sonifier 250; Branson, Danbury, CT). After ultracentrifugation at 21,000 g for 45 min at 4°C, the supernatant was loaded onto Ni-IMAC resin (Bio-Rad, Hercules, CA) and eluted with 20 mM Tris-HCl at pH 7.5, 250 mM NaCl, 1 mM MgSO₄, 100 μM ATP, 10% (w/v) sucrose, 250 mM imidazole-HCl at pH 7.5, and 0.5 mM dithiothreitol. The eluate was next loaded onto anti-FLAG agarose (Sigma, St. Louis, MO) and eluted with lysis buffer supplemented with 350 μg/mL 3× FLAG peptide (Sigma). The concentration of the products was determined by using the Bradford method with the Coomassie Plus protein assay reagent (Thermo Fisher Scientific, Waltham, MA).

Tubulin was purified from porcine brain tissue through two successive cycles of polymerization and depolymerization. A phosphocellulose column (Whatman, Maidstone, UK) or high-molarity PIPES buffer (47) was used to remove contaminating MT-associated proteins. Tubulins purified with high-molarity PIPES buffer were used to polymerize guanosine-5′-[(α,β)-methyleno]triphosphate (GMPCPP) MTs. To prepare fluorescently labeled MTs, tubulin was labeled with ATTO647N (ATTO-TEC) or ATTO565 (ATTO-TEC). ATTO647N- and ATTO565-labeled MTs were polymerized by copolymerizing labeled and unlabeled tubulin for 30 min at 37°C, and stabilized with 40 μM paclitaxel (Sigma). The labeling ratios were 5% and 10% for ATTO647N-MT and ATTO565-MT, respectively.

Observation of the spatiotemporal dynamics of the MT-kinesin network

Time-lapse confocal images of fluorescently labeled MTs and green fluorescence protein (GFP)-tagged kinesins were collected using a Nikon A1 confocal laser-scanning microscope system with a Plan Apo VC 20X DIC N2 objective lens (NA = 0.75, Nikon) and diode lasers (Sapphire 488-20, Sapphire 561-20, and Cube 640-40C; Coherent, Santa Clara, CA). The flow chamber was composed of two coverslips (32 mm × 24 mm and 18 mm × 24 mm) that were coated with Teflon (K. Furuta, personal communication) and spaced with double-coated tape (80 μm thick, W-12; 3M, St. Paul, MN). To prepare the Teflon-coated coverslips, the uncoated coverslips were first cleaned with 2% Hellmanex II (Hellma, Müllheim, Germany) in Milli-Q water for 20 min with heat (2510; Branson), followed by a 1:1 mixture of ammonium hydroxide and hydrogen peroxide for 20 min with heat. Then, the surface was activated with oxygen plasma for 1 min (PDC-32G; Harrick, Pleasantville, NY), followed by fluorosilanization. Finally, the coverslips were coated with 0.5% Teflon AF 1601 (Dupont, Wilmington, DE) in FC-40 (3M). The chamber was first passivated using 1% (w/v) Pluronic F127 dissolved in BRB80 (80 mM PIPES-KOH, 1 mM MgSO₄, 1 mM EGTA) buffer and then incubated for 5 min to prevent nonspecific adsorption of proteins. After the chamber was washed with BRB80 buffer supplemented with 10 μM taxol, a mixed solution of fluorescently labeled MTs and GFP-fused kinesin constructs in assay buffer (80 mM PIPES-KOH pH 6.8, 2 mM MgSO₄, 1 mM EGTA, 2 mM dithiothreitol, 70 units/mL creatine kinase (Roche, Basel, Switzerland), 5 mM creatine phosphate, 42.5 units/mL glucose oxidase (Sigma), 42.5 units/mL catalase, 25 mM glucose, and 2 mM ATP) was allowed to flow into the chamber. Most images were recorded at time intervals of 1 min. The observations were conducted in a region ∼30–40 μm away from the glass surface.

Measurement of the velocities of nodes

Eg5 tends to first accumulate at the intersection of the MTs and then move toward the plus end, forming motor-accumulated nodes in MT networks. To measure the velocities of these nodes, the drift in the movies was first corrected with the use of an ImageJ software plugin (StackReg, http://bigwww.epfl.ch/thevenaz/stackreg/). Then, the motor channel was split and filtered using a median filter. The detection of nodes in the images was based on finding local maxima using the Find Maxima function of ImageJ. The position of nodes at each time point was determined by two-dimensional Gaussian fitting, using custom software (48).

Characterization of the spatiotemporal dynamics of the node velocities

We quantified the randomness and persistency of the node velocities by calculating the spatial correlation function of the node velocity vectors, v = (v_x, v_y). To obtain the correlation function, we first calculated the pairwise node velocity correlations, v_x(r)v_x(r + d) and v_y(r)v_y(r + d), for all distance vectors, d, between any two velocity vectors separated at the node-node distance, |d|. Next, we averaged these pairwise velocity correlations over all nodes located around the distance |d| ± 10 μm to obtain the correlation functions C_xx(|d|) and C_yy(|d|)) for the x and y directions, respectively. We calculated the x and y components separately because the chambers we used in our experiments were highly elongated in the x direction compared with the y direction. We performed these calculations at each time point to obtain the temporal changes that occurred in the spatial correlation function of the node velocity.

Characterization of the spatiotemporal dynamics of the MT network

We characterized the spatiotemporal dynamics of the MT networks by measuring the time evolution of the number and size of the clusters, which we defined as connected structures in the MT images, and calculating the connectivity and contractility of the network. To determine these values, we first performed an image analysis combining binarization and morphology operations. Time-series images of MT channel were median-filtered with a radius of 20 pixels to reduce the background noise. The resultant images were binarized with a threshold value that was set as 0.85 times the mean grayscale value at the initial time point. The binarized images were morphologically closed using a 20-pixel-radius disk as a structuring element to merge components that were smaller than the structuring element. The factor 0.85 and the closing operation were needed to ensure the connectivity of the dense MT network in the first frame. Because the images processed by the closing operation usually contained many smaller connected components, all connected components smaller than 400 pixels were removed. The numbers and sizes of the connected components obtained by the method described above were calculated over all frames with the time-lapse images. The connectivity of the MT network was defined as the ratio of the largest cluster’s area measured at the recording end time, T_f, to the whole area at T_f. The contractility was defined as the ratio of the maximum value of the whole area throughout the recording time to the whole area at T_f.

Coarse-grained model

Eg5 is a tetrameric motor protein that has two motor units connected through a coiled-coil domain and moves along MTs (Fig. S1, A–C, in the Supporting Material). Due to these features, a single Eg5 can cross-link MTs (Fig. 1 A) and slide them (Fig. S1, D–F), as previously reported (49, 50). Given these motor properties, one of our main goals was to construct a coarse-grained model that would reproduce the macroscopic contractile patterns of filament-motor networks observed in the experiments on a spatial scale of several millimeters and within a temporal space of ∼2 h. For this purpose, we employed a semi-continuum description: motors were treated by their concentrations, whereas MTs were represented by a set of extensible lines. Herein, we refer to the line as a link. In contrast to earlier theoretical models (51, 52, 53) in which a single cytoskeletal filament was modeled by a flexible link, our model regards links as macroscopic representations of bundles of filaments cross-linked by motors (Fig. S13 A).

Figure 1.

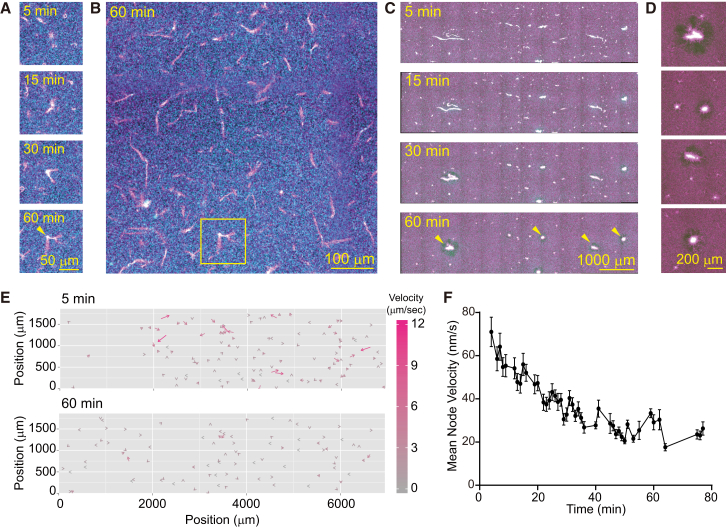
Self-organized structures emerged from the mixture of MTs and Eg5. (A) Time-series images showing the formation of bundled MT structures under low MT and Eg5 concentrations ([tubulin] = 10 nM, [Eg5] = 2.97 nM). The images for ATTO647N-labeled MT (magenta) and GFP-fused Eg5 (cyan) are merged. The times displayed in the images represent the time that elapsed after initial mixing. The arrowhead in the bottom image (60 min) indicates a jointed point of bundled MTs. (B) General image of bundled MT structures. The yellow box denotes the MT structure shown in (A). (C) Time-series images show the time-dependent evolutionary dynamics of astral structures in the crowded MTs ([tubulin] = 1 μM, [Eg5] = 8.91 nM). The times displayed in the images represent the time that elapsed after mixing. The arrowheads in the bottom image (60 min) indicate the formation of astral MT structures, with Eg5 accumulated at their centers. (D) Enlarged images of astral MT structures shown by the arrowheads in (C). (E) Vector field representation of node velocities in the static network shown in (C). The velocity of each node is shown by the length of the arrows and the color scale. (F) Temporal evolution pattern of the mean node velocity in the static network shown in (C). The mean value and standard deviation (SD) are shown. The total trace number of nodes is 216.

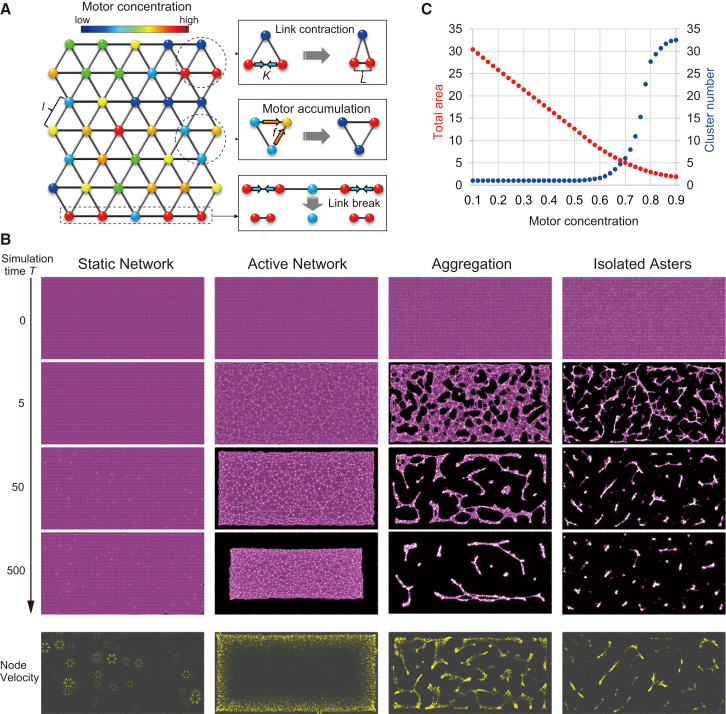
The initial configuration of the links was given by two-dimensional N_x × N_y nodes of a triangular lattice composed of links with equal length l (see Fig. 5 A), corresponding to a macroscopic description of highly dense and randomly oriented isotropic filaments in the initial system. We defined the local motor concentration C_i on the ith node. Based on previous theoretical findings for filament-motor systems (54, 55), which took into account the tendency of motors to bring filaments together and create a local motor-filament configuration (referred to as an aster; Fig. S12 A), we assumed that each lattice node acts as an aster and that plus-ended motors accumulate in the center of the asters, i.e., into nodes (Fig. S12 B). We attributed this accumulation to the facts that 1) a single aster has a radial array of filaments with their plus ends pointing inward, and 2) plus-end-directed motors move along the filaments toward the center of the aster according to their polarity. This motor accumulation process can be implemented by a constant flux, f, of motor concentration per unit of time, during which the motors can travel through adjacent lattice nodes, i and j, against the motor concentration gradient:

$$\frac{d{C}_i}{dt}=min\left(f,C_j/dt\right),\frac{d{C}_j}{dt}=-min\left(f,C_j/dt\right)If0\le C_j<C_i\le C_{max}-\text{min}\left(fdt,C_j\right).$$ (1)

Here, we set the maximum motor concentration, C_max, at all nodes to take into account the saturation of the motors at each aster. The initial condition, C_i, is randomly drawn from the uniform distribution between zero and C_ub. The parameter C_ub determines the motor concentration in the whole system, and served as the main control parameter during the simulations.

Figure 5.

Coarse-grained model of the filament motor system. (A) Schematic representations of the model and its dynamic rules. Two adjacent active nodes contract with each other with strength K. Motors accumulate against the concentration gradient with flux f. A link is severed when it is elongated above a threshold length L_c. The motor concentration at each node is represented by the color spectrum. (B) Spatiotemporal dynamics of the model for different motor concentrations (C_ub) and the parameters K and f. (C_ub, K, f) = (0.1, 15, 0.01), (0.4, 15, 0.01), (0.7, 15, 0.01), and (0.9, 30, 0.02) for the static network, active network, aggregation, and isolated cluster, respectively. Links are depicted by magenta lines and motors are depicted by white circles. Node velocities at T = 50 are shown by yellow arrowheads, sized in proportion to the velocity magnitude. (C) Total areas (red) and cluster numbers (blue) measured at T = 500 are displayed as a function of the motor concentration. (K, f) = (15, 0.01). Circles denote the mean value for 100 repeated simulations, starting with randomized initial distributions of the motor concentration.

Because filaments between two adjacent asters are arranged mostly in an antiparallel orientation, a link connecting two adjacent nodes contracts through the sliding action of the motors (Fig. S12 C). When the motors are abundant in both of the adjacent nodes, the link between the two nodes contracts as the nodes pull each other. However, when the motors are scarce at either of the adjacent nodes, there is only a small degree of contraction because of the lack of strong sliding activity. These contraction processes can be described by a dipole interaction (56, 57, 58, 59) between nodes i and j with a magnitude K_ij and a node-node distance L_ij, both of which are dependent on the motor concentrations C_i and C_j. Because the force dipoles acting on the ith and jth nodes are equal and opposite to each other, K_ij and L_ij are given by, to the lowest order, $\propto$ C_i + C_j and $\propto$ −(C_i + C_j) + constant, respectively. We generalize these relationships into the following equations:

$$K_{ij}=\frac{1}{4}\left(K-k\right)\left[1+\text{tanh}\left(\frac{C_i-\tilde{C}}{ϵ}\right)\right]\left[1+\text{tanh}\left(\frac{C_j-\tilde{C}}{ϵ}\right)\right]+k$$ (2)

$$L_{ij}=\frac{1}{4}\left(l-L\right)\left[1-\tanh \left(\frac{C_i-\tilde{C}}{\epsilon }\right)\right]\left[1-\tanh \left(\frac{C_j-\tilde{C}}{\epsilon }\right)\right]+L,$$ (3)

where K and k represent the maximum and minimum contractile strengths, respectively. K corresponds to the stall force of the motors, whereas k originates from the elastic restorative forces of MT filaments against their deformations. L represents the maximum compression length, which takes into account the limitation of compression due to the finite size effect of the MT filaments. $\tilde{C}$ and $ϵ$ are phenomenological parameters that control the onset and saturation of contractility. The hyperbolic tangent profiles used in Eqs. 2 and 3 are some of the simplest forms that can be used to describe the nonlinearities in the onset and saturation of contractility, as well as to stabilize numerical calculations for high motor concentrations. The saturation effect originates from the fact that the space on which motors work becomes restrictive at high motor concentrations. In contrast, the nonlinear onset of the contractile force K_ij can be attributed to the existence of positive feedback between the motor binding/unbinding kinetics and filaments: a higher density of motors recruits more filaments, which promotes motor binding to filaments and prevents the motors from escaping far away from the filaments, due to confinement by the filaments.

In this study, we assumed that the motion of the nodes was overdamped due to solvent friction. Furthermore, because we focused only on motor-driven filament rearrangements, we did not account for thermal fluctuations and restricted our model to deterministic motions. With these simplifications, the equation describing the motion of the position vector r_i of the ith node can be written in the following form:

$$\gamma \frac{d{r}_i}{dt}=-\sum _j{K}_{ij}\left(\left|r_i-r_j\right|-L_{ij}\right)\frac{r_i-r_j}{\left|r_i-r_j\right|},$$ (4)

where $\gamma$ is a friction coefficient and the summation runs over the nodes j that possess a link to node i. The total elastic energy, E, stored in the system is calculated by the following equation:

$$E=\sum _{i,j}\left[\frac{K_{ij}}{2}{\left(\left|r_i-r_j\right|-L_{ij}\right)}^2\right].$$ (5)

The summation is taken over all node pairs with links. It is reasonable to break a link when it is elongated and bears significant tension. Here, we employed a simple threshold criterion: if the length of a link was longer than a certain threshold value, L_c, we severed the link. Since a single link, which represents bundles of MT filaments, is thought to be sufficiently stiff, we did not consider the dynamics of link buckling. Equation 4 was numerically integrated using the forward Euler method with a time step of dt. All of the model parameters, except for K and f, were held constant throughout this study (l = 0.08, L = 0.008, L_c = 0.16, k = 0.5, $\tilde{C}$ = 0.5, C_max = 1, $ϵ$ = 0.1, $\gamma$ = 1, dt = 0.01, N_x = 100, and N_y = 58). All of these quantities are dimensionless in our model.

Results

The MT-kinesin system exhibited various spatiotemporal dynamics

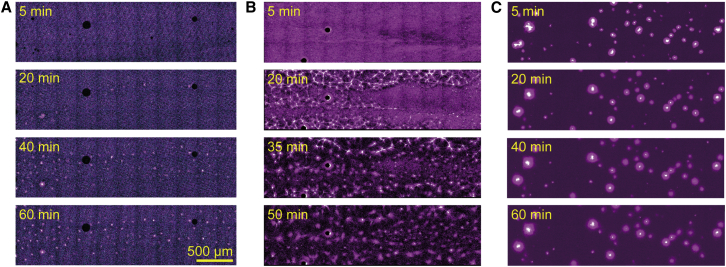
To explore the spatiotemporal dynamics of MT networks, we constructed a system that consisted of a minimal number of components, i.e., MTs and a single type of motile cross-linker, Eg5, which is a member of the kinesin-5 family (36). GFP-fused Eg5 moved processively along ATTO647N-labeled MTs (8.9 ± 0.4 nm/s; Fig. S1, A–C), cross-linked a pair of MTs, and promoted their sliding (Fig. S1, D and E) as previously reported (32, 50, 60). We then mixed a low quantity of taxol-stabilized MTs and Eg5 ([Eg5] = 2.97 nM, [tubulin] = 10 nM) in the presence of 2 mM ATP and an ATP-regenerating system, and observed their interactions and dynamics. In the mixture, Eg5 that was evenly distributed on MTs promoted cross-linking and sliding of the MTs. Once the bundle was formed, the Eg5 started moving along the MT bundle and finally accumulated at one end of the bundle (Fig. 1 A). The resultant shape of the MT-Eg5 complex resembled pine needles connected at a basal sheath. As time elapsed, the MT bundles were joined through tip-accumulated Eg5 (Fig. 1, A and B). Once formed, such tip-jointed MT structures were stable even 60 min after the initial mixing (Fig. 1 B).

When the MTs were dense ([tubulin] = 1 μM), the tip-joined MT structures were connected to each other and formed a globally connected MT network. This network was composed of MT links and various sizes of Eg5-accumulated nodes (Figs. 1 C and S2 A; Movies S1 and S2). At the beginning of network formation, radial MT structures extending from the Eg5-accumulated center (node) appeared (Fig. S2 B, yellow circles). Since Eg5 accumulates at the plus end of an MT, the radially extending MTs had a definite orientation with their plus end pointing to the center. Thus, when free MTs floating in the solution reached the extending MTs, Eg5 bound to the extending MTs, caught them, and transported them toward the center of the node (Figs. 1, C and D, and S2 B, yellow arrowheads). As time elapsed, the nodes attracted a number of MTs and increased in size up to 10–100 μm (Fig. 1 C). These enlarged nodes, referred to as active nodes, can exert active contractile force. The nodes started linking together through MTs in solution (Fig. S2 B, yellow arrowheads) and formed a global network (Movie S2). However, the contractile dynamics was limited to local contractility at [Eg5] = 2.97 nM, as indicated by the velocity field of nodes (Fig. 1 E). The mean node velocities were low throughout the observation time, indicating a lack of rapid movements of the nodes (Fig. 1 F). In addition, the time evolution of the velocity correlation function also shows that the directions of the node movements had no global correlation (Fig. S2 E). Furthermore, the stable temporal evolution of both the total network size and the size of the largest cluster indicated that no global change occurred in the network (Fig. S2 D). This dynamic pattern with global connectivity and local contractility is referred to as a static network (Table S1).

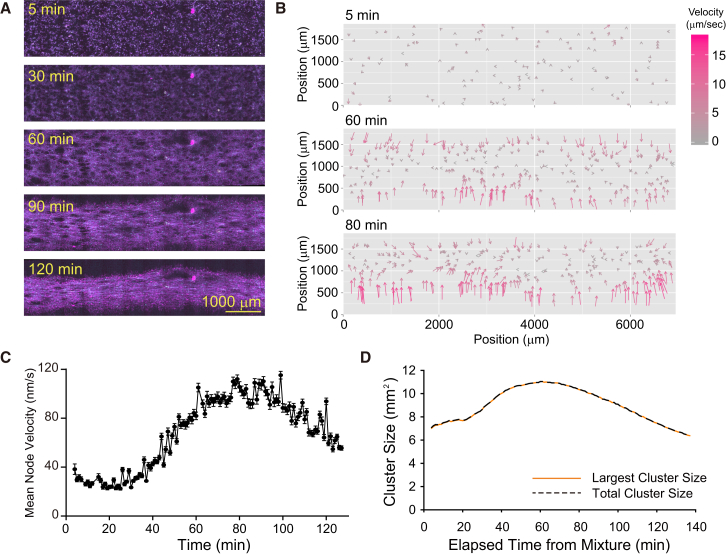
As the Eg5 concentration increased ([Eg5] = 22.5 nM), the node density became high enough to cause a global connection of active nodes, and the connected network subsequently contracted (Figs. 2 A and S3 A; Movie S3). In the early stage of the dynamics, the formation of a globally connected MT network occurred. Due to the increased Eg5 concentration, both the number and size of active nodes in the network increased compared with those observed in the static network. After a considerable amount of time had elapsed (∼20 min), the linking of contractile active nodes brought about a global contraction of the network. The velocity field of the nodes indicated an immotility of active nodes during network formation and rapid movements during the contraction step (Fig. 2 B; Movie S4). The temporal evolution of the mean node velocity and the velocity correlation function clearly showed the existence of a waiting period before contraction started (Figs. 2 C and S3 B). Since the temporal evolution of the total network size and that of the largest cluster size behaved almost identically (Fig. 2 D), one can conclude that the network contracted as a whole. This dynamic pattern with global connectivity and contractility is referred to as an active network (Table S1). In addition to the global contraction, occasional self-rupturing of the network was also observed (Fig. S3 C). Active-network dynamics was observed under several Eg5 concentrations (18, 22.5, and 29.7 nM; Fig. S4 and Table S1). Interestingly, under some Eg5 concentrations, both static and active networks were observed (Fig. S3 D), probably because of the initial distribution of node positions (Fig. S5).

Figure 2.

Formation and contraction of MT networks by a motile cross-linker. (A) Time-series images showing the formation of a globally connected contractile MT network ([tubulin] = 1 μM, [Eg5] = 22.5 nM). The images of ATTO647N-labeled MTs (magenta), ATTO565-labeled MTs (yellow), and GFP-fused Eg5 (cyan) are merged. The times displayed in the images represent the times that elapsed after mixing. (B) Time-dependent evolutionary pattern of the vector field representation of node velocities in the active network shown in (A). The velocity of each node is indicated by the length of arrows and the color scale. (C) Temporal evolution pattern of the mean node velocity in the active network shown in (A). The mean value and SD are shown. The total trace number of nodes is 1572. (D) Temporal evolution pattern of the size of total cluster and the largest cluster.

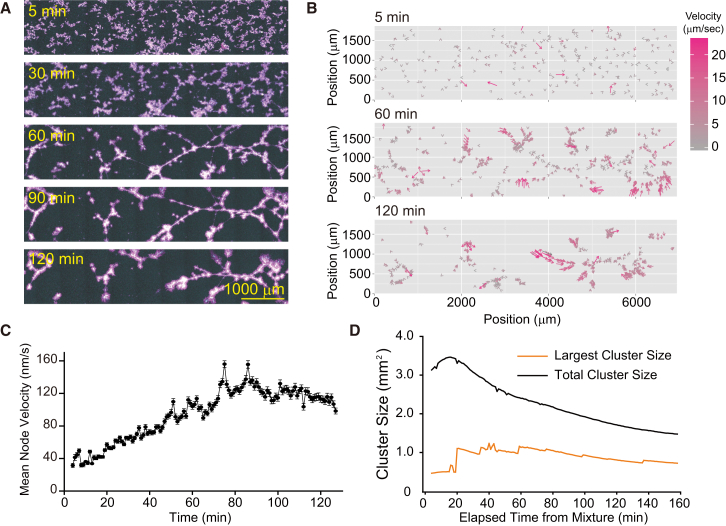
When the Eg5 concentration was further increased ([Eg5] = 45 nM), MT-Eg5 clusters of various sizes formed even before the observations began (Fig. 3 A, 5 min). Densely distributed active nodes in the clusters caused an immediate contraction of the network and separated it into aggregates of different sizes and shapes (Figs. 3 A and S6 A; Movie S4). In addition to the aggregates of various sizes, several spherical asters of similar size were segregated during the contraction (Fig. S6 B). The time-evolution pattern of the node velocity field and the mean node velocity showed that contraction started at the early stage of the dynamics and was localized (Figs. 3, B and C, and S6 C). Based on the large difference between the time series for the total network size and the largest cluster size, one can conclude that network segmentation occurred at the early stage of the dynamics (Fig. 3 D). This dynamic pattern with local connectivity and strong contractility is called aggregation (Fig. S6 D and Table S1).

Figure 3.

The strong contraction force caused by a motile cross-linker results in MT network fragmentation. (A) Time-series images showing the formation of a globally connected contractile MT network ([tubulin] = 1 μM, [Eg5] = 45 nM). Images of ATTO647N-labeled MTs (magenta), ATTO565-labeled MTs (yellow), and GFP-fused Eg5 (cyan) are merged. The times displayed in the images represent the time that elapsed after mixing. (B) Vector field representation of node velocities in the aggregation shown in (A). The velocity of each node is indicated by the length of the arrows and the color scale. (C) Temporal evolution pattern of the mean node velocities in the aggregation shown in (A). (D) Temporal evolution pattern of the size of the total cluster and the largest cluster.

Effects of MT properties on network dynamics

We next investigated the effects of MT properties on spatiotemporal dynamics by using MTs shortened by shearing and GMPCPP-MTs instead of taxol-stabilized (normal) GTP-MTs. We confirmed that the sheared MTs and GMPCPP-MTs were shorter in length than the GTP-MTs (Fig. S7, A and B). Before observing the spatiotemporal dynamics of the MT network, we observed Eg5 moving on both GMPCPP-MTs and taxol-stabilized GTP-MTs (Fig. S8). The mean velocities were 19.0 ± 0.2 nm/s (GMPCPP-MTs) and 9.4 ± 0.1 nm/s (taxol-MTs), respectively. Although the velocity of Eg5 was higher on GMPCPP-MTs than on GTP-MTs, a mixture of Eg5 and both kinds of shortened MTs displayed all three of the distinct patterns observed in the system composed of Eg5 and normal GTP-MTs (Fig. S9 and Table S1), suggesting that modulation of MT properties does not have a critical effect on the types of spatiotemporal patterns. However, the correspondence between the observed patterns and the concentration range of Eg5 was different (Fig. S9 and Table S1). Since the density of the MTs did not change with the use of shortened MTs (Fig. S7 C), this shift in the transition concentration of Eg5 probably resulted from differences in the lengths of the MTs.

Effects of motor properties on network dynamics

We next investigated how the spatiotemporal dynamics of MT networks can be affected by the activity of a motile cross-linker. To address this question, we altered the motor properties by replacing the motor head of Eg5 with that of KIF5B (Fig. S10, A and B), which is similar to a construct used in a previous study (32). This chimeric motor (KIF5B_head-Eg5_tail) exhibited processivity along MTs with a 10-fold higher velocity than the wild-type Eg5 protein, and with less affinity for MTs (Fig. S10, C–F). The mixture of MT and KIF5B_head-Eg5_tail showed temporal evolution patterns distinct from those of the MT-Eg5 system (Fig. 4), suggesting that the activity of the motile cross-linker critically affected the MT network dynamics. The eventual steady-state patterns of the system revealed many isolated astral structures with an isotropic shape, regardless of the motor concentration used ([KIF5B_head-Eg5_tail] = 6.25–37.5 nM). These results are consistent with a previous study that used a similar chimeric construct (32) and artificially oligomerized kinesins (29, 30). This dynamic pattern including the formation of such astral clusters is referred to as isolated asters. Although the spatial patterns of the final state were similar, the intermediate temporal patterns were dependent on the motor concentration. When the motor concentration was low ([KIF5B_head-Eg5_tail] = 6.25 nM), the motors localized to form asters. However, these asters were distributed so sparsely that a globally connected network did not form (Fig. 4 A; Movie S7). At an intermediate concentration ([KIF5B_head-Eg5_tail] = 12.5 nM), the motors accumulated to form numerous active nodes, which were interconnected through bundled MTs to form a global network. The formed network immediately started to contract, but the links between the active nodes broke readily upon contraction, such that the network structure collapsed into isolated asters (Fig. 4 B; Movie S6). At a high motor concentration ([KIF5B_head-Eg5_tail] = 37.5 nM), the MTs assembled on separate asters even before the start of observations (Fig. 4 C).

Figure 4.

Spatiotemporal dynamics of the MT network driven by KIF5B_head-Eg5_tail. Time-lapse images show the temporal evolution of isolated asters. Images of taxol-stabilized ATTO647N-labeled MTs (magenta), ATTO565-labeled MTs (yellow), and KIF5B_head-Eg5_tail (cyan) are merged. (A–C) The KIF5B_head-Eg5_tail concentration was 6.25 nM (A), 12.5 nM (B), or 37.5 nM (C).

Coarse-grained modeling of the spatiotemporal patterns observed experimentally

To understand the mechanism underlying the spatiotemporal dynamics of the MT-motor system and identify essential factors of the system, we developed a coarse-grained model for the contractile MT networks (Figs. 5 A and S12; see also the “Coarse-grained model” section in Materials and Methods) and examined the temporal evolution of MT networks under various motor concentrations with fixed motor properties (Movies S6, S7, and S8).

In our model, MT networks were described by a graphical representation with a set of nodes and links (Figs. 5 A and S12, A and B). Since almost all experimentally observed patterns included astral structures that exerted contractile forces, we regarded each network node as a contractile unit with radially extending links (an active node). Each link represents bundles of MTs interconnecting the active nodes.

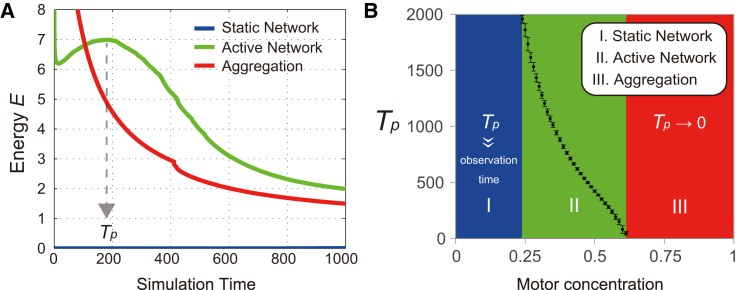
Motor concentrations were assigned to each node, and links were elastically extended depending on the motor concentration at each node (Eqs. 2 and 3). Because plus-end-directed motors move toward the centers of asters and tend to be localized (Fig. 1, A and B), we assumed that the motors move against the gradient of motor concentration with a constant flux f to accumulate in regions of higher concentrations. Furthermore, because neighboring filaments between adjacent nodes are mostly in an antiparallel configuration (Fig. S12 C), we modeled a link between two adjacent nodes to contract through the motors’ sliding activity, which induces overlapping of neighboring filaments. The links were broken when they extended beyond a critical length, L_c, in a manner similar to the bond-dilution process that is widely used to investigate biopolymer networks (54). Fig. 5 B shows representative pattern evolutions with different initial motor concentrations, C_ub. At a low motor concentration of C_ub = 0.1, the motors accumulated on a few nodes, and these nodes then attracted surrounding nodes (Fig. 5 B, Static Network, Node Velocity; Movie S8), corresponding to the local contractile dynamics observed in our experiments (Fig. 1 D). Because these active nodes were too sparsely distributed to link to each other, the system remained static, corresponding to the experimentally observed static network (Figs. 1 and S2). As the motor concentration was increased to C_ub = 0.4, many active nodes became interconnected to form a network that contracted as an entire domain (Fig. 5 B, Active Network, Node Velocity; Movie S9). This global contraction corresponded to the active networks observed in the experiments (Figs. 2 and S3). A slight increase of the motor concentration around C_ub = 0.6 caused some active nodes to exhibit strong local contracting forces, leading to the breakage of several links. Link breakage, in turn, caused local stress concentrations, resulting in occasional rupturing of the entire domain (Fig. S13 B). At a higher motor concentration of C_ub = 0.7, the active nodes pulled their surrounding nodes so rapidly upon the mixing of motors with MTs that the network no longer maintained global connectivity. The resultant structures contracted rapidly to form chain-like aggregates (Fig. 5 B, Aggregation, Node Velocity; Movie S10). These results are similar to the experimental patterns observed with the high motor concentration (Figs. 3 and S6). Changes in the total area and the cluster number at a simulation time of T = 500, as the motor concentration was varied, are summarized in Fig. 5 C.

Modulation of model parameters reproduced the isolated-asters pattern

Increasing the strength, K, of the contraction between adjacent active nodes and the motor flux, f, which mimics the elevated sliding activity of the motors, resulted in the formation of multiple asters of small filament-motor aggregates (Fig. 5 B, Isolated Asters, Node Velocity). These isolated asters were created through rapid, strong contractions followed by many link breaks. This dynamics reproduced the observation of isolated asters with KIF5B_head-Eg5_tail (Figs. 4 and S11).

The elastic energy storage in the MT network calculated by coarse-grained modeling recharacterized static networks, active networks, and aggregation

To compare the mechanical behaviors of the modeled MT networks, we calculated the elastic energy stored within them. We found three distinct patterns in the temporal evolution of the total elastic energy, E, stored in the system (Fig. 6). The energy in the static network remained small, whereas the energy in the active network increased to a maximum during the contraction phase and was released through dissipation via link breakage. In the aggregation phase, the network immediately collapsed under self-generated mechanical stress, whereas the energy decreased continuously (Fig. 6 A). Fig. 6 B depicts the time at which the energy peaked, T_p (Fig. 6 A), as the motor concentration was varied. Thus, three distinct phases were clearly identified as a static network (T_p ≫ observation time), an active network (T_p remaining finite), and aggregation (T_p → 0).

Figure 6.

Mechanical properties of the model MT networks. (A) Temporal changes in the total elastic energy (E) stored in the system for the static network (C_ub = 0.1), active network (C_ub = 0.59), and aggregation (C_ub = 1.0) patterns. (B) Relationship between the time at which E reaches a local maximum, T_p, and the motor concentration, C_ub. Bars reflect the standard deviation of the mean value for 100 repeated simulations, starting with randomized initial distributions of the motor concentration. The model parameters are the same as those in Fig. 5B.

Discussion

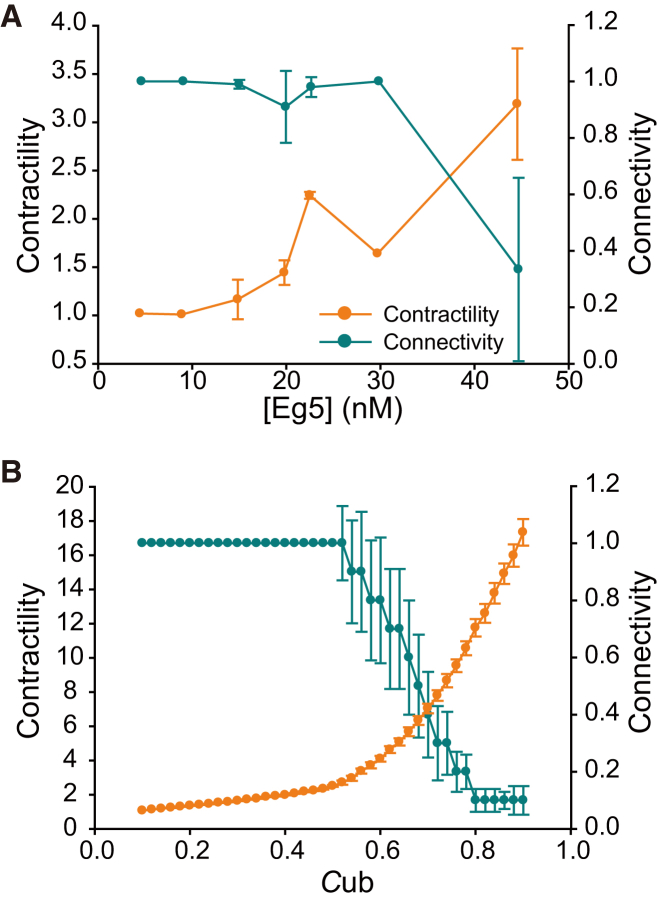
In this study, we demonstrated that a simple system composed of MTs and cross-linking motors exhibited a variety of spatiotemporal dynamics (Figs. 1, 2, 3, and 4; Table S1). The patterns were categorized as static networks, active networks, aggregation, and isolated asters, and characterized by the connectivity and contractility of the networks (Fig. 7). The static and active networks were similar in that the MTs were globally connected. However, after network formation, the dynamics of the static network showed a lack of global contractility, whereas the active network displayed contraction throughout the entire structure. Aggregations and active networks shared contractile dynamics, but aggregations showed a lack of global connectivity and only local contractions. In isolated asters, the strong contractility or weak connectivity that resulted from modulation of the motor properties caused connectivity breaks in the network, resulting in localized contraction, even when a globally connected network was formed. Regarding the connectivity and contractility of networks, the elemental structure is the active node, the motor-accumulated point from which MTs extend radially. The active nodes are thought to be formed via reorganization of MTs and motors (Fig. S13 C), based on the cross-linking and sliding activities of motor proteins, and have MTs with uniform polarity surrounding around them. Since the MTs in the active nodes have a defined polarity, contraction forces emerge between the adjacent active nodes linked through MT bundles, and this contractile interaction between active nodes is the origin of network contractility.

Figure 7.

Contractility and connectivity of MT networks. (A) Dependence of contractility and connectivity on the Eg5 concentration in the experiments. The mean and standard deviation are shown. Number of observed chambers: one (4.5 nM), one (8.9 nM), five (14.9 nM), three (19.8 nM), five (22.5 nM), one (29.7 nM), and five (45 nM), respectively. (B) Dependence of contractility and connectivity on the motor concentration, C_ub, in the simulations. Average values are shown, with bars reflecting the SD of the mean value for 100 repeated simulations, starting with randomized initial distributions of the motor concentration.

The geometric configuration of active nodes may play some role in the temporal evolution of the network dynamics. In the static network, the active nodes were distributed so sparsely that links between contractile active nodes rarely formed. In the active network, connected links of active nodes formed and rendered the network capable of undergoing global contractility. During aggregation, densely distributed active nodes formed local clusters and exerted strong contractile forces to break linkages among the clusters. The importance of the geometrical configuration of active nodes is further supported by evidence that differences in the initial spatial distribution of motors correlated with the subsequent temporal evolution pattern (Fig. S5). However, it is difficult to control the initial distribution of active nodes in the system used here. The relationship between the geometry of the node positions and the temporal evolution patterns of the networks will be addressed in more detail in future work.

Furthermore, the spatiotemporal dynamics of the MT-motor network were affected by modulation of the MT and motor properties (Figs. 4 and S9). The results obtained using GMPCPP-MTs and shortened MTs suggested that the experimental modulation of MT properties had little effect on the types of patterns observed (Fig. S9), although shifts in the transition concentration of the motor protein occurred. In contrast, the results obtained with the chimeric KIF5B_head-Eg5_tail protein indicated that modulation of the motor properties critically affected the spatiotemporal dynamics, which led to a different type of pattern, namely, isolated asters.

On the basis of the spatiotemporal dynamics of the MT-kinesin network, we developed a simple model of network contraction that reproduced our experimentally observed patterns. To construct a simple model of the macroscopic contractile patterns of filament-motor networks on a scale of several millimeters over ∼2 h, we employed a coarse-grained description in which the MTs were represented by a set of extensible links without buckling, based on our experimental observations that showed no apparent buckling of the bundles around active nodes (Fig. S13 A). Our model suggests that two essential features account for our experimental findings. First, motors must move between adjacent nodes to accumulate and form active nodes; otherwise, they fail to exert significant contractile forces. Second, the magnitude of contraction between nodes must depend on the motor concentration in a threshold-dependent manner (Eqs. 2 and 3). Without this nonlinear dependency, the model network would experience excessive link breakages during active node formation. The typical spatiotemporal dynamics of the modified model, where the contraction strength depends linearly on the motor concentration, is shown in Fig. S13 C. The modified model predicted the formation of large holes in the network during contraction over nearly all concentrations of the initial motor density, and eliminated the aggregation phase at a high motor concentration (Fig. S13 D). These results conflicted with our experimental observations, suggesting that nonlinearity is necessary to maintain network connectivity in global contractile dynamics. Furthermore, recent theoretical work on the actomyosin network (61) also provides support for our assumption of nonlinear dependency, showing that the net contractile force in the actomyosin system emerges in a threshold-dependent manner.

In addition, our model showed an energy-storage capacity of active networks (Fig. 6). During the temporal evolution of an active network, the interconnection of active nodes prevents local link breakages and enables the storage of elastic energy in the entire network, except when occasional ruptures occur (Figs. S3 C and S13 B). From a biological point of view, contraction of the MT network and energy storage might contribute to increased mechanical stability of cells when the network periphery is cramped, so that it cannot contract, but rather can span tightly throughout the whole cell surface.

Although contraction principles for actin-myosin networks have been widely studied experimentally (62, 63, 64, 65) and theoretically (66, 67, 68, 69, 70, 71), surprisingly few studies of the contraction mechanism of MT networks have been published. Foster et al. (41) recently demonstrated the contractile dynamics of large-scale MT networks in Xenopus extracts and modeled them using active hydrodynamic theory, providing insight into the macroscopic cytoskeletal organization (42). The in vitro motor-filament system that we studied here is composed of simpler and well-characterized components, i.e., MTs and a single kind of active cross-linker. This system exhibits not only similar contractile dynamics but also network ruptures, which can be understood by using an elastic network model.

Previous studies on MTs focused mainly on the role of MTs in establishing the mitotic spindle and intracellular transport. Recent cell biology studies, however, have provided evidence that network-like MT structures with multiple organizing centers can form, which can be viewed as network nodes in myocytes (43), muscle cells (44), and plants (72), suggesting possible biological functions of MT networks. It is known that in these networks, many MT organizing centers without any obvious organizing apparatus can play an important role in establishing network structures. This study of the MT-motor network with self-organized contractile active nodes will provide a new, to our knowledge, basic framework for understanding the spatiotemporal dynamics of MT networks with multiple acentrosome-organizing centers.

Author Contributions

T.T., D.T., and K.O. designed the study. T.T. designed and performed the experiments. T.T. and D.T. performed the image analysis. D.T. designed and performed the simulations. All of the authors contributed to the writing of the manuscript.

Editor: Stefan Diez.

Supporting Material

Movie S1. Spatiotemporal Dynamics of a Static Network

Three-dimensional reconstitution of the temporal evolution of the static network shown in Fig. 1 C ([Eg5] = 8.9 nM, [tubulin] = 1 μM). Images of ATTO647N-labeled MTs (magenta), ATTO565-labeled MTs (yellow), and GFP-fused Eg5 (cyan) are merged.

Movie S2. Spatiotemporal Dynamics of MTs in the Static Network

The movie displays the global connectivity of MTs in the static network ([Eg5] = 1.37 nM, [tubulin] = 1 μM; 1800 × real time). Images of ATTO647N-labeled MTs are shown.

Movie S3. Spatiotemporal Dynamics of an Active Network

Three-dimensional reconstitution of the temporal evolution of the active network shown in Fig. 2 A ([Eg5] = 22.5 nM, [tubulin] = 1 μM). Images of ATTO647N-labeled MTs (magenta), ATTO565-labeled MTs (yellow), and GFP-fused Eg5 (cyan) are merged.

Movie S4. Temporal Evolution Pattern of the Velocity Field of the Active Network

The time-dependent evolutionary pattern of node velocities in the active network shown in Fig. 2 A is represented by vector fields. The velocity values are indicated by the length of the vectors and colors.

Movie S5. Spatiotemporal Dynamics of Aggregation

Three-dimensional reconstitution of the temporal evolution of the aggregation shown in Fig. 3 A ([Eg5] = 45 nM, [tubulin] = 1 μM). Images of ATTO647N-labeled MTs (magenta), ATTO565-labeled MTs (yellow), and GFP-fused Eg5 (cyan) are merged.

Movie S6. Spatiotemporal Dynamics of Isolated Asters

Three-dimensional reconstitution of the temporal evolution of the isolated asters shown in Fig. 4 B ([KIF5Bhead-Eg5tail] = 12.5 nM, [tubulin] = 1 μM). Images of ATTO647N-labeled MTs (magenta), ATTO565-labeled MTs (yellow), and GFP-fused KIF5Bhead-Eg5tail (cyan) are merged.

Movie S7. Spatiotemporal Dynamics of MTs in Isolated Asters

The movie displays the lack of global connectivity in the isolated asters ([KIF5Bhead-Eg5tail] = 6.25 nM, [tubulin] = 1 μM; 1800 × real time). Images of ATTO647N-labeled MTs are shown.

Movie S8. Spatiotemporal Dynamics of a Static Network in the Coarse-Grained Model

Model simulation of the static network shown in Fig. 5 B. Links are represented in magenta and motors are represented in white. Model parameters: Cub = 0.1, K = 15, k = 0.5, f = 0.01, L = 0.008, Lc = 0.16, l = 0.08, Cmax = 1, $\tilde{C}$ = 0.5, $ϵ$ = 0.1, γ = 1, dt = 0.01, Nx = 100, and Ny = 58. The total length of the movie corresponds to 50,000 simulation steps.

Movie S9. Spatiotemporal Dynamics of an Active Network in the Coarse-Grained Model

Model simulation of the active network shown in Fig. 5 B. Links are represented in magenta and motors are represented in white. Model parameters: Cub = 0.4, K = 15, k = 0.5, f = 0.01, L = 0.008, Lc = 0.16, l = 0.08, Cmax = 1, $\tilde{C}$ = 0.5, $ϵ$ = 0.1, γ = 1, dt = 0.01, Nx = 100, and Ny = 58. The total length of the movie corresponds to 50,000 simulation steps.

Movie S10. Spatiotemporal Dynamics of Aggregation in the Coarse-Grained Model

Model simulation of the aggregation shown in Fig. 5 B. Links are represented in magenta and motors are represented in white. Model parameters: Cub = 0.7, K = 15, k = 0.5, f = 0.01, L = 0.008, Lc = 0.16, l = 0.08, Cmax = 1, $\tilde{C}$ = 0.5, $ϵ$ = 0.1, γ = 1, dt = 0.01, Nx = 100, and Ny = 58. The total length of the movie corresponds to 50,000 simulation steps.