Printing of stretchable silk membranes for strain measurements

Abstract

Quantifying the deformation of biological tissues under mechanical loading is crucial to understand its biomechanical response in physiological conditions and important for designing materials and treatments for biomedical applications. However, strain measurements for biological tissues subjected to large deformations and humid environments are challenging for conventional methods due to several limitations such as strain range, boundary conditions, surface bonding and biocompatibility. Here we propose the use of silk solutions and printing to synthesize prototype strain gauges for large strain measurements in biological tissues. The study shows that silk-based strain gauges can be stretched up to 1300% without failure, which is more than two orders of magnitude larger than conventional strain gauges, and the mechanics can be tuned by adjusting ion content. We demonstrate that the printing approach can accurately provide well bonded florescent features on the silk membranes using designs which can accurately measure strain in the membrane. The results show that these new strain gauges measure large deformations in the materials by eliminating the effects of sliding from the boundaries, making the measurements more accurate than direct outputs from tensile machines.

Introduction

Many biological tissues in the body are flexible and are subjected to large deformations under mechanical loading.^1-6 Quantifying these large strains in real time, such as those taking place in skin, muscle and nervous tissue, is very important for mechanical characterization of these tissues toward understanding of their mechanical functions under stress in physiological conditions and thereafter for designs of biomaterials with compatible mechanical response for further biomedical applications.^7-14 However, conventional strain measurements have limitations for biological tissues. For example, indirect strain measurements, such as strain computed via the displacement of tensile grips for uniaxial loading test, can lead to errors as the tissue can easily slide from the surface in contact with the grips. Contact measurements through a variety of electrical-based strain gauges, are limited to their strain range, humidity in the environment and surface chemistry for bonding, as well as the material selection which may affect the mechanical properties of the biological material used for the measurements as engineering materials are usually stiffer and less stretchable than biological tissues. On the other hand, non-contacting strain measurements including digital image correlation use cameras and computer algorithms to recognize the location of random points on material surface and compute the strain through their movement field.^15,16 Such methods require high-image resolution that depends on the quality of camera and light source, and small deformations of material samples for successfully setting up the correlation between two neighboring images, which becomes difficult for in-situ measurements of biological materials. Accurate measurements of the strain in biological tissues in physiological conditions requires a technique that introduces only a small disturbance to the native tissue while also being convenient for receiving and processing the data.

Here, we report a new method and a set of membrane materials based on silk protein, useful for accurate optical strain gauges. Pure silk fibroin (SF) derived from Bombyx mori cocoons was used and hence the material is biocompatible and biodegradable due to the absence of toxicity and immunogenicity,^17,18 making these devices useful candidates for in-situ and implantable strain measurements. We illustrate the use of printing,^8,19,20 to accurately print silk membrane materials with predictable structures based on our design. The study shows that the materials are extremely flexible to allow them to conform to irregular curved surfaces and bond well to them. The results show that we can use ultraviolet (UV) light and two-dimensional discrete Fast Fourier Transform (2D-FFT) to obtain the strain of the membrane during deformation. We further demonstrate that the material is more stretchable than most biological tissues and can accommodate strains at least to 250% in deformation, more than two orders of magnitude larger than almost commercially available strain gauges.^6,12,21

Materials and methods

Preparation of degummed silk fibers

B. mori silk fibers were degummed by boiling in two 30 min changes of 0.5% (w/w) NaHCO₃ (Sigma-Aldrich) solution. Then the degummed silk fibers were washed with distilled water and allowed to air dry at room temperature.

Preparation of silk membranes

The dry degummed silk fibers were dissolved in CaCl₂/formic acid (FA) solution to produce silk solution to form into membranes with desired SF/FA/CaCl₂ ratios. In a typical experiment, 1g CaCl₂ (Sigma-Aldrich) was added in 20g FA (Sigma-Aldrich) solution, followed by the addition of 3g degummed silk fibers. After shaking for 1 min at room temperature, the solution was cast onto a polystyrene petri dish with diameter of 150 mm, and the FA solvent allowed to evaporate at approximately 25°C and 50% relative humidity, resulting in films approximately 100 μm thick.

Preparation of florescent silk solution

One gram of CaCl₂ (Sigma-Aldrich) and 1 mg Rhodamine B (Sigma-Aldrich) were added in 20g FA solution, followed by the addition of 3g degummed silk fibers. The florescent silk ink was then prepared by shaking the solution at room temperature.

Printing process

A printer was designed and built for printing of silk solution. The printer is composed of a syringe pump, a standing moving rail and the substrate (Fig. 1b). The majority of the printer body is made of acrylic plates (0.25 inch) machined by a laser cutter. The motion of each part, including the standing rail moving in x-direction, the substrate moving in the y-direction and the syringe pump moving in the z-direction, is digitally controlled by a stepper motor with a minimum 1.8 step angle, a ball screw with 12 mm in diameter and 4 mm in lead and a computer numerical control (CNC) board that is connected through the parallel port to a computer installed with the Mach3 software. A paragraph of G-code for Mach3 software is generated by a Matlab script to control the printing pattern, injecting speed and the moving speed along each axis during the printing process. The system has a theoretical resolution of 20 μm in motion. The resolution of the printing pattern also depends on the viscosity of the silk solution and the hydrophobicity of the substrate. In the case of silk strain gauge, the resolution is mainly limited by the thickness of bands as two neighboring bands can be printed as narrow as possible and as long as they do not fuse and become optically distinguishable. The band thickness is limited by the inner diameter of the syringe tip as a thinner tip significantly increases the shear force, which needs larger compressing force and can cause silk clogging at the tip. For the current syringe tip (with inner diameter of 0.64 mm) that we successfully used, the distance of the neighboring lines in our printing gauge could be narrowed to 500 μm and the X-Y resolutions can reach up to 1 mm.

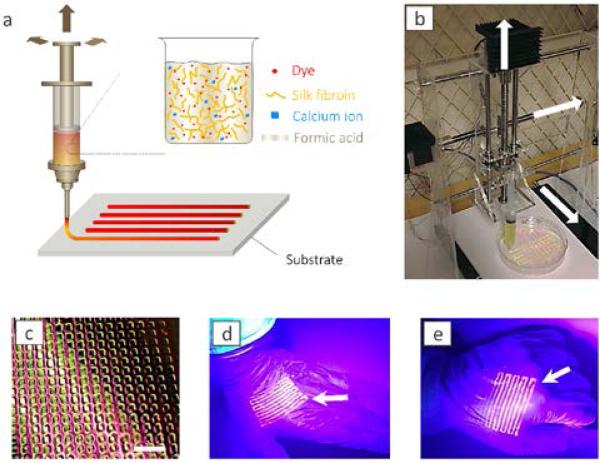
Fig. 1.

Printing of silk. (a) Schematic illustration of the printing process. A fluorescent silk/Ca²⁺/FA ink is printed onto a substrate. (b) Photograph of custom-built printing device. (c) Photograph of printed silk pattern on polypropylene film. The scale bar is 1 cm. (d, e) Photograph of printed silk pattern on gloves with palm open (d) and clenched fist (e). The fluorescent silk pattern deforms with the deformation of the gloves.

Remote strain measurements

A video camera was used to record the drawing process of printed samples. All tests were carried out in a dark room with UV light directed on the samples. To avoid UV light damage protective glasses and clothes were needed. The drawing process was controlled and recorded via an Instron 3366 machine in tensile mode at 25°C and 40% relative humidity with a drawing speed of 6 mm min⁻¹.

2D-FFT analysis of deformed silk patterns

Each snapshot of the deformed sample was read by Matlab in the format of a RGB (red, green, blue) color matrix with each pixel described by its RGB scale. 2D-FFT was applied only to the red color scale of the matrix and transforms the image into the frequency space. The cross section plot along the middle longitudinal axis of the 2D-FFT image contains the information of the average band-distance through the sample, which is given by the inversed x-axis value of the second peak in the plot.

Pig Skin for mechanical tests

Fresh pig skin shown in Fig. 5 was obtained from a local butcher shop. The material was preserved with a temperature of 4°C before testing. The abdominal area of the pig skin was cut to make specimens as shown in Fig. 5a with size of 100×25×2 mm³ (length×width×thickness). Most of the fat layer and hairs were carefully removed before testing.

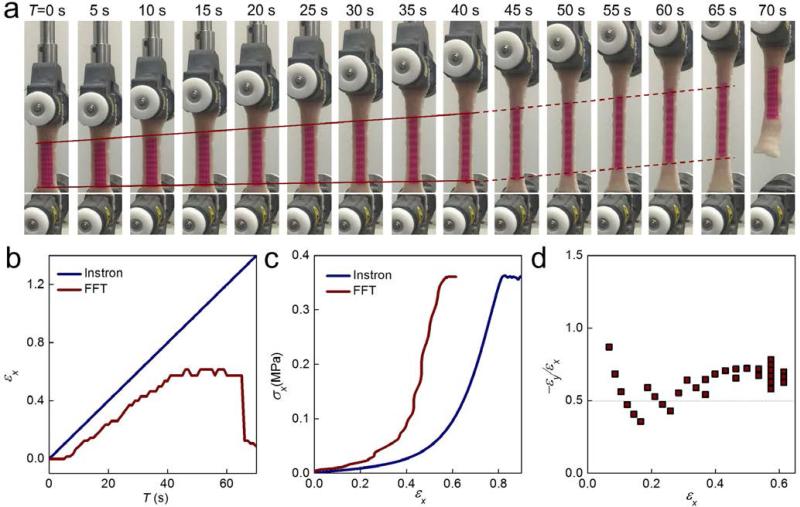
Fig. 5.

The application of a silk strain gauge in pig skin (abdomen perpendicular to spine) tensile tests. (a) Snapshots taken during the uniaxial tensile test on pig skin. The silk strain gauge was attached on the surface of pig skin. (c) Strain vs time curves obtained from the Instron monitoring and FFT analysis. (c) Stress-strain curves obtained from the Instron monitoring and FFT analysis (d) Poisson's ratio vs strain curves calculated from FFT analysis.

Characterization

The morphology and structure of the films were characterized by fluorescence microscopy (BZ-9000, Keyence, Itasca, IL), SEM (Ultra 55 filed emission scanning electron microscope, Harvard University Center for Nanoscale Systems) and FTIR spectroscopy (Jasco FTIR-6200, Jasco Instruments, Easton, MD). The mechanical properties of the films were tested with an Instron 3366 machine in tensile mode at 25°C and controlled relative humidity. The drawing speed was 6 m min⁻¹. The results were the average values from at least five measurements.

Results and discussion

Fig. 1 illustrates the general process of printing of the silk membrane as an optical strain gauge. The florescent silk solution was printed from a syringe loaded right before printing. The concentrations of silk and ions were tested to make sure the viscoelastic properties of the material were suitable to avoid clogging the tip of the syringe needle and to maintain a relatively stable form on the substrate surface after printing. Specifically, the degummed silk fibers were dissolved in CaCl₂/FA solvent²² with the concentration at 30 wt% without aggregation or gelling (Fig. 1a, see experimental section for detailed formula). The syringe was mounted to a custom-built printer that can move in all directions as well to control the ejection speed of the syringe during printing (Fig. 1b). These features of our printer are important for gauge fabrication, because regular 2D printers cannot tolerate the thickness difference of printing surfaces. All the motions of the printer were digitally controlled by stepper motors and a computer numerical control board. By using this system, different florescent patterns were printed, such as rectangular networks with different fluorescent colors in two different orthogonal directions and parallel bands (Fig. 1c, Fig. S1, supporting information and Movie 1). Patterns were able to be printed on different deformable substrates including polypropylene films, rubber and polydimethylsiloxane (PDMS) because of the high viscoelasticity of the silk solution. After rapid curing owing to the rapid evaporation of FA (about 10 min), the printed silk pattern could be deformed together with the substrate (Fig. S1, supporting information), even for a rubber glove (Fig. 1d) that was stressed in full tension (Fig. 1e).

Although SF materials have been developed, utilization of pure SF to obtain high stretchable materials remains a challenge.¹⁸ Here, highly stretchable silk membranes were developed with an approximate thickness of 100 μm and were used as the substrate for printing (Fig. 2). These silk membranes had super flexibility and strong adhesive capability and were suitable for printing. In addition, as with other types of SF membranes, they can be used as interfacial materials to attach to biological tissues.²³ The membrane is composed of SF and Ca²⁺ ions, and its mechanics can be tuned by adjusting the calcium ion content, because calcium ions in the membrane bond to the silk protein via chelation and charge interactions, and can capture water molecules from the atmospheric through coordination (See methods and Fig. 2a).^24,25 Hence, the more calcium ion is in SF membrane, the more water molecules, as plasticizers, can be captured, resulting in much softer and stretchable membranes. The progressive addition of calcium ions resulted in increased rupture strain for the silk membranes from 300±50% to 1300±300% when the SF/Ca²⁺ weight ratio went from 85:15 to 60:40 (Fig. 2). However, the modulus of toughness, which corresponds to the area below the stress-strain curve, was not a monotonic function as the SF/Ca²⁺ weight ratio. The modulus of toughness sensitively increased from 1.9 MJ/m³ for the 85:15 weight ratio to 3.0 MJ/m³ for the 80:20 weight ratio but decreased to 1.0 MJ/m³ for the 60:40 weight ratios, suggesting that there may be competing mechanisms for the ion effect on the membrane mechanics. Fig. 2c presents sample 80:20 as a representative example with a moderate calcium ion content. There was a systematic increase (up to nearly 2-3 times) in the tensile elongation to break when the relative humidity content was increased from 55% to 85%.

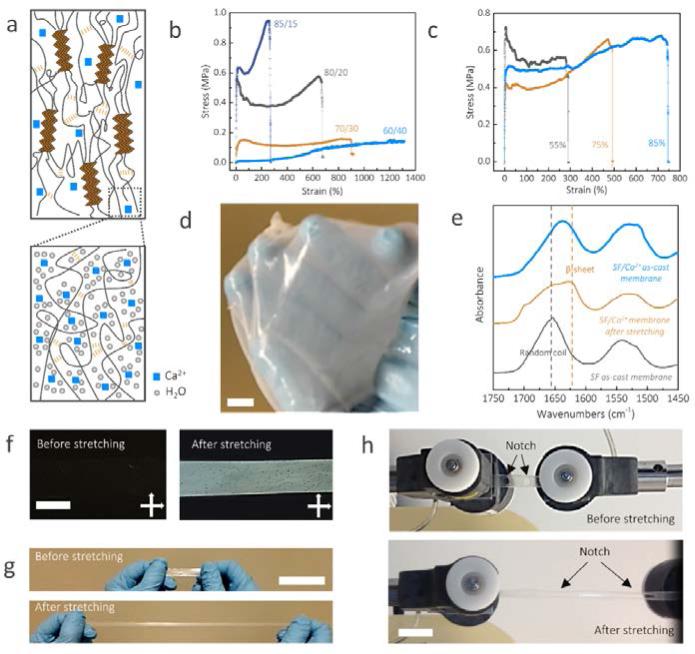
Fig. 2.

Structural and mechanical characterization of the highly stretchable silk membranes. (a) Schematic illustration of the components and interactions of SF/Ca²⁺ silk membranes. (b) Typical stress-strain plots of SF/Ca²⁺ membranes at varying SF/Ca²⁺ weight ratios with the same relative humidity (80%). (c) Typical stress-strain plots of SF/Ca²⁺ (80/20) membranes after incubation at various relative humidity levels controlled by specific saturated salt solutions with known relative humidity: KCl (85%); NaCl (75%), Mg(NO₃)₂ (55%). (d) The SF/Ca²⁺ membranes were stable after immersion in water for 4 hours. (e) FTIR spectra of silk films from 1750 to 1450 cm⁻¹, which includes amide I and amide II bands (1630 and 1655 cm⁻¹ are assigned to β-sheet and random coil, respectively). The black spectrum is the control sample prepared from SF/LiBr/water. The brief preparation process is to dissolve the dry degummed B. mori silk fibers in 9.3 mol/L LiBr aqueous solution. After dialysis against deionized water, the resultant SF solution was cast to obtain SF as cast membrane. (f) Photographs of SF/Ca²⁺ membranes under cross-polarized light before and after stretching. (g, h) the pictures of un-notched (g) and notched (h) SF/Ca²⁺ silk membranes before and after stretching. The scale bars are 1 cm.

Furthermore, unlike the as-cast SF membranes prepared from aqueous SF solution, which dissolved promptly when immersed in water, these new membranes were still stable and robust after soaking in water after 4 hours (Fig. 2d, Fig. S2, supporting information). To understand these differences, we used FTIR spectroscopy to monitor the secondary structure of these two kinds of membranes and found that our membranes contained a higher content of β-sheets²⁶ (Fig. 2e, details in the experimental section), which plays a role as a crosslinking point to form interlocking of protein chains and keeps the SF molecules stable in solvent (schematics in Fig. 2a)^27,28. The mechanism of β-sheet molecular structure is similar as what is found in natural silk fibers.^27-29 In addition, after the membrane was stretched, its maximum absorbance shifted further toward 1630 cm⁻¹, and the birefringence also sharply increased (Fig. 2f), indicating the content of β-sheet molecular structures was significantly increased by stretching, agreeing with previous studies of natural silk materials^30-32. As far as we can determine, the 1300% strain of our silk films is the highest strain value attained for silk materials (Fig. 2b, g and Movie 2). Such films were also notch-insensitive (Fig. 2h, and Movie 3 and 4). When two notches were cut into the films, at a strain of 400% the notches were blunted and remained stable during the deformation, indicating that such strain gauges can continue working in spite of local damages. In addition, this silk strain gauge could be directly transferred to different substrates, such as glass, polypropylene, rubber glove and polydimethylsiloxane, and were able to be reused without causing large deformation, (Fig. S3).

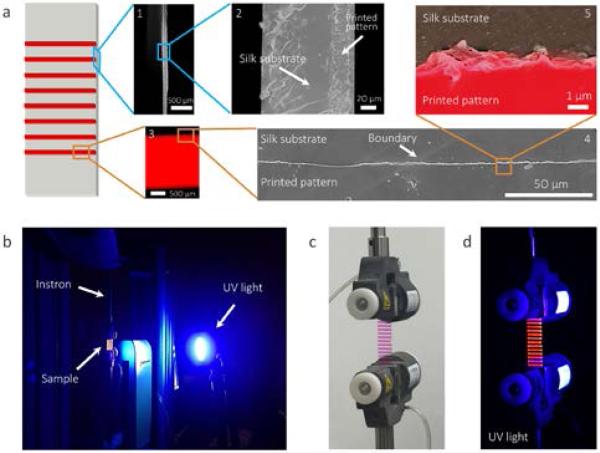
Fig. 3a presents the schematics and microscopic structure of the prototype printed silk strain gauges. The silk membrane and the printed fluorescent silk pattern were bonded well with each other as both fluorescence microscopy and scanning electron microscopy (SEM) images confirmed a sharp boundary without a significant gap between the two materials from millimeter to micrometer scales. The printed silk patterns had a uniform thickness of 30 μm. A camera was used to record the deformation of the silk strain gauge under UV-light (Fig. 3b). The printed silk lines emitted a strong red light due to the UV excitation of rhodamine B dye, however, the silk substrate remained transparent due to the weak UV excitation of silk (Fig. 3c,d). Such different florescent features between the substrate and the printed silk pattern resulted in the contrast between the two materials which significantly improved image resolution for strain analysis (Fig. 3d).

Fig. 3.

Morphologic characterization and strain measurement setup for printing silk membranes. (a) Cross-sectional (image 1 and 2) and top-view (image 4 and 5) SEM images and fluorescence microscopy image (image 3) of printed silk membranes. False color was used in SEM image 5 to distinguish printed patterns (red) and substrate (black). (b) The strain measurement setup. (c, d) Pictures of the printed silk membrane under visible (c) and UV light (d).

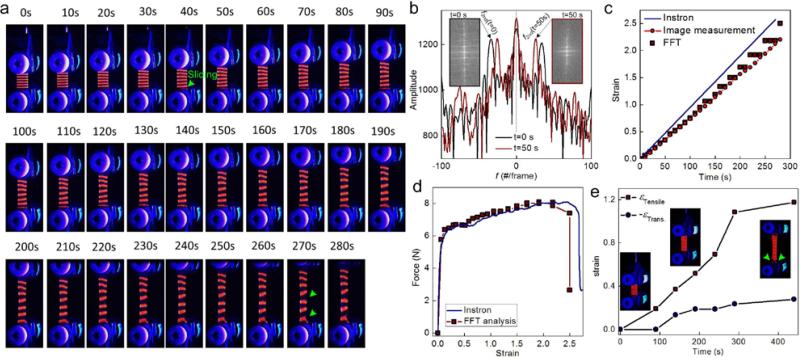
Mechanical tests were carried out by deforming the prototype strain gauge with a constant strain rate using a tensile machine. The deformation process was recorded (Fig. 4a and Movie 5). Guided by the florescence pattern, the entire sample had a uniform deformation at small deformations, which was shown by the equal distance between any two neighboring bands through the length of the material. This gauge started to fracture from the edge at large deformations (Fig. 4a, 270s), which related to heterogeneous deformation as shown by the irregular band distances. While sand paper was used with tightened clamped grips (overtightening would lead to material rupture at the interface with the grips), we could not prevent the silk membrane from sliding from the bottom grips (Fig. 4a, 40s) under deformation; such sliding at the interface can happen to any stretchable soft polymeric material under tensile tests. We analyzed the deformation of the florescent pattern by applying a 2D-FFT algorithm to the red content of each pixel in a snapshot (Fig. 4b) and obtained the average band distance as the inverse of the x-axis value (1/f_2nd) of the 2^nd peak from the center of the plot. The average strain in the strain gauge at a specific time (t) can thereafter be obtained as:

$$\epsilon \left(t\right)=\frac{f_{2\mathrm{nd}}\left(0\right)}{f_{2\mathrm{nd}}\left(t\right)}-1$$ (1)

Fig. 4.

The mechanical test and FFT analysis of printed optical strain gauges. (a) Snapshots taken during the uniaxial tensile test on the optical strain gauge. Sliding and rupture events are highlighted by green arrows. (b) FFT plots, which are obtained from the middle axis of the 2D-FFT images as the transform of the snapshots in panel (a), the average strain in the sample using Eq. (1). (c) Strain obtained from Eq. (1) as a function of time compared against the applied deformation by Instron and a direct measurement of the average distance between neighboring bands in the snapshots. Strain, computed according to the displacement of the loading grips of the Instron, overestimates the deformation of the sample. d) The calibrated force-extension curve using FFT analysis, which shows differences from that obtained directly from the Instron. e) A sample printed with a rectangular lattice to provide actual strain in tensile and transverse directions (sliding at the interface with grips as indicated by the green arrow), to show necking deformation under tension.

It is worth noting that the FFT measurement approach is based on tracking the average movement of the bands, which is different from direct measurement of the distance between two points (sharpie marker method) or digital image correlation. By repeating the FFT analysis for each snapshot, we managed to obtain as a function of t (Fig. 4c). The applied strain read from the tensile machine agreed with the FFT analysis for small deformations (t<40s) but over estimated the value for larger deformations (t>40s). Mean while, when the deformation is less than 100% (which is comparable with the strain of real tissue, such as pig skin presented below), the FFT analysis agrees well with the strain obtained from direct measurements of the varying distances between the center points of the top and bottom bands from images, suggesting that the strain gauge accounts for the sliding at the bottom boundary (Fig. 4a). When the deformation is larger than 100%, the FFT results start to slightly deviate with image measurement. This is because of FFT results that take the average distance between bands through the entire sample, so it has more tolerance to band deformation. Once the band is distorted, direct measurement can be biased to some extent. Further, we used ε(t) and the force data as that recorded by the sensor in the tensile machine to correct the force-extension curve by eliminating the sliding effect at the boundary (Fig. 4d), which yielded a slightly different curve from that obtained directly from the tensile machine and better reflected the material's mechanical response under load. Besides the uniaxial tensile tests, these printed silk patterns can also account for deformation in other directions, such as using a rectangular lattice to illustrate and compute the necking of the material in a tensile test. As shown in Fig. 4e, both tensile and transverse strain can be calculated via FFT analysis of rectangular lattice. The ratio between the transverse strain and tensile strain, as its value at small strain corresponds to the Poisson ratio, is decreased from 0.4 to 0.2 during the tensile process until slippage occurs at 290 s (indicated by green row), corresponding to fracture of the material in the tensile process.

To demonstrate the application of this strain gauge, a SF membrane (SF/Ca²⁺=70/30) with rectangular lattice pattern was selected to monitor the deformation of pig skin. One of the basic criteria when attaching a strain gauge to deformable materials is to make sure that the strain gauge itself will not change the strain in the system. Thus, we first compared two mechanical properties of pig skin before and after adherence of the strain gauge (Fig. S4). In this case, we used the same skin sample with strain less than 50% to make sure that the skin can totally recover after the tensile force was removed. By comparing the stress-strain curves of two rounds of testing, no significant difference was observed, indicating that the strain gauge does not affect the mechanical behavior of the pig skin. Additionally, after testing was completed, the gauge could be easily removed from pig skin without any damage to the pig skin or gauge. We also estimated the effect of the tissue-gauge stiffness mismatch on tissue strain via a calculation (Fig. S5). Such an effect was progressively weakened by increasing of tissue/gauge (substrate/patch) modulus ratio. Once the modulus ratio is larger than 0.7, the strain difference between the tissue with and without the gauge will be smaller than 5%. The stiffness of our strain gauge can be as low as 5 × 10⁻⁴ MPa (60:40 SF/Ca²⁺ film), which is more than 20 times smaller than that of most of soft tissues (larger than 0.01 MPa)³³. Accordingly, this strain gauge is suitable for most of tissues.

The use of a strain gauge in assessment of the deformation of a piece of pig skin is shown in Fig. 5. The membrane adhered well to the skin and deformed with stretching of the skin (Fig. 5a). The red lines in Y direction (horizontal direction) were elongated, and conversely, the lines in X direction (vertical direction) were contracted and slimmed, agreeing with skin necking under deformation. Moreover, FFT analysis (Fig. 5b) revealed that there were three stages in the tensile process. In the first stage (0-5 s), no strain was observed, since the skin was still slack in this stage. In the second stage (5-40 s), the deformation of the strain gauge increased linearly, the slope of calculated strain was consistent with the strain detected by Instron. However, significant deformation was detected after 40 s from FFT analysis (the second stage, after 40s). The calculated strain value was almost the same as value in the range of 40-65 s. Examination of snapshots (Fig. 5a) confirmed our calculated strain tendency. In the dark red solid line region (first stage, 0-40 s), the pig skin was drawn with tiny slippage (the difference between white base line and bottom red line). In the dark red dashed line region (second stage, 40-65s), the whole strain gauge was shifted to the middle region with no elongation observed. At the end of the tensile test, the entire skin sample slipped from the grips and the deformation returned to 0, as what was measured by FFT analysis. Stress-time curves recorded by Instron (Fig. S6) further supported our FFT calculation with evidence that the stress climbed in 0-40 s, but sharply dropped in 40-65s. The calibrated stress-strain curves obtained from the tensile machine and FFT analysis are presented in Figure 5c, where FFT analysis showed a very different curve from the one given by the tensile machine. This was obtained from the calibrated curve where the secant modulus of the pig skin at ε_x=0.2 is measured to be 0.102 MPa, which is higher than that of Instron measurement (0.046 MPa). It is noted that the calibrated result was obtained at a strain rate at ~0.15 s⁻¹, and the modulus agrees with previous tensile tests of pig skin as the secant modulus at ε_x=0.2 was measured to be 0.06 and 0.115 MPa for loading rate of 0.005 s⁻¹ and 0.5 s⁻¹, respectively³⁴. The Poisson's ratio (Figure 5d) estimated from FFT analysis was around 0.5, suggesting it is more like an incompressible material such as rubber. All of these results demonstrated that the printed strain gauge is suitable for the detection of large deformations in biological tissues.

Conclusions

Using silk materials and our custom-built printer, we managed to accurately print different florescent silk patterns on silk membranes. These silk membranes can be stretched up to 1300% strain without fracture and are suitable for use as prototype strain gauges which have a strain range more than two orders of magnitude larger than conventional strain gauges. We demonstrate in our experiments that such a strain gauge can help to measure deformation by using 2D-FFT analysis and our measurements reflect actual material deformation by accounting for sliding at the boundaries. Our measurements can provide a more accurate description of strain in flexible materials subjected to large deformations.

By increasing the complexity of the analysis algorithm and incorporating computational models we expect our method can be extended to obtain more complex strain fields as well as nonlinear constitutive laws of polymeric materials by incorporating the measured strain distribution with real-time measurements from force sensors or Brillouin spectroscopy for stiffness.^35,36 Moreover, these silk strain gauges would offer biocompatibility, even with some caveats due to the Rhodamine, which could be facilely replaced by biologically safe dyes, such as green fluorescent protein or quantum dots. Thus these gauges have the potential for in-situ strain measurements of biological tissues, which might be used to characterize the biomechanical function of different biological tissues under different physiological conditions including disease states.^2,37,38 Such understanding would be crucial for designing proper materials and treatments for biomedical applications.