Protein–protein docking by fast generalized Fourier transforms on 5D rotational manifolds

Significance

Expressing the interaction energy as sum of correlation functions, fast Fourier transform (FFT) based methods speed the calculation, enabling the sampling of billions of putative protein–protein complex conformations. However, such acceleration is currently achieved only on a 3D subspace of the full 6D rotational/translational space, and the remaining dimensions must be sampled using conventional slow calculations. Here we present an algorithm that employs FFT-based sampling on the 5D rotational space, and only the 1D translations are sampled conventionally. The accuracy of the results is the same as those of earlier methods, but the calculation is an order of magnitude faster. Also, it is inexpensive computationally to add more correlation function terms to the scoring function compared with classical approaches.

Abstract

Energy evaluation using fast Fourier transforms (FFTs) enables sampling billions of putative complex structures and hence revolutionized rigid protein–protein docking. However, in current methods, efficient acceleration is achieved only in either the translational or the rotational subspace. Developing an efficient and accurate docking method that expands FFT-based sampling to five rotational coordinates is an extensively studied but still unsolved problem. The algorithm presented here retains the accuracy of earlier methods but yields at least 10-fold speedup. The improvement is due to two innovations. First, the search space is treated as the product manifold $\mathbf{S}\mathbf{O}\left(\mathbf{3}\right)\mathbf{\times }\left(\mathbf{S}\mathbf{O}\left(\mathbf{3}\right)\mathrm{\setminus }{\mathbf{S}}^{\mathbf{1}}\right)$, where $\mathbf{S}\mathbf{O}\left(\mathbf{3}\right)$ is the rotation group representing the space of the rotating ligand, and $\left(\mathbf{S}\mathbf{O}\left(\mathbf{3}\right)\mathrm{\setminus }{\mathbf{S}}^{\mathbf{1}}\right)$ is the space spanned by the two Euler angles that define the orientation of the vector from the center of the fixed receptor toward the center of the ligand. This representation enables the use of efficient FFT methods developed for $\mathbf{S}\mathbf{O}\left(\mathbf{3}\right)$. Second, we select the centers of highly populated clusters of docked structures, rather than the lowest energy conformations, as predictions of the complex, and hence there is no need for very high accuracy in energy evaluation. Therefore, it is sufficient to use a limited number of spherical basis functions in the Fourier space, which increases the efficiency of sampling while retaining the accuracy of docking results. A major advantage of the method is that, in contrast to classical approaches, increasing the number of correlation function terms is computationally inexpensive, which enables using complex energy functions for scoring.

Determining putative protein–protein interactions using genome-wide proteomics studies is a major step toward elucidating the molecular basis of cellular functions. Understanding the atomic details of these interactions, however, requires further biochemical and structural information. Although the most complete structural characterization is provided by X-ray crystallography, solving the structures of protein–protein complexes is frequently very difficult. Thus, it is desirable to develop computational docking methods that, starting from the coordinates of two unbound component molecules defined as receptor and ligand, respectively, are capable of providing a model of acceptable accuracy for the bound receptor–ligand complex (1–4). In view of the large number of putative protein–protein interactions, the computational efficiency of docking is also a concern.

Most global docking methods start with rigid body search that assumes only moderate conformational change upon the association, accounted for by using a smooth scoring function that allows for some level of steric overlaps (3). Rigid docking was revolutionized by the fast Fourier transform (FFT) correlation approach, introduced in 1992 by Katchalski-Katzir et al. (5). The major requirement of the method is to express the interaction energy in each receptor–ligand orientation as a sum of P correlation functions, i.e., in the form

$$E\left(\alpha ,\beta ,\gamma ,\lambda ,\mu ,\nu \right)={\displaystyle \sum _{p=1}^P{\displaystyle \int \overline{R_p\left(x,y,z\right)}\widehat{T}\left(\lambda ,\mu ,\nu \right)\widehat{D}\left(\alpha ,\beta ,\gamma \right)L_p\left(x,y,z\right)dV,}}$$ [1]

where $R_p$ and $L_p$ are defined on the receptor and ligand, respectively, $\widehat{T}$ and $\widehat{D}$ denote translational and rotational operators, and $\alpha ,\beta ,\gamma$ and $\lambda ,\mu ,\nu$ are the rotational and translational coordinates. To illustrate how such functions can be used for docking, consider the very simple case with $P=1$, $R_p=-1$ on a surface layer and $R_p=1$ on the core of the receptor, $L_p=1$ on the entire ligand, and $R_p=L_p=0$ everywhere else. It is clear that this scoring function, which is essentially the one used by Katchalski-Katzir et al. (5), reaches its minimum on a conformation in which the ligand maximally overlaps with the surface layer of the receptor, thus providing optimal shape complementarity. In later FFT-based methods, the scoring function has been expanded to include electrostatic and solvation terms (6, 7) and, more recently, structure-based interaction potentials (8, 9), substantially improving the accuracy of docked structures. As mentioned, in all scoring functions, the shape complementarity term allows for some overlaps, thereby accounting for the differences between bound and unbound (separately crystallized) structures.

Most FFT-based methods (6–8, 10–12) define $R_p$ and $L_p$ on grids, and use a 3D Cartesian FFT approach to accelerate the sampling of the translational space. The method is based on the idea that the energy function, given by Eq. 1, can be expressed in terms of the Fourier transforms $r_p$ of $R_p$ and $l_p$ of $L_p$. Because the translational operator applied to $l_p$ in the Fourier space is given by

$$T\left(\lambda ,\mu ,\nu \right)l_p\left(n,m,l\right)=e^{-2\pi i/N\left(n\lambda +l\mu +m\nu \right)}{l}_p\left(x,y,z\right),$$ [2]

where $i=\sqrt{-1}$, accounting for the orthonormality of Fourier basis functions and interchanging the order of integration and summation yield

$$E\left(\alpha ,\beta ,\gamma ,\lambda ,\mu ,\nu \right)={\displaystyle \sum _{p=1}^P{\displaystyle \sum _{nlm}\overline{r_p\left(n,l,m\right)}{l}_p\left(\alpha ,\beta ,\gamma ,n,l,m\right)e^{-\frac{2\pi i}{N}\left(n\lambda +l\mu +m\nu \right)},}}$$ [3]

which is the expression for the inverse Fourier transform of the product of the Fourier images $r_p\left(n,m,l\right)$ and $l_p\left(\alpha ,\beta ,\gamma ,n,l,m\right)$ as stated by the convolution theorem. Thus, for a given rotation, E can be calculated over the entire translational space using P forward and one inverse FFT. If N denotes the size of the grid in each direction, then the efficiency of this approach is $O\left(N^{3}log{N}^3\right)$ compared with $O\left(N^6\right)$ when energy evaluations are performed directly. Owing to the high numerical efficiency of the FFT-based algorithm, it became computationally feasible, for the first time, to systematically explore the conformational space of protein–protein complexes evaluating the energies for billions of conformations, and thus to dock proteins without any a priori information on the expected structure of their complex.

Despite the usefulness of the above algorithm, using FFTs only in translational space has three major limitations. First, FFTs on a new grid must be computed for each rotational increment of the rotating molecule; thus acceleration applies only to half of the degrees of freedom (Fig. 1). Second, each term in the scoring function requires a separate FFT calculation. Thus, accounting for electrostatics, desolvation, and, particularly, pairwise interactions substantially increases the required computational efforts. Third, experimental techniques such as NMR Nuclear Overhauser effect measurements and chemical cross-linking yield information on approximate distances between interacting residues across the interface, and this information can be used to perform the docking subject to pairwise distance restraints. Unfortunately, each pairwise distance restraint requires a new correlation function term. Because the required computational effort is proportional to P, the number of correlation functions in the energy expression, the increasing complexity reduces the numerical advantage of the FFT approach.

Fig. 1.

Schematic representation of FFT-based docking methods. In Cartesian FFT sampling (upper path), the ligand protein is translated along three Cartesian coordinates in Fourier space using the translational operator T. The translation must be repeated for each rotation of the ligand. In 5D FMFT docking (lower path), the direction of the vector from the center of the receptor to the center of the ligand is defined by two Euler angles, and the ligand is rotated around its center, resulting in the search space $\left(SO\left(3\right)\mathrm{\setminus }S\right)\times SO\left(3\right)$. All rotations are performed in generalized Fourier space, where D denotes the rotational operator. The only traditional search is the 1D translation along the vector between the centers of the two proteins.

In principle, the above problems can be avoided by applying the transforms first, and then moving the proteins in the Fourier space without the need for recomputing the transforms. However, it is difficult to carry out rotations in the translational Fourier space, and, thus, to perform rotations efficiently, it is natural to use spherical coordinates. This approach was applied to crystallography in the early 1970s by Tony Crowther, who realized that the rotation function can be computed more quickly using the FFT, expressing the Patterson maps as spherical harmonics (13). A few groups also used this idea for the development of docking algorithms (14, 15). Most notable is the Hex method of Ritchie and Kemp (14), which represents protein shapes using Fourier series expansions of spherical harmonic and Gauss–Laguerre polynomials. This representation allows rotational searches to be accelerated by angular FFTs, and it enables translations to be calculated analytically in the Fourier basis (15). A similar approach has been developed by Chacon’s group (16, 17), in which translations are calculated numerically. However, both approaches were found to have lower accuracy than traditional Cartesian FFT sampling (15). This may be attributed to three main factors. Firstly, the energy functions used were less detailed than in some of the Cartesian approaches. In particular, we used only van der Waals and electrostatic terms (15). Secondly, because the computational cost of the polar Fourier translation matrices grows as $O\left(N^5\right)$, the polar Fourier representation is limited to using relatively low order expansions, which limits the achievable accuracy. Finally, the manifold structure of the 5D rotational space was not fully considered, and this resulted in a memory-intensive algorithm that mapped less efficiently onto modern multiprocessor computer architectures than simple 1D FFTs (18). Although we showed previously that the polar representation allows an elegant 5D factorization of multiterm potentials (15), previous efforts to exploit this property have, until now, had limited success.

In this paper, we describe a fast manifold Fourier transform (FMFT) algorithm that eliminates the above shortcomings and, on the average, results in a 10-fold decrease in computing time while retaining the accuracy of the traditional Cartesian FFT-based docking. As will be further emphasized, even more important is that, using FMFT, the computational efforts required are essentially independent of the number of correlation function terms in the scoring function, thus enabling the efficient use of more accurate but also more complex energy expressions, as well as accounting for any number of pairwise distance restraints. Developing the method, we took advantage of the generalization of the Cartesian FFT approach to the rotational group manifold $SO\left(3\right)$ by Kostelec and Rockmore (19). The basis for using this algorithm was recognizing that the 5D rotational search space can be regarded as the product manifold $SO\left(3\right)\mathrm{\times }\left(SO\left(3\right)\mathrm{\setminus }{S}^1\right)$, where the rotation group $SO\left(3\right)$ represents the space of the rotating ligand and $\left(SO\left(3\right)\mathrm{\setminus }{S}^1\right)$ is the space spanned by the two Euler angles that define the orientation of the vector from the center of the fixed receptor to the center of the ligand (Fig. 1 and Fig. S1). This is important, because the algorithm by Kostelec and Rockmore (19) can be easily extended to the $SO\left(3\right)\times \left(SO\left(3\right)\mathrm{\setminus }{S}^1\right)$ manifold.

Fig. S1.

(A) Matching of a pair of patterns via rotation around two different points. The patterns can be regarded as printed on the surfaces of two rotatable spheres with centers coinciding with the points of rotation. (B) A pair of spherical coordinate systems that are used for representation of functions f and g describing the patterns to be superimposed.

As already mentioned, a general shortcoming of using Fourier decomposition in spherical spaces is the relatively slow convergence of the series of spherical basis functions. Thus, using a large number of terms reduces computational efficiency, whereas truncating the series limits the accuracy of the energy values calculated by the method. Therefore, a key factor explaining the success of our manifold FFT docking method is that we select the centers of highly populated clusters of low-energy docked structures rather than simply low-energy conformations as predictions of the complex. Such clusters occur in low-energy regions around the local minima in the conformational space. The size of each cluster represents the width of the corresponding energy well, and hence provides some information on entropic contributions to the free energy. Model selection based on cluster size has been used in our very successful docking server ClusPro and, in a substantial fraction of docking problems, enabled the identification of the docked structure closest to the native complex (20). We note that a similar clustering step is implemented in the protein structure prediction program Rosetta (21). For a somewhat more formal justification of the cluster-based approach to model selection, we argue that, using FFT, we globally and systematically sample the energy landscape of the interacting protein pair on a grid, and hence we can calculate an approximate partition function of the form $Z={\displaystyle {\sum }_{j}exp\left(-E_j/RT\right)}$, where $E_j$ is the energy of the jth pose, and we sum over all poses. For the kth low-energy cluster, the partition function is given by $Z_k={\displaystyle {\sum }_{j}exp\left(-E_j/RT\right)}$, where the sum is restricted to poses within the cluster. Based on these values, the probability of the kth cluster is given by $P_k=Z_k/Z$. However, because the low-energy structures are selected from a relatively narrow energy range, and the energy values are calculated with considerable error, it is reasonable to assume that these energies do not differ from each other, i.e., $E_j=E$ for all j in the low-energy clusters. This simplification implies that $P_k=exp\left(-E/RT\right)\times \left(N_k/Z\right)$, and thus the probability $P_k$ is proportional to $N_k$, where $N_k$ is the number of structures in the kth cluster. Therefore, we select the centers of highly populated clusters of docked structures, rather than low-energy conformations, as predictions of the complex. Although neglecting the energy differences within the low-energy clusters seems to be arbitrary, the success of the ClusPro server demonstrates that the approximation is valid in a large fraction of cases. The significance of model selection based on cluster size rather than energy values is that it does not require very accurate energy evaluation, and hence, in FMFT, it is sufficient to use a limited number of spherical basis functions in the Fourier space, increasing numerical efficiency without noticeable loss of docking accuracy.

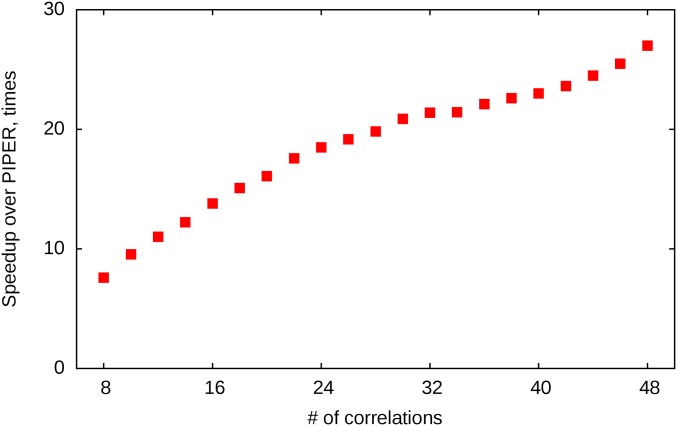
The high efficiency of the FMFT algorithm enables solving very demanding docking problems, way beyond what was considered feasible in the past. After demonstrating that the accuracy of FMFT is comparable to that of the traditional Cartesian FFT-based docking, we present here a few applications that require a large number of docking calculations. Such problems include docking ensembles of models obtained by NMR or homology modeling, and exploring a large number of putative peptide conformations in peptide–protein docking. As will be described, an additional and very favorable property of the FMFT algorithm is that the required computational efforts are almost completely independent of the number P of the correlation function terms in the energy expression given by Eq. 1, and hence the method can be efficiently used with scoring functions of arbitrary complexity. In contrast, in the traditional FFT approach, the efforts are proportional to P, and hence it is difficult to perform docking subject to pairwise distance restraints, as each restraint gives rise to an additional term in the scoring function. Using FMFT, we demonstrate that this problem can be solved effectively without significant increase in running times (Fig. S2).

Fig. S2.

Speedup of the FMFT appproach over PIPER as a function of the number of correlations. Although FMFT is generally faster than PIPER by an order of magnitude, the difference further increases with the increasing number of correlation terms, allowing for routine use of much more complex correlation-based energy functions. All execution times were measured on the E2A-HPr system and averaged over three runs. Additional correlation terms used were extra-repulsive van der Waals energy components, reweighted to provide a constant repulsive van der Waals contribution.

Results and Discussion

FFT-Based Docking on 5D Rotational Manifolds.

Here we demonstrate that, by taking advantage of the special geometry of the space characterizing molecular movement upon protein–protein association, it is possible to construct an extremely efficient FFT-based docking algorithm. We present the basic idea of this algorithm as the generalization of the translational FFT method described in the Introduction. Because we plan to work in the rotational space, we change the Cartesian coordinates to polar coordinates $\left(x,y,z\right)\to \left(r,\theta ,\varphi \right)$, and consider the generalization of the Fourier transform on the sphere

$$R\left(r,\theta ,\varphi \right)={\displaystyle \sum _{nlm}^{N}r\left(n,l,m\right)R_{nl}\left(r\right)d_{lm}\left(cos\theta \right)e^{-im\varphi }}$$ [4]

where $R_{nl}\left(r\right)$ are radial basis functions, $r\left(n,l,m\right)$ are generalized Fourier coefficients, $d_{lm}\left(cos\theta \right)$ are Legendre polynomials (22), and N is the order of expansion used. Eq. 4 looks like a Fourier transform, but $e^{-im\varphi }$ is replaced by $d_{lm}\left(cos\theta \right)e^{-im\varphi }$, which shows the non-Cartesian properties of the sphere (23).

Consider again the derivation of the convolution theorem (Eq. 1) but, this time, on the manifold $\left(SO\left(3\right)\mathrm{\setminus }S\right)\times SO\left(3\right)$ shown in the lower path of Fig. 1. The translation of the ligand can be represented as the rotation of the receptor, followed by the translation of the ligand along the z axis,

$$E\left(z,\beta ,\gamma ,\alpha \prime ,\beta \prime ,\gamma \prime \right)={\displaystyle \sum _{p=1}^P{\displaystyle \int \widehat{T}\left(-z\right)\widehat{D}\left(0,\beta ,\gamma \right)R_p\left(\rho ,\theta ,\varphi \right)\times \widehat{D}\left(\alpha \prime ,\beta \prime ,\gamma \prime \right)L_p\left(\rho ,\theta ,\varphi \right)dV}}.$$ [5]

Rotations of the receptor can be expressed as follows:

$$D\left(\alpha ,\beta ,\gamma \right)R\left(r,\theta ,\varphi \right)={\displaystyle \sum _{nlm}{R}_{nl}\left(r\right)Y_{lm}\left(\theta ,\varphi \right){\displaystyle \sum _{m_1}{D}_{m{m}_1}^l\left(\alpha ,\beta ,\gamma \right)r\left(n,l,m_1\right),}}$$ [6]

where $Y_{lm}\left(\theta ,\varphi \right)$ denotes spherical harmonics, and

$$D_{mm\prime }^l\left(\alpha ,\beta ,\gamma \right)=e^{-im\alpha }{d}_{mm\prime }^l\left(\beta \right)e^{-im\prime \gamma }$$ [7]

are Wigner rotation matrices with $d_{mm1}^l\left(\beta \right)$ denoting Wigner d functions, related to Jacobi polynomials (19). Eqs. 6 and 7 show that the rotational operator in the rotational group $SO\left(3\right)$ acts on generalized Fourier coefficients the same way as the translation operator acts on Fourier coefficients in the Cartesian space (Eq. 2), apart from the asymmetry of the middle angle β, which requires special treatment. Describing the translation of the ligand along the z axis in the Fourier space is far from simple, and requires updating a set of coefficients. However, it is only 1 degree of freedom (as opposed to 3 degrees in the Cartesian space), and hence it can be accomplished relatively efficiently (24). Now we apply the translation operator and the rotation operator (Eq. 7) to the integral in Eq. 5. Based on the orthonormality of the generalized Fourier basis functions, interchanging the order of integration and summation yields

$$\begin{array}{l}E\left(z,\beta ,-\gamma ,\alpha \prime ,\beta \prime ,\gamma \prime \right)=\\ ={\displaystyle \sum _{\stackrel{l{l}_1}{m{m}_1{m}_2}}\left({\displaystyle \sum _{n{n}_1}{\displaystyle \sum _p\overline{\hspace{0.17em}{r}_p\left(n_1,l_1,m_1\right)}{l}_p\left(n,l,m_2\right)T_{nl{n}_1{l}_1}^{\left|m\right|}\left(z\right)}}\right)\times d_{m{m}_1}^{l_1}\left(\beta \right)d_{m{m}_2}^l(\beta \prime )e^{-i\left(m\alpha \prime +m_1\gamma +m_2\gamma \prime \right)}}.\end{array}$$ [8]

Note that Eq. 8 is similar to Eq. 3 in Cartesian coordinates, with the difference that, instead of a 3D inverse Fourier transform, we have a generalized FMFT, which involves the Wigner d functions $d_{mm1}^l\left(\beta \right)$. However, the really important difference is in the order of the transforms and the summation of correlation functions. In Eq. 3, for each rotation of the ligand, we have to calculate the Fourier transforms $l_p\left(\alpha ,\beta ,\gamma ,n,l,m\right)$ for each of the P components of the ligand energy function separately, form the product with the transform $r_p\left(n,m,l\right)$ of the pth component of the receptor energy function, sum all terms, and take the inverse transform. In contrast, according to Eq. 8, we calculate the sum of initial precalculated generalized Fourier coefficients in the internal loop only once, and perform all rotations in Fourier space rather than calculating an FFT for each rotation. This allows us to calculate multiple energy terms using a single FMFT for each translation. Thus, as already emphasized, the computational efforts are essentially independent of the number P of the correlation function terms in the energy expression. Because inverse manifold Fourier transforms can be efficiently calculated by methods due to ref. 19, this approach provides substantial computational advantage, particularly if P is high.

Execution Times.

Execution times of the FMFT sampling algorithm were measured by docking unbound structures of component proteins in 51 enzyme–inhibitor pairs from the established Protein Docking Benchmark (25) (Table S1). The times were compared with those required for docking the same proteins using PIPER, a protein docking program based on the Cartesian FFT approach (8). The FFTW (Fastest Fourier Transform in the West) library (26) was used for FFT calculations. All runs were performed using the standard PIPER scoring function, consisting of eight correlation function terms. Execution times were measured on one or several Intel Xeon E5-2680 processors. Using the FMFT algorithm, the average execution time was 15.39 min. In comparison, the average execution time for the same set of proteins using PIPER was 232.15 min, indicating that FMFT speeds up the calculations ∼15-fold. Using parallel versions of the algorithms on 16 CPU cores, the average execution times measured were 2.67 min and 20.19 min for FMFT and PIPER, respectively, which shows about a 7.5-fold speedup.

Table S1.

Execution times (in minutes) for enzyme–inhibitor docking set (1BOYV excluded)

Complex	FMFT 1 core	PIPER 1 core	FMFT 16 cores	PIPER 16 cores
1acb	12.20	157.38	2.05	14.42
1avx	12.79	164.77	2.09	14.70
1ay7	10.99	74.50	1.62	5.99
1bvn	16.33	173.40	2.67	21.68
1cgi	12.81	121.18	2.01	10.47
1clv	16.51	119.63	3.50	10.00
1d6r	13.17	156.53	2.99	12.87
1dfj	21.82	274.47	2.64	25.72
1e6e	17.44	263.02	3.83	21.22
1eaw	13.44	105.32	2.33	9.84
1ewy	15.55	198.00	2.96	16.14
1ezu	18.41	343.48	3.34	28.63
1f34	18.89	334.80	3.38	26.67
1f6m	18.39	260.07	3.10	22.33
1fle	13.87	125.53	2.03	11.89
1fq1	15.45	803.63	2.93	25.67
1gl1	12.94	141.48	2.00	28.49
1gxd	22.42	479.30	4.23	43.49
1hia	14.52	134.32	2.75	11.44
1ijk	19.06	315.03	3.18	26.49
1jiw	16.79	226.43	3.54	30.13
1jtg	15.68	179.72	2.79	17.02
1kkl	18.58	259.15	3.76	22.56
1m10	18.15	414.60	3.14	51.70
1mah	16.70	541.47	2.95	17.08
1n8o	17.14	247.50	2.81	21.17
1nw9	16.21	167.52	2.86	33.74
1oc0	15.91	128.75	2.45	16.57
1oph	15.90	333.18	3.77	29.47
1oyv	14.69	306.47	2.17	24.81
1ppe	12.60	73.58	1.97	6.50
1pxv	12.78	249.45	2.14	20.81
1r0r	12.12	71.53	1.96	6.66
1tmq	15.21	269.40	3.39	24.83
1udi	13.91	137.22	2.21	13.56
1yvb	19.83	181.30	2.78	39.90
1zli	18.05	669.10	3.25	46.85
2abz	13.02	166.20	2.16	13.58
2b42	18.17	192.30	3.36	26.60
2j0t	13.94	144.35	2.01	13.94
2mta	15.18	209.27	2.67	18.73
2o3b	14.19	176.68	2.19	16.38
2o8v	14.29	148.28	2.05	13.66
2oul	15.89	494.57	2.85	17.63
2pcc	14.32	175.65	2.45	16.09
2sic	14.58	167.47	2.91	15.19
2sni	12.92	123.20	2.17	11.48
2uuy	14.23	108.97	1.99	9.43
3sgq	12.62	250.78	1.78	7.10
4cpa	12.96	132.55	2.16	26.43
7cei	11.18	147.08	1.91	11.97
Average	15.39	232.15	2.67	20.19

The table shows execution times for the FMFT algorithm and PIPER when applied to 51 enzyme–inhibitor pairs from the Protein Docking Benchmark version 4.0. All runs used the standard PIPER energy function consisting of eight correlation terms. Running times for both serial and parallel versions of the algorithms were measured on Intel Xeon E5-2680 processors.

Application 1: Constructing Enzyme–Inhibitor Complexes.

The quality of FMFT and PIPER results was determined by docking the same 51 enzyme–inhibitor pairs that we have used for comparing execution times (Table S2). In both cases, the scoring function was the same one normally used in PIPER for docking enzyme–inhibitor pairs, and it consisted of attractive and repulsive van der Waals, Coulombic electrostatics, generalized Born, and knowledge-based Decoys As the Reference State terms, the latter representing nonpolar solvation (27). The docking procedure for these cases was the one normally used by PIPER (20). First, the conformational space was sampled using either the FMFT or the PIPER protocol. After docking, the 1,000 lowest energy poses were retained and clustered using interface C_α rms deviation (RMSD) as the distance metrics with a fixed 9 Å clustering radius. The clusters were ranked according to cluster populations (i.e., number of poses in the cluster), and the centers of up to 30 largest clusters were reported as putative models of the complex (Table S2).

Table S2.

Docking results for enzyme–inhibitor docking set (1BOYV excluded)

Complex	FMFT				PIPER
	Hits	Top cluster	Cluster IRMSD	Cluster size	Hits	Top cluster	Cluster IRMSD	Cluster size
1ACB	251	2	8.15	130	180	1	7.04	127
1AVX	290	1	2.19	257	286	1	3.22	244
1AY7	32	7	7.62	32	81	3	5.96	85
1BVN	714	1	6.53	737	536	1	5.98	460
1CGI	377	1	1.84	208	235	2	9.25	173
1CLV	555	1	4.52	549	598	1	4.74	447
1D6R	21	—	—	—	15	18	8.10	17
1DFJ	170	2	2.10	162	122	2	3.76	116
1E6E	137	1	4.62	136	186	1	3.78	100
1EAW	221	2	6.65	131	248	2	5.80	132
1EWY	87	6	5.87	61	106	4	7.56	83
1EZU	11	—	—	—	30	8	2.77	27
1F34	25	7	6.70	38	24	13	5.84	26
1F6M	0	—	—	—	0	—	—	—
1FLE	373	1	5.20	287	292	2	5.32	194
1FQ1	0	—	—	—	0	—	—	—
1GL1	223	4	4.41	103	233	1	9.62	223
1GXD	0	—	—	—	10	12	9.68	23
1HIA	105	7	7.37	66	81	4	9.88	81
1IJK	13	17	7.20	13	32	10	1.87	32
1JIW	0	—	—	—	0	—	—	—
1JTG	278	1	3.38	278	127	1	3.78	127
1KKL	15	15	8.45	19	1	—	—	—
1M10	0	—	—	—	0	—	—	—
1MAH	40	9	2.65	39	83	2	7.08	84
1N8O	292	2	3.77	147	250	1	5.99	184
1NW9	40	13	8.55	32	42	11	9.70	36
1OC0	201	1	7.21	278	75	3	7.56	167
1OPH	0	—	—	—	36	8	8.69	33
1OYV	195	2	8.85	179	126	1	3.55	88
1PPE	957	1	3.40	958	743	1	2.25	611
1PXV	1	—	—	—	2	—	—	—
1R0R	81	2	4.51	73	65	4	1.59	65
1TMQ	98	2	3.27	98	48	7	3.20	47
1UDI	296	2	2.88	214	266	1	2.39	152
1YVB	30	7	4.75	36	165	3	3.87	109
1ZLI	0	—	—	—	0	—	—	—
2ABZ	5	—	—	—	15	19	5.44	15
2B42	199	1	4.25	198	143	2	5.16	101
2J0T	138	3	9.68	80	153	1	8.94	120
2MTA	14	13	6.50	18	127	3	5.73	111
2O3B	27	16	8.24	21	95	10	5.60	37
2O8V	0	—	—	—	30	13	5.54	30
2OUL	458	1	5.18	364	327	1	3.11	309
2PCC	100	10	8.06	33	115	6	5.81	78
2SIC	312	2	2.14	99	327	1	4.51	235
2SNI	464	1	3.27	348	288	1	4.11	183
2UUY	108	4	9.43	115	113	7	7.02	58
3SGQ	195	7	9.70	24	162	5	5.09	75
4CPA	45	7	3.68	31	101	6	2.76	52
7CEI	29	13	5.45	29	99	3	5.25	100

Comparison of enzyme–inhibitor docking results for FMFT and PIPER. The docking procedure consists of the sampling step yielding 1,000 low-energy poses and the following clustering step during which these 1,000 poses are clustered, and cluster centers are reported as final models ranked according to cluster populations. The columns are as follows: Hits, number of near-native solutions among the 1,000 lowest energy poses sampled by the algorithm; Top cluster, the rank of the near-native model (if any) obtained by clustering the sampled low-energy poses; Cluster IRMSD, C_α interface RMSD of this near-native model; and Cluster size, the population of the near-native cluster.

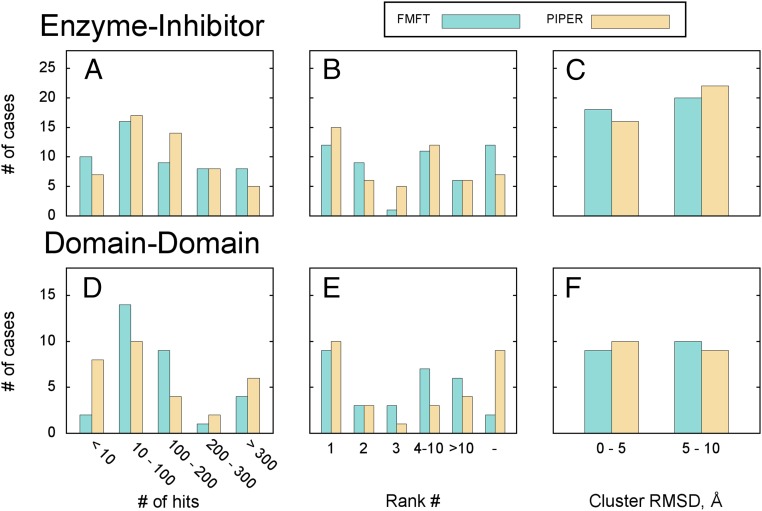
Fig. 2 A–C shows the results of docking. The number of hits shown in Fig. 2A is the number of near-native poses, defined as having less than 10 Å $C_{\alpha }$ interface RMSD (IRMSD) from the native complex, generated by each of the two algorithms. Note that IRMSD is calculated for the backbone atoms of the ligand that are within 10 Å of any receptor atom after superimposing the receptors in the X-ray and docked complex structures. We found that the number of poses with less than 10 Å IRMSD is a good measure of the quality of sampling of the energy landscape in the vicinity of the native structure. Fig. 2 B and C shows the properties of models obtained by clustering low-energy poses using pairwise IRMSD as a distance metric. A large number of low-energy poses typically yields a well-populated and thus highly ranked near-native cluster, reported as one of the final models. Based on all these results, FMFT and PIPER show comparable docking performance, both in terms of the number of near-native structures (Fig. 2A), the ranks of the clusters that define the final near-native models (Fig. 2B), and the IRMSD (Fig. 2C) of these models.

Fig. 2.

Results of docking enzyme–inhibitor and domain-domain pairs. Bar heights represent the number of docking cases that fall into an appropriate category. (A) The number of hits among the 1,000 low-energy poses generated for enzyme–inhibitor complexes. (B) Ranking of final near-native models for enzyme–inhibitor complexes. (C) $C_{\alpha }$ IRMSD of the final model for enzyme–inhibitor complexes (here only cases with both FMFT and PIPER producing a near-native model were taken into account). (D) The number of hits among the 1,500 low-energy poses generated for domain–domain complexes. (E) Ranking of final near-native models for domain–domain complexes. (F) $C_{\alpha }$ IRMSD of the final model for domain–domain complexes. As in C, only cases with both FMFT and PIPER producing a near-native model were taken into account.

Application 2: Docking Interacting Protein Domains.

We further compared FMFT and PIPER by docking interacting domains extracted from proteins that are defined as “Other” type in the Protein Docking Benchmark (25) (Tables S3 and S4). This problem is generally more challenging than docking inhibitors to enzymes because the Other category includes complexes with highly variable properties. Restricting consideration to individual domains eliminates the additional problem that the domains in multidomain proteins may shift relative to each other, affecting the docking results. Thirty cases representing domain–domain binding were selected from the Others section of the Protein Docking Benchmark (Table S4). Nineteen cases from this set represent binding of single-domain proteins (or single domains taken from larger proteins), and thus full protein structures were used for docking. In another 11 cases, receptor and/or ligand are composed of several domains, so reduced representations of protein structures were prepared: Only the binding domains were retained for docking, and the rest of the structure was cleaved. Residue ranges for binding domains were assigned according to structural classification of proteins (SCOP) domain classification (28). To prevent possible association at intraprotein domain–domain binding interfaces exposed by the cleavage, additional repulsion grids were used in the docking procedure. These were constructed by taking the backbone atoms of the original structure lying within 10 Å (but not closer than 5 Å) of the binding domain and placing repulsive spheres with 0.5-Å radius at the positions of those atoms. The 5-Å lower bound to the distance range specifying the thickness of this “repulsive padding” was introduced to ensure that additional repulsion doesn’t affect binding to the relevant portion of protein surface. During the docking process, such repulsive padding grid was correlated with the standard repulsive van der Waals grid of the binding partner. The docking procedure overall was the same as that used for enzyme–inhibitor targets, except that 1,500 low-energy poses were used for clustering, generated from three docking runs (500 poses from each) performed with differently weighted components of the scoring function (20). Similarly to the results obtained for enzyme–inhibitor complexes, FMFT and PIPER show comparable performance (Fig. 2 D–F and Table S3). Although PIPER generates large numbers (>200) of near-native structures for more complexes than FMFT, the number of complexes with very few (<10) such near-native structures is substantially smaller using FMFT than using PIPER. Thus, FMFT shows better performance for the more difficult-to-dock complexes (Fig. 2D). In addition, using PIPER, the number of models that are not ranked in the top 10 is much higher than using FMFT (Fig. 2E). Based on these results, FMFT performs as well as PIPER.

Table S3.

Docking results for domain–domain cases

Complex	FMFT				PIPER
	Hits	Top cluster	Cluster IRMSD	Cluster size	Hits	Top cluster	Cluster IRMSD	Cluster size
1A2K	196	2	4.75	135	167	1	4.38	125
1AK4	26	19	7.72	26	3	—	—	—
1AZS	106	1	6.15	105	128	2	6.52	130
1B6C	190	1	3.05	154	300	1	2.91	271
1BUH	63	7	7.9	64	21	27	9.48	15
1E96	106	3	8.19	83	93	5	4.85	54
1F51	15	15	7.7	31	0	—	—	—
1FFW	239	3	9.14	102	303	1	9.53	259
1GCQ	12	13	9.68	29	13	—	—	—
1GLA	74	6	8.63	67	119	1	8.54	197
1GPW	365	1	2.82	324	207	1	3.26	158
1H9D	0	—	—	—	4	19	9.78	21
1HE1	104	5	7.27	89	25	10	6.01	33
1J2J	131	1	7.32	166	144	1	8.32	142
1K74	497	1	2.86	477	380	1	3.14	330
1KAC	25	15	8.8	26	12	31	2.67	11
1PVH	19	7	9.36	47	0	—	—	—
1QA9	42	10	4.16	38	82	11	4.84	47
1WDW	171	1	2.01	149	340	1	6.59	190
1XD3	409	1	1.98	360	652	1	3.13	475
1XU1	92	6	7.71	92	0	—	—	—
1Z0K	37	2	9.74	92	72	2	9.92	108
1Z5Y	169	1	4.09	136	278	2	3.35	115
1ZHH	16	25	9.62	18	2	—	—	—
1ZHI	0	—	—	—	61	9	7.46	55
2A5T	32	2	6.92	77	1	—	—	—
2FJU	25	9	7.38	38	87	—	—	—
2HLE	102	3	8.37	90	91	3	8.41	100
2HQS	22	20	7.12	22	0	—	—	—
3D5S	720	1	4.36	586	425	1	3.93	349

The table shows a comparison of domain–domain docking results for FMFT and PIPER. Interacting domains were extracted from the Others section of the Protein Docking Benchmark. The docking procedure generally followed the one used for enzyme–inhibitor complexes, except that 1,500 low-energy poses were used for clustering, generated by three sampling runs, performed with differently weighted components of scoring function. From each run, the 500 lowest energy structures were retained for clustering. The columns are as follows: Hits, number of near-native solutions among the 1,500 lowest-energy poses sampled by the algorithm; Top cluster, the rank of the near-native model (if any) acquired by clustering the sampled low-energy poses; Cluster IRMSD, C_α interface RMSD of this near-native model; and Cluster size, the population of the near-native cluster.

Table S4.

Domains used for docking

Complex (original benchmark)	Unbound receptor			Unbound ligand
	PDB_CHAIN (original benchmark)	SCOP domain	Residues used	PDB_CHAIN (original benchmark)	SCOP domain	Residues used
Cleaved
1A2K_AB:C	1OUN_AB	d1ounb_	B	1QG4_A	d1qg4a_	A
1AZS_AB:C	1AB8_AB	d1ab8b_	B	1AZT_A	d1azta2	A:35–65, A:202–391
1F51_AB:E	1IXM_AB	d1ixma_	A	1SRR_C	d1srrc_	C
1GCQ_B:C	1GRI_B	d1grib2	B:157–217	1GCP_B	d1gcpa_	A
1GLA_G:F	1BU6_O	d1bu6o2	O:254–499	1F3Z_A	d1f3za_	A
1PVH_A:B	1BQU_A	d1bqua1	A:5–99	1EMR_A	d1emra_	A
1QA9_A:B	1HNF_	d1hnfa1	A:4–104	1CCZ_A	d1ccza1	A:1–93
1WDW_BD:A	1V8Z_AB	d1v8za1	A:1–386	1GEQ_A	d1geqa_	A
1XU1_ABD:T	1U5Y_ABD	d1u5yd_	D	1XUT_A(11)	d1xuta_	A
2FJU_B:A	2ZKM_X	d2zkmx3	X:11–141	1MH1_A	d1mh1a_	A
2HQS_A:H	1CRZ_A	d1crza1	A:141–409	1OAP_A	d1oapa_	A
Full
1AK4_A:D	2CPL_	d2cpla_	A	1E6J_P:11–147	d1e6jp2	P:11–147
1B6C_A:B	1D6O_A	d1d6oa_	A	1IAS_A	d1iasa_	A
1BUH_A:B	1HCL_	d1hcla_	A	1DKS_A	d1dksa_	A
1E96_A:B	1MH1_	d1mh1a_	A	1HH8_A	d1hh8a_	A
1FFW_A:B	3CHY_A	d3chya_	A	1FWP_A	d1fwpa_	A
1GPW_A:B	1THF_D	d1thfd_	D	1K9V_F	d1k9vf_	F
1H9D_A:B	1EAN_A	d1eana_	A	1ILF_A(1)	d1ilfa_	A
1HE1_C:A	1MH1_	d1mh1a_	A	1HE9_A	d1he9a_	A
1J2J_A:B	1O3Y_A	d1o3ya_	A	1OXZ_A	d1oxza_	A
1K74_AB:DE	1MZN_AB	d1mzna_	AB	1ZGY_AB	d1zgya1	AB
1KAC_A:B	1NOB_F	d1nobf_	F	1F5W_B	d1f5wb_	B
1XD3_A:B	1UCH	d1ucha_	A	1YJ1_A	d1yj1a1	A
1Z0K_A:B	2BME_A	d2bmea1	A	1YZM_A	d1yzma1	A
1Z5Y_D:E	1L6P	d1l6pa_	A	2B1K_A	—	A
1ZHH_A:B	1JX6_A	d1jx6a_	A	2HJE_A	d2hjea1	A
1ZHI_A:B	1M4Z_A	d1m4za_	A	1Z1A_A	d1z1aa1	A
2A5T_A:B	1Y20_A	d1y20a1	A	2A5S_A	d2a5sa1	A
2HLE_A:B	2BBA_A	d2bbaa1	A	1IKO_P	d1ikop_	P
3D5S_A:C	1C3D_A	d1c3da_	A	2GOM_A	d2goma1	A

The table provides a list of structures used for docking of protein domains. All domain–domain pairs were selected from the Others section of the Protein Docking Benchmark. Nineteen complexes originally required docking of single-domain proteins (or single domains of larger proteins), and thus full structures of the unbound component proteins were used as they appear in the benchmark, indicated as “full” in the table. Another 11 complexes represent binding of multidomain proteins, so reduced representations of the structures were prepared. Because only the interacting domains were retained and the rest of the structure was removed, these complexes are indicated as “cleaved” in the table. The columns are as follows: Complex, PDB entry and chains of the complex as they appear in the Protein Docking Benchmark; PDB_CHAIN, PDB entry and chain of the unbound receptor and ligand as they appear in the Protein Docking Benchmark; SCOP domain, name of the interacting domain in the SCOP database that was used for docking; and Residues used, chains and residue ranges of the unbound structures used for docking as specified in the SCOP database for the given domain.

Application 3: Accounting for Pairwise Distance Restraints.

An important consideration for selecting a docking method is the maximum complexity of the scoring function that still allows for solving problems with reasonable execution times. As mentioned, all FFT-based approaches require the use of scoring functions that can be written as sums of correlation functions. This is not a major limitation, because such functions may include many commonly used physics-based energy terms, such as steric repulsion, van der Waals interaction, and Coulombic electrostatics. It has also been shown that some energy terms that are not inherently correlation-based, such as the widely used pairwise interaction potentials, can be efficiently approximated by a sum of several correlation functions (27). Altogether, this makes the number of correlations a crucial parameter, because this number effectively defines the complexity of the scoring function in the particular sampling run.

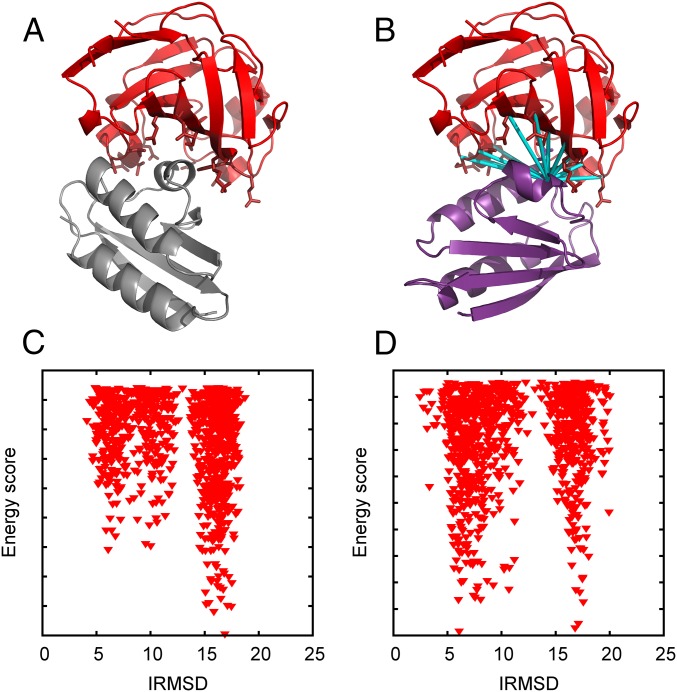
One important task, especially demanding in terms of scoring function complexity, is incorporating pairwise distance restraints, based on known interactions between residue pairs, into the docking procedure. Such restraints can be derived in a variety of experiments, including NMR, cross-linking, and mutagenesis assays (29). The restraints can be implemented as short-distance attractive terms in the scoring function, but each will add a correlation function term. As emphasized, in Cartesian FFT, the number of transforms required is proportional to the number P of correlation functions (Eq. 3), whereas, in FMFT, the number of transforms is independent of P. To demonstrate this difference, we determined the structure of the glucose-specific enzyme IIA (E2A)-histidine-containing phosphocarrier protein (HPr) complex [Protein Data Bank (PDB) entry 1GGR] (30) from the structures of its constituents in their unbound form (PDB entries 1F3G and 1POH) and 20 ambiguous interaction restraints (AIRs) based on NMR titration data (29). The docking procedure was the one used for docking enzyme–inhibitor pairs, but with 20 additional correlations terms in the scoring function due to the restraints (29). Each restraint is specified as a residue in one of the proteins, and a set of residues on the partner protein that are in contact with the first residue, where “contact” means ≤3 Å distance between any two atoms of the residue pair. To represent these restraints, receptor and ligand correlation components were constructed by placing 3-Å radius attractive spheres on the atoms of the particular residue on the first protein and the attracted point “charges” on the atoms of the interacting residues on the partner protein. Docking was performed using both FMFT and PIPER. Incorporation of restraints increased the population of the near-native cluster from 201 to 410, which became the most populated cluster and thus provided the putative model of the complex (Fig. 3 and Table S5) without any significant change in the IRMSD of the cluster center (5.25 Å for the unrestrained case versus 5.15 Å for the restrained). Adding the restraints increased the number of correlation function terms in the scoring function from 8 to 28. For PIPER, this resulted in a proportional increase in execution time (from 96.15 min to 373.80 min). In contrast, running FMFT, the execution time barely changed, from 12.32 min to 15.30 min. This result demonstrates that FMFT can be used with very complex scoring functions (Fig. S2).

Fig. 3.

Docking of E2A and HPr proteins. (A) Model defined by the most populated cluster obtained without restraints. (B) Model defined by the most populated cluster obtained with restraints. A set of cyan cylinders represents one of the 20 restraints. (C) IRMSD versus energy score for docking without restraints. (D) IRMSD versus energy score for docking with restraints. Incorporation of experimental restraints substantially increased the population of the near-native cluster.

Table S5.

Restrained docking results for E2A-HPr complex

Restraints	Cluster rank	Cluster IRMSD	Cluster population	No. correlations	Execution time, min
					FMFT	PIPER
No restraints	2	5.25	201	8	12.32	96.15
With restraints	1	5.15	410	28	15.30	373.80

Results for docking HPr to the E2A protein using the FMFT algorithm with and without AIRs (Application 3). Use of experimental restraints significantly increased the population of the native cluster, bringing it to the top rank. Although accounting for the restraints increased the number of correlation terms from 8 to 28 in the scoring function, the execution time remained almost unchanged when using the FMFT algorithm, whereas it increased almost proportionally with the number of correlation function terms when using the Cartesian FFT method PIPER. In the table, Cluster rank shows the rank of the near-native model, assigned according to cluster population. Cluster IRMSD is the interface C_α RMSD of this near-native model. Cluster population is the number of poses in the cluster. No. correlations is the number of components in the correlation-based energy function.

Application 4: Docking Ensembles of NMR Models.

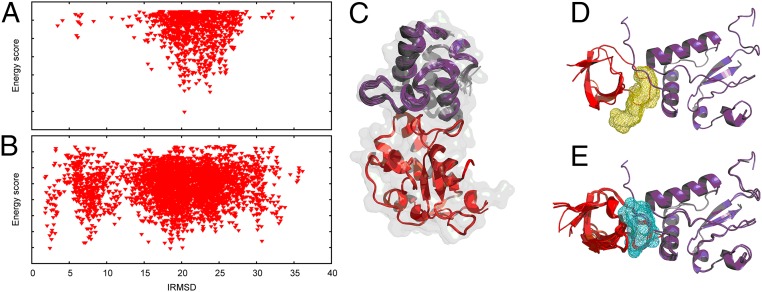
Multiple docking runs may be required when one or both component proteins are given as ensembles of structures, obtained by NMR experiments or by extracting snapshots from molecular dynamics simulations. Because accounting for multiple structures may substantially improve docking results, the high efficiency of the FMFT method is particularly useful. As an example, we considered calculating the complex formed by the Escherichia coli Colicin E9 DNase domain and its cognate immunity protein IM9. Four different X-ray structures of the unbound E9 DNase domain (chains B, C, D, and E of PDB entry 1FSJ) were docked in a pairwise manner to 20 NMR models of the IM9 protein (PDB entry 1E0H), thus performing 80 docking calculations. Unstructured termini of the receptor were masked and didn’t contribute to the calculated energy scores. The 50 lowest energy poses were extracted from each of the 80 docking runs and merged, yielding a total of 4,000 poses that were then clustered as usual in PIPER. Fig. 4 A–C shows the docking results. In short, merging the 50 lowest energy poses from each docking run, followed by clustering, provided a 2.94-Å IRMSD model of the complex ranked fifth, where the 1IBX structure of the native complex was used for comparison when evaluating the accuracy of results. To emphasize the advantage of ensemble docking, we also docked a single pair of structures, chain B of 1FSJ and the first NMR model of the ligand from the PDB file 1E0H. The standard docking protocol was used, and we retained the 1,000 lowest energy poses for clustering. Docking the single pair, the best near-native model obtained was ranked 13, and had the IRMSD value of 3.45 Å. Thus, in the case of structural uncertainty of the component proteins, ensemble docking can substantially improve the results, and, in this type of application, the higher speed of FMFT is a major advantage. Computational efficiency will be particularly important for genome-wide analyses of protein–protein interactions, but we think that, for such applications, it will be necessary to better understand the docking of homology models (see Application 5: Identification of Binding Sites by Docking Homology Models), because, generally, structures are not available for a substantial fraction of proteins.

Fig. 4.

Docking of structural ensembles. (A) Sampling the interaction energy landscape using a single E9 DNase domain structure and the first NMR model of IM9. The docking does not capture any near-native energy minimum. (B) Consensus energy values from the 80 pairwise dockings of four different X-ray structures of the E9 DNase domain to 20 NMR models of the IM9 protein. (C) Cartoon representation of the four E9 DNase domain and 20 IM9 structures used for docking, superimposed on the structure of the native complex (gray shade). (D) Binding site identification for the Nef–Fyn(R96I)SH3 complex obtained by docking the highest sequence identity models alone. (E) Using multiple homology models of the receptor and the ligand to identify the binding site for the Nef–Fyn(R96I) SH3 complex results in a more specific prediction.

Application 5: Identification of Binding Sites by Docking Homology Models.

It has been shown that protein–protein interaction sites can be found by determining the highly populated interfaces in the ensemble of structures generated by global docking (31, 32). We implemented this approach by clustering the “interfacial” atoms in the low-energy docked poses. Although this method usually requires structures of the component proteins, we extended the approach to proteins with yet undetermined structures by docking multiple homology models. The extended method was applied to determining the interface in the Nef–Fyn(R96I)SH3 complex (PDB entry 1EFN). Ten models of the receptor (SH3 domain) and 2 models of the ligand (HIV-1 Nef protein) were constructed using the MODELLER program (33) and based on homologous templates with 30–60% sequence identity (see Table S6 for the list of templates used). All possible receptor–ligand model pairs were docked using the approach developed for Other type of complexes (20). From each of the 20 docking runs, we selected the 1,500/20 = 75 lowest energy poses that were merged and clustered using RMSD as the distance metrics. The structures at the centers of these clusters were used to define interface atoms as atoms located within 5 Å of any atom of the partner protein. These interfacial atoms were then subjected to bottom-up hierarchial clustering using the Euclidian distance as the metrics. Clustering was terminated, i.e., neighboring clusters were not merged, if the minimal distance between a pair of their atoms was larger than the value of a separation parameter. The resulting clusters were ranked according to cluster population (i.e., the number of atoms in each cluster), and the largest cluster was considered to be the most probable prediction of the protein–protein interaction site. For comparison, we also predicted the interaction site by docking a single pair of homology models based on the templates with the highest sequence identity. In this case, a slightly larger value of the clustering separation parameter was used (1.35 Å rather than 1.30 Å). This change was due to the fact that a single docking run provided fewer interfacial atoms for hierarchical clustering, resulting in clusters that were too small. Therefore, the value of the cutoff parameter was increased to ensure that the relative population of the largest cluster was comparable to that obtained by merging the results from 20 docking runs. As shown in Fig. 4 D and E, docking of multiple homology models of the component proteins increased the accuracy of binding site prediction, compared with the result of using the maximum sequence identity models alone.

Table S6.

Structures used for homology modeling of Nef–Fyn(R96I) SH3 complex constituents

Homolog PDB	Identical, %	Positive, %
Fyn SH3 domain
1lck	50.9	70.2
1x27	50.9	70.2
2iim	50.9	70.2
4d8k	50.9	70.2
4j9b	46.6	67.2
4j9f	46.6	65.5
4j9g	46.6	65.5
4j9h	46.6	65.5
4j9i	46.6	65.5
2vkn	42.9	58.7
Nef protein
3ik5	47.3	61.1
3ioz	47.3	61.1

Homolog PDB specifies the PDB entry of the template structure used for homology modeling of the binding partners. Identical indicates the sequence identity of target and template sequences. Positive shows the level of similarity between the targets and the templates using Blosum62 as the measure of similarity. Models based on highest sequence identity homologs 1lck and 3ik5 were used for one-to-one docking.

Application 6: Docking Flexible Peptides.

The difficulty in docking short linear peptides is that their structure in solution is generally unknown and may be ill-defined. One possible solution is to dock a variety of peptide conformations, thus requiring multiple docking runs. We have recently developed an algorithm based on the use of structural templates extracted from the PDB with sequences that matched the known sequence motif in the peptide. These templates were docked individually using the FMFT algorithm. From each run, a number of low-energy poses were retained, the pooled peptide structures were clustered, and the highly populated cluster centers were reported as final models as in all applications of our docking algorithm.

Here we demonstrate this algorithm by docking the ace-PQQATDD peptide to the tumor necrosis factor receptor-associated factor 2 (TRAF2). For this peptide, the PXQ motif sequence known from the literature was extended to length 7 (PXQXXDD) and used to extract 316 structural templates from the PDB database. These templates were then used to model the target peptide. The models were aligned and clustered using the backbone RMSD as the distance measure, with 0.5 Å as the fixed clustering radius. Peptide structures corresponding to the centers of the 25 most-populated clusters were docked to the unbound receptor structure (chain A of PDB entry 1CA4).

The 250 lowest energy poses were retained from each docking run. The poses were merged and clustered using backbone RMSD as a distance measure with 3.5 Å as the fixed clustering radius. Cluster centers were ranked according to cluster populations and reported as final models. Docking results were evaluated using the backbone RMSD from the structure of the peptide in the native complex (chain A of PDB entry 1CZY). A near-native model of the protein–peptide complex was ranked fourth and had the backbone RMSD of 3.3 Å from the conformation in the X-ray structure (Table S7 and Fig. 5A). Note that docking only the most frequently occurring structural template provides less accurate models, as demonstrated in Fig. 5 B and C.

Table S7.

Peptide docking results

Rank	Backbone RMSD
1	21.40
2	26.82
3	24.74
4	3.30
5	16.96
6	25.63
7	15.84
8	9.21
9	24.28
10	18.10

The table shows the backbone RMSDs for 10 top-ranked models of the complex of TRAF2 and ace-PQQATDD peptide.

Fig. 5.

Docking of the ace-PQQATDD peptide to TRAF2. (A) Bound structure of the peptide (red) and the 3.3-Å model, ranked fourth (cyan). (B) Peptide backbone RMSD versus scoring function when docking the most common structural template alone. (C) Peptide backbone RMSD versus scoring function when using all 25 templates. Docking the ensemble substantially improves the results, and yields samples with less than 4.0-Å backbone RMSD.

Conclusions

Extending the classical 3D Cartesian implementation of the FFT correlation approach to perform rotations in Fourier space without the need for recalculating the transforms has been a long-outstanding and extensively studied problem. The main difficulty in developing such methods is that, to achieve numerical efficiency, one can use only a moderate number of spherical basis functions to span the search space, and this may reduce the accuracy of energy evaluation. However, because we base model selection on the population of low-energy clusters rather than on energy values, minor deviations in energy generally do not affect the accuracy of final models. Here we present an elegant manifold FFT implementation of 5D search that is more than 10-fold faster than the traditional 3D approach. A major advantage of the method is that adding correlation function terms in the scoring function is computationally inexpensive, and hence the method works efficiently with very complex energy evaluation models, possibly including pairwise distance restraints that are difficult to deal with in traditional FFT-based docking. The improved efficiency implies that we can solve new classes of docking problems, including the docking of large ensembles of proteins rather than just a single protein pair, docking homology models, and flexible peptides that may have a large number of potential conformations. We note that the beta version of a code implementing the FMFT algorithm can be downloaded from https://bitbucket.org/abcgroup_midas/fmft_dock/, thus providing an opportunity for testing and using the method. In addition, we are in the process of adding FMFT as a new option to the server.

Materials and Methods

This section summarizes the implementation of the FMFT approach. For the mathematical details of the algorithm, see SI Materials and Methods.

The procedure starts with receptor- and ligand-associated components of each correlation term of the energy function being represented as sets of coefficients $r\left(n,l,m\right)$, $l\left(n,l,m\right)$ that appear in the expansion shown as Eq. 4. Here $1\le n\le N$, $0\le l\le n-1$, and $-l\le m\le +l$, where N governs the order at which the series is truncated. These coefficients, together with the translation range to be sampled (i.e., minimal and maximal distances between protein centers, calculated from the geometrical properties of the proteins), are submitted as input parameters to the program performing the FMFT-based sampling. To improve efficiency, two stages of FMFT sampling are being executed: The first one, performed with a maximal coefficient order $N=20$ on a small FFT grid, is computationally inexpensive and provides a crude approximation of the energy landscape, which is then used to focus the search to the translation range potentially containing the energy minima, whereas the second one is executed with $N=30$ on a full-sized FFT grid but performs the sampling only in the refined translation range, thus saving computational resources.

The actual sampling stage can be described as follows: After loading the input parameters, the program starts to iterate the allowed translation range in steps of 1 Å. For each translation step, the ${\displaystyle {\sum }_{n{n}_1}{\displaystyle {\sum }_p{r}_p}\left(n_1,l_1,m_1\right)l_p\left(n,l,m_2\right)T_{nl{n}_1{l}_1}^{\left|m\right|}\left(z\right)}$ product of coefficients and translation matrix elements is calculated, followed by a manifold FFT, which provides the values of energy score for all receptor–ligand orientations corresponding to a fixed distance between the centers of the two proteins. The resulting samples are located on the $\left(\beta ,\gamma ,\alpha \prime ,\beta \prime ,\gamma \prime \right)$ Euler angle grid with dimensions of 30 × 59 × 59 × 30 × 59 (or 16 × 30 × 30 × 16 × 30 for the low-order scan). K (on the order of 1,000 for a typical sampling run) lowest energy samples are retained for each translation step. After the entire translation range is processed, the low-energy samples from individual translation steps are merged and resorted by energy value to select the K lowest energy samples that are presented as the final results.

It is important to note here that the sampling of the $S^2\times SO\left(3\right)$ manifold [in practice probed as $\left(SO\left(3\right)\mathrm{\setminus }{S}^1\right)\times SO\left(3\right)$], provided by the equispaced sampling of Euler angles, is inherently nonuniform. This becomes a significant problem if one seeks to obtain statistical information about the energy landscape of protein interaction, for example, to construct the partition function of the system. To battle this nonuniformity, a special procedure is used for the selection of low-energy scores. Specifically, once the 5D array of energy scores for a single translation step is acquired, the program starts selecting lowest-scoring conformations and excluding the samples corresponding to the surrounding region from further consideration. Here the “surrounding region” is defined as the subset of elements $\left\{\left(x,y\right)|x\left(\beta ,\gamma \right)\subset S^2,y\left(\beta ,\gamma ,\alpha \prime ,\beta \prime ,\gamma \prime \right)\subset SO\left(3\right)\right\}$ of the $S^2\times SO\left(3\right)$ manifold, for which $\left(dis{t}_{S^2}\left(x,x_{min}\right)<\mathit{\Delta }\right)\wedge \left(dis{t}_{SO\left(3\right)}\left(y,y_{min}\right)<\mathit{\Delta }\right)$, where $\mathit{\Delta }$ is a cutoff parameter chosen to be 6.0°, which is slightly less than the grid step of $360°/59=6.1°$. This procedure ensures that the sampling explores a substantial fraction of the conformational space rather than producing structures very close to each other.

SI Materials and Methods

FFT-Based Sampling on Manifolds.

The FMFT basis set.

As stated by the Peter–Weyl theorem, a complete set of Wigner D functions $D_{mm1}^l\left(\alpha ,\beta ,\gamma \right)$ forms a basis in the space of square integrable functions defined on the rotation group $SO\left(3\right)$. As a direct consequence, for the functions defined on the $\left(SO\left(3\right)\mathrm{\setminus }{S}^1\right)\times SO\left(3\right)$ manifold [i.e., a direct product of a rotation group and its 2D subspace $SO\left(3\right)\mathrm{\setminus }{S}^1$ sampled by Euler angles β and γ with α set to zero], the basis can be specified as the following collection of Wigner function products:

$$\overline{D_{m{m}_1}^l\left(0,\beta ,\gamma \right)}\hspace{0.17em}{D}_{m{m}_2}^{l_1}\left(\alpha \prime ,\beta \prime ,\gamma \prime \right).$$ [S1]

Here the fact that both D functions have the same index m accounts for the lacking degree of freedom associated with the α angle.

A function $f\in L^2\left(\left(SO\left(3\right)\mathrm{\setminus }{S}^1\right)\times SO\left(3\right)\right)$ can be written as the following expansion in terms of basis elements given by [S1]:

$$\begin{array}{l}f\left(\beta ,\gamma ,\alpha \prime ,\beta \prime ,\gamma \prime \right)=\\ ={\displaystyle \sum _{\stackrel{l{l}_1}{m{m}_1{m}_2}}f\left(l,l_1,m,m_1,m_2\right)\overline{D_{m{m}_1}^l\left(0,\beta ,\gamma \right)}\hspace{0.17em}{D}_{m{m}_2}^{l_1}\left(\alpha \prime ,\beta \prime ,\gamma \prime \right)}.\end{array}$$ [S2]

We refer to this expansion as the manifold Fourier expansion, and note that it specifies an inverse Fourier transform on the $\left(SO\left(3\right)\mathrm{\setminus }{S}^1\right)\times SO\left(3\right)$ manifold.

Correlations on $\left(\mathbf{S}\mathbf{O}\left(\mathbf{3}\right)\mathrm{\setminus }{\mathbf{S}}^{\mathbf{1}}\right)\times \mathbf{S}\mathbf{O}\left(\mathbf{3}\right)$.

Consider the problem of matching a pair of 3D patterns, each defined as a function on $S^2\times R$ (or, equivalently, $R^3$) (Fig. S1). We assume that the only transformation allowed for each function is the rotation around a certain point in space, and these points are different for the two functions. Here, by “matching,” we mean finding a combination of rotations that brings the patterns into alignment (i.e., maximizes the overlap). Such patterns can be regarded as printed on the surfaces of two spheres (Fig. S1A) that need to be rotated to achieve superimposition.

If the patterns are defined as real-valued density functions f and g, $f,g\in L^2\left(S^2\times R\right)$, and $\tilde{f},\tilde{g}$ denote the properly rotated functions that result in superimposing the two patterns, i.e., $\tilde{f}=\widehat{D}\left(\chi \right)f$, $\chi \in \left(SO\left(3\right)\mathrm{\setminus }{S}^1\right)$, $\tilde{g}=\widehat{D}\left(\omega \right)g$, and $\omega \in SO\left(3\right)$, then the whole problem can be reformulated as finding the maximum of a correlation function,

$$E\left(\psi =\left(\chi ,\omega \right)\right)={\displaystyle \underset{S^2\times R}{\int }\overline{\widehat{D}\left(\chi \right)f\left(y\left(x\right)\right)}\hspace{0.17em}\widehat{D}\left(\omega \right)g\left(x\right)dx,}\psi =\left(\chi ,\omega \right)\in SO\left(3\right)\mathrm{\setminus }{S}^1\times SO\left(3\right).$$ [S3]

In this expression, $f\left(y\right)$ and $g\left(x\right)$ are representations of f and g in two different spherical coordinate systems $\left(O_y,y\right)$ and $\left(O_x,x\right)$ with origins $O_y$ and $O_x$ coinciding with centers of rotation (Fig. S1B). $D\left(\chi \right)$ and $D\left(\omega \right)$, therefore, apply rotation around the origins of appropriate coordinate systems. Obviously, to perform the integration, we need both functions to be expressed in the same coordinate system. We will address this problem later by acquiring an explicit representation of $\widehat{D}\left(\chi \right)f$ in the $\left(O_x,x\right)$ coordinate system using its known representation in $\left(O_y,y\right)$.

Important for this work is that correlation function [S3] is defined on the $SO\left(3\right)\mathrm{\setminus }{S}^1\times SO\left(3\right)$ manifold. In the portion of the text that follows, we demonstrate that this correlation function can be efficiently expressed in terms of a manifold Fourier transform [S2], which allows significant acceleration of the search for the optimal $\psi =\left(\chi ,\omega \right)$ element.

As a first step, we recognize that, because both f and g are defined on $S^2\times R$, they can be rewritten in the form of generalized Fourier expansions,

$$\begin{array}{r}f\left(y=\left(r\prime ,s\prime \right)\right)={\displaystyle \sum _{n=1}^N{\displaystyle \sum _{l=0}^{n-1}{\displaystyle \sum _{m=-l}^{l}f\left(n,l,m\right)R_{nl}(r\prime )Y_{lm}(s\prime )}}}\\ g\left(x=\left(r,s\right)\right)={\displaystyle \sum _{n=1}^N{\displaystyle \sum _{l=0}^{n-1}{\displaystyle \sum _{m=-l}^{l}g\left(n,l,m\right)R_{nl}\left(r\right)Y_{lm}\left(s\right)}}}.\end{array}$$ [S4]

Here $Y_{lm}\left(s\right)$ and $R_{nl}\left(r\right)$ are spherical and radial harmonics, respectively, and we denote the spherical coordinates as $x=\left(r,s\right)$ and $y=\left(r\prime ,s\prime \right)$, where $s=\left(\theta ,\varphi \right)$, $s\prime =\left(\theta \prime ,\mathit{\varphi }\prime \right)$ are the elements of the $S^2$ sphere and r, $r\prime$ are the distances from the origin of the coordinate system. Following ref. 15, we use Gaussian-type orbitals as radial harmonics in this work. We also note that, here, we assume f and g to be band-limited functions in the selected basis set, which means that $f\left(n,l,m\right)=g\left(n,l,m\right)=0$ for $n>N$. If this is not true, expressions [S4] become approximate when finite N is used.

Next, we substitute [S4] into [S3] and take advantage of the linearity of rotation operators $\widehat{D}\left(\chi \right)$ and $\widehat{D}\left(\omega \right)$,

$$E\left(\psi =\left(\chi ,\omega \right)\right)={\displaystyle \underset{S^2\times R}{\int }\overline{\widehat{D}\left(\chi \right){\displaystyle \sum _{n_1{l}_1{m}_1}f\left(n_1,l_1,m_1\right)R_{n_1{l}_1}(r\prime )Y_{l_1{m}_1}(s\prime )}}}\times \widehat{D}\left(\omega \right){\displaystyle \sum _{nl{m}_2}g\left(n,l,m_2\right)R_{nl}\left(r\right)Y_{l{m}_2}\left(s\right)dx=}{\displaystyle \underset{S^2\times R}{\int }\overline{{\displaystyle \sum _{n_1{l}_1{m}_1}f\left(n_1,l_1,m_1\right)R_{n_1{l}_1}(r\prime )\widehat{D}\left(\chi \right)Y_{l_1{m}_1}(s\prime )}}}\times {\displaystyle \sum _{nl{m}_2}g\left(n,l,m_2\right)R_{nl}\left(r\right)\widehat{D}\left(\omega \right)Y_{l{m}_2}\left(s\right)dx}.$$ [S5]

Next, we capitalize on the rotational properties of spherical harmonics. More precisely, we use the fact that a rotated spherical harmonic can be expressed as linear combination of spherical harmonics of the same order,

$$\widehat{D}\left(\omega \right)Y_{lm}\left(s\right)={\displaystyle \sum _{|m\prime |\le l}{D}_{m\prime m}^l\left(\omega \right)Y_{lm\prime }\left(s\right)}.$$ [S6]

The weighting coefficients $D_{m\prime m}^l\left(\omega \right)$ here are elements of Wigner rotation matrices. Subsituting this into [S5] and changing the order of summation, we obtain the following relation:

$$\begin{array}{l}E\left(\psi =\left(\chi ,\omega \right)\right)\\ ={\displaystyle \int \overline{{\displaystyle \sum _{n_1{l}_1{m}_1}f\left(n_1,l_1,m_1\right)R_{n_1{l}_1}(r\prime ){\displaystyle \sum _m{D}_{m{m}_1}^{l_1}\left(\chi \right)Y_{l_{1}m}(s\prime )}}}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\times {\displaystyle \sum _{nl{m}_2}g\left(n,l,m_2\right)R_{nl}\left(r\right){\displaystyle \sum _{m\prime }{D}_{m\prime m_2}^l\left(\omega \right)Y_{lm\prime }\left(s\right)dx}}\\ ={\displaystyle \int \overline{{\displaystyle \sum _{n_1{l}_1{m}_1}{\displaystyle \sum _{m}f\left(n_1,l_1,m_1\right)D_{m{m}_1}^{l_1}\left(\chi \right)R_{n_1{l}_1}(r\prime )Y_{l_{1}m}(s\prime )}}}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\times {\displaystyle \sum _{nl{m}_2}{\displaystyle \sum _{m\prime }g\left(n,l,m_2\right)D_{m\prime m_2}^l\left(\omega \right)R_{nl}\left(r\right)Y_{lm\prime }\left(s\right)dx}}.\end{array}$$ [S7]

At this point, we perform a change of coordinates, which we discussed previously: $y=y\left(x\right)=\left(r\prime \left(x\right),s\prime \left(x\right)\right)=\left(r\prime \left(r,s\right),s\prime \left(r,s\right)\right)$. In relation to this, it is important to mention that, although we explicitly specified the location of the origins of our coordinate systems, up until now, no restrictions were imposed on their orientation. We will use this to our advantage and choose the $\left(r,\theta ,\varphi \right)=\left(r,\mathrm{0,0}\right)$ and $\left(r,\theta \prime ,\varphi \prime \right)=\left(r,\mathrm{0,0}\right)$ axes to coincide with the line connecting the origins of the two coordinate systems and the $\left(r,\theta ,\varphi \right)=\left(r,\pi /2,0\right)$ and $\left(r\prime ,\theta \prime ,\varphi \prime \right)=\left(r,\pi /2,0\right)$ axes to be parallel. In practice, that would mean that the $\left(r\prime ,s\prime \right)$ coordinate system is simply a copy of $\left(r,s\right)$ shifted along the $\left(r,\theta ,\varphi \right)=\left(r,\mathrm{0,0}\right)$ axis (Fig. S1B). This makes each of the $R_{nl}(r\prime )Y_{lm}(s\prime )$ basis elements an appropriately shifted copy of the $R_{nl}\left(r\right)Y_{lm}\left(s\right)$ basis element, that is,

$$R_{nl}(r\prime )Y_{lm}(s\prime )=\widehat{T}\left(-z\right)R_{nl}\left(r\right)Y_{lm}\left(s\right).$$ [S8]

Here $\widehat{T}$ is an operator specifying translation along the $\left(r,\mathrm{0,0}\right)$ axis and z is the distance between the origins of coordinate systems. For the case of Gaussian-type orbitals, an analytical expression is available for this type of transformation (24),

$${\widehat{T}}_z\left(-z\right)R_{nl}\left(r\right)Y_{lm}\left(s\right)={\displaystyle \sum _{nl}{T}_{n\prime l\prime ,nl}^{\left|m\right|}\left(-z\right)R_{n\prime l\prime }\left(r\right)Y_{l\prime m}\left(s\right)}.$$ [S9]

Substituting [S9] into [S7] and using the symmetry of translation matrix elements (24),

$$T_{n\prime l\prime ,nl}^{\left|m\right|}\left(-z\right)=T_{nl,n\prime l\prime }^{\left|m\right|}\left(z\right),$$ [S10]

we get the following:

$$\begin{array}{l}E\left(\psi =\left(\chi ,\omega \right)\right)\\ ={\displaystyle \int \overline{{\displaystyle \sum _{n_1{l}_1{m}_1}{\displaystyle \sum _{m}f\left(n_1,l_1,m_1\right)D_{m{m}_1}^{l_1}\left(\chi \right)}}}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times \overline{{\displaystyle \sum _{n\prime l\prime }{T}_{n_1{l}_1,n\prime l\prime }^{\left|m\right|}\left(z\right)R_{n\prime l\prime }\left(r\right)Y_{l\prime m}\left(s\right))}}\\ \hspace{1em}\hspace{1em}\times {\displaystyle \sum _{nl{m}_2}{\displaystyle \sum _{m\prime }g\left(n,l,m_2\right)D_{m\prime m_2}^l\left(\omega \right)R_{nl}\left(r\right)Y_{lm\prime }\left(s\right)dx}}\\ ={\displaystyle \sum _{\stackrel{n_1{l}_1{m}_1}{nl{m}_2}}{\displaystyle \sum _{mm\prime }{\displaystyle \sum _{n\prime l\prime }\overline{f\left(n_1,l_1,m_1\right)}{T}_{n\prime l\prime ,n_1{l}_1}^{\left|m\right|}\left(z\right)g\left(n,l,m_2\right)}}}\\ \times \hspace{0.17em}\overline{D_{m{m}_1}^{l_1}\left(\chi \right)}{D}_{m\prime m_2}^l\left(\omega \right){\displaystyle \int \overline{R_{n\prime l\prime }\left(r\right)Y_{l_1^{\prime }m}\left(s\right)}}{R}_{nl}\left(r\right)Y_{l{m}_2}\left(s\right)dx.\end{array}$$ [S11]

Finally, taking into account the orthonormality of basis functions and changing the order of summation yields

$$\begin{array}{l}E\left(\psi =\left(\chi ,\omega \right)\right)\\ ={\displaystyle \sum _{n_1{l}_1{m}_1}{\displaystyle \sum _{nl{m}_2}{\displaystyle \sum _{mm\prime }{\displaystyle \sum _{n\prime l\prime }\overline{f\left(n,l,m\right)}{T}_{n\prime l\prime ,nl}^{\left|m\right|}\left(z\right)g\left(n,l,m_2\right)}}}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\times \overline{D_{m{m}_1}^{l_1}\left(\chi \right)}{D}_{m\prime m_2}^l\left(\omega \right){\delta }_{nn\prime }{\delta }_{nn\prime }{\delta }_{nn\prime }dx\\ ={\displaystyle \sum _{\stackrel{l_{1}l}{m{m}_1{m}_2}}\left({\displaystyle \sum _{n_1,n}\overline{f\left(n_1,l_1,m_1\right)}{T}_{n_1{l}_1,nl}^{\left|m\right|}\left(z\right)g\left(n,l,m_2\right)}\right)}\\ \hspace{1em}\hspace{1em}\hspace{1em}\times \hspace{0.17em}\overline{D_{m{m}_1}^{l_1}\left(\chi \right)}{D}_{m{m}_2}^l\left(\omega \right).\end{array}$$ [S12]

As already mentioned, this expression is an inverse manifold Fourier transform. This result can be rewritten in a more conventional Fourier-like form by using the following expression for Wigner rotation matrices (34):

$$D_{mm\prime }^l\left(\alpha ,\beta ,\gamma \right)=e^{-im\alpha }{d}_{mm\prime }^l\left(\beta \right)e^{-im\prime \gamma }.$$ [S13]

Subsituting into [S12], using $\chi =\left(0,\beta ,\gamma \right)$ and $\omega =\left(\alpha \prime ,\beta \prime ,\gamma \prime \right)$, we can write

$$\begin{array}{l}E\left(\beta ,\gamma ,\alpha \prime ,\beta \prime ,\gamma \prime \right)\\ ={\displaystyle \sum _{m{m}_1{m}_2}{\displaystyle \sum _{l_{1}l}\left({\displaystyle \sum _{n_1,n}\overline{f\left(n_1,l_1,m_1\right)}{T}_{n_1{l}_1,nl}^{\left|m\right|}\left(z\right)g\left(n,l,m_2\right)}\right)}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\times \hspace{0.17em}\overline{D_{m{m}_1}^{l_1}\left(0,\beta ,\gamma \right)}\hspace{0.17em}{D}_{m{m}_2}^l\left(\alpha \prime ,\beta \prime ,\gamma \prime \right)\\ ={\displaystyle \sum _{m{m}_1{m}_2}{\displaystyle \sum _{l_{1}l}\left({\displaystyle \sum _{n_1,n}\overline{f\left(n_1,l_1,m_1\right)}{T}_{n_1{l}_1,nl}^{\left|m\right|}\left(z\right)g\left(n,l,m_2\right)}\right)}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\times d_{m{m}_2}^l(\beta \prime )d_{m{m}_1}^{l_1}\left(\beta \right)e^{-i\left(-m_1\gamma +m_2\gamma \prime +m\alpha \prime \right)}.\end{array}$$ [S14]

A certain asymmetry associated with the γ angle arises from complex conjugation and can be dealt with by simply substituting γ with $-\gamma$,

$$\begin{array}{l}E\left(\beta ,-\gamma ,\alpha \prime ,\beta \prime ,\gamma \prime \right)\\ ={\displaystyle \sum _{m{m}_1{m}_2}{\displaystyle \sum _{l_{1}l}\left({\displaystyle \sum _{n_1,n}\overline{f\left(n_1,l_1,m_1\right)}{T}_{n_1{l}_1,nl}^{\left|m\right|}\left(z\right)g\left(n,l,m_2\right)}\right)}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\times d_{m{m}_2}^l(\beta \prime )d_{m{m}_1}^{l_1}\left(\beta \right)e^{-i\left(m_1\gamma +m_2\gamma \prime +m\alpha \prime \right)}.\end{array}$$ [S15]

This substitution does not have any significant consequence, due to the periodicity associated with rotations by the γ angle (i.e., if we substitute γ with $-\gamma$, all of the associated rotations are still sampled, albeit in reverse order).

Before we finish the discussion of correlations on $SO\left(3\right)\mathrm{\backslash }{S}^1\times SO\left(3\right)$, it might be useful to take one last look at the relations between the coordinate systems that we have been using. Recall that we introduced a translation operator $\widehat{T}$ to perform the change of coordinates and express the $R_{nl}(r\prime )Y_{lm}(s\prime )$ basis elements as shifted $R_{nl}\left(r\right)Y_{lm}\left(s\right)$ elements. Now, because our function f is a linear combination of these basis elements, we can view it as a shifted version of some other function h, that is, $f=\widehat{T}h$, or, for the rotated versions, ${\widehat{D}}_{O_y}\left(\chi \right)f=\widehat{T}{\widehat{D}}_{O_x}\left(\chi \right)h$. The interesting part here is that h is being rotated around the same point as g. This allows us to rewrite expression [S5] using just one coordinate system but explicitly introducing a translation operator instead,

$$E\left(z,\psi \right)={\displaystyle \underset{S^2\times R}{\int }\overline{\widehat{T}\left(-z\right)\widehat{D}\left(\chi \right)h\left(x\right)}\widehat{D}\left(\omega \right)g\left(x\right)dx,}d\in R^1,\psi =\left(\chi ,\omega \right)\in SO\left(3\right)\mathrm{\setminus }{S}^1\times SO\left(3\right).$$ [S16]

Such representation, although equivalent to [S5], provides a more convenient way for thinking about problems in which the initial position of the two patterns relative to each other is not given explicitly, but, instead, multiple different configurations need to be sampled. One example of such a problem is the problem of protein docking, where both proteins are rotated around their centers of mass and different initial distances between centers of mass need to be sampled.

Application to Protein Docking.

Development of the docking protocol.

Consider the case where f and g describe the matching physical characteristics of a pair of interacting proteins, such that their overlap integral over the 3D space gives a component of receptor–ligand interaction energy. For example, the electrostatic potential of one protein and the charge distribution of the other give the electrostatic energy of the system. We will denote a pair of such characteristics of receptor and ligand as $\mathrm{ℛ}$ and $\mathrm{ℒ}$, respectively, and use them as a specific example of f and g; that is, from now on, we consider $f=\mathrm{ℛ}$ and $g=\mathrm{ℒ}$. If the centers of mass of these proteins are selected as centers of rotation, then applying the manifold Fourier transform [S15] gives the energy scores for all orientations corresponding to a fixed distance between receptor and ligand centers of mass,

$$\begin{array}{l}E\left(\beta ,-\gamma ,\alpha \prime ,\beta \prime ,\gamma \prime \right)\\ ={\displaystyle \sum _{m{m}_1{m}_2}{\displaystyle \sum _{l_{1}l}\left({\displaystyle \sum }_{n_1,n}\overline{r\left(n_1,l_1,m_1\right)}{T}_{n_1{l}_1,nl}^{\left|m\right|}\left(z\right)l\left(n,l,m_2\right)\right)}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\times d_{m{m}_2}^l(\beta \prime )d_{m{m}_1}^{l_1}\left(\beta \right)e^{-i\left(m_1\gamma +m_2\gamma \prime +m\alpha \prime \right)}.\end{array}$$ [S17]

Here $r\left(n_1,l_1,m_1\right)$ and $l\left(n,l,m_2\right)$ are expansion coefficients of $\mathrm{ℛ}$ and $\mathrm{ℒ}$.

To develop a protocol for sampling of the full 6D space of mutual receptor–ligand orientations, one needs to complement the FMFT based sampling of five rotational degrees of freedom with explicit sampling of the only translational degree of freedom that is associated with the distance between receptor and ligand centers of mass. In fact, we do not have to do any additional manipulation to achieve this goal, because expression [S17] already contains a translation matrix that specifies the distance between the rotation centers, or, in our specific case of protein docking, between protein centers of mass. By simply changing the value of parameter z, we are able to sample configurations corresponding to different receptor–ligand distances,

$$\begin{array}{l}E\left(z,\beta ,-\gamma ,\alpha \prime ,\beta \prime ,\gamma \prime \right)\\ ={\displaystyle \sum _{m{m}_1{m}_2}{\displaystyle \sum _{l_{1}l}\left({\displaystyle \sum _{n_1,n}\overline{r\left(n_1,l_1,m_1\right)}{T}_{n_1{l}_1,nl}^{\left|m\right|}\left(z\right)l\left(n,l,m_2\right)}\right)}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\times d_{m{m}_2}^l(\beta \prime )d_{m{m}_1}^{l_1}\left(\beta \right)e^{-i\left(m_1\gamma +m_2\gamma \prime +m\alpha \prime \right)}.\end{array}$$ [S18]

This expression can be further expanded to incorporate multiple correlation-based components of the energy function,

$$\begin{array}{l}E\left(z,\beta ,-\gamma ,\alpha \prime ,\beta \prime ,\gamma \prime \right)={\displaystyle \sum _p^P{E}_p\left(-d,\beta ,-\gamma ,\alpha \prime ,\beta \prime ,\gamma \prime \right)}\\ ={\displaystyle \sum _p^P{\displaystyle \sum _{\stackrel{m{m}_1{m}_2}{l{l}_1}}\left({\displaystyle \sum _{n_{1}n}\overline{r_p\left(n_1,l_1,m_1\right)}\hspace{0.17em}{l}_p\left(n,l,m_2\right)T_{n_1{l}_1,nl}^{\left|m\right|}\left(z\right)}\right)}}\\ \hspace{1em}\hspace{1em}\times \hspace{0.17em}{d}_{m{m}_2}^l\left(\beta \prime \right)d_{m{m}_1}^{l_1}\left(\beta \right)e^{-i\left(m_1\gamma +m_2\gamma \prime +m\alpha \prime \right)}\\ ={\displaystyle \sum _{\stackrel{m{m}_1{m}_2}{l{l}_1}}\left({\displaystyle \sum _{n_{1}n}\left[{\displaystyle \sum _p^P\overline{r_p\left(n_1,l_1,m_1\right)}\hspace{0.17em}{l}_p\left(n,l,m_2\right)}\right]T_{n_1{l}_1,nl}^{\left|m\right|}\left(z\right)}\right)}\\ \hspace{1em}\hspace{1em}\times \hspace{0.17em}{d}_{m{m}_2}^l(\beta \prime )d_{m{m}_1}^{l_1}\left(\beta \right)e^{-i\left(m_1\gamma +m_2\gamma \prime +m\alpha \prime \right)}.\end{array}$$ [S19]

Note here that the summation over different correlation terms is performed in the inner loop, which allows us to execute the manifold Fourier transform only once for all correlation components of the scoring function, which makes the total execution time much less sensitive to the number of correlations used in the scoring function.

In practice, the algorithm is organized as follows: For each translation distance of interest, we calculate the product of expansion coefficients and translation matrix elements,

$$\begin{array}{l}{S}^z\left(l,l_1,m,m_1,m_2\right)\\ \hspace{1em}={\displaystyle \sum _{n_{1}n}{\displaystyle \sum _p\overline{r_p\left(n_1,l_1,m_1\right)}{l}_p\left(n,l,m_2\right)T_{n_1{l}_1,nl}^{\left|m\right|}\left(z\right),}}\end{array}$$ [S20]

and then apply the manifold Fourier transform,

$$\begin{array}{l}E\left(z,\beta ,-\gamma ,\alpha \prime ,\beta \prime ,\gamma \prime \right)={\displaystyle \sum _{\stackrel{m{m}_1{m}_2}{l{l}_1}}{S}^z\left(l,l_1,m,m_1,m_2\right)}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times \hspace{0.17em}{d}_{m{m}_2}^l(\beta \prime )d_{m{m}_1}^{l_1}\left(\beta \right)e^{-i\left(m_1\gamma +m_2\gamma \prime +m\alpha \prime \right)}.\end{array}$$ [S21]

Implementing the FMFT explains the actual procedure being used to compute Fourier transform on the $SO\left(3\right)\mathrm{\setminus }{S}^1\times SO\left(3\right)$ manifold.

Implementing the FMFT.

Before the discussion of implementation details, a few words need to be said about the sampling of β and $\beta \prime$ angles. Unlike $\gamma ,\alpha \prime$ and $\gamma \prime$ angles, for which the descretization is imposed based on the size of FFT array and gives an angular step of $2\pi /\left(2N-1\right)$ (note that indices m, $m_1$, $m_2$ change from $-N+1$ to $N-1$), β and $\beta \prime$ require a “manual” choice of samples. To achieve a similar sampling frequency, these are selected to be in steps of $\pi /\left(N-1\right)$,

$${\beta }_u=\pi u/\left(N-1\right),{\beta }_v^{\prime }=\pi v/\left(N-1\right);u,v=\mathrm{0..}N-1,$$ [S22]

and Wigner d functions are precalculated for these values and stored in memory for future reuse.

The actual FMFT procedure is implemented in two steps.

First, we evaluate the expression

$$\begin{array}{l}{\mathit{ϵ}}_{u,v}^z\left(m,m_1,m_2\right)\\ \hspace{1em}\hspace{1em}={\displaystyle \sum _{l{l}_1}{S}^z\left(l,l_1,m,m_1,m_2\right)d_{m{m}_1}^{l_1}\left({\beta }_u\right)d_{m{m}_2}^{\left(l\right)}\left({\beta }_v^{\prime }\right)}\end{array}$$ [S23]

for all of the chosen values of β and $\beta \prime$ angles using the precalculated Wigner d functions, thus performing an inverse 2D Discrete Wigner transform. Although a straightforward approach to this problem has a complexity of $O\left(N^7\right)$, as one can check by counting the number of subscripts in [S23], the same result can be achieved in two $O\left(N^6\right)$ steps using a temporary array,

$$\begin{array}{r}{\tilde{W}}_v^z\left(l_1,m,m_1,m_2\right)={\displaystyle \sum _l{d}_{m{m}_2}^l\left({\beta }_v^{\prime }\right)S^z\left(l,l_1,m,m_1,m_2\right)}\\ {\mathit{ϵ}}_{u,v}^z\left(m,m_1,m_2\right)={\displaystyle \sum _{l_1}{d}_{m{m}_1}^{l_1}\left({\beta }_u\right){\tilde{W}}_v^z\left(l_1,m,m_1,m_2\right)}.\end{array}$$ [S24]

The calculation of the $S^z$ array elements can be accelerated in a similar way (15), but, in this case, the complexity of the problem scales as $2\times O\left(P{N}^6\right)$. The result of the first step is a 5D array consisting of $N^2$ logically 3D arrays.

The second step is application of $N^2$ “conventional” 3D FFTs to the aforementioned arrays. As a result, we get scoring function values for all of the sampled values of $\beta ,\gamma ,\alpha \prime ,\beta \prime ,\gamma \prime$ parameters [the total amount of samples is $N\times N\times \left(\left(2N-1\right)\times \left(2N-1\right)\times \left(2N-1\right)\right)$], basically scoring all of the orientations corresponding to a given distance z between the centers of receptor and ligand. Because the complexity of each 3D FFT is $O\left({\left(2N-1\right)}^3\ln \left({\left(2N-1\right)}^3\right)\right)\approx O\left(N^3\ln \left(N\right)\right)$, the total complexity of this step is $O\left(N^5\text{ln}\left(N\right)\right)$.

In summary, our inverse FMFT algorithm consists of $O\left(N^6\right)$ and $O\left(N^5\ln \left(N\right)\right)$ steps, which makes the overall asymptotic complexity $O\left(N^6\right)$. Minor details aside, an approach presented here is effectively an extension of the method presented in ref. 19 for calculation of FFTs on the SO(3) group. The distinctive trait of this approach is use of explicit Wigner d functions for calculation of the inverse Wigner transform. It should also be noted that, although we deal with multiplication by Wigner d functions (i.e., with inverse discrete Wigner transform) by using a simple $O\left(N^6\right)$ approach, an asymptotically superior algorithm is available (35), which potentially opens an opportunity for an even faster method.

Symmetries of Fourier arrays.

It is important to mention that receptor and ligand properties that are being correlated are described by real functions, and, consequently, the values of the energy function should be real as well. This means that an array of real values is to be expected as a result of the FFT procedure, which can only be true if, for fixed u and v indices, the complex ${\mathit{ϵ}}_{u,v}^z\left(m,m_1,m_2\right)$ arrays, which are subject to 3D FFTs, possess Hermitian symmetries, i.e., their elements satisfy the following relations:

$$\begin{array}{l}{\mathit{ϵ}}_{u,v}^z\left(m,m_1,m_2\right)=\overline{{\mathit{ϵ}}_{u,v}^z\left(-m,-m_1,-m_2\right)},\\ {\mathit{ϵ}}_{u,v}^z\left(m,m_1,-m_2\right)=\overline{{\mathit{ϵ}}_{u,v}^z\left(-m,-m_1,m_2\right)},\\ {\mathit{ϵ}}_{u,v}^z\left(m,-m_1,m_2\right)=\overline{{\mathit{ϵ}}_{u,v}^z\left(-m,m_1,-m_2\right)},\\ {\mathit{ϵ}}_{u,v}^z\left(-m,m_1,m_2\right)=\overline{{\mathit{ϵ}}_{u,v}^z\left(m,-m_1,-m_2\right)}.\end{array}$$ [S25]

In practice, this property allows us to fill only the elements corresponding to nonnegative values of the m index and to use specialized complex-to-real FFT algorithms (36), reducing the number of calculations and the amount of memory used by almost twofold.