Significance
Biological sensory systems have the capacity to respond to signals over a broad range of intensities, be it vision in animals or signal transduction in cells. Such a broad response range is thought to be mediated by the system’s ability to sense signal logarithmically. We seek to understand the implementation of logarithmic sensors in cells. We find that a pervasive class of proteins, those that are allosterically regulated, have dynamics that facilitate response on a logarithmic (as opposed to absolute) scale, allowing sensitive response across a broad range of signal.
Keywords: allosteric regulation, fold-change detection, logarithmic sensing
Abstract
Many sensory systems, from vision and hearing in animals to signal transduction in cells, respond to fold changes in signal relative to background. Responding to fold change requires that the system senses signal on a logarithmic scale, responding identically to a change in signal level from 1 to 3, or from 10 to 30. It is an ongoing search in the field to understand the ways in which a logarithmic sensor can be implemented at the molecular level. In this work, we present evidence that logarithmic sensing can be implemented with a single protein, by means of allosteric regulation. Specifically, we find that mathematical models show that allosteric proteins can respond to stimuli on a logarithmic scale. Next, we present evidence from measurements in the literature that some allosteric proteins do operate in a parameter regime that permits logarithmic sensing. Finally, we present examples suggesting that allosteric proteins are indeed used in this capacity: allosteric proteins play a prominent role in systems where fold-change detection has been proposed. This finding suggests a role as logarithmic sensors for the many allosteric proteins across diverse biological processes.
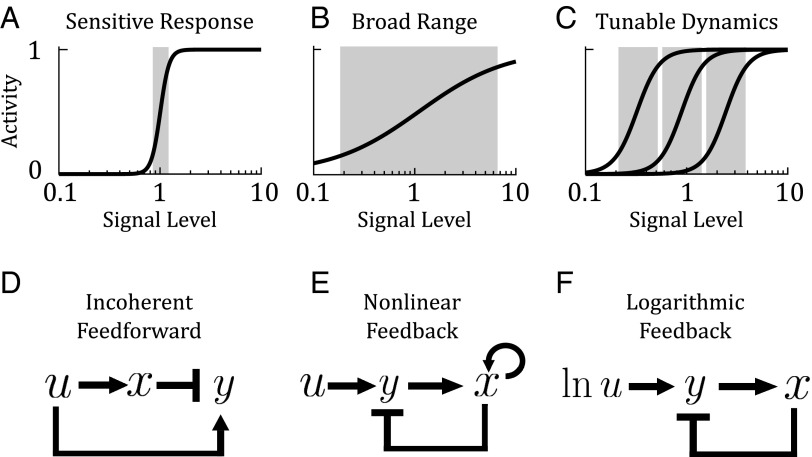
Sensory systems in biology are faced with two seemingly conflicting goals: they must be sensitive to detect small changes in signal (Fig. 1A), and at the same time, they must have a broad response range because many natural signals vary over several orders of magnitude (Fig. 1B) (1). To achieve these conflicting goals, it has been proposed that many sensory systems have evolved to tune their sensitivity over a wide range (Fig. 1C). In these systems, the pathway can adapt the regime to which it is most sensitive depending on the magnitude of the signal they receive.
Fig. 1.
Sensory systems have conflicting goals. (A) A sensitive system detects small changes in signal but has a narrow response range. (B) A broad-ranged system responds to a large range of signal but is not sensitive to small changes. (C) A tunable sensor is both sensitive to small changes in signal and is capable of adjusting its response curve logarithmically across a broad range. Proposed molecular circuits for fold-change detection. (D) An incoherent feedforward loop is a common motif in gene regulatory systems, where an input activates an output, and at the same time a repressor of the output. (E) A nonlinear feedback loop has also been proposed as a mechanism for fold-change detection. (F) A logarithmic-feedback circuit, built from a logarithmic sensor coupled to linear feedback. In this study, we ask how a logarithmic sensor might be implemented at the molecular level.
The ability to tune sensitivity over a broad range of signal is a key property of the phenomenon known as fold-change detection, where the change in activity of a system is not a function of the level or absolute difference in signal, but of the ratio of signal to background (2, 3). For example, a change in signal level from 1 to 3 or from 10 to 30 would yield an identical outcome. Fold-change detection is related to the well-known Weber’s Law, which describes how our sensory systems tune their detection thresholds to the background state (4). Weber’s Law has been proposed in many sensory systems, including vision, weight perception, and taste, as well as numerical and temporal cognition (4–7). Beyond sensory systems in whole organisms, fold-change detection has recently emerged at the cellular level, governing signal transduction in animal cells. Specifically, studies in several signaling pathways have presented evidence that gene transcription responds to the fold change in the level of a transcription factor, rather than its absolute level (8–11). Finally, evidence for fold-change detection has also been observed in the sensory response of fungi (12), bacteria (3, 13), and social amoeba (14).
Given the wide-ranging occurrence of fold-change detection, it is therefore of interest to understand how fold-change detection is implemented at the molecular level. It has been proposed that fold-change detection can be mediated by specific classes of incoherent feedforward loops (Fig. 1D) and nonlinear feedback loops (Fig. 1E) (3, 15). The authors also hypothesized that fold-change detection can be realized using another type of circuit, where an upstream logarithmic sensor is coupled with linear feedback (Fig. 1F). Whereas feedforward and feedback circuits are commonly found in biological systems, it is not clear how a logarithmic sensor would be implemented. We define here a logarithmic sensor as having two properties: (i) it must be able to respond to changes in signal on a logarithmic scale; and (ii) it must be logarithmically tunable, i.e., shift its response curve on a logarithmic scale (Fig. 1C). We will rigorously define and analyze these properties in the next section.
In this study, we explore the possible roles of allostery in fold-change detection. An allosteric protein is one that has an effector which regulates its activity by acting on a site physically distant from the protein’s ligand-binding site. Allostery is found in a vast range of processes, including metabolism, signal transduction, oxygen and membrane transport, cell cycle regulation, and transcription (16, 17). Allostery has been thought to mediate cooperativity, for example, in hemoglobin and metabolic enzymes. Allostery has also been thought to facilitate biological control loops, for example mediating feedback in glycolysis (18).
We propose a function for allosteric proteins as logarithmic sensors. In the context of bacterial chemotaxis, Lazova et al. (15) and Tu et al. (19) have proposed that a logarithmic transformation can emerge from the aspartate-sensing Tar receptors that follow the Monod–Wyman–Changeux (MWC) model of allostery. Here, we find that logarithmic sensing is a general property of allostery, regardless of whether the conformational change is thermally or kinetically driven, independent of the specific model of allostery (e.g., conformational selection or sequential binding) and can even be implemented in either a single protein or a network of proteins. Essentially, we find that the capacity to act as a logarithmic sensor arises from the fundamental feature of allostery, the ability to tune the activity of a protein without directly affecting its binding kinetics. The broad presence of allosteric proteins raises the possibility that diverse cellular processes may sense input in a fold-change manner, akin to how our sensory systems work.
Results
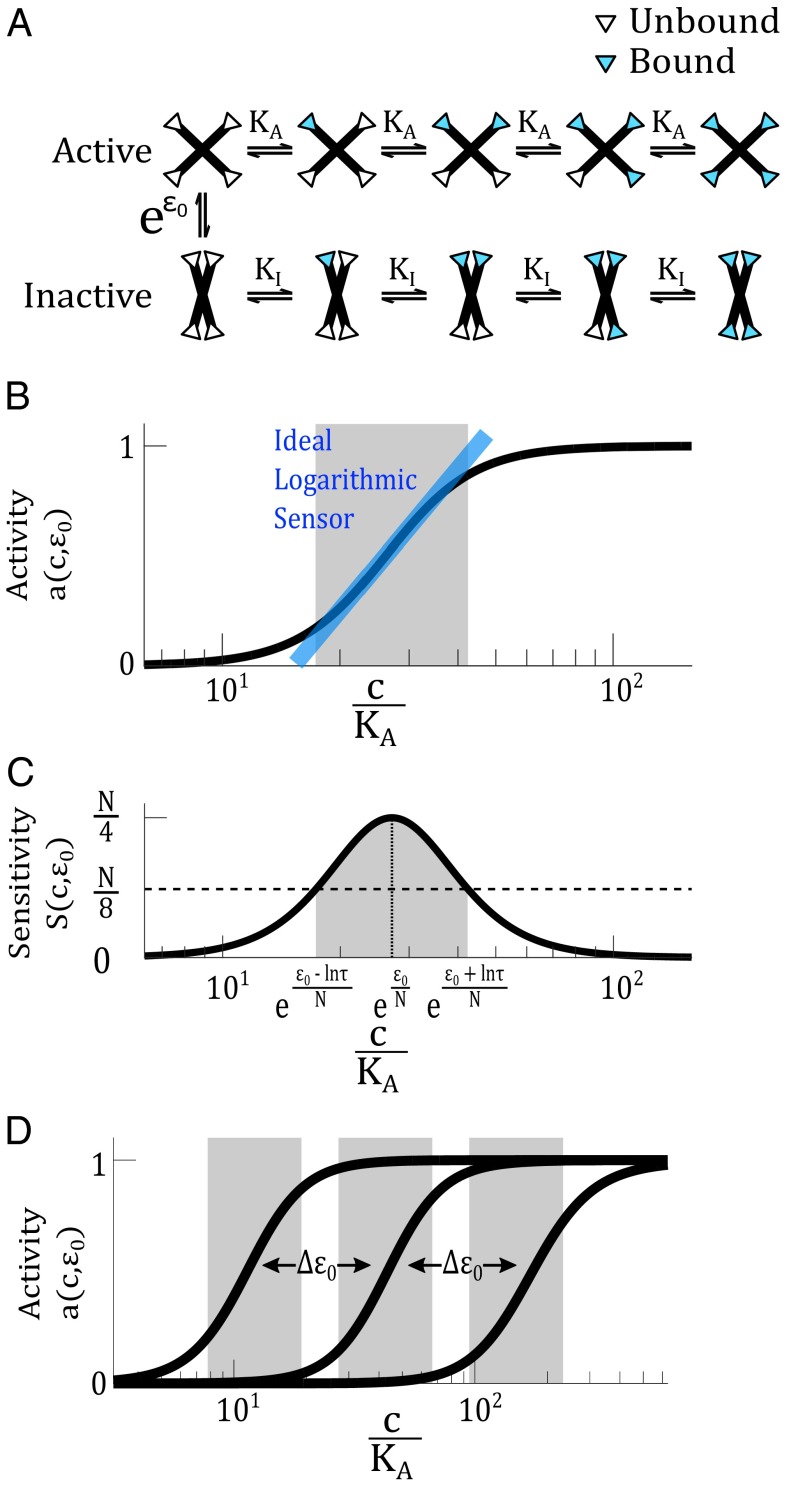
To investigate whether an allosteric protein can act as a logarithmic sensor, we begin by analyzing a widely used model of allostery, the MWC model, proposed by Monod, Wyman, and Changeux to explain cooperativity in metabolic enzymes and hemoglobin (20, 21). The MWC model is based on conformational selection. The model considers a large homogeneous population of proteins, where each protein has N identical subunits that can independently bind ligand (Fig. 2A). Each protein can either be in the active (A) or inactive (I) conformation, each of which have different binding affinities for ligand. Conformational change occurs in an all-or-none fashion when there is no ligand bound and is regulated by the binding of an allosteric effector.
Fig. 2.
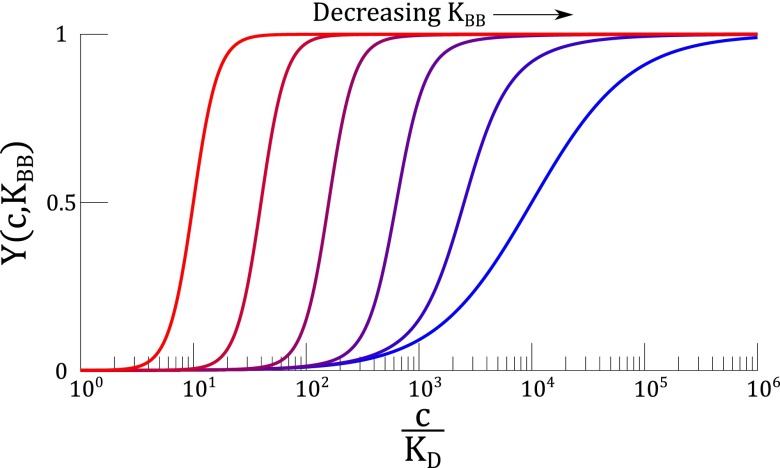
An MWC protein can act as a logarithmic sensor. (A) The MWC model describes a protein that can switch between an active and inactive conformation at a rate determined by the allosteric constant . The active state has a ligand-binding affinity and the inactive state has an affinity . The white and blue triangles represent binding sites unoccupied and occupied by ligand, respectively. (B) Within a certain range, activity of the MWC protein, , depends logarithmically on the ligand concentration. The blue line indicates the ideal logarithmic sensor, whose activity directly corresponds to the logarithm of ligand concentration. The gray range indicates the range where activity of the MWC protein coincides with that of the ideal logarithmic sensor with a certain tolerable error. In this illustration, we set the error to be at most 10% (corresponding to in Eq. S9). (C) The sensitivity function is related to the derivative of the activity function, . The sensitivity function allows us to define a range (in gray) where the sensitivity is above a certain threshold. In this illustration, the threshold is set to , corresponding approximately to . In both B and C, we use , , , and . (D) The activity curve of an MWC protein can be tuned on a logarithmic scale, by modulating the allosteric parameter .
Let c be the concentration of ligand, and be the dissociation constants associated with the active and inactive conformations, and be the equilibrium ratio between the inactive and active conformations when no ligand is bound. This parameter is known as the allosteric constant. represents the free-energy difference when the system is at thermodynamic equilibrium, or the reaction equilibrium constant when the system is at steady state. The fraction of proteins in the active state is
| [1] |
The MWC model is typically analyzed in a static context. Tu and coworkers analyzed a dynamic version of the model in the context of bacterial chemotaxis (19, 22) by taking partial derivatives with respect to c,
| [2] |
With this dynamic framework, we now examine the range where the ligand concentration is large enough to facilitate binding to the active conformation, but not so large as to allow binding to the inactive conformation.
This range can be substantial in some proteins, e.g., up to three orders of magnitude in phosphofructokinase (PFK1) (23). In this range, Eqs. 1 and 2 simplify respectively to
| [3] |
where we define the sensitivity function , which describes the steepness of the activity curve:
| [4] |
Representative plots of and are shown in Fig. 2 B and C. We give a detailed analysis in SI Materials and Figs. S1 and S2 of how varies with c and for the full range of ligand concentration.
Fig. S1.
Effects of on the sensitivity function. (A) Activation curves for the MWC model in Eq. 1. The parameters used here are . (B) Sensitivity functions corresponding to the MWC activation curves in A.
Fig. S2.
Saturation effects in the sensitivity function. (A) Activation curves for the MWC model in Eq. 1, across a full range of ligand concentration, c. The parameters used here are . (B) as c nears lower saturation. The solid black curves are for the same parameters as in A, the dashed blue line is from Eq. S15, and the dotted black line is the scaling function . (C) as c nears upper saturation. The solid black curves are plots of for the same parameters as in A, the dashed red line is from Eq. S16, and the dotted black line is the scaling function .
Examining the dynamics of activity with respect to ligand changing in time, we get the equation
| [5] |
This equation shows explicitly that the rate of change in the activity of an MWC protein is a function of the logarithm of ligand concentration c.
The logarithmic dependence of an MWC protein occurs within a certain range,
| [6] |
where τ parametrizes the limits of the logarithmic range. This range is illustrated by the gray regions in Fig. 2 B and C, where we have chosen as an example . We provide a detailed derivation in SI Materials for how the range (Eq. 6) translates into the gray regions in Fig. 2 B and C.
τ can be related to the deviation of the MWC response curve from a hypothetical ideal logarithmic sensor (the blue line in Fig. 2B, derived in SI Materials). If we tolerate, for example, at most error [at the lower and upper limits of the range (Eq. 6) when ], then an MWC protein with cooperativity (e.g., hemoglobin and PFK1) would have a logarithmic range of ∼2.5-fold change in ligand concentration. A monomeric protein without any cooperativity () would have a logarithmic range of 36-fold change in ligand concentration. Therefore, the range over which the activity of an MWC protein is logarithmically dependent on ligand concentration can be quite substantial. We see further that this range can be increased at the expense of cooperativity, telling us that there is an intrinsic tradeoff between sensitivity and logarithmic range.
The logarithmic dependence of activity on ligand concentration is, however, not a unique feature of MWC proteins. Any monotonic binding curve, e.g., that of a Hill model
| [7] |
would also show some range for which activation depends logarithmically on ligand. The requirement for a logarithmic sensor we are considering here is a more stringent one: the activity of the protein must also be logarithmically tunable (Fig. 1C). This property will allow a protein that can already sense logarithmically over some regime of ligand to extend its responsiveness to a much greater range.
MWC proteins have the additional feature of logarithmic tunability, facilitated by the presence of an allosteric effector. Inequality Eq. 6 shows that the net effect of varying the allosteric parameter is a shift in the midpoint of the logarithmic range, without changing its width (Fig. 2D). The logarithmic tuning of the activity curve comes from the independent multiplicative relationship between and c in Eq. 3. To contrast, a Hill protein with a fixed has no capacity to tune its response curve logarithmically. This property can be seen in Eq. 7, which is analogous to the activation of an MWC protein in Eq. 3, except that there is no allosteric parameter . Allosteric regulation, which modulates the structural conformation of a protein, produces logarithmic tuning in the protein’s response range.
Now we may ask whether the capacity to act as a logarithmic sensor is a unique feature of the MWC model. First, we find that logarithmic tuning of the response curve does not depend on the specific form of the equilibrium ratio . Either an exponential form or a polynomial form of this function, as originally used by Monod, Wyman, and Changeux, work equally well (SI Materials) (21). This result implies that an MWC protein can act as a logarithmic sensor whether it is thermally or kinetically driven.
Second, we find that other models of allostery also show the capacity for logarithmic sensing. An alternative model of allostery was proposed by Koshland, Némethy, and Filmer, known as the KNF or sequential binding model (24). In this model, ligand binding induces processive conformational changes, as opposed to the all-or-none transition in the MWC model. We find that activity of the KNF model can be tuned logarithmically, although the model requires the regulation of more parameters (see derivation in SI Materials and Fig. S3).
Fig. S3.
Logarithmic tuning in the KNF model. Here, we show the capacity of the KNF model to be logarithmically tuned. This plot uses . For these parameters, we observe approximately three orders-of-magnitude in logarithmic shifting before the response curve begins to change shape. Much like the MWC and GPCR models, the KNF model can potentially act as a logarithmic sensor over a broad range of signal.
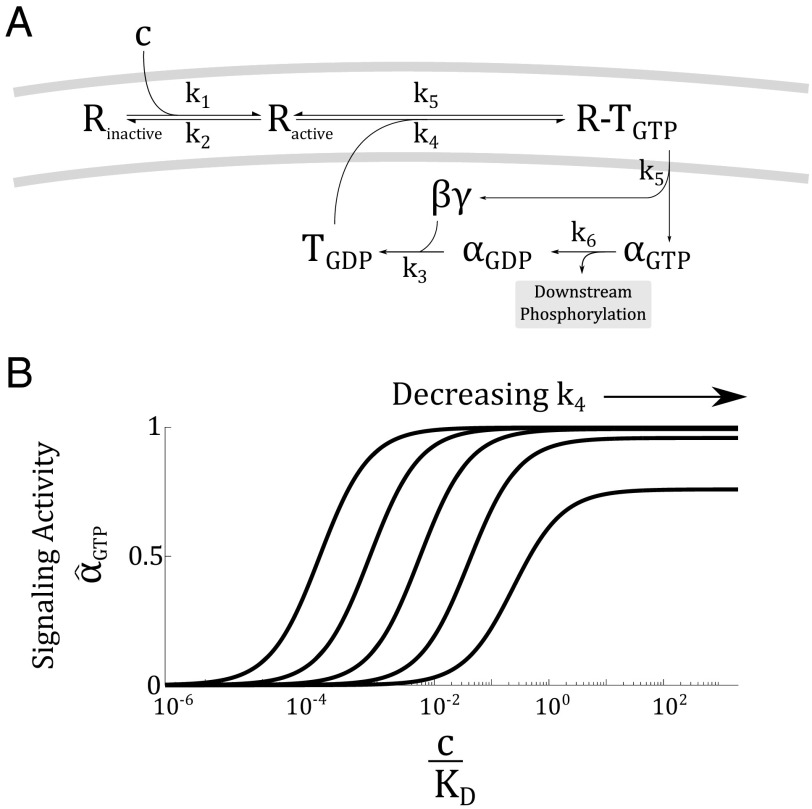
Finally, beyond a single protein, we find that a network of proteins with appropriate connectivity can act as a logarithmic sensor. We illustrate this finding by analyzing the G protein-coupled receptor (GPCR) system (Fig. 3A). GPCRs are a large family of seven-transmembrane domain receptor that couples to a G protein. The G proteins are composed of α, β, and γ subunits. Ligand binding induces a conformational change in the receptor, which results in the exchange of GDP for GTP in the alpha subunit. This exchange causes the α subunit to break off and activate downstream targets.
Fig. 3.
The regulatory circuit of the GPCRs can act as a logarithmic sensor. (A) Upon activation by ligand (c), the receptor (R) changes conformation and activates a G protein (T), which then break into an α and a subunit. The α subunit is responsible for downstream signaling, after which, it recombines with a subunit and recover the pool of G proteins. (B) Activity of the GPCR system, (i.e., the concentration of ) is logarithmically tuned by , the effective allosteric constant in the system. The logarithmic tuning breaks down when is much slower than . In this plot, and .
The GPCR system is described by a mass-action model (Fig. 3A) (25):
where R is the fraction of active receptors, c is the ligand concentration, and are the concentrations of G protein with GDP and GTP bound, and and are the concentrations of α subunits dissociated from the G protein complex with GDP and GTP bound. Additionally, let be the total concentration of G protein.
Although this system of differential equations appears unrelated to the MWC model, we find upon solving the equations that the steady-state activity of the GPCR system is
| [8] |
which is analogous to Eq. 3 in the MWC model (see detailed derivation in SI Materials). The effective allosteric parameter here is , which regulates the availability of G proteins. As plotted in Fig. 3B, varying logarithmically tunes the activity curve of the GPCR. This tuning eventually breaks down when becomes too low. In a later section, we will discuss the physiological significance of tuning the rate .
Therefore, the capacity to act as a logarithmic sensor can be realized when conformational changes in an allosteric protein is either thermally or kinetically driven, whether allosteric regulation is manifested through all-or-none or processive conformational change, and whether allosteric regulation is realized by a single protein with multiple subunits or a network of many proteins. We formally define a logarithmic sensor as a system that satisfies the property
| [9] |
where κ is a scaling factor that corresponds to the rate at which logarithmic shifting occurs. The particular value of κ will depend on the parameters of the underlying system. With some manipulation, we get
| [10] |
In any system where Eq. 9 holds, a linear shift in ε results in a logarithmic tuning of the response curve. We show in SI Materials that the different models we have considered satisfy these requirements in Eq. 9 (e.g., the MWC model, the GPCR network, the KNF model).
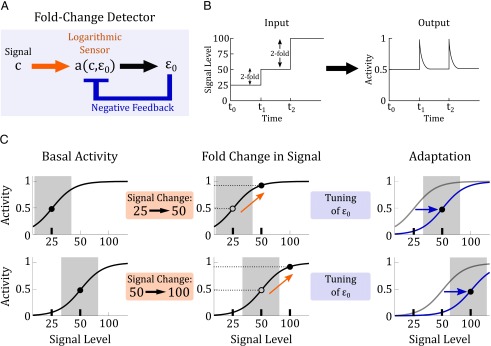
How might a logarithmic sensor be used in biological systems? A logarithmic sensor can mediate fold-change detection when it is coupled to a downstream feedback module (Fig. 4 A and B). For example, consider a system that experiences a twofold change in signal, from 25 to 50 (Fig. 4C, upper row). The logarithmic sensor computes a twofold change, and produces an activity change of . Subsequently, the feedback module adapts the system to the new signal level by allosterically tuning the response curve and restoring the protein to the original level of activity. The system is now poised to respond to signal changes again. If, from the basal activity of 50, the system experiences another change in signal to 100 (Fig. 4C, lower row), the logarithmic sensor will again compute a twofold change, producing an identical change in activity of , and the feedback module again adapts the system to the new signal level. We simulate the interaction of allostery and negative feedback, and confirm that they can indeed produce fold-change detection (SI Materials and Figs. S4 and S5). Therefore, the combination of a logarithmic sensor and adaptive feedback produces fold-change detection by continually tuning the response curve to a new background level, avoiding saturation and maintaining sensitivity to subsequent changes in signal.
Fig. 4.
Logarithmic-feedback circuit. (A) A logarithmic sensor can produce fold-change detection when coupled with negative feedback. In our model, the logarithmic sensor is an allosteric protein and the feedback comes from downstream modulation of an allosteric effector. (B) In fold-change detection a step increase in signal from 25 to 50, or from 50 to 100, will produce identical outputs. (C) An illustration of how the logarithmic-feedback circuit can produce fold-change detection. In the upper row, a logarithmic sensor experiences a twofold change in signal from 25 to 50. This stimulus produces a change in the sensor’s activity (orange arrow). The change in activity turns on downstream feedback which allosterically tunes the activation curve on a logarithmic scale (blue arrow), returning the sensor’s activity to its basal level. In the lower row, the same sensor now experiences another twofold change in signal, from 50 to 100. Despite the different in signal magnitude, this twofold change produces a change in activity that is identical to the previous one (dashed lines). Feedback will eventually takes effect and the system will return again to its basal level of activity.
Fig. S4.
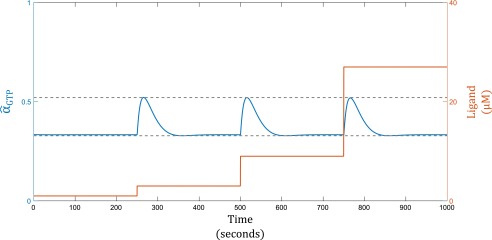
Fold-Change detection with an MWC Tar/Tsr Sensor. In this simulation, . The blue line indicates the activity of the Tar/Tsr receptor. The orange line indicates ligand concentration, varied by threefold at each step increase.
Fig. S5.
Fold-Change detection with a GPCR sensor. In this simulation, . The blue line indicates the activity of the GPCR system. The orange line indicates ligand concentration, varied by threefold at each step increase.
Evidence That Allosteric Proteins Are Used as Logarithmic Sensors.
Although our theoretical results show that allosteric proteins can act as logarithmic sensors, in practice, there may be physical limitations where the systems may not operate in an appropriate parameter regime to facilitate this behavior. For example, it may be that the inactive conformation is so heavily preferred that ligand binding follows a Michaelis–Menten model. Alternatively, the binding of allosteric effectors may be saturated, making it impossible to tune the activity curve.
We therefore explored evidence in the literature to see whether known allosteric proteins act as logarithmic sensors in physiological contexts. We found two lines of evidence. First, we found many measurements of allosteric proteins show response curves that are logarithmically tunable. Second, we find examples where allosteric proteins play a prominent role in processes where fold-change detection has been proposed or established.
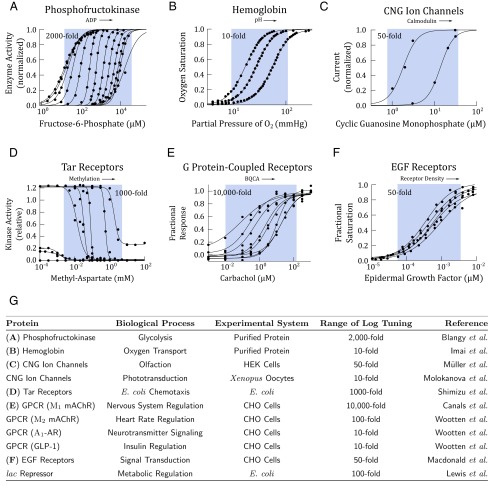
Shown in Fig. 5 are measured activity curves of some allosteric proteins. We reproduced these measurements with original data when available, or by retrieving data with Web Plot Digitizer. In some instances the curves were originally plotted in linear scale, and we have replotted them here in logarithmic scale to examine whether they are logarithmically tunable. Although there is wide literature on allosteric proteins, we present here examples where quantitative measurements have been performed over a broad range of ligand concentrations.
Fig. 5.
Biophysical measurements show that allosteric proteins are logarithmically tunable. In A–F, activity of an allosteric protein is plotted against ligand concentration. Within each plot, each activity curve corresponds to a different level of allosteric modulation. The arrow indicates modulation of the concentration of allosteric effectors. Data points (black circles) were extracted from the original studies using Web Plot Digitizer, except in A and B, where the original data were available. The data were fit with Hill equations using a nonlinear least-square fit in Matlab. The range of logarithmic tuning is defined as the ratio of , which we estimated from the published measurements with empirical values from the Hill equation and is depicted in the blue regions. These regions are meant to be a visual aid to highlight the effects of allosteric regulation and are not analytical. (A) PFK1 is a key enzyme in glycolysis and is allosterically regulated by ADP and ATP. In this study, ADP was varied from 0 to 2 mM (23). (B) Hemoglobin is the primary oxygen transport protein in vertebrates. Hemoglobin is allosterically regulated by blood pH. In this study, pH was varied from 6.6 to 7.8 (26). (C) Cyclic nucleotide-gate ion channels are allosterically modulated by calmodulin. In this study, the ion channels were treated with 0 and 0.5 μM calmodulin (27). (D) The Tar receptor in the Escherichia coli chemotaxis pathway is allosterically regulated by methylation level. In this study, the methylation level was varied through receptor mutants (28). (E) Muscarinic acetylcholine receptors are GPCRs responsible for signaling often found in neurons. The receptors are allosterically regulated by benzyl quinolone carboxylic acid (BQCA). In this study, BQCA was varied from 0 to 10 μM (29). (F) EGFRs are allosterically regulated by receptor density (30). In this study, receptor density was varied by overexpression from to receptors per cell. (G) A table summary of more allosteric proteins, whose measured activity shows logarithmically tuning. When measurements were performed in vivo, the systems were either Chinese hamster ovary (CHO) cells, human embryonic kidney (HEK) cells, Xenopus oocytes, or E. coli. Data for CNG ion channels in phototransduction from ref. 31; data for mAChR, -AR, and GLP-1 GPCRs from ref. 32; and data for the lac repressor from ref. 33.
Not only do some allosteric proteins tune their response on logarithmic scale, they can do so over a substantial range. One striking example we found is the glycolytic enzyme PFK1, whose response can be tuned over a remarkable 2,000-fold range of ligand concentration. This tuning eventually fails at low concentrations, where leaky enzyme activity begins to appear. More examples are summarized in the table in Fig. 5G. Presented in the table is the approximate range of ligand concentrations over which allosteric proteins tune their response logarithmically. We found examples across a wide range of biological processes including metabolism, ion transport, neurotransmission, insulin signaling, and olfaction.
In addition to evidence that some allosteric proteins operate in the parameter regime where they are logarithmically tunable, we find that they play a prominent role in systems where fold-change detection has been proposed. Furthermore, in each example, the allosteric proteins are coupled to feedback mechanisms, suggesting that their capacity as a logarithmic sensor is functionally used. We describe three examples here.
Bacterial Chemotaxis.
Bacterial cells detect and track chemical gradients in their environment. Mesibov et al. (13) first observed that the bacterial motile behavior depended on fold changes in attractant concentration. The fold-change detection was later confirmed through elegant FRET experiments (15, 28, 34).
Structural studies have now established a physical basis for MWC allostery in the aspartate-sensing Tar receptors (Fig. 5D) (22, 35). Furthermore, the allosteric receptor is connected to a well established feedback mechanism. Feedback is largely mediated by methylation and demethylation of the Tar receptors, which yield precise adaptation (36–38).
Vision.
Logarithmic response is well established in vision, in particular in the context of dark adaptation in rod photoreceptors (5, 39). Light detection is mediated by the GPCR rhodopsin in retinal photoreceptor cells. Examining the rhodopsin regulation network, we found two possible roles for allostery. First, recent studies find evidence that GPCRs follow the MWC model, existing in distinct conformational states, containing physically distant regulatory sites, and forming oligomers (29, 40–43). Indeed, several regulators tune activity curves of GPCRs on a logarithmic scale (Fig. 5E). Second, as described earlier, the regulatory network of interactions between GPCRs and G proteins can give the net effect of allosteric regulation (Fig. 3).
Moreover, the allosteric rhodopsin is coupled to a known feedback mechanism mediated by β-arrestin. Activation of rhodopsin induces receptor phosphorylation and binding of arrestin, which blocks further binding of transducin and results in adaptation to the prestimulus state. The action of arrestin modulates in Fig. 3A, the regulatory step that facilitates logarithmic tuning of the GPCR response curves (Fig. 3B).
Epidermal Growth Factor Signaling.
The EGF receptor (EGFR) pathway is a major signaling pathways in animal cells. Cohen-Saidon et al. showed that upon ligand stimulation, single cells show a precise fold-change response relative to the basal level, despite large variation in the absolute magnitude of the response (9). Recent evidence suggests that the EGFR is allosterically regulated (30). The EGFR exists in monomeric and dimeric forms. Binding of the ligand stabilizes the dimers, leading to activation of downstream effectors. It is proposed that modulation of dimerization rate results in allosteric regulation, which produced logarithmic tuning in the receptor activity (Fig. 5F).
Moreover, the allosteric receptor is upstream from various known feedback mechanisms, including ubiquitylation and endocytosis of receptors (44, 45), dephosphorylation of active receptors (46), and feedback by ERK (47). Interestingly, one member of the EGFR family, ErbB2 receptor, lacks a ligand-binding domain but can dimerize with other receptors. Overexpression of ErbB2 has been associated with therapy-resistant cancers (48), suggesting that disrupting the allosteric regulation of the EGF receptors may play a role in disease.
SI Materials
Analysis of the Sensitivity and Error Functions.
We now define the sensitivity function , which summarizes the steepness of the slope of the activity curve is as a function of c and ,
| [S1] |
Looking at the dynamics of activity with respect to ligand changing in time, we get the equation
| [S2] |
Here, we see the first requirements for a protein to give rise to logarithmic sensing: the rate of change of activity is naturally a function of the logarithm of the ligand concentration c. Eq. 5 is complicated by the sensitivity function , which varies with c and is therefore not a simple proportional factor. An ideal logarithmic sensor requires that the activity function depends strictly on , as illustrated by the blue dashed line in Fig. 2B. To measure how well an MWC protein can act as a logarithmic sensor, let us quantify the extent to which varies as a function of c.
First, we note that an ideal logarithmic sensor coincides exactly with an MWC protein at the midpoint of the activity curve (, at the inflection point of a). This point also corresponds to the maximum of the sensitivity function in Eq. 4 (i.e., the peak in Fig. 2C). Any variation in ligand which pushes activity away from the midpoint will lower the sensitivity and will do so in a nonlinear way. Our first task here is to define a regime of the sensitivity curve (the gray region in Fig. 2 B–D) where the MWC protein can approximate a logarithmic sensor, and compute the corresponding error.
To parametrize variation from , we define the effective ligand concentration to be
| [S3] |
Deriving Eq. 4 in terms of , we obtain a natural representation of the sensitivity function,
| [S4] |
In this representation, the sensitivity is now maximized at . Next, we derive a lower limit on the sensitivity function. Let us define the parameter τ, such that for distance from the midpoint of the activity curve, we have a minimum sensitivity,
| [S5] |
With these lower and upper limits on sensitivity, we now define the regime in the response curve over which the MWC protein approximates a logarithmic sensor as
| [S6] |
Using Eq. S3, we can derive a corresponding lower limit on for the range of over which the bound holds, . These limits give the ligand concentration range over which an MWC protein behaves as a logarithmic sensor,
| [S7] |
This range is shown in Fig. 2 B and C, where the sensitivity regimes for different values of are shaded in gray. We see that the range of ligand over which the MWC systems functions as a logarithmic sensor is set by a threshold for sensitivity . The error between the MWC activity curve and the idealized sensor is parametrized by τ. The range over which the MWC protein behaves as a logarithmic sensor depends on how much error the system can tolerate.
To derive the error, we first write the formal expression for an ideal logarithmic sensor,
| [S8] |
We will now use this expression to define an error function to quantify the deviation of the actual activity function a from the idealized one . Combining Eq. 3 and Eq. S8, we have
| [S9] |
At the midpoint of activity () the error function is minimized at , because this is the point where MWC activity coincides exactly with the ideal logarithmic sensor. We observe that the error increases as moves away from 1. Consequently, the error at the threshold τ, , corresponds to the worst case error in the sensitive regime. For example in Fig. 2E, where we set , we have , so the MWC response differs by at most from the ideal logarithmic response in the sensitive regime. The threshold τ serves as a way to analyze how much the response of an MWC protein differs from an ideal logarithmic sensor as we expand the range of ligand concentration over which it is used. The maximum error increases at an asymptotic rate of
This limit shows that the error increases slowly with τ and that the MWC protein can approximate well an ideal logarithmic sensor over a wide range of the activity curve.
With the error function, we can now define the logarithmic regime of an MWC protein, as the ratio of the maximum and minimum ligand concentrations in the sensitive regime
| [S10] |
If we tolerate, for example, error from the ideal logarithmic sensor (corresponding to ), then an MWC protein with cooperativity (as is the case, for example, with hemoglobin and PFK1), we have , so the protein can act as a logarithmic sensor over a 2.45 range of fold change in signal. If, for example, the protein of interest were a monomer (i.e., ) that lacks cooperativity, we would have , so the protein can act as a logarithmic sensor over a 36-fold range of signal. We see from these results that an MWC protein can approximate an ideal logarithmic sensor over a substantial range of ligand concentration. Reducing cooperativity effectively increases the regime over which an MWC protein responds logarithmically to ligand. Eq. S10 tells us that there is an intrinsic trade-off between sensitivity and signaling range. Because N corresponds to cooperativity and corresponds to the width of the sensitivity regime, we see directly that increasing N for a given τ narrows the range over which the sensor can function.
Effects of the Allosteric Constant on the Sensitivity Function.
We first analyze the effects of on when c is in the range and then analyze the general case where c could be near saturation. In the former case, as we derive in the main text,
Fig. S1 shows that shifts logarithmically as is varied, in the same way as the activity curve does.
Next, we analyze the general case for all values of ligand concentration c. The general sensitivity function is defined in terms of the expression,
| [S11] |
For an MWC protein, we have from Eq. 2 that
| [S12] |
| [S13] |
Next, assuming that , we can rewrite the sensitivity function as
| [S14] |
We see that, in the limit (i.e., ), Eq. S14 reduces to the sensitivity function we derive in the main text,
Logarithmic tuning fails for very high or low values of , when c is near saturation. To see why logarithmic tuning fails, we derive the limit of as , corresponding to the ligand concentration being near the lower saturation limit. We can make the simplification , which yields
| [S15] |
Fig. S2B shows the full sensitivity function (Eq. S14) as a solid black line and the approximation in Eq. S15 as a blue dotted line. We see that, as approaches 1, is scaled down by a factor of (shown as a dotted black line). This effect will become noticeable when is small enough to push the center of the sensitivity function close to .
At the upper limit, as , which give the simplification , we can derive
| [S16] |
Fig. S2C shows the Eq. S16 in red. As c approaches , scales down by a factor of . This effect will become noticeable when is large enough to push the center of the sensitivity function close to .
This analysis shows how c and combine to determine the shape of the full sensitivity function and how logarithmic sensing breaks down as ligand concentration nears saturation.
Allosteric Activators and Inhibitors in the MWC Model.
In their original model (21), Monod et al. did not express their “allosteric constant” in the general form but rather proposed a more detailed model where the binding of allosteric activators and inhibitors are explicitly accounted for, in much the same way as the primary ligand. In terms of our notation, their model can be expressed in the form
| [S17] |
where . This version of the model assumes that the activator and inhibitor have and binding sites with dissociation constants and , respectively. Rewriting the expression for L, we get
| [S18] |
If the allosteric effectors are far from saturation, then from the Taylor expansion of we have
| [S19] |
This approximation gives a mechanism for the linear dependence of free energy on the concentrations of allosteric regulators. Shimizu et al. found just such a dependence in experiments on receptor methylation in the bacterial chemotaxis pathway (28).
Logarithmic Tuning in the KNF Model.
Shortly after Monod, Wyman, and Changeux published their MWC model of allostery via conformational selection, Koshland et al. put forth what is now called the induced fit or KNF model of allostery to explain hemoglobin binding kinetics (24). This model proposes that instead of undergoing spontaneous conformational change, individual binding events in one subunit could directly change the binding kinetics of another. This model has the advantage that it can both encapsulate positive cooperativity (like the MWC model) and negative cooperativity, where a given binding even could potentially inhibit the next. In the years after both models of hemoglobin were published, structural work by Perutz gave evidence that the MWC model was indeed more accurate. In reference to the work of Monod et al., Perutz wrote, “These words ring prophetically if we look at the mechanism in terms of quaternary structure” (51).
Be that as it may, the concept of induced fit proved useful for describing other classes of allosteric systems, in particular, those in which negative cooperativity plays an important role (52). Here, we show under what conditions the KNF model can be logarithmically tuned. The KNF model differs from other models of binding typically discussed because the specific geometry of the protein plays an important role, we will use as an example the tetrahedral geometry discussed in the original paper by Koshland et al. (24), which results in the saturation function
| [S20] |
where is the ligand dissociation constant, and the subunit conformations are denoted A and B. By convention, A will be the low affinity inactive state and B will be the high-affinity active state. The interaction strengths and represent the relative strengths of interactions between the A and B conformations and the B conformation with itself, respectively. Here, we allow allosteric effects to enter through . The motivation for this assumption is the underlying model that the allosteric effectors alter the stability of the bonds between the active conformation.
The authors use as a reference interaction strength against which to measure the other two, so it does not have to be explicitly accounted for in Eq. S20. In this model, high cooperativity comes from high stability of the active state B (i.e., and ). Under these conditions, the intermediate terms in the KNF model drop out the saturation function and we have the simplified expression
| [S21] |
where . Here, we see that, in the limits of strong cooperativity, the KNF model satisfies the logarithmic tuning requirement in relationship 9. This observation is consistent with the data originally fitted by Koshland et al. (24), where they use and, for the tetrahedral case, find . Even for the lower end of this range, we have , which is much greater than the next largest coefficient in Eq. S20, .
Detailed Analysis of the GPCR Model.
Here, we present a more detailed derivation of the activation function derived in Eq. 8. We begin again from the system of differential equations for GPCR activation:
From this system of equations, we will solve for , the relative level compared with the total level of G protein . Just by setting derivatives equal to zero, we get
We then use the fact steady-state relationship
to find
just as in Eq. 8. Because is effectively a for the receptors, it is taken as a fixed quantity. On the other hand, β-arrestin signaling alters the rate () at which binds to active receptors. To this end, we will rewrite Eq. 8 to see whether it can be made to look like the form described in relationship 9, with the definition ,
| [S22] |
Here, we see that, if we allow to play the role that plays in the MWC model, with variations in β-arrestin signaling effectively shifting the free energy ε, then the GPCR model almost fits the logarithmic tuning requirement in relationship 9. The confounding element is the factor of that depends on and thus could potentially complicate things. Rearranging this term, we get
From this equation, we see that there dependence on will vanish so long as either or , and consequently under these conditions the system will behave as a logarithmic sensor. In terms of the biochemistry of the GPCR pathway, this means that β-arrestin binding is far from saturation so that is always able to find active receptors, be it at an attenuated rate.
Fold-Change Detection Arises from Logarithmic Sensing and Negative Feedback.
We present here simulations showing fold-change detection arising from a circuit containing allosteric regulation and negative feedback. We use as specific examples the Tar/Tsr receptor system (discussed in Results) and the GPCR system.
Tar/Tsr Receptor and Negative Feedback.
We model the allosteric regulation of the receptor using the MWC model and the negative feedback as described in Shimizu et al. (28) and Pontius et al. (38). The negative feedback via methylation acts on a slower time scale than receptor activation, such that instantaneously responds to changes in ligand and allosteric effector concentrations. Furthermore, and a are related by a linear feedback coupling, such that
| [S23] |
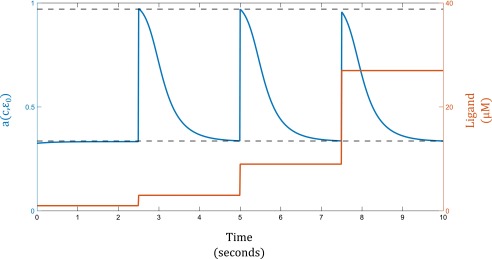
where is the basal activation level to which the system adapts and m is a constant corresponding to the rate of adaptation. When , we have , and the system will show precise adaptation, as expected. Fig. S4 shows the change in Tar/Tsr receptor activity (blue) in response to sequential threefold step increases in ligand concentration (orange). The system gives identical responses for all three steps, performing fold-change detection.
GPCR and Negative Feedback.
The dynamics of the GPCR system are described in the main text (Eq. 8). As described in the main text, allosteric regulation is implemented through , which characterizes the rate of receptor phosphorylation and β-arrestin binding. Although we could express feedback in terms of directly, we may run into problems because is a reaction rate and therefore must be nonnegative. To avoid running into negative values, we rewrite , for some constant β. The differential equations describing the GPCR system are now
| [S24] |
where . Fig. S5 shows the response of the GPCR system to sequential threefold step increase in signal. We see again that a logarithmic sensor coupled with negative feedback yields fold-change detection.
Discussion
In this study, we set out to search for a molecular implementation of a logarithmic sensor that can mediate fold-change detection in sensory systems. We identify that a ubiquitous class of regulation, allostery, has the necessary properties to act as a logarithmic sensor. Allostery has traditionally been thought as a mechanism for generating cooperativity and implementing feedback in signaling systems. Our analysis suggests that allosteric proteins can act as logarithmic sensors. We find that the capacity for logarithmic sensing is not dependent on the specific physical implementations of allostery. Rather, this capacity arises from the basic feature of allostery: the presence of an independent regulation to tune the protein’s activity without altering the ligand-binding kinetics. It is remarkable that the seemingly complex task of computing a logarithm can be encoded within a single protein, and further that this can be accomplished through such a pervasive form of regulation in biological systems. Moreover, beyond proteins, allostery also applies to RNAs. For instance, there is recent evidence that riboswitch activity can be tuned via conformational selection (49). This opens up the possibility of an RNA-based logarithmic sensor that senses metabolite concentration.
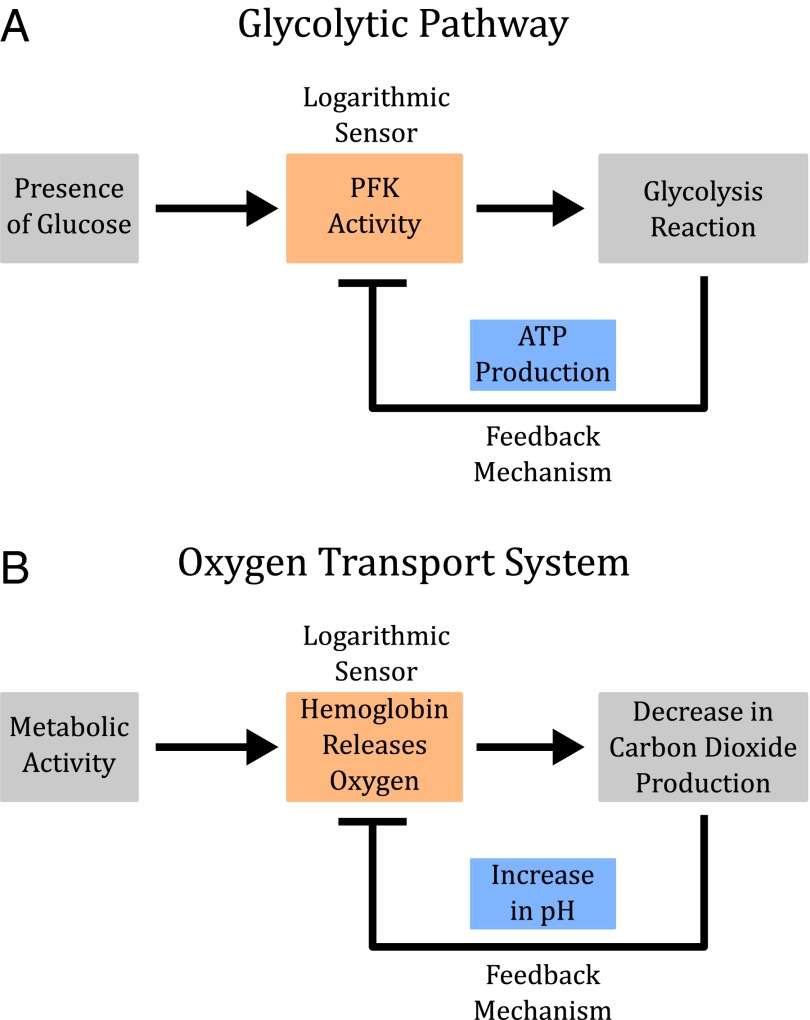
When coupled with linear feedback, allosteric regulation can produce fold-change detection (Fig. 4A). This logarithmic-feedback circuit is an appealing architecture because feedback regulation is another ubiquitous feature of biological systems, and raises the questions of whether logarithmic sensing and the related phenomenon of fold-change detection occurs more broadly in biological processes than is currently appreciated. For instance, in glycolysis, PFK1 is inhibited by ATP and ADP, end products of the pathway, producing a logarithmic-feedback circuit (Fig. 6A) (18). We imagine that fold-change detection might be beneficial in glycolysis to maintain sensitive metabolic activity across a broad range of glucose concentrations. In another example, hemoglobin is regulated by blood pH, in what is known as the Bohr effect (26, 50). High levels of carbon dioxide cause changes in blood pH, which in turn regulate the activity of hemoglobin, producing a logarithmic-feedback motif (Fig. 6B). We imagine that fold-change detection might be beneficial for hemoglobin to maintain sensitivity across a range of altitude, metabolic state, physical activity, lifestyle, or body size, where oxygen level varies.
Fig. 6.
Allostery and feedback in glycolysis and oxygen regulation. (A) PFK1 (PFK) is a key enzyme in glycolysis. PFK1 both catalyzes downstream production of ATP and is allosterically regulated by ATP itself. This system of interactions resembles a logarithmic-feedback circuit, which has the capacity to produce fold-change detection. (B) Oxygen transport in vertebrates is mediated by hemoglobin and feedback via multiple effectors (including carbon dioxide level). This system of interactions forms a logarithmic-feedback circuit, which can produce fold-change detection.
Therefore, beyond their commonly thought of roles as enzymes, transporters, it would be interesting to see whether allosteric proteins may also generally act as quantitative sensors, adjusting detection on a logarithmic scale to maintain sensitivity over a broad response range.
Acknowledgments
We thank Kibeom Kim, Christopher Frick, Harry Nunns, Michael Abrams, Ty Basinger, Enoch Yeung, Tal Einav, Nicholas Frankel, Rob Phillips, and Henry Lester for discussions and suggestions on the manuscript. We also thank Meritxell Canals and Arthur Christopoulos for sharing their raw experimental data on allostery in GPCRs. This work was supported by the Benjamin M. Rosen Fellowship (N.O.), James S. McDonnell Scholar Award in Complex Systems 220020365 (to L.G.), and NSF CAREER Award NSF.145863 (to L.G.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1601791113/-/DCSupplemental.
References
- 1.Martins BM, Swain PS. Trade-offs and constraints in allosteric sensing. PLOS Comput Biol. 2011;7(11):e1002261. doi: 10.1371/journal.pcbi.1002261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Goentoro L, Shoval O, Kirschner MW, Alon U. The incoherent feedforward loop can provide fold-change detection in gene regulation. Mol Cell. 2009;36(5):894–899. doi: 10.1016/j.molcel.2009.11.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Shoval O, et al. Fold-change detection and scalar symmetry of sensory input fields. Proc Natl Acad Sci USA. 2010;107(36):15995–16000. doi: 10.1073/pnas.1002352107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Weber EH, Ross HE, Murray DJ. EH Weber on the Tactile Senses. Psychology Press; East Sussex, UK: 1996. [Google Scholar]
- 5.Pugh EN, Jr, Nikonov S, Lamb TD. Molecular mechanisms of vertebrate photoreceptor light adaptation. Curr Opin Neurobiol. 1999;9(4):410–418. doi: 10.1016/S0959-4388(99)80062-2. [DOI] [PubMed] [Google Scholar]
- 6.Dehaene S. The neural basis of the Weber-Fechner law: A logarithmic mental number line. Trends Cogn Sci. 2003;7(4):145–147. doi: 10.1016/s1364-6613(03)00055-x. [DOI] [PubMed] [Google Scholar]
- 7.Kandel ER, et al. Principles of Neural Science. Vol 4 McGraw-Hill; New York: 2000. [Google Scholar]
- 8.Goentoro L, Kirschner MW. Evidence that fold-change, and not absolute level, of β-catenin dictates Wnt signaling. Mol Cell. 2009;36(5):872–884. doi: 10.1016/j.molcel.2009.11.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cohen-Saidon C, Cohen AA, Sigal A, Liron Y, Alon U. Dynamics and variability of ERK2 response to EGF in individual living cells. Mol Cell. 2009;36(5):885–893. doi: 10.1016/j.molcel.2009.11.025. [DOI] [PubMed] [Google Scholar]
- 10.Thurley K, et al. Reliable encoding of stimulus intensities within random sequences of intracellular Ca2+ spikes. Sci Signal. 2014;7(331):ra59. doi: 10.1126/scisignal.2005237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lee RE, Walker SR, Savery K, Frank DA, Gaudet S. Fold change of nuclear NF-κB determines TNF-induced transcription in single cells. Mol Cell. 2014;53(6):867–879. doi: 10.1016/j.molcel.2014.01.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Delbrück M, Reichardt W, Rudnick D. System Analysis for the Light Growth Reactions of Phycomyces. Princeton Univ. Press; Princeton: 1956. pp. 3–44. [Google Scholar]
- 13.Mesibov R, Ordal GW, Adler J. The range of attractant concentrations for bacterial chemotaxis and the threshold and size of response over this range. Weber law and related phenomena. J Gen Physiol. 1973;62(2):203–223. doi: 10.1085/jgp.62.2.203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Adler M, Mayo A, Alon U. Logarithmic and power law input-output relations in sensory systems with fold-change detection. PLOS Comput Biol. 2014;10(8):e1003781. doi: 10.1371/journal.pcbi.1003781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lazova MD, Ahmed T, Bellomo D, Stocker R, Shimizu TS. Response rescaling in bacterial chemotaxis. Proc Natl Acad Sci USA. 2011;108(33):13870–13875. doi: 10.1073/pnas.1108608108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Marzen S, Garcia HG, Phillips R. Statistical mechanics of Monod-Wyman-Changeux (MWC) models. J Mol Biol. 2013;425(9):1433–1460. doi: 10.1016/j.jmb.2013.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Changeux JP. Allostery and the Monod-Wyman-Changeux model after 50 years. Annu Rev Biophys. 2012;41:103–133. doi: 10.1146/annurev-biophys-050511-102222. [DOI] [PubMed] [Google Scholar]
- 18.Chandra FA, Buzi G, Doyle JC. Glycolytic oscillations and limits on robust efficiency. Science. 2011;333(6039):187–192. doi: 10.1126/science.1200705. [DOI] [PubMed] [Google Scholar]
- 19.Tu Y, Shimizu TS, Berg HC. Modeling the chemotactic response of Escherichia coli to time-varying stimuli. Proc Natl Acad Sci USA. 2008;105(39):14855–14860. doi: 10.1073/pnas.0807569105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Monod J, Changeux JP, Jacob F. Allosteric proteins and cellular control systems. J Mol Biol. 1963;6(4):306–329. doi: 10.1016/s0022-2836(63)80091-1. [DOI] [PubMed] [Google Scholar]
- 21.Monod J, Wyman J, Changeux JP. On the nature of allosteric transitions: A plausible model. J Mol Biol. 1965;12(1):88–118. doi: 10.1016/s0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
- 22.Mello BA, Tu Y. Effects of adaptation in maintaining high sensitivity over a wide range of backgrounds for Escherichia coli chemotaxis. Biophys J. 2007;92(7):2329–2337. doi: 10.1529/biophysj.106.097808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Blangy D, Buc H, Monod J. Kinetics of the allosteric interactions of phosphofructokinase from Escherichia coli. J Mol Biol. 1968;31(1):13–35. doi: 10.1016/0022-2836(68)90051-x. [DOI] [PubMed] [Google Scholar]
- 24.Koshland DE, Jr, Némethy G, Filmer D. Comparison of experimental binding data and theoretical models in proteins containing subunits. Biochemistry. 1966;5(1):365–385. doi: 10.1021/bi00865a047. [DOI] [PubMed] [Google Scholar]
- 25.Keener J, Sneyd J. Mathematical Physiology I: Cellular Physiology. Vol 1. Springer Science & Business Media; New York: 2009. pp. 905–907. [Google Scholar]
- 26.Imai K. The Monod-Wyman-Changeux allosteric model describes haemoglobin oxygenation with only one adjustable parameter. J Mol Biol. 1983;167(3):741–749. doi: 10.1016/s0022-2836(83)80107-7. [DOI] [PubMed] [Google Scholar]
- 27.Müller F, Bönigk W, Sesti F, Frings S. Phosphorylation of mammalian olfactory cyclic nucleotide-gated channels increases ligand sensitivity. J Neurosci. 1998;18(1):164–173. doi: 10.1523/JNEUROSCI.18-01-00164.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Shimizu TS, Tu Y, Berg HC. A modular gradient-sensing network for chemotaxis in Escherichia coli revealed by responses to time-varying stimuli. Mol Syst Biol. 2010;6(1):382. doi: 10.1038/msb.2010.37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Canals M, et al. A Monod-Wyman-Changeux mechanism can explain G protein-coupled receptor (GPCR) allosteric modulation. J Biol Chem. 2012;287(1):650–659. doi: 10.1074/jbc.M111.314278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Macdonald-Obermann JL, Pike LJ. The intracellular juxtamembrane domain of the epidermal growth factor (EGF) receptor is responsible for the allosteric regulation of EGF binding. J Biol Chem. 2009;284(20):13570–13576. doi: 10.1074/jbc.M109.001487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Molokanova E, Trivedi B, Savchenko A, Kramer RH. Modulation of rod photoreceptor cyclic nucleotide-gated channels by tyrosine phosphorylation. J Neurosci. 1997;17(23):9068–9076. doi: 10.1523/JNEUROSCI.17-23-09068.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wootten D, Christopoulos A, Sexton PM. Emerging paradigms in GPCR allostery: Implications for drug discovery. Nat Rev Drug Discov. 2013;12(8):630–644. doi: 10.1038/nrd4052. [DOI] [PubMed] [Google Scholar]
- 33.Lewis M. Allostery and the lac Operon. J Mol Biol. 2013;425(13):2309–2316. doi: 10.1016/j.jmb.2013.03.003. [DOI] [PubMed] [Google Scholar]
- 34.Kalinin YV, Jiang L, Tu Y, Wu M. Logarithmic sensing in Escherichia coli bacterial chemotaxis. Biophys J. 2009;96(6):2439–2448. doi: 10.1016/j.bpj.2008.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Keymer JE, Endres RG, Skoge M, Meir Y, Wingreen NS. Chemosensing in Escherichia coli: Two regimes of two-state receptors. Proc Natl Acad Sci USA. 2006;103(6):1786–1791. doi: 10.1073/pnas.0507438103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Springer MS, Goy MF, Adler J. Sensory transduction in Escherichia coli: Two complementary pathways of information processing that involve methylated proteins. Proc Natl Acad Sci USA. 1977;74(8):3312–3316. doi: 10.1073/pnas.74.8.3312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Endres RG, Wingreen NS. Precise adaptation in bacterial chemotaxis through “assistance neighborhoods”. Proc Natl Acad Sci USA. 2006;103(35):13040–13044. doi: 10.1073/pnas.0603101103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Pontius W, Sneddon MW, Emonet T. Adaptation dynamics in densely clustered chemoreceptors. PLOS Comput Biol. 2013;9(9):e1003230. doi: 10.1371/journal.pcbi.1003230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Fain GL, Matthews HR, Cornwall MC, Koutalos Y. Adaptation in vertebrate photoreceptors. Physiol Rev. 2001;81(1):117–151. doi: 10.1152/physrev.2001.81.1.117. [DOI] [PubMed] [Google Scholar]
- 40.Lane JR, et al. A new mechanism of allostery in a G protein-coupled receptor dimer. Nat Chem Biol. 2014;10(9):745–752. doi: 10.1038/nchembio.1593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Nussinov R, Tsai CJ. Allostery in disease and in drug discovery. Cell. 2013;153(2):293–305. doi: 10.1016/j.cell.2013.03.034. [DOI] [PubMed] [Google Scholar]
- 42.Nussinov R, Tsai CJ, Ma B. The underappreciated role of allostery in the cellular network. Annu Rev Biophys. 2013;42:169–189. doi: 10.1146/annurev-biophys-083012-130257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Rajagopal S, Rajagopal K, Lefkowitz RJ. Teaching old receptors new tricks: Biasing seven-transmembrane receptors. Nat Rev Drug Discov. 2010;9(5):373–386. doi: 10.1038/nrd3024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Carpenter G, Cohen S. 125I-labeled human epidermal growth factor. Binding, internalization, and degradation in human fibroblasts. J Cell Biol. 1976;71(1):159–171. doi: 10.1083/jcb.71.1.159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Avraham R, Yarden Y. Feedback regulation of EGFR signalling: Decision making by early and delayed loops. Nat Rev Mol Cell Biol. 2011;12(2):104–117. doi: 10.1038/nrm3048. [DOI] [PubMed] [Google Scholar]
- 46.Stuible M, et al. PTP1B targets the endosomal sorting machinery: Dephosphorylation of regulatory sites on the endosomal sorting complex required for transport component STAM2. J Biol Chem. 2010;285(31):23899–23907. doi: 10.1074/jbc.M110.115295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Dougherty MK, et al. Regulation of Raf-1 by direct feedback phosphorylation. Mol Cell. 2005;17(2):215–224. doi: 10.1016/j.molcel.2004.11.055. [DOI] [PubMed] [Google Scholar]
- 48.Slamon DJ, et al. Studies of the HER-2/neu proto-oncogene in human breast and ovarian cancer. Science. 1989;244(4905):707–712. doi: 10.1126/science.2470152. [DOI] [PubMed] [Google Scholar]
- 49.Wilson RC, et al. Tuning riboswitch regulation through conformational selection. J Mol Biol. 2011;405(4):926–938. doi: 10.1016/j.jmb.2010.10.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Milo R, Hou JH, Springer M, Brenner MP, Kirschner MW. The relationship between evolutionary and physiological variation in hemoglobin. Proc Natl Acad Sci USA. 2007;104(43):16998–17003. doi: 10.1073/pnas.0707673104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Perutz MF. Stereochemistry of cooperative effects in haemoglobin. Nature. 1970;228(5273):726–739. doi: 10.1038/228726a0. [DOI] [PubMed] [Google Scholar]
- 52.Koshland DE, Jr, Hamadani K. Proteomics and models for enzyme cooperativity. J Biol Chem. 2002;277(49):46841–46844. doi: 10.1074/jbc.R200014200. [DOI] [PubMed] [Google Scholar]