A location-centric network approach to analyzing epidemic dynamics

Abstract

Recent health threats, such as the SARS, H1N1, and Ebola pandemics, have stimulated great interest in network models to study the transmission of communicable diseases through human interaction and mobility. Most current network models have focused on an individual-centric perspective where individuals are represented as nodes, and the interactions among them as edges. Few of these models are concerned with the discovery of the spatial patterns and dynamics of epidemics.

We propose a location-centric, transmission network approach, in which nodes denote locations and edges denote possible disease transmissions between locations. We then identify the dynamics of transmission flows, the dynamics of critical locations, and the spatial-temporal extent of transmission pathways to assess the impact of these spatial dynamics on the evolution of an epidemic.

Results show that transmission flows shift from elementary schools to middle schools and finally universities and professional schools at different phases of an epidemic. Critical locations, identified using network analysis, are responsible for the upsurge in transmission flows during the peaks of the epidemic. The length of transmission pathways shows a power law distribution and their spatial extent is rather small. Insights gained from this study will help devise spatially sensitive strategies to control communicable diseases.

Introduction

Human interaction and mobility behaviors are essential to the transmission of communicable diseases (Gushulak and Douglas 2000). Interactions at homes, workplaces, and schools may cause local transmission, while individuals’ mobility between these places may propagate the transmission to an area-wide epidemic (Eubank et al. 2004; Cauchemez et al. 2008). Recent health threats, such as the SARS, H1N1, and Ebola pandemics have stimulated great interest in network models to study communicable disease transmissions (Salathé et al. 2010; Bian et al. 2012; Gomes et al. 2014; Liu et al. 2014).

A network consists of nodes and edges. Most recent network models have focused on an individual-centric perspective where individuals are denoted as nodes, and the interactions among them are denoted as edges. Individuals’ behaviors (e.g. interaction, mobility) and attributes (e.g. demographics, infection status) are used to simulate an individualized transmission process. Collectively, these individual transmissions contribute to a dispersion pattern at the population level. Although the attributes may include spatial information, such as the location of transmission, it is treated as a spatial stamp of the transmission process because these models focus primarily on health outcomes, such as the number of infected cases during an epidemic (Cooley et al. 2008; Salathé et al. 2010).

Few of these models are concerned with the discovery of the spatial patterns and dynamics of epidemics. For example, how do disease transmissions ‘flow’ in space, are there critical locations of transmission, to what extent do transmissions expand spatially and temporally, and ultimately how do these spatial dynamics influence an epidemic? It is well understood that this information is crucial to devising spatially informed policies to control and prevent communicable diseases (Bian 2013). Current individual-centric networks are inadequate to address the aforementioned questions. An alternative, location-centric perspective is required to easily represent and identify spatial dynamics of the disease transmission process.

The objective of this study is twofold. Firstly, we propose a location-centric, transmission network approach, in which nodes denote locations and edges denote possible disease transmissions between locations. The spatial and temporal co-occurrence and mobility information embedded in the discrete infection cases are used to construct the networks. Secondly, we (1) examine the dynamics of transmission flows drawn from the reconstructed location-centric networks, (2) identify critical locations by applying network centrality analysis, and (3) extract transmission pathways based on the spatial and temporal continuity in the transmission flows. The influence of these spatial dynamics on the epidemic is analyzed. Results are visualized using 2D and 3D approaches.

The study area is a metropolitan area in Midwest China that was affected by both a seasonal influenza epidemic and the H1N1 pandemic at the same time in 2009 (Smith 2009; CDC 2011). Both diseases shared many similar symptoms, such as cough, fever, and headache, except that the symptoms of H1N1 were unusually severe (Fiore et al. 2010). The seasonal influenza infection cases reported during the epidemic are used to support the intended study because of their representativeness and data availability. Insights gained from this study will help design data models in network forms, so that spatial patterns can be easily discerned. From the perspective of disease control, the identification of transmission flows, critical locations, and transmission pathways will help policy makers to develop location-oriented prevention and control strategies.

Study Area and Data

The study area encompasses 60 square kilometers with a population of about 890,000. The dataset used for this study consists of 4,315 anonymous cases; each was clinically diagnosed as seasonal influenza. The epidemic extended over 73 days between September 1 and November 12. Each case is associated with a residential address, a workplace address, the type of workplace, the symptom onset date, and the gender, age, and occupation of the infected person. Although each address has a specific location, but the data available for this study only identifies the residential address within a named residential community and identifies the workplace address in an area equivalent to the census block group in U.S. Based on the occupation information, most cases involve students. Their workplace type typically includes elementary schools, middle schools (Grade 7–12), professional schools, or universities. This dataset was obtained from the China Information System for Diseases Control and Prevention.

Methods

To investigate spatial characteristics of influenza transmission, a total of 73 daily location-centric, transmission networks are constructed using the co-occurrence and mobility information observed in the discrete influenza cases. Critical nodes and transmission pathways are then derived and visualized. The impacts of spatial dynamics on the epidemic are discussed. Each is detailed below.

Construct location-centric transmission networks

Spatial and temporal co-occurrence and mobility are key components in the construction of location-centric, transmission networks. Spatial and temporal co-occurrence refers to the spatial and temporal range shared between discrete events. Social ties have been inferred based on a small number, but high frequency co-occurrences (Crandall et al. 2010). Because interactions between individuals at homes and workplaces have a long duration and high frequency, co-occurrences at these locations are deemed to foster localized disease transmission (Cauchemez et al. 2011; Bian et al. 2012). Presently, the co-occurrence concept has been limited to the construction of static, single-link social ties. Our study extends the concept to the construction of dynamic, extended transmission networks. Mobility, in the context of this study, refers to individuals’ daily travel between homes and workplaces. Mobility facilitates the disease transmission between locations, thus propagating localized transmissions to an area-wide epidemic.

By projecting the location of the 4,315 cases into space, a total of 1,026 distinct locations are identified (including residential and workplace locations). These locations serve as nodes in the 73 daily transmission networks and the disease transmission flows between locations serve as edges. The transmission flows are reconstructed by a spatial co-occurrence constraint and a temporal co-occurrence constraint, as explained below.

Firstly, an influenza case is denoted using the following formula:

$$\mathit{C}\mathit{n}=\mathit{(}\mathit{T}\mathit{n},\mathit{R}\mathit{n},\mathit{W}\mathit{n}\mathit{)},$$

where Cn is the nth case; Tn denotes the symptom onset date of Case n; Rn and Wn denote the residential address and workplace address of Case n, respectively.

Based on the denotation of each case, a transmission flow from Ci to Cj occurs if:

$$\mathit{(}\mathit{R}\mathit{i}\cup \mathit{W}\mathit{i}\mathit{)}\cap (\mathit{R}\mathit{j}\cup \mathit{W}\mathit{j})\ne \mathit{N}\mathit{U}\mathit{L}\mathit{L},$$ (1)

$$\mathit{\text{and }}\mathit{0}<\mathit{T}\mathit{j}-\mathit{T}\mathit{i}\le \mathit{7}\mathrm{.}$$ (2)

The (Ri∪Wi) and (Rj∪Wj) in the first constraint represent individuals’ mobility paths between their residences and workplaces for individuals i and j, respectively. The intersection of the two mobility paths indicates that individuals i and j must share at least one location. For example, they might live or work together. Along with the spatial co-occurrence defined in the first constraint, the second constraint focuses on the temporal co-occurrence. This constraint requires that individual j shows symptoms within seven days after individual i shows symptoms. This indicates that Case j falls within the infectious period of Case i, which is typically seven days. The infectious period of seven days is adopted from the literature (Heyman 2004; Fiore et al. 2010; CDC 2011), including a review of 71 influenza reports (Carrat et al. 2005) and our preliminary sensitivity analysis that experimented with the infectious period from two to ten days. The infectious period of seven days best supports the actual epidemic patterns.

The reconstructed transmission edges derived from the above two constraints are projected into space. They are directed straight lines between two locations rather than the transportation routes actually used by individuals. Of the two location nodes associated with each transmission edge, one is a source location and the other is a target location. The target location is where Ci and Cj co-locate, either at a residence or a workplace, and Ci‘s other location on the mobility path is the source location. Each transmission edge starts on the symptom onset date of Ci at the source location and ends on the symptom onset date of Cj at the target location.

Multiple transmission edges may share the same mobility path when multiple individuals travel along the same path and bring infections between the two locations. This situation is hereafter called multi-edge flows. Internal transmissions at a single location are considered transmission edges without spatial length and direction. The number of cases is represented as an attribute of location nodes. The assemblage of location nodes and the reconstructed transmission edges constitute the location-centric, transmission networks, one network for each of the 73 days of the epidemic. The 1,026 distinct locations remain the same in the 73 daily networks, but the edges between them change over time, as the transmission flows may change locations across time.

Identify critical locations

Two network centrality indices, degree centrality and bridging centrality, are used to identify critical nodes in the transmission networks. Network centrality indices measure how central individual nodes are in a network (Newman 2010). The degree centrality is the count of a node’s connecting edges, which is a measure of a node’s ability to generate out-flows to or receive in-flows from neighboring nodes. A higher value means more active flows (Scott and Carrington 2011). Degree centrality seems the best indicator for disease transmission probability in the context of interaction- and mobility- induced transmissions, while the role of betweenness and closeness centralities remains inconclusive (Christley et al. 2005, Bian et al. 2012).

The bridging centrality is the product of the bridging coefficient and the betweenness centrality. The bridging coefficient indicates whether a node is positioned between high-degree neighboring nodes, and the betweenness centrality measures the extent to which a node is located on the shortest paths of any pairs of other nodes (Borgatti, Everett, and Johnson 2013). A high bridging centrality value implies a node’s ability to control flows between high-degree clusters in a network (Hwang et al. 2008).

Degree centrality and bridging centrality are calculated for all nodes of all 73 daily networks. For each index, 74,898 values are derived (73 days × 1,026 locations = 74,898). Summary statistics of each index, including the sum and standard deviation, are calculated for each location throughout the 73 day period to identify critical nodes in the transmission networks. Locations with continuously high degree centrality values (i.e. great sums and relatively small standard deviations) are considered the critical locations in terms of the magnitude of their transmission flows. Similarly, locations with continuously high bridging centrality values are considered the critical locations in terms of their ability to control transmission flows. Both sets of critical locations are visualized using a 3D approach to show their spatial dynamics (Kwan 2000, 2004).

Extract transmission pathways

A transmission pathway is composed of a series of spatially and temporally continuous transmission edges, including the internal transmission edges. Two spatial transmission edges are considered continuous if both of the following constraints are met: the target location of one transmission edge is identical to the source location of the other transmission edge, and further, one edge starts before or on the day the other edge ends. In the situation of multi-edge flow, each edge represents a segment of a distinct pathway.

The spatial extent and temporal duration of the transmission pathways are analyzed to examine whether the pathway duration has an impact on their spatial extent. The spatial extent of a transmission pathway is measured by the area of the rectangular convex hull that encloses the path. The temporal duration of a path is the total number of days the path lasts, and is referred to as the pathway length. The transmission pathways are displayed in 3D to disclose the spatial and temporal patterns of transmission flows during the epidemic, following the visualization method of Kwan (2000, 2004).

Results and Discussion

Transmission flows

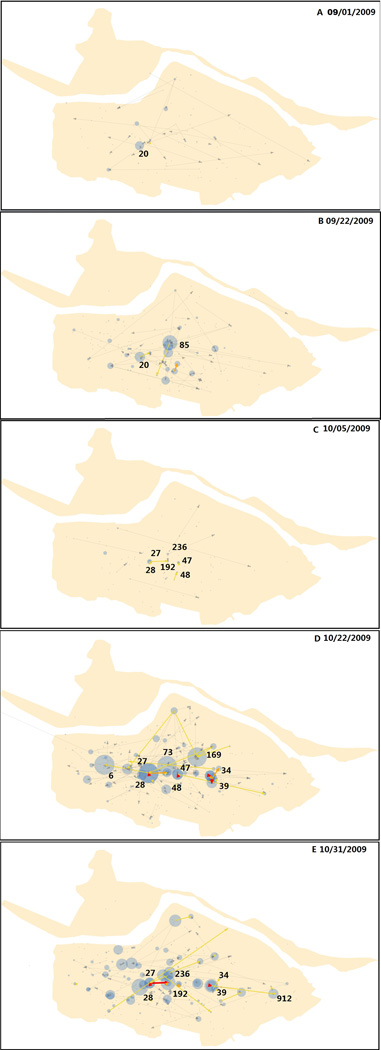
The result includes 73 daily location-centric, transmission networks, one network for each day during the entire epidemic. Figure 1 shows the daily networks of five days, 1 September, 22 September, 5 October, 22 October, and 31 October (hereinafter “9/1”, “9/22”, “10/5”, “10/22”, and “10/31”). The five dates correspond to the dynamics of the epidemic: two minor peaks in the early phase, one major trough, and then two major peaks at the later phase.

Figure 1.

A–E. Transmission networks on 9/1, 9/22, 10/5, 10/22, and 10/31. Blue circles denote location nodes. Their size indicates the number of cases at the location. Arrows denote transmission edges. The yellow, orange and red arrows indicate 1, 2–10, and ≥11 transmission edges, respectively. Note a river runs through the northern part of the study area from west to east.

According to local news sources, the first reported case of the epidemic in the region occurred at the center of the study area in mid-August (a case not included in the dataset). By the time the epidemic had evolved into the first peak on 9/1, the transmission had expanded from its initial location outward to cover a large area. Most target locations are elementary schools because when schools start on 9/1, students already infected with influenza during the summer bring the disease to schools, thus creating the first peak of the epidemic on the school starting date. The elementary school at Location 20 contributes the most to the peak in terms of both the number of cases and flows (Figure 1A). Among all flows, few are out-flows, indicating extensive internal transmissions within the school (Table 1).

Table 1.

Number of transmission flows and cases on the five days.

Date	Total transmission edges	External transmission edges (outflow)	Internal transmissions	Internal transmission rate
1-Sep	105	26	79	0.75
22-Sep	208	52	156	0.75
5-Oct	24	11	13	0.54
22-Oct	493	105	388	0.79
31-Oct	305	75	230	0.75

After a series of mild fluctuations, the epidemic reaches its second peak on 9/22. The transmission flows are more active and more focused than the first peak (Figure 1B, Table 1), as shown by a greater number of in-flows to a target location, a greater number of multi-edge flows, and a greater number of large-case target locations. They remain as elementary schools, such as the one at Location 85 that has the most cases and flows. The second peak could be the result of further spread of the first peak. Extensive internal transmissions at schools might have brought infections to students’ residential locations, as shown by increased out-flows, especially multi-edge ones.

After affecting mostly elementary schools, the epidemic arrives at a trough on 10/5, reaching an epidemic-wide low number of transmission cases and flows (Figure 1C, Table 1). Flows remain active between the campus-dorm location pairs of two universities and a professional school at Locations 27–28, 192–236, and 47–48. The trough might be the result of depletion of susceptible students in the elementary schools after the two initial peaks.

By late October, the magnitude of transmission rises again and the epidemic reaches its highest peak on 10/22 (Figure 1D, Table 1). There is a widespread upsurge of transmission flows between a large number of locations over a large area. Most target locations are middle schools, such as those at Locations 73, 6, and 169, and universities and professional schools, such as Locations 27, 47 and 39. High schools have larger pools of susceptible students, as their student population is two or more times as great as elementary schools in the study area, while universities and professional schools are typically 5–10 times as great as middle schools (or 10–20 times as great as elementary schools).

The most active transmission flows are between campus-dorm pairs of universities and professional schools (e.g. Locations 27–28, 47–48, 39–34). Unlike elementary schools and middle schools where students commute between schools and home, students in university and professional schools reside in dorms (a mandate in the study area). The dorms are either on or near a campus, as shown on the maps. This mobility behavior significantly increases the likelihood of mass interaction among a large number of students, and may explain the extensive transmission once universities and professional schools are affected.

Shortly after this major peak begins to decline, another major peak rises around 10/31 (Figure 1E, Table 1) that is associated with another considerable increase in transmission flows. The transmission flows, although fewer in number, are active at more focused locations with a greater magnitude, effectively maintaining the same magnitude of cases observed at the 10/22 peak (Table 1). Transmissions at middle schools have reduced considerably. Flows between the campuses and dorms of universities and professional schools dominate the transmission, such as those at Locations 27–28, 192–236, and 39–34. Particularly, the two universities (at Locations 27 and 192) share the same dorms, thus generating a considerably large number of cases and flows. This significantly contributes to the second highest peak of the epidemic before the epidemic declines to its end around mid-November.

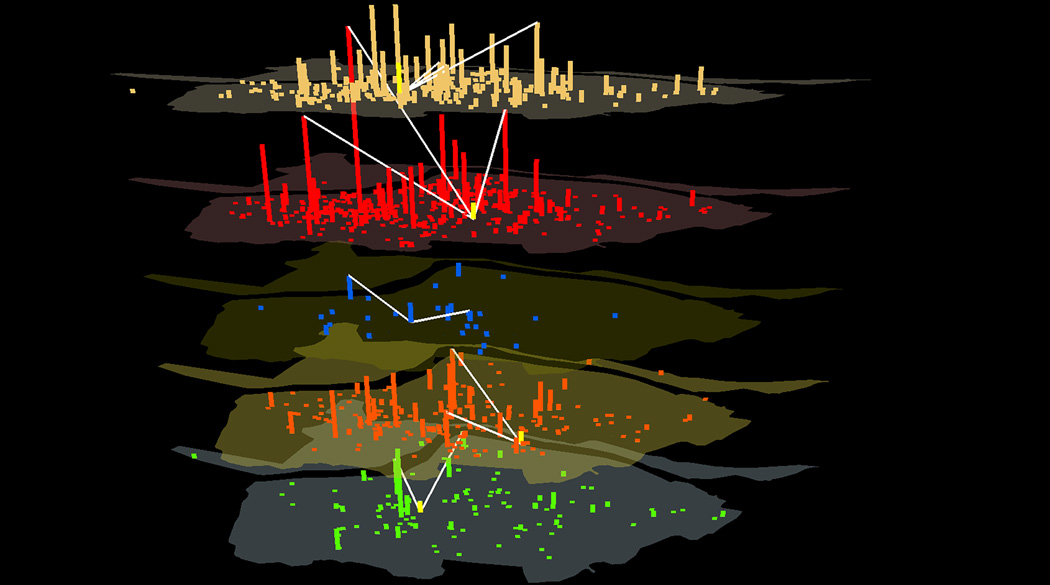
Critical Locations

The top 10 critical locations in terms of the degree centrality that measures the magnitude of transmission flow are listed in Table 2 and shown in Figure 2. These locations have the highest sum of degree centrality and a relatively low standard deviation. Locations identified earlier as having high flows (See the Transmission Flows section) are among those listed. For example, the elementary school at Location 20 has the highest degree at the 9/1 peak, while the elementary school at Location 85 is the highest at the 9/22 peak. Middle schools at Location 73, along with 99, 6, and 41 are among the highest at the 10/22 peak. The university at Location 27 ranks the highest at the last peak on 10/31. If intervention strategies, such as travel restrictions or vaccination, are applied to these schools, the transmission flows might be controlled effectively and reduce their impact on other locations.

Table 2.

Top 10 critical locations ranked by degree centrality and their sum and standard deviation of degree centrality.

Rank	Location ID	Sum	Std	9/1	9/22	10/5	10/22	10/31
1	99	838	18.91656				Active
2	20	746	9.874556	Active
3	73	635	10.47575				Active
4	27	583	5.157231				Active	Active
5	85	529	7.395158		Active
6	41	525	7.811419				Active	Active
7	26	470	5.030425				Active	Active
8	6	429	9.858647				Active	Active
9	142	427	5.633903				Active
10	35	401	5.270788	Active

Figure 2.

Spatial distribution of degree centrality in colored vertical bars for five days from bottom to top: 9/1, 9/22, 10/5, 10/22, and 10/31. Also shown is the location of the highest bridging centrality (yellow vertical bar) for the five days and locations bridged by the high-bridging location (white links).

The critical locations with high degree centrality values extend through the center of the study area (Figure 2). This observation concurs with previous findings that nodes that are central in a network (e.g. have a high degree centrality) tend to be at the geographic center as well (Barthélemy 2010). This is because spatial constraints, such as mobility cost, often favor geographically central locations for important nodes that have a high spatial accessibility in addition to its high network accessibility.

The top 10 critical locations in terms of the bridging centrality are listed in Table 3 and shown in Figure 2. These locations possess the highest sum of bridging centrality, and a relatively low standard deviation. These locations, mostly residential communities, bridge between high-flow middle schools, fostering cross transmissions. For example, the top ranked residential community at Location 191 (Table 3) bridges between the top ranked high-flow middle schools at Locations 99, 73, and 41 (Table 2). All 10 critical locations are active at the 10/22 peak, each connecting up to seven middle schools with each other. These may explain why middle schools account for a considerable proportion of the target locations during the major peak on 10/22. For a clearer view, only the location with the highest bridging centrality is shown for each day (Figure 2). The high-bridging locations play an influential role in sustaining the momentum of epidemic. Spatially oriented intervention strategies at these locations might have the divide and conquer effect to dissect spatially continuous disease transmissions into localized transmissions.

Table 3.

Top 10 critical locations by bridging centrality and the sum and standard deviation of bridging centrality.

Rank	Location ID	Sum	Std	9/1	9/22	10/5	10/22	10/31
1	191	9417.908	17.3513				Active
2	88	6378.168	17.36493				Active
3	222	6364.241	17.71181				Active	Active
4	28	4566.322	12.20597				Active
5	759	4081.006	15.98819				Active
6	255	4025.136	11.84818				Active
7	26	4006.323	9.782303		Active		Active
8	97	3710.142	12.72711				Active	Active
9	163	3321.843	9.417358				Active
10	27	3150.414	9.508776				Active	Active

Transmission Pathways

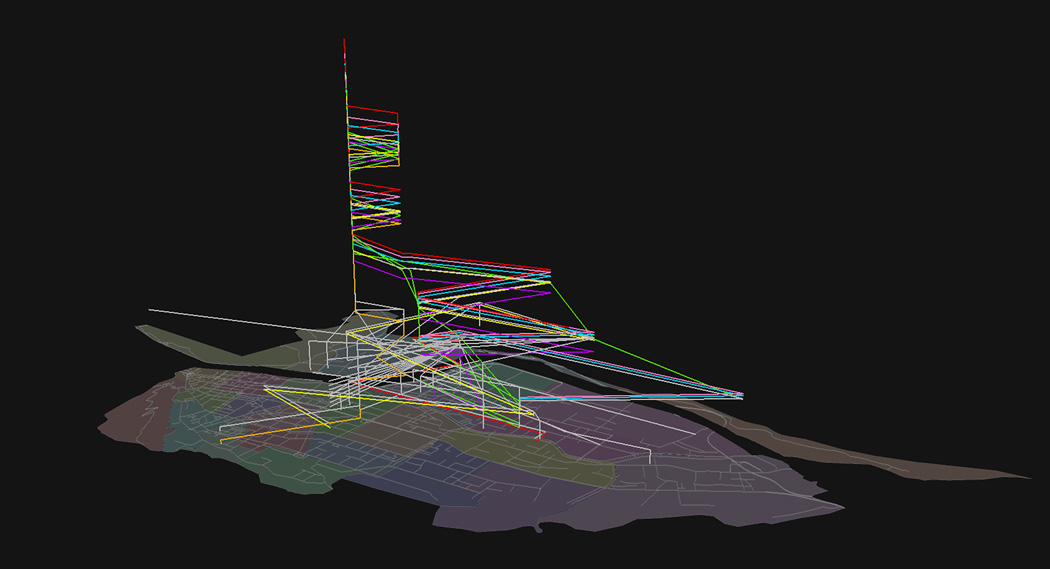
In total, 17,985 transmission pathways are generated. For viewing clarity, the top 5 percent (955 in total) longest pathways are visualized in 3D (Figure 3). The value in the third dimension records the date when the transmission flow reaches a location. The horizontal segments are transmission flows between locations. The vertical segments indicate internal transmissions lingering at a single location for multiple days.

Figure 3.

Top 5 percent longest transmission pathways. The vertical dimension shows the temporal range of 73 days. The color-encoded seven longest pathways are slightly shifted in the vertical direction to distinguish between them. Other pathways are displayed in light grey.

The seven longest pathways (40–42 days) converge to one location, the university at Location 27, and form the longest internal transmission of the epidemic. This is due to the large student population on campus and the mass flow between the campus and dorms.

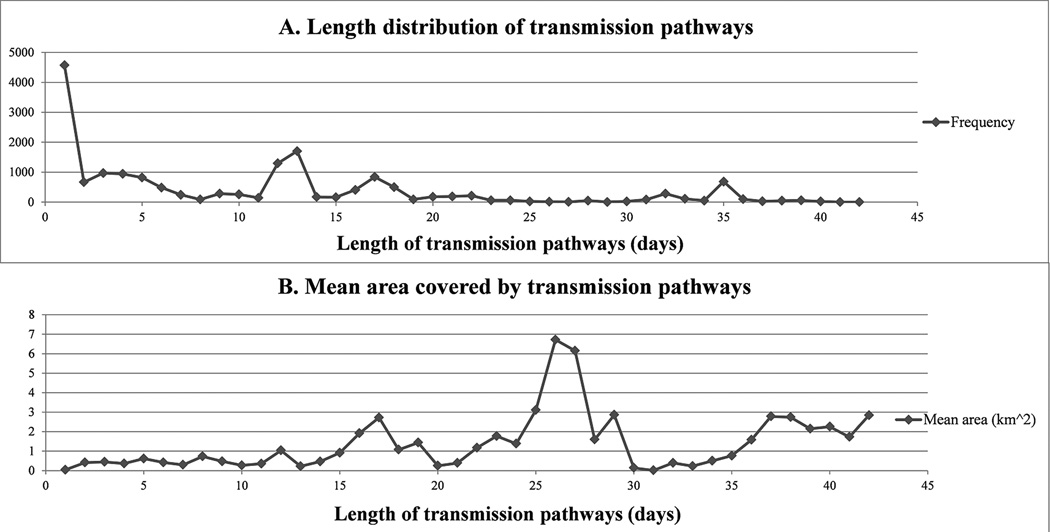
Approximately 25 percent of transmission pathways last only one day. The next length range of 2–10 days accounts for another 25 percent. The third length range of 11–20 days represents more than 30 percent of all pathways. The longest 5 percent of pathways are from 35 to 42 days. The length of the pathways follows a trend closely resembling a power law distribution (α=2.69, p-value from the Kolmogorov-Smirnov test =0.99) (Figure 4A). This implies that while most flows are short-lived, a few have a long duration. This observation is similar to the reported human travel trajectory patterns (Gonzalez et al. 2008; Barthélemy 2010), and reflects the individual mobility pattern behind the transmission pathways.

Figure 4.

A. Frequency distribution of transmission pathway length, p(Y) ~ X^−2.69. B. Average area covered by pathways.

The average area covered by the rectangular convex hull of transmission pathways (Figure 4B) does not increase monotonically with the pathway length. Most pathways, short or long, are within an area of 3 km². It implies that the long pathways tend to move between locations (e.g. campus and dorms) repeatedly over time, thus having a long duration within a small area. The greatest degree of spatial spread is caused by several individuals who have long mobility paths. This coincides the previous finding that the spread of the disease in space is usually caused by a few long-distance travelers (Holmes 1997; Eubank et al. 2004).

Critical locations with high-degree flows, by both internal and external transmission, may lengthen an epidemic, as in the situation of Location 27 shown in Figure 3. This in turn gives rise to the possibility of long-distance travelers’ infections, expanding the spatial extent of the epidemic. Thus, closing high-flow locations during an epidemic can not only control the internal transmissions, but also reduce the spatial and temporal extent of the epidemic.

Conclusions

The location-centric approach proposed in this study is critical to improve our understanding of transmission dynamics of communicable diseases in space, as well as to stimulate new designs for epidemiological modeling. The location-centric network approach is a progress toward this goal, but it is also in a great need of devising spatially and temporally sensitive network indices that could quantitatively characterize the spatial dynamics of epidemics.

Biographies

SHIRAN ZHONG is a Ph.D. candidate in the Department of Geography, University at Buffalo, the State University of New York, Amherst, NY 14261. E-mail: shiranzhbuffalo.edu. His research interests include spatial networks, individual-based epidemiological modeling, and forecasts of influenza epidemics.

LING BIAN is a professor in the Department of Geography, University at Buffalo, the State University of New York, Amherst, NY 14261. E-mail: lbianbuffalo.edu. Her research interests include spatial networks, individual-based epidemiological modeling, and inter-operable environmental models.