The Precision of Mapping Between Number Words and the Approximate Number System Predicts Children’s Formal Math Abilities

Abstract

Children can represent number in at least two ways: by using their non-verbal, intuitive Approximate Number System (ANS), and by using words and symbols to count and represent numbers exactly. Further, by the time they are five years old, children can map between the ANS and number words, as evidenced by their ability to verbally estimate numbers of items without counting. How does the quality of the mapping between approximate and exact numbers relate to children’s math abilities? The role of the ANS-number word mapping in math competence remains controversial for at least two reasons. First, previous work has not examined the relation between verbal estimation and distinct subtypes of math abilities. Second, previous work has not addressed how distinct components of verbal estimation – mapping accuracy and variability – might each relate to math performance. Here, we address these gaps by measuring individual differences in ANS precision, verbal number estimation, and formal and informal math abilities in 5- to 7-year-old children. We found that verbal estimation variability, but not estimation accuracy, predicted formal math abilities even when controlling for age, expressive vocabulary, and ANS precision, and that it mediated the link between ANS precision and overall math ability. These findings suggest that variability in the ANS-number word mapping may be especially important for formal math abilities.

Introduction

Educated adults and children have at least two means of representing and processing numerical information. They can use the Approximate Number System (ANS), which forms quick, imprecise numerical estimates without relying on serial counting (Dehaene, Dehaene-Lambertz, & Cohen, 1998), or they can use an exact number system that represents numerical information precisely via counting and number words, and that is essential for much of school mathematics (Dehaene, 1992).

The ANS and exact number representations can be distinguished in several ways. The ANS is present in humans from birth (Izard, Sann, Spelke, & Streri, 2009) and also has been demonstrated in non-human animals including fish (Dadda, Piffer, Agrillo, & Bisazza, 2009), rodents (Meck, Church, & Gibbon, 1985), whales and dolphins (Abramson, Hernandez-Lloreda, Call, & Colmenares, 2013), and non-human primates (Cantlon & Brannon, 2006)—its presence in these pre-verbal and non-verbal populations shows that the ANS does not rely on language or an understanding of external symbols. Non-verbal ANS comparison tasks – in which participants typically are presented with two arrays of stimuli that differ by varying numerical ratios (e.g., two arrays of dots, or two sequences of tones) and must indicate which is more numerous – reveal that the ANS represents number in a noisy, continuous fashion along a mental number line, with increasing overlap between neighboring numerical representations as the target quantity grows (Dehaene, 1992; Piazza, Izard, Pinel, Le Bihan, & Dehaene, 2004; van Oeffelen & Vos, 1982). As a result, performance on ANS comparison tasks is ratio-dependent – quantities that differ by larger ratios are more easily distinguished than quantities that differ by finer ratios. The precision of ANS representations (i.e., the degree of non-overlap between neighboring representations) is often measured as the Weber fraction (w), which improves over human development (Halberda & Feigenson, 2008; Halberda, Ly, Willmer, Naiman, & Germine, 2012; Libertus & Brannon, 2010; Odic, Libertus, Feigenson, & Halberda, 2013; Xu & Spelke, 2000) and also varies among individuals in a given age group (e.g., Halberda, Mazzocco, & Feigenson, 2008; Libertus, Feigenson, & Halberda, 2011; Starr, Libertus, & Brannon, 2013).

In contrast, the exact number system is uniquely human, and is slowly acquired over the course of several years as children learn to use number words to represent numerical concepts (Carey, 2009; Feigenson, Dehaene, & Spelke, 2004; Le Corre & Carey, 2007; Wynn, 1992). The exact number system appears to depend on language, as people living in communities that lack a verbal counting routine lack exact large number concepts (Frank, Everett, Fedorenko, & Gibson, 2008; Gordon, 2004; Pica, Lemer, Izard, & Dehaene, 2004; Spaepen, Coppola, Spelke, Carey, & Goldin-Meadow, 2011). Critically, whereas the Approximate Number System lacks the precision to precisely represent large numbers (e.g., to represent exactly 50, as distinct from 49 and 51), exact numbers support such precision.

Despite the differences between the ANS and exact number words, children eventually learn a correspondence between the two systems. The development of this mapping is protracted (Crollen, Castronovo, & Seron, 2011; Le Corre & Carey, 2007; Odic, Le Corre, & Halberda, 2015; Pinheiro-Chagas et al., 2014) and may not be causally linked (Gunderson, Spaepen, & Levine, 2015), but, once complete, it allows children and adults both to label approximate number representations with exact number words, and to produce approximate representations given an exact number word. For example, a five-year-old child shown a display of 10 dots presented too quickly to count can translate the resulting imprecise ANS representation of about 10 dots to arrive at a verbal estimate of “ten,” and a child asked to produce a particular number of actions, e.g., quickly tapping “ten times without counting” will produce an approximately correct number of taps (Odic, Le Corre, et al., 2015).

Although all people who use exact number words can form a mapping between these words and the Approximate Number System, the ease with which people map between number formats and the quality of this mapping may differ from person to person (Lyons, Ansari, & Beilock, 2012). Much as we can index individual differences in ANS precision using a non-verbal ANS comparison task, we can index individual differences in the mapping between the ANS and exact number words using a verbal estimation task¹. In a typical version of this task, participants are shown some number of dots too quickly to count and must verbally report how many there were. This yields two measures of performance. First, performance reflects verbal estimation accuracy (e.g., a participant should produce a number word close to “twelve” for 12 dots, “twenty-three” for 23 dots, etc.). By plotting the participant’s verbal response against the target number, mapping accuracy can be measured through the intercept, slope, and error rate of their responses (i.e., error rate = response - target; Crollen et al., 2011; Izard & Dehaene, 2008; Odic, Le Corre, et al., 2015). If perfectly accurate, participants’ average intercept and error rate will be 0, and their slope will be 1 (i.e., for every additional item in the target array, the participant should increment their estimate by one number word in their known list). Estimation accuracy depends on several factors including children’s ability to calibrate the mapping between the ANS and number words (Sullivan & Barner, 2014), potential observer biases (Barth & Paladino, 2011), and the range of number words known (Lipton & Spelke, 2005).

Verbal estimation tasks also produce a second measure of performance: estimation variability. Estimation variability reflects the degree to which a participant’s verbal responses vary from trial-to-trial (Cordes, Gelman, Gallistel, & Whalen, 2001; Odic, Im, Eisinger, Ly, & Halberda, 2015). For example, a child who is shown 15 dots on three occasions and reports seeing “five,” “fifteen,” and “twenty-five” will be (on average) perfectly accurate, but his estimation variability will be high compared to a child who says “fourteen,” “fifteen,” and “sixteen.” Though often measured as a Coefficient of Variance (CV; the standard deviation of all responses for a given stimulus number divided by that number), we have previously shown that estimation variability can be more robustly captured through a simple maximum-likelihood estimation (MLE) method that returns an estimate that we call σ (Odic, Im, et al., 2015)². Children with a lower σ are less variable/more precise in their verbal estimates.

What is the relation between the ANS, exact number words, and math abilities?

Do individual differences in the mapping between the ANS and exact number words affect math performance? One reason to think so is that the ANS itself appears related to math performance. Prior studies that measured ANS representations without requiring any mappings to words or symbols found evidence of a link between individual differences in ANS precision and school math abilities (for a review, see Feigenson, Libertus, & Halberda, 2013). For example, Halberda, Mazzocco, and Feigenson (2008) showed that adolescents’ ANS precision in a number task using non-symbolic dot arrays related to their prior performance on standardized symbolic math assessments. Subsequent work revealed that this relation between the ANS and math is present prior to schooling (Bonny & Lourenco, 2013; Libertus et al., 2011) and is maintained throughout adulthood (DeWind & Brannon, 2012; Halberda et al., 2012; Libertus, Odic, & Halberda, 2012; Lourenco, Bonny, Fernandez, & Rao, 2012; Lyons & Beilock, 2011). Further, ANS precision measured in infancy or in the early preschool years also predicts later math performance (Libertus, Feigenson, & Halberda, 2013a; Mazzocco, Feigenson, & Halberda, 2011b; Starr et al., 2013). Although some studies failed to find a link between ANS precision and math ability (e.g., Castronovo & Göbel, 2012; Gilmore et al., 2013; Price, Palmer, Battista, & Ansari, 2012; Sasanguie, De Smedt, Defever, & Reynvoet, 2012), recent meta-analyses support the existence of this link (Chen & Li, 2014; Fazio, Bailey, Thompson, & Siegler, 2014; Schneider et al., 2016).

If having more precise ANS representations is linked to better symbolic math performance, this raises the question of whether the mapping between the ANS and exact number words predicts additional variance in math abilities. Better mappings could plausibly provide children with a more accurate or reliable sense of the approximate magnitude corresponding to a number word or symbol, thereby improving mathematical intuitions. Indeed, children’s exact number abilities – especially those related to their emerging understanding of exact number symbols – have also been shown to be important for math achievement. For example, Holloway and Ansari (2009), Brankaer and colleagues (2014), and Sasanguie and colleagues (Sasanguie et al., 2012; Sasanguie, Defever, Maertens, & Reynvoet, 2013) found that children’s performance on a symbolic number comparison task (e.g., showing participants two Arabic numerals and asking them to quickly judge which is greater) correlated with math abilities. Similarly, Kolkman and colleagues (2013) found that kindergarteners’ performance on a symbolic number comparison task and a symbolic number line estimation task (but not on a non-symbolic number comparison task or a non-symbolic number line estimation task) predicted math performance in first grade. Other studies have found that children with math learning disabilities show significantly worse performance on symbolic number tasks than children without math learning disabilities (De Smedt & Gilmore, 2011; Iuculano, Tang, Hall, & Butterworth, 2008; Landerl & Kölle, 2009; Rousselle & Noel, 2007). These findings have sometimes been taken to indicate that the mapping of number words and symbols to their meanings is critical for math achievement—perhaps even more important than the ANS itself for the math skills tested (for a review, see De Smedt, Noel, Gilmore, & Ansari, 2013). However, some have recently questioned whether symbolic number comparison tasks actually reflect any use of approximate number representations. Lyons, Nuerk, and Ansari (2015) suggested that ratio effects in symbolic tasks (e.g., taking longer to respond that 19 is more than 17 than to respond that 19 is more than 11) do not reflect a mapping to approximate number representations, but instead stem from more general issues of symbolic processing (like frequency effects of particular number symbols). If so, then previously observed correlations between ratio effects in symbolic number tasks and math performance may not reveal anything about the role of the mapping between the ANS and number words in mathematical thinking.

One way to address this issue is to use tasks that more directly probe the mapping between the ANS and exact number words. The verbal estimation task described earlier requires explicit translation between non-symbolic quantities and symbolic quantities, and as such may be better suited to asking whether individual differences in the ANS-number word mapping relate to math abilities. However, previous studies using verbal estimation tasks have yielded mixed results with regard to math performance. Some verbal estimation studies have found a significant relation between ANS-number word mapping and math ability in children. For example, Mazzocco, Feigenson and Halberda (2011a) found that in a sample of ninth-graders, individual differences in ANS precision and verbal estimation independently explained variability in children’s standardized math test performance. Similarly, Pinheiro-Chagas and colleagues (2014) found that 10-year-old children’s ANS and verbal estimation performance each correlated with calculation skills, with verbal estimation partly mediating the relation between ANS and calculation. Mundy and Gilmore (2009) found that the accuracy of 6- to 8-year-old children’s mappings between non-symbolic quantities and number words predicted a small but significant amount of variance in math performance. And Bartelet and colleagues (2014) found that kindergarteners’ verbal number estimation skills predicted their arithmetic performance in first grade, whereas their efficiency on a non-symbolic ANS comparison task did not. However, other studies found no evidence of this association—Lyons and colleagues (2014) observed no reliable link between success at estimating the numerosity of a dot array and math ability in first- through sixth-grade children (Lyons, Price, Vaessen, Blomert, & Ansari, 2014). And other studies found mixed evidence within a single sample—in a study by Castronovo and Göbel (2012), adults’ verbal estimation error rates correlated with math abilities, but their estimation variability did not. Together, these findings do not offer a coherent picture of the relation between the ANS, verbal estimation, and mathematics.

At least two possibilities may help explain these divergent findings. First, verbal estimation abilities may be more important for some math skills than others. In preschool and early elementary school instruction, mathematics is often described as comprised of informal and formal components (Baroody, 1987; Baroody & Wilkins, 1999). Informal math knowledge is acquired from children’s everyday experiences with collections or events in their environment. For example, preschool-aged children’s informal math abilities include counting, comparing number words to determine which is greater, and determining the answers to simple arithmetic problems using tokens or fingers. In contrast, formal math knowledge requires an understanding of symbols and mathematical conventions, and hence is learned through explicit instruction. Children’s formal math abilities include reading and writing Arabic numerals, understanding the place value system, and recalling memorized addition, subtraction, and multiplication facts.

The distinction between formal and informal aspects of mathematics plays an important role in interpreting the correlations between ANS precision and math ability. In a recent study, Libertus, Feigenson, and Halberda (2013b) found that 3- to 7-year-old children’s ANS precision predicted their informal but not their formal math abilities up to two years later. In adults, Lourenco and colleagues (2012) showed that ANS precision correlated with performance on the Woodcock-Johnson (WJ) calculation subtest and KeyMath geometry subtest, but not with the WJ math fluency, applied math problems, or quantitative concepts subtests (but see Inglis, Attridge, Batchelor, & Gilmore, 2011, for a failure to find a link between any WJ math subtest and ANS acuity in adults). In contrast, Holloway and Ansari (2009) found that children’s performance on a symbolic number comparison task, but not on a non-symbolic ANS comparison task, significantly correlated with performance on the WJ math fluency subtest and marginally with the calculation subtest. Taken together, these findings suggest that the link between ANS precision and exact number representations does not play a uniform role across all aspects of mathematics. Verbal estimation abilities may likely be more closely related to those aspects of math that heavily rely on understanding the meaning of number words and symbols (i.e., formal math abilities).

A second potential explanation for the discrepancies in the literature is that only some indices of verbal number estimation may be linked to math abilities. In particular, the accuracy of the mapping between the ANS and exact number words may play a distinct role from the variability in this mapping. If, for example, a child uses the mapping between number words and the ANS to perform quick mental arithmetic (accessing approximate representations to estimate the answer to math problems that use exact number symbols), a highly variable mapping would lead to many more errors over time, even if the mapping is on average accurate. Similarly, a highly variable mapping may lead to a low-confidence internal signal, leading children to blindly guess or to use other non-optimal strategies (e.g., see Odic, Hock, & Halberda, 2014). As a result, individual differences in the variability of children’s mappings between ANS representations and exact number words may affect math abilities differently than estimation accuracy.

Goals of the current study

The goals of the present study were twofold. First, we aimed to identify whether children’s symbolic math abilities depend on both verbal estimation accuracy (intercept, slope, error rate) and verbal estimation variability ( σ), even when ANS precision is controlled for. Second, we aimed to investigate the degree to which children’s ANS precision and verbal estimation accuracy and variability are differentially linked to informal versus formal math abilities. To this end, we tested 5- to 7-year-old children on a verbal number estimation task (to measure their accuracy through intercepts, slopes, error rates and their variability through σ), a non-symbolic ANS comparison task (to measure their ANS precision, or w), and a standardized assessment of informal and formal math abilities. We focused on this age range because previous work shows that 5-year-olds have established a mapping between the ANS and number words (Le Corre & Carey, 2007; Odic, Le Corre, et al., 2015), and because 5- to 7-year-old children are at the point of transitioning from mostly informal math skills to more formal ones.

Method

Participants

We tested 51 children (23 females, average age = 6 years 8 months, range: 5 years, 1 month to 8 years, 0 months). Data from two additional children were excluded because the children were unable to complete all three tasks. Most children came from families of middle to high socio-economic status, all from the Baltimore area. Parents of all children provided informed written consent prior to their child’s participation, and all children received a small gift (e.g., toy or book) to thank them for their participation.

Materials and Procedure

Children were tested in the laboratory and completed three tasks, all in the same order: a verbal Number Estimation task, then a standardized assessment of math ability (Test of Early Mathematics Ability, TEMA-3, Ginsburg & Baroody, 2003), and finally an Approximate Number System (ANS) Comparison task. The tasks were administered in this order so that our primary measure of interest—performance in the Number Estimation task—would not be biased by children first completing another numerical task that used either number words or dot arrays. We administered the ANS Comparison task last so that it would not immediately follow the Number Estimation task (as both tasks involved dot arrays, and might therefore lead to decreased engagement). In addition, parents completed an assessment of children’s expressive vocabulary (the Developmental Vocabulary Assessment for Parents, the “DVAP”, Libertus, Odic, Feigenson, & Halberda, 2015). It took children about 5–10 minutes to complete the Number Estimation task, 20–30 minutes to complete the TEMA-3, and 5–10 minutes to complete the ANS Comparison task.

Number Estimation task (“How many?”)

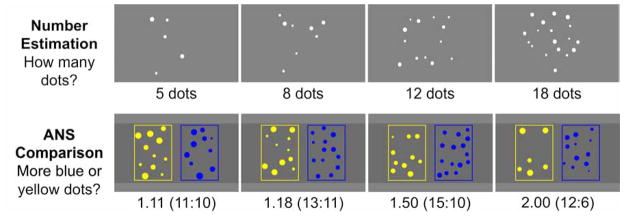
Children were told that they would see briefly flashed displays of dots on a computer screen, and should say how many dots appeared in each flash (Figure 1). Unlike in the ANS Comparison task (see below), children were asked to produce a number word on each trial. The experimenter initiated each trial when children appeared to be attentive (i.e., quietly looking at the screen), and recorded their response by pushing a button as soon as they answered. In addition, the experimenter wrote down all responses on a piece of paper and the computer recorded children’s responses in an audio file. The stimuli were arrays of 5, 8, 12, or 18 white dots on a gray background, and each array was presented for 2000 ms on a 13-inch laptop screen (i.e., long enough for comfortable viewing, but too short for serial counting). We chose these stimulus numerosities to ensure that the arrays triggered ANS representations rather than non-cardinal representations of individual objects (as is often the case for arrays containing four or fewer items), and so that the numerosities fell within the range of known number words for all of our participants (i.e., numbers < 20). To verify that children in fact knew the number words for all target values, children were asked to count up to the biggest number they knew; all children reliably counted to at least 22. We avoided choosing stimulus numerosities that were too close to each other to be reliably distinguishable; hence the numerosities all had a ratio of at least 1.5 from the next nearest numerosity. The dots were heterogeneous in size and were drawn from a uniform distribution of 20 to 50 pixels. Finally, although we only presented four different stimulus numerosities, we expected that the inherent noisiness of the Approximate Number System would lead children to experience more variability between the stimuli (i.e., children would be unaware that they had been shown just four different numerosities).

Figure 1.

Sample stimuli for the Number Estimation task (top panel) and ANS Comparison task (bottom panel)

Children received four practice trials containing three and four dots, followed by 32 test trials (8 trials for each numerosity, presented in random order). After each 2000 ms target stimulus, a blank screen remained visible until children responded. Regardless of the correctness of their response, children always received neutral positive feedback after each practice and test trial (e.g., “Great!” “Awesome!”). We used neutral positive feedback rather than accurate feedback in order to avoid discouragement, and because previous studies show that feedback can modify estimation abilities within a single experimental session (Izard & Dehaene, 2008). Because we were interested in individual differences in children’s existing mappings, we avoided providing feedback that might change children’s responses.

Standardized mathematics assessment

To assess children’s mathematics abilities we administered Form A of the Test of Early Mathematics Ability (TEMA-3; Ginsburg & Baroody, 2003), which has been normed for children between the ages of 3 years 0 months and 8 years 11 months. The TEMA-3 is comprised of 72 items divided into two broad categories. One category tests informal math abilities such as numbering skills (e.g., verbally counting the number of objects on a page), number-comparison facility (e.g., determining which of two spoken number words is larger), informal calculation (e.g., solving word problems with the aid of tokens or fingers), and informal number concepts (e.g., the cardinality principle, i.e., knowing that the last number in a count sequence is the number of items in the set). The other TEMA-3 category tests formal math abilities such as numeral literacy (e.g., reading and writing Arabic numerals), mastery of number facts (e.g., retrieving addition, subtraction, and multiplication facts), calculation skills (e.g., solving mental and written addition and subtraction problems), and number concepts (e.g., answering how many tens are in one hundred). Although the authors of the TEMA have not published factor analyses of TEMA items, subsequent studies found that children’s performance was better fit by a model containing multiple subtypes of mathematical abilities, as opposed to a single math ability score (Ryoo et al., 2015).

We administered the TEMA-3 using the standardized procedure, i.e., the first item administered was determined by the child’s age, after which we administered items consecutively and stopped after the child incorrectly answered five items in a row. Items before the age-defined starting point were only administered if children did not initially succeed on five consecutive items. No feedback was given.

ANS Comparison task (“Which is more?”)

To measure the precision of children’s Approximate Number System (ANS) representations, we administered a version of Panamath (the Psychophysical Assessment of Number-sense Acuity; panamath.org; Halberda & Ly, in preparation) – an approximate number discrimination task. Children were shown arrays of spatially separated blue and yellow dots on a 13-inch laptop screen and were asked to indicate whether more of the dots were blue or yellow (Figure 1). The experimenter initiated each trial when children appeared attentive (i.e., quietly looking at the screen). Each stimulus array was visible for 2000 ms and was followed by a blank screen that remained until children gave a verbal response (e.g., “yellow”). The experimenter immediately pressed the corresponding key on an external keyboard (e.g., “y” for “yellow”). The computer provided positive (e.g., ‘That’s right!’ ‘Fantastic!’) or negative feedback (e.g., ‘Oh, that’s not right.’). We provided accurate feedback in this task in accordance with the methods used in previous studies of ANS discrimination (e.g., Halberda & Feigenson, 2008; Halberda et al., 2008; Libertus et al., 2011, 2013a). Children were familiarized to the task and feedback on four practice trials during which the experimenter provided additional verbal feedback to ensure that children understood the task and were motivated to participate.

Following these practice trials, children completed 56 test trials. On each of these trials, the presented numerosities were drawn randomly from one of seven numerical ratio bins: 1.08, 1.11, 1.15, 1.18, 1.25, 1.5, and 2.0 (with the absolute number of dots in each collection varying between 5 and 22, such that a trial with, e.g., 5 yellow versus 10 blue dots would contribute to the 2.0-ratio bin). On half of the trials the yellow dots were more numerous and on the other half the blue dots were more numerous. Orthogonally, the dots in each array varied in size in order to discourage children from using dot size as a cue. The default radius of the dots was 60 pixels and the maximum variability in size between the dots was +/−35%. Previous research has found that non-numerical aspects of an array can affect numerical performance (Clayton, Gilmore, & Inglis, 2015; Gebuis & Reynvoet, 2012; Smets, Sasanguie, Szücs, & Reynvoet, 2015). As such, on half of the trials the two arrays were equated for individual dot size (i.e., the average size of the dots in each collection was equal). On the other half of the trials, the cumulative surface area of the blue dots and the yellow dots was equated.

Expressive vocabulary

We measured children’s expressive vocabulary using the Developmental Vocabulary Assessment for Parents (DVAP, Libertus et al., 2015). The DVAP questionnaire contained a list of 212 nouns, verbs, and adjectives taken from Form A of the Peabody Picture Vocabulary Test (PPVT-4; Dunn & Dunn, 2007), and parents were asked to indicate which of the listed words they had heard their child say. Previous work has established the DVAP as a stable and accurate indicator of children’s expressive verbal knowledge that correlates with children’s PPVT-4 performance (Libertus et al., 2015). Parents completed the DVAP either before the child’s testing session began or, if they did not accompany their child into the testing room, during the testing session.

Results

We first report the data from each task, comparing performance in our sample to performance previously reported in the literature. Subsequently, we examine the relations between the three tasks. Where the underlying distribution of scores was found to be left- or right-skewed, we used Spearman rank-order coefficients instead of Pearson coefficients (Inglis & Gilmore, 2014). We report the correlations that were identified a priori as our primary interest in the main text, but a full overview of all zero-order correlations can be found in the Appendix. Finally, although all participants were tested in the Number Estimation task first, the Standardized Math Assessment second, and the ANS Comparison task third, for ease of explication we report results from the Number Estimation and ANS Comparison tasks first.

Number Estimation task

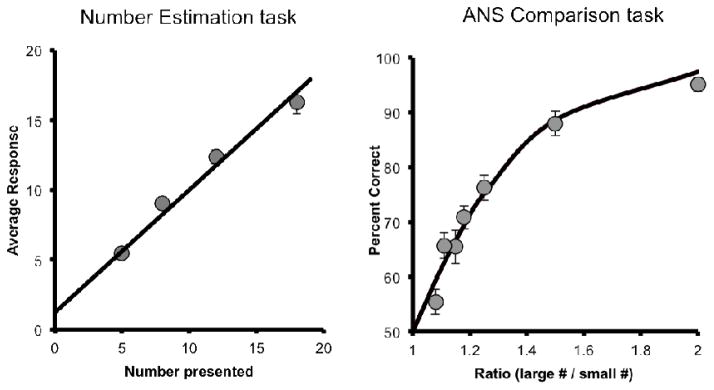
Children’s performance on the verbal Number Estimation task is shown in Figure 2 (left panel). Before analysis, we removed any responses that were more than 2.5 standard deviations from the child’s average response across all trials (less than 1% of trials). We found that children showed a linearly increasing relation between the target numerosity and the number word produced (F(3,150) = 127.21; p < .001; linear contrast F(1,50) = 155.50, p < .001). Children’s responses also exhibited linearly increasing variability (F(3,150) = 17.62; p < .001; linear contrast F(1,50) = 21.78; p < .001). Both of these patterns are considered signatures of the Approximate Number System, confirming that children did not count in our task but instead used the mapping between the imprecise ANS and exact number words (Barth, Starr, & Sullivan, 2009; Crollen et al., 2011; Huntley-Fenner, 2001; Izard & Dehaene, 2008).

Figure 2.

Performance in the verbal Number Estimation task (left) and non-symbolic ANS Comparison task (right). Error bars in the Number Estimation graph depict standard errors of the mean and show an expected linear increase in the number word produced as the number of target dots increased. The best fitting linear function had a slope of 0.9 and an intercept of 1.22. Error bars in the ANS Comparison task graph depict standard errors of the mean and the line reflects the best fitting psychophysical model with w = 0.25.

The mathematical model of verbal number estimation predicts that children’s responses will track with slope/intercept and that their variability will be normally distributed with standard deviation σ. To estimate the slope, intercept, and σ of each child’s verbal number estimates, we used the R-PsiMLE software (Odic, Im, et al., 2015). This method maximizes the parameters that fit the Normal Distribution CDF function with slope, intercept, and target number determining the mean of the distribution, and σ, proportional to the mean, determining the standard deviation:

$$L(\alpha ,\beta ,\sigma \mid \mathit{Resp},\mathit{Num})=\prod _{i=1}^n\frac{1}{\sqrt{2\pi {(\alpha +\beta \ast {\mathit{Num}}_i\ast \sigma )}^2}}exp\left(-\frac{{({\mathit{Resp}}_i-\alpha +\beta \ast {\mathit{Num}}_i)}^2}{2{(\alpha +\beta \ast {\mathit{Num}}_i\ast \sigma )}^2}\right)$$

Here, Num corresponds to the number of dots presented (i.e., either 5, 8, 12, or 18), α corresponds to the intercept of the linear regression, β corresponds to the slope, σ corresponds to the linearly increasing scalar variability (equivalent to CV) and Resp corresponds to children’s number word response. The R-PsiMLE software (freely available online at http://panamath.org/psimle) uses maximum-likelihood estimation to simultaneously estimate all three parameters of interest. Separately, we also calculated the average error rate for each child by subtracting the target numbers from the actual responses and averaging them. Positive error rates indicate over-estimation and negative error rates indicate under-estimation³. σ – our measure of estimation variability correlated strongly with the more traditionally used Coefficient of Variance measure (relation of σ to CV; r = 0.96, p < .001). Because the PsiMLE method yields better reliability in estimates (Odic, Im, et al., 2015), we used σ throughout our analyses. However, the pattern of results was nearly identical when we analyzed CV instead.

Data from all children were included in our analyses. We found that children in our sample were, on average, accurate in their verbal estimates, with roughly equal numbers of children producing over- vs. under-estimates. Across children, the average β (i.e., slope) was 0.90 (SD = 0.53), average α (i.e., intercept) was 1.22 (SD = 3.61), and average error rate was 0.05 (SD = 2.77). The average estimation variability – i.e., σ – was 0.26 (SD = 0.12), slightly higher than the typical adult average of 0.22 (Cordes et al., 2001).

ANS Comparison task

Performance on the ANS Comparison task is shown in Figure 2 (right panel). Preliminary analyses revealed no significant differences in accuracy for trials in which individual dot size was equated (M = 74%, SEM = 2%) and in which cumulative surface area was equated (M = 73%, SEM = 1%; t(50) = 0.94; p = .35), nor any correlation between age and the difference in performance on these two trial types (r(51) = .005). Thus, we collapsed across these trial types in our further analyses. The Spearman-Brown corrected random split-half reliability for the ANS Comparison task was 0.69, in line with previous estimates (Libertus et al., 2012).

As shown in Figure 2 and as predicted by Weber’s law, children’s accuracy at judging the greater of the two arrays decreased as the ratio between the numerosities approached equality (F(6,342) = 50.48; p < .001). To determine each individual child’s Weber fraction (w), an estimate of their ANS precision, we fit each child’s responses over all 56 trials with a widely used psychophysical model (1) (cf., Green & Swets, 1966; Halberda & Feigenson, 2008; Halberda et al., 2008; Pica et al., 2004).

$$\mathit{expected}\mathit{accuracy}=\mathrm{\Phi }\left(\frac{\mathit{ratio}-1}{w\sqrt{{\mathit{ratio}}^2+1}}\right)$$ (1)

In this model, ratio is the ratio between the presented numerosities (larger number/smaller number), w the Weber fraction, and Φ the standard cumulative distribution function of a Gaussian distribution. The best-fitting w parameter was found via non-linear least squares. The model assumes that the underlying representations are distributed along a continuum of Gaussian random variables. An important implication of this model is that the two numerosities presented on each trial will often yield similar and overlapping representations. In other words, as the ratio of two quantities becomes increasingly close (i.e., approaches 1.0), the Gaussian representations of the numerosities will increasingly overlap and children will have greater difficulty determining which array is more numerous, resulting in decreased accuracy. A greater w indicates greater imprecision in a child’s ANS representations. Data from one child could not be fitted because the child performed at chance across all ratios.

Collapsing across all of the ages we tested, we found that children had an average w of 0.25 (SD = 0.15), a value consistent with previous estimates for children of this age in tasks using similar methods (Halberda & Feigenson, 2008; Piazza et al., 2010).

Standardized Mathematics Assessment

To measure children’s overall math abilities, we calculated their raw math scores following the TEMA-3 procedures. We distinguished children’s informal versus formal mathematics abilities using the item categorization given in the TEMA-3 Examiner’s Manual (Ginsburg & Baroody, 2003). As described above, the standardized administration of the TEMA-3 requires starting and ending with different items in the test sequence depending on children’s age and performance. To account for the resulting difference in the total number of items children completed, and for the number of informal versus formal math items administered to each child, we averaged children’s scores (such that children were scored as having either a 0 or 1 for each administered item), and multiplied these averages by 100 to create separate percentage scores for informal and formal mathematics skills. Only data from children who were tested with at least three items in a given category were included, to avoid including informal or formal math scores that were based on very few items. Additionally, because children started at different points according to their age, the resulting informal and formal math scores are, in practice, roughly controlled for age at time of testing.

Children’s average raw TEMA-3 score was 43.06 (SD = 14.34), which corresponds to an average standardized score of 107.14 (SD = 14.11), about half a standard deviation above the expected population mean. Children solved an average of 66.09% informal math problems (SD = 17.24%) and 44.72% formal math problems (SD = 16.53%). The higher rate of correctly solved informal problems is expected given that these problems tend to be easier than formal problems.

Expressive Vocabulary

To measure children’s expressive vocabulary we summed the number of words that parents had marked on the DVAP questionnaire as having heard their child say (as described by Libertus et al., 2015). Children’s average score on the expressive vocabulary questionnaire was 130.51 (SD = 26.65). This is somewhat higher than the average score reported in previous investigations using the DVAP (Libertus et al., 2011; Libertus et al., 2015); this is not surprising given that the children in this sample were on average older than those in the previous studies.

Correlations between Verbal Number Estimation and Non-symbolic ANS Precision

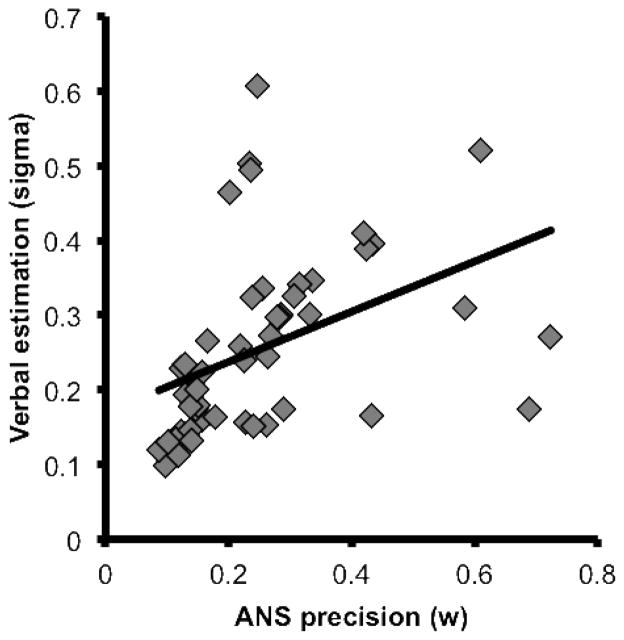
To ask whether the precision of children’s Approximate Number System was related to the accuracy of their verbal number estimation independent of children’s age, we examined the relation between w and the slope, intercept, and error rates of children’s verbal number estimates, controlling for age at the time of testing. These analyses revealed no significant correlation between w and slope (r_s = −.26, p = .10) or error rate (r_s = −.10, p = .52), but a significant correlation between w and intercept (r_s = .38, p < .01). We next asked whether ANS precision was related to the variability of children’s verbal number estimates. Here we found a significant correlation between w and σ (r_s = .56, p < .001; Figure 3): more imprecise approximate number representations (i.e., higher w scores) were associated with more variability in the number words children produced. This finding suggests that variability in number estimation is partly determined by the ANS.

Figure 3.

Scatterplot depicting the relation between ANS precision (w) and verbal number estimation variability (sigma). Children with greater ANS precision (i.e., lower w) tended to show less variable verbal estimation performance.

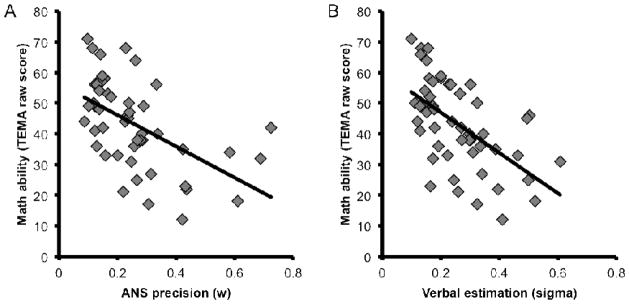
Relation between Non-symbolic ANS Precision and Mathematical Ability

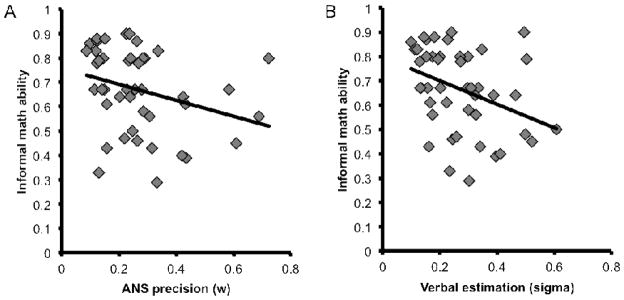
In replication of previous work (Bonny & Lourenco, 2013; Libertus et al., 2011, 2013a), we observed a significant correlation between children’s w and their TEMA-3 scores, controlling for age (r_s = −.51, p < .01; Figure 4a): children with more imprecise approximate number representations performed more poorly on the standardized math test. We further replicated a divergence in the relation between w and formal versus informal math abilities. Consistent with the findings of Libertus and colleagues (2013b), we found that w significantly related to informal math abilities even when controlling for age (r_s = −.36, p < .05; Figure 5a), but w showed no significant relation to formal math abilities (r_s = −.06, p = .71; Figure 6a). This asymmetry motivated us to probe for a similar divergence in the link between informal versus formal math abilities and their relation to verbal number estimation.

Figure 4.

Scatterplots depicting the relation between overall math ability (TEMA-3 raw scores) and ANS precision (A) and verbal number estimation (B). Children with greater ANS precision (i.e., lower w) or lower verbal estimation variability (i.e., lower sigma) tended to have greater overall math ability.

Figure 5.

Scatterplots depicting the relation between informal math ability and ANS precision (A) and verbal number estimation (B). Children with greater ANS precision (i.e., lower w) or lower verbal estimation variability (i.e., lower sigma) tended to have greater informal math ability.

Figure 6.

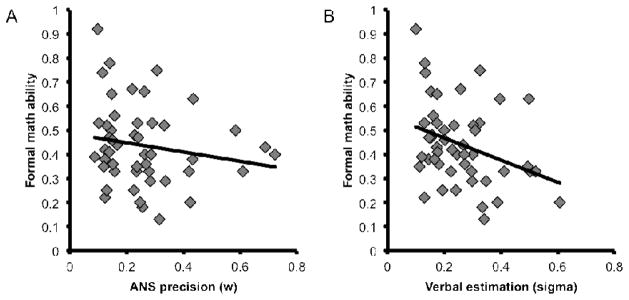
Scatterplots depicting the relation between formal math ability and ANS precision (A) and verbal number estimation (B). Children with lower verbal estimation variability (i.e., lower sigma) tended to have greater formal math ability, but no relation was observed between ANS precision and formal math ability.

Relation between Verbal Number Estimation and Mathematical Ability

To ask whether children’s performance in the verbal Number Estimation task was related to their math abilities, we first examined whether number estimation accuracy (slope, intercept, and error rates) correlated with individual differences in TEMA-3 performance, controlling for children’s age. We found no significant correlation between overall TEMA scores and any of the three measures of estimation accuracy (intercept: r = −.04, p = .79; slope: r = .004, p = .98; error rate: r = −.04, p = .81). This lack of a relation held for both informal (intercept: r = −.16, p = .33; slope: r = .10, p = .51; error rate: r = .02, p = .93) and formal math abilities (intercept: r = .17, p = .29; slope: r = −.15, p = .34; error rate: r = −.07, p = .67). Together, these results suggest that the accuracy of children’s verbal number estimation – at least in the range of number words that they reliably know - does not relate to their informal or formal math abilities.

We next examined the relation between math performance and our second measure of verbal number estimation: mapping variability Here we found a robust correlation between estimation variability – measured by σ - and overall TEMA-3 scores, even when controlling for children’s age (r = −.44, p < .01; Figure 4b). And even when controlling for age, estimation variability was marginally correlated with informal math ability (r = −.30, p = .054; Figure 5b) and significantly correlated with formal math ability (r = −.34, p < .05; Figure 6b).

To assess whether estimation variability was a significant predictor of children’s math performance above and beyond differences in age, expressive vocabulary, and ANS precision, we conducted three hierarchical linear regression analyses: one for overall TEMA-3 scores, one for informal TEMA-3 scores, and one for formal TEMA-3 scores. In the first step, we entered age and expressive vocabulary (DVAP) as variables. In the next step, we added ANS precision (w). In the final step, we entered estimation variability (σ) to test whether σ explained a significant amount of variability in math performance above and beyond the predictors entered in the first two steps. As can be seen in Table 1, σ was a significant predictor of children’s overall math performance even when controlling for age, expressive vocabulary, and w. Similarly, σ was a significant predictor of children’s formal math performance even when controlling for age, expressive vocabulary, and w (see Table 3). In contrast, σ was not a significant predictor of children’s informal math performance, and neither was w (see Table 2).

Table 1.

Summary of hierarchical linear regression analyses for variables predicting overall math ability

Variable	Model 1			Model 2			Model 3
	B	SE B	β	B	SE B	β	B	SE B	β
Age	.04	.005	.75***	.03	.005	.64***	.03	.005	.53***
Expressive vocabulary (DVAP)	.02	.06	.03	.01	.05	.03	.05	.05	.10
ANS acuity (w)				−24.16	9.54	−.25*	−16.54	9.35	−.17
Estimation variability (sigma)							−32.06	11.70	−.28**
R2		.58			.63			.68
F for R2 change		32.00***			6.42*			7.52**

^***p < .001,

^**p < .01,

^*p < .05

Table 3.

Summary of hierarchical linear regression analyses for variables predicting formal math ability

Variable	Model 1			Model 2			Model 3
	B	SE B	β	B	SE B	β	B	SE B	β
Age	<.001	<.001	.20	<.001	<.001	.16	<.001	<.001	.02
Expressive vocabulary (DVAP)	.001	.001	.11	.001	.001	.11	.001	.001	.20
ANS acuity (w)				−.10	.18	−.09	.01	.18	.01
Estimation variability (sigma)							−.47	.23	−.34*
R2		.07			.07			.15
F for R2 change		1.56			.30			4.12*

^***p < .001,

^**p < .01,

^*p < .05

Table 2.

Summary of hierarchical linear regression analyses for variables predicting informal math ability

Variable	Model 1			Model 2			Model 3
	B	SE B	β	B	SE B	β	B	SE B	β
Age	<.001	<.001	.25	<.001	<.001	.14	<.001	<.001	.03
Expressive vocabulary (DVAP)	−.001	.001	−.14	−.001	.001	−.14	<.001	.001	−.07
ANS acuity (w)				−.30	.19	−.26	−.21	.20	−.18
Estimation variability (Sigma)							−.36	.24	−.26
R2		.06			.11			.16
F for R2 change		1.24			2.46			2.22

^***p < .001,

^**p < .01,

^*p < .05

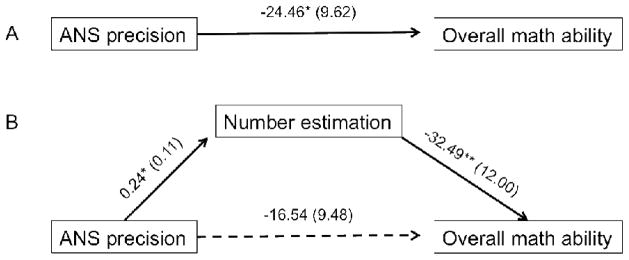
Finally, to test whether verbal number estimation, specifically estimation variability (σ) mediated the relation between ANS precision (w) and overall math performance, we conducted a mediation analysis following the approach outlined by Preacher and Hayes (2008). The overall regression model, including both ANS precision and σ as predictors and age and expressive vocabulary scores as covariates, was significant (R² = .67, p < .001). The direct path between ANS precision and overall math ability was no longer significant when the indirect path via verbal number estimation was added (p = .09, see Figure 7) and the 95% confidence interval ranged from −35.75 to −0.34, suggesting a significant mediation effect (p < .05).

Figure 7.

Mediation model for the relation between ANS precision and overall math ability by number estimation, controlling for age and expressive vocabulary scores. Unstandardized path coefficients for the direct effect of ANS precision on overall math ability (A) and for the indirect effects via verbal number estimation (B). Standard errors are given in parentheses. ** = p < .01, * = p < .05

Discussion

By their fifth birthday, children have two ways of representing number: intuitive non-verbal representations produced by the Approximate Number System (ANS), and exact number words and symbols whose meanings are acquired gradually, usually over the preschool years. Although each of these systems has been shown to independently relate to early mathematics ability, the role of the mapping between the two systems (e.g., as measured by the accuracy and variability of children’s verbal number estimations) has remained controversial.

Here, we report three main findings. First, we demonstrate that only some aspects of verbal number estimation correlate with early mathematics ability. We found that whereas children’s estimation accuracy (indexed by slopes, intercepts, and error rates) did not correlate with their math abilities, the variability in their estimates (indexed by σ) did. Second, we found that this variability in children’s mappings between the ANS and number words —σ— uniquely correlated with formal math abilities. σ was a significant predictor of formal math abilities (but not informal math abilities) even when ANS precision, age, and expressive vocabulary were controlled for. Third, σ mediated the relation between children’s ANS precision and their overall math ability. As we elaborate below, these findings suggest that the link between the ANS and number words may uniquely contribute to children’s math skills.

One of the primary motivations for our investigation was the mixed and sometimes contradictory findings on the relation between verbal number estimation and math performance (Castronovo & Göbel, 2012; Lyons et al., 2014; Mazzocco et al., 2011a; Mejias, Mussolin, Rousselle, Gregoire, & Noel, 2012; Mejias & Schiltz, 2013; Mundy & Gilmore, 2009; Pinheiro-Chagas et al., 2014). Our results suggest at least two reasons for these discrepancies. First, the relation between number estimation and math appears to be restricted to estimation variability; estimation accuracy showed no relation with math in our analyses. Second, when ANS precision is controlled for, estimation variability related to formal math skills, but not to informal math skills. This suggests that future studies might clearly delineate these components of math ability, especially across development.

Our results also confirm that non-verbal ANS comparison and verbal number estimation tasks share some common cognitive resources—including, critically, the degree of precision of the underlying ANS representations themselves (Ansari, Donlan, & Karmiloff-Smith, 2007). This is evidenced by the correlation between ANS precision (w) and σ. However, our results also show that estimation variability (σ) measures more than just ANS precision. In our regression analyses, σ was a significant predictor of formal math ability even when ANS precision, age, and vocabulary were controlled for. We conclude that the variability in σ unaccounted for by ANS precision is not just measurement noise. We suggest instead that it may reflect shifting calibration in children’s mappings (e.g., children may be unable to maintain a stable association between the ANS and number words; Sullivan & Barner, 2014), or may reflect the effects of children’s precision in being able to categorize the continuous ANS representation into a single number word (Odic, Le Corre, et al., 2015). As an example, children may vary in whether their mental category for the word “ten” neatly aligns with only the section of the ANS mental number line coding for 10 items, or whether it bleeds over onto nearby ANS representations. As a result, children may be – on average – correct in their verbal estimates, but very imprecise in what they consider “ten” to be. Future studies could investigate whether verbal number estimation is unique in this regard, or whether other number estimation tasks including symbol production (in which children are required to write a number in response to a non-symbolic stimulus), matching tasks (in which children match numerosities to Arabic numerals or vice versa; Brankaer, Ghesquiere, & De Smedt, 2014), and non-symbolic numerosity production tasks (in which children produce an approximate number of objects or actions to match a given number symbol) yield similar results.

Our findings also suggest that, in line with previous investigations, symbolic number skills may mediate the relation between the ANS and math abilities. For example, previous studies found that verbal number abilities mediated the relation between ANS precision and math achievement in preschoolers and elementary school aged children (van Marle, Chu, Li, & Geary, 2014; Pinheiro-Chagas et al., 2014). Similarly, performance on a symbolic number comparison task mediated the relation between ANS precision and various aspects of math achievement in third graders (Price & Fuchs, 2016). Here, we found evidence of a similar relation: σ mediated the relation between ANS precision and overall math ability. This mediated relation makes sense given that σ reflects the precision of the ANS, plus additional variability in the mapping between the ANS and number words.

Finally, we note that in previous work (Libertus et al., 2013b), ANS precision(w) correlated with informal but not formal math abilities; this association remained significant even when controlling for children’s age and non-verbal IQ. In the present work, we found that ANS precision was no longer a significant predictor of children’s informal math abilities when controlling for age and expressive vocabulary. It is possible that the lack of an observed relation between ANS precision and informal math performance in the present study was due to the smaller sample size relative to previous work (Libertus et al., 2013b). Indeed, the qualitative pattern we observed here mirrored that in our previous investigation: ANS precision was a better predictor of children’s informal math abilities than their formal math abilities (see Tables 2 and 3). Future studies should continue to explore the predictive value of ANS precision for different subtypes of math abilities.

Possible explanation for the link between number estimation variability and formal math abilities

It is of course important to note that the observed relation between the variability in children’s number estimation and their formal math abilities is correlational, and that therefore any suggestions about the mechanisms linking them will be speculative. However, one possible explanation may be children’s confidence in their number estimation abilities. Children with low variability in their mappings between the Approximate Number System and exact number words can rapidly form fairly precise estimates of numerical magnitude (i.e., can reliably narrow in on a small region of the ANS mental number line) in response to a number word or symbol. This mapping precision may cause children to experience a sense of confidence in their “gut sense” of number when interacting with number words and symbols, leading them to make fewer guesses when engaging in formal mathematics (Hacker, Dunlosky, & Graesser, 1998). Recently, work studying children’s non-verbal numerical approximation abilities has demonstrated the importance of confidence for ANS comparison in young children (Halberda & Odic, 2014; Odic et al., 2014). Accessing the approximate magnitudes associated with exact number symbols may be less important for children when they engage in informal math processing (as when using tokens or fingers to solve word problems, or engage in rote counting); hence individual differences in mapping variability may specifically affect formal math processing.

Another possible explanation for the relation between verbal estimation variability and math performance is the potential shared need to inhibit irrelevant information. In the verbal number estimation task, representing the approximate numerosity of a stimulus array requires inhibiting irrelevant perceptual information including cumulative surface area, density, and convex hull of the array (Szucs, Nobes, Devine, Gabriel & Gebuis, 2013). Inhibitory control also appears to play a role in children’s math performance (Blair & Razza, 2007; Clark et al., 2010; St Clair-Thompson & Gathercole, 2006). Thus, it is plausible that variability in inhibitory control may contribute to the link between performance on ANS comparison tasks, number estimation tasks, and math ability. Although this has not been directly examined for number estimation tasks, previous studies examining the role of inhibitory control in explaining the link between ANS precision and math ability have yielded mixed results (Gilmore et al., 2013; Fuhs & McNeil, 2013; Keller & Libertus, 2015; Libertus et al., 2013); hence further work is needed.

We also note that the understanding of exact number words or symbols may influence math ability via routes other than just the mapping between ANS representations and number words, as we assessed here. Previous work by Lyons and Beilock (2011) showed that in adults, symbolic ordering skills (e.g., determining whether three Arabic numerals are presented in numerically increasing order) are a mediator between ANS precision and math ability. Thus, future research could determine whether symbolic ordering and verbal number estimation skills independently mediate the relation between ANS precision and math ability. Alternatively, symbolic ordering and verbal number estimation skills may be independently associated with distinct aspects of mathematics, and/or different mediators may be at play at different stages of development.

Conclusion

In sum, we found that the precision of 5- to 7-year-old children’s mapping between the Approximate Number System (ANS) and exact number words correlated with their math abilities. More specifically, the variability in the ANS-number word mapping predicted formal math abilities, even with ANS precision, age, and verbal abilities controlled for, and mediated the relation between ANS precision and overall math abilities. These findings demonstrate that verbal number estimates – and especially the variability in producing these estimates - reflect additional cognitive processes beyond ANS precision, and that these additional processes play an important role in math performance. Future studies are necessary to replicate and extend these findings to more clearly delineate the relation between ANS precision, number estimation, and subcategories of informal and formal mathematical abilities across developmental time. This work will further our understanding of the mechanisms that link basic math cognition with the variety of skills required by abstract mathematical thought.

Research highlights.

• Verbal number estimation variability correlates with overall math abilities.

• Estimation predicts formal math, even when ANS, age and vocabulary are controlled.

• Estimation mediates the link between ANS precision and overall math abilities.

• Estimation variability indexes ANS precision and the ANS-number word mapping.

Appendix

Pearson correlation results for all measures of interest, controlling for age at the time of testing. Note that all correlations involving ANS precision (w) are Spearman rank-ordered correlations because the distribution of the Weber fraction scores was slightly skewed. Correction for multiple correlations using the correction by Benjamini and Hochberg (1995) shifts the significance level to p < .009.

	Estimation accuracy (Intercept)	Estimation accuracy (Slope)	Estimation accuracy (Error rate)	Estimation variability (sigma)	ANS precision (w)	Expressive vocabulary (DVAP)
1) Overall math	−.04	.004	−.04	−.44**	−.51**	.02
2) Informal math	−.16	.10	.02	−.30†	−.36*	−.12
3) Formal math	.17	−.15	−.07	−.34*	−.06	.09
4) Estimation accuracy (Intercept)	--	−.92***	−.57***	−.04	.38*	.10
5) Estimation accuracy (Slope)		--	.84***	.23	−.26	.005
6) Estimation accuracy (Error rate)			--	.38*	−.10	.14
7) Estimation variability (sigma)				--	.56***	.31*
8) ANS precision (w)					--	.04
9) Expressive vocabulary (DVAP)						--

^***p < .001,

^**p < .01,

^*p < .05,

^†p < .06