Target size matters: target errors contribute to the generalization of implicit visuomotor learning

Implicit motor adaptation is considered to be driven by the mismatch between a subject's aiming direction and the perceived feedback and not by the distance of the cursor from the target (target error). Using an unconstrained reaching task, we show that while the size of the target does not affect the adaptation to a gradual rotation, it does affect postrotation “blind” reaching movements. This result suggests that implicit adaptation of internal models is sensitive to target errors.

Abstract

The process of sensorimotor adaptation is considered to be driven by errors. While sensory prediction errors, defined as the difference between the planned and the actual movement of the cursor, drive implicit learning processes, target errors (e.g., the distance of the cursor from the target) are thought to drive explicit learning mechanisms. This distinction was mainly studied in the context of arm reaching tasks where the position and the size of the target were constant. We hypothesize that in a dynamic reaching environment, where subjects have to hit moving targets and the targets' dynamic characteristics affect task success, implicit processes will benefit from target errors as well. We examine the effect of target errors on learning of an unnoticed perturbation during unconstrained reaching movements. Subjects played a Pong game, in which they had to hit a moving ball by moving a paddle controlled by their hand. During the game, the movement of the paddle was gradually rotated with respect to the hand, reaching a final rotation of 25°. Subjects were assigned to one of two groups: The high-target error group played the Pong with a small ball, and the low-target error group played with a big ball. Before and after the Pong game, subjects performed open-loop reaching movements toward static targets with no visual feedback. While both groups adapted to the rotation, the postrotation reaching movements were directionally biased only in the small-ball group. This result provides evidence that implicit adaptation is sensitive to target errors.

NEW & NOTEWORTHY

Implicit motor adaptation is considered to be driven by the mismatch between a subject's aiming direction and the perceived feedback and not by the distance of the cursor from the target (target error). Using an unconstrained reaching task, we show that while the size of the target does not affect the adaptation to a gradual rotation, it does affect postrotation “blind” reaching movements. This result suggests that implicit adaptation of internal models is sensitive to target errors.

the efficiency of the human motor system critically depends on its capacity to adapt to changes in the environment. Indeed, our motor system adapts to a large variety of changes in the body of the actor and in its surrounding environment. Accumulating theoretical and experimental works in recent years suggest that adaptation depends on a forward model, which generates a prediction of the sensory outcome of a movement based on the outgoing motor commands (Wolpert et al. 1995). Thus a discrepancy between the expected and the observed sensory outcome results in an error that drives the adaptation process. The ability to adapt to a range of environments and to maintain a desired performance indicates that the central nervous system builds and maintains internal models of the kinematics and dynamics of its surroundings (Kawato 1999).

A common approach for studying motor adaptation is to perturb the sensory feedback that subjects receive during a reaching task (Krakauer et al. 2000; Shadmehr and Mussa-Ivaldi 1994). In such tasks, participants typically learn to compensate for this perturbation and to regain their baseline performance levels. The presence of aftereffects, e.g., performance errors in the opposite direction to the distortion following the removal of the perturbation, indicates that subjects have changed their sensorimotor mapping and that after adaptation, motor commands are generated on the basis of the newly acquired sensorimotor mapping. The gradual decay of the aftereffect serves as another indication of the adaptive process. Thus the existence of aftereffects and their gradual decay during washout are considered the hallmark of an adaptation of an internal model.

When studying the processes of motor adaptation that are driven by signals of errors, two types of errors can be regarded as the input. The first is a sensory prediction error, which is the difference between the predicted sensory feedback from the planned movement (according to the motor command) and the actual sensory feedback from the executed movement. This signal is mostly considered to produce the changes in the sensorimotor mapping and to drive the adaptation of internal models (Berniker and Kording 2008; Izawa and Shadmehr 2011; Schaefer et al. 2012; Wolpert and Ghahramani 2000). The second error signal is a target error, which is the difference between the target and the movement feedback and is related to the goal of the movement. According to some studies, awareness of target errors promotes the use of cognitive strategies (Hwang et al. 2006; Malfait and Ostry 2004) and enhances the rate of error reduction during learning (Peled and Karniel 2012; Werner and Bock 2007). For instance, subjects who gain an explicit knowledge of the imposed distortion show better performance during the learning phase than subjects who report little or no awareness of the perturbation (Peled and Karniel 2012; Werner and Bock 2007).

Nevertheless, several studies argue that the adaptation of a forward model relies exclusively on sensory prediction errors. When a condition of an abrupt onset of the perturbation, in which case awareness is likely, is compared to a condition of a gradual increase of the perturbation until it reaches the same perturbation level but with less awareness of the perturbation, the aftereffects in the gradual protocol have been shown to be bigger (Kagerer et al. 1997; Michel et al. 2007) and longer-lasting (Michel et al. 2007). Furthermore, recent studies showed that implicit adaptation occurs even when it is in conflict with the explicit task goal, suggesting that implicit and explicit adaptation processes are independent and are driven by different error signals (Mazzoni and Krakauer 2006; Taylor and Ivry 2011).

Supposing that sensory prediction errors derive an automatic and implicit adaptation process that is separated from the task's demands and explicit processes and is impenetrable to target errors (Mazzoni and Krakauer 2006; Schaefer et al. 2012; Taylor and Ivry 2011), an interesting question is whether exposure to an unnoticed perturbation while interacting with targets of different sizes, a manipulation that influences target errors only, equally affects the adaptation to the perturbation. On one hand, if subjects are unaware of the perturbation, then the learning process should occur implicitly (Frensch 1998; Willingham 2001). Therefore, the adaptation process should not be affected by target errors and success rates. On the other hand, although the perturbation itself is unnoticed, error and reward signals are salient and may drive additional learning processes that will eventually affect the adaptation process. We therefore reasoned that the separation between implicit processes that are driven by sensory prediction errors and explicit processes that are driven by target errors (Mazzoni and Krakauer 2006; Taylor and Ivry 2011) does not preclude the possibility that implicit adaptation processes are also sensitive to global task requirements that affect target errors but not sensory prediction errors.

As opposed to the canonical reaching tasks in the lab where the targets of the reach are static, our everyday activities often involve interacting with moving objects. In these cases, the object's features, such as trajectory and size, directly affect the planning of the movement and errors in reaching the object can be due to failure to predict the dynamics of the object and not only due to a failure in one's internal model. For example, to achieve the goal of hitting a ball with a racquet, the performer's body and limb movements must spatially and temporally coincide with the trajectory of the ball. Thus in dynamic environments it is plausible that target errors are utilized by the motor system more than is currently assumed by the motor control community. Therefore, in dynamic environments target parameters may affect implicit adaptation processes.

In this study, we hypothesized that in a dynamic reaching environment, where subjects have to hit moving targets and the targets' dynamics affect the task's success, implicit processes will benefit from target errors. We tested our hypothesis in a virtual game inspired by the classical Pong game (Farshchiansadegh 2012; Pressman 2012), in which subjects had to hit a moving ball (the target) and perceived hits (success) with visual, auditory, and haptic impact. Subjects were randomly divided into two groups: One group played the Pong with a small ball and the other with a big ball. In the two groups, the visual feedback of the hand's direction was gradually rotated to eliminate the involvement of explicit processes in the adaptation (Kagerer et al. 1997; Kasuga and Nozaki 2011; Michel et al. 2007; Saijo and Gomi 2010). Subjects were exposed to a similar distribution of sensory prediction errors while playing the Pong game with balls of different sizes, a manipulation that influenced success rates and target errors, defined as the distances of the paddle from the ball when the target was missed. Before and after the rotation training, subjects performed unperturbed games together with pre- and postrotation “blind” reaching movements. These reaching movements were directed to static targets and did not include visual feedback of the hand, to avoid feedback corrections. These movements provided us with a controlled assessment of directional changes in visuomotor mapping.

The Pong results indicate that both groups adapted to the rotation, which is consistent with the assumption that sensory prediction error drives adaptation to an unnoticed perturbation. Interestingly, the results show that only the blind reaching movements of the small-ball group were affected by the perturbed Pong. Since both groups adapted to the rotation, as can be seen through the Pong performances at the end of the adaptation session and through the aftereffects, we regard this result as an evidence for the fact that target properties affect generalization across tasks. This finding is inconsistent with previous results suggesting that implicit error correction does not interact with task goal (Taylor and Ivry 2011) and suggests that in dynamic environments implicit adaptation is influenced by target errors.

METHODS

Subjects

Twenty healthy right-handed subjects (aged 22–30 yr; 13 men and 7 women) participated in the experiment after signing an informed consent form, as reviewed and approved by the Institutional Helsinki Committee. Subjects were randomly assigned to one of two groups and were paid for their participation.

Apparatus

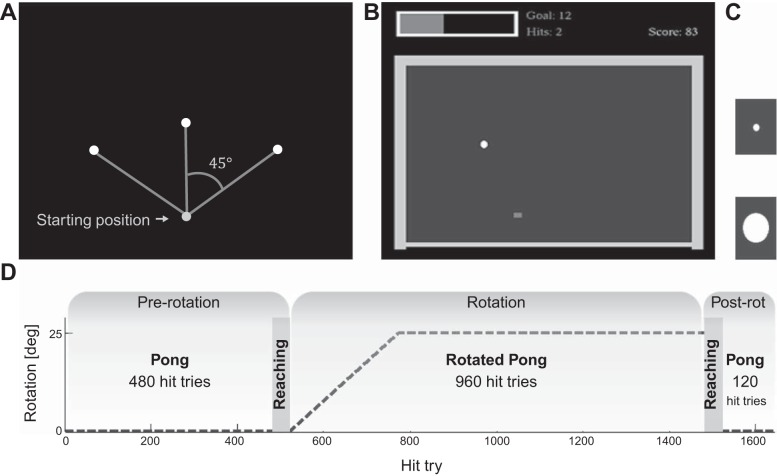
Subjects set in front of a horizontal board that was used as a screen for a projector that was hung above it. The chair height was set so that subject's shoulders were ∼10 cm above board plane. A SensAble PHANTOM Premium 1.5 was placed below the board and was hidden from the subject's sight. Subjects held the robotic handle with their right hand. The arm was covered up to the shoulder with a dark fabric to occlude visual feedback of the hand. Its handle was set to enable a two-dimensional movement in a horizontal plane, 27 cm underneath the board (see Fig. 1). During parts of the experiment in which visual feedback of the hand location was provided and was not perturbed, the movement of the virtual paddle on the screen was consistent with the movement of the handle of the haptic device within the plane of interest (see Procedure). The robotic handle also provided a haptic feedback to simulate the act of hitting a ball. The code for the experiment was written in C++. The data were recorded at 200 Hz and analyzed off-line with MATLAB (The MathWorks).

Fig. 1.

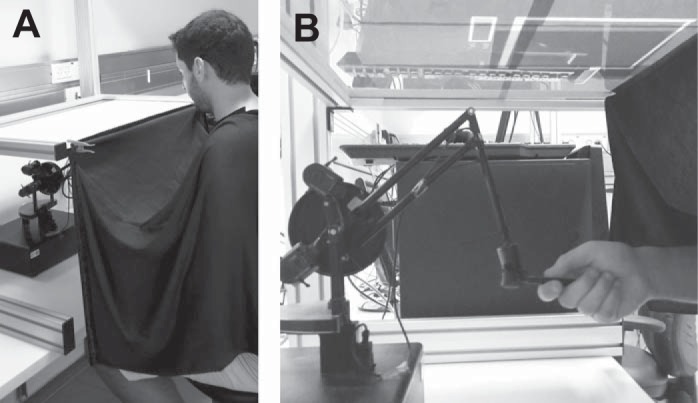
Experimental setup. A: a subject is sitting in front of the display board. His upper body is covered with a dark fabric. B: a subject holds the handle of the robot positioned underneath the board.

Procedure

The experiment was composed of the following two tasks: a Pong game and a blind reaching session. Two groups of subjects carried out the experiment, 10 subjects in each group. The only difference between the groups was in the size of the ball that was displayed during the Pong game task.

Pong game.

display.

Subjects played a virtual Pong game using their right hand. The visual display of the Pong experiment is presented in Fig. 2B. A rectangular border (17.5 × 25-cm inner area) limited the space in which the ball (a white circle, 0.6 cm in diameter in the small condition group and 2.4 cm in the large condition group) could move. The movement of the paddle (a blue bar, 0.5 × 0.7 cm) was controlled by the subject through the robotic handle. It could move both within and outside the rectangular area. Each game (single trial) lasted 30 s, during which the subject was required to achieve or surpass a certain number of hits. At the end of each game, a score was updated based on the compliance with this goal. Above the play zone, the subjects were presented with a timer bar (a magenta horizontal bar), an online hits counter, the goal of the current game, and the score of the previous game.

Fig. 2.

General experimental procedure. A: reaching task. The circle at bottom is the starting position of the reaching movements. This circle was permanently presented during the task and was colored yellow. Each trial started with the hand arriving at the starting position; then, 1 of the 3 targets (white circles) appeared. B: Pong game task. The small filled rectangle represents the position of the paddle, which was colored blue, and the white circle represents the virtual ball. The ball could only move within the arena, which was bounded by 3 gray walls and a bottom border that was shown in cyan. A magenta bar timer was presented in the upper left corner. Next to the timer are the goal and the current number of hits. The score up to the previous game is displayed at top right. C: ball sizes of the 2 groups, proportional to the display in B. Each subject played with only 1 of the balls, as determined by his/her experimental group. D: experimental protocol. The experiment was composed of blind reaching sessions and Pong sessions with and without rotation.

score.

Subjects were instructed to hit the ball with the paddle and to achieve a certain number of hits (the goal) that was redefined separately for each game. The calculation of the presented score was based both on the performance at the previous game and on previous scores. At the end of each game, the score was updated to be the average between the last game's performance and the previous score:

$${\text{Performance}}_i=\frac{{\text{Hits}}_i}{{\text{Goal}}_i}\times 100$$ (1)

$${\text{Score}}_i=\frac{{\text{Score}}_{i-1}+{\text{Performance}}_i}{2},{\hspace{0.17em}\text{Score}}_1={\text{Performance}}_1$$ (2)

where Performance is the success of a specific game, Hits and Goal are the number of hits and the goal of that game, Score is the average between the performance in the current game and the previous score. The i index indicates the number of the game.

The hits Goal was calculated based on the individual's performance in order to equalize as much as possible the reward feedback between the two groups and to motivate the subjects to improve their performance throughout the experiment. The goal in each trial was calculated as the mean of the number of hits in the preceding five trials plus 3 (for the small-ball group) or 5 (for the big-ball group) points. To encourage the subjects, on every third game we set the goal to the mean of the five preceding hits number, subtracted by 2 points. At the first game the goal was 6 for the small-ball group and 15 for the big-ball group. When subjects reached the goal, the message “Well done!” was presented. To motivate the subjects further, they were told that a good score in the Pong task, together with successful performance in the reaching task (during which no feedback of success was provided, see Reaching task), would earn them an extra 14% payment. All the subjects eventually got the extra payment.

hit conditions.

Hitting the ball was possible only when fulfilling certain conditions. The ball had to move toward the bottom border and the paddle toward the upper border. Moreover, only if the paddle vertical velocity at the moment of the hit was above a minimum threshold velocity of 0.02 m/s could a hit occur. The subjects were told that slow movements could not hit the ball and they had to learn the required speed during the first game. The minimum velocity criterion was applied to ensure that the visuomotor rotation occurred simultaneously with the hits events. In addition to the constraints on the movement at the moment of the hit, before the hit the paddle had to cross an invisible line, located 2 cm above and parallel to the bottom cyan border. To comply with this condition, subjects were instructed to start the movements toward the ball from the bottom border. Compliance with all these conditions, together with bringing the paddle to the same vertical position of the bottom of the ball, was considered as a hit try. Intercepting the ball also at the horizontal dimension led to a hit.

ball movement.

When hits occurred, the ball bounced on the paddle and its velocity was influenced by the paddle velocity as follows:

$$V{x}_{\text{ball}}^{\text{new}}=0.7\left(V{x}_{\text{ball}}^{\text{prev}}+0.6V{x}_{\text{paddle}}\right)$$ (3)

$$V{y}_{\text{ball}}^{\text{new}}=-0.7\left(V{y}_{\text{ball}}^{\text{prev}}-0.6V{y}_{\text{paddle}}\right)$$ (4)

where V_ball^new and V_ball^prev are the velocities of the ball after and before the hit, respectively, V_paddle is the paddle velocity at the moment of the hit, and x and y indicate the direction of the velocity components, vertical or horizontal, respectively. Note that, accordingly with the hit conditions, if we consider a positive vertical direction as the direction that is further away from the subject, Vy_ball^prev in Eq. 4 has a negative sign while V_paddle is always positive. Additionally, when hitting the ball, a haptic force was delivered through the robotic handle, which also produced a tapping sound. The hitting force increased linearly from 0 to F_max and backward within Δt s.

$$\text{F}{i}_{\max }=\frac{\text{Mass}}{\Delta t}\left(\left|V{i}_{\text{ball}}^{\text{new}}\right|+\left|V{i}_{\text{ball}}^{\text{prev}}\right|\right),\hspace{0.17em}i=\left\{x,y\right\}$$ (5)

where Mass represents the ball mass, which was determined to be 0.18 kg (in both conditions), and Δt is the amount of time that the hitting force was produced, which was 0.05 s. Failure to comply with the conditions of the hit resulted in a visual overlap between the ball and the paddle, as if they are moving in different planes.

When the ball hit one of the four borders, it bounced according to the laws of elastic collisions, with an exception of the upper border, where the angle of reflection was altered by a random component. This was achieved by adding the variable J to the x component of the ball velocity following the top border hits.

$$J=-V{y}_{\text{ball}}^{\text{prev}}/\tan \left(\frac{\pi }{2}-\text{Jitter}\right)$$ (6)

$$V{x}_{\text{ball}}^{\text{new}}=V{x}_{\text{ball}}^{\text{prev}}+J$$ (7)

where Jitter is a random number taken from a normal distribution with a zero mean and a 0.05π variance. The purpose of this interference was to encourage the subjects to explore the entire arena and to avoid drifting to certain strategies that use only parts of the Pong arena.

trial initiation and task duration.

At the end of each trial, the paddle and the ball disappeared. Subjects initiated the following trial by moving their hand toward the top border. The Pong task duration in each part of the experiment (prerotation, rotation, and postrotation) was determined according to a number of hit tries (480, 960, or 120, see Protocol) in order to equalize the amount of movements between the groups in each of the experimental sessions. Before the last trial in the session, the message “Last Pong game” was presented above the play zone. The message prompted the subjects that they would have to perform reaching movements as soon as the next Pong game was over.

the perturbation.

During the rotation session (see Protocol), a clockwise rotation between the movement direction of the hand and the paddle was applied. The coincidence in the positions was set at the bottom center of the rectangular area.

small- and big-ball conditions.

Two groups of subjects participated in the experiment. The difference between the two was the diameter of the ball: 0.6 cm in the small-ball group and 2.4 cm in the big-ball group (see Fig. 2). For the small-ball group, an overlap between the x positions of the paddle length (0.7 cm) and the center bottom of the ball was considered a hit. In the big-ball group, an overlap range of 2.5 cm was considered a hit. Thus the hit range of the big-ball group was 3.57 times longer than the hit range of the small-ball group.

The sizes of the balls were chosen to create a significant difference in the difficulty of hitting the ball between the two groups and yet keep the game challenging for both groups.

Reaching task.

In the reaching task, subjects were asked to reach and stop at the indicated targets using their right hand. The starting position of all the trials was identical. It was presented as a yellow circle, 0.7 cm in diameter (the same as the length of the paddle in the Pong task), centered at the same location as the center of the bottom border of the Pong arena and 2 cm above it. The targets were white circles, 0.7 cm in diameter, separated by 45° and placed at one of three possible positions: 7 cm above and left to the starting position, 7 cm above and right to it, or 10 cm above it (see Fig. 2). No visual feedback of the hand position was provided during the movement. Subjects could only know that a trial started from the appearance of the yellow circle, which was presented for the entire task.

Each trial started when the haptic device was applying a force on the subject's hand that moved it to the starting position, together with a written message “Move with the robot.” Then, one of the three targets appeared and the subjects were instructed to reach and stop at the target as fast and as accurately as they could, with a single movement (with no corrections). When subjects stopped moving (all velocity components were lower than 0.15 m/s, for at least 0.5 s), the target disappeared and another game started immediately.

To enhance subjects' cooperation, subjects were told that success in the task was based on their accuracy and speed and it could earn them an extra payment. In contrast to the Pong task, in the reaching task subjects had no feedback about the position of the hand or about their overall success. Eventually, all subjects received the extra payment, with no consideration of their performance.

Protocol.

The protocol consisted of four sessions: training, prerotation, rotation, and postrotation (see Fig. 2). The training session was designed to introduce the subjects to the robotic handle and the experimental display and to ensure that they understand the instructions for reaching. For this purpose, three sets of six reaching trials were performed. The first set provided a continuous visual feedback of the entire hand trajectories (using a blue circled cursor, 0.7 cm in diameter). In the second set, visual feedback was not provided during the movement but only after the subjects stopped, indicating the end-point position of the hand. The last set was identical to the reaching trials on the next sessions, i.e., with no visual feedback at any point during the task.

The second session, prerotation, consisted of Pong games that included at least 480 hit tries (see Pong game for more details about the Pong game's duration) and was followed by 42 reaching trials, 14 trials to each of the three targets. The order for presenting the targets was chosen randomly, with the constraint that each of the three targets had to appear twice every six trials.

The next session, rotation, included Pong game trials in which a clockwise visuomotor rotation between the hand movements and the visual feedback was applied. The perturbation was applied around the bottom center position of the Pong space. The rotation was gradually increased within the first 250 hit tries, 0.1° every hit try, up to 25°. Afterwards, an additional 710 hit tries, or more, with a constant rotation of 25° were performed. If 710 hit tries were completed before the end of a trial (30 s of Pong game), the session continued until its end.

The last session, postrotation, was composed of a reaching session that was followed by Pong games with no rotation for at least 120 hit tries.

Pong Performance Analysis

The Pong performance was evaluated with the four following measures: success rate, target error, x-distance, and movement length.

Performance was estimated based on success rate and target error.

Success rate was determined as the percentage of successful hits out of the hit tries and was calculated every 20 hit tries. Success rates are expected to be higher in the big-ball group. Furthermore, because of a ceiling effect in the big-ball group performance, improvement (e.g., the difference between success rates at the beginning and at the end of the epoch) within the pre- and postrotation sessions is expected to be higher in the small-ball group.

Target error was determined as the distance between the edge of the paddle and the ball along the x-axis when the ball was missed. The averaged absolute target error is expected to be larger in the big-ball group.

Directional error was estimated based on the x-distance.

To estimate directional errors in the Pong task, we looked at the attempts to hit the ball (hit tries). We assumed that the hit tries were directed to cross the bottom center of the ball. Therefore, the horizontal distance between the ball center and the paddle center, when the hit tries were both successful and unsuccessful, served as a measure of directional errors. We use the term x-distance to quantify this horizontal distance (see Fig. 3 for an illustration of this measure).

Fig. 3.

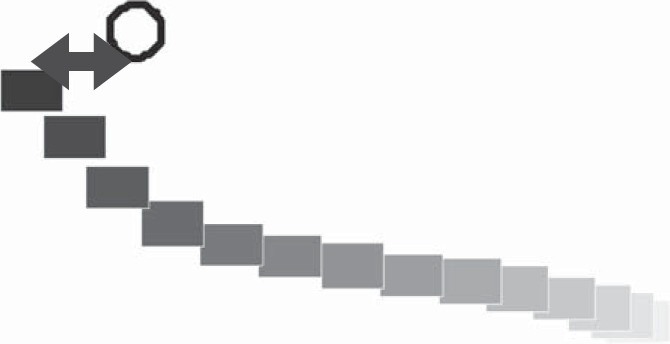
An illustration of the Pong performance measures. A movement toward the ball from a Pong game of a subject from the small-ball group is presented to demonstrate the Pong measures. The paddle positions are presented every 35 ms with a rectangle. Later positions are colored in a darker color tone. The x-distance is marked by the horizontal arrows. In this example, the position of the paddle is on the left side of the ball, and therefore the x-distance is negative. The movement length is the length of this presented trajectory.

At the end of the rotation session, subjects are expected to adapt to the visuomotor rotation, and therefore the x-distance mean should not be different from the mean at the beginning of the rotation session (where the perturbation was gradually increasing from 0°). Accordingly, at the beginning of the postrotation session a negative mean compared with the final prerotation performance is expected. These comparisons were assessed using the means of five x-distances from the end of the preadaptation, the end of the adaptation, and the beginning of the postadaptation performance.

Online corrections were estimated using movement length.

Movement length was determined as the length of the trajectory of the paddle preceding a hit try event. Movement length was defined as the distance from the point where the paddle started to move upward until the hit try was counted (crossing the horizontal line of the ball; see Fig. 3). Characteristics of the efficiency of movements, such as measures of the trajectories' curvature or duration, are commonly used to assess a rise in online corrective motor commands in the presence of large performance errors compared with the baseline behavior (Hinder et al. 2010; Kagerer et al. 1997). We estimated changes in online corrections between the end of the prerotation session and the beginning of the postrotation session by comparing movement lengths.

Reaching Performance Analysis

The reaching performance was also evaluated according to the movement directions. A reaching movement direction was calculated as the direction of the velocity vector at the moment of the maximum velocity.

We assessed the effect of the Pong rotation training on the reaching task in a manner that is representative of movements to all directions using the averaged-target bias (Hinder et al. 2010; Krakauer et al. 1999), which was calculated as the averaged difference between pre- and postrotation reaching directions across the three targets. We also examined the directional bias of each of the targets separately. Target bias was defined as the difference between pre- and postrotation reaching directions that were directed toward the same target.

Kinematic Comparison Between Groups and Tasks

We compared kinematic measures between the groups and the tasks in order to examine the explanation that different generalization patterns between the group conditions could be driven by similarities between the Pong and the reaching movements. We computed the Euclidian distances between the starting point of the blind reaching movements and the starting points of the movements in the Pong game as well as the distance between the end point of the Pong reaching movements and their closest target in the blind reaching condition. Furthermore, we compared the averaged velocity of the movements at the end of the Pong rotation session with the velocity of the reaching movements in the two groups.

Statistical Tests

For the Pong measures and the target biases the comparisons were analyzed with repeated-measures ANOVA. When significant differences were found, post hoc analyses were performed with two-tailed, two-sample, or paired-sample t-tests together with Bonferroni corrections for multiple comparisons. Two-tailed, one-sample t-tests were performed on the averaged-target biases to assess the significance of each of the biases (assessing whether the biases are significantly different from zero). Also, two-tailed, two-sample t-tests were performed to compare averaged-target biases of the two groups, and the level of significance was corrected using Bonferroni adjustment to account for multiple comparisons.

Unless otherwise noted, all aforementioned metrics followed a normal distribution, as confirmed by the Lilliefors test. Otherwise, a two-tailed Wilcoxon signed-rank paired test was used for comparisons within groups and a two-tailed Wilcoxon rank sum test was used for comparisons between groups (both tests for 1-factor comparisons). For all analyses, P values < 0.05 were considered to indicate a significant difference.

RESULTS

Subjects were gradually exposed to a visuomotor rotation while playing a virtual Pong game. Subjects controlled a virtual paddle by moving their right arm in a two-dimensional plane and received continuous visual feedback of the position of the paddle and a haptic feedback when the paddle hit the ball. During the game, the direction of movement of the paddle with respect to the hand was gradually perturbed, reaching a rotation of 25°. To manipulate target errors, subjects were randomly divided into two groups: the first played Pong with a big ball and the second with a small ball. Before and after the Pong rotation session, subjects performed reaching movements toward static targets with no visual feedback of hand position. Subjects also played Pong games without rotation before and after the rotation session for training and for assessment of aftereffects, respectively. In the next section, we present the effect of the size of the ball on task success and compare the adaptation patterns across groups. We present behaviors in the training task (the Pong) that indicate that both groups adapted to the rotation, i.e., completed the rotation session with no directional biases and began the subsequent session of Pong games with negative aftereffects. Nevertheless, differences in the performance of the reaching task suggest that there are differences in adaptation processes of the two groups.

Higher Task Success with Big Ball

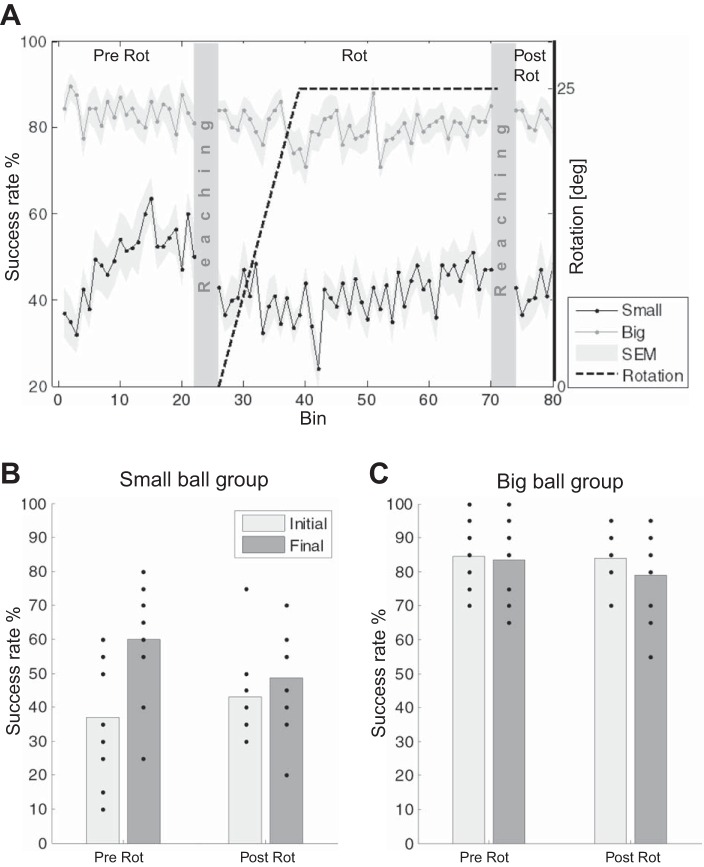
The sizes of the balls were chosen to create a noticeable difference in the difficulty of hitting the ball between the groups. Figure 4A demonstrates the success rates (the ratios of hits to hit tries) during the three experimental sessions averaged across subjects for the two groups. As expected, the big-ball group was much more successful than the small-ball group. Success rates from the beginning and the end of the pre- and postrotation Pong sessions (summed over the first and last 20 hit tries) are presented in Fig. 4, B and C. We found a significant difference between the performance of the two groups in these sessions (F = 135.56, P < 0.001), indicating that, as planned, subjects were more successful when playing with the big ball. Additionally, there was no significant main effect of improvement within sessions (F = 3.38, P = 0.07). The significant interaction between the groups and the improvement within sessions (F = 7.95, P = 0.006) demonstrates that subjects in the small-ball group improved their performance whereas subjects in the big-ball group did not. The above differences suggest that the big-ball group experienced fewer target (ball) misses.

Fig. 4.

Success rates along the experiment, demonstrating that the big-ball group better achieved the task's goal and thus experienced fewer target errors. A: connected dots represent success rates averaged across subjects for the 2 groups. Light gray area around the dots represents SE. Gray and black dots represent the performance of the big- and small-ball groups, respectively. During the rotation session, the size of the rotation is indicated by the dashed line and the right y-axis. Between the Pong sessions, gray rectangles represent trials in which the reaching task was carried out. B and C: success rates during the initial and final stages of the prerotation and postrotation sessions, shown for the small- and big-ball groups, respectively. Each dot represents a success rate of a single subject. Bars represent group averages.

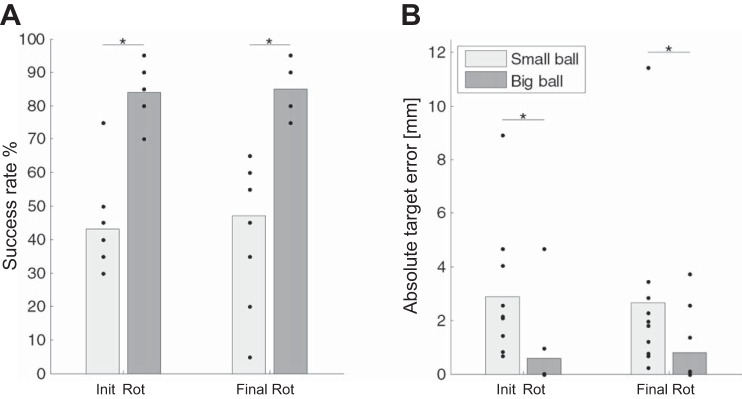
We next examined the success rates within the Pong rotation session. Figure 5A presents success rates at the beginning and at the end of this session. These results are presented separately from the other sessions since the last success rates of the small-ball group and the first success rates of the big-ball group did not follow a normal distribution according to Lilliefors test, and therefore a nonparametric Wilcoxon test was applied. Consistent with the results from the other Pong sessions, here again the success rates of the big-ball group were higher than the success rates of the small-ball group both at the beginning of the Pong session (Z = −3.704, P = 0.0002) and at its end (Z = −3.763, P = 0.00017). Differences between the groups were also noticeable when computing target errors, which are defined as the distance between the paddle and the edge of the ball along the x-axis when the ball was missed. Comparison of the target errors from the first and last five hit tries of the rotation session across the two groups, using a nonparametric Wilcoxon test, reveals a significant group effect (Z = 2.97, P = 0.0029 for initial target errors and Z = 2.25, P = 0.0246 for final target errors; see Fig. 5B). Finally, to estimate learning during the adaptation session, where the perturbation was gradually applied, we tested whether there was a change in success rates between the beginning of the session (in the presence of 0–0.2° rotation) and its end (in the presence of 25° rotation). The comparison reveals no significant difference in success rates for both groups (W = 34.5, P = 0.51 for small-ball group and W = 16, P = 0.81 for big-ball group). The lack of significant differences suggests that subjects learned to compensate for the gradual perturbation that was introduced during the rotation session.

Fig. 5.

Performance during the Pong rotation session. A: success rate of the initial and final performances of each group in the rotation session, demonstrating a significant group effect. Dots represent single subjects. Bars represent group averages. B: absolute target error rates of the initial and final performances of each group in the rotation session, demonstrating a significant group effect. The number of points is smaller than the number of subjects in each group (10) because of overlapping results. Significance is depicted by asterisks (P < 0.05).

Both Groups Adapted to Rotation

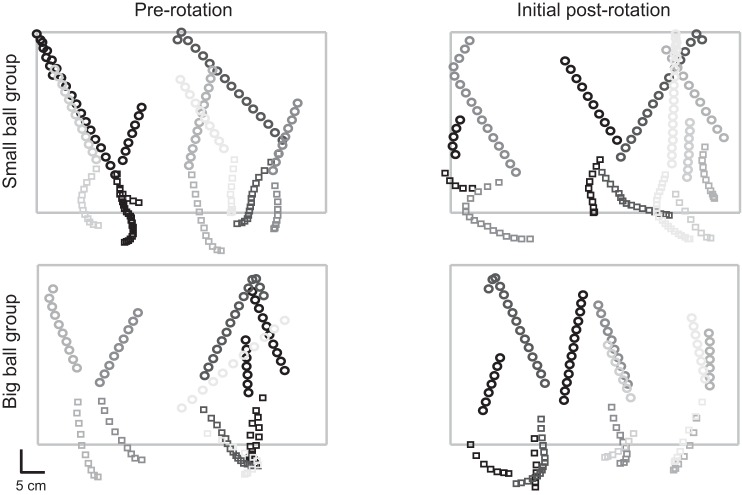
The experimental question of this study is whether differences in success rates will affect the adaptation process to the unnoticed, gradual, rotation perturbation of the feedback from the paddle. The movements in the Pong task were subjected to very few constraints and therefore were relatively free and, accordingly, the trajectories were very diverse. Figure 6 presents trajectories of ball-directed movements of subjects from both groups at the prerotation session and at the beginning of the postrotation session. The presented trajectories represent the paddle's movements toward the ball from the point where it started to move upward until it crossed the vertical position of the ball. Multiple trajectories are presented to demonstrate the variance between successive movements and differences between the presented sessions.

Fig. 6.

Hit tries trajectories. Six successive trajectories of hit tries from the final prerotation session (left) and the initial postrotation session (right) of representative subjects from the small-ball (top) and big-ball (bottom) groups. The ball and paddle positions are presented from the moment that the vertical component of the paddle velocity became positive (upward) until the paddle crossed the vertical position of the ball. The positions of the ball center (circles) and the paddle center (squares) are presented every 35 ms. The gray rectangles represent the borders that limited the ball movement. Successive trajectories differ in their color tone, such that later ones are lighter. The sequence of the trajectories is particularly meaningful at the postrotation performances, in which substantial error corrections take place both during and between the movements.

Assessing Directional Errors

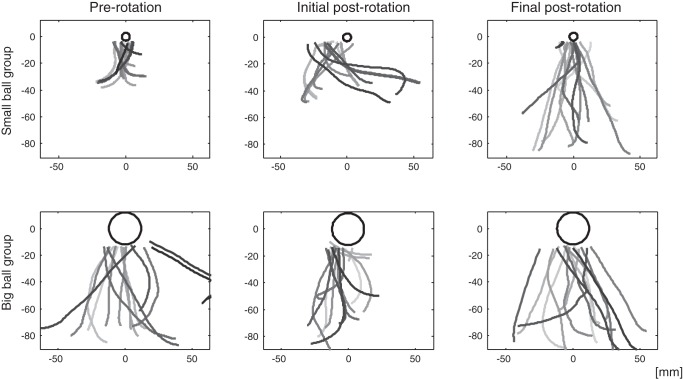
A noticeable difference between the pre- and postrotation movements in Fig. 6 is the bias of the final position of the paddle to the left at the end of the movements at the postrotation session, which reflects the presence of an aftereffect. For better observation of the progress of this measure (the x-distance) within and between the experimental sessions, Fig. 7 presents successive trajectories that are placed on top of each other, such that the place of the ball at the moment of the hit tries count was placed in the origin, (0,0). x-Distance is defined as the horizontal distance between the trajectories' ends and the bottom center of the ball. The shift of the distribution of the x-distances following the rotation suggests that the x-distance mean captures the directional errors that were caused by the visuomotor rotation and that both groups adapted their visuomotor mapping. Moreover, as the postrotation movements were carried out earlier (colored in a darker color tone) the errors were bigger, implying a washout process.

Fig. 7.

The x-distance as a measure of the directional errors that were caused by the visuomotor rotation; 15 successive hit try trajectories are presented in each panel. In each panel, as the color tone is lighter the trajectory was carried out later. Trajectories are placed on top of each other, such that the place of the ball at the moment of the hit try count is placed in the origin, (0,0). Each row of panels presents movements of a single subject from a different group. Columns represent different experimental phases: final prerotation, initial postrotation, and final postrotation (from left to right). x- and y-Axes are in millimeters.

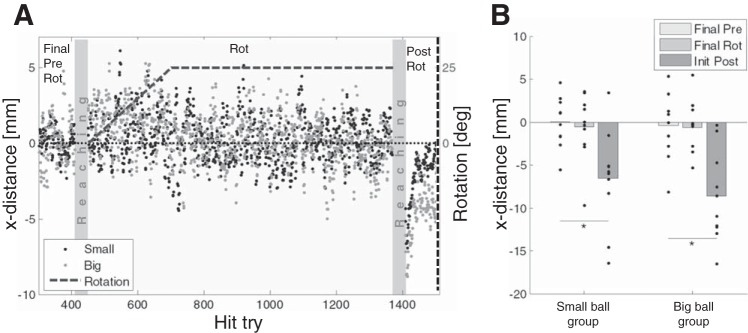
Figure 8A shows the x-distance during the three experimental sessions, averaged across subjects for each of the two groups. The changes along the experiment are consistent with the above assessments, showing that the x-distance may approximate directional errors and that the participants adapted to the rotation. The means of five successive x-distances from the final prerotation, the final rotation, and the initial postrotation session of all subjects are presented in Fig. 8B. Analysis of the differences between these means revealed significant differences between the compared experimental phases (F = 19.11, P < 0.001). Post hoc analysis revealed no difference between the final prerotation time and the final rotation time (P = 0.73 for small-ball group and P = 0.93 for big-ball group), indicating that subjects adapted to the perturbation, and a significant difference between each group's final prerotation time and initial postrotation time (P = 0.01 for small-ball group and P = 0.001 for big-ball group), indicating aftereffects. Additionally, there was no main effect of group (F = 0.61, P = 0.44) and no interaction between the groups and the experimental phases (F = 0.31, P = 0.73), suggesting that both groups were similarly affected by the rotation.

Fig. 8.

x-Distance averages along the experiment. A: the x-distance during the 3 experimental sessions, averaged across subjects for the 2 groups. The dots present the averaged x-distance of every hit try for each group (depicted by color). At the rotation session, the size of the rotation is indicated by the dashed line and the right y-axis. Between the Pong sessions, gray rectangles represent trials in which the reaching task was carried out. Data were filtered with a moving average filter with window length of 5 points. B: means of 5 successive x-distances from final prerotation, final rotation, and initial postrotation results. Each dot represents a mean x-distance of a single subject. Bars represent the grand average. Significance is depicted by asterisks (P < 0.05).

As stated above, the adaptation of a rotated visuomotor mapping is clearly noted at the initial postrotation session in both groups. Notably, the x-distance measure reflects the errors at the end of the movements and may be affected by online corrections. For a better assessment of the initial postadaptation differences between the groups, the next section addresses indications of online error corrections of the groups at the postrotation session.

Changes in Online Corrections

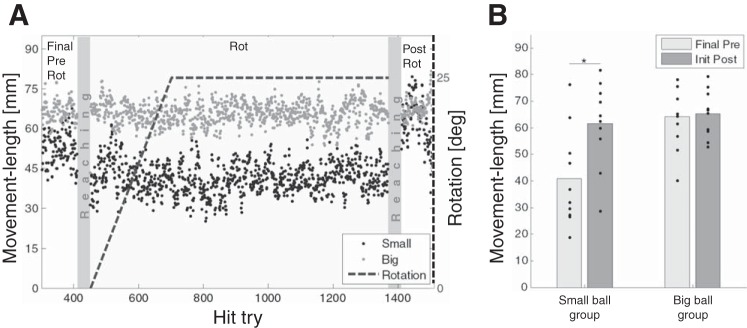
Changes in the duration and in the shape of movements in the presence of large performance errors compared with the baseline are commonly attributed to online corrective motor commands (Hinder et al. 2010; Kagerer et al. 1997). We therefore expected to find kinematic changes between the baseline and the washout phases due to the increase in error rates that subjects experienced after the abrupt removal of the perturbation. These changes are expected to be more pronounced in the small-ball group, since in this group directional errors have a stronger effect on the task's success. Figure 9A shows averaged movement lengths during the three experimental sessions. The means of five successive movements from the final prerotation and initial postrotation results of every subject are presented in Fig. 9B. Analysis of the differences between these means revealed a main effect of group (F = 8.84, P = 0.005), suggesting that subjects performed shorter movements with the small ball. Since hitting a small ball is more difficult and reaching a closer target is more accurate (Fitts 1954), the shorter trajectories of the small-ball group may be a result of waiting until the ball is close before trying to hit it. In addition, there was a main effect of the experimental phase (F = 5.98, P = 0.019) and an interaction between the groups and the experimental phase (F = 4.71, P = 0.037). Together with the post hoc analysis that indicated that only the small-ball group had a significant increase in this measure at the initial postrotation phase compared with the final prerotation phase (P = 0.015 for small-ball group and P = 0.8 for big-ball group), these observations suggest that only the small-ball group's movements were significantly longer at the postrotation session compared with the baseline movements. This increase in movement length may result from an increase in online corrections following the removal of the perturbation. The apparent differences in online corrections between groups may suggest that the x-distance performance results, which are measured at the end of the movement, represent an underestimation of initial errors in the small-ball group.

Fig. 9.

Average movement lengths along the experiment, demonstrating a postrotation rise in the online feedback corrections at the small-ball group. A: the movement length during the 3 experimental sessions, averaged across subjects for the 2 groups. The dots represent the averaged data of every hit try of each group (depicted by color). At the rotation session, the size of the rotation is indicated by the dashed line and the right y-axis. Between the Pong sessions, gray rectangles represent trials in which the reaching task was carried out. Data were filtered with a moving average filter with window length of 5 hit tries. B: average of 5 successive movement lengths from the final prerotation and the initial postrotation results. Individual means are presented by the dots, and bar values represent the mean of all subjects. Significance is depicted by asterisks (P < 0.05).

Generalization of Adapted Changes to Reaching Task Only in Small-Ball Group

After observing directional changes in the visuomotor mapping of both groups in the training task (the Pong), we examined the representational changes that occurred after the rotation using reaching movements toward static targets without visual feedback from the hand. This blind reaching provides an assessment of the feedforward control component in the movement and does not include online corrections. Furthermore, the static aimed positions enable us to better measure the difference between the visual (desired) direction and the hand direction.

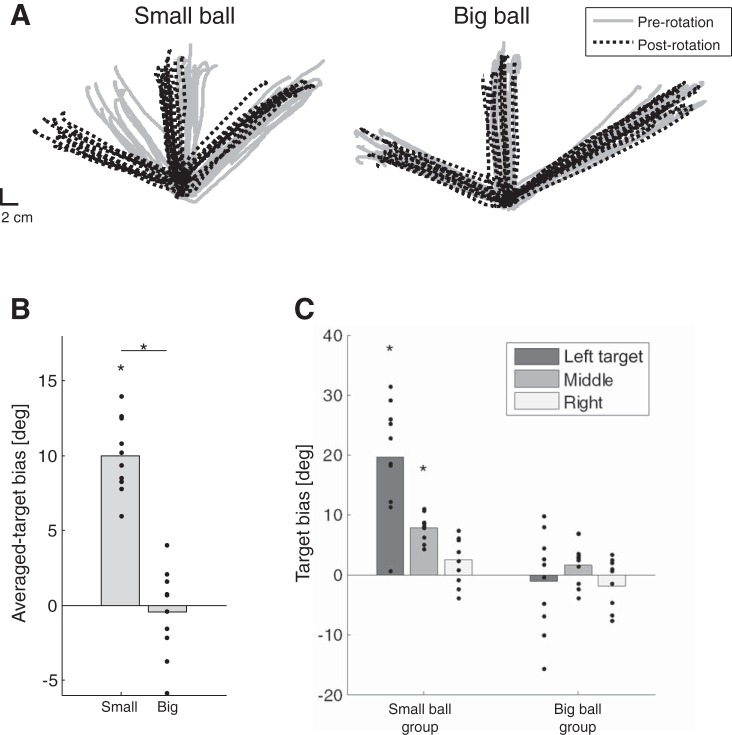
The reaching movements of subjects from the small-ball group demonstrate directional biases in the postrotation movements, whereas in the big-ball group subjects did not show any significant bias in their reaching directions (Fig. 10A). The averaged-target bias between the pre- and postrotation reaching directions (Fig. 10B) is significantly different from zero only for the small-ball group [t(9) = 12.57, P < 0.001 for small-ball group and t(9) = −0.49, P = 0.64 for big-ball group], and this measure is significantly different between the groups [t(18) = 8.56, P < 0.001]. These differences indicate that, averaged across the probe directions, the two groups were affected differently by the visuomotor rotation. The lack of any bias in the big-ball group is not consistent with the postrotation bias seen in the Pong movements.

Fig. 10.

Directional biases in the postrotation reaching movements are observed only in the small-ball group. A: trajectories of the pre- and postrotation reaching movements toward the 3 targets taken from individual subjects. Left: reaching movements of an individual subject from the small-ball group. A counterclockwise bias is observed between the pre- and postrotation performances. Right: reaching movements of an individual subject from the big-ball group, demonstrating an overlap between the performances. B: averaged-target biases. Each dot represents a subject's averaged-target bias between the pre- and postrotation reaching directions. Mean results are presented by bars. C: target biases. Each dot represents the bias between the pre- and postrotation performances of movements toward the same target (according to bar color) of a single subject. The mean of each group's results at each target is presented by bars. Significant biases (P < 0.05) are depicted by asterisks.

Looking at the biases between the pre- and postrotation movements separately for each target (Fig. 10C) also reveals a significant difference between the groups (F = 47.94, P < 0.001). In addition, the biases of the small-ball group for the left and middle targets are significantly different from zero [t(9) = 6.57, P < 0.001 and t(9) = 11.53, P < 0.001, respectively] while for the right target this difference was not significant [t(9) = 2.05, P = 0.07]. For the big-ball group, the difference from zero was not significant for all three targets [t(9) = −0.43, P = 0.68, t(9) = 1.5, P = 0.16, and t(9) = −1.31, P = 0.22 for left, middle, and right targets, respectively]. As expected, these observations are consistent with the averaged-target analysis. In addition, there are significant differences between the targets (F = 11.5, P < 0.001) and an interaction between the groups and the targets (F = 11.61, P < 0.001), suggesting that the directional effect of the rotation was not generalized in an equal manner to all directions. Together, these results demonstrate that although both groups adapted a rotated visuomotor mapping in the trained environment, only with the small ball did subjects generalize these changes to untrained movements.

Kinematic Difference Between Big- and Small-Ball Group Performance During The Pong Adaptation Phase

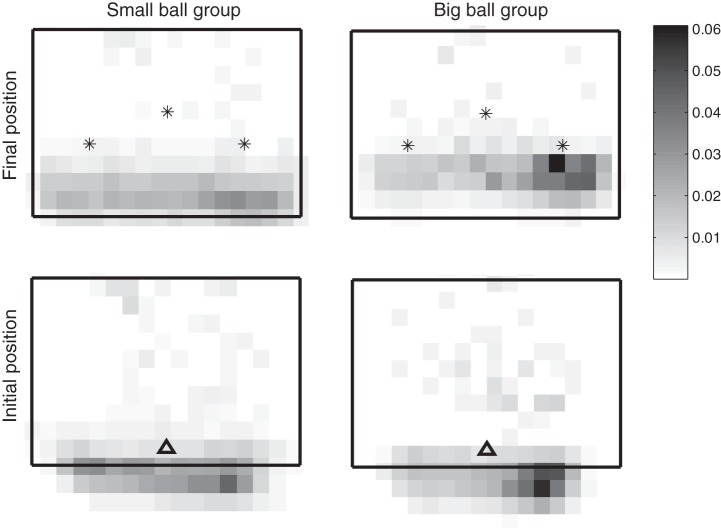
A central concern is that the movements that subjects made in the small-ball group in the Pong game were more similar to the movements that they performed in the blind reaching condition than the movements that the big-ball subjects made. Thus it could be that the similarity between the Pong and the reaching movements drove the generalization between these conditions and not the perceived target errors due to the manipulation of the size of the ball. To address this concern, we computed the Euclidian distances between the starting point of the blind reaching movements and the starting points of the movements in the Pong game (Fig. 11). The distance between the starting position of the blind reaching and the starting positions in the Pong game in the big-ball group was smaller than the distance from the small-ball group starting points [63.8 ± 34.1 mm (SD) for small-ball group and 61.3 ± 29.5 mm (SD) for big-ball group; Z = 2.592, P = 0.0096, nonparametric Wilcoxon test]. We next computed the distance between the end point of the Pong reaching movements and their closest target in the blind reaching condition. The end points in the big-ball group Pong movements were closer to the targets of the blind reaching condition compared with the end points of the small-ball condition [57.7 ± 19.5 mm (SD) for small-ball group and 40.6 ± 18.6 mm (SD) for big-ball group; Z = 62.363, P < 0.0001 for final position distance, nonparametric Wilcoxon test]. These analyses show that the movements that subjects made in the big-ball group during the Pong rotation session were more similar to the reaching movements than the movements that subjects performed in the small-ball group. These results are opposite to the predictions of the alternative explanation and therefore suggest that the differences in generalization cannot be attributed to an increased similarity between the Pong and the reaching movements of the small-ball group.

Fig. 11.

Three-dimensional histograms of Pong initial or final positions of all hit tries of all subjects. Color intensity represents the averaged probability of counts in 1 pixel. The rectangle represents the Pong borders. Top: distribution of final positions of the Pong reaching movements together with the targets in the blind reaching condition (asterisks). Bottom: distribution of initial movement positions together with the starting point in the blind reaching condition (triangles).

As another test of this alternative explanation, we compared the averaged velocity of the movements at the end of the Pong rotation session with the velocity of the reaching movements during the postrotation reaching session in the two groups (Fig. 12). This analysis reveals a main effect of group (F = 16.69, P = 0.0002), pointing to the fact that subjects in the big-ball group made faster movements both at the Pong and at the reaching sessions. Nevertheless, there was no significant effect of task (F = 0.04, P = 0.845) and no significant interaction between the groups and the tasks (F = 3.42, P = 0.072), suggesting that the velocities in the small- and big-ball groups were comparable between the Pong and the reaching sessions. Together with the previous analyses, our results suggest that the changes in generalization are not related to the kinematic similarity between the Pong and the blind reaching movements.

Fig. 12.

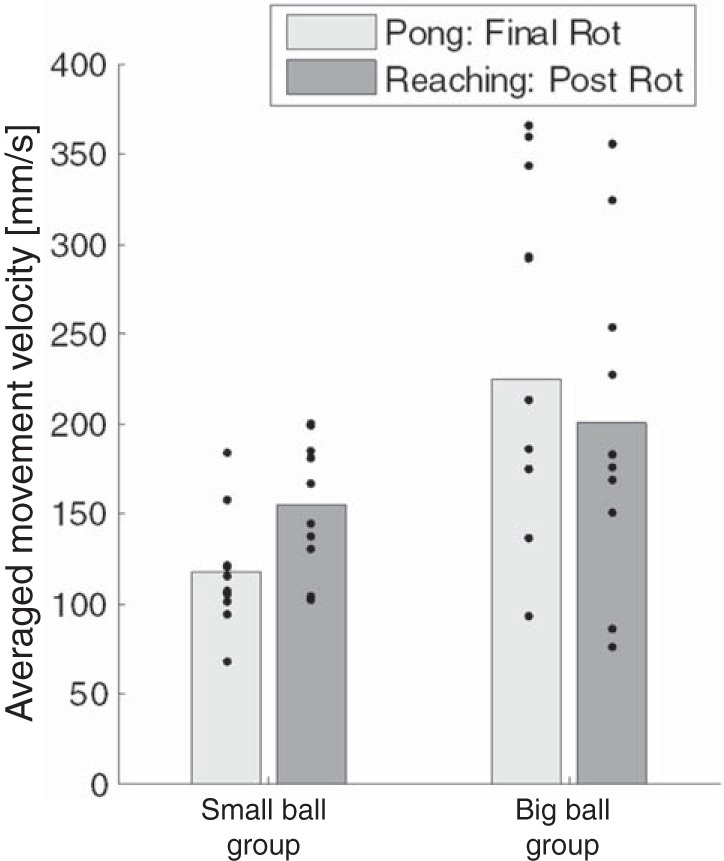
Averaged movement velocity during the final Pong rotation (last 5 hit tries) and the postrotation reaching sessions.

DISCUSSION

Summary

In this study we examined the effect of target error on implicit adaptation processes by examining the effect of target size on gradual adaptation learning and feedforward control processes with an adapted version of the Pong game. We tested two groups of subjects who played Pong while the visual feedback of their movement direction was gradually rotated. The ball size was different between the groups such that directional errors had a different effect on task success and on target errors. Before and after adaptation, subjects played an unperturbed version of the Pong game and also performed reaching movements toward static targets with no visual feedback of the hand. At the end of the Pong adaptation session (in the presence of 25° clockwise rotation) both groups adapted to the perturbation, as indicated by the fact that, on average, forward movements of the paddle ended, on the horizontal dimension, around the ball center. Additionally, at the beginning of the washout phase, reaching directions were biased to the left of the ball in both groups. Interestingly, in the blind reaching session, conducted straight after the Pong adaptation session, only the subjects who played with the small ball showed a directional bias. Our results therefore suggest that, unlike previous claims (Mazzoni and Krakauer 2006; Taylor et al. 2014; Taylor and Ivry 2011), target errors, defined as the distance of the paddle from the ball when the target was missed, do affect implicit adaptation processes. We suggest that this effect may reflect a target error modulation of implicit adaptation processes, or an indirect effect of target error on the representational changes that occurred after the adaptation process.

Target Error Modulation of Implicit Adaptation Processes

Despite the differences in success rates between the groups, both groups adapted to the rotation, as can be seen through the horizontal deviations of the paddle from the target. At the end of the adaptation session, the average position of the paddle, when approaching the ball, was around the ball center, suggesting that both groups learned to completely compensate for the rotation. Furthermore, at the beginning of the postadaptation session, cursor positions were biased to the left of the ball, indicating that both groups adapted their internal model. While this result suggests that implicit learning is indeed driven solely by sensory prediction errors, the directional error measures that were used in the analysis (the x-distance) are related to the final position of the paddle and therefore reflect both feedforward biases and online feedback corrections. Furthermore, the rise in movement length of the small-ball group at the postadaptation session suggests that this group used feedback corrections. Thus the initial feedforward bias in the small-ball group may be bigger than the bias of the big ball. This proposed difference suggests that the difference in blind reaching biases is in fact associated with different magnitude of adaptation in the Pong game. According to this explanation, the blind reaching biases reflect a stronger adaptation in the small-ball group and not an indirect effect of target errors on the representational changes that led to adaptation. Thus target errors may affect the implicit adaptation process directly, by enhancing the adaptation process that is associated with higher target errors.

Target Error Modulation of Motor Plan

Following the idea that implicit learning is based mainly on sensory prediction errors (Mazzoni and Krakauer 2006; Taylor and Ivry 2011), that is, on differences between the motor plan and the perceived feedback, it is possible that the differences between the groups result from a difference between their sensory prediction errors as a result of different planning of the movements. For instance, when aiming a movement toward a big target, less accuracy is required and therefore movement plan can be less precise. Thus the sensory prediction errors, computed between the planning and the feedback from the cursor, might be less certain. According to this conjecture, the sensory prediction errors that drive the adaptation of internal models are contributed by specifications of the goal of the movement that subsequently affect the quality of the plan of the movement. As the goal requirements are more specific, the quality of the plan improves and the sensory prediction errors influence the motor plan to a greater extent. Consistent with previous studies (Fitts 1954; Soechting 1984), we found that manipulating the target size affected the spatial characteristics of the reaching movements. The idea that the certainty of the movement planning contributes to implicit adaptation is consistent with results of a study by Taylor and Ivry (2011). In their study, subjects were provided with different levels of strategy for planning their movements to achieve the task's goal. The different strategies included different certainties regarding the desired movement. After an adaptation session, which began with successful performance owing to the strategies, postadaptation aftereffects showed that all the groups adapted their internal model to account for the perturbation. However, the aftereffects were bigger as the group was provided with more certain instructions for their movement planning. While our results suggest that subjects in the two groups adapted equally to the perturbation, it may be that the certainty of the motor plan affected the retention and generalization of the adaptation process, and not the rate of adaptation itself.

Generalization as a Probe of the Internal Model

Neural network models have been engaged in revealing how the neural representation constrains the extent of task generalization (Poggio and Bizzi 2004). In our study, the reaching task was designed to provide a controlled measurement of the representational changes that are associated with the adaptation process. Training in the Pong task under a visuomotor rotation led to adaptation of an internal model of the Pong reaching movement that was manifested in a bias in movement direction to the opposite direction of the rotation. Thus the reaching task enabled a better quantification of the change of the internal model than the Pong task since movements were spatially constrained and online corrections were prevented by eliminating visual feedback. Nevertheless, evaluating the size of the change in this way depends on the generalization of the adapted model to the reaching task, i.e., to a task in which the initial hand direction and targets are static and there is no visual feedback of the movement.

Specifically, two key features are thought to define the pattern of generalization. First, generalization will be constrained by the properties of the underlying neural units that control the movements (Thoroughman and Shadmehr 2000). Second, error signals that are used to update the sensorimotor map alter the relation between the tuned units and desired directions of movement (Pouget and Snyder 2000). As such, if the underlying units represent movement space broadly, generalization will be broad because many units are affected by the error signal (Thoroughman and Shadmehr 2000).

Generalization of visuomotor rotations has been shown to be quite narrow (Krakauer et al. 2000), with strong generalization for movements similar to the training direction and falling off rapidly as the probe directions deviate from this direction (Krakauer et al. 2000). Nonetheless, most studies have found a small degree of generalization throughout the entire workspace (Krakauer et al. 2000; Tanaka et al. 2009). Learning a visuomotor rotation with the Pong task exposes subjects to wide training directions, together with further dynamic and spatial properties that vary between movements. In this sense, the nature of the trained movements is not expected to restrict the generalization to the probe reaching movements or cause a difference between the groups. However, the Pong task does not constrain movements in space like the studies described above (classical reaching movements). Therefore, the existence of generalization in one group and not in the other, which cannot be explained by kinematic differences, suggests that the internal model can adapt in a task-specific and in a task-unspecific manner, and that this property is affected by the task requirements.

Importance of Target Error Signals to Generalization

Few studies have considered the contribution of error signals to task-dependent effects on generalization. The strength of generalization was shown to be influenced by the availability of the feedback (Shabbott and Sainburg 2010; Taylor et al. 2013). As discussed above, the big-ball group perceived fewer and smaller target errors. Therefore, it is reasonable to assume that difference in the target error signals caused the generalization difference between the groups. Compared with the abovementioned studies, in our study the hand feedback was the same for the two groups. Moreover, both groups adapted a new visuomotor mapping at the Pong performance. Thus this difference in the error signals does not explicitly explain why both groups adapted an internal model but just one group generalized it to static reaching movements.

A possible explanation can be that different error signals drive different internal models, such that the differences were not only in the strength of the model but also in the way that it compensated the perturbation. Studies of visuomotor rotations have, for the most part, reported generalization patterns that are consistent with the direction of the rotation. However, a few studies suggest that generalization may entail another component, one that indicates that participants may be inferring a translational shift, either in addition to a rotation (Brayanov et al. 2012) or in lieu of a rotation (Taylor et al. 2013; Taylor and Ivry 2013). In our experiment, the lack of generalization in the big-ball group might reflect a similar effect. It could be that the lack of target errors prevented a correct representation of the perturbation and, instead, a different internal model was used and counteracted the rotation.

Influence of Context

Different generalization patterns are also associated with contextual effects. For example, different arrangements of the probe targets, rather than different error signals, were reported to have more effect on the extent of generalization across the workspace (Taylor and Ivry 2013). Regarding our results, we assume that the explanation of the generalization results should consider the contextual differences between the Pong and the reaching tasks: In the reaching task, movements are constrained and do not require precise timing, in contrast to the Pong task, in which subjects move freely in space and the dynamic characteristics of the environment determine how movements must be performed to successfully achieve the goal. Thus these contextual differences, which apply to both groups, might constrain the generalization of the adapted visuomotor mapping across the two tasks for both groups. Since the size of the target of the Pong task was manipulated between the groups, these contextual constraints may have been different between the groups. For instance, it is possible that the contextual constraints were more influential when hitting the ball was harder compared with when it was easier.

Conclusions

While future research is required to explore the mechanisms of contextual and goal effects, the present study shows that adaptation to an unnoticed visuomotor rotation depends not only on the visuomotor distortion and the feedback of the movement but also on the goal requirements. In particular, adaptation in the context of high goal requirements advances generalization across tasks. While the effect of task properties on learning has not been studied much, this effect is clearly important for implementing current adaptation theories in everyday learning behaviors. We therefore believe that future work with the Pong task as well as other unconstrained tasks has the potential of bridging the gap between current motor control theories that are based on lab-based artificial tasks and complex daily tasks that typically involve multiple implicit and explicit learning processes.

GRANTS

This research was supported by the United States-Israel Binational Science Foundation (M. Reichenthal, G. Avraham, A. Karniel), by the Kreitman fellowship (G. Avraham), by the German-Israeli Foundation for Scientific Research (L. Shmuelof), and by the Helmsley Charitable Trust through the Agricultural, Biological and Cognitive Robotics Initiative of Ben-Gurion University of the Negev.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

M.R., G.A., A.K., and L.S. conception and design of research; M.R. performed experiments; M.R. analyzed data; M.R., G.A., and L.S. interpreted results of experiments; M.R. prepared figures; M.R. drafted manuscript; M.R., G.A., and L.S. edited and revised manuscript; M.R., G.A., and L.S. approved final version of manuscript.