Sensory reweighting dynamics following removal and addition of visual and proprioceptive cues

Novel methods were applied to investigate the time course of changes in sensory contributions to balance (sensory reweighting) following a sudden addition and removal of visual or proprioceptive orientation information. Results demonstrate the influence of reweighting in adjusting to changes in sensory conditions but also reveal the influence of additional mechanisms, including an effect of expectation of upcoming changes, that affect balance control behavior when environmental conditions change.

Abstract

Removing or adding sensory cues from one sensory system during standing balance causes a change in the contribution of the remaining sensory systems, a process referred to as sensory reweighting. While reweighting changes have been described in many studies under steady-state conditions, less is known about the temporal dynamics of reweighting following sudden transitions to different sensory conditions. The present study changed sensory conditions by periodically adding or removing visual (lights On/Off) or proprioceptive cues (surface sway referencing On/Off) in 12 young, healthy subjects. Evidence for changes in sensory contributions to balance was obtained by measuring the time course of medial-lateral sway responses to a constant-amplitude 0.56-Hz sinusoidal stimulus, applied as support surface tilt (proprioceptive contribution), as visual scene tilt (visual contribution), or as binaural galvanic vestibular stimulation (vestibular contribution), and by analyzing the time course of sway variability. Sine responses and variability of body sway velocity showed significant changes following transitions and were highly correlated under steady-state conditions. A dependence of steady-state responses on upcoming transitions was observed, suggesting that knowledge of impending changes can influence sensory weighting. Dynamic changes in sway in the period immediately following sensory transitions were very inhomogeneous across sway measures and in different experimental tests. In contrast to steady-state results, sway response and variability measures were not correlated with one another in the dynamic transition period. Several factors influence sway responses following addition or removal of sensory cues, partly instigated by but also obscuring the effects of reweighting dynamics.

NEW & NOTEWORTHY

Novel methods were applied to investigate the time course of changes in sensory contributions to balance (sensory reweighting) following a sudden addition and removal of visual or proprioceptive orientation information. Results demonstrate the influence of reweighting in adjusting to changes in sensory conditions but also reveal the influence of additional mechanisms, including an effect of expectation of upcoming changes, that affect balance control behavior when environmental conditions change.

humans integrate visual, vestibular, and proprioceptive sensory cues to maintain balance in upright stance (Horak and Macpherson 1996). The balance mechanism is robust, in that it is able to compensate for the sudden loss of orientation information from one or two of these sensory systems. Such a loss of sensory information is common in everyday life for the visual system when closing the eyes or entering a dark room and for proprioceptive orientation cues when, for example, moving to or from a compliant surface. Failure to make timely and adequate adjustments in the balance control mechanism makes a person vulnerable to falls and injury in such changing environments (Honeine and Schieppati 2014).

Nashner and Berthoz (1978) suggested that the contributions of the individual sensory systems change when the available sensory information changes. This concept of “sensory reweighting” has been confirmed by quantitative measures of the individual sensory contributions (“sensory weights”) during tilts of the support surface, galvanic vestibular stimulation (GVS), and/or the visual surround (Assländer and Peterka 2014; Cenciarini and Peterka 2006; Hwang et al. 2014; Peterka 2002). Most studies investigating balance control were performed under steady-state conditions, in which test conditions remained unchanged and balance perturbations were continuously applied over time (Cenciarini and Peterka 2006; van der Kooij and de Vlugt 2007; Kuo 2005; Maurer et al. 2006; Mergner et al. 2003, 2009; Nashner and Berthoz 1978; Oie et al. 2002; Peterka 2002). In contrast, less attention has been given to the dynamic changes in balance control that occur after transient changes in the available sensory information (Honeine and Schieppati 2014).

Studies that have addressed transient changes include those that measured changes in spontaneous sway when adding and removing visual information (Hay et al. 1996; Honeine et al. 2015; Sozzi et al. 2011, 2012; Teasdale et al. 1991) or when adding or removing sensory input from a space-stationary touch pad (Honeine et al. 2015; Schieppati et al. 2014; Sozzi et al. 2011). Teasdale and colleagues (Hay et al. 1996; Teasdale et al. 1991) measured center of pressure (CoP) excursions in quiet stance of healthy young subjects and showed that sway variability was reduced or increased 4 s after addition or removal of visual cues, respectively. However, temporal resolution was limited in these studies because averages across several seconds were used to determine the changes in variability. The limitation of low temporal resolution was overcome by the approach used by Sozzi et al. (2011, 2012), who reported the time course of sway variability for transitions between eyes open and eyes closed. The time courses of changes in CoP variability following transitions were quantified with fits of an exponential function to experimental measures of sway variability. Results showed that the time constants were in the range of 3–4 s in the anterior-posterior (AP) and 1–2 s in the medial-lateral (ML) sway direction. In addition, Sozzi et al. (2011) found an asymmetry in the exponential time constants when adding and removing visual cues. Variability in the ML direction increased faster after an eyes open-to-eyes closed transition (1 s) compared with the variability decrease after an eyes closed-to-eyes open transition (2 s). These results were confirmed in a recent study of the same group (Honeine et al. 2015). Changes in sway variability can be caused by neural adjustments that affect the gain of the feedback control loop (Maurer et al. 2004) or by sensory reweighting that shifts reliance among sensory systems that have greater or lesser levels of sensory noise (van der Kooij and Peterka 2011).

To focus on the transient changes in sensory reweighting, several recent studies investigated reweighting dynamics evoked by a change in the amplitude of different balance-perturbing stimuli (Assländer and Peterka 2014; Jeka et al. 2008; Polastri et al. 2012). These studies employed the simultaneous presentation of surface-tilt and visual motion stimuli with one stimulus changing in amplitude while the other stimulus remained at a constant amplitude. For example, Assländer and Peterka (2014) used a pseudorandom surface- or visual-tilt stimulus that transiently changed amplitude to evoke sensory reweighting. The second stimulus component, a constant-amplitude sinusoidal surface or visual-tilt stimulus, was used as a “probe” to measure changes in sway sensitivity to the sine stimulus. Changes in the sway response to the constant-amplitude sine component were assumed to indicate changes in the sensory contribution to balance control, and thus sensory reweighting. Specifically, an increase in the sway response to support surface tilt or visual scene tilt following a change in amplitude of the pseudorandom stimulus indicated a shift toward increased reliance on proprioceptive or visual cues, respectively, for balance control. The time course of the sway response to the sine component allowed a detailed analysis of the dynamics of sensory reweighting with a high temporal resolution. Several studies (Assländer and Peterka 2014; Jeka et al. 2008) reported an asymmetry in the sway response dynamics following transitions. The asymmetries were similar to those observed in sway variability (Honeine et al. 2015; Sozzi et al. 2011, 2012; see above). Transitions to conditions that presented a greater challenge to balance showed faster changes in sway responses compared with transitions to less challenging conditions.

While the studies of the Jeka group and of Assländer and Peterka (2014) gave insight into the reweighting dynamics following amplitude transitions of external perturbations, the results were limited in that they only investigated proprioceptive and visual reweighting dynamics and thus provided no insight into reweighting dynamics of the vestibular contribution to balance control. Furthermore, all previous results were limited to stimuli that evoked AP sway and thus provided no insight into the control of balance in the ML plane.

In the present study, we investigated the reweighting dynamics and changes in sway variability associated with ML plane balance control following the sudden addition and removal of one source of sensory orientation information. Sensory reweighting was evoked by adding or removing the visual contribution by switching room lights on and off, respectively, or by adding or removing proprioceptive space orientation cues by switching body sway referencing of the support surface off and on, respectively (see methods). A constant-amplitude sinusoidal probe stimulus was continuously applied to measure transient changes in evoked sway indicative of the changes in sensory contributions of proprioception (using sinusoidal support surface tilts), vision (using sinusoidal visual surround tilts), or the vestibular system (using a sinusoidal binaural galvanic vestibular stimulus; Fitzpatrick and Day 2004). The time course of sway responses to the probe stimuli following transitions was used to analyze the dynamics of reweighting.

METHODS

Subjects

Twelve subjects (age 27.0 ± 3.8 yr; 7 women, 5 men) participated in this study after giving their written informed consent. The study was approved by the Internal Review Board of the Oregon Health & Science University and is in accordance with the 1964 Declaration of Helsinki.

Experimental Setup

Subjects stood with hands crossed at waist level in a balance test device (Fig. 1B), which allowed servo-controlled ML tilts of the support surface and the visual scene. The visual scene consisted of a half cylinder (70-cm radius) with high-contrast horizontal and vertical stripes of several gray shades and various spatial frequencies. The visual scene was illuminated by two bright white LED lights (Neutral White 4,000 K; Bridgelux, Livermore, CA) attached to the visual surround. Subjects wore a harness, which was loosely attached to the ceiling such that subjects had no additional orientation cues. ML body displacements at hip and shoulder levels were measured with two sway rods that hung from potentiometers (model CP-2URX-04, Midori America) attached to an Earth-fixed post behind the subject (Goodworth and Peterka 2010). Hooks attached at midline to the subject's harness at shoulder level and to a waist belt at greater trochanter height guided ML displacements of the sway rods. Trigonometric calculations were used to transform the potentiometer signals into ML displacement measures, and these ML displacements were used for later calculations of center of mass (COM) motion.

Fig. 1.

A: table of experimental conditions and corresponding stimulus combinations. EC and EO refer to eyes-closed and eyes-open conditions. B: schema of the experimental setup. C: example of the applied stimulus sequence, showing the transient On and Off switching of sway referencing (Exps. 1–3) or lights (Exps. 4–6), the constant amplitude sinusoidal stimulus, and the measured COM sway of 1 representative subject.

Self-adhering oval electrodes (3.2 × 5.7 cm; Bio-Flex BF-7, Lead-Lok) were applied to the mastoid process behind each ear to deliver bipolar, binaural GVS. Impedance of the skin was reduced below 3 kΩ with an abrasive gel and skin cleansing with alcohol pads. The GVS was generated with a custom-made battery-powered and optically isolated voltage-to-current amplifier, with the command voltage delivered by the data collection computer. Bipolar, binaural GVS is known to activate vestibular afferents and to evoke ML body sway when the subject's head is facing forward (Fitzpatrick and Day 2004).

Data collection and stimulus delivery were controlled by a custom program written in LabVIEW (National Instruments, Austin, TX) and executed on a National Instruments PXI system running real-time LabVIEW and a host PC. The LabVIEW program performed all online calculations, created and delivered the sinusoidal stimuli, and sampled data (actual surface and visual surround angles, CoP displacements, GVS current, and hip and shoulder displacements) for later analysis. Stimulus output and data recordings were at 200 Hz. During the experiments, subjects wore headphones and listened to an audio book to prevent auditory orientation cues and to distract from the balancing task.

Stimuli

Four experiments made use of “surface sway referencing” to minimize proprioceptive cues encoding body sway relative to the Earth vertical (Nashner and Berthoz 1978). Sway referencing was performed by commanding the angular position of the surface to match the online-measured tilt of the lower body based on ML displacements obtained from the hip sway rod.

Six experimental conditions were tested (Fig. 1A), with stimuli applied during each experiment consisting of two components. The first component was a rectangular signal, which switched on and off either sway referencing (Exps. 1–3) or the lights (Exps. 4–6) at intervals of 21.6 s, to transiently change the sensory cues available for balance control. The second stimulus component was a constant-amplitude sine wave that was continuously applied to the visual scene (Exp. 3), the support surface (Exp. 5), or the galvanic current amplifier (Exps. 1, 2, 4, 6). The sine stimulus had a frequency of 12 sine cycles/21.6 s = ∼0.56 Hz and a peak-to-peak amplitude of 0.3° for the visual scene and the support surface or 0.5 mA for the galvanic vestibular stimulus. The low amplitude and 0.56 Hz midfrequency stimuli were chosen to provide a good trade-off between evoking sway large enough to reveal changes in sway responses across time and small enough to minimally disturb the system's behavior (Assländer and Peterka 2014). The Off/On switching sequence consisted of eight consecutive 21.6-s Off/21.6-s On cycles that ended with one additional 21.6-s Off period (Fig. 1C).

Calibration Routine

The time course of the whole body COM sway angle with respect to Earth vertical was considered the main output for further analysis. Information needed for the COM calculations was obtained from the results of a 120-s-duration calibration trial performed at the beginning of the test session. During the calibration trial subjects were instructed to voluntarily perform slow ML sways such that a wide variety of combinations of upper and lower body orientations were recorded. The slow movements provided quasi-static conditions in which the recorded CoP was assumed to provide a measure of the vertical projection of the COM (Brenière 1996). A regression, relating the measured CoP displacement to a linear combination of the measured body displacements at shoulder and hip levels, gave the regression coefficients that were used on subsequent experimental tests to calculate the ML COM displacements as a function of measured hip and shoulder displacements. Anthropometric measures obtained from each subject were used to calculate the subject's COM height above the ankle joint level (Winter 2005), and then COM height and COM displacements were used to calculate COM sway angular trajectories.

Protocol

Subjects were asked to remove shoes and socks, and anthropometric measures were obtained. GVS electrodes were applied and the harness, waist belt, sway rod hooks, and earphones were attached. After the measurement of weight (including attached equipment), subjects were asked to step into the balancing device. The feet were aligned by placing the inner margin of the feet against a 12-cm-wide guide that was placed symmetrically with respect to the tilt axis. The guide was removed before the experiment was started. The calibration trial was performed, followed by a warm-up trial, consisting of a combination of all experimental tests, to familiarize subjects with the experimental setup. The six experimental tests (Exps. 1–6; Fig. 1A) and two additional tests (results not included in this report) were performed in random order. Three subjects had difficulty maintaining balance in Exps. 1 and 6, requiring repetition in order to obtain sufficient data for analysis. We concatenated cycles from different attempts to perform the challenging experimental tests in five cases where subjects did not successfully complete a full experimental test.

Data Analysis

Recorded data were analyzed with custom MATLAB (The MathWorks, Natick, MA) programs. The first and the last 10.8 s of each test were discarded to avoid uncontrolled transient effects, and sway velocity was calculated as the sample difference per sampling time without additional filtering. Velocity traces were chosen since they involve fewer drifts compared with position traces and therefore simplify all further analysis steps. The mean and standard deviation of COM sway velocity responses (Fig. 2) were calculated for each point in time across the remaining 96 individual 43.2-s-long cycles of all subjects (8 cycles of 12 subjects). This pooling of data across subjects ignores potential intersubject differences and could also lead to additional effects, such as an increase in variability due to different dynamics of individual subjects. An increase in variability could potentially reduce the accuracy of parameters that were used to characterize the time course of responses following transitions. The second half of the 21.6-s period following an Off or On transition was considered to be a steady-state period in which there were minimal cycle-to-cycle changes in amplitude or timing of responses to the sinusoidal stimulus component. The mean amplitude and phase values of the COM sway velocity at the sinusoidal stimulus frequency were obtained by first calculating the complex real and imaginary components from Fourier transforms of each individual steady-state period and then averaging these components across all steady-state periods. Amplitude was calculated as the absolute value of the mean complex components and phase as the inverse tangent of the imaginary divided by the real component. Significance tests for the differences between sine responses in the Off and On steady-state periods were performed in two steps. Hotelling's T² was used to test the difference between the two complex mean values of the Fourier transform at the stimulus frequency (Calkins 1998). Second, post hoc tests were performed for the amplitude and phase separately with bootstrap hypothesis tests (Zoubir and Boashash 1998). To obtain the 95% confidence intervals of the steady-state amplitude and phase values, distributions of the mean values were also calculated with bootstrap methods. From the 96 cycles of the original data, 96 cycles were randomly drawn (with replacement) and the amplitude and phase were calculated in the same way as for the original data. The procedure was repeated 5,000 times, gain and phase values were sorted in descending order, and the 125th and 4,876th values were taken as upper and lower bounds of the 95% confidence interval (Zoubir and Boashash 1998). Bootstrap methods were implemented in MATLAB with the function “bootstrp” from the “Statistics Toolbox.”

Fig. 2.

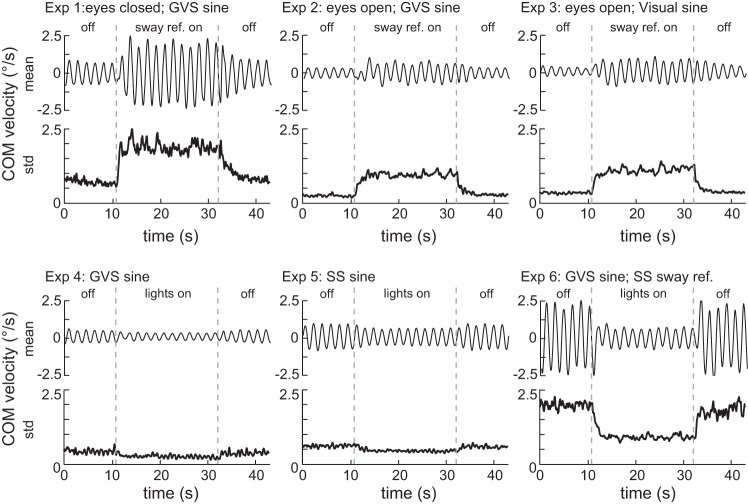
COM sway velocity averaged across subjects and cycles (mean, top) and variability of COM sway velocity, calculated as the standard deviation across subjects and cycles (std, bottom) for each of the 6 experimental tests. The mean (sine response) resembles the component evoked by the constant-amplitude sinusoidal stimulus. The standard deviation (sway variability) across time resembles the component that is not evoked by the sinusoidal stimulus.

Descriptions of Sine Responses Following Transitions

For a quantitative analysis of the dynamic change in amplitude and phase following an Off or On transition, functions were fitted to the experimental data according to previously presented methods (Assländer and Peterka 2014). The mean COM sway velocity responses across the 21.8-s periods following Off or On transitions were used as input to the fitting procedure. The functions had the following form:

$$\begin{array}{l}y\left(t\right)=a\times \sin \left(\mathrm{\omega }t+\phi \right)\text{for}t<\Delta t_{\text{A},\text{P}}\\ y\left(t\right)=A\left(t\right)\times \sin (\mathrm{\omega }t+\Phi \left(t\right))\text{for}t\ge \Delta t_{\text{A},\text{P}}\end{array}$$ (1)

where a and φ are the amplitude and phase of the previous steady state, ω the frequency of the sine stimulus, and Δt_A,P a time delay after which the transitions in response amplitude and phase begin. The temporal dynamics of the amplitude A(t) and phase Φ(t) were described with exponential functions given by

$$A\left(t\right)=a+\Delta a\times \left(1-e^{\frac{-\left(t-\Delta t_{\text{A,P}}\right)}{{\tau }_{\text{A}}}}\right)$$ (2)

$$\Phi \left(t\right)=\phi +\Delta \phi \times \left(1-e^{\frac{-\left(t-\Delta t_{\text{A,P}}\right)}{{\tau }_{\mathrm{p}}}}\right)$$ (3)

where a and φ are the amplitude and phase in the steady-state period at the end of the 21.8-s period following the transition, Δa and Δφ are the differences between amplitude and phase in the steady-state period following the transition and the previous steady-state period, and τ_A and τ_P are the time constants for the exponential terms describing amplitude and phase changes, respectively. A fitting procedure was used to obtain the parameters of the above equations. The steady-state amplitude and phase values calculated as described above were used in the fitting procedure to define the parameters a, φ, Δa, and Δφ. Therefore only Δt_A,P, τ_A, and τ_P were varied to fit the experimental data. All fitting procedures were performed in MATLAB with the “Curve Fitting Toolbox” with a least-squares criterion implemented with the function “fit” with the “trust-region-reflective” algorithm. To obtain confidence intervals of the fit results, the COM sway velocity data from the ninety-six 21.6-s periods following Off or On transitions were bootstrapped 5,000 times, the mean was calculated, and a fit was performed on each of the obtained 5,000 mean sine responses. Confidence limits were obtained equivalently as for the steady-state parameters.

In addition to the functions presented in Eqs. 1–3 to describe the time course of COM sway velocity following Off or On transitions, we considered two other equations with fewer parameters. One included no time delay (Δt_A,P = 0) and the other assumed that τ_A = τ_P. F-statistics were used to compare whether additional parameters (i.e., Δt_A,P ≠ 0 and/or τ_A ≠ τ_P) would improve the description of the experimental data significantly, where the statistical test accounts for the trade-off between a smaller fit error and adding a parameter to the model (Johannson 1993). Variance accounted for was calculated as a quantitative estimate of the quality of the fit with

$$\text{VAF}\left(\%\right)=\left(1-\frac{\text{RSS}}{{\sigma }_{\mathrm{E}\mathrm{X}\mathrm{P}}}\right)\times 100$$ (4)

where RSS is the residual sum of squares of the model fits and σ_EXP the variance of the experimental sway responses across the stimulus cycle.

Description of Variability Following Transients

Statistical comparisons of the steady-state variability differences between Off and On conditions and the fitting of the dynamic changes of the variability following transitions were performed with procedures analogous to those used for the sine responses. Bootstrap hypothesis tests were performed to test for differences between steady-state variability in the Off and On conditions. To fit the time course of variability following transitions, an equation of the form of Eq. 2 was used, with a equal to the steady-state variability value in the previous period and Δa equal to the change in steady-state variability. In case of the fits including a time delay Δt_V, the function value for t < Δt_V was the previous steady-state value a. F-test statistics were performed to compare fits with and without time delay to determine whether inclusion of the time delay parameter significantly improved the fit, and the variance accounted for was calculated with Eq. 4.

RESULTS

Figure 2 shows the mean and standard deviation of the body sway velocity across all repetitions of the stimulus cycles for each of the six experimental tests. The mean body sway velocity is the component of body sway that is evoked by the sinusoidal stimulus. The standard deviation of body sway velocity was used as a measure of sway variability. No obvious modulation of variability with the sinusoidal stimulus was observed. This indicates that variability appeared to be independent from the sine response and showed no clear evidence for signal-dependent noise or variability caused by changes in response gain across repeated trials. Both sway components clearly show modulation between On and Off periods in all experimental tests. Furthermore, the dynamics of the change of the sine responses and the sway variability following On and Off transitions are clearly visible in all experimental tests. In the following, the results of the quantitative analysis of the On and Off steady-state conditions, defined as the 10.8-s period prior to a transition, are presented, followed by the description of the identified temporal dynamics that reflect the time course of changes in amplitude and phase of sway velocity responses and of sway variability.

Analysis of Steady-State Sway

Figure 3A shows the mean amplitude and phase of the sine responses (see also Table 1) and the mean sway variability (see also Table 2) during the steady-state period with 95% confidence intervals. Both sway components, sine responses (Hotelling's T²-test in Table 1) and sway variability (Table 2), showed significant differences between On and Off conditions in all six experimental tests. In all tests that switched surface sway referencing On and Off (Exps. 1–3), the steady-state amplitudes and phase lag of the sine response as well as sway variability were greatly increased, with sway referencing On compared with sway referencing Off (P < 0.01; phase in Exp. 3: P < 0.05). In tests that switched lights On and Off (Exps. 4–6), steady-state sine response amplitudes and sway variability were decreased during lights On compared with lights Off (P < 0.01). The phase of the sine responses showed small differences in Exps. 4–6, which were only significant in Exps. 4 and 6 (P < 0.05). These results confirm that switching sway referencing or lights On and Off significantly affects sine response amplitude and sway variability and, in most cases, response phase during constant-amplitude sinusoidal surface tilt, visual tilt, or GVS perturbations.

Fig. 3.

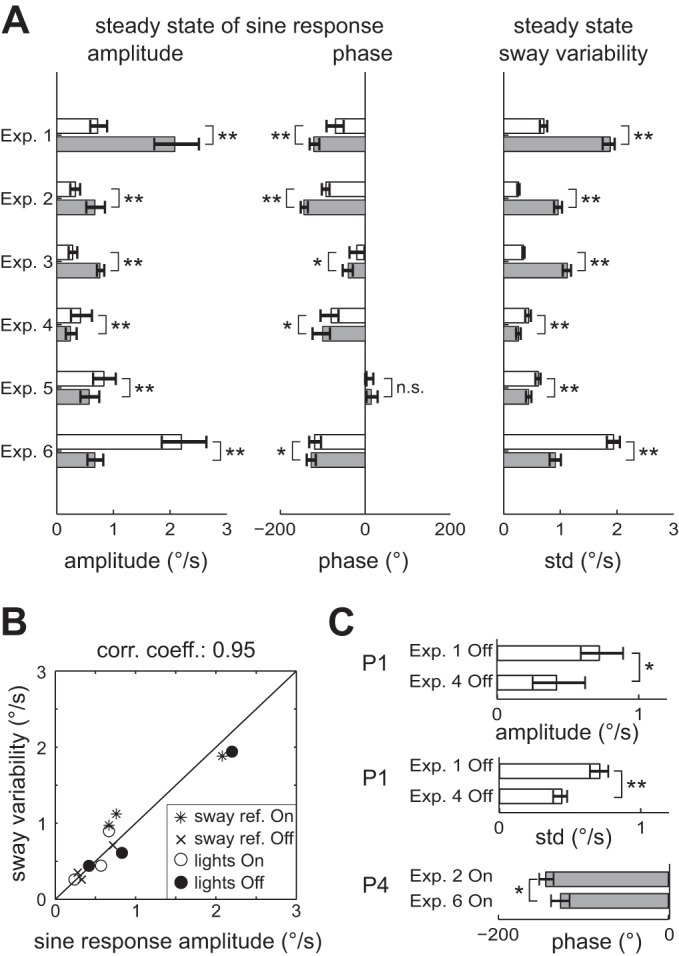
Steady-state values of sine response amplitude, sine response phase, and sway variability. A: Off (open bars) and On (gray bars) steady-state values, defined as the average values during the 10.8 s prior to a transition; error bars indicate 95% bootstrap confidence limits. Results of bootstrap significance tests for differences between On and Off values are represented by * (P < 0.05) or ** (P < 0.01). B: comparison of sway variability and sine response amplitude for each steady state. Diagonal line indicates identity of both parameters. C: selected parameters, with 95% confidence limits, for the comparison of pairs with identical steady-state conditions that were realized twice in different experimental tests. The only difference within each pair is that for one steady-state condition the upcoming transition is switching sway referencing On (P1) or Off (P4), while the other is switching lights On (P1) or Off (P4). Only parameters of pairs with significant differences are shown. Other combinations of identical steady-state conditions are indicated in Tables 1 and 2.

Table 1.

Sine response steady-state sway velocity, amplitude, and phase

			Steady-State Amplitude			Steady-State Phase
Experiment	Hotelling T2-Test	No.	Off, °/s	On, °/s	ΔAmpl Bootstrap Hypothesis Test	Off, °/s	On, °/s	ΔPhase Bootstrap Hypothesis Test
1	EC SS s.r. on/off, GVS sine	P < 0.01	0.72P1	2.08P3	P < 0.01	−70P1	−120P3	P < 0.01
			0.59/0.89	1.72/2.51		−91/−51	−131/−108
2	EO SS s.r. on/off, GVS sine	P < 0.01	0.33P2	0.67P4	P < 0.01	−92P2	−144P4	P < 0.01
			0.24/0.41	0.52/0.85		−102/−84	−152/−135
3	EO SS s.r. on/off, VS sine	P < 0.01	0.28	0.76	P < 0.01	−19	−40	P < 0.05
			0.21/0.36	0.71/0.84		−37/−2	−53/−29
4	Lights on/off GVS sine	P < 0.05	0.42P1	0.24P2	P < 0.01	−79P1	−100P2	P < 0.05
			0.25/0.62	0.16/0.35		−105/-63	−124/−83
5	Lights on/off SS sine	P < 0.01	0.83	0.57	P < 0.01	4	13	n.s.
			0.64/1.04	0.42/0.75		0/19	3/29
6	Lights on/off GVS sine; SS s.r.	P < 0.01	2.20P3	0.67P4	P < 0.01	−118P3	−126P4	P < 0.05
			1.85/2.64	0.54/0.82		−132/−104	−138/−116

Values are mean and lower/upper limits of 95% confidence intervals from bootstrap analyses. P1–P4 indicate pairs with identical sensory condition and identical sinusoidal stimulus during the steady state. EC, eyes closed; EO, eyes open; SS s.r., support surface sway referencing; VS, visual scene; n.s., not significant.

Table 2.

Steady state and sway variability

		Steady-State std
No.	Experiment	Off, °/s	On, °/s	Δstd Bootstrap Hypothesis Test
1	EC SS s.r. on/off, GVS sine	0.71P1	1.88P3	P < 0.01
		0.64/0.77	1.75/1.96
2	EO SS s.r. on/off, GVS sine	0.26P2	0.96P4	P < 0.01
		0.24/0.28	0.89/1.03
3	EO SS s.r. on/off, VS sine	0.35	1.12	P < 0.01
		0.33/0.37	1.04/1.19
4	Lights on/off, GVS sine	0.44P1	0.26P2	P < 0.01
		0.38/0.48	0.22/0.30
5	Lights on/off, SS sine	0.61	0.44	P < 0.01
		0.56/0.65	0.39/0.49
6	Lights on/off, GVS sine, SS s.r.	1.94P3	0.91P4	P < 0.01
		1.82/2.05	0.81/1.01

Values are mean and lower/upper limits of 95% confidence intervals from bootstrap analyses. P1–P4 indicate pairs with identical sensory condition and sinusoidal stimulus.

Figure 3B shows the sway variability plotted with respect to the sine response amplitude. A significant correlation was found between these two sway components (P < 0.01) for the On and Off steady states of all experimental tests, with a correlation coefficient of 0.95.

Across the four experimental tests that applied sinusoidal GVS, there were four pairs of steady-state conditions where the available sensory cues were identical, although these identical conditions occurred in different experimental tests. These four pairs are indicated in Tables 1 and 2 with P1 (fixed surface, no vision), P2 (fixed surface, with vision), P3 (sway referenced surface, no vision), and P4 (sway referenced surface, with vision). Figure 3C shows the comparison of steady-state parameters for pairs with identical steady-state conditions but with significantly different parameters. Differences were found in P1 (no vision, stable support surface), where sway response amplitude and sway variability were ∼40% smaller in the lights On/Off experimental test (Exp. 4) compared with the sway referencing On/Off test (Exp. 1). The third difference was found in the sway response phase of P4. These differences were unexpected and are addressed in discussion.

Analysis of Temporal Dynamics

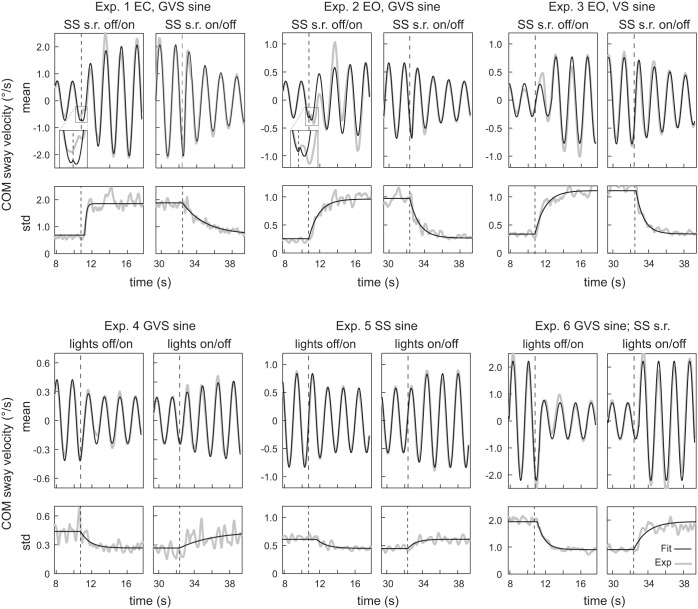
Figure 4 shows the sine response and the sway variability following On-to-Off and Off-to-On transitions together with the mathematical functions that were used to quantify the temporal dynamics of the experimental data. Identified parameters of the exponential functions that best described the transition dynamics of the sway response velocity are shown in Table 3. The mathematical functions were able to account for the dynamic changes in most tests. However, when switching sway referencing On (Exps. 1–3), the functions were not able to capture all characteristics of the observed sine responses (Fig. 4, top). Close inspection (see magnifications in Fig. 4) revealed a small discontinuity in the sine response ∼180 ms after the transition in Exps. 1 and 2 that was not properly accounted for by the fitted function. In addition, the sine response amplitude after switching sway referencing On in Exp. 2 was overestimated in the first cycle and underestimated in the second cycle. After the Off-to-On transition in Exp. 3 the sine response was underestimated by the mathematical function with identified best-fit parameters. The difficulties in accounting for the dynamics of Exps. 2 and 3 are reflected in the relatively low VAF values of 81.9% and 92.5%, respectively (Table 3).

Fig. 4.

Time course of the identified exponential fit functions (black line) that best described the experimental COM sway velocity data (gray line). Shown are the Off-to-On and On-to-Off transitions of the sine responses (mean, top) and of the sway variability (std, bottom) for all experimental tests. Note that the scale of the y-axis changes across tests.

Table 3.

Fit parameters of sine response sway velocity

		Off-to-On Transition			On-to-Off Transition
No.	Experiment	τA, s	τP, s	ΔtA,P, s	τA, s	τP, s	ΔtA,P, s	VAF, %
1	EC SS s.r. on/off, GVS sine	1.61	0.26	*	2.88	0.08	0.17	96.4
		0.74/2.68	0.01/1.28		2.14/3.60	0.05/0.31	0.00/0.24
2	EO SS s.r. on/off, GVS sine	2.43	0.04	*	2.11	0.09	0.24	81.9
		1.85/3.53	0.02/0.07		1.35/2.97	0.04/0.21	0.13/0.30
3	EO SS s.r. on/off, VS sine	0.01	0.82	1.93	5.64	0.27	*	92.5
		0.01/1.05	0.14/3.61	0.43/2.00	4.15/7.22	0.09/0.42
4	Lights on/off, GVS sine	0.56**	0.56**	*	2.50	0.44	*	99.1
		0.28/2.28	0.28/2.28		0.55/3.93	0.22/0.85
5	Lights on/off, SS sine	0.47	6.21	0.81	0.42	5.80	0.85	99.4
		0.01/2.02	0.01/10.00	0.00/1.30	0.01/2.89	0.01/10.00	0.00/1.82
6	Lights on/off, GVS sine, SS s.r.	0.21	0.01	0.45	0.01**	0.01**	0.57	99.0
		0.01/0.47	0.01/3.34	0.29/0.63	0.01/0.22	0.01/0.22	0.29/0.64

Values are mean and lower/upper limits of 95% confidence intervals from bootstrap analyses. VAF, variance accounted for by model fits.

^*Adding parameter did not improve fit significantly;

^**varying time constants of amplitude and phase independently from each other did not improve the fit significantly.

Sine responses to the GVS stimulus when switching sway referencing Off showed similar dynamics in eyes closed (Exp. 1) compared with eyes open (Exp. 2), with a time delay of ∼200 ms, very fast phase changes (τ_P < 0.1 s), and sine response amplitude changes with a time constant of 2.88 s (eyes closed) and 2.11 s (eyes open) (see Table 3). For the response to the visual scene sine when switching sway referencing Off (Exp. 3) no time delay was identified, the time constant of the phase was 0.27 s, while the time constant of the amplitude change was very slow with a time constant of 5.64 s.

In summary, switching sway referencing On in Exps. 1–3 showed abrupt changes in the sine responses, which were not fully described with exponential functions. Switching sway referencing Off showed abrupt changes in phase and a more gradual decline in sine response amplitudes to GVS and visual scene stimuli with sine responses that were characterized well by exponential functions.

For both lights On-to-Off and Off-to-On transitions (Exps. 4–6) the time courses of sine responses were generally well characterized by exponential functions. In Exp. 4 the changes in phase of sine responses following both transitions were best described without a time delay and with a time constant of ∼0.5 s. The change in sine response amplitude in Exp. 4 differed between transitions, with a relatively small time constant of 0.56 s after switching the lights On and a time constant of 2.5 s after switching the lights Off. In Exp. 5, the sine response amplitude to the surface tilt stimulus following both transitions showed changes after time delays of ∼0.8 s and with time constants of ∼0.45 s. For the phase in Exp. 5, the large confidence intervals of the time constant (0.01–10 s) and the small, nonsignificant difference in phase during the steady states limit the relevance of the identified phase transition dynamics. In Exp. 6 lights were switched On and Off during a sinusoidal GVS perturbation while subjects were standing on a sway-referenced support surface. Sine response changes in this experimental test showed fast time constants (0.01–0.21 s) for both phase and amplitude and a time delay of 0.5 s.

The graphs of each experimental test in Fig. 4, bottom, show the sway variability trajectories following the transitions and the exponential functions that were fitted to the data. In general, sway variability dynamics were well described by the mathematical functions in all experimental tests. Visually, only the time course of sway variability when switching lights Off in Exp. 6 showed characteristics of a time delay and a fast increase, which was not confirmed by the fitting procedure. A reason for this result could be a second, slow increase in sway variability ∼10 s after the transition (see Fig. 2).

Table 4 shows the results of the quantitative description of transition dynamics of the sway variability (standard deviation across cycles). Most time constants that were identified for the changes observed in sway variability were in the range of 0.8–1.5 s, which is the range reported in earlier studies (Honeine et al. 2015; Sozzi et al. 2011, 2012). A major exception was found in Exp. 1, where sway variability changed with a time constant of 0.17 s (the shortest of all variability time constants) when switching lights On and a time constant of 2.61 s when switching lights Off. A second exception was the variability change in Exp. 4 when switching lights Off, where the time constant was 3.83 s. The difference in sway variability between the steady states of this experimental test was very small and resulted in large confidence bounds, which might have led to an overestimation of this time constant as well as the relatively low VAF values in Exps. 4 and 5 (Table 4).

Table 4.

Fit parameters of sway variability

		Off-to-On Transition		On-to-Off Transition
No.	Experiment	τV, s	ΔtV, s	τV, s	ΔtV, s	VAF, %
1	EC SS s.r. on/off, GVS sine	0.17	0.42	2.61	*	93.6
		0.11/0.43	0.30/0.48	2.21/3.12
2	EO SS s.r. on/off, GVS sine	1.14	*	1.08	*	96.5
		0.85/1.60		0.84/1.38
3	EO SS s.r. on/off, VS sine	1.17	*	0.88	0.12	96.3
		0.84/1.71		0.64/1.13	0.00/0.21
4	Lights on/off, GVS sine	1.06	*	3.83	*	59.3
		0.70/2.17		0.74/5.00
5	Lights on/off, SS sine	1.10	0.90	0.91	*	78.7
		0.15/2.82	0.16/1.17	0.56/2.55
6	Lights on/off, GVS sine, SS s.r.	0.83	0.34	1.49	*	94.0
		0.51/1.14	0.18/0.67	0.86/3.05

Values are mean and lower/upper limits of 95% confidence intervals from bootstrap analyses. VAF, variance accounted for by model fits.

^*Adding parameter did not improve fit significantly.

Figure 5 shows the relationship between the temporal dynamics of changes in sine response phase and sine response amplitude (Fig. 5B) and in sway variability and sine response amplitude following transitions (Fig. 5C). To simplify making comparisons of transition dynamics, a “transition time” was defined as the time required to complete 95% of the total amplitude change. The transition time was calculated from the exponential function parameters shown in Table 3 for sine response amplitude and in Table 4 for sway variability using Δt + 3 × τ (see Fig. 5A; see also Honeine et al. 2015), as an exponential decay reaches 95% of the total change after three time constants (transition time for phase is not shown in Fig. 5A).

Fig. 5.

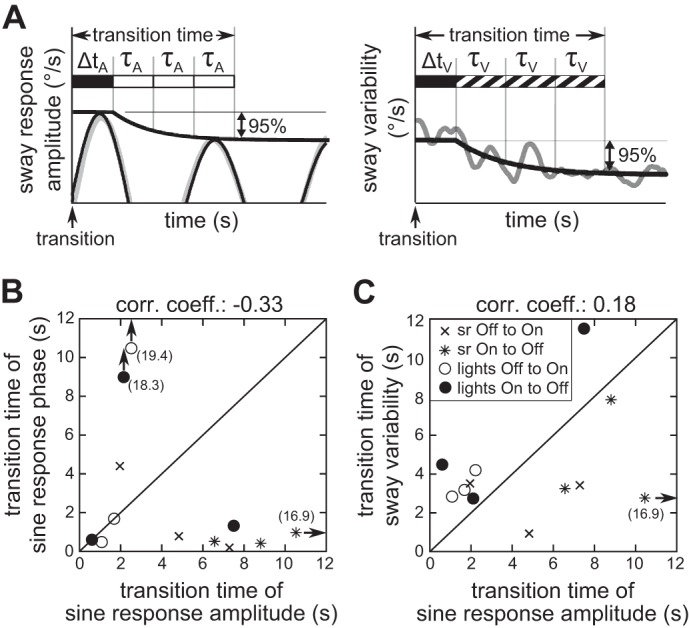
Transition times of all experimental tests. A: definition of transition times for the sine response amplitude (left) and sway variability (right). B and C: summary of transition times with sine response phase plotted over sine response amplitude (B) and sway variability plotted over sine response amplitude (C). Very large transition times are indicated with arrows and the corresponding values in parentheses.

Transition times of the sine response phase were not correlated to the transition times of the sine response amplitude (Fig. 5B; correlation coefficient −0.33, not significant). While transition times of the sine response amplitude are spread over a wide range (1–16.9 s), most phase transition times were small (<2 s). The two most notable exceptions were the very large values of phase transition times of Exp. 5, which may be explained by the difficulty of accurately measuring a transition time when there was only a small and not significant difference between the steady-state values of the phase during On and Off periods.

Figure 5C shows the relation of the transition times of sine response amplitude and sway variability. Overall, there was no clear relationship between these transition times, as indicated by the general scatter of points in Fig. 5C and the low correlation coefficient of 0.18 (not significant). This finding is in contrast to the high correlation found between the steady-state values of sine response amplitudes and sway variability (see Fig. 3B). Another pattern visible in Fig. 5C is the difference between lights On/Off and sway referencing On/Off transition times. For lights On/Off transitions (Exps. 4–6) the sway variability transition times were greater than the sway response amplitude transition times in all six On-to-Off and Off-to-On transitions. In contrast, for sway referencing On/Off transitions (Exps. 1–3) the sway response amplitude transition times were greater than the sway variability transition times in five of six of the transitions.

DISCUSSION

The present study investigated the time course of sensory reweighting following a transient change in sensory contributions, where proprioceptive (Exps. 1–3) or visual (Exps. 4–6) cues were suddenly removed or added. Responses to sinusoidal surface tilts, visual scene tilts, or sinusoidal GVS were used to estimate the time course of the proprioceptive, visual, or vestibular sensory contributions, respectively. Sway responses to the sinusoidal stimulus and sway variability showed significant differences between On and Off steady states in all experimental tests (see Figs. 2 and 3 and Tables 1 and 2). Below, results from the steady-state period are discussed, followed by considerations regarding the temporal dynamics of changes in sway following transitions in sensory conditions. Finally, the temporal dynamics are compared to previous results from the literature, especially with respect to an asymmetry between On-to-Off and Off-to-On transitions, as reported in earlier studies.

Steady-State Period

The sway responses to sinusoidal stimuli were considered to have reached a steady state in the time period 10.8–21.6 s after a transition. The observed sway amplitudes were in good agreement with previous studies investigating steady-state sway during support surface tilt, visual scene tilt, and GVS perturbations (Cenciarini and Peterka 2006; Peterka 2002). The following sections describe some observations related to the steady-state sway velocity response to the sinusoidal stimulus and sway variability.

Phase lag in experimental tests with GVS.

In all tests where the sinusoidal stimulus component was applied as GVS (Exps. 1, 2, 4, and 6), the phase of the sine response showed a considerable phase lag compared with responses from surface and visual stimuli (Table 1 and Fig. 3A). Several factors could have contributed to larger GVS phase lags. One possibility is that GVS evoked sway with a long time delay. Day and Cole (2002) found a relatively long 240-ms onset delay of head and trunk tilt in response to a step change in GVS. This delay was similar to results from an early study that found that a dynamic model that incorporated a 250-ms delay in response to a step change in GVS was able to account for experimental results (Nashner and Wolfson 1974).

In addition to a long time delay, the observed phase lag could also be influenced by central processing of GVS-evoked vestibular responses. Because vestibular nerve activation by GVS does not correspond to activation evoked by natural head motion (Fitzpatrick and Day 2004), the brain's processing of GVS-evoked vestibular signals could be distorted compared with the wide-bandwidth encoding of head motion obtained from natural vestibular stimulation. Consistent with this, Peterka (2012) found that the bandwidth of sway responses to GVS was reduced relative to the bandwidth of sway evoked by surface-tilt stimuli. Specifically, to explain the sway response to GVS, an existing balance control model required the addition of low-pass filtering of the GVS waveform with a cutoff frequency of ∼0.15 Hz. Such a low-pass filter accounted for a frequency-dependent phase lag that was roughly in the range of −70° at the sine frequency used in the experiments of the present study (0.56 Hz). Note, however, that the result of Peterka (2012) was based on limited data.

Steady-state sine response amplitudes and sway variability.

Sine response velocity amplitudes and the average magnitude of sway variability were similar in steady-state conditions, and the correlation between them was very high (Fig. 3B). This finding suggests that there is a close coupling between the two sway components across a variety of sensory conditions. A similarly close and nearly 1:1 coupling between steady-state sway response amplitude and sway variability was previously documented in an experimental setup in which the sensory conditions remained the same (eyes-closed stance with surface-tilt stimuli) but the sway amplitude was increased by increasing the stimulus amplitude (see Fig. 4A in van der Kooij and Peterka 2011). A model-based interpretation in this previous study indicated that both the pattern of sensory reweighting and the coupling between stimulus-evoked sway and sway variability could be accounted for by a sensory reweighting process that minimized mean square sway velocity.

Some authors, on the basis of studies of voluntary arm and hand movements, suggested that motor noise is a major source of human movement variability (Harris and Wolpert 1998; Wolpert and Ghahramani 2000). If these results applied to the present study, this would suggest that the increased sine response amplitude would cause higher variability due to the higher muscle forces that are necessary to generate the evoked sway. However, there are other potential sources of movement variability. For example, there is evidence that variability of eye movements controlled by the smooth pursuit system is dominated by errors in sensory estimates, i.e., sensory noise (Osborne et al. 2005).

Variability observed during human stance also appears to be dominated by sensory noise. In a model-based interpretation of experimental results of body sway evoked by surface-tilt stimuli during eyes-closed standing balance, motor noise only accounted for ∼10% of the overall observed sway variability, while sensory noise was the major source of sway variability (van der Kooij and Peterka 2011). Furthermore, vestibular system noise was ∼10 times larger than proprioceptive noise and the increased sway variability observed with increasing stimulus amplitudes was accounted for by a reweighting process that increased the vestibular contribution to balance control relative to the proprioceptive contribution.

Although this previous study did not apply a similar analysis to results from experiments in which subjects had access to visual information, it is known that sway variability is reduced in eyes-open vs. eyes-closed conditions. By analogy to this previous study, and from estimates of sensory contributions during eyes-open stance showing lower vestibular weights compared with eyes-closed conditions (Peterka 2002), it is reasonable to expect that a reduction in sway variability with eyes open is due to both a reduction in the influence of vestibular noise (downweighting the vestibular contribution) and the addition (sensory substitution) of lower-noise visual information for the noisy vestibular cues (Assländer et al. 2015).

Both notions, vestibular noise as a major contributor to response variability and the variability reduction associated with increased reliance on proprioceptive and/or visual cues, are consistent with the results of the present study. Specifically, variability was increased whenever the vestibular contribution was increased, with the increased vestibular contribution indicated by the increased sine response amplitude to the GVS stimulus in Exps. 1, 2, 4, and 6. Also, among all the combinations of sensory information available in the different steady-state periods of the six experiments, steady-state sway variability was largest in the two periods where we expect essentially full reliance on vestibular information for balance (sway referencing On in Exp. 1 and lights Off in Exp. 6).

While sway variability and sine responses to the GVS stimulus are consistent with the explanation of the vestibular system as the major noise source, there was also modulation of sway variability in experiments that applied a visual scene stimulus (Exp. 3) and a surface-tilt stimulus (Exp. 5). As in experiments applying GVS, the steady-state response amplitudes evoked by visual or surface stimuli were modulated by the changing conditions and the changes in response amplitudes were correlated with changes in sway variability. Because no external vestibular stimulus was applied in Exps. 3 and 5, it is uncertain whether the observed changes in sway variability were attributable to a change in the vestibular contribution to balance or to a reapportioning of the visual and proprioceptive contributions to balance. For example, in Exp. 5 the sway response to surface sine stimulus increased with lights Off and sway variability increased. It is possible that the vestibular contribution to balance, and therefore the sway variability attributable to vestibular noise, remained constant throughout. If proprioceptive noise was greater than visual noise, then a shift toward increased reliance on proprioception with lights Off, consistent with the increased response to the surface stimulus, would also cause increased sway variability even though the vestibular contribution did not change. Alternatively, an increase in sway variability would also occur if both the vestibular and proprioceptive contributions to balance increased to compensate for the loss of visual information. More complex experiments using multiple stimuli have been used to simultaneously estimate the contribution of visual, vestibular, and proprioceptive contributions (Hwang et al. 2014). Similar experiments could be used to clarify the rearrangement of multiple sensory contributions to balance as conditions change.

Expectation-dependent influence on steady-state responses.

Four pairs of steady-state conditions were identical in terms of available sensory cues and the application of sinusoidal GVS, although each pair was realized in different experimental tests. The pairs were P1 (lights Off, fixed surface), P2 (lights On, fixed surface), P3 (lights Off, sway referenced surface), and P4 (lights On, sway referenced surface), where each pair contained one experimental test with an upcoming transition in sway referencing and one experimental test with an upcoming transition in the visual condition. Two of these pairs (P2 and P3) showed no differences in sway responses or variability, suggesting that results were entirely a function of the presented sensory conditions. However, the other two pairs (P1 and P4) did show differences. Specifically, P1 showed considerable differences in steady-state sway amplitude and variability and P4 showed differences in the sine response phase (see Fig. 3C). These differences occurred despite the fact that the available sensory information and the applied stimulus (GVS) were identical for each pair.

The observed differences could result from adjustments that produced either different dynamics of the control system (e.g., different levels of cocontraction and/or active neural control that affects overall stiffness) or different combinations of sensory weighting factors. Independent of the specific cause that produced the observed differences in responses in two of the four paired conditions, these differences provide evidence that the state of the balance control system can be influenced by factors other than the specific sensory information that is available in a particular condition. In our experiments, where transitions between two different conditions occurred repeatedly, such a factor could be an expectation of the upcoming transition and knowledge about whether an upcoming transition threatens stability.

In the paired conditions that showed differences in amplitude and variability (P1) or phase (P4), there was evidence that an expectation of a threat to stability did influence sway responses. Specifically in P1 and P4 pairs, two sources of sensory information were available. In one of the experiments in each pair the expected transition involved removal of one of these two sources and was associated with a large change in sway amplitude, while in the other experiment of each pair the expected transition involved the addition of a third sensory source and was associated with a small reduction of sway amplitude. Since condition changes were periodically repeated, subjects could have developed an expectation for the upcoming transition. Such “habituation” was also reported for transient visual scene motions, where the first repetition evoked a large sway response in standing subjects while succeeding stimuli did not (Bronstein 1986). One interpretation of Bronstein's and our results is that, with two sources of sensory orientation information available, the sensory weights of these sources could have been adjusted in expectation of the upcoming transition.

The behavioral advantage of having an expectation of an upcoming transition is likely more beneficial if the expected transition poses a threat to stability, i.e., expecting the removal of sensory information. In pair P1 the transition to sway referencing On in Exp. 1 necessitated a rapid shift to exclusive use of vestibular cues for balance. This rapid shift was possibly facilitated by the subject's balance control system being already biased toward increased reliance on vestibular information prior to the transition to sway referencing. In contrast, when stability is not threatened, as in Exp. 4 (the second experiment in pair P1), the behavioral advantage of knowing that the upcoming transition will add sensory information is probably small since stability is not threatened. In this situation the subject's balance control system could have discounted the value of expectation and rather optimized sensory utilization based on a criterion that did not include an expectation of a threat to stability (e.g., reduced sway variability; see van der Kooij and Peterka 2011). Thus in the P1 condition of Exp. 1 the vestibular weight is higher than in the P1 condition in Exp. 4 and, consistent with this, the sway response amplitude to GVS and sway variability is higher in the P1 condition in Exp. 1 than in the P1 condition in Exp. 4.

Previous results have demonstrated that GVS-evoked responses differ in situations where fear of falling is increased when standing on a high platform vs. standing at ground level (Horslen et al. 2014; Osler et al. 2013). While there is some controversy regarding the interpretation of these results (Horslen et al. 2015; Reynolds et al. 2015), our results from the P1 paired conditions appear to be generally consistent with both prior studies. Specifically, our results indicated that the vestibular contribution to balance was increased in tests where there was an expectation of a greater threat to stability. This heightened vestibular contribution is likely accompanied by sensory integration changes that include a reduced reliance on proprioceptive cues (Cenciarini and Peterka 2006).

In the paired conditions that showed no differences in amplitude, phase, or variability (P2 and P3) it may be informative to note that in the P2 pair only vestibular information was available for balance control and in the P3 pair all sources of sensory information were available. With only one source of sensory information available, subjects had no option other than relying entirely on vestibular information for balance and thus were unable to make any adjustments in their balance control system that affected steady-state responses. When all sources of sensory information were available (P3 pair), body sway amplitudes were small and transitions that occurred in those experimental tests (Exps. 2 and 4) produced only modest increases in body sway. Thus there was no behavioral necessity to make adjustments to the balance control system to facilitate stability after transitions.

Transition Period

In the design of the study, the expectation was that the sway responses to the applied constant-amplitude sine stimulus would be indicative of sensory contributions. Therefore, the time course of sway responses following the addition and removal of sensory information were expected to provide insights into the dynamics of sensory reweighting. The quantitative description of the transition period assumed a time delay (accounting for conduction times, neural processing, muscle activation dynamics, etc.) and an exponential term to account for reweighting dynamics. While our transition time measures did provide insights into the overall time required for reweighting, there were some inconsistencies in individual time delay estimates such as an implausibly long 2-s time delay in the sine response of Exp. 3 and no time delays identified in various other transitions. The dynamics of the transitions indicate that factors other than reweighting influence the dynamics of sway responses following transitions. These factors, which include passive torque contributions, imperfect coordination of sensory reweighting, and prediction of periodic stimulation, are discussed below. The relatively simple equations that were also used in an earlier study (Assländer and Peterka 2014) may not be adequate to account for transition dynamics that include such factors, with the result that estimated parameters have reduced reliability. In the last part of this section, the observed differences between transition dynamics of sine responses and sway variability, as well as the asymmetry between Off-to-On and On-to-Off transitions, are discussed.

Influence of passive torque changes following sway referencing transitions.

In Exps. 1 and 2 abrupt changes in different aspects of evoked sway were observed when switching sway referencing On and Off. Discontinuities were present when switching sway referencing On in Exps. 1 and 2 (Fig. 4, insets), and curve fits identified large phase changes (40–50°) that occurred with short transition times after both On and Off transitions. One plausible explanation for these sudden changes is the sudden removal of passive ankle joint impedance when switching sway referencing On. This removal occurs because sway referencing essentially eliminates the ankle joint angle changes that normally occur with stance on a flat surface. Without a change in ankle joint angle, the muscle/tendon structures surrounding the joints are not stretched in relation to body sway, thereby largely reducing the contribution of the passive structures to the overall torque maintaining the body upright. Considering that balance is maintained by a feedback control mechanism (Johansson and Magnusson 1991; Peterka 2002), the sudden removal of the passive contribution produces a sudden decrease in total gain of the feedback control loop such that less corrective torque is generated per unit of body sway. This decrease in loop gain would affect the dynamic characteristics of the balance system such that a greater phase lag of sway with respect to the stimulus is present because of a reduced bandwidth of the control system. Additionally, a greater phase lag would be expected with loss of the passive torque contribution because the passive structures generate torque as an instantaneous (zero time delay) function of ankle joint angle changes while the sensory-derived contribution to torque production is time delayed.

The observed abrupt phase changes when switching sway referencing Off are also consistent with an explanation based on passive ankle impedance. Switching sway referencing Off results in a sudden addition of the passive contribution to ankle torque, which in turn evokes a rapid change in sine response phase due to a greater loop gain and a torque component acting with zero time delay.

Influence of imperfect sensory reweighting following transitions.

An additional effect potentially contributing to the observed abrupt changes following sway referencing On and Off transition may be related to results presented by Peterka and Loughlin (2004). These authors found that humans show 1-Hz resonant sway when sway referencing is switched off. They suggested that this resonant behavior can result from an increased feedback loop gain through an “imperfect” sensory reweighting mechanism that causes the sum of weights to be >1 in the initial period after switching sway referencing off. Each sensory weight represents the relative contribution of the various sensory systems contributing to balance control, such that the sum is unity in steady-state conditions. If the sum of weights is transiently >1 then the feedback loop gain is transiently increased, thus changing the dynamic characteristics of the balance control system. Similarly, results in Peterka and Loughlin (2004) indicated that the loop gain may be transiently too low when sway referencing is turned on. Therefore, an imperfect coordination of sensory integration mechanisms could contribute to the transient generation of too much or too little corrective torque that could influence the evoked sway dynamics following transitions in a manner similar to the addition and removal of the passive torque contribution. However, passive torque changes occur instantaneously, while the effects of imperfect sensory weighting would occur with a delay and would last as long as the imperfect weighting remained.

Influence of prediction in extending sensory estimates of periodic motion.

The sinusoidal probe stimuli that were applied to investigate the time course of reweighting have a simple periodic pattern. It is reasonable to assume that predictive mechanisms could be involved in the generation of sway responses to such stimuli. Evidence for such a mechanism has, for example, been found in smooth pursuit eye movements (Barnes and Asselman 1991). Barnes and Asselman (1991) recorded eye movements during tracking of a periodic visual target stimulus that occasionally was interrupted or had an amplitude change. The results showed that after stimulus interruptions or amplitude changes the eye movements initially continued as if the stimulus remained present. These results suggested that the nervous system developed a prediction of expected target motion when the periodic visual target stimulus was present, and this internal prediction contributed to the sustained generation of eye movement in addition to compensating for delays in the visual system to keep the eyes exactly on target. Such a mechanism could be relevant to the lights On/Off transitions in our experiments, where sway responses continued rather smoothly when switching lights Off (Figs. 2 and 4). The smooth transition indicates that, despite the sudden removal of the visual space reference, no major loss of overall torque seems to have occurred. A predictive component could have continued the visual contribution for a short period until other sensory systems compensated for the loss.

Feedforward aspects of sensory transitions.

Alternative terminologies have been used to describe mechanisms that determine the responsiveness to sensory disturbances following transitions that alter the availability of sensory orientation information. In their study of how the quality of visual cues influences the time course of responses to GVS, Day and Guerraz (2007) considered how “feedforward” and “feedback” mechanisms modulate GVS-evoked sway. The authors' description of feedforward effects pertains to the observation that the initial response to GVS depended on the prior state of the system, which in turn depended on the quality of available sensory cues in the prior state (Prochazka 1989). This view is consistent with our concept of sensory weighting where weights were set according to the experimental conditions and determined the steady-state responsiveness to our sinusoidal stimuli. When a transition occurred, the weights set in the prior condition accounted for the initial continuation of responses to the sine perturbations. After a transition, the change in available sensory signals affected the sine responses due to changes in the dynamic characteristics of the continuously active feedback control system. Day and Guerraz (2007) recognized that the time course of body sway following a transition could be influenced by a dynamic adjustment of control gain that may be determined by a “feedforward gain control mechanism.” We refer to this adjustment as a dynamic reweighting process. The central mechanism for this reweighting is unknown. However, it seems unnecessary to attribute this reweighting to a feedforward mechanism since reweighting, as well as the setting of sensory weights in steady-state conditions, could occur as a function of the central processing of sensory signals within a feedback control framework (Mahboobin et al. 2009; Mergner 2010; Mergner et al. 2003).

Transition time comparison of sine response amplitudes and sway variability.

The identified transition times for the sine response amplitude changes showed considerable differences compared with those of sway variability (Fig. 5C). Given the high correlation between response amplitude and variability measures in steady-state conditions (Fig. 3B), one might expect that these measures would also be correlated throughout the transition period, with the result that transition times would be similar. This expectation would likely require that, throughout the transition period, the dynamic characteristics of the balance system remained similar to those in steady-state conditions. A specific requirement for maintaining similar dynamic characteristics in a feedback control system under different conditions is that the corrective torque, generated per unit of sensory error, remains constant (i.e., the “torque normalization hypothesis”; Peterka 2002). However, the two factors mentioned previously, loss or restoration of the passive torque contribution following transitions to and from sway-referenced conditions and imperfect sensory reweighting, would both contribute to a violation of torque normalization such that the dynamic characteristics of the balance system would change throughout the transition period. Furthermore, these changing dynamics would likely influence sway variability and responses to external stimuli differently since the dynamic characteristics of evoked sway differ depending on whether sway is evoked by an internal signal (sensory or motor noise) vs. an external stimulus (e.g., see appendix B in van der Kooij and Peterka 2011). The observed dissociation between stimulus-evoked sway and sway variability following transitions revealed the complexity of processes involved in adjusting to changing environments. While we have suggested factors that likely contributed to this complexity, a more detailed understanding will require additional experiments that independently probe the time course of multiple sensory contributions and application of existing models (Carver et al. 2006; Mergner 2010; Peterka 2002) or development of new models that are able to account for all aspects of the experimental data.

Asymmetry of On-to-Off and Off-to-On transitions.

Earlier studies reported an asymmetry, where switching to a condition that endangered balance evoked fast transitions to new steady-state response profiles, consistent with rapid sensory reweighting, while transitions were slower when the new condition did not endanger balance (Assländer and Peterka 2014; Honeine et al. 2015; Jeka et al. 2008; Sozzi et al. 2011, 2012). The hypothesized behavioral utility for asymmetric responses is that when a transition adds accurate orientation information, humans may not need to react quickly to rearrange sensory contributions since the balance system is already in a stable state and adjustments can occur slowly. However, if sensory information is lost, more rapid adjustments in sensory contributions are needed since losing information could result in reduced corrective torque and therefore instability. In the present study, removing the contribution of one sensory system can be considered as a situation that endangers stability. For sway referencing On/Off experiments (Exps. 1–3), the Off-to-On transition removed proprioceptive information whereas the On-to-Off added accurate proprioceptive information. The opposite is true for lights On/Off experiments (Exps. 4–6). The lights On-to-Off transition removed visual information, while visual information was added with the lights Off-to-On transition.

To test for asymmetries in the six experimental tests, a ratio was calculated of the transition time of the sine response amplitude when adding sensory cues to the transition time when removing sensory cues. A ratio > 1 indicates that the transition to new steady-state conditions occurred faster in the situation that removed sensory information and that potentially endangered balance, while a ratio < 1 indicates the opposite. Ratios > 1 would be consistent with the hypothesized behavioral utility for asymmetric responses.

The ratios of the six experimental tests are shown in Table 5. Exps. 1, 3, and 6 had transition time ratios clearly >1 and were therefore in full agreement with the hypothesized asymmetry. The ratios in Exps. 2 and 5 were ∼1, indicating symmetric transition dynamics. The ratio of Exp. 4, in contrast, was 0.22, i.e., opposed to the assumption of faster reweighting in the situation that endangers balance. However, the accuracy of the Exp. 4 ratio is questionable since the response amplitudes to GVS in Exp. 4 were very small and changed very little between lights On and Off conditions. In summary, these results partially support the idea of faster reweighting in situations that endanger stability but are condition dependent and show a wide range including a minority of results that do not support this idea.

Table 5.

Ratios of sine response transition times

		Transition Time
No.	Experiment	Removal	Addition	Transition Time Ratio Addition/Removal
1	EC SS s.r. on/off, GVS sine	4.83	8.81	1.82
2	EO SS s.r. on/off, GVS sine	7.29	6.57	0.90
3	EO SS s.r. on/off, VS sine	1.96	16.92	8.63
4	Lights on/off, GVS sine	7.50	1.68	0.22
5	Lights on/off, SS sine	2.11	2.22	1.05
6	Lights on/off, GVS sine, SS s.r.	0.60	1.08	1.80

Removal (addition) of sensory information occurs when switching sway referencing On (Off) in Exps. 1–3 and when switching lights Off (On) in Exps. 4–6.

Conclusions

Our results highlight the complexity of dynamic changes in human balance control following sudden transitions that added or removed sensory cues. The time courses of sway responses and variability to continuously applied low-amplitude sinusoidal perturbations provided evidence for changes in sensory weights following transitions. However, the exact time course of sensory weight changes was partially obscured by factors that influenced the dynamics of balance control. These factors included changes in the passive torque contributions to balance in sway referencing On/Off experiments, the likely occurrence of imperfectly coordinated reweighting among sensory systems that transiently produced an under- or overproduction of corrective torque, and the potential contribution of prediction in sustaining, for a short time, a visual motion estimate when lights were turned off. This added complexity is a major difference compared with an earlier approach (Assländer and Peterka 2014), where relatively small changes in sensory weights were evoked by changing stimulus amplitudes. A better understanding of reweighting in the presence of the various obscuring factors will require new experimental approaches that can isolate their contributions to the observed overall responses. An unanticipated finding was that different sway responses could occur under identical sensory conditions in different experiments when the expected changes in sensory conditions differed between the experiments. This finding suggested that an expectation of an impending change in environmental conditions can influence the selection of sensory information used for balance control.

GRANTS

This work was supported by National Institute on Deafness and Other Communication Disorders Grant R01 DC-010779 and European Union FP7 Grant 610454.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

L.A. and R.J.P. conception and design of research; L.A. and R.J.P. performed experiments; L.A. and R.J.P. analyzed data; L.A. and R.J.P. interpreted results of experiments; L.A. and R.J.P. prepared figures; L.A. and R.J.P. drafted manuscript; L.A. and R.J.P. edited and revised manuscript; L.A. and R.J.P. approved final version of manuscript.