Computational Design of Selective Peptides to Discriminate Between Similar PDZ Domains in an Oncogenic Pathway

Abstract

Reagents that target protein-protein interactions to rewire signaling are of great relevance in biological research. Computational protein design may offer a means of creating such reagents on demand, but methods for encoding targeting selectivity are sorely needed. This is especially challenging when targeting interactions with ubiquitous recognition modules—e.g., PDZ domains, which bind C-terminal sequences of partner proteins. Here we consider the problem of designing selective PDZ inhibitor peptides in the context of an oncogenic signaling pathway, in which two PDZ domains (NHERF-2 PDZ2—N2P2 and MAGI-3 PDZ6—M3P6) compete for a receptor C-terminus to differentially modulate oncogenic activities. Because N2P2 increases tumorigenicity and M3P6 decreases it, we sought to design peptides that inhibit N2P2 without affecting M3P6. We developed a structure-based computational design framework that models peptide flexibility in binding, yet is efficient enough to rapidly analyze tradeoffs between affinity and selectivity. Designed peptides showed low-micromolar inhibition constants for N2P2 and no detectable M3P6 binding. Peptides designed for reverse discrimination bound M3P6 tighter than N2P2, further testing our technology. Experimental and computational analysis of selectivity determinants revealed significant indirect energetic coupling in the binding site. Successful discrimination between N2P2 and M3P6, despite their overlapping binding preferences, is highly encouraging for computational approaches to selective PDZ targeting, especially because design relied on a homology model of M3P6. Still, we demonstrate specific deficiencies of structural modeling that must be addressed to enable truly robust design. The presented framework is general and can be applied in many scenarios to engineer selective targeting.

Introduction

Interaction preferences of signaling proteins—i.e., their interaction specificity profiles—are tuned for precise control of cellular function, with altered specificity frequently leading to disease states [1]. Thus, in order to perturb cellular pathways in desired ways, we must be able to tune specificities of targeting reagents [2, 3]. When the goal is to target a single binding site, the reagent should be selective—i.e., it should evade interactions with other, possibly similar structural regions of cellular proteins. Though different specificity profiles may be needed for different applications (e.g., one may want to target multiple sites), the ability to design selectivity appears to be a fundamental requirement for effective biomolecular targeting. It would enable precise interrogation of individual molecular interactions in the cell, opening a broad range of possibilities in therapeutic development and mechanistic investigation [4].

Large families of conserved protein-recognition domains (PRDs) have emerged as key modulators of cellular protein interactions [5, 6]. Some PRD families are responsible for hundreds or even thousands of interactions [7], with the specificity of each family member likely suited for its precise function [8, 9]. Such modularity may have arisen for better evolvability [3], but it presents challenges for selective biomolecular targeting. For example, when targeting a single PRD family member with the aim of inhibiting its interactions, the possibility of inhibiting interactions of other family members (with unpredictable functional effects) arises naturally.

PDZ domains, named for the first three proteins in which they were found (PSD95, Dlg1, and ZO-1), are among the most ubiquitous PRDs. These domains typically recognize the C-terminal sequences of partnering proteins, binding them in an extended conformation [10]. The last six residues of the partner, typically labeled P0 through P-5 starting from the C-terminus, encode much of the interaction specificity (Fig. 1A) [11], and strong biases exist within this short recognition sequence. Many of the over 260 PDZ domains in humans [12] are known to be involved in signaling and disease [13-15], making them important targets for functional modulation [16, 17]. However, their ubiquity and high conservation, along with a short and biased recognition sequence, may drastically complicate selective targeting. Encouragingly, Sidhu and co-workers showed PDZ domains to be much less promiscuous than previously thought [18], demonstrating at least 16 PDZ specificity classes. Also, in a recent experimental study, Madden and co-workers were successful in engineering selectivity among five PDZ proteins [19]. Nevertheless, experimental optimization of selectivity remains non-trivial and laborious. There is thus a great need for robust computational methods for selective PDZ targeting.

Figure 1. PDZ-peptide recognition, encoded by N2P2 and M3P6, regulates LPA signaling.

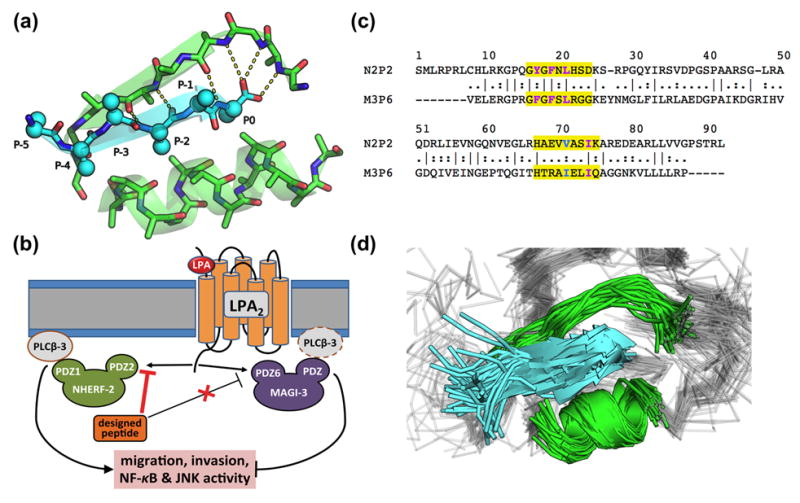
(a) A canonical PDZ-peptide binding conformation (peptide shown in cyan and a portion of the domain binding site in green; only backbone and Cβ atoms are rendered). Standard labeling of peptide residues is indicated. (b) A putative model for LPA-induced signaling in colon cancer cells. NHERF-2 and MAGI-3 compete for binding to the C-terminus of active LPA₂, antagonistically modulating the downstream oncogenicity through differential regulation of phospholipase C β3 (PLC-β3) [29]. (c) Sequence alignment between N2P2 and M3P6. The indicated numbering was adopted throughout the study to refer to residues of both domains. The regions used to align the binding sites (yellow), the four hydrophobic residues lining the P0 binding pockets (magenta), and the position critical for modulating P0 binding specificity (cyan) are highlighted. (d) The binding sites (green) of the 70 PDZ-peptide structures used to generate diverse starting peptide conformations (cyan) are shown aligned, illustrating the considerable flexibility of PDZ-bound peptides.

Several investigators have developed computational tools for the analysis and design of PDZ-peptide interactions. Kortemme and co-workers demonstrated that structure-based modeling can predict peptide sequence features recognized by individual PDZ domains in good agreement with high-throughput studies [20]. Stanefa and Wallin studied PDZ/peptide binding free energy landscapes using implicit-solvent Monte Carlo simulations, showing qualitative agreement with experiments [21]. Other studies have demonstrated reasonable ability to describe the space of peptide binders using structure-based calculations [22-24] or sequence-based models trained on high-throughput experimental data [11, 25]. Machine-learning methods can even enable sequence-based prediction of affinities, as demonstrated by Kamisetty et al. [25]. PDZ domains have also been subjects of structure-based computational design studies. Reina et al. redesigned a PDZ domain to bind new peptide sequences [26]. Smith et al. engineered phosphorylatable serines into a PDZ domain, providing phosphorylation-based control of peptide affinity [27]. Roberts et al. designed binding peptides for the CAL PDZ domain, a known target in cystic fibrosis, showing them to rescue the disease phenotype in cells [28]. Despite these notable successes, computational design methods that explicitly consider PDZ targeting selectivity are generally lacking, which prevents in-silico approaches from maximizing their impact on downstream biomedical applications. A structure-based solution to this problem would be ideal, due to the potential to generalize to other protein-interaction systems where design of selectivity is relevant.

As a motivating example for developing such solutions, in this work we consider a colon-cancer associated signaling pathway for which selective PDZ targeting may provide a means of reducing oncogenicity [29]. This pathway is associated with lysophosphatidic acid (LPA)—a critical regulator of colon cancer tumorigenesis and metastasis [29-31]. Binding of LPA to its receptor LPA₂ recruits a PDZ-containing scaffolding protein NHERF-2 to the LPA₂ C-terminus (Fig. 1B) [32, 33]. Several studies have shown the NHERF-2:LPA₂ complex to be required for oncogenic LPA signaling in colon cancer cells [29, 32-34]. Recently another PDZ-containing protein, MAGI-3, was found to compete with NHERF-2 for binding to LPA₂ and alter the functional outcome (Fig. 1B). Binding of LPA₂ to NHERF-2 via its second PDZ domain (N2P2) increases oncogenic signaling, while binding to MAGI-3 through its sixth PDZ domain (M3P6) decreases it [29]. These data underscore the importance of selective inhibition within PRD families, as one would ideally like to inhibit N2P2 without affecting M3P6.

A common strategy for generating PDZ domain inhibitors is to begin with the C-terminal sequence of a native partner [17]. However, because N2P2 and M3P6 both recognize the same C-terminal peptide of LPA₂ and are generally quite similar (Fig. 1C), this may not be a good starting point. Indeed, the overlap in specificites of these domains means attaining selectivity between the two may not be trivial. Motivated by both the biomedical relevance of LPA/LPA₂ signaling as well as the broader need to target PDZ domains selectively, we aimed to solve this problem with a general structure-based framework, seeking broadly applicable insights. Importantly, our approach decouples the complexity of the structure-based simulation used to model interactions from the computational efficiency requirements imposed by protein design, through the application of Cluster Expansion (CE) [35, 36]. CE produces simple sequence-based expressions that closely agree with results of complex structural calculations. Here we used CE in conjunction with rigorous structural sampling of a flexible peptide in the PDZ pocket [37], but even more sophisticated and demanding methodologies are admissible. Further, the framework explicitly considers interactions with both the target (here N2P2) and any competitors (here M3P6) via the general-purpose CLASSY approach [38], finding sequences optimal in terms of both affinity and selectivity.

Our three designed peptides exhibited high affinity for N2P2 (7-14 μM), binding it 2-to-4-fold tighter than the native LPA₂ C-terminus. One peptide, predicted to be the least selective of the three, bound M3P6 weakly (~600 μM), while the remaining two designs showed no detectable binding to the domain. These results are especially encouraging given that a homology model of M3P6 was used in the computational framework, as no experimental structure was available. To better test the robustness of our framework, we considered the reverse design objective of targeting M3P6 and not N2P2. All three designs considered in this case bound M3P6 with high affinity (5-13 μM), and two peptides showed preference for M3P6. Taking advantage of our computational model, we went on to study the determinants of designed selectivity. We found clear evidence of coupling between parts of the interface that occurs through indirect means via the peptide’s overall conformation. Experiments with peptide and domain mutants confirmed these computational hypotheses. Overall, though the structure-based simulation of binding proved reasonably predictive in this pursuit, the need for better accuracy was apparent, especially with respect to effects associated with dynamics.

LPA/LPA₂ signaling is just one example where PDZ-encoded recognition is implicated in cancer [39, 40], and these domains are also promising targets in other disease processes [41, 42]. Thus, strategies for modulating PDZ pathways will have broad utility in dissecting and ultimately manipulating disease-relevant interactions. Our results suggest that the use of structure-based computation for routine design of selective PDZ inhibitor peptides may be within reach, but will likely require further improvements in the accuracy of structural modeling techniques used in protein design. We hope that the method of Cluster Expansion can provide an avenue for implementing such improvements, by effectively reducing the burden of computational efficiency in protein design and enabling the application of more detailed and accurate structure-based models.

Results

Homology modeling

A crystal structure of peptide-bound N2P2 existed in the PDB (ID 2HE4), but no structures of M3P6 were available at the time of our study. We thus proceeded to build a structural representation of M3P6 by homology modeling. Using 14 PDZ domains, each with both a peptide-bound and an apo structure in the PDB, we found that the PDZ binding site tends to widen upon peptide association (see Fig. S1). Thus, as the template for modeling M3P6, we chose the closest-in-sequence peptide-bound structure in the PDB—i.e., the first PDZ domain of MAGI-1 (PDB ID 2I04, 40% sequence identity to M3P6), although a closer apo structure was available (PDB ID 1WFV with 66% sequence identity to M3P6). A homology model was built using the SWISS-MODEL automated server [43], and the resulting structure was subjected to a full-atom minimization in PyRosetta [44] after the LPA₂ C-terminal 6-mer peptide was modeled in the binding site (see Materials and Methods).

A template with sequence identity of 40% is generally considered sufficiently close for the application of homology modeling [45]. However, because our intention was to use the M3P6 model in structure-based protein design, we sought to estimate its likely quality. Benchmarks of homology modeling accuracy as a function of sequence identity are widely available [46]. However, we reasoned that performance might differ significantly when working within a well-defined protein domain. Further, we were most interested in the prediction accuracy within and around the binding site. For these reasons, we performed a homology modeling benchmark specific to PDZ domains. We collected 29 distinct crystal structures of PDZ-peptide complexes from the PDB and applied the MODELLER package [47] to build homology models for each domain using every other domain as template (the benchmark was done with MODELLER and not SWISS-MODEL due to ease of automation, but the two approaches produced nearly identical models for M3P6). The 841 resulting models revealed the dependence of prediction quality on sequence identity between the modeled sequence and the template (see Fig. S2). For cases in the 35-45% sequence identity range, the median Cα RMSD of the binding-site and the peptide-contacting region (an average of 19 residues) was 1.4 Å (1.6 Å over all heavy backbone atoms), suggesting that the M3P6 model is likely of high quality (see Fig. S2B-C).

A structure-based model of PDZ-peptide binding

Considerable variation in the precise PDZ-peptide binding conformation exists even within the canonical binding mode, as demonstrated in the superposition of known PDZ-peptide complexes (Fig. 1D). We thus reasoned that a computational model of PDZ-peptide binding must thoroughly sample peptide conformations. As a vehicle for this sampling we chose the FlexPepDock ab-initio protocol of the Rosetta modeling suite (hereafter referred to as FPD) [37, 48]. FPD takes as input a starting structural model of the domain-peptide complex and samples peptide conformations (rigid body orientation and backbone/side-chain dihedral angles) as well as domain rotamers in and around the binding site, seeking to minimize an empirical scoring function [37]. Six-mer peptides were used in all calculations throughout this study, as the last six residues have been shown to encode much of the binding specificity [11, 18, 25]. To reduce the possibility of getting trapped in local minima, we used 70 existing PDZ-peptide complex structures to generate a diverse set of starting domain-docked peptide conformations, each initiating an independent FPD simulation (Fig. 1D; see Materials and Methods). We found this diversification of sampling trajectories to be important as scores and conformations reached from different starting points varied considerably, and different starting models gave the best solutions for different peptides (see Fig. S3).

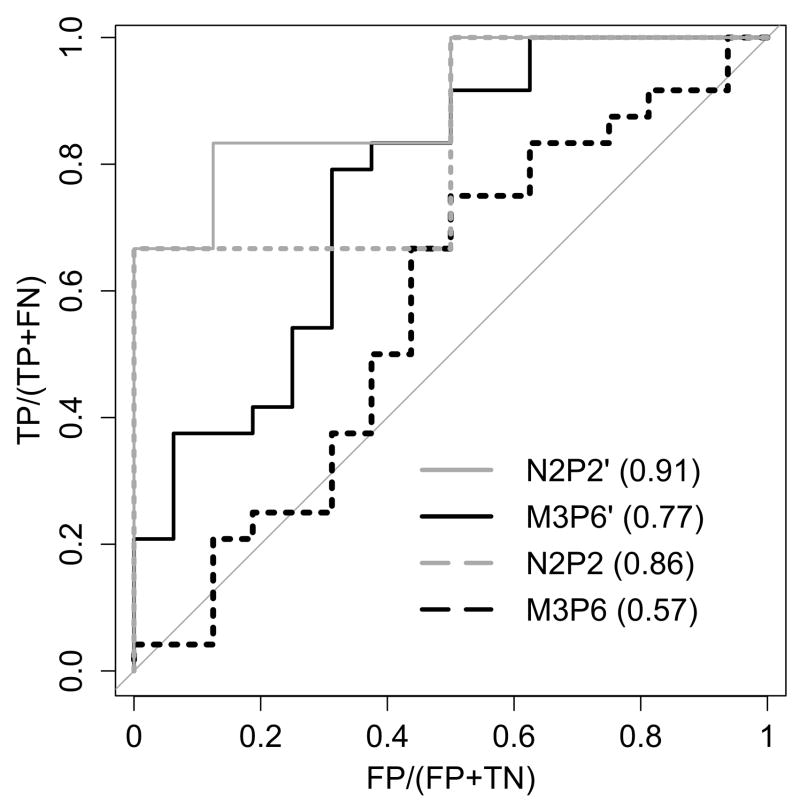
To assess the accuracy of our model, we used sets of peptide binding affinities for N2P2 and M3P6 reported in the literature [19, 49]. 100 μM was used as the dissociation constant cutoff to classify peptides into “binders” and “weak/non-binders” for each domain. Applying our FPD-based protocol to model each complex enabled us to benchmark the approach. Using the default Rosetta scoring function in FPD (“score12”) led to effective classification for N2P2, but performed poorly for M3P6, as illustrated by receiver operating characteristic (ROC) curves in Fig. 2. Scrutinizing the energetics of FPD-produced structural models revealed that two empirical terms, “rama” and “omega” (capturing the statistical preferences for backbone φ/ϕ and ω dihedral angles, respectively), fluctuated unrealistically strongly across M3P6-peptide models. Simply omitting these two terms improved classification performance for both domains, with a significant improvement for M3P6 (see Fig. 2). The reasonable performance for M3P6 further suggests that the homology model is of high quality, though the higher performance for N2P2 is not surprising given that a peptide-bound high-resolution crystal structure was used in that case.

Figure 2. A benchmark of the FPD-based PDZ-peptide modeling protocol.

Dotted lines (N2P2 and M3P6) show the results using the default Rosetta scoring function, and solid lines (N2P2’ and M3P6’) represent the performance upon omitting “rama” and “omega” terms. The area under curve (AUC) for each case is indicated in the legend in parenthesis. There were 15 and 41 data points for N2P2 and M3P6, respectively. Of those, 7 and 25, respectively, were classified as “binders” based on having measured affinities below 100 μM. TP: number of true positives; FP: number of false positives; TN: number of true negatives; FN: number of false negatives.

FPD Score Significance Threshold

In order to calibrate our interpretation of structure-based scores, we assessed to what extent predicted score differences track with differences in affinity. Using the same set of experimental PDZ-peptide affinities as above, we considered all pairs of peptides (for each domain) and asked how frequently FPD scores predicted the correct order of affinities as a function of the score difference (solid line in Fig. S4). We found the threshold of significance to be around 1.5 – 2 energy units (eu), such that score differences above this range were very likely to establish the correct relative order of affinities.

Cluster Expansion and CLASSY

The modeling procedure described above is highly computationally demanding, taking over 400 CPU hours per peptide/domain complex on an Intel Xeon 2.70GHz processor. This is because we found that extensive conformational sampling was necessary to achieve reasonable performance. In fact, our procedure involved a total of 35,000 independent Monte Carlo simulations (see Materials and Methods), with attempts at reducing the amount of sampling leading to clear degradation in performance. This is consistent with Raveh et al. reporting the use of 50,000 independent MC simulations to model a variety of domain-peptide complexes [37]. To address the issue of computational efficiency and enable the application of our structure-based model in design, we turned to the method of Cluster Expansion (CE) described previously [35, 36, 50]. In short, CE expresses the result of any protein structure-based computation as a series expansion in terms contributions from amino-acid clusters of increasing size (cluster functions). For example, if E(σ⃗)is the final score from the above FPD protocol applied to the peptide sequence σ⃗ for a given domain, the CE expression would state:

$$E\left(\overrightarrow{\sigma }\right)=C+\sum _{\underset{{\sigma }_i\ne {\rho }_i}{i=1}}^L{f}_i\left({\sigma }_i\right)+\sum _{\underset{{\sigma }_i\ne {\rho }_i}{i=1}}^{L-1}\sum _{\underset{{\sigma }_j\ne {\rho }_j}{j=1}}^L{f}_{ij}({\sigma }_i,{\sigma }_j)+\cdots$$ (1)

where ρ⃗ is a suitably chosen reference sequence, with σ_i and ρ_i being the amino acids in i-th position of σ⃗ and ρ⃗, respectively, and L is sequence length. The term C is the reference cluster function, which can be interpreted as the score of the reference sequence ρ⃗. For all other sequences, additional terms in the expansion contribute to the total score. So, if amino acid at position i in σ⃗ differs from that in ρ⃗, this carries an additional contribution from the point cluster function f_i(σ_i). Similarly, if amino acids at positions i and j in σ⃗ both differ from the corresponding ones in ρ⃗, then besides the two point contributions, there is also an additive contribution form the pair cluster function f_ij(σ_i, σ_j). The full expansion contains all of the higher-order terms (up to L-tuples) and has exactly as many cluster functions as there are possible sequences, so that it is in principle exact. However, to be practical, the expansion can be truncated (e.g., to include all up to pair terms) and the values for the remaining cluster functions can be obtained by least-squares fitting given a set of training sequences with pre-computed E(σ⃗)[35, 36, 50]. Though generation of this training set takes time, once a CE is derived, the evaluation of additional sequences is extremely fast.

We have previously shown that a CE not only increases computational efficiency by many orders of magnitude, but also enables the simultaneous design of affinity and specificity via the method CLASSY [38]. CLASSY works by finding the sequences that display optimal trade-offs between affinity and selectivity—that is, sequences that cannot be simultaneously improved in both categories (i.e., the Pareto optimal front). Because of this property, no other sequences need to be considered as design candidates.

To apply CLASSY here we first needed to derive cluster expansions for both N2P2 and M3P6. Given that our initial goal was to design a peptide to selectively target N2P2, we based the amino acids allowed at each position (i.e., the design alphabet) on the range of peptides previously shown to bind N2P2 in a high-throughput study [18] and the native LPA₂ C-terminus (see Fig. 3A). Though this gave only 8,400 possible sequences, the direct application of the FPD protocol would be infeasible (even on a 1,000-CPU cluster it would take over 140 days). Instead, we applied the protocol to just 192 randomly generated sequences from this space with both domains, enabling us to train corresponding cluster expansions (see Materials and Methods). Fig. 3B illustrates the resulting agreement between CE and FPD-based scores. The CE-based evaluation, involving the addition of a handful of terms per sequence, is at least 10¹⁰ times faster than the explicit FPD-based protocol, while the agreement between the two is very high. Further, the true error introduced by CE is likely lower than what is shown in Fig. 3B, because a cluster expansion is expected to reduce the effect of stochastic noise in FPD-derived scores. This reduction happens because the CE training process effectively averages cluster function contributions in different contexts. To test the extent of this effect, we trained cluster expansions using the same training set as above (and the same procedure), but added normally distributed random noise with mean of 0 and standard deviation of 0.5 eu to the FPD-derived scores. Repeating this 100 times shows that the standard deviation of CE-predicted sequence scores across different expansions (with different realizations of noise) is less than 0.3 eu—a 40% reduction of stochastic noise (Fig. S5).

Figure 3. Design of N2P2-vs-M3P6 selectivity.

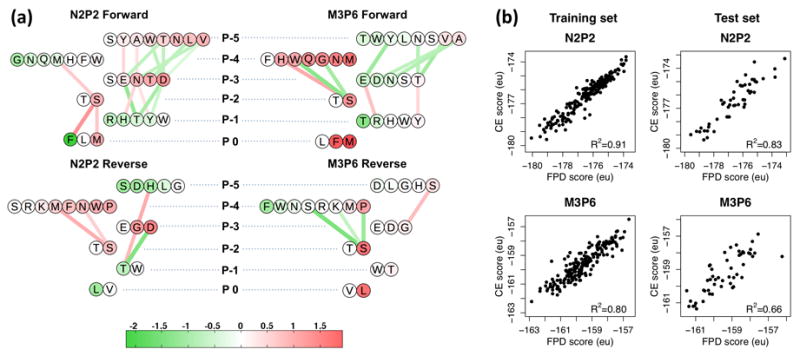
(a) Design alphabets and CE parameters for forward design (upper row) and reverse design (lower row). Encircled letters represent amino acids allowed at corresponding positions, and edges represent pairwise terms between the two connected amino acids. Circles and edges are colored to indicate the signs and magnitudes of corresponding self and pair cluster functions, respectively, according to the colorbar shown (Rosetta energy units, eu). Edge thickness also reflects pair cluster function magnitude. (b) Correlations between FPD and CE scores for both domains in training and test sets for forward design. Each point represents a peptide sequence. The squares of correlation coefficients are indicated.

Design

Given the speed of CE evaluation, the entire sequence space considered in design could be quickly enumerated and sequences with optimal affinity/selectivity tradeoffs obtained directly, without needing to apply the integer linear programming approached we previously described [38]. Here the affinity score of peptide σ⃗for domain X was defined as:

$$A_X(\overrightarrow{\sigma })=C{E}_X(\overrightarrow{\sigma })-C{E}_X(\mathrm{LMDSTL})$$ (2)

where CE_X(σ⃗) is the score for σ⃗ predicted by the cluster expansion for domain X, and LMDSTL is the native C-terminus of LPA₂ (native peptide). The selectivity score of σ⃗ for domain X relative to domain Y was defined as S_XY(σ⃗) = A_X(σ⃗) − A_Y(σ⃗). The native LPA₂ C-terminus is a relevant reference point for both affinity and selectivity because its interactions with both N2P2 and M3P6 are clearly physiologically relevant.

Fig. 4A shows the relationship between affinity and selectivity for the entire sequence space considered, with the black curve delineating the six sequences making optimal tradeoffs. Though the affinity and selectivity appear to be significantly correlated, considerable amount of variation in selectivity exists within any given value of predicted affinity (and vice versa). These observations parallel the seemingly contradictory results in the literature, where selectivity against an undesired partner is sometimes obtained “for free” purely by seeking increased affinity for the desired target [26, 51-53], whereas at other times increased affinity for the target tracks with that for the competitor [54-56]. The peptide with the highest predicted affinity already exhibits considerable N2P2 selectivity, though it is predicted to bind to M3P6 with similar affinity as the native peptide (see point 1 in Fig. 4A; note score definitions above). At the cost of relatively small amounts of affinity to N2P2, designs are predicted to increase N2P2 selectivity further, significantly reducing affinity for M3P6.

Figure 4. Predicted affinity/selectivity landscapes.

Each dot represents a single peptide sequence, and the sequences for which affinities and specificities cannot be optimized simultaneously (Pareto optimal front; white points) are connected with black lines. Because scores are expressed relative to the native peptide (see Eq. 2), sequences falling on/near the diagonal are predicted to bind the competitor roughly as well as the native peptide. (a) and (b) correspond to forward design (8400 sequences) and reverse design (960 sequences), respectively. The sequences selected for experimental validation (3 in each case) are labeled with numbers.

We wondered whether the feasibility of selective N2P2 targeting suggested by calculations was an artifact of using a crystal structure to score binding to the desired target (N2P2) but a homology model to assess undesired interactions with M3P6. Thus, to truly test the generality of our selectivity design framework (and the reliability of the homology model), we decided to also tackle the opposite design problem—finding peptides that selectively associate with M3P6 relative to N2P2. We refer to this as “reverse design” as opposed to “forward design” considered above. Using a similar procedure as above to choose a design alphabet, train cluster expansions, and apply the CLASSY framework (see Materials and Methods and Fig. S6), produced the affinity/selectivity landscape shown in Fig. 4B. In contrast to forward design, the sequence with the highest predicted target affinity here, though it is expected to have some selectivity, is predicted to bind the competitor better than does the native peptide. The Pareto optimal front suggests that additional selectivity can be gained at the cost of apparently small losses of affinity, but even the maximum level of selectivity here is on par with the level obtained “for free” by the peptide with the highest target affinity in forward design (compare optimal fronts in Figs. 4A-B). This predicts that M3P6 may be more difficult to target selectively than N2P2 (at least, using our design alphabets) and suggests that, in general, the ease of selective targeting may vary among representatives of a domain family.

In both design exercises there were six sequences forming the Pareto optimal front (Figs.4A-B), the CE-predicted affinity scores for all of which were verified to be in close agreement with full FPD calculations (Table S1). Three sequences were chosen for experimental characterization in each case (FD1–FD3 for forward design and RD1–RD3 for reverse design, denoted in Figs. 4A-B) as representing the range of predicted affinity/selectivity tradeoffs.

Experimental Validation

Peptide affinities for the two domains were determined by Fluorescence Polarization (FP) using well characterized assays [42, 49, 57] (see Materials and Methods). The affinity of each domain for a fluorescently labeled reporter peptide was measured first, enabling competition assays to determine apparent inhibition constants, K_i, of designed and native peptides (see Materials and Methods).

Table 1 summarizes the measured affinities (see also Figs. S7-S9). All three forward designs are highly selective for N2P2, as expected by design. The first of these (FD1), designed without explicit consideration of selectivity, does interact with M3P6. However, this interaction is approximately an order-of-magnitude weaker than that between M3P6 and the native peptide, whereas the corresponding complexes were scored similarly by the model (see Fig. 4A). The remaining two designs, predicted to widen the selectivity gap between N2P2 and M3P6, do so and show no appreciable M3P6 association.

Table 1.

Domain-peptide affinities measured by fluorescence polarization (FP) assay.

Ki of all tested peptidesa
Abbreviation	Sequence	Ki for N2P2	Ki for M3P6	Ki for M3P6m
		(μM)
LPA2 6-mer	LMDSTL	28.4 ± 1.8	47.4 ± 2.6	67.7 ± 5.4
FD1	TGETTF	14.2 ± 2.2	600 ± 300	151 ± 15.9
FD2	SGSTRF	6.8 ± 0.7	> 1000
FD3	SGSTHF	9.1 ± 1.0	> 1000
RD1	DFETWV	5.4 ± 1.2	1.8 ± 0.5
RD2	GFETWV	12.5 ± 2.0	2.7 ± 0.4
RD3	GFDTWV	4.6 ± 1.5	6.8 ± 1.5
CST	DFSTTV	54.8 ± 3.0		241.7 ± 17.6
CSR	DFSTRV	52.1 ± 5.3		510.4 ± 51.4
CAT	DFATTV	253.8 ± 6.6		351.4 ± 17.9
CAR	DFATRV	69.3 ± 8.7		284.6 ± 24.5
Kd of all reporter peptidesb
Abbreviation	Sequence	Kd for N2P2	Kd for M3P6	Kd for M3P6m
		(μM)
LPA2 10-mer	NGHPLMDSTL	11.5 ± 0.7
Claudin23	QNSLPCDSDL		3.6 ± 0.2	4.1 ± 0.4
FD2 8-mer	GGSGSTRF	3.6 ± 0.5

^asee Fig. S8 for raw data and fits

^bsee Fig. S7 for raw data and fits

Reverse designs show a significant shift in selectivity towards M3P6. All designs are more selective for M3P6 than the native peptide, with RD1 and RD2 showing 5-and 8-fold shift in selectivity. Also, affinities of designed peptides for M3P6 are ~20-fold (for RD1 and RD2) and ~7-fold (for RD3) higher than that of the native peptide (see Table 1). However, in line with predictions, selectivity here is not as large as in forward design. Notably, peptides did not weaken affinity for the competitor (N2P2) relative to the native peptide. This was expected only for RD1, while RD2 and RD3 were predicted to bind N2P2 more weakly than the native peptide (see Fig. 4B). Still, the reduction in affinity for the competitor, relative to the native peptide, was predicted to be lower here than in forward design, as was the overall degree of target selectivity (Fig. 4B).

Binding Mode Validation via NMR

To confirm the binding mode intended by design, we employed NMR-based footprinting to characterize the association of FD2 and native LPA₂ C-terminus with N2P2 (see Materials and Methods). This assay identified residues significantly perturbed upon peptide binding (defined as a chemical shift perturbed by more than one standard deviation above the average; see Materials and Methods), with the results mapped onto the surface of the modeled N2P2:peptide complex shown in Fig. 5. Clearly, the affected residues for N2P2:FD2 cluster around the canonical binding site, verifying the binding mode as intended by design. Further, the significantly perturbed region is similar upon binding the native and designed peptides (see Fig. S10), illustrating that FD2 binds in a manner similar to the native peptide.

Figure 5. Binding mode validation for FD2:N2P2 with NMR footprinting.

(a) ¹H,¹⁵N HSQC spectra of N2P2 alone (blue) and in the presence of the FD2 (red), with select residues labeled. (b) Design model of FD2:N2P2 with N2P2 residues exhibiting significant chemical shifts highlighted in red (see Materials and Methods).

Determinants of selectivity

We sought to understand the reasons behind the general success of our selectivity design, looking for potentially generalizable insights. In this respect, CE proves highly useful as it readily extracts effective sequence-level contributions from complex structure-based simulations. In fact, we found that CE enables a simple visualization of the entire scoring model for a given domain, with models for N2P2 and M3P6 in forward and reverse designs illustrated in Fig. 3A. Here each design position is shown on one line, with its allowed amino acids colored to indicate the magnitude of the corresponding CE self term (see Eq. 1). Lines connecting amino acids at different positions indicate pair CE terms, with both color and thickness indicating magnitude.

A feature of the forward design problem immediately apparent from this visualization is that the best amino-acid choice for binding N2P2 (in terms of self contributions) is often close to the worst choice for binding M3P6 (in particular, this is so for positions 0, -3, -4, and -5) (Fig. 3A). In reverse design, however, the best choice for M3P6 is significantly suboptimal for N2P2 in only in positions 0 and -5 (Fig. 3B). Though pairwise CE contributions certainly complicate the picture, this simple observation is in line with the result of gaining less selectivity in reverse design both computationally (Fig. 4B) and experimentally (Table 1). This also suggests that selective targeting may be innately “easier” for some domains than others.

Indirect effects responsible for differential Phe@P0 preferences

Fig. 3A shows that a very significant contributor to N2P2 selectivity in forward designs comes from Phe at position P0, which is highly favored for N2P2 and disfavored for M3P6. A retrospective analysis of the work by Sidhu and co-workers confirmed a preference for Phe@P0 in N2P2 and lack of this amino acid in 22 peptides selected for binding to PDZ5 of K01A6.2, a C. elegans domain with 81% sequence identity to M3P6 [18]. Given the ability of our model to anticipate this preference, we sought to understand the structural basis for this selectivity, particularly in light of the high similarity between binding sites of N2P2 and M3P6. In fact, of the four residues lining the hydrophobic pocket for position P0, three are identical between the two domains (Phe19, Leu21 and Ile74; residues numbered as in Fig. 1C), and one is highly similar (Tyr17 in N2P2 and Phe17 in M3P6; see Fig. 6A). The pockets also have visually similar shapes (Figs. 6A and S11A), and best-scoring structures of N2P2:FD1 and M3P6:FD1 complexes adopt very similar peptide conformations, including the rotamer of Phe@P0 (see Fig. 6A). Our inspection of computational models did, however, identify a critical difference between the two domains at position 71—occupied by Val in N2P2 and Ile in M3P6 (Fig. 6A). Though not a position that would typically be considered a part of the P0 binding pocket, we reasoned that the extra methyl group in M3P6 might form an unfavorable contact with Phe@P0. We thus modeled the in-silico I71V mutant of M3P6 (M3P6m), and found its preference at P0 to indeed be shifted towards Phe, as its interaction with FD1 was predicted to improve but not its interaction with TGETTL (FD1_L)—a peptide different from FD1 only in having a Leu the C-terminal position (see Table S2). However, decomposing the total scores of M3P6:FD1 and M3P6m:FD1 revealed that the interaction energy between Phe@P0 and domain position 71 became substantially less favorable upon the removal of the hydrophobic methyl group (Table S2). That is, I71V was predicted to increase the preference for Phe@P0, but not through a direct interaction with the residue. Rather, the improvement came from the packing between Phe@P0 and the canonical P0 binding pocket residues (Table S2). This suggested that the reason for the poor accommodation of Phe@P0 by wild-type M3P6 was a conformational frustration between optimizing packing interactions with canonical binding-pocket residues (19, 21, and 74) and the boundary residue Ile71. In fact, this frustration is evident in the top 10 best-scoring M3P6:FD1 complexes, where Phe@P0 does not appear to have a single best binding orientation but rather samples several sub-optimal ones (Fig. S11B). On the other hand, top 10 best-scoring structures of M3P6m:FD1 do show a clear preference for a single binding pose, as do top-scoring poses of N2P2:FD1 (see Fig. S11C-D).

Figure 6. Specificity determinants predicted by structural modeling.

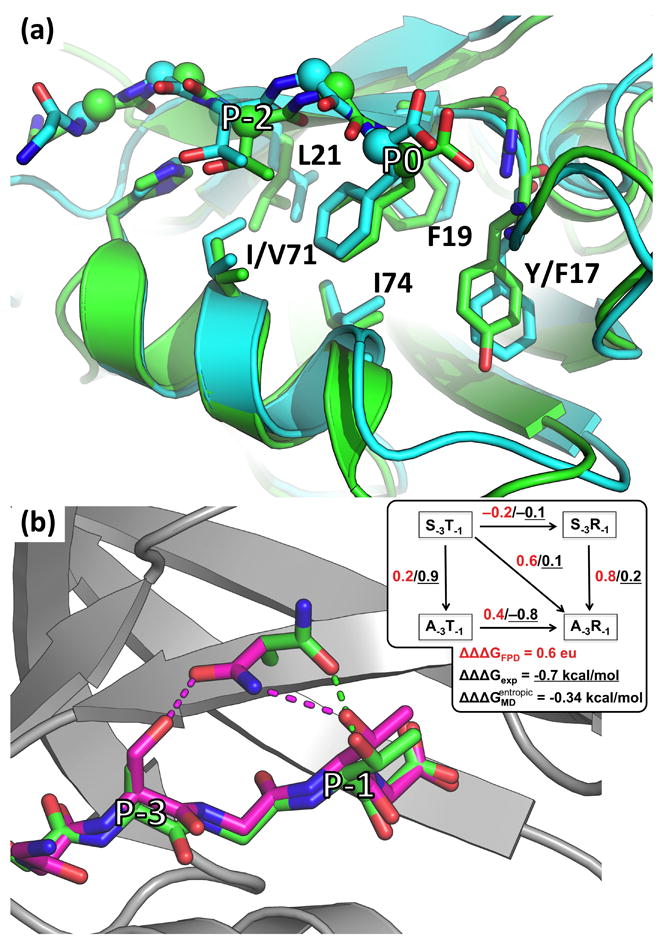
(a) Models of FD1 in peptide-binding pockets of N2P2 (green) and M3P6 (cyan). (b) Models of C_ST (magenta) and C_AT (green) in the peptide-binding pocket of N2P2. Shown are best-scoring models. According to FPD calculations, in the model of C_ST, Ser@P-3 and Thr@P-1 both hydrogen bond to the same Asn20, while in the model of C_AT Asn20 adopts a different rotamer to form a more optimal hydrogen bond with Thr@P-1. Inset in (b) depicts the results of double mutant coupling energy calculations using FPD (red) as well as corresponding experimental values (black, underlined).

Experimental measurements showed that the affinity of M3P6m for FD1 was indeed ~4-fold higher than that of the wild-type domain. Further, the difference between affinities of M3P6m for FD1 and the native 6-mer (a peptide with Leu@P0) was only ~2-fold (see Table 1), indicating that much of the preference for Phe versus Leu at P0 was abrogated by the I71V mutation, just as predicted. On the other hand, the native 6-mer bound both M3P6 and M3P6m domains with roughly equal affinity, indicating that I71V did not simply increase affinity for peptides broadly, but rather modulated the specificity, substantially increasing the preference for Phe@P0. Indeed, FD1 would not have been nearly as selective had M3P6m been the relevant competitor in forward design.

Peptide positions energetically coupled via peptide conformational ensemble

These results suggested that indirect coupling effects (i.e., energetic coupling between regions of the binding site not explained by direct interactions) might play a significant role in shaping binding preferences. Coupling between peptide positions would manifest itself via higher-order terms in CE (Fig. 3A). This is because a CE pair term f_ij(σ_i,σ_j) indicates that the effective joint energetic contribution of amino acids σ_i and σ_j at positions i and j, relative to reference amino acids ρ_i and ρ_j at these positions, cannot be explained solely in terms of context-independent contributions from σ_i and σ_j (see Eq. 1). These terms are thus akin to double mutant coupling energies [35, 58], though their direct interpretation here is complicated by the choice of a non-trivial reference sequence in our expansions (i.e., the native LPA₂ C-terminus). Nevertheless, it is clear from Fig. 3A that CE predicts considerable influence of coupling on affinity (see Fig. 3A). On the other hand, this effect could have arisen erroneously due to, for example, insufficient structural relaxation of the peptide or the domain. We thus sought to test whether predicted intra-peptide coupling exists.

It was not surprising to see pair terms between pocket-facing positions (i.e., P0, P-2, and P-4), as steric constraints of the binding site should couple these residues via the overall bound peptide conformation. On the other hand, it was less obvious that away-facing positions (i.e., P-1, P-3, and P-5), which are expected to make “softer” contacts, should be significantly coupled. We thus focused on positions P-3 and P-1, seeking to determine whether the contribution of Ser@P-3 (having the best CE self term for N2P2 binding, but almost the worst for M3P6) depended on the amino acid at position P-1. Specifically, we considered the effect of the mutation Ser→Ala@P-3 with either Thr or Arg at position P-1 (amino acids chosen in FD1 and FD2, respectively; see Fig. 6B inset).

We used the FPD framework to choose the remaining sequence context, aiming to ensure appreciable predicted affinity for both N2P2 and M3P6 and enable measurement of coupling in both contexts. The resulting peptides C_ST, C_AT, C_SR, and C_AR are shown in Table 1 along with their affinities for the domains. FPD-based calculations suggested that Ser→Ala@P-3 reduced affinity for N2P2 more in the context of Arg@P-1 than with Thr@P-1 (though predicted differences were below the significance threshold of 1.5-2 eu; see Fig. 6B inset and Table S3). Reduction of affinity in both contexts was borne out in experiments, but the direction of coupling was predicted incorrectly (see Table 1). Namely, loss of affinity due to Ser→Ala@P-3 is substantially larger in the context of Thr@P-1 than Arg@P-1, with a coupling constant between the two mutations of −0.7 ± 0.1 kcal/mol (definition in Materials and Methods).

Ser→Ala@P-3 was predicted to reduce affinity for M3P6 by roughly the same amount in both contexts, though again differences were below the significance threshold (see Table S3). Interestingly, experiments showed that reduction in affinity is observed only in the context of Arg@P-1, whereas there is a small increase in affinity in the context of Thr@P-1. The corresponding coupling here was –0.6 ± 0.1 kcal/mol.

The combination of Ser@P-3 and Arg@P-1 was predicted to be the best for binding N2P2 and most selective against M3P6—predictions borne out experimentally, with C_SR exhibiting a ten-fold preference for M3P6. CLASSY picked this combination in FD2 to increase N2P2 selectivity relative to FD1, and this was indeed observed experimentally (see Table 1). So it would appear that the scoring model performs well in finding selectivity modulating residues, but its ability to evaluate context-dependent inter-residue couplings is limited.

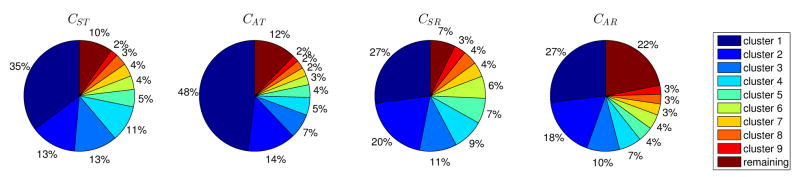
Optimal complex structures of N2P2:C_ST found by FPD involved both Ser@P-3 and Thr@P-1 hydrogen bonding to Asn20 on the domain (Fig. 6B). This was the basis of FPD’s coupling prediction—the contribution of Ser@P-3 in C_ST is diminished by the fact that ideal hydrogen bonding geometry is not achievable (within the constrains of the sampling) for both residues (see Table S3). Explicit-solvent Molecular Dynamics (MD) simulations provided a plausible explanation for why this prediction was incorrect. Complexes between N2P2 and the four coupling peptides (C_ST, C_AT, C_SR, and C_AR) were each subjected to a total of 100 ns of simulation in the NTP ensemble (see Materials and Methods). We observed that both peptides with Ala@P-3 were highly flexible at the N-terminus, while those with Ser@P-3 preserved the β-sheet structure (Fig. S12). Analysis of the trajectories invalidated the basis for FPD’s coupling prediction, showing the Asn20-with-Ser@P-3 interaction to be, in fact, somewhat stronger with Thr@P-1 than with Arg@P-1 (see Fig. S13). Further, changes in peptide dynamics upon the Ser→Ala@P-3 mutation provided a significant difference between the two environments at P-1. Due to its length and flexibility, Arg@P-1 sampled interactions with several domain residues (e.g., Gln15, Asn20, and Asp37), without significantly restricting the peptide conformation. On the other hand, Thr@P-1 could only interact with Asn20, and this hydrogen bond imposed a much stronger restraint. As a result, the bound ensemble was much broader for C_AR than C_AT, with clustering of the trajectories revealing a far more diverse set of microstates for the former than the latter (see Figs. 7 and S14). For example, the most common microstate accounted for 54% of the observed ensemble for C_AT, but only 27% for C_AR. A simple estimate of conformational entropy contributions due to these differences revealed that they would account for a coupling energy of −0.34 ± 0.09 kcal/mol (see Table S4 and Materials and Methods). Although other contributions to the total coupling surely exist, this analysis demonstrates a substantial effect (of the right sign and significant magnitude) that was missed in our FPD analysis and would likely be missed by any current protein design scoring method.

Figure 7. Clustering the MD trajectories of N2P2 with coupling peptides reveals different distributions of peptide microstates.

The fraction of the total ensemble covered by each of the top nine clusters is shown in a pie-chart (peptide name indicated above each chart). The last pie segment corresponds to the remaining fraction of the ensemble not covered by the top nine microstates.

The significantly higher structural heterogeneity of Ala@P-3 versus Ser@P-3, observed by MD, is not unexpected given that Ala is unable to make side-chain salt bridge interactions with binding-site residues. Interestingly, however, the well-scoring structural ensemble sampled by FPD did not reveal a similar higher heterogeneity for Ala@P-3. In fact, all four coupling peptides exhibited roughly equivalent distributions of microstates as revealed by the same clustering analysis as above (see Fig. S14). More work is required to determine whether this is due to insufficient sampling performed in FPD or an inherent problem with the underlying energy function, but the ability to reproduce correct ensemble properties certainly appears to be a requirement for capturing the sort of entropic coupling we have observed by MD.

Discussion

Our computational framework was successful in achieving the practical design goal of this study—designed peptides were highly selective for binding N2P2 over M3P6, providing potential tools for interrogating the LPA signaling network and for investigating a therapeutic approach to colon cancer. That this success was reached by means of thorough structural sampling via the FlexPepDock ab-initio protocol, exploring both local adjustments in the binding site and global docking and folding of the peptide [37] (Fig. 2), is encouraging for the general applicability of the framework. We did, however, find it important to seed the protocol with a diverse population of reasonable starting conformations built form previously solved PDZ-peptide structures (see Fig. S3). Schueler-Furman and co-workers have shown considerable success in modeling domain-peptide interaction specificity using an alternative sampling approach, whereby they use the FlexPepBind protocol to perform local refinement, but use a priori structural constraints derived from known important features of the binding pose [59, 60]. In both cases prior structural information is used and is important, and the two approaches represent alternative means of incorporating such information. Details of the system at hand and the application—e.g., whether it is important for the framework to tackle non-canonically binding modes—would dictate which method would apply best. However, the fact that both approaches perform well offers considerable promise for tackling the PRD-peptide binding problem, particularly given the continually accumulating structural data on diverse PRDs.

A marked advantage of structure-computational approaches to protein design is that they can provide testable hypotheses on the determinants of designed properties and lead to general insights. Thus, to better understand the problem of selective PDZ targeting, we sought to uncover the determinants of selectivity in our system. Scoring the entire sequence space considered in design against both N2P2 and M3P6, made possible by the application of CE, enabled a global view of the affinity/selectivity landscape (Fig. 4). There are two fundamental ways to improve selectivity—by increasing affinity for the target or decreasing affinity for the competitor. Because we calculated domain-peptide scores relative to the native interaction (see Eq. 2), points falling on diagonal lines in Fig. 4 correspond to sequences predicted to bind the competitor roughly as well as the native peptide. Thus, our model predicts that optimizing target affinity alone, though it does lead to some selectivity, leaves affinity for the competitor generally on par with the wild-type interaction, in both reverse and forward design. In other words, if decreasing competitor affinity is not an explicit design requirement, it is predicted not to happen automatically. On the other hand, as the Pareto-optimal fronts in Fig. 4 demonstrate, once the requirement of selectivity is explicitly imposed, with small losses in affinity considerable destabilization of the competing interaction is expected. These predictions were partially borne out in experiments, though model inaccuracies were apparent. The affinity-only peptide in forward design (FD1) did detectably associate with M3P6, though about an order of magnitude more weakly than the native peptide. Peptides further down the Pareto-optimal front, FD1 and FD2, did further destabilize the competitor complex, showing no detectable M3P6 association, while affinities for the target were roughly unchanged. In general, forward design appeared to be a case where achieving selectivity was “easy”, in the sense that even the peptide that would have been chosen purely based on consideration of affinity already showed selectivity. This was not the case with targeting M3P6, where achieving selectivity appeared more difficult. First, the model predicted a significantly lower level of selectivity achievable in this case (see Fig. 4B). As in forward design, here the affinity-only variant, RD1, was expected to interact appreciably with the competitor (even somewhat better than does the native peptide; see Fig. 4B), and peptides further down the Pareto-optimal front (RD2 and RD3) were predicted to destabilize this interaction. Experiments showed that RD1 did indeed associate with N2P2 more tightly than the native peptide (~5 μM versus ~28 μM; Table 1). Further, RD2 did destabilize this complex and increase selectivity as predicted, though this increase was not substantial (from 3-fold to 4.6-fold; Table 1).

From these results it is apparent that predictions of our structure-based model are only qualitatively accurate. So what, if anything, can we state with confidence regarding the general issue of achieving selectivity? For one, our data clearly show that selectivity does not, in general, come “for free” with high affinity. Peptide engineered in both reverse and forward design bound the target with high affinity, much higher than did the native peptide and roughly equivalent between the two design problems. On the other hand, the achieved level of selectivity was considerably lower in targeting M3P6 than N2P2. Graphical representations of CE models suggest sequence-based reasons for these observations (see Fig. 3A). One important difference between N2P2 and M3P6 is in the preferences at position P0. N2P2 can accommodate Phe here, while for M3P6 this residue is highly unfavorable. On the other hand, residues that are accommodated well by M3P6 (i.e., Leu and Val) are also accommodated well by N2P2. Though the possibility remains that a more rare (or unnatural) amino acid at P0 would show preference for M3P6, this nevertheless suggests that some domains may be more inherently “selectively targetable” than others.

It has been suggested that when designing high-affinity binders, sequence changes made to optimize the target complex should be, on average, random with respect to competitors [53]. This argument would appear strongest when the target and competitors are sufficiently different. On the other hand, when these are similar, one might expect significant correlation between changes advantageous for target and competitor binding [38]. Our present study further suggests that directionality is important in defining the relationship between target and competitors. That is, though A may be an easy target when B is the competitor, B may not necessarily be an easy target with A as a competitor. By mapping these relationships between all PDZ domains, it may thus be possible to succinctly describe the landscape of selective targeting of these functionally important modules.

The amino-acid identity at position P0 is perhaps the most significant contributor to PDZ-peptide recognition [61]. This residue is hydrophobic in classical PDZ binding motifs [18]—a constrain originating from the hydrophobic binding pocket into which the P0 side-chain packs. Our computational model recapitulates the importance of P0 for binding, showing Phe@P0 to provide a significant preference for N2P2 over M3P6. However, interrogation of the model as to the source of this selectivity revealed a surprising mechanism involving a residue from what would typically be considered the P-2 binding pocket (Fig. 6A). Residue 71, Val in N2P2 and Ile in M3P6, appeared to encode much of this preference by indirectly modulating the binding landscape of Phe@P0. Even though Ile71 in M3P6 interacts favorably with Phe@P0 in bound peptides (better than the corresponding Val71 in N2P2), and this interaction is weakened in the I71V mutant M3P6m, the mutation does enable substantially better packing of Phe@P0 into its standard binding pocket (Table S2). Thus, Ile71 serves as a “gatekeeper” residue that causes a conformational frustration for Phe@P0, whereby interactions with its canonical binding pocket and the gatekeeper cannot be optimized simultaneously. M3P6m resolves this frustration, and experiments confirm its shift in specificity towards Phe@P0 (see Table 1).

We went on to look for further evidence of indirect coupling by predicting non-additivity between energetic contributions of residues at P-1 and P-3. Measurements revealed that the change in N2P2 affinity due to the Ser→Ala@P-3 mutation depended significantly on whether Thr or Arg was present at P-1 (see Table 1). In fact, the magnitude of the coupling between the two mutations (–0.7 ± 0.1 kcal/mol) was on par with values measured for known specificity-determining interactions in other systems [62]. Significant energetic coupling has not, to our knowledge, been shown in PDZ-binding peptides, and intra-peptide coupling effects have been largely ignored in PDZ-binding models. However, Gfeller et al. recently demonstrated significant correlation between positional identities in peptides selected to bind individual PDZ domains via high-throughput experiments [63]. The authors argue this to be evidence of “multiple binding specificities” within a single domain, such that the space of peptide sequences compatible with binding a given PDZ domain is better characterized with multiple sequence motifs rather than a single motif. Our findings also suggest that the affinity/specificity landscape of PDZ-binding peptides cannot be well described using positional preferences alone.

As with positional preferences, one generally expects coupling contributions to be domain-specific. Therefore, properly accounting for these will improve our ability to design selective targeting peptides. This will become especially important when aiming to achieve more global selectivity, likely to be necessary for downstream biomedical applications. On the other hand, capturing coupling effects well is a difficult task in the context of computational protein design. Because insufficient structural relaxation will tend to produce apparently significant but erroneous coupling in models, thorough sampling of backbone degrees of freedom is likely a minimal requirement. Due to their high computational cost, such models are not commonly used in protein design. Using the technique of Cluster Expansion, we were able to surmount this computational cost, allowing for the use of FPD—a state-of-the-art flexible domain/peptide modeling tool—in our design calculations. Nevertheless, we still found that the sign of the predicted coupling between Ser/Ala@P-3 and Thr/Arg@P-1 was incorrect. This illustrates the complexity of the underlying problem, but also underscores the need for more accurate structural models. In fact, using explicit-solvent MD simulations, we discovered that accounting for the degeneracy of bound peptide ensembles introduces significant non-additive entropic contributions that are on the order of the observed coupling and of the right sign (Fig. 7 and Table S4). Interestingly, FPD-based sampling did not reveal a similar variation in structural heterogeneity between peptides (Fig. S14). This suggests that aiming to correctly describe ensemble properties, rather than just the ground-state structure, would be an important next goal in developing FPD and similar docking/sampling approaches.

Conclusions

Given the roles of N2P2 and M3P6 in LPA₂-associated tumorigenicity (Fig. 1B), the design problems posed in this study are biomedically relevant and the resulting peptides are potential tools for functional modulation. On a broader scale, our study represents a critical test of computational design for the selective targeting of PDZ domains—a problem of relevance in a wide range of biological systems. We found that selectivity, in general, does not arise “for free” from optimizing affinity for the target alone. Further, our results suggest that some domains are likely more selectively targetable than others, which may be a significant consideration in choosing therapeutic targets in the cell. We also found clear evidence of the importance of indirect coupling between binding-site residues in modulating affinity and selectivity. Coupling effects are likely to provide additional ammunition for achieving selectivity, but they are difficult to catalog experimentally, which further motivates the developing of accurate structure-based models.

The success of our computational framework demonstrates the feasibility of PDZ selective targeting by design, even in cases with considerable specificity overlap and with partial structural information. Nevertheless, we find that accuracy of structure-based modeling continues to be a significant limitation. Using a state-of-the-art modeling platform predicted qualitative positional preferences well, but the non-quantitative nature of the model was highly limiting when weighing the trade-offs between affinity and selectivity. Ultimately, to solve the problem of selective targeting by design, more accurate computational methods will be required. For example, we show here that considerations of dynamics, generally absent in protein-design scoring functions, can have significant effects on the energetics of peptide binding. Because protein design imposes significant computational constraints on scoring models, explicit consideration of such effects is currently considered prohibitive. On the other hand, the method of Cluster Expansion can be used to bridge the gap between detailed structure-based simulations and the computational efficiency required for protein design. We thus hope that this technique can enable further improvement in the accuracy of scoring functions used in design.

Materials and Methods

Structure-based Modeling

The structure of N2P2 was taken from the Protein Data Bank entry 2HE4. The boundaries of M3P6 were defined according to UniProt (residues 1047-1126 from entry Q5TCQ9). A common numbering of residues was adopted for the two domains according to their sequence alignment in Fig. 1C. The six PDZ domains of MAGI-3 are sometimes denoted in the literature as M3P0–M3P5, due to the fact that the most N-terminal domain was identified last. Here we use the more canonical nomenclature of M3P1–M3P6, so that M3P6 refers to the most C-terminal PDZ domain of MAGI-3.

Using the SWISS-MODEL automated server [43], a homology model of M3P6 was built with the structure of MAGI-1 PDZ1 bound to a human papillomavirus E6 polypeptide (PDB ID: 2I04) as the template. The resulting structure was aligned to the template by optimizing the root-mean squared deviation (RMSD) of the binding site region (residues 16-24 and 67-75) and the peptide backbone from the template was copied to the M3P6 model. Side-chains of the LPA₂ C-terminus (LMDSTL) were then repacked onto the peptide backbone and the resulting M3P6-peptide complex was subjected to continuous full-atom minimization in PyRosetta using dfpmin with tolerance as 0.01, where the movement of backbone torsion angles and chi-angles were allowed [44]. The M3P6 structure produced in this way was used for subsequent peptide scoring.

Rosetta FlexPepDock ab-initio protocol (FPD) [37] was used for scoring domain-peptide combinations. To reduce the possibility of being trapped in a local minimum, a diverse set of starting peptide-bound conformations was generated for each peptide, on the basis of 70 existing PDZ-peptide complex structures (identified with the help of the Extended PDZ Database [64]; shown superimposed in Fig. 1D). The binding mode within each of these 70 structures was transferred to either N2P2 or M3P6 by first aligning the corresponding binding sites and then copying the coordinates of the peptide backbone. The alignment was performed to minimize the binding-site RMSD, with the correspondence between N2P2 and M3P6 binding sites (i.e., residues 16-24 and 67-75 in Fig. 1C) and those of existing complex structures defined using MaDCaT [65]. Thus, for each domain-sequence pair, 70 independent FPD simulations were initiated, each starting with a different initial conformation. As each simulation was asked to general 500 structural models (from 500 independent MC simulations), a total of 35,000 models were produced for a given domain-peptide combination.

Models were scored as the total score of the complex less the total reference state weight. We found this to perform better on our benchmark datasets than the “reweighted score” used in other studies [37, 66], which magnifies the contribution of interface residues. The default scoring function (score12) was used in FPD, but we found that dropping statistical terms “rama” and “omega” upon model re-evaluation improved the performance. The lowest score among all 35,000 models for a given domain-peptide pair was assigned as the final metric.

PDZ Homology Modeling Benchmark

Of the 70 experimental PDZ-peptide structures used elsewhere in this study (Fig.1D), 29 were PDZ/peptide co-crystal structures and were used for a homology modeling benchmark. We focused the benchmark on peptide-bound structures only because of our finding that the binding site tended to widen upon peptide association (Fig. S1B). Each domain was used to build a homology model for every other domain, resulting in 841 predictions. Modeller 9.10 was used, with the input file generated by using sequences extracted from the target and template PDB files. The comparative modeling module “automodel” was used for the entire modeling process. The alignment between template and target sequences was built with the standard Needleman-Wunsch dynamic programming method, using the BLOSUM62 mutation matrix with a gap-opening and gap-extension penalties of -11 and -1, respectively. Sequence identity was computed from this alignment.

Model accuracy was determined based on backbone RMSD of the most relevant PDZ binding pocket region. This region was defined on the target structure based on being in contact with the last five amino acids of the bound peptide. More specifically, any residue with a heavy atom within 6 Å of any atom of the bound C-terminal five-mer was considered relevant. RMSD’s were calculated over the backbone of this region relative to the corresponding residues on the modeled structure. CA and full-backbone RMSD’s involved 19 and 77 atoms on average, respectively.

Design Procedure

The reference and all point clusters were considered in CE, but pair clusters were restricted to position pairs separated by a single residue. Such pairs would map to one side of the binding interface and were deemed more likely to couple. The amino-acid alphabet in forward and reverse design was based on residues observed in peptides chosen to bind N2P2 and M3P6, respectively, in a previous phage-display study [18], augmented by residues from the LPA₂ C-terminus. Sequences for CE training where initially chosen randomly from design alphabets. Following this, additional random sequences constrained to have CFs underrepresented in the initial set were added until all candidate CFs were present at least three times. The resulting training sets for forward design and reverse design consisted of 192 and 84 peptide sequences, respectively. FPD was run to score the binding of each training-set sequence to both N2P2 and M3P6. To prevent overtraining in CE derivation, we used our previously described strategy, in which constant and all point cluster functions were included in the model, but pair cluster functions were included only if they improved the cross-validation root-mean-square (CV RMS) [35]. The final quality of each CE was evaluated using 50 additional randomly-generated sequences not present in CE training sets, with performance on these test sets shown in Fig. 3C.

Derived cluster expansions were used to score the entire sequence space in both design problems. For sequences on the affinity/selectivity Pareto-optimal front (six sequences in each case), FPD was run to confirm CE-estimated binding scores, with close agreement between CE and FPD seen in all cases (Table S1).

Molecular Dynamics

Explicit-solvent molecular dynamics simulations were run using NAMD 2.9, developed by the Theoretical and Computational Biophysics Group in the Beckman Institute for Advanced Science and Technology at the University of Illinois at Urbana-Champaign [67]. To speed up calculations, explicit non-bonded interactions were cut off at 10 Å, with a switching function starting at 6 Å (CHARMM22 force-field). Particle Mesh Ewald method was used to account for long-range electrostatics and an analytical correction was applied to account for long-range van der Waals energies [68]. Pande and co-workers showed, on the example of computing amino-acid analog solvation free energies, that with these long-range corrections a 6/10 Å non-bonded interaction schedule was essentially as effective as using much longer explicit cutoffs (e.g., 12/14 Å) [69]. Each simulated complex (N2P2 with one of the four coupling peptides) was padded with 10 Å of TIP3 water on all sides and simulations were run in the NTP ensemble (pressure 1 atm, temperature 298.15 K). Each peptide was subjected to ten independent 10-ns simulations, starting with the FPD predicted model, with an integration step of 1 fs. Frames were saved every 100 fs.

The combined trajectory for each peptide, produced by concatenating the second half of all 10-ns runs, was clustered using a greedy algorithm implemented by the “measure cluster” command in VMD [70]. Specifically, every 10^th frame was read (corresponding to 1 ps between frames) and clustering was performed using best-fit RMSD over the binding region (peptide plus select domain residues) as a metric of distance between frames. Domain residues were added to the binding region definition based on making important contacts with the bound peptide, and these were Tyr17, Asn20, His22, Arg34, and His67 (see Fig. S15). Distance threshold for clustering was 1.5 Å, meaning that all frames within a given cluster were within no more than 1.5 Å RMSD of the cluster centroid. The same approach was used for clustering FPD-sampled structures (see Fig. S14). Of the 3,500 models produced for each peptide, only those within 2.5 eu of the best-scoring conformation were clustered, and a threshold of 0.8 Å was used due to the lower overall heterogeneity (with a threshold of 1.5 Å nearly all conformations are placed into a single cluster).

The frequency of each cluster was used as an approximation of its probability, and an entropic contribution was estimated as S = −R Σ_i f_i · ln(f_i) where the sum extends over all clusters and f_i is the frequency of cluster i (see Table S4). Given this value for each of the coupling peptides (S_ST, S_AT, and S_AR, corresponding to peptides C_ST, C_AT, C_SR, and C_AR, respectively), the coupling contribution was computed as T · [(S_AR − S_SR) − (S_AT − S_ST)] (T, the absolute temperature, was 298.15 K). To provide a measure of the random error of this estimate, we first calculated the apparent correlation time of cluster identity. That is, for a given lag time t, we computed the probability of two frames separated by t occupying the same cluster. The resulting curves of probability as a function of t fit well to single exponential decay, and the fits were used to derive the time corresponding to the point of half decay, which was defined as the correlation time τ. This time varied between 80 and 150 ps for the four coupling peptides. We then split the combined trajectory of each peptide into windows of duration τ, and randomly discarded half of these windows. This was meant to sub-sample the trajectory, but in a way that recognized its internally correlated nature. Entropy contributions from sub-sampled trajectories were estimated as above, and performing this procedure 1,000 times gave a standard deviation of the sub-sampled estimate, which was taken as an indicator of statistical error (reported in Table S4). The error estimate for the entire coupling contribution was obtained by standard error propagation.

Experimental Coupling Constants

The coupling constant between Ser/Ala@P-3 and Arg/Thr@P-1 was defined as $\mathrm{\Delta \Delta }{G}_C=(\mathrm{\Delta }{G}_{\mathit{AT}}^b-\mathrm{\Delta }{G}_{\mathit{ST}}^b)-(\mathrm{\Delta }{G}_{\mathit{AR}}^b-\mathrm{\Delta }{G}_{\mathit{SR}}^b)$, where $\mathrm{\Delta }{G}_{AT}^b$, $\mathrm{\Delta }{G}_{ST}^b$, $\mathrm{\Delta }{G}_{AR}^b$, and $\mathrm{\Delta }{G}_{SR}^b$ were the standard-state dissociation free energies of C_AT, C_ST, C_AR, and C_SR to the domain in question (either N2P2 or M3P6), respectively. Dissociation free energies were estimated from the apparent inhibition constants shown in Table 1. Error bounds on the estimated coupling constants were computed using 95% confidence intervals from K_i fits and the standard error propagation.

Protein Expression and Purification

DNA vectors

A DNA fragment encoding a 10x His tag followed by a 3C protease recognition site and an N-terminal portion of N2P2 was purchased from Integrated DNA Technologies (IDT). Using the Nco1 and Xma1 restriction sites the fragment was inserted into a pET16b expression vector already containing N2P2 (generously provided by Dr. Dean Madden, Dartmouth College, and previously described by Cushing et al. [71]). The final expression vector thus contained the N2P2 domain (residues 143-280 from UniProt entry Q15599; Fig. 1C) tagged at the N-terminus with a 10x His tag and a 3C protease recognition site linker to enable tag removal.

A DNA fragment encoding M3P6 (residues 1040-1149 of UniProt entry Q5TCQ9-2; Fig. 1C) was produced through overlap extension PCR of two fragments purchased from IDT, followed by gel purification using QIAquick Gel Extraction Kit (Qiagen). The M3P6 fragment, having appropriate sequence overlaps with the pET 48b(+) multiple cloning site, was combined with the plasmid through a Gibson Assembly reaction (NEB). The final expression vector contained M3P6 fused with a thioredoxin solubility tag and a 6x His purification tag on the N-terminus, separated by a 3C protease site.

M3P6m was created by site directed mutagenesis of pET48b(+)-M3P6. Briefly, a primer introducing the change was purchased from IDT and the region was substituted in the parent vector using Gibson Assembly.

Sequences of all constructs were verified at the Dartmouth Molecular Biology Core Facility.

Expression

All domains were expressed in Rosetta 2 (DE3) cells (Novagen). 10mL starter cultures of Terrific Broth supplemented with ampicillin and chloramphenicol (for N2P2) or kanamycin and chloramphenicol (for M3P6) were inoculated from single colonies or stored glycerol stocks and grown up overnight at 37°C with shaking. The next day the starter culture was used to seed a 1L culture of Terrific Broth (TB) media containing chloramphenicol at (34 μg/mL) and either ampicillin (100 μg/mL for N2P2) or kanamycin (50 μg/mL for M3P6). Cultures grew at 37°C with shaking to an OD₆₀₀ of 0.6-0.8 before being shifted to 16°C. After cooling for 20 minutes cultures were induced with 0.1mM IPTG and continued to incubate at 16°C for 20-24 hours.

Lysis

Cells were centrifuged for 20 minutes at 6,000 RPM and then resuspended in lysis buffer—Bugbuster (Novagen), 25mM Tris, pH 7.5, 150mM NaCl, 2mM MgCl2, 0.5% v/v Protease Inhibitor Cocktail Set III, EDTA-free (Calbiochem), 1mM THP (Novagen), 50U/mL benzonase (Novagen). Lysis proceeded for 20 minutes on ice and suspension was then clarified by centrifugation for 20 minutes at 18,000g at 4°C.

Purification

Clarified supernatant was supplemented with imidazole to a final concentration of 10mM. 1mL of Nickel Sepharose 6 Fast Flow resin (GE) was prepared for each 1 L of culture by pre-equilibrating with five column volumes of distilled water followed by binding buffer (25mM Tris, pH 7.5, 150mM NaCl, 20mM imidazole, 1mM THP). Clarified supernatant was batch bound to prepared resin by incubating the two together with stirring at 4°C for 1 hour. After 1 hour, the supernatant and resin mixture was loaded into a plastic column (Pierce) and allowed to drain by gravity. Resin was washed two times with five column volumes (CV) of binding buffer and then two times with five CV of wash buffer (25mM Tris, pH7.5, 150mM NaCl, 40mM imidazole, 1mM THP). Protein was eluted with ten CV of elution buffer (25mM Tris, pH7.5, 150mM NaCl, 400mM imidazole, 1mM THP) and 1mL fractions were collected and supplemented with 50mM EDTA to chelate nickel that may have dissociated from the column. Fractions were run on a 10% tricine SDS-PAGE gel and evaluated for purity and concentration. Fractions with high concentration and purity were carried forward for digestion.

Digestion with 3C protease

Fractions carried forward were pooled, yield was estimated and 6x His tagged 3C protease was added at 1:50 w/w ratio to the protein prep. The mixture was transferred to 3.5K MWCO dialysis tubing (Thermo Scientific) and dialyzed in 1L protein buffer (25mM Tris, pH 7.5, 150mM NaCl, 1mM THP) with stirring overnight at 4°C. The next day the mixture was incubated with prepared Nickel Sepharose 6 Fast Flow Resin at 4°C with stirring for 15 minutes. The resin and protein mixture was poured into a plastic chromatography column and the flow-through was collected.

Storage

The collected protein was concentrated and two buffer exchanges of 1:10 each were completed with freezer storage buffer (25mM Tris, pH 7.5, 150mM NaCl, 0.1mM TCEP, 10% glycerol, 0.02% sodium azide) using Amicon Ultra 10,000 MWCO centrifugal filters. Concentration was determined by measuring A₂₈₀ using a Nanodrop 2000 and applying theoretical extinction coefficients (calculated using the ExPASy ProtParam tool; 2980 M⁻¹cm⁻¹ for N2P2 and 5960 M⁻¹cm⁻¹ for M3P6 and M3P6m). Protein stocks were stored as aliquots at -80C.

Analytical FPLC

Purified proteins were analyzed on an Akta Explorer (GE Healthcare) by injecting 500 μg of protein over a Superdex 75 10/300 GL column. Absorbance of fractions was measured at 280 nm and 218 nm and chromatograms were analyzed using Unicorn 5.10 software (GE Healthcare). All proteins eluted in a single peak at a retention time consistent with a monomer.

MALDI-TOF

The identity of purified proteins was confirmed by MALDI-TOF analysis on an Applied Biosystems Voyager-DE Pro MALDI-TOF mass spectrophotometer at the Dartmouth Molecular Biology & Proteomics Core Facility. Samples were prepared by mixing 1:1 with sinapinic acid matrix (Thermo Scientific).

Peptide Synthesis

All peptides were synthesized by GenScript USA. For K_d and K_i experiments, peptide concentrations were determined by dividing the weight of lyophilized peptide powder by the volume of suspending buffer. Because the three reverse design peptides contained a Trp residue, we were also able to determine their concentration spectroscopically using their theoretical extinction coefficient at 280 nm, showing the two methods of concentration determination to be within 15-20% of each other (see Supplementary Material). For experiments aimed at determining double-mutant coupling free energies, because additional accuracy was required, peptide concentrations were established using quantitative amino acid analysis [REF] performed by GenScript USA.

Fluorescence Polarization

Fluorescence Polarization (FP) assays were performed to measure domain-peptide dissociation and inhibition constants (K_d and K_i, respectively) generally as described elsewhere in the literature [42], with some minor changes. Purified domain proteins were dialyzed into FP buffer A (25 mM Tris, pH 7.5, 150 mM NaCl, 0,1 mM TCEP). Appropriate amounts of domain proteins were incubated in FP buffer B (FP buffer A plus a final concentration of 0.1 mg/mL IgG, 0.5 mM Thesit, and 30 nM fluorescently labeled reporter peptide) for 20 min to equilibrate. In a K_d assay, equilibrated domain was serially diluted into FP buffer B, incubated in the dark with gentle shaking for 10 minutes, spun briefly to remove air bubbles and then 30uL was transferred to an assay plate. We measured fluorescence anisotropy as a function of domain concentration to determine the domain-reporter dissociation constant (K_d). In a K_i assay, the domain protein, at a concentration ranging between 1.5-3 times of the domain-reporter K_d, was equilibrated in FP buffer B, and a competitor peptide serially diluted in FP buffer B was added to the equilibrated solution. We measured the anisotropy as a function of competitor concentration to determine the apparent inhibition constant (K_i). Fluorescein isothiocyanate (FITC)-labeled C-terminal 10mer of LPA₂ (FITC-Ahx-NGHPLMDSTL) and FITC-labeled C-terminal 10mer of claudin23 (FITC-Ahx-QNSLPCDSDL) were used as reporters for N2P2 and M3P6, respectively (Ahx: aminohexanoic acid). When measuring the affinities of LPA₂ 6mer to N2P2, we used FITC-labeled FD2 8-mer (FITC-Ahx-GGSGSTRF) as the reporter. All dilutions were incubated on black 96-well plates for 10 min with gentle agitation. After centrifugation for 2 min at 1,500 rpm to remove bubbles, 30 μL of each well was transferred to assay plates, then centrifuged again for 2 min at 1,500 rpm. Assay plates were incubated in the dark for 20 min, then scanned in a Tecan Infinite M1000 Microplate Reader with a 10 min pre-read equilibration at 27 °C.

Data were processed in MATLAB. A nonlinear least-squares algorithm was used to fit the experimental anisotropy to the anisotropy calculated by the equation below:

$$S_{\mathit{calc}}=S_L+(S_{PL}-S_L)[\mathit{PL}]/{[L]}_0$$

where [L]₀ was total labeled peptide concentration, [PL] the concentration of domain-labeled peptide complex, S_L and S_PL the innate anisotropies due to pure unbound peptide and domain-peptide complex, respectively. For K_d experiments, [PL] was calculated by considering the simple binding equilibrium of labeled peptide L and domain P:

$$\begin{array}{c}P+L\stackrel{K_d}{\leftrightarrow }\mathit{PL}\\ K_d=\frac{[P][L]}{[\mathit{PL}]}=\frac{({[P]}_0-[\mathit{PL}])({[L]}_0-[\mathit{PL}])}{[\mathit{PL}]}\\ [\mathit{PL}]=\frac{{[P]}_0+{[L]}_0+K_d-\sqrt{{({[P]}_0+{[L]}_0+K_d)}^2-4{[P]}_0{[L]}_0}}{2}\end{array}$$

where [P] and [P]₀ where unbound and total domain concentrations, discarding the meaningless solution to the quadratic equation. K_d, S_L, and S_PL were fit to minimize the sum-squared error between calculated and experimental anisotropies using MATLAB’s Curve Fitting Toolbox. For K_i experiments, [PL] is the solution to a cubic equation resulting from considering linked equillibria of labeled and unlabeled peptide (L and C, respectively) binding to domain P:

$$\begin{array}{c}P+L\stackrel{K_d}{\leftrightarrow }\mathit{PL}\\ P+C\stackrel{K_i}{\leftrightarrow }\mathit{PC}\\ K_d=\frac{[P][L]}{[\mathit{PL}]}=\frac{\left({[P]}_0-[\mathit{PL}]-[\mathit{PC}]\right)\left({[L]}_0-[\mathit{PL}]\right)}{[\mathit{PL}]}\\ K_i=\frac{[P][C]}{[\mathit{PC}]}=\frac{\left({[P]}_0-[\mathit{PL}]-[\mathit{PC}]\right)\left({[C]}_0-[\mathit{PC}]\right)}{[\mathit{PC}]}\\ (K_d-K_i){[\mathit{PL}]}^3+({[C]}_0{K}_d-K_d{[L]}_0+2K_i{L}_0-K_d{P}_0+K_i{P}_0-K_d^2+K_d{K}_i){[\mathit{PL}]}^2+\\ (K_d{[L]}_0{[P]}_0-{[C]}_0{K}_d{[L]}_0-K_i{[L]}_0^2-2K_i{[L]}_0{[P]}_0-K_d{K}_i{[L]}_0)[\mathit{PL}]+K_i{L}_0^2{P}_0=0\end{array}$$

where [C]₀, [C], [PC] were total, free, and domain-bound concentrations of unlabeled peptide. The MATLAB function “roots” was used to calculate the three roots to the above cubic equation, discarding the two that were meaningless. K_i, S_L, and S_PL were fit to minimize the sum-squared error between calculated and measured anisotropies using a combination of MATLAB’s Optimization and Curve Fitting Toolboxes.

We used global fitting to fit replicates measuring the K_d or K_i of the same domain-peptide combination. To this end, K_d or K_i were constrained to be the same across all replicates, whereas S_L and S_PL were allowed to vary among them to account for small experiment-to-experiment variations (S_L and S_PL in different replicate tended to agreed closely). K_i, S_L, and S_PL were fit to minimize the sum-squared error between calculated and measured anisotropies over all replicates.

For binding between M3P6 and forward design peptides, we were unable to reach the plateau region in competition assays (Fig. S8). In the case of FD1, though some reduction in anisotropy was observed at high peptide concentration, control measurements (involving the same dilutions as in normal K_i experiments but lacking the domain) revealed a strong viscosity effect above ~1 mM FD1, preventing us from making measurements at higher concentrations. For FD2 and FD3, as no significant decrease of anisotropy was seen even at ~1mM peptide, we found it unnecessary to determine affinity accurately. We did want to estimate a reasonable range of affinities from available data in these cases, however. To this end, we performed a series of fitting procedures, in which K_i was fixed at a specific value (scanned in a wide range) and the remaining parameters were fit to optimize error (S_L was constrained to the range of 10-20 anisotropy units, based on anisotropy values seen when the reporter peptide was mixed with the competitor peptide alone). We then considered fitting error as a function of the fixed K_i looking for regions that can be safely discarded from consideration—i.e., regions where the fitting error is higher than the error expected from typical experimental variations (calculated as the mean experiment-to-experiment difference between all pairs of independent measurements for a given peptide/domain pair); Fig. S9. The remaining region was considered a plausible interval for K_i (see Fig. S9).

95% confidence bounds for K_d and K_i estimates were calculated as $\pm t\sqrt{{(X^{T}X)}^{-1}{s}^2}$, where t is the inverse of Student’s T cumulative distribution at p = 0.95, X is the Jacobian of the fitted values with respect to the variable coefficients, and s² is the mean squared error [72].

NMR Footprinting

The NMR based peptide binding assays were carried out on a Bruker Avance III 700 MHz NMR, with a 5 mm cryoprobe. Samples were in the following buffer: 25 mM NaPi, 50 mM NaCl, 0.1 mM TCEP, 0.02% w/v NaN3, 5% v/v D₂O, at pH 6.8. Concentration of N2P2 and peptide in samples was 100μM. Chemical shift perturbations from ¹H,¹⁵N HSQC experiments were used to determine the location of peptide binding. 16 scans were collected with 1024 points in the ¹H-dimension and 128 in the ¹⁵N-dimension. Spectra comparisons were carried out with Sparky 3.115 [73]. The following equation was used to normalize chemical shift perturbation values [74]:

$${\mathrm{\Delta }}_{\mathit{obs}}=\sqrt{\frac{{\mathrm{\Delta }}_{1H}^2+{\left(\frac{{\mathrm{\Delta }}_{15N}}{5}\right)}^2}{2}}$$

where Δ_obs is the normalized chemical shift, Δ_1H is the change of the chemical shift in the ¹H-dimension, Δ_15N is the chemical shift change in the ¹⁵N-dimension. Normalized chemical shift perturbations were considered significant if they were greater than one standard deviation above the mean. Details of N2P2 assignment will be reported elsewhere. The NHERF2 PDZ2 assignments have been deposited in the Biological Magnetic Resonance bank under entry number 19871.