A meta-analysis of leaf nitrogen distribution within plant canopies

Abstract

Background and aims Leaf nitrogen distribution in the plant canopy is an important determinant for canopy photosynthesis. Although the gradient of leaf nitrogen is formed along light gradients in the canopy, its quantitative variations among species and environmental responses remain unknown. Here, we conducted a global meta-analysis of leaf nitrogen distribution in plant canopies.

Methods We collected data on the nitrogen distribution and environmental variables from 393 plant canopies (100, 241 and 52 canopies for wheat, other herbaceous and woody species, respectively).

Key Results The trends were clearly different between wheat and other species; the photosynthetic nitrogen distribution coefficient (K_b) was mainly determined by leaf area index (LAI) in wheat, whereas it was correlated with the light extinction coefficient (K_L) and LAI in other species. Some other variables were also found to influence K_b. We present the best equations for K_b as a function of environmental variables and canopy characteristics. As a more simple function, K_b = 0·5K_L can be used for canopies of species other than wheat. Sensitivity analyses using a terrestrial carbon flux model showed that gross primary production tended to be more sensitive to the K_b value especially when nitrogen content of the uppermost leaf was fixed.

Conclusion Our results reveal that nitrogen distribution is mainly driven by the vertical light gradient but other factors such as LAI also have significant effects. Our equations contribute to an improvement in the projection of plant productivity and cycling of carbon and nitrogen in terrestrial ecosystems.

INTRODUCTION

In a leaf canopy, leaf nitrogen content per unit leaf area (N_area) is highest at the top of the canopy and decreases with depth (Mooney et al., 1981; DeJong and Doyle, 1985; Charles-Edwards et al., 1987; Hirose and Werger, 1987b). Such a gradient of N_area contributes to an efficient use of nitrogen at the whole-plant level, as photosynthetic carbon gain of a leaf increases with increasing N_area at high irradiance but is less dependent at low irradiance (Mooney and Gulmon, 1979; Hirose and Werger, 1987a; Hikosaka and Terashima, 1995). Given that nitrogen is one of the most limiting resources for plant growth (Aerts and Chapin, 2000), the distribution of N_area within a leaf canopy is one of the most important determinants of canopy carbon gain.

To date, many studies have discussed optimal N_area distribution that maximizes canopy carbon gain. Field (1983) indicated that canopy photosynthesis is maximized when N_area is distributed such that the marginal gain of nitrogen investment is identical among leaves. Assuming linear relationships between A_max (light-saturated rate of CO₂ assimilation) and N_area, Farquhar (1989) suggested that canopy photosynthesis is maximized when A_max is proportional to relative light intensity. Anten et al. (1995) derived a mathematical solution of the optimal N_area distribution. When the gradient of light availability and N_area are described with an exponential function as

$$I=I_{\text{o}}\text{exp}\left(–K_{\text{L}}F\right)$$ (1)

$$N_{\text{area}}=\left(N_{\text{o}}–N_{\text{b}}\right)\text{exp}\left(–K_{\text{b}}F\right)+N_{\text{b}},$$ (2)

optimal K_b that maximizes canopy carbon gain is given as follows:

$$K_{\text{b}}=K_{\text{L}}$$ (3)

where F is the cumulative leaf area index (LAI) from the canopy top, I and I_o are photosynthetically active photon flux density (PPFD) at F and the canopy top, respectively, N_o is N_area of the top leaves, N_b is the x-intercept of the A_max–N_area relationship, which can be regarded as representing non-photosynthetic nitrogen content, and K_L and K_b are the light extinction coefficient and photosynthetic nitrogen distribution coefficient, respectively (see Anten et al., 1995, for how this solution is derived). Several simulation studies have reported that the N_area distribution observed in actual canopies significantly improves canopy photosynthesis compared with the uniform N_area distribution (for a review, see Hirose, 2005). This optimality theory has been used to describe canopy N_area distribution in various models of plant functioning because of its simplicity (Sellers et al., 1992; Anten, 2002; Franklin and Ågren, 2002; Hikosaka, 2003; Hikosaka and Anten, 2012).

Nevertheless, the N_area gradients in actual canopies have been shown to be less steep than the optimal gradients (e.g. Hirose and Werger, 1987b; Yin et al., 2003; Niinemets, 2012; Buckley et al., 2013). Furthermore, Hikosaka (2014) demonstrated that the optimal N_area distribution is steeper under direct and diffuse light than under diffuse light only. The difference between actual and optimal N_area distribution is therefore even larger than considered in previous studies that assumed only diffuse light in their calculation of optimal N_area distributions. Many studies have intensively discussed the physiological and physical constraints explaining discrepancies between theoretical and actual N_area distribution (Pons et al., 1989; Stockhoff, 1994; Hollinger, 1996; Schieving and Poorter, 1999; Kull, 2002; Buckley et al., 2002, 2013; Lloyd et al., 2010; Dewar et al., 2012; Peltoniemi et al., 2012; Niinemets, 2012; Tarvainen et al., 2013; Coble and Cavaleri, 2015).

Given that actual N_area distribution is suboptimal, several questions arise: how steep is the N_area gradient in actual canopies? Is the gradient different between species or between functional groups? Can we predict N_area gradients in plant canopies located in different environmental conditions? As N_area distribution is one of the critical elements for determining canopy photosynthesis (i.e. equivalent to gross primary productivity, GPP) in crop growth models (Yin and Struik, 2010) and vegetation–climate models (Sitch et al., 2003; Krinner et al., 2005; Ito et al., 2005; Bonan et al., 2011), this information is required to improve the accuracy of the model predictions. Anten et al. (2000) demonstrated that K_b was significantly correlated with K_L across various plant stands, implying that N_area distribution is regulated depending on the light gradient. However, they used a limited number of plant stands and did not investigate stands of woody species (i.e. forest). In contrast, by examining N_area distribution in canopies of many wheat cultivars, Moreau et al. (2012) reported that the N_area distribution depended on LAI in the canopy rather than K_L. Recently, Niinemets et al. (2015) conducted a meta-analysis of leaf trait gradient within a canopy, in which they focused on the relationship between traits and light availability of leaves. However, their results are not necessarily useful for canopy photosynthesis modelling because they did not study how N_area distribution is related to K_L and LAI in the canopies. Here, we conducted a meta-analysis of nitrogen distribution coefficients in plant canopies. We collected data of N_area distribution from many plant stands and analysed interspecific variation and environmental dependence of the nitrogen distribution coefficient. We further analysed the sensitivity in canopy carbon gain in vegetation types to the value of nitrogen distribution coefficient.

MATERIALS AND METHODS

Data collection

We collected data for canopy traits of 393 stands from 41 studies including published (37 studies) and unpublished results (four studies) (Supplementary Data Table S1). The published papers were sourced from the Web of Science, Google Scholar and citations within other studies. The quality of data in unpublished studies was considered to be equivalent to that in published studies. We chose data that had total LAI of the canopy and N_area values for at least two positions in the canopy in terms of cumulative LAI from the top. The locations of the stands ranged from 43°S to 58°N in latitude and from –0·6 to 1025 m in altitude (Table 1). Ten stands were multispecies forests consisting of species belonging to the same functional group, whereas the other stands consisted of or were dominated by single species (43 species). The dataset included natural (44 canopies) and artificial stands (349 canopies) that were established in the field (290 canopies) or in greenhouses (103 canopies), and included both wild and domesticated (crop) species. We did not collect data from stands grown only under artificial light sources.

Table 1.

Basic statistics of the data

	Mean	SD	Min.	Max.
Latitude (°, absolute value)	39.2	9.3	3.0	58.0
Altitude (m)	172.1	173.1	–0.6	1025
[CO2] (μmol mol–1)	398.0	72.2	350	705.6
Air temperature (°C)	21.6	5.0	5.7	30.6
Leaf area index (m2 m–2)	4.18	2.64	0.19	14.2
KL	0.58	0.18	0.29	1.31
KN	0.26	0.21	–0.14	1.71
Kb	0.41	0.35	0.01	2.55

The number of stands was 264, 393 and 236 for K_L (light extinction coefficient), K_N (coefficient of leaf nitrogen distribution) and K_b (coefficient of photosynthetic nitrogen distribution), respectively.

We studied two nitrogen distribution coefficients, K_b and K_N. K_b is the slope of photosynthetic nitrogen content (N_area–N_b) given by eqn (2). N_b was obtained as the x-intercept of the relationship between photosynthetic capacity and N_area (Anten et al., 1995). K_N is the slope of N_area in the canopy given as follows:

$$N_{\text{area}}=N_{\text{o}}\text{exp}\left(–K_{\text{N}}F\right).$$ (4)

K_N values were available for all the studied stands, whereas K_b values were available for 236 stands because of a lack of photosynthetic data. K_L values, which were given in the literature or calculated according to eqn (1) based on direct measurements, were available for 264 stands.

We obtained latitude (Lat) and altitude (Alt) of the site, date of measurement, mean daily or monthly air temperature (Temp) at the date or month of measurement and growth CO₂ concentration (CO₂), if available. If not, monthly air temperature data near the site were collected from other sources such as websites and growth CO₂ concentration was obtained from the global mean (http://ds.data.jma.go.jp/gmd/wdcgg/pub/global/globalmean.html; Japan Meteorological Agency). We calculated noon solar angle (SA) at the measurement date or month. Precipitation was not considered because some crop stands were irrigated. The effects of field/greenhouse and that of natural/artificial canopies were not assessed because they were not significant in a preliminary test.

Species were categorized according to growth form (annual herb, A; perennial herb, P; deciduous woody species, D; and evergreen woody species, E), phylogeny (Phyl: gymnosperm, G; monocot, M; and dicot, D) and photosynthetic metabolism (C₃ or C₄). Growth phase was divided into vegetative or reproductive based on the presence of reproductive organs in the studied plants. Additionally, we conducted a separate analysis using data only for Triticum aestivum (wheat) and for other species, because wheat showed different trends from the other species (see Results).

Statistics

We applied multiple regression analyses to detect factors responsible for nitrogen coefficients (K_b and K_N) and the light extinction coefficient (K_L) using a generalized linear model (GLM). As explanatory variables, we used K_L (only for nitrogen coefficients), LAI, Temp, SA, Lat, Alt, CO₂, Phyl, C₃/C₄ and growth phase in the full model of the GLM. The absolute value of latitude was used. We selected the best model that provided the lowest values of Akaike’s information criterion (AIC) by a backward stepwise process. In the present study, we did not incorporate the random effects for the studies in the GLM. This is because the reported species in each study were highly dependent on the literature (i.e. some papers only reported Oryza sativa). Therefore, we assumed that every study had a common true effect size in this study. Multicollinearity was assessed using the variance inflation factor (VIF). When the VIF value was higher than 10, the model was rejected and the best model was selected eliminating a parameter that was related to others. The analyses were performed using the R statistical software version 3.2.0 with packages mgcv and car (R Core Team, 2015).

Sensitivity analysis

To examine quantitative influences of K_b values on ecosystem-scale carbon flux, we conducted a sensitivity analysis using a process-based terrestrial carbon cycle model at three contrastive sites. We used the Vegetation Integrative SImulator for Trace gases (VISIT; Ito, 2010) to simulate GPP through the year. In the model, a sun/shade canopy scheme by de Pury and Farquhar (1997) was incorporated. The analysis was conducted using data from three sites: (1) a cool-temperate deciduous broadleaved forest in Takayama, Japan, (2) an evergreen tropical forest in Lambir, Malaysia, and (3) a cool grass/shrubland at Chokurdakh, Russia. These sites are occupied by C₃ plants.

We conducted seven simulations for each site: Sim1, a baseline simulation using the K_b value obtained from our meta-analysis; Sim2 and Sim5, the value of K_b was changed by + 10 % from Sim1; Sim3 and Sim6, the value of K_b was changed by –10 % from Sim1; and Sim4 and Sim7, a reference simulation according to the model of de Pury and Farquhar (1997), where nitrogen distribution in the canopy is described using another nitrogen distribution coefficient, K_a:

$$N_{\text{area}}=N_{\text{o}}\text{exp}\left(–K_{\text{a}}F/F_{\text{t}}\right)$$ (5)

where F_t is the total LAI in the canopy. The value of K_a was fixed at 0·713 in Sim4 and Sim7 (de Pury and Farquhar, 1997); note that K_b values change with LAI when K_a is fixed. For the baseline simulation (i.e. Sim1), ecophysiological parameters such as canopy-top nitrogen concentration were calibrated, so that the estimated GPP came close to observations (Saigusa et al., 2005 for Takayama; Katayama et al., 2013 for Lambir; Iwahana et al., 2014 for Chokurdakh). In Sim2–4, total leaf nitrogen in the canopy was identical to that in Sim1. In Sim5–7, N_area of top leaves (N_o) was identical to that in Sim1. Sim5–7 were applied because N_o values are available rather than canopy nitrogen in most experimental sites and thus many simulation models use N_o values for estimating GPP. Because the simulated carbon flux was stabilized through a sufficient length of initialization (i.e. spin-up), for clarity we focused on annual GPP in this sensitivity analysis.

RESULTS

Nitrogen distribution coefficients

The global means of K_N and K_b values in the database were 0·26 and 0·41, respectively (Table 1). The mean value of LAI was 4·18, which was very close to our previous meta-analysis of LAI for forests (4·21; Iio et al., 2014). The mean value of K_L was 0·58.

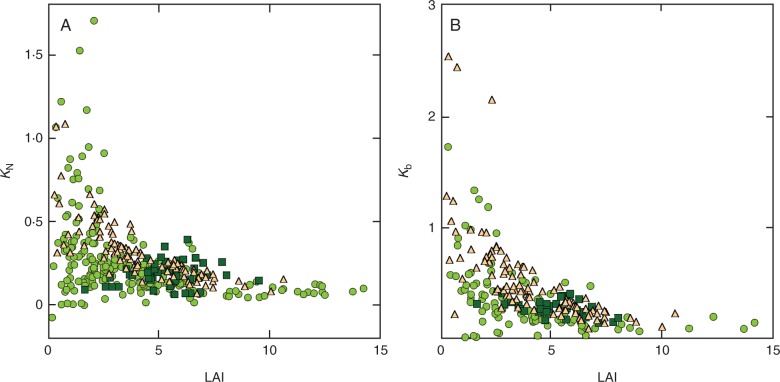
When all the data were pooled, K_L, LAI, SA and growth form were selected in the best model for the variation in K_N (Table 2). K_L, LAI, latitude and solar angle were selected for the variation in K_b (Table 2). Because the relationship between the nitrogen distribution coefficients and K_L was very different between wheat and the other species (Fig. 1), we analysed these groups separately. In wheat, K_N and K_b were not related to K_L (Fig. 1) but rather to LAI (Fig. 2). Air temperature at harvest was also selected as a significant factor for the variation in K_b in wheat (Table 2). In contrast, in the species other than wheat, K_N was related to K_L, LAI, growth form and growth phase (Table 2) and K_b was related to K_L, LAI, temperature, Lat and Alt (Table 2). K_N and K_b were nearly proportional to K_L; the regression line was K_b =0·5K_L (Fig. 1). K_N and K_b were negatively correlated with LAI not only in wheat but also in other species (Fig. 2). We further separated species other than wheat into herbaceous and woody species. In all cases, K_L was a significant factor for the variation in the nitrogen distribution coefficients (Table 2). LAI was also selected in every case, although it was not significant in the analysis for K_b of herbs. Some of the geographical and environmental factors were selected in the best models; however, the selected factors were different depending on whether K_N or K_b was considered. Air temperature at harvest was suggested to significantly influence both K_N and K_b in woody species; an increase by 1 °C in temperature decreased nitrogen coefficients by 0·006–0·015, whereas it was positively related to K_b in herbs (Table 2). Altitude was found to be negatively related to K_b in herbs. Perennial herbs were found to have lower K_N than annual herbs. Evergreen woody species were found to have lower K_N than deciduous woody species. Coefficients of other factors selected in the model were not significant.

Table 2.

Results of multiple regression analysis for nitrogen distribution coefficients

		Full model	AIC	Selected model	d.f.	AIC	Coefficient
KN	All	KL + LAI + Temp + Lat + SA + CO2 + Alt + GF + Phyl + Phase + C3/C4	–133·6	KL + LAI + SA + GF	183	–196·1	Intercept	KL	LAI	SA	GF C	GF D	GF E	GF P
							0·455	0·136	–0·0323	–0·00210	–0·06270	–0·190	–0·0679	–0·103
							***	*	***	**				***
							VIF	1·313	1·410	1·164	1·199
	Wheat	KL + LAI + Temp + Lat + SA + CO2 + Alt + Phase	10·2	LAI + Lat	98	–110·7	Intercept	LAI	Lat
							0·563	–0·0573	–0·00009
							*	***
							VIF	1·034	1·034
	Non-wheat	KL + LAI + Temp + Lat + SA + CO2 + Alt + GF + Phyl + Phase + C3/C4	–158·5	KL + LAI + GF + Phase	129	–176·9	Intercept	KL	LAI	GF D	GF E	GF P	Veg
							0·231	0·242	–0·0252	0·00862	–0·1370	–0·0766	–0·0361
							***	***	***		*	***
							VIF	1·486	1·513	1·506			1·319
	Herbs (except wheat)	KL + LAI + Temp + Lat + SA + CO2 + Alt + GF + Phyl + Phase + C3/C4	–101·4	KL + LAI + GF + Phase	104	–120·7	Intercept	KL	LAI	GF P	Veg
							0·239	0·240	–0·0255	–0·0700	–0·0494
							**	**	***	*
							VIF	1·460	1·420	1·350	1·330
	Woody species	KL + LAI + Temp + Lat + SA + CO2 + Alt + GF + Phase	–114·8	KL + LAI + Temp + GF	42	–159·4	Intercept	KL	LAI	Temp	GF E
							0·337	0·176	–0·0195	–0·00599	–0·09950
							***	***	***	***	***
							VIF	1·228	1·130	1·246	1·399
Kb	All	KL + LAI + Temp + Lat + SA + CO2 + Alt + GF + Phyl + Phase + C3/C4	43·6	KL + LAI + Lat + SA	124	20·7	Intercept	KL	LAI	Lat	SA
							1·319	0·251	–0·0381	–0·0042	–0·0121
							***	+	**		***
							VIF	1·529	1·781	2·187	2·912
	Wheat	KL + LAI + Temp + Lat + SA + CO2 + Alt + Phase	62·9	LAI + Temp	97	53·5	Intercept	LAI	Temp
							1·651	–0·1070	–0·0424
							***	***	*
							VIF	1·159	1·159
	Non-wheat	KL + LAI + Temp + Lat + SA + CO2 + Alt + GF + Phyl + Phase + C3/C4	–82·7	KL + LAI + Temp + Lat + Alt	95	–114·4	Intercept	KL	LAI	Temp	Lat	Alt
							–0·181	0·454	–0·0208	0·00834	0·00347	–0·00014
								***	***	+	*	*
							VIF	1·877	1·683	2·050	1·945	1·114
	Herbs (except wheat)	KL + LAI + Temp + Lat + SA + CO2 + Alt + GF + Phyl + Phase + C3/C4	–36·9	KL + LAI + Temp + Lat + Alt	61	–52·2	Intercept	KL	LAI	Temp	Lat	Alt
							–0·276	0·538	–0·0149	0·0100	0·00333	–0·00019
								***				*
							VIF	2·492	1·909	2·438	1·913	1·193
	Woody species	KL + LAI + Temp + Lat + SA + CO2 + Alt + GF + Phase	–76·5	KL + LAI + Temp + CO2	29	–99·1	Intercept	KL	LAI	Temp	CO2
							0·459	0·251	–0·0205	–0·01500	0·00226
							***	**	*	***
							VIF	1·399	1·568	1·164	1·310

A generalized linear model with stepwise selection was applied to obtain the best model based on Akaike’s information criterion (AIC). Coefficient values (not standardized) with significance are shown (***P < 0·001, **P < 0·01, *P < 0·05, ⁺P < 0·1). Coefficients for the categorical variable are the value relative to annual plant (growth form), dicot species (phylogeny) and reproductive phase (phase). All the variables were treated as a fixed factor. Alt, altitude (m); CO₂, atmospheric CO₂ concentration (μmol mol^–1); GF, growth form (C, conifer; D, deciduous tree; E, evergreen tree; P, perennial herb); K_b, coefficient of photosynthetic nitrogen distribution; K_L, light extinction coefficient; K_N, coefficient of leaf nitrogen distribution; LAI, leaf area index; Lat, latitude (degrees); Phase, vegetative or reproductive phase; Phyl, phylogeny (gymnosperm, monocot or dicot); SA, solar angle at harvest (degrees); Temp, air temperature at harvest (°C); Veg, vegetative phase; VIF, variance inflation factor.

Fig. 1.

Relationship between nitrogen distribution coefficients and light extinction coefficient (K_L). (A) The coefficient of leaf nitrogen distribution (K_N) and (B) the coefficient of photosynthetic nitrogen distribution (K_b). Circles, herbaceous species except wheat; triangles, wheat; and squares, woody species. Regression lines are K_N = 0·368K_L (r² = 0·22) and K_b = 0·499K_L (r² = 0·37), with data for wheat not included. Note that three data points that had K_b values higher than 1·5 were omitted from B (see Supplementary Data Fig. S1 for the whole data set).

Fig. 2.

Relationship between nitrogen distribution coefficients and leaf area index (LAI). (A) The coefficient of leaf nitrogen distribution (K_N) and (B) the coefficient of photosynthetic nitrogen distribution (K_b). Circles, herbaceous species except wheat; triangles, wheat; and squares, woody species.

Variation in K_L among species was analysed. When all the species were pooled, K_L was significantly related to LAI, temperature, SA, growth form and phylogeny (Supplementary Data Table S2). Annual plants had a higher K_L than deciduous woody species. When separated into different growth forms, K_L in wheat was related to LAI and SA. In herbs other than wheat, K_L was related to LAI, temperature, growth form, phylogeny (gymnosperm, monocot or dicot) and growth phase. In woody species, K_L was related to SA and growth form.

Sensitivity analysis

Here, we assess the effect of incorrect values of nitrogen distribution on GPP estimation. At the three sites, the baseline simulation by the VISIT model retrieved intersite differences in annual GPP (Table 3): high productivity of Lambir tropical forest, low productivity of cool grass/shrubland, and intermediate productivity in the Takayama temperate forest. In Sim2–4, K_b values were altered with the same value of canopy nitrogen as for Sim1. An increase in K_b increased GPP, indicating that the predicted K_b is less steep than optimal. However, the deviations in GPP from Sim1 were small except for Sim4, suggesting that the effects of small changes in K_b on GPP are generally small. On the other hand, in Sim5–7, where K_b values were altered with the same N_o value as for Sim1, the deviations were larger than those in Sim2–4. Whereas optimality models fix canopy nitrogen as in Sim2–4, many simulations of ecosystem carbon cycling use leaf properties of top leaves rather than canopy nitrogen as in Sim5–7. Therefore, correct K_b values are necessary for accurate projection of carbon cycling.

Table 3.

Sensitivity analysis for effects of photosynthetic nitrogen distribution coefficient (K_b) on gross primary production (GPP) in three ecosystems, Takayama (deciduous broadleaved forest), Lambir (evergreen tropical forest) and Chokurdakh (grass/shrubland)

Site	Mean Kb	GPP (g C m−2 year−1)
		Same canopy nitrogen				Same No
		Sim1	Sim2	Sim3	Sim4	Sim5	Sim6	Sim7
Takayama	0·371	1006	1011	1000	1125	973	1042	1162
			+0·5 %	–0·6 %	+11·9 %	–3·4 %	+4·0 %	+17·6 %
Lambir	0·180	3442	3460	3423	3430	3365	3417	3377
			+0·5 %	–0·5 %	–0·3 %	–0·8 %	+0·8 %	+0·4 %
Chokurdakh	0·222	382	382	382	372	287	325	216
			+0·05 %	–0·05 %	–2·7 %	–5·7 %	+6·6 %	+29·1 %

Sim1, a baseline simulation using K_b values obtained from the meta-analysis (the equation of ‘woody species’ for Takayama and Lambir and that of ‘non-wheat’ for Chokurdakh; Table 2); Sim2 and Sim5, the K_b value was changed by + 10 % from Sim1; Sim3 and Sim6, the K_b value was changed by –10 % from Sim1; Sim4 and Sim7, a reference simulation using K_a value (0·713) assumed in de Pury and Farquhar (1997) (see text for details). For Sim2–4, canopy nitrogen content per ground area was the same as that for Sim1, whereas for Sim5–7, nitrogen content of top leaves (N_o) was the same as that for Sim1. Note that the K_b value in Sim1–3 changes for each site depending on other variables such as temperature and the mean value is shown. For Takayama, the mean K_b value was calculated for seasons with LAI > 1.

DISCUSSION

Our meta-analysis clearly demonstrated that the nitrogen distribution coefficients are sensitive to species traits and environmental factors. In particular, wheat has a different dependence of nitrogen coefficients on the traits and factors from other species. We presented the best models to explain the variation in nitrogen partitioning coefficients in Table 2. These models contribute to prediction of nitrogen partitioning in canopies of species belonging to different functional groups under various environmental conditions.

For species other than wheat, K_N and K_b were mostly explained by K_L. K_b was nearly proportional to K_L. Therefore, we can use a simple model, K_b = 0·5K_L, to predict nitrogen partitioning in plant canopies when information on other factors is lacking. Given that K_b = K_L is optimal under diffuse light (Anten et al., 1995; Hikosaka, 2014; see Introduction), the K_b to K_L ratio <1 indicates that nitrogen distribution in actual canopies is suboptimal. However, a strong correlation between K_b and K_L suggests that light distribution in the canopy is an important driver of nitrogen distribution within the canopy across a wide variety of species, as has been indicated by many researchers (Hirose and Werger, 1987b; Hirose et al., 1988, 1989; Ackerly, 1992; Ackerly and Bazzaz, 1995; Pons et al., 1993; Hikosaka et al., 1994; Anten et al., 1995; Niinemets et al., 2015).

It was found that K_N and K_b were negatively related to LAI. This was partly explained by the fact that greater K_L values were found only with lower LAI, especially in herbaceous species. A canopy with both greater K_L and LAI values may be unrealistic because carbon gain in leaves at lower positions becomes negative due to very low light availability (Monsi and Saeki, 1953). Higher K_N and K_b at low LAI may be related to nitrogen availability. When plants are exposed to low nitrogen availability, senescence of old leaves and thus retranslocation of nitrogen from old to new leaves is accelerated (Thomas and Staddart, 1980). Moreau et al. (2012) showed that wheat stands in low nutrient availability had higher K_b.

Several environmental and geographical factors were found to influence nitrogen distribution coefficients. Air temperature at harvest was negatively related to K_N and K_b in woody species. This is consistent with a study showing that an experimentally warmed Scots pine stand had a less steep gradient of leaf nitrogen content (Kellmäki and Wang, 1997). Although effects of other factors such as latitude and altitude were found to be significant in some cases, their effects were not consistent between K_N and K_b. For example, effects of altitude were significant for K_b in herbaceous species but not for K_N, although K_N and K_b are closely related to each other (see eqns 2 and 4). In our dataset, K_N values were available in all stands, whereas K_b values were available for 60 % of the studied stands. This implies that the results for K_N are more reliable than those for K_b and that the environmental and geographical factors may influence a limited number of species.

Many researchers have discussed why nitrogen distributions in leaf canopies are generally more uniform than the optimal distribution (see Introduction). Although the present study did not directly analyse the underlying mechanisms, comparisons between different functional groups may provide some insights. It has been indicated that leaf ageing may contribute to forming the nitrogen gradient because N_area generally decreases with leaf age (Mooney et al., 1981). Hikosaka et al. (1994) raised a vine plant (Ipomoea tricolor) horizontally to avoid shading between leaves and found that nitrogen gradient was formed along leaf age when the plants were grown at low nutrient availability. As a vertical leaf age gradient is formed in herbaceous dicot stands but not in most woody species stands, one may expect that herbaceous stands have a steeper gradient of nitrogen content than stands of woody species. In the present study, annual herbs had a higher K_N than evergreen woody species (Table 2). However, such a difference was not found for K_b. Furthermore, deciduous woody species had higher K_N values than annual herbs, although this was not significant (Table 2). Therefore, we can reject a hypothesis that leaf age gradient plays an important role for forming the nitrogen gradient in field stands. Peltoniemi et al. (2012) demonstrated theoretically that suboptimal distribution of hydraulic conductance between upper and lower leaves may explain suboptimal nitrogen distribution. However, a similar nitrogen gradient between annual herbs and deciduous trees may suggest that hydraulic constraints are not an important factor as hydraulic limitations are less important in herbs than in taller trees. Further studies may be necessary for understanding the ecological significance of suboptimal nitrogen distribution in the canopy.

In wheat canopies, in contrast to other species, nitrogen distribution was not related to K_L but to LAI, as has been indicated by Moreau et al. (2012). In addition, their K_N and K_b values were generally greater than that of other species even though they have lower K_L values. Intriguingly, the results for wheat were contrary to those for other Poaceae species included in the present study. For example, rice had a similar K_b to K_L ratio to other species, 0·34 ± 0·12. Berthloot et al. (2008) reported that there was no gradient of N_area within flag leaves of wheat although there was a large gradient in light. They considered that light signal is integrated at the whole leaf lamina level and that the nitrogen gradient is mainly due to differences between leaves. If this is true, the vertical gradient of N_area may be steeper in a canopy consisting of smaller individual leaves where LAI is lower. Another explanation may originate from the fact that the wheat ear has a high photosynthetic ability and its contribution to grain filling is greater than that of flag leaves (e.g. Sanchez-Bragado et al., 2014). Previous optimization models assume that the slope of the relationship between photosynthetic ability and N_area is constant across leaves. However, if the slope is very different between ear and flag leaves, this assumption may not hold true, and a more complex model would need to be used to determine optimal N distributions. Although the mechanisms remain unclear, our meta-analysis clearly showed that the relationship between canopy structure and the nitrogen distribution differs from that of the other species in the present study. This effect will need to be considered when wheat productivity is modelled.

The equations to predict K_N and K_b values (Table 2) include information on geography, abiotic environment and canopy characteristics. Whereas the geographical and environmental variables can be estimated using geographical information systems (GIS), canopy characteristics, LAI and K_L may need to be determined with field investigation. Recently, Iio et al. (2014) conducted a meta-analysis of forest LAI where LAI was expressed as a function of mean annual temperature, wetness index (the ratio of annual precipitation to potential evapotranspiration) and plant functional type, which may be useful to predict LAI in a given ecosystem. K_L varies considerably among plant stands (see Table 1) mainly depending on leaf angle (Monsi and Saeki, 1953). The equations shown in Table S2 may be useful to predict K_L values in plant stands.

How K_L values theoretically influence canopy photosynthesis varies depending on model assumptions. In previous optimality studies, the sensitivities of canopy photosynthesis to K_L values were studied keeping a constant canopy nitrogen per ground area, because nitrogen is regarded as a cost for photosynthesis (Field, 1983; Hirose and Werger, 1987b). In Sim2–4, canopy nitrogen was the same as Sim1 and an increase in the K_b value increased GPP (Table 3) because the K_b value was lower than the optimum. On the other hand, in vegetation models that consider canopy photosynthesis, N_area of the top leaves (N_o) is given (e.g. de Pury and Farquhar, 1997). In these models, a decrease in the K_b value resulted in a decrease in canopy nitrogen per ground area (see eqn 2), which leads to a decrease in canopy photosynthesis. In Sim5–7, N_o was the same as that in Sim1 and an increase in the K_b value decreased canopy nitrogen and thus GPP (Table 2).

Our sensitivity analysis clearly revealed that GPP is sensitive to the value of K_b especially when N_o is given. Therefore, accuracy of the K_b value is indispensable for accurate projection of canopy gas exchange rates, plant production and ecosystem carbon budget. Furthermore, the K_b value also contributes to estimation of leaf nitrogen content in the canopy, which is an important variable for ecosystem nitrogen cycling. This information may contribute to a functional coupling of models for carbon and nitrogen cycling in terrestrial ecosystems.

CONCLUSION

The present study has demonstrated that the nitrogen distribution coefficients of a plant canopy are influenced by various factors. It is surprising that wheat has a different dependence of nitrogen distribution coefficients on the factors from other species. In other species, the nitrogen distribution coefficients were significantly correlated with the light extinction coefficient, suggesting that the vertical light gradient is a main driver of nitrogen distribution in the canopy. Other factors such as LAI were also found to influence nitrogen distribution coefficients. The best models shown in the present study contribute to an accurate estimation of nitrogen distribution coefficients in a given vegetation and to an improvement of projection of plant productivity and cycling of carbon and nitrogen in terrestrial ecosystems.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. Figure S1: relationship between the coefficient of photosynthetic nitrogen distribution and light extinction coefficient. Table S1: dataset of leaf area index, light extinction coefficient, coefficient of leaf nitrogen distribution and coefficient of photosynthetic nitrogen distribution. Table S2: result of multiple regression analysis for light extinction coefficient.