Detection of transposable elements by their compositional bias

Abstract

Background

Transposable elements (TE) are mobile genetic entities present in nearly all genomes. Previous work has shown that TEs tend to have a different nucleotide composition than the host genes, either considering codon usage bias or dinucleotide frequencies. We show here how these compositional differences can be used as a tool for detection and analysis of TE sequences.

Results

We compared the composition of TE sequences and host gene sequences using probabilistic models of nucleotide sequences. We used hidden Markov models (HMM), which take into account the base composition of the sequences (occurrences of words n nucleotides long, with n ranging here from 1 to 4) and the heterogeneity between coding and non-coding parts of sequences. We analyzed three sets of sequences containing class I TEs, class II TEs and genes respectively in three species: Drosophila melanogaster, Cænorhabditis elegans and Arabidopsis thaliana. Each of these sets had a distinct, homogeneous composition, enabling us to distinguish between the two classes of TE and the genes. However the particular base composition of the TEs differed in the three species studied.

Conclusions

This approach can be used to detect and annotate TEs in genomic sequences and complements the current homology-based TE detection methods. Furthermore, the HMM method is able to identify the parts of a sequence in which the nucleotide composition resembles that of a coding region of a TE. This is useful for the detailed annotation of TE sequences, which may contain an ancient, highly diverged coding region that is no longer fully functional.

Background

Transposable elements (TE) are mobile genetic entities present in genomes. The process of transposition is accomplished by various molecular mechanisms. Some elements, known as class I elements (or retrotransposons), use an RNA molecule as an intermediate in the process; this is a "copy and paste" mechanism. The TE encodes a reverse transcriptase, which is used to convert the transcribed RNA into a DNA molecule which is then inserted into the genome. Class II elements use a DNA intermediate, generally by means of a "cut and paste" mechanism. Many elements encode themselves the transposase responsible for their excision and insertion. The transposition process leaves a double-strand break at the excision site, subsequently repaired by the host's DNA repair mechanisms such as homologous recombination. The TE sequence can be partially or completely restored at the excision site, using another copy as a template (for instance, the homologous chromosome).

Several observations have been reported concerning the base composition of TEs. Ashburner [1] and Shields et al. [2] observed by comparing sequences of TEs (mainly class I) and sequences of Drosophila melanogaster genes that TEs have more codons ending in A or T than do their host genes. Lerat et al. [3] compared codon usage in TEs and in their host genes in five species. They confirmed that a high frequency of codons ending in A/T is indeed a feature of TEs, regardless of their host genome. More precisely, in TEs the third codon position always has a higher A/T content than the first position, whereas for genes, this is only true in GC-poor genomes like A. thaliana and C. elegans. They also studied dinucleotide composition by comparing the frequency of dinucleotides to that of single nucleotides [4]. These relative frequencies seem to be specific for a given genome: this is the "genomic signature" defined by Karlin et al. [5]. They found out that coding regions of TEs and host genes were clustered together for C. elegans and A. thaliana whereas they formed a distinct group for D. melanogaster and H. sapiens, the retrovirus-like elements being the furthest from the host genes. On the other hand, TEs and host genes show some similar patterns of relative dinucleotide abundance. In both genomes and TEs, dinucleotide TA is thus underrepresented and CG appears to be suppressed in A. thaliana and H. sapiens but not in D. melanogaster and C. elegans.

We investigated whether these base composition peculiarities of TEs could be used to detect TEs in genomic sequences. If appropriate, this would make it possible to detect TEs that are too divergent from those already known, and which cannot therefore be identified by homology-based methods. The methods used to date to analyze TE composition (such as principal component analysis) require the user to carry out the analysis, and would therefore be impractical when dealing with large genomic fragments. Moreover, some of these methods consider codon usage bias, which precludes their application to unannotated sequences. We have therefore developed a method that could be applied in an automated way to unannotated genomic sequences.

We used probabilistic models of nucleic acid sequences as a means of evaluating the compositional characteristics of the studied sequences. A model M defines the probability of a sequence S given some parameter values θ : P(S|M, θ). If we have several parameter sets (θ₁,θ₂,...), we can compare the various probabilities obtained for the same sequence S: P(S|M,θ₁), P(S|M,θ₂),... and so identify the parameter set yielding the highest probability. These parameters are obtained by a training process, using biological sequences: parameters values are estimated using a carefully chosen set of biological sequences (a training set). The actual probabilistic model is chosen so that its parameters are in some way linked to the nucleotide composition of the training set. Thus, if a parameter set θ_i yields the highest probability for a sequence S, then sequence S is closer in composition to training set i than to the other training sets.

This approach was applied to three organisms (Drosophila melanogaster, Cænorhabditis elegans and Arabidopsis thaliana), using hidden Markov models (HMMs) as the probabilistic models. Models were trained on three training sets composed of class I TEs, class II TEs and host genes and then tested to evaluate their predictive capability. We showed that HMMs were adequate probabilistic models for representing the different base compositions of the training sets. Indeed, the three types of sequences were clearly distinguished by the HMMs after training. However, the particular base composition for a given set did not seem to be shared by the various organisms. With the intention of using these models to classify unknown sequences, the models were then further tested on various TE copies, genes and intergenic sequences extracted from sequenced genomes. The HMMs were still able to identify the TE copies, provided that they were not too small. This means that this approach can be used to assist in detecting and annotating TE sequences. These HMMs can also analyze a given sequence, and predict regions where the composition resembles that of a TE or host coding region, even in the presence of frameshifts or large indels.

Results

Model training

The detailed structure of the HMMs used for training is described in the Methods section. All models have a similare structure: 3 states representing the coding regions (one state per codon position) and one or more state for the non-coding regions. Each state is a plain Markov chain on the nucleotide sequence.

For each species, model parameters were estimated from a set of biological sequences (the training set). For Arabidopsis thaliana and Cænorhabditis elegans, the training set of TEs consisted of selected sequences from REPBASE UPDATE [6,7]: sequences of transposable elements were kept but small repetitive sequences and satellite-like repeats were removed. For Drosophila melanogaster, we used the transposon set curated by BDGP [8] which is a collection of transposable elements only. The training sets only contain one sequence per TE family (the canonical sequence of the element). We did not use multiple copies of the same element in the training set as this could bias the training process: a family with many copies would influence the model's parameters more than a family with few copies. Copies tend to be very close to the canonical sequence in terms of sequence identity, so they would add only little information on the composition anyway. Several TEs have conserved domains in their proteins (e.g. reverse transcriptase domains for class I TEs, transposase domains in the mariner superfamily) but at the DNA level, the sequences generally do not align. In some training sets, a few sequences have some local similarity: a block of a few hundreds nucleotides can be seen in a local alignment. But this never represents more than half the sequence and the identity level is not very high (around 80%). Ultimately, within a training set, sequences have low or no similarity between each other.

Since sequences that were part of a training set should not be used to evaluate the predictive capability of the trained models, in all the following tests the test set and training set for a model were distinct. The training sets for host genes consisted of 500 sequences, randomly drawn from the annotation database of the species; the test sets for host genes also consisted of 500 sequences, but the training and test sets did not share any common sequence. The training sets for TEs were unfortunately rather small compared to the set of genes, making it impossible to split them in a training set and a test set. Whenever we needed to test a TE sequence with a TE model of the same class, we therefore resorted to using a jackknife technique: in a set of n TE sequences, we successively tested each sequence by keeping apart this sequence and training a model on the remaining n-1 sequences. This allowed us to keep a maximum of TE sequences for training and to test the model with sequences not part of the training set. This scheme was however only used on sets consisting of a few elements, as it is very compute-intensive: for a set of n sequences, n models have to be trained instead of just one.

The TE models were trained several times, using different orders for the Markov chains, from 0 to 3, so as to select the best order (data not shown). Models with Markov chains of order 0 or 1 had too few parameters to enable them to distinguish correctly between the different sequence groups, and they therefore performed poorly. Higher order Markov chains contained more parameters, yielding HMMs with more information. With order 3 Markov chains, we were faced by the problem of overfitting: the model has too many parameters to be accurately estimated on the available data. So, the overall performance of a TE HMM was found to be best for Markov chains of order 2. Gene models can be trained using higher levels than TE models before encountering overfitting, because of the larger quantity of training sequences available. The subsequent analyses were therefore carried out with order 2 Markov chains for the TE models and order 3 Markov chains for the gene models. Interestingly, order 1 Markov chains were much more informative for D. melanogaster TEs than for C. elegans or A. thaliana. Order 1 Markov chains were enough for separating the different groups in D. melanogaster, suggesting that the dinucleotide composition is very different between genes and TEs in this organism; a contrario, in the other two species higher orders are necessary, meaning that the composition difference is more subtle. This is in accordance with the results of the principal component analysis of dinucleotides frequencies made by Lerat et al [4] where it was shown that among these three organisms, only in D. melanogaster did the TEs cluster separately from genes.

Testing the models

For each sequence S in the three test sets (genes, class I TEs, class II TEs), the probabilities P(S|M) were calculated for each of the three models M (genes, class I TEs, class II TEs), with the special case of the "jackknife" model when S was a TE sequence of the same class as M. These probabilities were used to choose the best model for S: the model with the highest probability. This prediction was then compared with the known nature of sequence S. We determined the quality of the predictions over the whole test sets by calculating the specificity and sensitivity of the predictions (see Methods). The results are summarized in Table 1.

Table 1.

Sensitivity and specificity of sequence class prediction.

	model	sensitivity	specificity
Drosophila melanogaster	gene	93.80%	84.50%
	class I TE	64.29%	97.67%
	class II TE	93.33%	94.78%
Cænorhabditis elegans	gene	83.20%	70.00%
	class I TE	88.89%	99.41%
	class II TE	45.45%	83.89%
Arabidopsis thaliana	gene	87.20%	86.87%
	class I TE	68.75%	92.29%
	class II TE	84.21%	93.28%

The models are relevant

The specificity of TE detection was high for all the species, (over 90%, except for C. elegans class II TEs). This means that, given a test sequence, the trained models are unlikely to erroneously tag the sequence as a TE; in other words, the system generates few false positive TE detections. On the other hand, its sensitivity is somewhat lower (ranging from 45% to 93%), which means that a fraction of the actual TEs were not detected. Despite this, the rather high values of sensitivity and specificity indicate that these models are relevant: a TE test sequence was usually correctly classified, even if it was not part of the training set. This means that the elements constituting the training sets had sufficiently distinct nucleotide compositions to be detected by the HMM. Prediction was also good for the genes.

Jackknife bias

Most of the sets of TEs contained only a few elements (less than 20). When testing for one of these elements, we used a jackknife technique to train the TE model, so as to keep as much information as possible, while separating the sequence being tested from the training set. This approach could introduce bias: we feared that the difference in size between the training sets for the genes and the TEs could affect the findings. More specifically, could any small set of sequences yield a homogeneous HMM? To test this, we took ten 20-sequence samples from the gene set and tested them using the jackknife technique. Each sequence in these samples was tested using the general gene model and a model trained using the remaining sequences in the sample. We found that the the proportion of sequences in a sample having greater probability with the model trained on the sample was much less than that found previously for the TE sets (cf. sensitivity values in table 1). The median was 25% for D. melanogaster, 37.5% for C. elegans and 20% for A. thaliana. This means that these random samples were not homogeneous in composition, and consequently, when an element was withdrawn from the set, the composition of this element differed more from the composition found by HMM after training using the remaining elements than from the general HMM.

This means that the fact that TE sequences display a high prediction sensitivity with the jackknife model is not attributable to an effect of the small size of the TE sets. Rather, it reinforces the fact that they are homogeneous in composition, and distinct from the other training sets.

Interspecific tests

To find out whether TEs of a given species can be used as a training set for the recognition of TEs of another species, we tested TE sequences using HMMs trained on TEs of other species. More specifically, for all 6 TE sets, we calculated the probabilities using the HMMs trained using TEs from the other 2 species and with the HMM trained using the host species' own genes (see Table 2). The model with the highest probability was usually the model trained using the genes of the same species (particularly in the case of A. thaliana: 87% of its TE sequences and C. elegans: 75%). This shows that each species has its own particular TE composition and that TEs do not share a common composition.

Table 2.

Interspecific tests. Predictions (as a %) of TE sequences for one species obtained using the host gene model of the same species versus the value found using the TE models of the other two species (counts are given in parentheses).

	host genes, same species	same TE class, another species	other TE class, another species
D. melanogaster	39% (28)	34% (24)	28% (19)
C. elegans	75% (15)	20% (4)	5% (1)
A. thaliana	87% (86)	9% (9)	4% (4)

Dinucleotide composition

We tried to make a better use of the composition information captured by the HMMs than the simple comparison of probabilities on whole sequences. However HMMs are bit unwieldy when it comes to comparing them in detail: our models have more than 200 independent parameters. Furthermore, the parameters linked to nucleotide composition (the emission probabilities of the HMMs) are conditional probabilities, not frequencies. Yet it is possible to recover some frequency information.

In our HMMs, each state is a Markov chain of order k. The parameters of this Markov chain are the conditional probabilities of observing a nucleotide given the k previous nucleotides. Using these parameters, we were able to calculate the non-conditional probabilities of observing k-letter words. For instance, with Markov chains of order 2, we were able to calculate the probabilities of dinucleotides in each state (see Methods). Given two HMMs, it was then possible to compare these dinucleotide probabilities and to identify the dinucleotides for which the probabilities were the most different (the most discriminating). Tables 3, 4 and 5 show the four most discriminating dinucleotides identified by pairwise comparisons of the three HMMs (class I TEs, class II TEs and host genes), for each HMM state and for each species.

Table 3.

Class I vs genes: The four most discriminating dinucleotides when comparing the HMM trained on class I TEs and the HMM trained on genes for each state of the HMM. E1, E2, E3 are the three coding states; I is the non-coding state. Log2 of the frequency ratio is given in parentheses. A value of +1 (resp. -1) thus indicates a twofold increase (resp. decrease) of the frequency in the TE model.

HMM state	A. thaliana
E1	CG (-0.79)	CC (-0.32)	AC (0.20)	TC (0.17)
E2	CA (0.28)	TA (0.26)	AC (0.17)	TC (-0.14)
E3	CG (-0.31)	GC (-0.30)	TC (-0.23)	CC (-0.18)
I	CG (2.23)	CC (1.76)	TT (-1.62)	TA (-1.35)
HMM state	C. elegans
E1	TG (-1.71)	CT (1.12)	CC (0.96)	AG (-0.85)
E2	GA (-1.66)	GG (-1.17)	TA (0.80)	TC (0.73)
E3	TA (1.03)	CC (0.90)	TT (-0.68)	AT (-0.67)
I	TT (-1.73)	CG (1.22)	TA (-0.87)	CC (0.87)
HMM state	D. melanogaster
E1	AG (0.89)	AA (0.87)	TA (0.66)	GG (-0.58)
E2	AG (0.59)	TG (0.38)	GA (-0.25)	GG (-0.24)
E3	TA (1.06)	CA (0.73)	GG (0.72)	TG (-0.68)
I	GG (-1.03)	GC (-0.56)	AA (0.55)	CG (-0.51)

Table 4.

Class II vs genes (cf. legend of table 3).

HMM state	A. thaliana
E1	CG (-0.75)	CT (-0.51)	CC (-0.48)	CA (-0.29)
E2	CT (-0.59)	TA (0.35)	TC (-0.28)	TG (0.27)
E3	TC (-0.72)	CC (-0.58)	CG (-0.48)	AT (0.38)
I	CC (-1.06)	CA (-0.48)	GC (-0.41)	GT (0.38)
HMM state	C. elegans
E1	GT (0.42)	GC (0.41)	CC (0.35)	TG (-0.35)
E2	CG (0.54)	TG (0.43)	AG (0.38)	TA (0.33)
E3	GG (0.67)	GC (0.57)	CG (0.38)	CA (-0.36)
I	AA (-0.26)	CG (0.22)	TC (0.15)	AC (0.13)
HMM state	D. melanogaster
E1	AA (1.59)	TA (1.32)	GG (-1.28)	AT (1.24)
E2	GG (-0.84)	TT (0.67)	AA (0.64)	CT (-0.62)
E3	TA (1.47)	CC (-1.34)	AA (1.28)	TT (1.01)
I	GC (-1.08)	CC (-1.00)	CG (-0.95)	TC (-0.76)

Table 5.

Class I vs Class II (cf. legend of table 3).

HMM state	A. thaliana
E1	CT (0.46)	CA (0.36)	AT (-0.28)	AC (0.22)
E2	CT (0.52)	TG (-0.30)	GA (-0.20)	AG (-0.16)
E3	TC (0.50)	CC (0.39)	AT (-0.24)	GG (-0.23)
I	CC (2.81)	CG (2.58)	TT (-1.94)	GC (1.56)
HMM state	C. elegans
E1	TG (-1.37)	CT (0.97)	GG (-0.91)	CG (-0.84)
E2	GA (-1.62)	GG (-0.95)	GT (-0.71)	TC (0.69)
E3	TA (1.01)	CC (0.73)	GT (-0.66)	AT (-0.58)
I	TT (-1.75)	CG (1.00)	GG (0.94)	CC (0.87)
HMM state	D. melanogaster
E1	TT (-1.28)	CC (0.91)	AA (-0.72)	AT (-0.70)
E2	TT (-0.76)	GC (0.69)	CT (0.65)	GG (0.60)
E3	CC (0.89)	AT (-0.82)	TT (-0.79)	GG (0.75)
I	CA (0.87)	AC (0.85)	TT (-0.79)	CC (0.78)

No clear trend in dinucleotide frequency was observed. The differences in base composition between TEs and genes seem to be host-specific, and more subtle than a simple disequilibrium in the frequency of a few dinucleotides. Indeed, certain dinucleotides that have special biological meaning in the context of TEs show no general marked frequency pattern. For instance, the dinucleotide CG is a potential methylation site for A. thaliana. Methylation plays an important role in the repression of gene transcription, and has been proposed as a possible mechanism for repressing TE activity in plants [9]. Here, we can see that CG representation varies considerably, and seems to be more specific to the host than to the TE class. In A. thaliana, CG dinucleotides are more frequent in the coding regions of genes than in the coding regions of class II TEs. The opposite is true in C. elegans, CG dinucleotides are more frequent in the coding regions of TEs, although there is no known CG methylation in C. elegans. In D. melanogaster, in which CG methylation is rare [10], the CG dinucleotide does not appear to be as discriminating as in the other two species.

TE copies

With the perspective of using HMM for detecting unknown TEs in sequenced genomes, we submitted a broader range of sequences to the HMMs. We searched the 3 genomes for copies of known TEs using a BLAST-based approach, using the program BLASTER with BLASTN as described in Quesneville et al. (2003) [11]. This yielded a set of sequences of various sizes. We added gene sequences from the annotation databases and "intergenic" sequences. The intergenic sequences were derived from the genomic sequence by removing the annotated genes and the TE sequences detected by BLASTER. The intergenic sequences were found to have a composition very similar to that of the intronic state of the gene HMM (data not shown), therefore no specific model was trained on these sequences.

We investigated the detection of TEs copies using HMM with the same technique as before and with the same 3 models (a gene model and 2 TE models). The sensitivity and specificity of TE detection was computed for each organism. The sensitivity was worse than with the full-length TE elements (40% for D melanogaster, 60% for A thaliana, 45% for C. elegans). Indeed, the BLAST approach identified many small fragments of TE that were not correctly distinguished by the HMMs, as there was too little material to work on. We repeated the calculations of sensitivity and specificity after removing all sequences shorter than a given threshold (see Figure 1). In D. melanogaster and A. thaliana, the sensitivity of the detection was much improved for sequences more than 500 bp in length: it rose from 40% to 70% in D. melanogaster and from 60% to 80% in A. thaliana. Most of the short test sequences were in fact TE fragments, and these were often wrongly predicted as "not TE" (false negatives), so that increasing the minimum length of the sequences tested eliminated these false negatives and improved the sensitivity. On the other hand, the specificity was less affected by the minimum size of the sequences; this is because most of the false positives were longer than the threshold value, and so eliminating the short sequences had little effect on the specificity. For C. elegans, the sensitivity of the class I TEs fell for sequences longer than 500 bp and for sequences longer than 1000 bp for class II TEs. It turns out this was because TE copies are much smaller in C. elegans than in the other two species. The number of sequences under analysis therefore fell rapidly as the minimum size increased. The longer sequences happen to originate from a couple of TE families that had been incorrectly classified, resulting in the observed decrease in sensitivity. Particularly, it appeared that all copies of the non-LTR retrotranposon RTE were mispredicted as class II elements. Other class I TE copies have however a better prediction rate: 70% of non-RTE class I sequences longer than 500 bp are correctly predicted.

Figure 1.

Specificity and sensitivity of sequence predictions with varying minimal length for: (a) Drosophila melanogaster TEs, (b) Arabidopsis thaliana TEs, (c) Cænorhabditis elegans TEs. The unbroken line indicates the sensitivity, the dotted line the specificity.

The size of 500 bp appears to be a reasonable threshold, yielding a good prediction quality without dismissing too many sequences.

Prediction of coding regions

We also used the trained models to analyze isolated TE sequences. Given a nucleotide sequence S, HMM is used to calculate the most likely sequence of hidden states, i.e. we determine the optimal path by the Viterbi algorithm. Since our HMMs include some states that represent coding regions, and other states that represent non-coding regions, the hidden state sequence divides the sequence into "coding state" regions and "non-coding state" regions, thus predicting which parts of the TE sequence under analysis have a coding-like composition. The HMM is trained on a set of unlabeled sequences (TEs of the same class). The prediction is then compared with the available CDS annotations. Unfortunately, few of the TEs in REPBASE UPDATE have such an annotation, but most of the elements in the BDGP set of Drosophila TEs do. The following results are therefore applicable only to Drosophila elements.

To assess the effectiveness of the prediction, we tested the approach on TE sequences of the BDGP set, using the jackknife technique, so that the sequence under test was never included as part of the training set. The quality of the prediction was measured by comparing the predicted coding regions with the annotation of the TE under test; we calculated the average sensitivity and specificity for coding sites for all TE sequences.

It turned out that the sensitivity of the coding site detection was good (> 95%) for both classes of TE (see Table 6). However, the specificity was around 50% for class I TEs, which means that nearly half of the non-coding sites were incorrectly predicted as coding. The HMM thus correctly identifies nearly all the coding sites, but also wrongly classifies a high proportion of non-coding sites as coding sites. This low specificity may be the result of unannotated ORFs, such as the short ORFs that have been characterized in several TE class I families [12]. An HMM with a different structure was also tried. This HMM had an additional "terminal" state to account for non-intronic, non-coding sites that are typically located at the beginning and end of the sequences (Figure 2b). This HMM yields more balanced predictions: the sensitivity is lower (75%), but the specificity is better (80%).

Table 6.

Quality of coding region prediction

	sensitivity	specificity
TE class II	97%	85%
TE class I	95%	51%
TE class I (alt. model)	75%	80%

Figure 2.

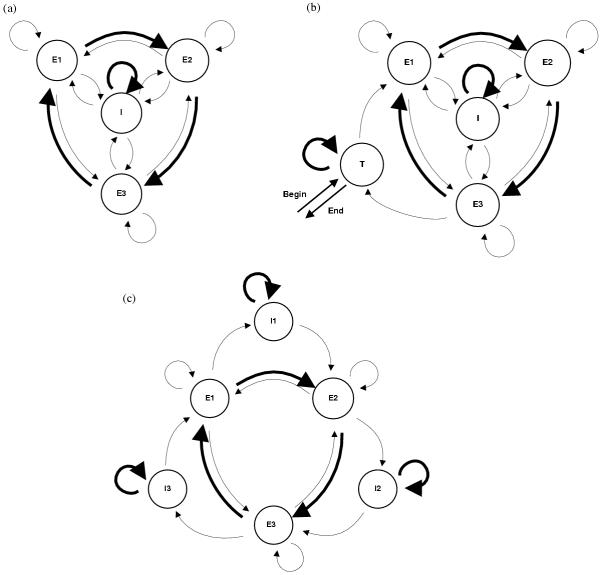
HMM structures. States are depicted by circles and transitions by arrows. The thickness of the arrows indicates the probability of the transition. The initial transition probabilities used for starting the estimation algorithm are 0.995 for thick arrows, the remaining 0.005 being equally divided between the thin arrows. Three different HMM structures were used. (a) 3 coding states, 1 non-coding state (b) 3 coding states, 2 non-coding states (intronic and non-intronic) (c) 3 coding states, 3 non-coding states. In (b) a path in the HMM starts and ends in the T state ; in (a) and (c) a path can begin and end in any state.

Discussion

Using HMMs as probabilistic models, we found that in the three species investigated, TEs differed markedly from genes in terms of base composition. The bias was not the same for the two TE classes. These models were able to distinguish between the three kinds of sequences with reasonable accuracy. The bias was also very host-specific, as shown by the dinucleotide compositions and interspecific tests: a TE was likely to have a composition more similar to that of its host's genes than to that of TEs of the same class occurring in other species.

Origin of the compositional bias

A couple of hypothesises can be made concerning the origin of the observed composition bias in TEs. It may be related to the molecular mechanisms involved in TE transposition which do not affect host genes. TEs are subject to DNA synthesis both during genome replication and during transposition. The transposition mechanisms make use of unusual DNA polymerases (such as reverse transcriptase or DNA repair polymerases) that are less efficient and less faithful than the DNA polymerases that replicates the chromosomes. Indeed, Strathern et al. [13,14] have shown that the DNA synthesis associated with the homologous repair of chromosomal double strand breaks is less faithful than replicative DNA synthesis in yeast. Several class II TEs (notably the P element family) make use of homologous DNA double strand break repair in their transposition process. Similarly, the reverse transcriptases involved in the transposition of class I TEs display unusual patterns of misincorporation [15]. Consequently, mutational bias due to DNA synthesis may be greater in TE sequences than in "regular" genes.

Selection may also account for this compositional difference. Indeed, TEs are mobile and so specific selection pressures may operate on their sequences. Selection may operate on the mobility of the element itself, or may reduce its impact on the host. For example, the CG dinucleotide may be a target for selection, because it plays a role in host-controlled TE repression in some species [9]. Additionally, it has been shown that some TEs have come from other species by horizontal transfer. This could explain the biased nucleotidic composition of some TEs.

TE detection

We envision two ways of using the trained HMMs for TE detection. The first approach is to build a composite HMM, integrating the three HMMs (genes, TE class I and TE class II). This integrated HMM can then "annotate" a sequence (like a genomic contig) by partitioning it into TEs, genes and intergenic regions. This will provide a rough annotation, identifying regions whose composition is similar to that of TEs. The limits of the region thus annotated will most probably be quite imprecise since the HMM is only concerned with the nucleotidic composition and is not using structural characteristics of TEs (target site duplication, inverted terminal repeats, long terminal repeats, etc.). So this method is to be used alongside other TE detection methods, as supplemental evidence for the presence of a TE.

Another approach is to use the HMMs to determine the best of the three models on a candidate sequence. That way, the HMMs can act as "filters", by post-processing the output of another TE detection program (such as one using a repeat-based method). This would alleviate the fact that the sensitivities of the HMMs are a bit low but that their specificity is good. It is difficult to alter these properties since they directly depend on the HMM parameters, which are estimated and cannot be easily modified. So, by combining the HMM prediction with a high-sensibility TE detection method, we could take advantage of the HMM's high specificity to select the most promising sequences.

As the HMM prediction is not based on sequence similarity, it could therefore detect new TE families, too divergent from known TEs to be found by homology-based methods. This relies on the fact that the composition bias detected by our HMM is homogeneous within TE classes: a new TE of the same class is expected to have a somehow similar composition. Applying the method on genomes with little information on their TEs may be problematic, though. Indeed, the method requires a reasonably large training set of TEs and TEs from other species cannot be used since we've shown that different genomes have distinct compositional bias for their TEs. Nevertheless, TEs from close species should be adequate. We tested this using TEs (in REPBASE) from Drosophilidæ other than D. melanogaster and we obtained predictions of a quality comparable to that obtained with melanogaster-only TEs (data not shown).

Finally, this method of detection has some bias. We've seen it is too unreliable for sequences shorter than 500 pb, so very fragmented TE copies would be missed. Inactive elements may also be difficult to detect: if the compositional bias is introduced by transposition processes, one would expect these elements to lose their distinct composition over time. However, inactive elements degradation seems to be caused primarily by accumulation of deletion than by punctual mutations [11,16,17]; consequently, old, inactive elements would not be detected because they become too short rather than because of a change in their composition.

TE annotation

The difference in nucleotide composition between host genes and TEs must be taken into account when trying to annotate the coding structures of TE sequences. Programs that use base composition to detect coding regions generally use a training set of gene sequences. These training sets do not capture the specific bias of TE sequences, and so these programs may perform poorly when predicting coding sequences within TEs. Moreover, TE copies in genomic sequences are often partially deleted. In such sequences, signals such as promoters, polyadenylation sites and splice sites may be missing. Moreover, frameshifts in coding reading frames must also be taken into account. Our simple HMM structure is very suitable for detecting the potential coding regions for these partial TEs.

Conclusions

We have shown that the difference in base composition between TEs and their host genes can be used to train specialized probabilistic models of sequences, notably HMMs. These structured models are able to reliably discriminate between TE class I, TE class II and host gene sequences. These models can thus be used in complement of other TE detection methods as additional evidence of the TE nature of a sequence or to sift through candidate sequences. Furthermore, the HMM can help analyze individual TE sequences by predicting the potential coding regions.

Methods

Biological sequences

We studied TE sequences and genes from three eukaryotic organisms: Drosophila melanogaster, Cænorhabditis elegans and Arabidopsis thaliana. The gene sequences were extracted from the raw sequence of assembled contigs or chromosomes, using gene annotation data. Table 7 indicates the sources of genomic sequences and annotations. The sequences of TEs for D. melanogaster were taken from the BDGP tranposon set [8]. For C. elegans and A. thaliana, the sequences of TEs were taken from REPBASE UPDATE version 7.8 [6,7], a database of sequences corresponding to repetitive DNA from various eukaryotic species. For the Repbase sets, we eliminated non-TE sequences (such as satellite DNA). When several sequences from the same family were present, we selected the longuest known copy. We also distinguished between class I TEs and class II TEs. See Table 8 for a summary of elements counts and sizes per set, and additional file 1 for a complete list of the TE sequences used. Intergenic sequences that are part of some tests were obtained by removing from the genomic sequence the annotated genes and the TE copies detected by BLASTER [11].

Table 7.

Sources of genomic sequences and annotations

Bdgp [22]	release 3
Tigr [23]	release ATH1
EnsEMBL/ Wormbase [24]	release WS85

Table 8.

Contents of TE training sets

		length (in bp)
	number of sequences	smallest	median	longest
D. melanogaster class I	56	2483	6411	10654
D. melanogaster class II	15	912	2167	4347
C. elegans class I	9	261	3259	4082
C. elegans class II	11	1242	5625	7227
A. thaliana class I	78	330	4496	10633
A. thaliana class II	19	265	4548	9233

Sequence analysis

Markov chains are simple models for modeling the base composition of sequences. The probability of a nucleotide occurring in position n is conditioned by the previous k nucleotides; k is called the order of the chain. For instance, the parameters of an order 1 Markov chain for a sequence S are: θ_{i, j} = P(S_n = i|S_n-1 = j) with i, j ∈ {A,C,G,T} A Markov chain thus has N^k+1parameters, where N is the number of letters of the alphabet considered (4 for DNA nucleotide sequences). The number of parameters increases rapidly with the order of the chain so, in practice, this order remains low. Estimation involves calculating the relative frequencies of k+1-letter words in a set of sequences (a training set), that is, the number of occurrences of the k+1 letter word divided by the number of occurrences of its k letter prefix. Thus, these parameters directly reflect the base composition of the training set: a Markov chain of order k models a sequence with a given composition in k+1 letter long nucleotides.

However, biological sequences, such as a gene or a TE, do not have a homogeneous base composition: the coding and non-coding parts have differing compositions. Hidden Markov models (HMMs) are more complex models that can take this heterogeneity into account. HMMs are used in many gene detection software (see, among many others [18,19]) ; ours are similar in spirit but with less features as we do not seek to detect gene-related signals (for instance splice sites), we're only interested in the base composition. HMMs can combine several Markov chains (called states of the HMM). Each Markov chain has its own set of parameters, reflecting the base composition for that state. This is a M1-Mk model [20]: the state sequence is an order 1 Markov chain and each state generates nucleotides according to an order k Markov chain. Given a sequence of states in the HMM (a path), the joint probability of the sequence S and the path is calculated as follows: is the probability of nucleotide S_i using the Markov chain parameters of state π_i(emission probability). reflects the probability of switching from state π_i to state π_i+1 (transition probability). Thus, the parameters of an HMM model with n states are: n² transition probabilities and n sets of Markov chain parameters. The overall probability of a sequence is the sum for all possible paths: . Introductory material concerning HMM can be found in [21].

Three different HMM structures were used in this study. The three structures consists of 3 states (one for each position in a codon, labeled E) for modeling coding parts of sequences and additional states for non-coding parts. A transition departing from a coding state can go to the next coding state (most probable), or to a non-coding state; it may also remain in the same state or revert to the preceding coding state, to account for frameshifts. For training on TE sequences, the HMM (see Figure 2a) has 4 states: the 3 coding states and a single non-coding state (labeled I). When predicting coding regions, an "alternate" model was trained on TE class I sequences; this model has 5 states: the 3 coding states, an "intronic" non-coding state and a "terminal" non-intronic non-coding state (labeled T) representing the parts at the beginning and end of the sequences. Finally, for training on gene sequences, the model was further refined: it has 3 coding states and 3 non-coding states so that the position in the current codon was conserved across non-coding parts (Figure 2c). This is desirable for gene sequences, because coding regions are interrupted by introns; this was not done for TE models because TE sequences may be non-functional, and so non-coding parts may not be actual introns.

In each state, the emission probabilities are given by plain Markov chains (of order 2 for TEs, and order 3 for genes). HMMs for TEs were trained with the Baum-Welch algorithm (see [21]), using TE sequences as unlabeled sequences. The Baum-Welch algorithm is a special case for HMMs of the expectation-maximization algorithm for parameter estimation. The starting point for the iterative Baum-Welch algorithm is an HMM with random emission probabilities, but fixed transition probabilities, yielding the structure shown in Figure 1. The training process estimates the emission probabilities and refines the transition probabilities, but the overall structure of the HMM is maintained. The training is repeated 10 times with different random starting points and the estimate with the highest probability is retained. The training for gene HMMs is straightforward: it doesn't need the Baum-Welch algorithm since the gene sequences are labeled by the genomic annotations.

The trained model is then used to calculate the probability of a given sequence; this probability is then compared with that of the same sequence, using other models with different parameters (obtained by estimations using other training sets).

The software used in this study is available upon request. It is written in the Objective Caml language and can be compiled on PCs running the GNU/Linux OS.

Prediction quality

To assess the quality of a prediction method, we calculate its sensitivity and specificity. The sensitivity is the proportion of true positives (TPs) amongst the subset of interest: true positives plus false negatives (FNs). Conversely, specificity is the proportion of true negatives (TNs) amongst the complement of the subset of interest: true negatives plus false positives (FPs). Thus a high sensitivity (resp. specificity) is indicative of a low proportion of false negatives (resp. false positives).

Calculation of dinucleotide frequencies

We considered an order-2 Markov chain with parameters (m_{i, j, k}) with i, j, k ∈ {A, C, G, T}. The probability of having dinucleotide ji in position n of sequence S is:

If the Markov chains are homogeneous, then we have:

P(S_n-1 = j, S_n-2 = k) = P(S_n = j, S_n-1 = k). If θ_i,j = P(S_n = i, S_n-1 = j), the previous equation can be written as: . This is a linear system of equations for θ_{i, j}. To have a system of independent equations, one equation is replaced by equation .

Resolution of this system yields θ_{i, j}, the expected frequency of dinucleotides under this Markov chain.

This method cannot be applied directly to the Markov chains describing coding sequences because the HMM cycles through the three Markov chains, changing at each position. Thus, the property used in the previous calculation that P(S_n-1 = j, S_n-2 = k) = P(S_n = j, S_n-1 = k) no longer holds. However, if we consider the three chains simultaneously, we still can solve the system: where are the dinucleotide probability (resp. Markov chain parameter) for exon state n. This is still a linear system of equations, but with 3 × 6 = 48 variables. Solving this system yields the expected frequencies of dinucleotides for each of the three positions in the codon.

List of abbreviations

TE transposable element

HMM hidden Markov model

Authors' contributions

OA wrote the software, carried some of the sequence analysis and drafted the manuscript. AF participated in the test of TE copies. DA and HQ conceived the study and participated in its design and coordination. All authors read and approved the final manuscript.

Supplementary Material

Additional File 1

This contains the list of TE sequences used in the training sets. The identifiers refer to sequences from the BDGP transposon set [8] and from REPBASE UPDATE [6,7].