Dynamics of Hydrophobic Core Phenylalanine Residues Probed by Solid-State Deuteron NMR

Abstract

We conducted a detailed investigation of the dynamics of two phenylalanine side chains in the hydrophobic core of the villin headpiece subdomain protein (HP36) in the hydrated powder state over the 298–80 K temperature range. Our main tools were static deuteron NMR measurements of longitudinal relaxation and line shapes supplemented with computational modeling. The temperature dependence of the relaxation times reveals the presence of two main mechanisms that can be attributed to the ring-flips, dominating at high temperatures, and small-angle fluctuations, dominating at low temperatures. The relaxation is non-exponential at all temperatures with the extent of non-exponentiality increasing from higher to lower temperatures. This behavior suggests a distribution of conformers with unique values of activation energies. The central values of the activation energies for the ring-flipping motions are among the smallest reported for aromatic residues in peptides and proteins and point to a very mobile hydrophobic core. The analysis of the widths of the distributions, in combination with the earlier results on the dynamics of flanking methyl groups (Vugmeyster et al., J. Phys. Chem. B 2013, 117, 6129–6137), suggests that the hydrophobic core undergoes slow concerted fluctuations. There is a pronounced effect of dehydration on the ring-flipping motions, which shifts the distribution toward more rigid conformers. The cross-over temperature between the regions of dominance of the small-angle fluctuations and ring-flips shifts from 195 K in the hydrated protein to 278 K in the dry one. This result points to the role of solvent in softening the core and highlights aromatic residues as markers of the protein dynamical transitions.

Introduction

The hydrophobic core of a protein plays an essential role in a variety of biological functions and in defining protein stability and folding.¹ It is known to be a very complex dynamical milieu with motions occurring on a variety of timescales from femtoseconds to seconds.² The most common types of groups studied in regards to the hydrophobic environment in proteins are methyl groups. The dynamics of these groups are known to be sensitive not only to local fluctuations but also to the overall hydrophobic core environment.^3–12 The assessment of the dynamics of aromatic side chains in a protein is relatively technically challenging, and much fewer studies are dedicated to these sites^13–23 compared with the investigations of protein methyl groups. Aromatic side chains comprise about 25% of the core volume on average and are often solvent-protected in the core by flanking methyl groups. The packing in the core is known to allow for a large extent of flexibility, even for the bulky aromatic groups of phenylalanines and tyrosines, which often participate in ring-flipping motions. The motions of these bulky groups likely require accommodations of the entire core and thus their characterization is very important for the detailed assessment of the overall free energy landscape of the core. The notion of concerted core fluctuations or “breathing” has been suggested since the 1970s and several works, such as those by Wagner et al.,^{22, 24} Hattori et al.,¹⁸ and Otting et al.,¹⁹ have characterized not only the activation enthalpy of ring-flipping motions but also the size of the cavity that has to be created in the core for ring-flipping motions to occur. A recent work by Kasinath et al.²³ detected a dynamical transition at elevated temperatures, at which aromatic side chains undergo rotations consistent with continuous diffusion that do not require the formation of a cavity.

Recent advances in solution NMR spectroscopy and isotopic labeling strategies allow for a more precise characterization of ring-flipping motions and encompass a wider range of timescales.^{13, 14} Solid state offers additional approaches for the characterization of motions in aromatic side chains on slow timescales due to the absence of overall molecular tumbling in the solid phase. In solution, overall molecular tumbling can often complicate the observation of motional modes on timescales close to or slower than those of the tumbling. Solid state also permits covering a much broader temperature range, thus, in principle, providing means for more thorough investigations of the energy landscape and its temperature dependence. Solid-state deuteron NMR techniques stand out as an important tool for the characterization of dynamics because deuteron NMR spectra and relaxation rates are usually dominated by one single-particle mechanism: the interaction of the nuclear electric quadrupole moment with the electric field gradient at the site of the nucleus. Available deuteron NMR techniques cover a very broad range of timescales, from pico- to milliseconds.²⁵ The relaxation measurements of Zeeman and quadrupolar order coherences are most sensitive to fast motions in the pico- to nanosecond range, while line shape experiments report on slower timescales. Static deuteron NMR line shape and relaxation measurements have been used since the early 1980s to characterize the motions of aromatic side chains in a variety of systems from crystalline amino acids^{26, 27} and amino acids bound to an enzyme¹⁷ to a multitude of polymer materials, as for example in the following works^28–30, to peptides^31–34, and, finally, to protein molecules.^{16, 26, 35} In particular, the work of Gall and Opella¹⁶ demonstrated that phenylalanine residues have a distribution of ring-flip rates. A recent work by Li et al.³⁶ utilized a magic-angle spinning deuterium NMR approach to compare the dynamics of phenylalanine residues in microcrystalline and surface-bound states. While in the microcrystalline state, only a single rotamer is populated and the dynamics are dominated by ring-flipping motions, rotameric transitions are observed in the bound state.

In this work, we investigate the dynamics of two hydrophobic core phenylalanine residues in the chicken villin headpiece subdomain protein (HP36). We utilize static solid-state deuteron NMR and probe a very wide temperature range from room temperature down to 80 K. The challenge of obtaining sufficient sensitivity for the relaxation measurements for the full-width powder pattern spectra is partially overcome by the employment of the multiple-echo acquisition (QCPMG) technique.³⁷ We then employ computational modeling to develop precise motional models consistent with the data over the entire temperature range. As a result, we characterize motional modes such as ring-flips and small-amplitude ring rotations and identify the cross-over temperature separating the regions of dominance of these two modes.

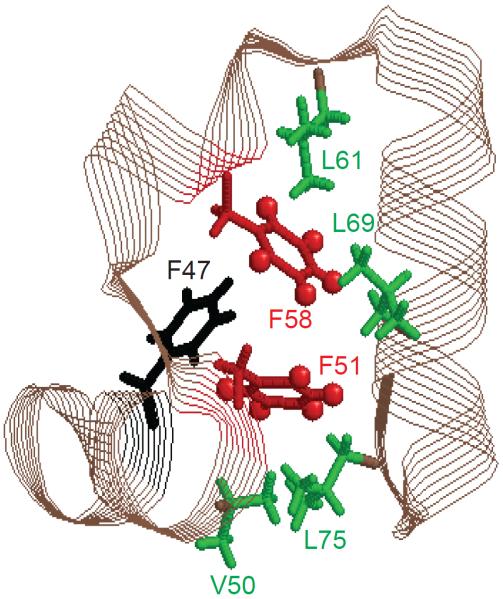
The hydrophobic core of the HP36 protein is spanned by three helices with three phenylalanine side chains, F47, F51, and F58, forming the basis of the core (Figure 1).^38–40 Several methyl groups flank the phenylalanine side chains and we have previously conducted detailed investigations of their dynamics.^41–46 Based on the deuteron longitudinal relaxation rates in the 300–60 K temperature range, the dynamics of the core, as probed at all of the methyl sites, is characterized by a distribution of sub-states with different values of the activation energies for methyl rotations.⁴² We hypothesized that the origin of these sub-states may be caused by concerted variations in core packing. If this is the case, the dynamics of the bulky aromatic groups should also reflect the presence of multiple sub-states. We show the sub-states are indeed observed for both small-amplitude ring rotations and large-angle ring-flip modes.

Figure 1.

Ribbon diagram of the HP36 protein with the key hydrophobic core side chains labeled. F51 and F58, investigated in this work, are shown in red.

Materials and Methods

Sample preparation and conditions

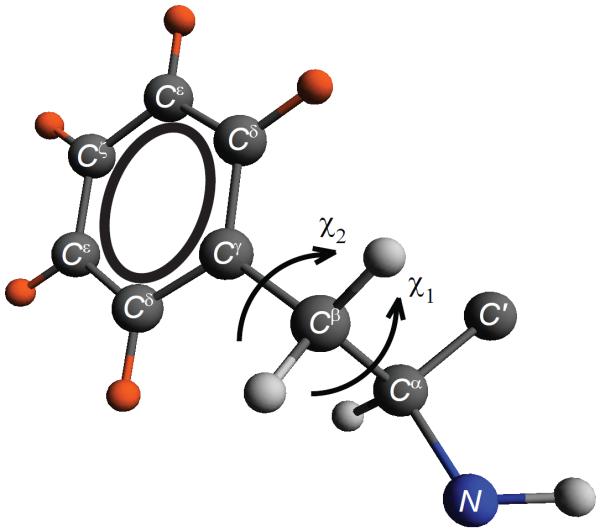
The two core phenylalanines probed in this study are F51 and F58 (Figure 1). In each of the protein samples, the deuteron labels have been incorporated into only one of the two phenylalanine side chains. Thus, the results are residue-specific. The labeling pattern (Figure 2) resulting from fluorenylmethyloxycarbonyl (FMOC)-Phenylalanine-ring-d₅ in the solid-state peptide synthesis corresponds to the deuterons incorporated in all five positions of the aromatic ring. The main sample conditions are hydrated powders with a water content of 40%, which is a typical amount of water for protein powder samples.^47–50 We confirmed the refolding procedure by measuring the ¹⁵N backbone chemical shifts of the three core phenylalanines and additional leucine residues^{45, 51} (Supporting Information SI1). An additional dry sample labeled at the F58 residue corresponds to lyophilized powder without the reintroduction of water.

Figure 2.

Phenylalanine side chain with deuteron labeling pattern marked in orange. Also shown are the torsional angles χ₁ and χ₂.

The protein was prepared using solid-state peptide synthesis (performed by Thermofisher Scientific Co, Rockford, IL) and FMOC-Phenylalanine-ring-d₅ was purchased from Cambridge Isotopes Laboratories (Andover, MA). The peptides were purified by reversed-phase HPLC and identity and purity was confirmed by mass spectroscopy and reversed-phase HPLC. Lyophilized powders were dissolved in water and the pH was adjusted to about 6 using NaOH/HCl. A hydrated state was achieved by exposing lyophilized powder to water vapor in a sealed chamber at 25°C until the water content reached saturating levels corresponding to about 40% by weight. The samples, in amounts of 20–25 mg, were packed in 5 mm NMR tubes (cut to 21 mm length) using teflon tape to center the sample volume in the coil.

Deuteron Solid-state NMR spectroscopy

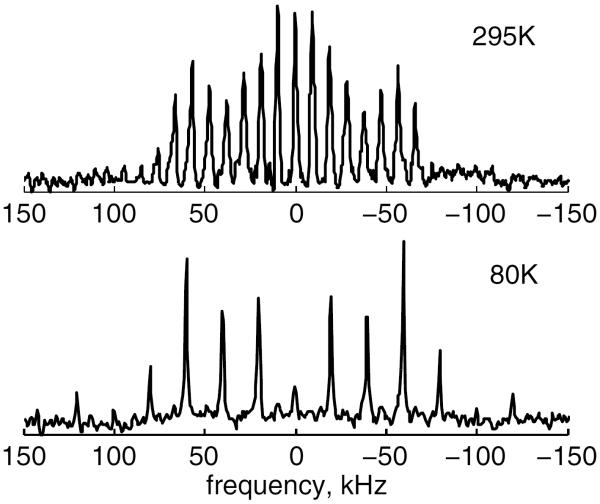
Experiments were performed at the 11.7 and 17.6 T magnetic fields. The 17.6 T WB750 Bruker spectrometer was equipped with AVANCE I electronics and a static probe operating in the range of temperatures between 145 and 380 K. The 11.7 T WB Varian Unity Plus spectrometer was equipped with a static cryogenic helium-cooled probe⁵² for temperatures below 150 K. T_1Z (Zeeman) measurements under static conditions were performed by the saturation recovery sequence. Due to the low sensitivity of the protein samples with dilute single-residue labels, an enhancement of the signal is necessary for the collection of accurate relaxation data. We made use of the multiple-echo acquisition scheme (QCPMG),³⁷ which is a static analog of magic-angle spinning. The scheme breaks a static powder pattern into a series of spikelets that follows the line shape (Figure 3).

Figure 3.

Experimental ²H QCPMG spectra for the hydrated HP36 protein labeled at the F58-ring-d₅ site; data are shown for 295 and 80 K.

Fifteen echoes were collected with 104 μs pulse spacing on the 17.6 T spectrometer and 50 μs on the 11.7 T spectrometer, corresponding to QCPMG spikelets (sidebands) spaced at 10 kHz and 20 kHz intervals, respectively. The number of echoes was optimized to avoid sample heating. The durations of 90° pulses were between 2.0 and 2.5 μs. Six to nine relaxation delays were collected. The number of scans varied greatly between 32 and 4096 depending on the signal to noise ratio in each sample and at each temperature as well as the precision of the data needed to define the non-exponential decays.

Room-temperature line shape measurements with the quadrupolar echo acquisition scheme were performed at 17.6 T with an eight-step phase cycle and a delay of 31 μs between 90° pulses. The number of scans varied between 40·1024 and 250·1024, which was determined by the amount of the sample and whether it was in the dry or hydrated state. The delay between the scans was set to at least 2.5 times the effective relaxation time at each temperature. We confirmed that this is sufficient to obtain non-distorted line shapes. For the echo-delay dependence of line shapes, echo delays between 21.5 and 56.5 μs were employed. For the line shape measurement of FMOC-Phenylalanine at 373 K, the inter-scan delay was set to 120 s and the number of scans to 2048. The spectra were processed with 1 kHz exponential line broadening.

On the 17.6 T spectrometer, temperature calibration was done by recording static lead nitrate line shapes⁵³ and using the freezing point of D₂O, 3.8°C, as the fixed point for the calibration. The cryogenic probe on the 11.7 T spectrometer had a temperature sensor in immediate proximity to the sample area. Its reading was taken as the sample temperature.

Simulations

I. Relaxation

The spin-lattice relaxation rate T₁ is given by^{7, 54}

$$\frac{1}{T_1}=\frac{C_q^2}{3}\left(J_1\right({\omega }_0)+4J_2(2{\omega }_0\left)\right)$$ (1)

where ω₀ is the Larmor frequency, J₁ and J₂ are spectral density functions, and C_q refers to the quadrupole coupling constant (units are Hz) in the absence of motion. J₁ and J₂ are dependent on the timescales and types of underlying motional processes as well as on the crystallite orientations. Spectral density functions can be obtained analytically for several simple models of motion.⁵⁵ However, a description of the processes with multiple motional modes and/or multiple conformers usually requires computer simulations.

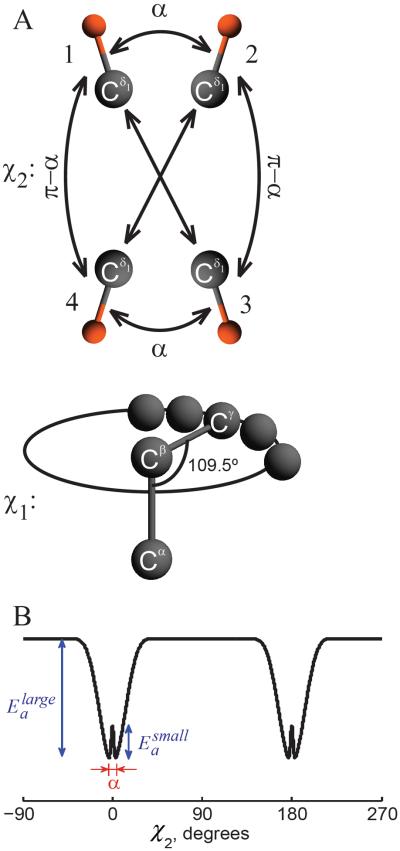
The model consistent with the relaxation data over the entire temperature range involves two modes of motions with rotations around the χ₂ dihedral angle of the phenylalanine side chain. We describe these rotational modes in the so-called strong collision limit, such that they correspond to jumps between four sites, schematically represented in Figure 4A. The large-angle flips occur between sites 1–3 and 1–4 with an equal probability; this also holds for the 2–3 and 2–4 pairs. The small-angle jumps with the amplitude α occur between sites 1–2 and 3–4. The change in the χ₂ angle for transitions 1–3 and 2–4 is exactly 180° due to the symmetry of the ring.

Figure 4.

A) Motional model for the fluctuations of the phenylalanine side chains. The motions around the χ₂ dihedral angle consist of large-angle ring-flips and small-angle fluctuations, parameterized by angle α. The diagram displays sites' connectivities according to the strong collision model, illustrated for one of the C^δ-D bonds. The motion around the χ₁ dihedral angle is modeled via the restricted diffusion of the C^β – C^γ axis along an arc and is approximated by small nearest neighbor jumps. B) Potential corresponding to the model of motions around the χ₂ angle, in which $E_a^{l\text{arg}e}$ and $E_a^{\mathit{small}}$ are the activation energies for the large-angle ring-flips and small-angle fluctuations, respectively.

The rotations around the χ₂ angle do not involve the ζ (para) deuteron. Thus, only the D^δ and D^ε deuterons participate in the jumps. We assume that the principal axis system of the quadrupolar tensor for each deuteron is aligned along the position of the C-D bond. In order to simulate the jumps between the four sites, one has to define the angle between the C-D bond and C^β – C^γ axis as well as the angles of rotation around the C^β – C^γ axis for each of the sites. The angle between the C-D bond and C^β – C^γ axis remains the same for all four exchange sites and, assuming an ideal ring geometry, equals 60° for the C^ε-D bonds and 120° for the C^δ-D bonds. In order to specify the angle of rotation around the C^β – C^γ axis (the χ₂ rotation), only one parameter is required because the rotation angles between sites 1–2 and 3–4 are equal and the transitions 1–3 and 2–4 are exactly 180°. For example, if we model small-angle jumps by the amplitude of α, this is the only parameter that needs to be specified.

The rate constants of transitions between the four positions are specified in the transition rate matrix:

$$\left(\begin{array}{cccc}\hfill -k^{\mathit{small}}-k^{\mathit{large}}\hfill & \hfill k^{\mathit{small}}\hfill & \hfill k^{\mathit{large}}∕2\hfill & \hfill k^{\mathit{large}}∕2\hfill \\ \hfill k^{\mathit{small}}\hfill & \hfill -k^{\mathit{small}}-k^{\mathit{large}}\hfill & \hfill k^{\mathit{large}}∕2\hfill & \hfill k^{\mathit{large}}∕2\hfill \\ \hfill k^{\mathit{large}}∕2\hfill & \hfill k^{\mathit{large}}∕2\hfill & \hfill -k^{\mathit{small}}-k^{\mathit{large}}\hfill & \hfill k^{\mathit{small}}\hfill \\ \hfill k^{\mathit{large}}∕2\hfill & \hfill k^{\mathit{large}}∕2\hfill & \hfill k^{\mathit{small}}\hfill & \hfill -k^{\mathit{small}}-k^{\mathit{large}}\hfill \end{array}\right),$$ (2)

where k^small is the small-angle jump rate and k^large / 2 is the rate for large-angle jumps. For example, if small-angle jumps have the amplitude of 5°, then k^large / 2 corresponds to the rate of jump from 0° to either 175 or 180°. The diagonal elements are chosen to satisfy the transition rate matrix conditions.

It is possible to derive analytical expressions for the correlation functions determining the spectral densities J₁ and J₂ of Eq. (1) for this model. The correlation functions of the fluctuations around the phenyl axis are defined by C_p,q (t) = 〈e^{−ipχ₂ (t)} e^{−iqχ₂ (0)}〉, where 〈 〉 stands for the ensemble average and p and q denote the components of Wigner matrices responsible for the transformations between the laboratory and deuteron principal axis systems. Note that with the transition 1–4 and 2–3 taken into account, the correlation function cannot be decomposed into the product of independent terms responsible for small- and large-angle fluctuations. For example, the term C_1,1(t) has the form

$$C_{1,1}\left(t\right)=C_{-1,-1}\left(t\right)=S^2{e}^{-2{k^{l\text{arg}e}}_t}+(1-S^2)e^{-(k^{l\text{arg}e}+2k^{\mathit{small}})t}$$ (3)

in which S = cos(α / 2) has the meaning of the order parameter for small-angle fluctuations. In the limit of timescale separation in which k^large <<k^small, the two motional modes become decoupled. The full analytical treatment of the model is presented in SI2.

The full model also includes a distribution of conformers distinguished by their values of the activation energies for both large- $E_a^{l\text{arg}e}$ and small-angle jumps $E_a^{\mathit{small}}$. The distribution arises due to heterogeneity of the free energy landscape of the hydrophobic core. A more detailed description of the distribution of the activation energies can be achieved by introducing a coupling term between the degrees of freedom describing the motion of the nuclei of interest and their changing molecular environment. As an example, a recently developed extension (MOMD) to slowly relaxing local structure (SRLS) approach may be considered as a possible framework for such a coupling.^{56, 57} The assumption of temperature independence of the distribution of the activation energies worked very well for our previous studies of methyl groups over the wide temperature range of 300–90 K,⁴³ suggesting that the conformational sub-states giving rise to the distribution do not change their structures substantially over the entire temperature range. As we will see in the “Results and Discussion” section, the assumption of temperature independence is also adequate for the description of the data on the phenylalanine residues. We also note that for a phenomenological application of the Arrhenius law, the linear term in the dependence of activation energy on temperature is equivalent to the rescaling of the pre-exponential factor and is, therefore, undetectable.

The temperature dependence of the rate constants for large- and small-angle jumps in each conformer is taken to be Arrhenius: $k(E_a^{l\text{arg}e},T)=k_0^{l\text{arg}e}{e}^{-E_a^{l\text{arg}e}∕T}$ and $k(E_a^{\mathit{small}},T)=k_0^{\mathit{small}}{e}^{-E_a^{\mathit{small}}∕T}$. The values of $k_0^{l\text{arg}e}$ and $k_0^{\mathit{small}}$ were assumed to be the same for all conformers.

As magnetization build-up curves depend on the rate constants, the distributions in the activation energies become the source of the non-exponentiality of the magnetization build-up. For the case of a continuous distribution of conformers, the overall observable magnetization M(t) is defined by

$$M\left(t\right)=\int \int m(E_a^{l\text{arg}e},E_a^{\mathit{small}},t)d{E}_a^{l\text{arg}e}d{E}_a^{\mathit{small}}$$ (4)

in which $m(E_a^{l\text{arg}e},E_a^{\mathit{small}},t)$ is the magnetization density. The magnetization density is proportional to the distribution functions for the activation energies.⁴³ A simple Gaussian form of the distribution was used for the large-angle jumps with the central values denoted by $\langle E_a^{l\text{arg}e}\rangle$ and the width of σ_{l arg e}, but an asymmetric gamma distribution was more appropriate for the small-angle jumps with the central value of $\langle E_a^{\mathit{small}}\rangle$ and the width of σ_small. They are related to the more conventional shape and rate parameters of the gamma distribution by ${\left(\langle E_a^{\mathit{small}}\rangle ∕{\sigma }_{\mathit{small}}\right)}^2$ and $\langle E_a^{\mathit{small}}\rangle ∕{\sigma }_{\mathit{small}}^2$, respectively. The longitudinal relaxation rate depends on the activation energies through the jump rate constants k^small and k^large / 2.

All simulations were performed using the EXPRESS program,⁵⁸ which allows for the incorporation of the QCPMG acquisition scheme. The value of the quadrupolar coupling constant C_q and asymmetry parameter η of the tensor were chosen based on the spectral data at the high and low temperature limits, which were consistent with the values of C_q = 180 kHz and η = 0. The continuous distribution was approximated by 21 conformers in the $E_a^{l\text{arg}e}$ dimension and 11 conformers in the $E_a^{\mathit{small}}$ dimension, analogous to the manner described previously for the methyl groups. The obtained M(t) profiles were fitted by the stretch-exponential function defined in Eq. (5) to yield simulated values of $T_1^{\mathit{eff}}$ and β. Thus, a library of simulated parameters $T_1^{\mathit{eff}}$ and β was created as a function of the small- and large-angle jump rates in order to fit the experimental data. The fitting was performed using χ² minimization.

II. Line shapes

An additional motional mode was required to simulate the line shape data. This mode involves motions in the plane perpendicular to the π-flips axis and corresponds to fluctuations of the χ₁ dihedral angle. The fluctuations were modeled as a restricted diffusion of the C^β – C^γ axis on an arc, with the arc length as a fitting parameter that signifies the extent of variations in the χ₁ angle. We thus approximate the actual potential restricting the dihedral angle fluctuations by flat potential (inside the arc) with rigid boundaries.

In EXPRESS, the introduction of this additional mode requires a two-frame simulation set-up, in which the rotations around the χ₂ angle are input in the first frame, which is nested inside the second frame defining the rotations around the χ₁ angle. This embedding is parameterized by two angles, one of which is the angle between the C^α – C^β and C^β – C^γ bonds and is defined by the tetrahedral geometry (fixed at 70.5°). The second angle defining the variations of χ₁ is specified by the azimuthal angle of rotations of the C^β – C^γ axis around the C^α – C^β axis. In this case, the average χ₂ angle has to be specified and we took it as 90°, which represents the most dominant rotameric configurations⁵⁹ and is also consistent with what is found from the structural coordinates (1YRF.pdf⁴⁰). The diffusion motion along the restricted arc was modeled by 5° degree steps. EXPRESS uses the following convention: k = 1/τ_c. Within this notation, the diffusion coefficient in rad²/s is given by D = k(5π /180)². The extent of variations in χ₁ and the diffusion constant were chosen by visual inspection of an array of simulated spectra. The array consisted of variations from 10° to 60° in 5° steps and variations in the diffusion constant from 80 to 1.5 × 10³ in nine steps on a logarithmic scale. Simulated line shapes were processed with 1 kHz exponential line broadening to match the experimental data processing and an additional 1.5 kHz Gaussian broadening in order to approximate the effect of homonuclear dipolar coupling on the line width.⁶⁰

When included in the relaxation simulations, the correction due to this mode is on the order of 1%. We also note that the motions around the χ₁ angle include contributions from all ring positions, including the D^ζ position. However, experimental line shapes at 295 K were collected with the relaxation delay on the order of 0.7–1.8 (2.5 times the apparent central T₁ values, as detailed in the Deuteron NMR spectroscopy section), which saturates all signals from the D^ζ deuterons and eliminates their contribution.

Results and Discussion

Longitudinal relaxation measurements over the 300–80 K temperature range

The main relaxation mechanism in phenylalanine rings is usually considered to be the symmetrical π-flips of the ring around the C^β – C^γ axis (Figure 4). We will see that our quantitative data over a very broad temperature range unveil many fine features of the landscape that complement the traditional view of phenylalanine ring-flips.

I. Non-exponentiality of magnetization build-up curves reports on the presence of multiple conformational sub-states

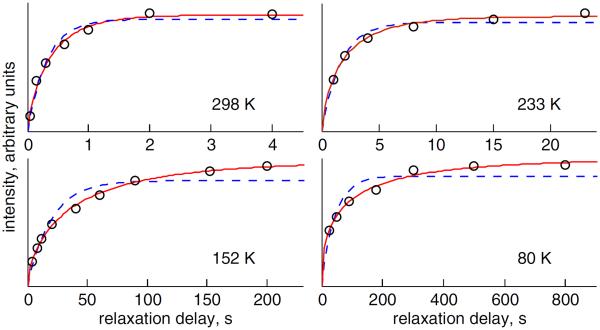
The saturation recovery build-up curves (Figure 5) reveal non-exponential behavior. The non-exponentiality of the magnetization build-up curves is evident starting at room temperature and its extent gradually increases at lower temperatures. For consistency, all data shown correspond to the spikelets at ±60 kHz, which are majors singularities at all temperatures except for the highest temperature of 295 K (Figure 3). There is no anisotropy in the data within the precision of the measurements. The data above 145 K were collected at 17.6 T and the data below 145 K were collected on a 11.6 T spectrometer equipped with a cryogenic helium-cooled probe.⁵²

Figure 5.

Longitudinal magnetization recovery curves at different temperatures are shown for the F58-ring-d₅ site in the hydrated state. Signal intensities (in arbitrary units) are plotted as a function of the relaxation delay. The fits of the experimental data (black circles) to the mono-exponential function are shown in blue dashed lines and the fits to the stretched exponential function are shown in red solid lines.

Analogous to glassy systems, the non-exponential build-up curves can be fitted to a stretched-exponential function of the form:^61–63

$$I\left(t\right)=I\left(\infty \right)\left(1-e^{-{(t∕T_1^{\mathit{eff}})}^{\beta }}\right)$$ (5)

in which I(t) is the signal intensity, $T_1^{\mathit{eff}}$ is the effective relaxation time, and β is the parameter that reflects the degree of non-exponentiality, 0 < β ≤ 1. β less than 1 corresponds to non-exponential behavior. In the absence of conformational exchange, this function can be viewed as an integral of ordinary mono-exponential relaxation functions over a distribution of the relaxation rates.⁶⁴

We have previously observed the non-exponentiality of the longitudinal relaxation for the hydrophobic core methyl groups. The relaxation data for these groups over 300–60 K temperature range were fitted using a model consisting of a distribution of conformers distinguished by different values of activation energies for methyl three-site jumps. The widths of the distribution were on the order of 1.5 kJ/mol for all four of the methyl residues probed. The existence of such distributions reflected multiple sub-states in the free energy landscape of the core and we hypothesized that these sub-states represent concerted core repacking. The observation of non-exponentiality in the relaxation for the core phenylalanine ring deuterons suggests the presence of multiple sub-states for these residues, which can likely be modeled using a distribution of activation energies for ring rotations. Combined with the methyl data, the presence of multiple sub-states for the bulky aromatic side chains strongly supports the hypothesis of concerted core repacking.

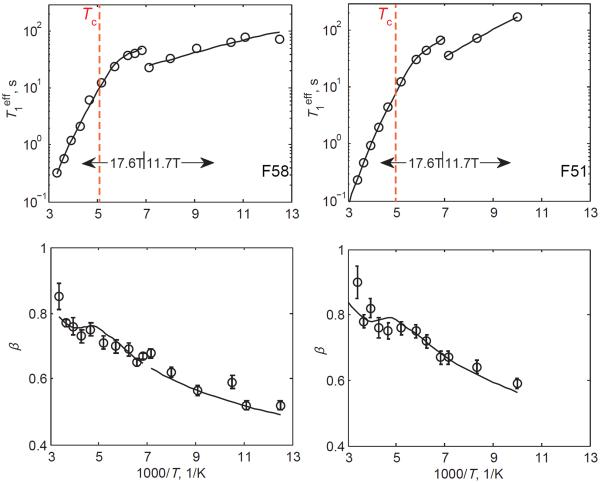
II. Temperature dependence of the relaxation profiles indicates the presence of two mechanisms

Plotting the values of the effective relaxation times $T_1^{\mathit{eff}}$ and β as a function of inverse temperature (Figure 6) reveals an interesting pattern: the values of $\ln T_1^{\mathit{eff}}$ increase in a roughly linear fashion between room temperature and 170 K and start to level out below about 165 K; the values of β decrease with a decrease in temperature. This pattern of the temperature dependence of relaxation times suggests two different mechanisms: one with strong temperature dependence that dominates at high temperatures and another one with much weaker temperature dependence that is dominant at low temperatures. The likely dominant mechanism at high temperatures, consistent with the steep temperature dependence of relaxation times, is the large-angle fluctuations of the ring, which are essentially the π-flips. The relaxation mechanism with weak temperature dependence likely corresponds to the small-angle fluctuations of phenyl rings, which are expected to be dominant at low temperatures when the π-flips are suppressed due to their high activation energy barriers.

Figure 6.

Plots of $T_1^{\mathit{eff}}$ vs. 1000/T on the semilog scale and β vs. 1000/T for hydrated samples with perdeuterated rings of F51 and F58. Experimental data (circles) are fit to the model (solid lines), which involves large- and small-angle fluctuations around the χ₂ angle, as described in the text and in Figure 3. The small-angle amplitude α=5°. The errors in $T_1^{\mathit{eff}}$ are within the size of the symbol. The red dotted vertical lines indicate the cross-over temperature T_c.

The decrease in the values of β upon lowering the temperature indicates that for both types of mechanisms the distribution in rate constants becomes wider as the temperature is lowered. We remind that the distribution in the rate constants is responsible for the non-exponential behavior and causes β to deviate from unity. As both processes appear thermally activated based on the temperature-dependent pattern of $T_1^{\mathit{eff}}$, the observed temperature dependence of β suggests distributions in the values of the activation energies for both mechanisms. This will be discussed in more detail in the following section.

III. Fitting the relaxation profiles to the two-mode motional model

We model both large- and small-angle fluctuations as changes in the χ₂ torsional angle (Figure 4). The symmetry of the ring implies that the crude picture of the phenylalanine ring potential should contain two minima of the χ₂ angle 180° apart, i.e. represent a double well potential. The large-angle fluctuations represent transitions between the wells and the small-angle fluctuations represent intra-well motions. However, the activation character of both types of fluctuations observed in the experiment means that the shape of the potential governing the ring dynamics is more complex than the traditional two minimum double well shape, as illustrated in Figure 4B. Inside each rather deep well, the potential display an additional more shallow double well structure. Such a potential is a cause of the two different rate constants, k^small and k^large.

The motion in this potential can, in principle, follow two different scenarios: i) the restricted diffusion case, in which the large-angle mode is coupled to the small-angle mode as described by Kramers' escape theory.⁶⁵ In this limit, both large- and small-angle fluctuations are described by a single diffusion constant. ii) The large-angle fluctuations occur in the strong collision limit and there are two independent rate constants of large- and small-angle fluctuations. The strong collision limit implies that large-angle jumps can occur from any angle position inside the first well into any angle position inside the second well.

The first scenario puts strong restrictions on the possible values of the diffusion constant, because one needs to accommodate the widely different activation energies of the two motions and describe the experimentally observed cross-over point between the dominance of the two regimes. In fact, we found that this scenario is incompatible with the experimental data and therefore concluded that the strong collision limit is most appropriate. Hattori et al.¹⁸ and Wagner²⁴ also suggested that large-angle ring-flips occur in the strong collision limit. Their analysis was based on the comparison of the calculated and experimental volumes of the cavity formed in the core in order for the ring-flipping motion to take place. We have previously shown that the leveling of relaxation times at low temperatures in methyl groups can be explained by small-angle intra-well fluctuations in the restricted diffusion limit.⁶⁶ The results of this work generalize this statement to either diffusion or strong collision limits.

We model the small-angle fluctuations as jumps between two discrete sites, and the strong collision limit for the large-angle fluctuations implies the following jump pattern: α ⇔ π, 0 ⇔ π, α + π ⇔ 0, α + π ⇔ α, where α is the angle of small amplitude fluctuations (Figure 4A). This pattern is reflected in the potential depicted in Figure 4B.

As discussed in the previous section, the non-exponentiality of the magnetization build-up curves is reflective of a distribution of conformers with different rate constants. The most logical description of this distribution within the concept of the energy landscape is to distinguish them by the different values of the activation energies. As elaborated in the Materials and Methods section, from a technical standpoint the simulations are accomplished in the two-dimensional activation energy space denoted by the variables $E_a^{l\text{arg}e}$ and $E_a^{\mathit{small}}$ (also defined in Figure 3B). The form of the distribution for the large-angle jumps is taken as Gaussian. However, for the small-angle jumps, we do not expect the average values of the activation energies to be much larger than the width of the distribution, and, therefore, we selected the gamma distribution, which excludes the negative values of the activation energies. The temperature dependence of β is driven by the temperature dependence of the width of the distribution of the rate constants, which are directly related to the width of the distributions in the activation energies by σ^large /T and σ^small /T. Thus, we see that for a fixed width of the distribution in the activation energy space, the distribution in the rate constants, in general, becomes wider as the temperature is lowered, which leads to a decrease in the values of β. This is consistent with the experimentally observed pattern. We note that the temperature dependence of β can become more complicated around the temperature of the cross-over between the two mechanisms, as discussed in SI3.

In the search for the value for the amplitude of the small-angle fluctuations, we fitted the data with small- angle jumps of α =5, 10, 20, 30, and 40°. The data are consistent with the small-angle values of 5 and 10°, but start to show discrepancies for larger values of α (SI4). The fitted parameters are weakly dependent on whether 5 or 10° are used and we, thus, use 5° as the lower limit of the small-angle jumps. The onset of the dominance of the small-angle fluctuation mechanism occurs when the temperature is lowered to 194 K for F58 and 200 K for F51. We defined the cross-over temperature between the two mechanisms (T_c) as the point at which the relaxation times corresponding to the large- and small-angle jump mechanisms are equal for the mean values of $\langle E_a^{l\text{arg}e}\rangle$ and $\langle E_a^{\mathit{small}}\rangle$ (SI3).

The comparison between the simulated and experimental relaxation anisotropies is one of the ways to validate the model. As indicated above, we did not observe any anisotropy within the precision of our measurements, which puts a constraint on the simulated anisotropy values to be below about 15%. We defined the relaxation anisotropy as the deviation of the relaxation times from $T_1^{\mathit{eff}}$ at the ±60 kHz spikelets. The simulated value of the anisotropy is in the range of 2–8% for low temperatures at which the small-angle jumps dominate and in the range of 5–15% for high temperatures dominated by the ring-flipping motions.

The fitted values of the activation energies (Table I) are in the range of 21–23 kJ/mol for large-angle jumps and 3–5 kJ/mol for small-angle jumps. For both modes, the widths are around 1.5–2 kJ/mol. It is interesting that these widths are very similar to what was found for the flanking methyl groups of V50, L61, L69, and L75, supporting the hypothesis of the concerted fluctuations in the core. The fitted values of the activation energies are comparable for the F58 and F51 rings, with the values for F51 being slightly higher. There is no evidence of conformational exchange between the sub-states with different activation energy values for phenylalanine dynamics. Fast conformational exchange would average out the differential T₁ contribution of the multiple conformers and render the magnetization build-up mono-exponential. At the opposite limit, at which the rate constant of the conformational exchange is much less than $T_1^{\mathit{eff}}$, the distribution appears to be static. We thus conclude that any possible conformational exchange processes between the sub-states at the phenylalanine sites should be slower than about 1.5 s at room temperature. This number is about 5 times larger than that estimated for some of the flanking methyl groups.

Table 1.

Fitted parameters characterizing the large- (175 ° and 180°) and small-angle (5°) fluctuations in the perdeuterated phenylalanine rings of the HP36 protein in the hydrated and dry powder states.

Residue/conditions	ln $k_0^{l\text{arg}e}$, s−1	$\langle E_a^{l\text{arg}e}\rangle$, kJ/mol	σlarge, kJ/mol	ln $k_0^{\mathit{small}}$,s1	$\langle E_a^{\mathit{small}}\rangle$, kJ/mol	σsmall, kJ/mol
F51 hydrated	25.4±1.5	23.9±3.1	1.9±0.4	19.6±0.9	5.2±1.0	1.4±0.3
F58 hydrated	23.9±1.7	20.8±3.5	2.0±0.4	18.0±0.7	3.25±0.6	1.8±0.4
F58 dry	29.0±2.5	36.5±4.0	3.0±0.5	21.4±0.7	6.9±1.2	1.8±0.3

Note that similar motional modes have been observed for phenylene rings of glassy polymers such as bisphenol-A polycarbonate and bisphenol-A polysulfones as probed by neutron scattering studies.^{67, 68} The dynamics was described by the two main modes of ring-flips and relatively small-angle over-damped oscillations, with individual distributions of activation energy barriers for each mode. This underscores a fundamental similarity between proteins and polymers. However, one would expect marked differences in the parameters, especially in the characteristic widths of the distributions, as the hydrophobic core is expected to have a higher degree of order. Indeed, the widths of the distributions in the polymers are on the order of 10 kJ/mol for both the oscillations and the flips, which is several times larger than in the protein. In addition, the oscillations are of much higher amplitude from 30 to 50°, as opposed to 5–10° in the protein. Also, the experimental results^61,62 suggested that $k_o^{l\text{arg}e}=k_o^{\mathit{small}}$, which is in favor of the diffusion origin of the ring-flipping motion in polymers, contrary to our results on the protein, for which a strong collision scenario related to the concerted changes of the hydrophobic core environment is more likely.

In our model (Figure 3), we suggest that both small- and large-angle jumps occur around the same dihedral angle χ₂, as this is the simplest assumption. Small-angle jumps are not subject to strong suppression by steric interactions as large-angle jumps are. Therefore, there is no a priori reason to limit small-angle motions to rotations around the phenyl axis. Small-angle jumps will contribute comparably to the relaxation process independent of their exact geometry with a caveat that for motions that involve a change in the direction of the C^β – C^γ axis, the D^ζ deuteron will contribute to the relaxation on the same timescale as the other phenyl ring deuterons.

A wide range of values between 27 and 155 kJ/mol has been reported in the literature for the activation energies of the ring-flipping motions of tyrosine and phenylalanine in peptides and proteins.^{18–22, 32–34} This wide range indicates that the ring-flipping motion is highly dependent on the environment. For example, an insightful investigation by Bajaj et al.³² compared two structurally similar peptides that display very different ring-flipping rates attributed to differences in packing. Our central values of 21–23 kJ/mol are at the lowest end of this range and indicate a relatively flexible environment in the hydrophobic core of HP36.

IV. Line shapes report on additional fluctuations around the χ₁ angle

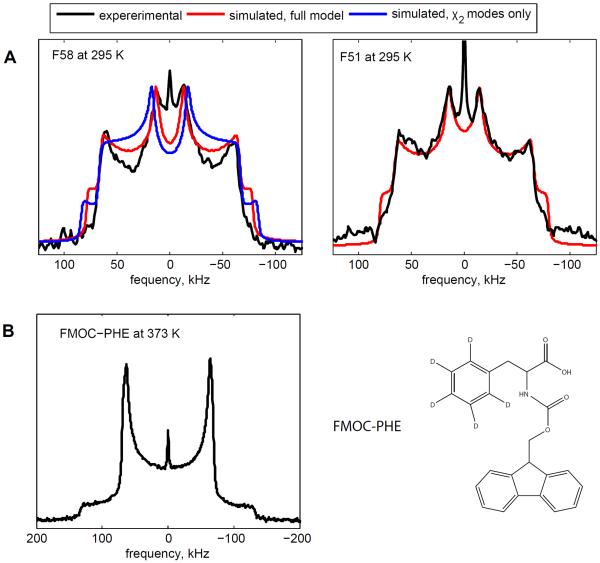
Experimental quadrupolar echo line shapes provide an additional independent test of the validity of the motional model and can point to aspects that need further refinement. The quadrupole echo acquisition scheme with one echo is better for this purpose compared with the multiple-echo detection, as it provides more detailed information. Due to the low signal-to-noise ratio and increasingly large relaxation delays at low temperatures, reliable experimental line shapes were collected only at 295 K (Figure 7). The experimental line shapes display two types of singularities: the inner ones originating from the perpendicular edges (horns) of the flip-averaged deuteron tensors and outer ones due to the perpendicular edges of the static tensors.

Figure 7.

A) Experimental deuteron NMR line shapes (black) acquired with the quadrupolar echo acquisition scheme at 295 K are overlaid with the simulated line shapes. The red lines correspond to the full motional model with fluctuations around both the χ₁ and the χ₂ angles and about 1° deviations from the ideal ring geometry, as discussed in the text. The blue line, shown for the F58 residue, was simulated using only the modes of motions around the χ₂ angle (both the large-angle flips and the small-angle fluctuations) with the parameters fixed from the relaxation data. An ideal ring geometry of 60° was used in this case. The narrow peak at the center of the spectra is the signal from HOD. B) Line shape spectrum for the FMOC-Phe-ring-d₅ amino acid at 373 K and its chemical structure.

When we compare the experimental line shapes with the model developed based on the relaxation data (shown in Figure 7A by the blue line for F58), we obtain good agreement in the overall pattern. The agreement in the relative heights of the inner and outer singularities indicates that the overall distribution of ring-flip rates is captured well in this model. Note that the peak at zero frequency corresponds to the residual HOD signal. However, two features in the experimental line shapes require further refinements of the model: i) the positions of the inner horn relative to the outer horns are narrowed in the experimental spectrum compared with the simulated one and ii) the depth of the valleys between the inner and outer singularities is more pronounced in the experimental spectrum compared with the simulated one.

To address the first feature, we note that the agreement with the experimental line shape cannot be achieved by the introduction of any additional motion of the ring axis, as this would lead to an overall narrowing of the powder pattern. Two possible explanations can selectively narrow the position of the inner horns. The first one involves the adjustment of the intrinsic asymmetry parameter. An alternative explanation is a slight deviation from the ideal ring geometry. Several sets of tensor parameters have been reported for crystalline phenylalanine amino acid. For example, Gall et al.²⁶ and Kinsey et al.⁶⁹ reported C_q of 180 kHz and η = 0.05 based on line shape data at 100 K and 298 K, respectively. Alternatively, Hiyama et al.²⁷ reported C_q = 171 kHz and η < 0.02 in conjunction with deviations from the ideal ring geometry based on the spectral data in the range of 293–421 K. Our experimental quadrupole echo data for both residues at 295 K can be fitted equally well with either C_q = 180 kHz, η = 0 and about 1° difference from the ideal ring geometry or with about 170 kHz, η = 0.06 – 0.07 and the ideal ring geometry. To distinguish between these two possibilities, we turn to our low temperature spectra, which were collected with the QCPMG acquisition scheme. While the spectra are not sensitive to the range of η between 0 and 0.07, they point toward a value of the quadrupolar coupling constant of 180 kHz as opposed to 170 kHz (SI5). We, thus, keep the following final parameters: C_q = 180 kHz, η = 0 and the angles between either the C^δ–D or C^ε–D bonds and the C^β – C^γ axis of 58.5° for F58 and 59° for F51. As can be seen from Figure 7A, the relative positions of the inner and outer horns agree well in the experimental and simulated spectra, as shown by the red line.

The second discrepancy between the simulations and experiment, namely the depth of the valleys between the inner and outer singularities, suggests additional asymmetric motions on the timescale of the quadrupolar coupling constant. When we include an additional motional mode corresponding to restricted diffusion around the axis perpendicular to the direction of the flips, the quality of the fit is significantly improved (Figure 7A, red line). This motional mode corresponds to restricted rotations around the χ₁ angle and represents the fluctuations of this angle within the rotameric well. It has been modeled as the diffusion of the C^β – C^γ axis along a restricted arc (Figure 4A). The best-fit parameter for the length of the arc, representing the variations in χ₁, is 30° and the diffusion rate is 760 rad²/s for both residues. The amplitude of 30° requires either relatively low packing density or the overall flexibility of the core to accommodate these motions. Thus, this result supports the conclusion obtained on the basis of the relaxation data, which pointed toward a relatively flexible core based on the values of the activation energies for the ring-flipping motion. However, the core environment is not so unconstrained as to allow for large-amplitude jumps of the ring axes, such as rotameric transitions that do not reproduce the experimental line shape data. This is consistent with the recent studies by Li et al.,³⁶ which showed that rotameric transition does not exist in a free (i.e., non-surface bound) peptide.

We also looked at the dependence of the line shapes on the inter-pulse delay τ in the quadrupolar echo experiment $({90}_x^0-\tau -{90}_y^0)$. As noted by Schadt et al.,⁷⁰ the dependence of the line shapes on this delay enables us to validate the width of the distribution of the conformers with different ring-flip rates. If the distribution in the rate constants is wider than two decades, then the corresponding line shapes are no longer dependent on the value of τ. In contrast, our relatively narrow width of the distribution preserves the dependence on τ. Experimental and simulated line shapes as a function of τ delays are presented in SI6 and they demonstrate good agreement. Further validation of the model for the description of the line-shapes could be obtained by magic-angle spinning experiments at lower temperatures.

It is also interesting to compare the dynamics of the phenyl rings in the protein core with the behavior of the ring in the FMOC-Phenylalnine amino-acid. The bulky hydrophobic FMOC group creates hydrophobic contacts for packing yet lacks the complexity of the core. The line shapes of FMOC-Phe are completely rigid, even at 373 K (Figure 7B). This result underscores that the environment of the protein core can allow for much more enhanced dynamics compared with general hydrophobic-type packing.

V. Hydration dependence of the dynamics and manifestation of the protein dynamical transition

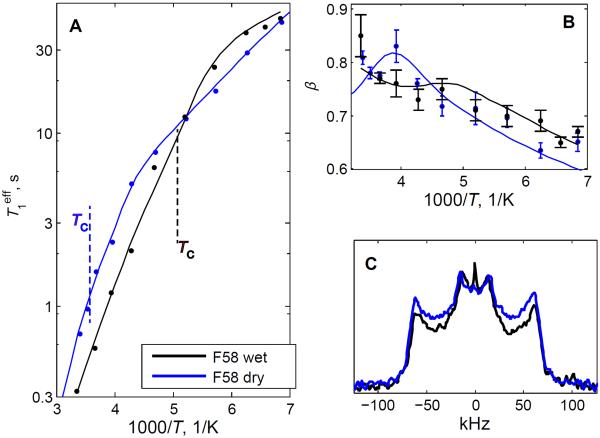
To assess how the motions depend on hydration, we compared both the relaxation and the line shape data for the side chain of F58 in the hydrated and dry powder states. For the dry sample, the data were obtained only at one field of 17.6 T in the 295–145 K range (Figure 8A). The value of $T_1^{\mathit{eff}}$ is about 2.5 higher at room temperature for the dry protein and the fitted value of the activation energy for the ring-flip motions is also significantly larger in the dry sample, with an increase of about 15 kJ/mol (Table I). The value of 15 kJ/mol can be viewed as the magnitude of change in the local potential of the hydrophobic core environment induced by dehydration. Small-amplitude fluctuations in the dry protein take place under this modified environment and the activation energy for these fluctuations is somewhat different (by 3.6 kJ/mol) but well within the 15 kJ/mol magnitude. It is also important that the widths of the distributions in the activation energies are of the same order of magnitude for both the π-flips and the small-angle fluctuations (2–3 kJ/mol), reinforcing the notion that the energy landscape of the small-angle fluctuations adjusts to changes in the overall potential caused by dehydration.

Figure 8.

Relaxation and line shape data for the F58-ring-d₅ site in the hydrated (black lines) and dry (blue lines) powder states. A) Plots of $T_1^{\mathit{eff}}$ vs. 1000/T on the semilog scale. The errors are within the size of the symbol. The dotted lines indicate the cross-over temperatures T_c. B) β vs. 1000/T. The data are shown for the temperature range between 295 to 145 K and the magnetic field strength of 17.6 T. C) quadrupolar echo line shapes at 295 K. The spectra are scaled to yield identical heights of the inner singularities (horns).

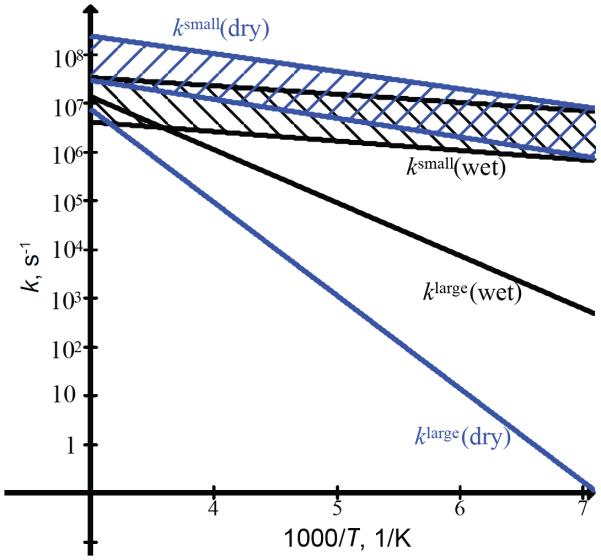
The effect of dehydration on the rate constants themselves is shown in Figure 9 for the entire temperature range, using the parameters listed in Table 1. Note that for the small-angle fluctuations the rate constant k^small obtained from the fits is strongly influenced by the uncertainty in the value of angle α. The bands in Figure 9 represent the uncertainties in k^small when α is taken in the range of 4–11°. While a pronounced effect of dehydration is observed for the ring-flipping motion, the rate constants for small-angle fluctuations are similar for dry and wet proteins within the uncertainties. Looking at the relative intensities of singularities in the line shape data at 295 K (Figure 8C), it is also evident that the distribution of the conformers is shifted toward slower ring-flip rates in the dry sample. The line shape data are not sensitive to small-angle fluctuations.

Figure 9.

Rate constants k^large and k^small over the temperature range of 295–145 K for the F58-ring-d₅ site in the hydrated (black) and dry (blue) states. The hatch bands in between the dotted lines represent the limits of uncertainties in k^small introduced by uncertainty in α in the 4–11° range.

Another interesting feature in the comparison between the relaxation behavior of the dry and wet proteins is that the cross-over from the dominance of the small-angle fluctuations to the ring-flipping motions occurs at a much higher temperature for the dry sample. The estimated temperature of the cross-over is around 278 K for the dry protein compared with about 194 K for the wet protein (SI3). We also note that due to the larger differences in the values of $\langle E_a^{l\text{arg}e}\rangle$ and $\langle E_a^{\mathit{small}}\rangle$ in the dry protein, the non-monotonous temperature dependence of β is expected to be more pronounced around the cross-over temperature.

Dynamical transitions in proteins are characterized by the onset of large-scale motions upon heating from cryogenic temperatures.⁷¹ They remain a topic of very active investigations by means of neutron scattering, NMR spectroscopy, and other techniques.^{5, 71–77} Notably, the cross-over point between the small-amplitude fluctuations and ring-flipping motions in the hydrated HP36 protein is close to the temperature of the dynamical transition for the backbone dynamic mode recently studied by Kämpf et al.⁷² by deuterium NMR relaxation and molecular dynamics simulations. Their work also pointed to the importance of the role of the hydration shell in inducing these motions. In addition, Lewandowski et al.⁷⁵ recently proposed a hierarchical model of protein dynamics that also emphasizes the importance of the hydration shell for inducing backbone and side chain motion with activation energies above 20 kJ/mol. Interestingly, the temperature of onset for these motions reported for the hydrated microcrystalline GB1 protein is 195 K, which coincides with the cross-over temperature for HP36 in the hydrated state.

In contrast to the present results on phenylalanine side chains, our previous investigation of the effect of hydration on the relaxation behavior of a core methyl-bearing side chain of L69 showed identical results for dry and hydrated proteins.⁴² Thus, our data suggest that the ring-flipping motions in aromatic residues is hydration-dependent, whereas the three-site jumps of methyl groups do not depend on hydration.

For the ring-flipping motion to occur, the hydrophobic core has to be able to adjust to the instantaneous rotational state of the ring in order to release steric hindrance, which otherwise precludes the motions of the bulky ring.^{78, 79} Hydration likely aids in rendering the core softer, resulting in more efficient adjustments of the environment. This implies propagation of the hydration effect from the protein surface into the hydrophobic core.^{80, 81} Fast three-site methyl jumps do not require large adjustments in the core due to much smaller size of the methyl groups compared to the aromatic groups, which can be the reason for their hydration-independent behavior. However, the motions of the methyl axes, which involve large-angle rotameric rearrangements, are dependent on hydration.⁴⁴ In analogy with the ring-flipping motion, large-angle rearrangements of the entire methyl-bearing side-chain of leucine would involve releasing the steric hindrance of neighboring atoms. On the other hand, the existence of the distributions of activation energies with similar widths for both the methyl jumps and phenyl flips implies additional slow concerted core fluctuations (slower than the ring-flipping motion) that give rise to these distributions. Molecular dynamics simulations in the solid-state are necessary to obtain further molecular insights into all these different motional modes inside the core and the extent of correlations among them. Results on phenylalanine side-chains presented in this work demonstrate that aromatic residues can be important markers of protein dynamical transitions.

Conclusion

This work presents one of the most detailed quantitative characterizations of aromatic side chain motions in the solid state. The side chains of F58 and F51 participate in two main motional modes, with ring-flips dominating at high temperatures and small-angle jumps dominating at low temperatures. The ring-flipping motion occurs in the strong collision limit as opposed to restricted diffusion. The onset of the dominance of the small-angle jump mechanism occurs at about 200–195 K in the hydrated protein and shifts to a much higher temperature of about 280 K in the dry protein. The cross-over point between the small-amplitude fluctuations and ring-flipping motions in the hydrated HP36 protein is close to the temperature of the dynamical transition temperature reported for the high activation energy motional modes of side chains and backbones in other proteins. The 80 K change in the onset of ring-flipping motions between the hydrated and dry proteins points to the role of solvent in softening the core and emphasizes the role of aromatic residues as useful markers of protein dynamical transitions.

The observed non-exponentiality of the magnetization build-up curves has led to the model involving the distributions of conformers distinguished by their values of activation energies for the ring-flips and small-angle fluctuations. The central values of the distributions are similar for the two residues and fall in the ranges of 21–23 kJ/mol and 3–5 kJ/mol for the ring-flips and small-angle jumps, respectively. These activation energies for the ring-flipping motion are among the smallest reported for phenylalanine and tyrosine side chains in peptides and proteins and indicate a relatively flexible core. Dehydration of the protein leads to the shift of the distribution toward a lot more rigid conformers for the ring-flipping motion, manifesting in a 15 kJ/mol increase in the central value of the activation energy. The line shape data at 295 K suggest the presence of one dominant rotameric configuration of the side chains without any rotameric inter-conversions on μs-ms timescales. The widths of the rotameric well for the χ₁ angle are about 30° for both residues, also supporting the notion of a relatively flexible core environment in the hydrated protein.

This study complements our previous investigations of the dynamics of hydrophobic core methyl groups. The combined analysis of aromatic and methyl sites allows for a very thorough view of the free energy landscape in the hydrophobic core. Within our model, the heterogeneity of the local free energy landscape is characterized by the widths of the distribution of the activation energies. These widths are on the order of 1.5–2 kJ/mol for both modes of motions in the phenylalanine residues as well as for the methyl rotational jumps. The presence of the distributions at multiple sites strongly suggests the existence of slow motional modes common to the entire core. The presented experimental results set the stage for molecular dynamic simulations in the solid state and at low temperatures, which can elucidate the structural details of the conformational sub-states that give rise to the distributions.