Estimating time to the most recent common ancestor (TMRCA): comparison and application of eight methods

Abstract

Investigating how an ancestral population diverges to give rise to distinct subpopulations remains a fundamental pursuit in population genetics. There is broad consensus for the ‘Out-of-Africa' hypothesis that states that modern humans arose ∼200 000 years ago in Africa and spread throughout the continent ∼100 000 years ago. This was followed by several waves of major population dispersals across the globe, although the exact nature of the population divergence remains debatable. Existing methods to estimate population divergence time differ in their methodological frameworks and demographic assumptions, and require different types of genetic data as input. These fundamental differences often result in the methods producing inconsistent estimates of the population divergence time, further confounding attempts to robustly uncover the history of human migration, especially when most population genetic studies do not employ multiple methods to estimate the time to the most recent common ancestor (TMRCA). Here, we chose eight popular methods for estimating TMRCA and evaluated their robustness and accuracy in correctly identifying the true TMRCA through a series of simulations that mimicked different evolutionary scenarios. We subsequently applied all eight methods to estimate the population divergence time between Southeast Asian Malays and South Asian Indians using deep whole-genome sequencing data.

Introduction

Population divergence is the process where populations of the same ancestry accumulate genetic mutations independently over a period of time, producing sufficient genetic distinction between these populations as a result of an extended period of reproductive isolation. The inference of the divergence time between populations has been of fundamental interest in the study of population evolution. Although there is a general consensus around the origin and expansion of modern humans in Africa, dated respectively at ∼200 000 and 100 000 years ago, there have been several conflicting theories on the exact nature of modern human dispersal across the globe.^{1, 2} The availability of genome-wide data by technologies ranging from genotyping to next-generation sequencing provides the unprecedented opportunity to study the demographic changes and migration patterns of modern humans shaped by the environment and subsequent evolutionary process of genetic drift and natural selection.^{3, 4} Valuable new insights have been derived from large complete genome sequencing surveys of populations in Africa,^{5, 6} Asia,^{7, 8} Europe,⁹ and the Americas.¹⁰

Many of the existing population genetics inference and methodologies have been built on the foundation of the coalescent theory,^{11, 12, 13} although these can be generally classified according to the type of genetic data used as input and the assumptions about population demography (Table 1). For example, one class of methods for estimating the time to the most recent common ancestor (TMRCA) considers multiple neutral loci each of ∼1000 bases only in multiple populations, such as MIMAR^{14, 15} and GPho-CS.¹⁶ Another class of methods infers the TMRCA from full chromosomal information, such as CoalHMM,¹⁷ PSMC,¹⁸ and MSMC.¹⁹ The third class of methods essentially infers the TMRCA on the extent of linkage disequilibrium (LD), population diversity measured by the F_ST parameter and population allele frequency, such as the approaches by Hayes and colleagues (abbreviated subsequently as T-LD),^{20, 21} by McEvoy and colleagues (abbreviated subsequently as T-FST),²² and DADI.²³ These methods differ by the type of input data required (sequence-level information or summary statistics), and by the assumption around the presence of genetic recombination during migration.²³

Table 1. Comparison of TMRCA methods.

Name	Methodology	Input classification	Input information	TMRCA	Demographic model
T-LD	Statistical estimator from LD	Summary statistics of alignments scalable to genomic size	LD of variants with genetic distance within 0.005–0.1 cM	Point estimation	Isolation–migration model
T-FST	Statistical estimator from FST and LD	Summary statistics of alignments scalable to genomic size	LD of variants with genetic distance within 0.005–0.1 cM SNP-wise FST of the two populations	Point estimation	Isolation–migration model
MIMAR	MCMC	Summary statistics at multiple neutral loci of size ~1000 bp	The summary statistics at each locus: the numbers of polymorphisms unique to the samples from populations 1 and 2; the number of shared alleles between the two samples and the number of fixed alleles in either sample	Posterior distribution mean±SD	Isolation–migration model or more complex model specified by user
GPho	MCMC	Full data at multiple neutral loci of size ~1000 bp	Each locus provides several samples of diploid or haploid sequences of multiple populations Out-group sequence can be used for mutation rate calibration	Posterior distribution mean±SD	Phylogeny tree given by user Constant population size to be estimated
DADI	Diffusion approximation	Summary statistics of alignments scalable to genomic size	Allele frequency spectrum of multiple populations Out-group information can be used for polarization	Point estimation	Demographic function specify by user with sets of parameters to be estimated
CoalHMM	HMM–MCMC	Full data of alignments scalable to genomic size	Two genomic size haploid sequences: one from population_1 and the other one from population_2	Posterior distribution mean±SD	Isolation model
PSMC	HMM–maximize likelihood estimation	Full data of alignments scalable to genomic size	Pseudo-diploid sequences constructed from two genomic size haploid sequences: one from population_1 and the other one from population_2	Qualitative estimation. PSMC provides an estimation of historical population size as a step function of time. The time when population size tends to infinity is the divergence time	A step function with boundaries of the intervals specified by users and function values to be estimated
MSMC	HMM–maximize likelihood estimation	Full data of alignments scalable to genomic size	Small samples of genomic size phased sequences from two populations. Normally equal numbers of sequences in each of the two populations (2–4 haploid sequences for each population)	Qualitative estimation. MSMC provides a metric, relative cross-coalescence rate to measures the gene exchange between two populations. It is a step function of time having value in [0,1]. It shows the dynamic process of relative gene flow changes between two populations, indicating the process of population divergence	A step function with boundaries of the intervals specified by users and function values to be estimated

These different methods can also be classified by the statistical framework used in the design of the methods. Notably, MIMAR and GPho-CS are Markov chain Monte Carlo (MCMC)-based methods that implement an MCMC algorithm to model the posterior distribution of the TMRCA parameter, and possess the advantage of incorporating greater complexity in the model to allow for recombination and gene flows through migration. However, such methods are typically computationally expensive and scaling up to allow whole-genome sequences to be considered as input remains intractable. Conversely, methods such as CoalHMM, PSMC, and MSMC adopt a hidden Markov model (HMM) framework that assumes a Markovian behaviour when considering recombination events. This reduces the computational burden and has been extended to allow the whole-genomic sequence to be analysed. T-LD and T-FST derive the TMRCA by computing statistics measuring the extent of LD or F_ST, whereas DADI infers the TMRCA between two populations from a diffusion approximation of the allele frequency spectrum.

In this paper, we perform a comparison of eight popular methods used to estimate TMRCA (T-LD, T-FST, MIMAR, GPho-CS, DADI, CoalHMM, PSMC, and MSMC), to gauge their relative performance as measured by the robustness and accuracy of the TMRCA estimates in order to identify the best performing method. This is achieved through a series of simulations under four different population demography scenarios: (1) simple-isolation model, (2) isolation–migration model, (3) bottleneck–nonbottleneck model, and (4) bottleneck–bottleneck model. The simple-isolation model is the simplest that assumes a random mating ancestral population that splits instantaneously into two descendant populations with no subsequent gene flow. The isolation–migration model extends the simple isolation model by allowing for migration after the population split. The bottleneck–nonbottleneck model simulates the demographic history of African and non-African populations, where studies have suggested the presence of demographic bottlenecks in non-African populations but not in African populations.^{24, 25, 26} The bottleneck–bottleneck model simulates the demographic history of non-African and non-African populations. These eight methods are subsequently applied to estimate the TMRCA between Southeast Asian Malays and South Asian Indians, with deep whole-genome sequencing data from these two populations.

Materials and methods

Simulating demographic models

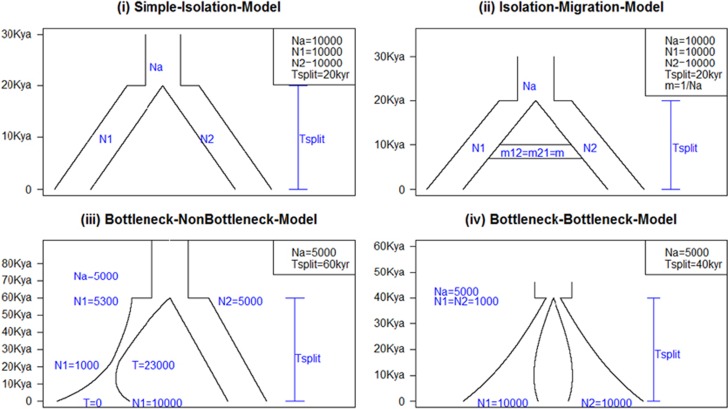
We simulated genetic sequences for two populations under four different demographic scenarios (Figure 1) with the ms program,²⁷ where 10 iterations were generated for each scenario. In each iteration, 1001 sequences of length 10 Mb are generated, comprising one sequence from an outgroup population and 500 sequences each from the two target populations. Our simulations were specifically designed to evaluate the ability to estimate the TMRCA for two populations that diverged between 20 000 and 60 000 years ago, and we assumed the outgroup population to have diverged from the two target populations 4 100 000 years ago. We assumed a mutation rate per site per year (m) of 10⁻⁹, a generation time of 25 years, and a recombination rate of 5 × 10⁻⁹. The four demographic models are: (1) simple-isolation model that assumed an ancestral population with an effective population size (N_e) of 10 000 that split into two populations 20 000 years ago with the same effective population size of 10 000; (2) isolation–migration model that assumed the same set-up as the simple-isolation model except with the addition of migration (migration rate=0.01%) between the two populations immediately after the split; (3) bottleneck–nonbottleneck model that assumed an ancestral population with N_e=5000 that split into two populations 60 000 years ago such that one population has an N_e=5000 and the other population has N_e declining exponentially from 5300 to 1000 at t=23 000 years ago, and increasing exponentially to 10 000 at present; (4) bottleneck–bottleneck model that assumed an ancestral population with N_e=5000 that split into two populations 40 000 years ago such that both populations have an N_e=1000 immediately after the split, and that increased exponentially to 10 000 at present. Our simulations produced an average of 98 175 SNPs in the simple-isolation model, 98 705 SNPs in the isolation–migration model, 57 677 SNPs in the bottleneck–nonbottleneck model, and 62 920 SNPs in the bottleneck–bottleneck model. The correct mutation rate is given to each model for converting TMRCA from coalescence unit to years.

Figure 1.

Four scenarios of demographic model. Illustrate the four demographic scenarios considered in our simulation study. An ancestral population diverged into two populations (population_1 and population_2) at time Tsplit. N1, N2, and Na are the effective population size of population_1, population_2, and the ancestral population, respectively. (i) Simple-isolation model: ancestral population split into two populations at 20 Kya. (ii) Isolation–migration model: a symmetric migration rate is added after the split. (iii) Bottleneck–nonbottleneck model: ancestral population split into two populations at 60 Kya after which population_2 has constant effective population size and population_1 experienced a bottleneck. (iv) Bottleneck–bottleneck model: ancestral population split into two populations at 40 Kya, after which both population_1 and population_2 have population size declined instantly and afterwards increased exponentially.

Estimating TMRCA of Southeast Asian Malays and South Asian Indians with whole-genome sequencing data

In order to estimate the TMRCA of Southeast Asian Malays and South Asian Indians, whole-genome sequencing data for 96 Malays from the Singapore Sequencing Malay Project (SSMP)²² and 36 Indians from the Singapore Sequencing Indian Project (SSIP)²³ were used. These individuals were sequenced on the Illumina HiSeq 2000 at a target depth of 30-fold (Illumina, San Diego, CA, USA), where the alignment and variant calling were performed with CASAVA and SAMtools for the Malay data, and with CASAVA and GATK for the Indians. The consensus calls were used as input for T-LD, T-FST, DADI, and MIMAR, whereas PSMC, MSMC, GPho-CS, and CoalHMM used the variant calls obtained from their individual analysis pipeline. For T-LD, T-FST, and DADI, all 96 Malays and 36 Indians were used to estimate the TMRCA. To avoid any effect of uneven sample sizes, we randomly selected 36 Malays to match the 36 Indians for the analysis with MIMAR. For the analysis with PSMC, MSMC, CoalHMM, and GPho-CS, one individual each from SSMP (SS6002734) and SSIP (SS6003427) were randomly selected. The analyses were performed independently across 22 autosomal chromosomes that were subsequently used to derive the mean and 95% confidence interval (CI) for the TMRCA estimate. A fixed mutation rate of 5 × 10⁻¹⁰ per site per year was assumed.

Evaluating performance of TMRCA estimation

The estimation of the TMRCA by each of the eight methods is evaluated using the simulation data with two metrics: (1) the mean error rate (expressed in percentage) and (2) the corresponding 95% CI across the 10 iterations in each of the four demographic scenarios. The error rate for the ith iteration is defined as 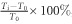, and T_i, i=1,…,10 represents the TMRCA estimated in the ith iteration, and T₀ represents the simulated population divergence time.

Technical details in the analysis of TMRCA

Comprehensive information to how each of the eight methods has been implemented can be found in the Supplementary Methods online. This includes the specific parameter settings that we have assumed for each of the methods, the specific data input considered, as well as the command lines used to implement each of the methods. All simulation data for the four demographic models, as well as the command line inputs and customized scripts for executing or implementing the eight methods, are also available online for download at http://www.statgen.nus.edu.sg/~tmrca/tmrca.html.

Results

Comparisons of eight methods with simulations

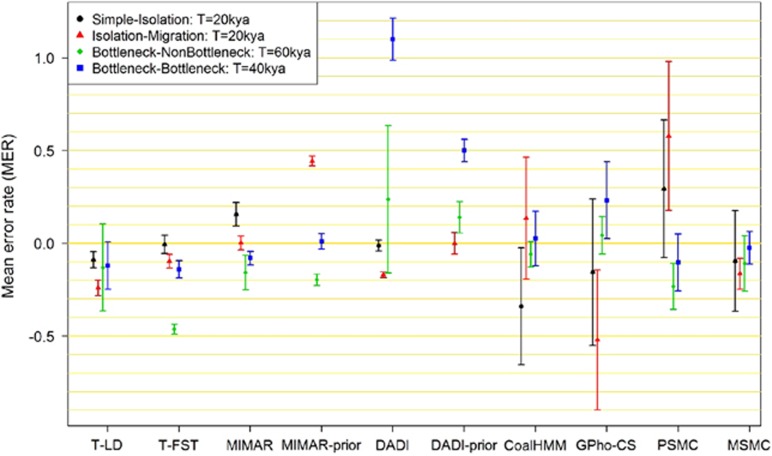
We compared the performance of the eight different methods for estimating TMRCA with 10 sets of simulated data from each of four demographic settings that assumed a: (1) simple-isolation model, (2) isolation–migration model, (3) bottleneck–nonbottleneck model, and (4) bottleneck–bottleneck model. The two simulated populations were designed to diverge 20 000 years ago for the simple-isolation and isolation–migration models, 60 000 years ago for the bottleneck–nonbottleneck model, and 40 000 years ago for the bottleneck–bottleneck model. The performance of the eight methods was then measured using two metrics: (1) the mean error rate (MER) and (2) the corresponding 95% CI (see Materials and methods for details), where MER closer to zero with narrower confidence intervals spanning zero is more desirable, across all four scenarios.

We separated the evaluation of the eight methods according to the type of input data considered, such as: (1) genotyping data, (2) sequencing data across tens of thousands of short loci, and (3) whole-genome sequencing data.

Three methods (T-LD, T-FST, and DADI) are applicable when only chip-based genotyping data are available. We observed that T-FST and DADI yielded more accurate TMRCA estimations in the setting assuming a simple-isolation model between two populations (Figure 2 and Supplementary Table 1), with the former exhibiting the lowest MER of −0.5% (95% CI: −5.5%, 4.4%) and the latter exhibiting a MER of −1.2% (95% CI: −4.2%, 1.8%). T-LD yielded a higher MER (−8.9%, 95% CI: −13.3%, −4.6%). However, in the setting assuming an isolation–migration model, all three methods performed poorly with moderate MERs (9.7–24%) but with corresponding confidence intervals that were significantly distant to zero. In the setting assuming a bottleneck–nonbottleneck model, although all three models yielded MERs >10%, the confidence intervals for T-LD and DADI encapsulated zero, with that for T-LD narrower than that for DADI. T-FST yielded a significant underestimation of the TMRCA with the MER of −46.3%, and worryingly exhibited a tight 95% CI (−48.9%, −43.6%). For the bottleneck–bottleneck scenario, only the 95% CI from T-LD encapsulated zero MER, whereas DADI yielded a gross overestimation of the TMRCA (MER=110.0%, 95% CI: 98.6%, 121.4%). In an ideal situation where DADI was implemented knowing what the underlying demographic model was, the error rates and the variability of the TMRCA estimations were reduced, although this did not yield estimates that were close to the true TMRCA except for the isolation–migration model.

Figure 2.

Mean error rate (MER) and corresponding 95% confidence interval of the eight methods. Mean error rate and 95% confidence interval are obtained from 10 iterations. Except MIMAR-prior and DADI-prior, the estimations are obtained with simple isolation model. MIMAR-prior and DADI-prior show the results obtained with prior knowledge of the demographic model for scenarios (ii), (iii), and (iv) of Figure 1.

When sequence data are available for short regions in the genome, GPho-CS produced TMRCA estimates with moderate error rates for three scenarios (except the isolation–migration model; MERs <24%), where the corresponding confidence intervals for the simple-isolation and bottleneck–nonbottleneck encapsulated zero MER (Figure 2). Another MCMC-based approach, MIMAR, yielded relatively smaller MER and variability than GPho-CS (MERs <16%), although the estimates tend to be consistently over (simple-isolation) or under (bottleneck–nonbottleneck and bottleneck–bottleneck). Intriguingly, implementing MIMAR with prior knowledge of the underlying demographic model yielded considerably poorer estimates for the isolation–migration and bottleneck–nonbottleneck scenarios, and only improved the estimate for the bottleneck–bottleneck scenario.

For the three HMM-based methods that allow whole-genome sequence data, CoalHMM and MSMC yielded comparable performance where each of the two methods yielded confidence intervals that encapsulated zero for three scenarios and where the corresponding MERs were also small. CoalHMM appeared to be most uncertain in the simple-isolation model, whereas MSMC performed poorer in the isolation–migration scenario. Compared with these two methods, PSMC exhibited greater variability and MERs across all four demographic models.

Estimating TMRCA for Southeast Asian Malays and South Asian Indians

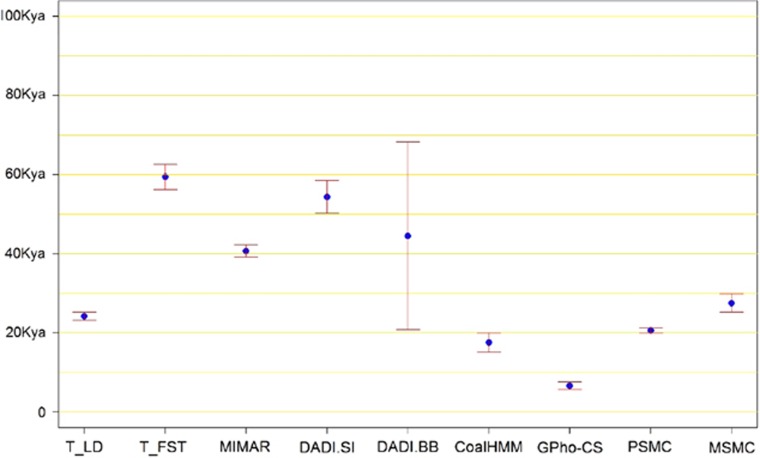
The eight methods were applied to whole-genome sequencing data for 96 Southeast Asian Malays and 36 South Asian Indians, where data from the 22 autosomal chromosomes were analysed independently by each of the eight methods and combined subsequently to derive the mean and 95% CIs of the estimates (Figure 3). DADI was implemented assuming both the simple-isolation model (DADI.SI) and the bottleneck–bottleneck model (DADI.BB). The analyses with the different methods yielded a broad range of TMRCA estimates, with GPho-CS reporting the lowest estimate of 6594 (95% CI: 5652, 7537) years ago (ya), to T-FST reporting the highest estimate of 59 429 ya (95% CI: 56 242, 62 615). Our previous simulation results suggested that T-LD, CoalHMM, and MSMC were likely to yield the most robust estimates regardless of the underlying demographic model, and it was reassuring that the TMRCA estimates for Malays and Indians from these three methods were comparable (T-LD=24 173 ya, CoalHMM=17 546 ya, MSMC=27 508 ya, Supplementary Table 2). PSMC also yielded a comparable estimate of 20 715 ya (95% CI: 20 011, 21 419), whereas the remaining methods yielded estimates exceeding 30 Kya.

Figure 3.

Malay–Indian TMRCA estimation by the eight methods. Illustrate the point estimation and corresponding 95% confidence interval of TMRCA for Southeast Asian Malays and South Asian Indians by the eight methods. DADI.SI and DADI.BB show the estimates of DADI with isolation model and bottleneck–bottleneck model, respectively.

Discussion

Estimating the TMRCA between two populations has always been a topic of great interest in population genetics, and there are presently a number of methods that leveraged on different genetic features and are built on a variety of statistical frameworks to perform this estimation. We set out to compare the accuracy and robustness of eight of these methods with a series of simulations that assumed different underlying demography between two diverged populations. The results of our simulations suggested that T-LD, CoalHMM, and MSMC were more likely to deliver estimates that were robust to a variety of background demography. The consistency in performance and accuracy across different demographic models is important, as often one does not know a priori what the underlying demographic model between two populations will be. The high variability in the TMRCA estimates observed in either the simulations or the analysis of the Malay and Indian data by some of the methods (such as DADI and GPho-CS) is worrying, as this suggests that the derived point estimates by these methods are susceptible to fluctuations even though the independent inputs were essentially from the different chromosomes of the same individuals.

In general, HMM-based methods tend to be more computationally efficient compared with MCMC-based methods. For example, the analysis of the Malay and Indian whole-genome sequencing data using HMM-based methods such as CoalHMM, PSMC, and MSMC can be completed in hours on a standard Linux-based processor, whereas MCMC-based methods such as MIMAR and GPho-CS required several days to a few weeks to complete the same analysis across 22 chromosomes. The computational burden also means that MCMC-based methods could not model recombination effectively, and the analysis was necessarily restricted to short segments. Conversely, the computational dexterity of HMM-based approaches allows both recombination events to be modelled and for full chromosomal data to be analysed.

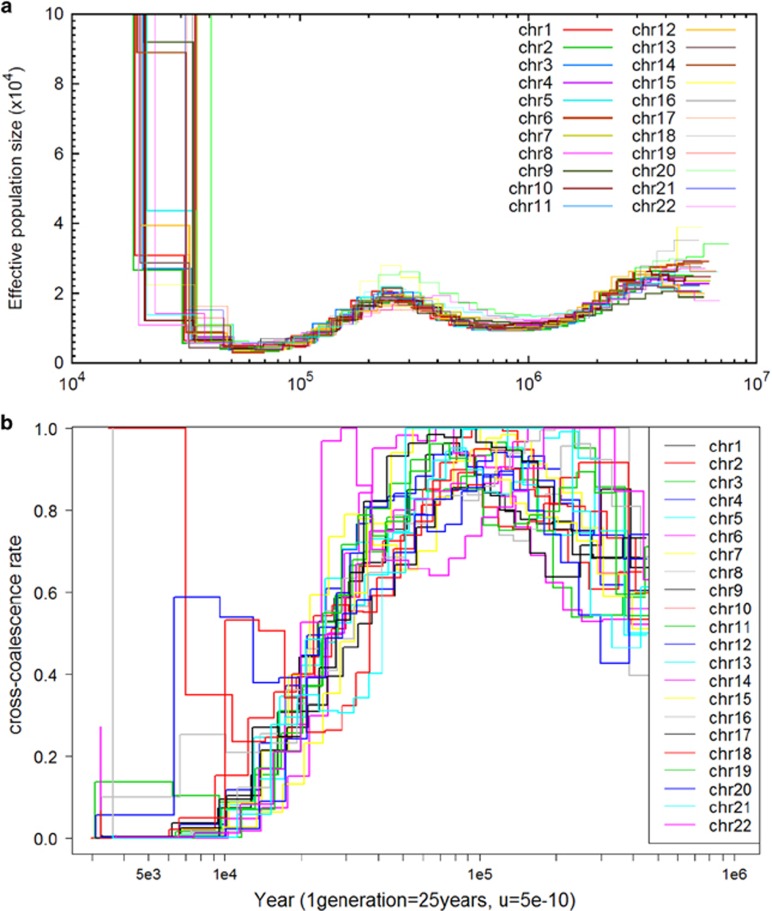
A key challenge in the implementation of PSMC and MSMC is in the selection of the thresholds for the effective population size and cross-coalescence rate respectively to determine divergence time (Figure 4). Presently, there are no recommended or default thresholds for these two approaches, and the TMRCA estimates are sensitive to the choice of the thresholds. For example, the TMRCA estimate for the PSMC analysis of the Malay and Indian data changes from 20 715 ya to 36 824 ya if the threshold on the effective population size changes from 1 000 000 to 50 000.

Figure 4.

Malay–Indian TMRCA estimation by PSMC and MSMC. Illustrate the estimation of TMRCA by (a) PSMC and (b) MSMC on whole-genome sequencing data for the 22 autosomal chromosomes from Southeast Asian Malays and South Asian Indians. Both the effective population size (a) and the cross-coalescence rate (b) are modelled as step functions. The divergence time for the two populations is defined for (a) PSMC as the time when the effective population size increases to infinity that, in practice, is implemented as a threshold such as 100 000 in our study; (b) MSMC as the most recent time when the cross-coalescence rate decreases below an arbitrarily selected threshold that in our study the threshold is selected as 0.5.

GPho-CS produced a considerably lower TMRCA estimate for the Malay and Indian whole-genome sequencing data, and this may be because of two reasons: (1) GPho-CS has previously reported lower accuracy to infer recent events¹⁶ and (2) GPho-CS relied on a different mutation rate. Presently, the method calibrates the mutation rate from the number of mutation events from an outgroup species to which the divergence time has to be assumed.¹⁶ By including a chimpanzee sequence in the model and assuming the divergence time from chimpanzee to be 6.5 Mya, this produced an average mutation rate of 6.96 × 10⁻¹⁰ that is only 70% of the default mutation rate of 10⁻⁹ for the chimpanzees. Although this may be a reasonable calibration given the exclusion of CpG and regions under selection, this is based on the assumption that chimpanzees and modern humans exhibited identical mutation rates per site per year and generation time. A recent study suggested revising the mutation rate to 5 × 10⁻¹⁰ per site per year for studies on modern human evolution,²⁸ the value we have used for the genome-wide average mutation rate. As such, a comparable mutation rate for neutral sites should thus be lower than 5 × 10⁻¹⁰. We scaled the mutation rate used in GPho-CS to correspond 70% of 5 × 10⁻¹⁰ that produced a point estimate of 13 188 ya (95% CI: 11 304, 15 074). However, this highlights the dependency that TMRCA estimation has on the parameters assumed.

Our simulation analyses with the different methods have assumed a constant mutation rate that reduced the complexity by not having to calibrate mutation rates and instead focussed on the inference of TMRCA measured in coalescent unit (time scaled by 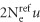). This was similarly the case in the inference of the TMRCA between Malays and Indians, a common assumption in evolutionary studies. However, we highlight the possibility that the choice of mutation rates can bias the estimation of divergence time, especially as (1) evolutionary rates may actually be time dependent and (2) the evolutionary rate estimate can depend on the timescale of measurement.²⁹ A comprehensive characterization of time-dependent biases in evolutionary rate is likely to be important but regretfully beyond the scope of the current study.

We have evaluated eight statistical methods commonly used in population genetics to estimate TMRCA. The performance of these methods varies according to the parameter settings assumed, as well as the background demographic model producing the split of the two populations. Our simulations have considered only four relatively simple demographic scenarios, and incorporating more complex demographic and migration models were beyond the scope of this study. The effective population size is confounding in TMRCA analysis, and an accurate effective population size is crucial for estimating divergence time. Among those methods, DADI, PSMC, and MSMC have higher resolution in effective population size. However, a note of caution is that the divergence times estimates differed depending on the methods used. Taken together, we recommend the T-LD, CoalHMM, and MSMC methods for TMRCA estimation when using genome-wide SNP or whole-genome sequencing data respectively.

The authors declare no conflict of interest.