Skip to main content
PMC home page
European Journal of Human Genetics logoLink to European Journal of Human Genetics
. 2016 Jan 6;24(8):1188–1194. doi: 10.1038/ejhg.2015.270

The effect of phenotypic outliers and non-normality on rare-variant association testing

Paul L Auer 1, Alex P Reiner 2, Suzanne M Leal 3,*
PMCID: PMC4970685  PMID: 26733287

Abstract

Rare-variant association studies (RVAS) have made important contributions to human complex trait genetics. These studies rely on specialized statistical methods for analyzing rare-variant associations, both individually and in aggregate. We investigated the impact that phenotypic outliers and non-normality have on the performance of rare-variant association testing procedures. Ignoring outliers or non-normality can significantly inflate Type I error rates. We found that rank-based inverse normal transformation (INT) and trait winsorisation were both effective at maintaining Type I error control without sacrificing power in the presence of outliers. INT was the optimal method for non-normally distributed traits. For RVAS of quantitative traits with outliers or non-normality, we recommend using INT to transform phenotypic values before association testing.

Introduction

Although Genome-Wide Association Studies (GWAS) have been successful in identifying associations between common variants and complex traits and diseases, much of the heritability of these traits and diseases remains unexplained.1 Recently, there has been a deepening interest in evaluating the extent to which rare variants contribute to variation in complex traits and diseases.2, 3, 4, 5, 6, 7, 8, 9 This has motivated development of statistical methods for testing rare-variant associations at the gene level.10, 11, 12, 13, 14, 15, 16 Although these methods are useful for increasing statistical power to detect associations relative to single-variant analyses, valid well-powered statistical analyses are contingent on careful examination of phenotypes and underlying assumptions. Here we explore some commonly encountered issues with how phenotypes are distributed and how these issues affect inferences from rare-variant association tests.

One assumption underlying many rare-variant association studies is that rare variants exert larger effect sizes than common variants. For some traits, this hypothesis is borne out by genetic evidence. For instance, the LDLR gene harbors multiple rare variants that are strongly associated with circulating low-density lipoprotein (LDL)-cholesterol levels.7 The genetic effects of these rare variants are so strong that individuals carrying certain LDLR mutations appear as outliers in population level summaries of LDL-cholesterol levels.7 Rare-variant association studies of complex traits are particularly interested in phenotypic outliers because they may harbor rare variants with strong genetic effects.

Furthermore, many rare-variant association tests rely on asymptotics that work best with normally (or approximately normally) distributed phenotypes.12, 16 However, many quantitative phenotypes are not normally distributed in healthy populations (even after controlling for confounders that may contribute to non-normality).17, 18 We show that rare-variant association tests are uniquely susceptible to biases caused by outliers and non-normality.

Materials and Methods

Simulations

We considered two different types of trait distributions. To simulate outliers, we generated a mixture of normal random variables by choosing 95% of the values to be drawn from a standard N(0,1) distribution and the other 5% from N(0, σ=8). To simulate non-normal phenotypes that are similar to those observed in genetic studies, we randomly generated highly skewed random variables from the 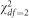Inline graphic distribution. As a secondary analysis, we simulated phenotypes using a left-skewed Gompertz distribution and a mixture of χ2 distributions by drawing 95% of the trait values from a 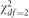Inline graphic and 5% from a 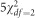Inline graphic distribution. Histograms of simulated trait distributions are shown in Supplementary Figure S5. Genotypes were drawn as 0, 1, or 2, from the multinomial distribution, with probabilities derived from Hardy–Weinberg equilibrium with specified minor allele frequencies.

Given our randomly generated genotypes, we also simulated heteroskedasticity (unequal error variance between genotypes) by drawing the ith phenotypic value Yi from N(0,1) if Xi=0, from N(0,1.5) if Xi=1, and from N(0,2) if Xi=2. In this manner, we simulated quantitative traits with no mean shift in trait value between genotypes, but where the genotype predicts the variance of the trait values.

We considered several different approaches for dealing with outliers. Winsorising (WINS) is a technique that limits the influence of extreme values by setting all outliers to a specified percentile of the observed data. We considered a 95% winsorization, where we set all observations below the 5th percentile or above the 95th percentile to the values observed at the 5th and 95th percentile, respectively. We also evaluated deleting outliers (DEL), where all values below the 5th percentile or above the 95th percentile were removed. In comparison to winsorising or deleting outliers, we also obtained empirical P-values by permuting the quantitative trait values (PERMUTE) one million times. In addition, we performed robust regression using the M-estimator (HUBER),19 as implemented in the rlm() package in R (R Foundation for Statistical Computing, Vienna, Austria). Finally, we performed the rank-based inverse normal transformation (INT), where all values of the trait are ranked, and the ranks are mapped to percentiles of the standard normal distributions. Specifically, the transformed value of the phenotype for the ith subject was:

graphic file with name ejhg2015270e1.jpg

where ri is the rank of the ith observation among a sample of size n, and Ф−1 denotes the standard normal quantile function. We also considered the natural logarithm transformation (LOG-NORM), as well as the Kruskal–Wallis non-parametric test (K–W; implemented with the kruskal.test() function in R, R Foundation for Statistical Computing). Note that while WINS, DEL, LOG-NORM, and INT can be considered trait transformations, PERMUTE, HUBER, and K–W are procedures that do not transform the phenotype values.

For simulations of single-genetic variants, we considered minor allele frequencies of both 0.005 and 0.05. We ran 100 000 iterations for both the Type I error and Power simulations. Type I error and Power were evaluated with simulated sample sizes n=10 000 and n=2000, respectively. For gene-level tests of association, we chose a modestly sized gene (MC4R) and a larger gene (ALK). Genotypes were simulated as previously described in Auer et al,20 with allele frequencies for non-synonymous variants taken from the Exome-Variant Server.

We evaluated single-variant associations using simple linear regression for every method except K–W. Gene-level associations were evaluated using the combined multivariate collapsing (CMC) burden test,12 the burden of rare-variants test20 (BRV, an adaptation of GRANVIL,21) and the sequence kernel association (SKAT)16 variance components test. Due to computational intensity, we did not evaluate the performance of SKAT under permutations. We also did not attempt to generalize the SKAT method with an M-estimator, so we do not report results for the HUBER method with SKAT. Note that SKAT is incompatible with K–W, therefore we did not evaluate its performance. Gene-level tests were implemented using a custom script in R for the CMC and BRV tests, and using the SKAT() function in R.

To evaluate the power, we assessed statistical significance at α=5 × 10−4 (this was the lowest significance level that we could implement across our simulations in a reasonable amount of time). Genetic effects were generated under the following additive genetic models: For single-variant analyses, we simulated the ith phenotypic value as Yi=Xiβ+ɛi, where Xi denotes the randomly generated genotype for the ith observation, β is the effect size and ɛi is the randomly generated error term (either from the mixture of normals for outliers or from a 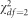Inline graphic for non-normality).

For gene-level tests, we used a similar model with 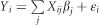Inline graphic, where Xij is the randomly generated genotype for the ith observation at the jth variant site, and βj is the effect at the jth variant site. We chose βj as a 0.1*Bernoulli(p) random variable (when simulating fixed effects) or as a 0.1*Multinomial(1,2,3,4,5,6,7,8,9,10)*Bernoulli(p) random variable (when simulating variable effects). For the gene-level simulations, p was set to one of 0.1, 0.25, 0.5, 0.75, or 1, corresponding to the percent of causal variants within the gene.

Data analysis

To evaluate the various approaches for outliers and non-normality, we analyzed Exome-Chip genotypes from the Women's Health Initiative (WHI).22 Our analyses focused on association testing for both circulating platelet counts (PLT) and white blood cell counts (WBC). These data have already been used in a meta-analysis that reported several robustly replicated rare-variant associations with PLT and WBC.3 Of the 161 808 participants in the WHI who were eligible and consented to genetic research, 18 513 were included in this analysis.

Blood counts were performed with automated hematology cell counters and standardized quality assurance procedures. WBC and PLT were recorded during the WHI baseline examination, conducted during 1993–1998. DNA samples were genotyped using the Illumina HumanExome v1.0 SNP array (Illumina, San Diego, CA, USA). Genotypes were assigned using GenomeStudio v2010.3 (Illumina). Markers with a genotyping success rate of less than 99% were excluded, as were samples with a genotyping success rate of less than 98%. Crytpic relatedness was assessed using the PLINK IBS/IBD functionality.23 For each related or duplicate pair of samples, we excluded the sample with the lower call rate. Samples with WBC >200 (× 109 cells/l) or PLT >1000 (× 109 cells/l) were excluded from the analysis, as these values are biologically implausible in healthy individuals.

Raw values for both PLT and WBC were regressed on age, genotyping batch, and the first two principal components. Neither PLT nor WBC are normally distributed. WBC is severely right skewed, and there are outliers for both PLT and WBC (Supplementary Figure S8), making them excellent phenotypes for illustrative purposes. The residuals from these regressions were either transformed (using INT, WINS, DEL, or LOG-NORM), and the transformed values were used for association testing, or the raw residuals were used for association testing with the K–W, PERMUTE, or HUBER approaches.

For testing single-variant associations, we considered single-nucleotide variants with a minor allele count >2. For gene-level association testing, we considered all missense, nonsense, or splice variants with an observed minor allele frequency ≤1%. Gene-level association testing was conducted with the CMC, BRV, and SKAT methods.

Results

Simulations

When there are outliers in the data, tests for rare-variant associations (both for single variants and for gene-level tests), suffer from inflated Type I error rates unless a correction is applied (Figure 1 and Supplementary Figure S1). We compared WINS, DEL, PERMUTE, INT, HUBER, and K–W to performing linear regression with outliers included (IGNORE). Ignoring outliers leads to inflation in Type I error for single-variant analyses, SKAT, and CMC (Figure 1 and Supplementary Figure S1, Table 1). Each method (WINS, DEL, PERMUTE, INT, HUBER, K–W) effectively controlled Type I error (Figure 1 and Supplementary Figure S1, Table 1).

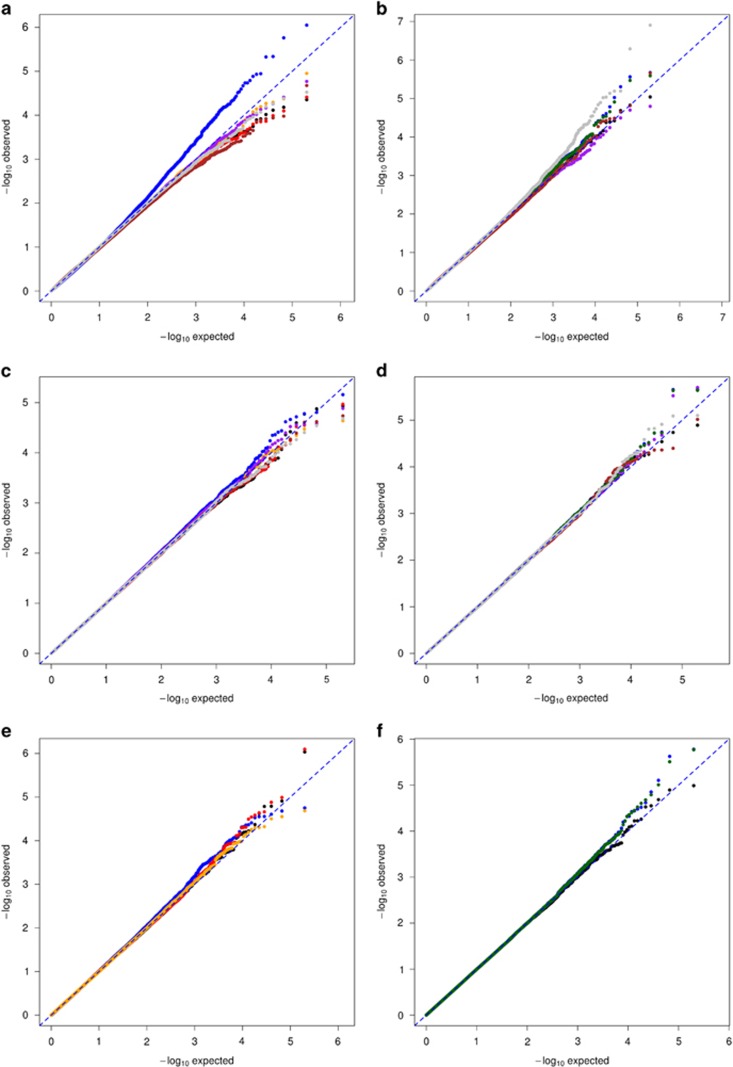
Figure 1.

Figure 1

Open in a new tab

QQplots of rare-variant associations with a quantitative phenotype under the null hypothesis of no association. INT is shown in black, WINS in red, DEL in orange, PERMUTE in purple, K–W in brown, LOG-NORM in green, and HUBER in gray; ignoring outliers or ignoring non-normality is shown in blue. Ignoring outliers leads to inflation of Type I error for single-variant analyses with MAF=0.005, all of the corrections successfully controls Type I error (a). For non-normal phenotypes, ignoring, HUBER, and LOG-NORM lead to modest inflation of Type I error for single-variant analyses with MAF=0.005; all other corrections control Type I error (b). The CMC approach for rare variants in MC4R, does not show inflation of Type I error when outliers or non-normality are ignored (c, d, respectively). The SKAT approach for rare variants in MC4R shows modest inflation of Type I error in the presence of outliers (e) and non-normality (f).

Table 1. Type I error probabilities at significance levels of 5 × 10−2, 5 × 10−3, and 5 × 10−4.

  SNV (outliers) CMC (outliers) SKAT (outliers) SNV (non-normal) CMC (non-normal) SKAT (non-normal)
(α=0.05) (α=0.005) (α=0.0005) MAF=0.05 MAF=0.005 MC4R ALK MC4R ALK MAF =0.05 MAF=0.005 MC4R ALK MC4R ALK
INT 4.9e-02 5.0e-03 5.0e-04 5.1e-02 5.1e-03 4.7e-04 4.9e-02 4.9e-03 5.1e-04 5.0e-02 5.0e-03 4.5e-04 5.1e-02 4.9e-03 5.2e-04 4.9e-02 4.9e-03 5.2e-04 4.9e-02 5.2e-03 4.1e-04 5.0e-02 5.2e-03 5.2e-04 5.0e-02 5.0e-03 4.7e-04 5.0e-02 5.1e-03 5.5e-04 4.9e-02 4.7e-03 5.6e-04 5.1e-02 4.9e-03 5.3e-04
WINS 4.9e-02 5.2e-03 5.0e-04 5.0e-02 5.1e-03 5.0e-04 4.9e-02 5.0e-03 5.2e-04 5.9e-02 4.9e-03 4.1e-04 5.0e-02 4.9e-03 6.1e-04 4.9e-02 5.0e-02 6.0e-02 NA NA NA NA NA NA
DEL 4.9e-02 4.8e-03 4.7e-04 5.0e-02 4.8e-03 4.0e-04 5.0e-02 5.4e-03 5.6e-04 4.9e-02 4.9e-03 4.6e-04 5.0e-02 5.2e-03 5.7e-04 4.9e-02 4.9e-03 5.8e-04 NA NA NA NA NA NA
IGNORE 4.9e-02 5.1e-03 6.e3-04 5.3e-02 7.6e-03 1.2e-03 5.0e-02 5.3e-03 5.6e-04 5.0e-02 5.1e-03 5.2e-04 5.3e-02 5.9e-03 8.4e-04 5.1e-02 5.0e-03 5.7e-04 4.9e-02 5.3e-03 6.1e-04 5.0e-02 5.6e-03 8.1e-04 5.0e-02 5.2e-03 4.7e-04 5.0e-02 5.2e-03 6.7e-04 4.9e-02 5.0e-03 6.3e-04 5.0e-02 5.3e-03 6.0e-04
PERM 4.8e-02 4.8e-03 5.3e-04 5.0e-02 5.0e-03 4.7e-04 4.9e-02 5.0e-03 4.9e-04 5.0e-02 5.0e-03 4.9e-04 NA NA 4.9e-02 5.2e-03 5.7e-04 5.1e-02 5.2e-03 5.2e-04 5.0e-02 5.1e-03 4.2e-04 5.0e-02 5.2e-03 6.5e-04 NA NA
LOG-NORM NA NA NA NA NA NA 4.9e-02 5.2e-03 6.3e-04 5.0e-02 5.6e-03 8.0e-04 5.0e-02 5.2e-03 4.5e-04 5.0e-02 5.2e-03 6.6e-04 4.9e-02 5.0e-03 6.2e-04 5.0e-02 5.3e-03 5.5e-04
K–W 4.9e-02 4.9e-03 4.3e-04 4.6e-02 4.5e-03 3.8e-04 4.9e-02 4.9e-03 5.8e-04 4.9e-02 5.0e-03 4.2e-04 NA NA 4.8e-02 4.7e-03 5.1e-04 4.6e-02 4.2e-03 3.8e-04 5.0e-02 5.0e-03 4.4e-04 4.9e-02 4.9e-03 5.0e-04 NA NA
HUBER 5.0e-02 5.1e-03 5.4e-04 5.0e-02 4.8e-03 3.2e-04 5.0e-02 5.1e-03 5.5e-04 4.9e-02 5.0e-03 4.6e-04 NA NA 5.1e-02 5.2e-03 5.1e-04 5.1e-02 6.1e-03 9.2e-04 4.9e-02 5.2e-03 5.0e-04 5.0e-02 5.4e-03 6.1e-04 NA NA
Open in a new tab

Abbreviations: CMC, combined multivariate collapsing; DEL, deleting outliers; INT, inverse normal transformation; NA, not applicable; PLT, platelet counts; WBC, white blood cell counts; WINS, winsorising.

Results are shown for single-variants tests, as well as the CMC and SKAT tests. Single-variant tests were conducted for MAFs of 0.05 and 0.005. The CMC and SKAT tests were conducted using variant data from the MC4R and ALK genes. Results are shown for both outlier and non-normal distributions. Inflated Type I error rates are highlighted in bold.

For data generated under a non-normal distribution, we compared INT, LOG-NORM, PERMUTE, HUBER, and K–W, to ignoring non-normality. When quantitative traits follow a distinctly non-normal distribution, we observed modest inflation of Type I error for single-variant analyses, SKAT, and CMC when non-normality is ignored. INT, PERMUTE, and K–W uniformly controlled Type I error across simulation settings. LOG-NORM and HUBER were only effective in some circumstances. (Figure 1, Supplementary Figures S1 and S2, Tables 1 and 2). The results were similar when we simulated non-normal trait distributions that also contained outliers (Table 2).

Table 2. Type I error probabilities at significance levels of 5 × 10−2, 5 × 10−3, and 5 × 10−4.

  SNV (gompertz) SNV (right tail+outliers)
(α=0.05) (α=0.005) (α=0.0005) MAF=0.05 MAF=0.005 MAF=0.05 MAF=0.005
INT 5.1e-02 5.2e-03 4.5e-04 5.0e-02 5.1e-03 5.3e-04 5.1e-02 5.2e-03 5.7e-04 5.0e-02 5.0e-03 4.3e-04
WINS NA NA 5.0e-02 4.9e-03 5.6e-04 4.9e-02 5.0e-03 5.3e-04
DEL NA NA 5.0e-02 4.9e-03 5.3e-04 5.0e-02 5.1e-03 4.4e-04
IGNORE 5.1e-02 5.1e-03 4.6e-04 4.9e-02 5.2e-03 6.7e-04 5.0e-02 5.5e-03 7.9e-04 4.8e-02 9.2e-03 2.6e-03
PERM 5.1e-02 5.1e-03 4.7e-04 4.9e-02 5.1e-03 5.8e-04 5.1e-02 5.1e-03 5.8e-04 5.0e-02 5.1e-03 4.1e-04
LOG-NORM 5.1e-02 5.1e-03 4.8e-04 4.9e-02 5.2e-03 6.7e-04 5.0e-02 5.2e-03 5.6e-04 4.8e-02 8.1e-03 1.9e-03
K–W 4.9e-02 4.7e-03 4.8e-04 4.5e-02 4.4e-03 4.8e-04 4.9e-02 5.0e-03 4.7e-04 4.6e-02 4.2e-03 3.2e-04
HUBER 5.1e-02 5.1e-03 6.1e-04 4.9e-02 5.2e-03 5.9e-04 5.0e-02 5.4e-03 6.3e-04 5.0e-02 5.7e-03 7.3e-04
Open in a new tab

Abbreviations: CMC, combined multivariate collapsing; DEL, deleting outliers; NA, not applicable; PLT, platelet counts; WBC, white blood cell counts; WINS, winsorising.

Results are shown for single-variant tests that were conducted for MAFs of 0.05 and 0.005. Results are shown for a left-tailed distribution that was simulated using the Gompertz distribution, as well as a right-tailed distribution (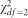Inline graphic) with outliers added. Inflated Type I error rates are highlighted in bold.

Although not the primary aim of our study, we also considered the Type I error control under heteroskedasticity. Similar to the results reported in Beasley et al.24 we found that none of these methods (WINS, DEL, PERMUTE, INT, HUBER, K–W, LOG-NORM) were effective at controlling Type I error when genotype predicts the variance of the trait values (Supplementary Figure S2).

The methods we considered for controlling Type I error in the presence of outliers and non-normality demonstrated varying performance in their power to detect associations. When outliers are present in the data, DEL, and PERMUTE suffer a dramatic loss of power for single-variant analyses with MAF=0.005; HUBER, INT, K–W, and WINS were very similarly powered in this circumstance (Figure 2). The same was true for the CMC, BRV, and SKAT rare-variant tests (Figure 2, Supplementary Figure S6). We simulated different proportions of causal variants, as well as both fixed and random genetic effects for variants within a gene region. Changing these parameters did not affect the primary conclusion: that HUBER, INT, K–W, and WINS were all most powerful in detecting associations in the presence of outliers (Supplementary Figures S3).

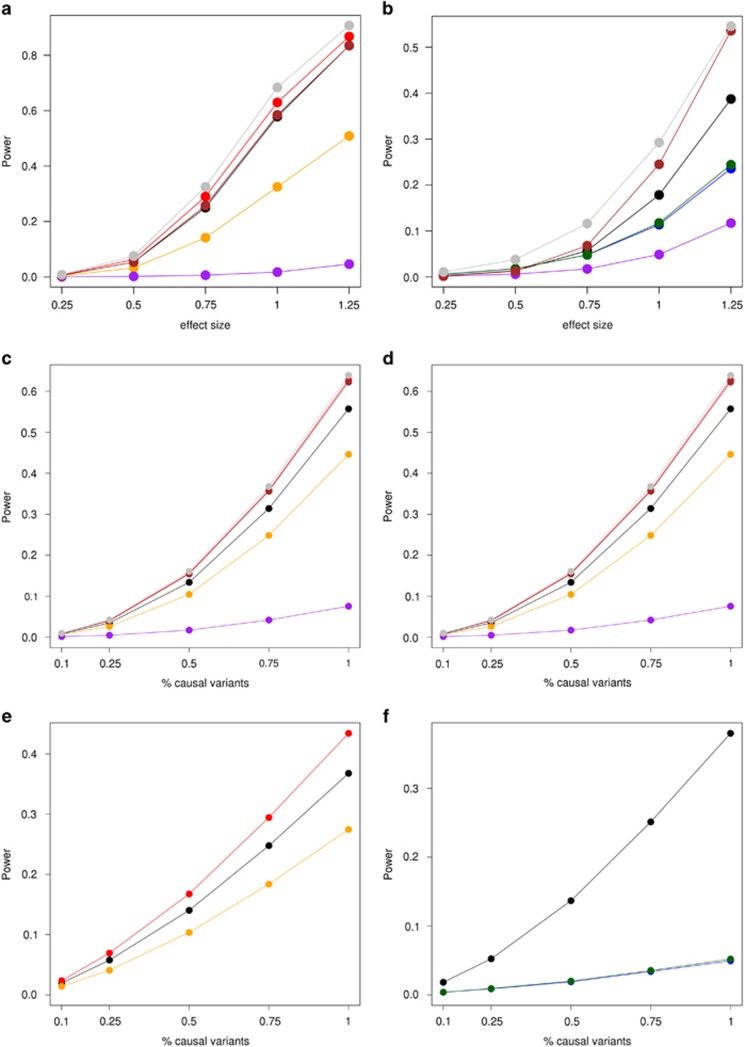
Figure 2.

Figure 2

Open in a new tab

Power plots of rare-variant associations with a quantitative phenotype. Power is shown on the y axis, INT is shown in black, WINS in red, DEL in orange, PERMUTE in purple, K–W in brown, LOG-NORM in green, and HUBER in gray; ignoring outliers or ignoring non-normality is shown in blue. For single-variant analyses with MAF=0.005 and outliers, permutations and deletion of outliers suffer from a dramatic loss of power (a). Of note PERM displays the lowest power of all methods. When the phenotype violates normality, INT, HUBER, and K–W demonstrate the highest power to detect an association (b). For a and b, effect sizes (ie, beta values) are taken in terms of trait SD's. For the CMC test in ALK, INT, HUBER, and K–W demonstrate the highest power with phenotypic outliers (c) or non-normal trait values (d). For the SKAT approach in ALK, INT, and WINS had the highest power to detect associations with phenotypic outliers (e); INT had the highest power to detect associations with non-normal trait values (f). For variants in ALK, we ran simulations with 10, 25, 50, 75, and 100% causal variants. All causal variants had the same effect size (ie, beta value) of 0.25 trait SD's.

For non-normally distributed phenotypes, HUBER, K–W, and INT were most powerful in detecting associations across our simulation settings (Figure 2, Supplementary Figures S3 and S4, S6 and S7). Similar to the results for outliers, LOG-NORM and PERMUTE suffered a loss in power (Figure 2, Supplementary Figures S3 and S4, S6 and S7). Note that because HUBER and K–W are incompatible with SKAT, INT is the most powerful method for detecting associations using SKAT in the presence of a non-normally distributed phenotype.

Finally, we compared the power of the various approaches when phenotypes were simulated with error terms from the N(0,1) distribution. In this instance, one would expect that running a simple regression and ignoring any outliers or non-normality (IGNORE) would be most powerful. Indeed, we found that for MAF of 0.005 and 0.05 across a range of effect sizes, IGNORE was most powerful (Table 3). In comparison to IGNORE, the INT, PERM, HUBER, and LOG-NORM approaches did not suffer any notable loss of power; K–W, WINS, and DEL all displayed marked loss of power.

Table 3. Power results at significance levels of 5 × 10−4.

(β=0.1) (β=0.5) (β=1.0) MAF=0.005 MAF=0.05
INT 1.5e-03 0.11 0.80 1.8e-02 1.0 1.0
WINS 1.1e-03 8.9e-02 0.74 1.7e-02 1.0 1.0
DEL 7.6e-04 2.5e-02 0.24 7.e3-03 0.93 1.0
IGNORE 1.5e-03 0.11 0.80 1.8e-02 1.0 1.0
PERM 1.4e-03 0.10 0.79 1.6e-02 1.0 1.0
LOG-NORM 1.4e-03 0.11 0.80 1.8e-02 1.0 1.0
K–W 8.8e-04 7.6e-02 0.71 8.4e-03 1.0 1.0
HUBER 1.1e-03 0.10 0.76 1.5e-02 1.0 1.0
Open in a new tab

Abbreviations: CMC, combined multivariate collapsing; DEL, deleting outliers; INT, inverse normal transformation; PLT, platelet counts; WBC, white blood cell counts; WINS, winsorising.

Results are shown for single-variant tests that were conducted for MAFs of 0.05 and 0.005 under a standard normal phenotypic distribution with effect sizes (β)=0.1, 0.5, and 1.0 SD's.

Data analysis

Both PLT and WBC were analyzed for association at both the variant- and gene-level. For PLT and WBC, INGORE, LOG-NORM, and HUBER were ineffective at controlling Type I error for variants with MAF <5% (Supplementary Figure S9). INT, PERMUTE, and K–W most closely followed the diagonal line on the qqplots. For variants with MAF > 5% it is difficult to visually establish Type I error control from qqplots, because these are both highly polygenic traits with hundreds of underlying common variants. For the gene-level tests (CMC, BRV, and SKAT), INT, DEL, WINS, PERM, and HUBER demonstrated control of Type I error as displayed by qqplots that closely followed the identity line (Supplementary Figure S10).

To evaluate the power of these approaches to detect associations, we considered a number of true positive associations that have been robustly replicated in multiple studies. The CXCR2 gene harbors multiple rare, missense variants that are associated with WBC, show signal in gene-level tests of association, and are represented on the Exome-Chip.3 In addition, we considered three different variants that are each strongly associated with PLT (rs41303899 (TUBB1), rs3184504 (SH2B3), and rs148636776 (SH2B3)).3 As displayed in Table 4, INT shows the strongest signal for association between WBC and a burden of rare variants in CXCR2, although almost all of the methods detect the association at gene-level exome-wide significance (5 × 10−6). For PLT, the P-values appear similar across approaches, with the exception of PERM which shows the weakest signal for association (Table 4). Taken together, these results suggest that INT and WINS effectively control Type I error while picking up on true associations in a large-scale real data analysis of rare-variant associations.

Table 4. P-values from the analysis of WHI Exome-Chip data for rare-variant associations with WBC and PLT.

Trait gene/variants test/MAF INT WINS DEL IGNORE PERM LOG-NORM K–W HUBER
WBC CXCR2 SKAT 1.1e-05 2.3e-04 8.8e-05 1.3e-03 NA 1.1e-03 NA NA
    CMC 7.3e-07 1.4e-05 6.0e-06 1.0e-04 1.3e-03 8.6e-05 9.7e-07 2.1e-06
    BRV 7.2e-07 1.4e-05 5.7e-06 9.9e-05 1.7e-03 8.3e-05 5.8e-06 2.2e-06
PLT rs41303899 0.0016 1.2e-04 1.7e-04 1.3e-05 9.2e-04 1.5e-03 3.3e-04 9.5e-05 2.2e-04
  rs3184504 0.4976 3.7e-14 1.0e-13 9.8e-15 2.9e-13 9.9e-07 1.0e-13 6.9e-13 1.2e-13
  rs148636776 0.0005 5.8e-03 3.4e-03 2.2e-02 4.0e-03 7.5e-03 4.8e-03 9.2e-03 4.4e-03
Open in a new tab

Abbreviations: CMC, combined multivariate collapsing; DEL, deleting outliers; INT, inverse normal transformation; NA, not applicable; PLT, platelet counts; WBC, white blood cell counts; WINS, winsorising.

Because we performed at most 1 million permutations, PERM cannot take on values <9.9e-07.

Discussion

Although it has become a common approach for the analysis of GWAS data,25 there are reservations about the impact of INT on the results from association testing.24 Both Beasley et al.24 and Buzkova26 investigated the effect of INT when there is heteroskedasticity and demonstrated that Type I error was not well-controlled. Not surprisingly, they also report that for normally distributed traits, INT is less powerful than using untransformed data. Our results for large sample sizes and rare variants are consistent with these observations. Beasley et al.24 noted, ‘The intricacies of the differences among the power functions of the t-test and the t-test performed on INTs with different sample sizes, effect sizes, and error distributions need further investigation.'

In standard regression analyses, normality is often assessed on the residuals rather than the raw trait values.27 Indeed, covariates with large effects may induce a multi-modal trait distribution, which disappears after adjustment. In our analyses, we adopted the following approach: (1) regress the trait values on the set of covariates, (2) transform the residuals from this regression; and (3) test for association between the transformed residuals and the genetic variable of interest. Although this method suffers from a loss of power when covariates are correlated with the genetic variable of interest,28, 29 in the absence of such pathological correlation, we have found this to be a convenient and flexible approach for genetic association testing.

There are a number of considerations when deciding whether an untransformed phenotype is suitable for rare-variant association testing. As we did for the Exome-Chip analyses of WBC and PLT, outliers should be checked for biological plausibility. QQplots offer a powerful method for assessing normality. After regression of trait values on covariates, the ranked residuals can be plotted against the percentiles of a normal distribution. Although visually detecting deviation from the diagonal line is often sufficient, the Shapiro–Wilk test for normality30 is a more formal approach. Because it is not a strict assumption of these methods, minor deviation from normality can be tolerated. We recommend using a combination of a formal approach (such as the Shapiro–Wilk test) along with visual inspection of qqplots to assess whether the trait is ‘normal enough' to conduct rare-variant association testing without a transformation (INT, WINS, DEL, and LOG-NORM) or alternate approach to testing (K–W, PERMUTE, and HUBER).

Under a variety of simulations, we found that INT effectively controlled Type I error and was the most powerful method, or very close to the most powerful method. For phenotypic outlier WINS and INT had comparable Type I and Type II error rates. However, phenotypic data may be both non-normal and contain outliers. In these cases, WINS only deals with the outliers, leaving the non-normality issue un-addressed. The INT is the only single approach we investigated that effectively deals with both outliers and non-normality simultaneously. Interestingly, PERMUTE was poorly powered in the presence of outliers or non-normality. Although PERMUTE is a gold standard method for controlling Type I error in genetic association studies, we recommend only using PERMUTE if the trait is approximately normally distributed and contains few, if any, outliers.

Unlike previous investigations,24 we evaluated power and Type I error at low alpha-levels. In addition, because many genome-wide genetic studies are using large sample sizes (even for rare-variant investigations)3, 6 our simulations featured large sample sizes as well. Rather than focusing our attention only on single-variant tests of association, we also investigated how aggregate rare-variant association tests (such as SKAT, CMC, and BRV) behave in the presence of phenotypic outliers or non-normality. For large-scale genome-wide studies for both common and rare variants, we recommend using INT or WINS as an effective means of correcting for trait outliers and INT for addressing non-normality.

Acknowledgments

We wish to thank Gao Wang for assistance with simulations. PLA was supported by NHLBI R21 HL121422-02. The WHI program is funded by the National Heart, Lung, and Blood Institute, the US National Institutes of Health, and the US Department of Health and Human Services (HHSN268201100046C, HHSN268201100001C, HHSN268201100002C, HHSN268201100003C, HHSN268201100004C, and HHSN271201100004C). Exome-chip data and analysis were supported through the Exome Sequencing Project (NHLBI RC2 HL-102924, RC2 HL-102925, and RC2 HL-102926), the Genetics and Epidemiology of Colorectal Cancer Consortium (NCI CA137088), and the Genomics and Randomized Trials Network (NHGRI U01-HG005152). We thank the WHI investigators and staff for their dedication and the study participants for making the program possible.

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies this paper on European Journal of Human Genetics website (http://www.nature.com/ejhg)

Supplementary Material

Supplementary Figure 1
Click here for additional data file. (14MB, pdf)
Supplementary Figure 2
Click here for additional data file. (11.3MB, pdf)
Supplementary Figure 3
Click here for additional data file. (4.9MB, pdf)
Supplementary Figure 4
Click here for additional data file. (4.9MB, pdf)
Supplementary Figure 5
Click here for additional data file. (878.4KB, pdf)
Supplementary Figure 6
Click here for additional data file. (8.2MB, pdf)
Supplementary Figure 7
Click here for additional data file. (11.4MB, pdf)
Supplementary Figure 8
Click here for additional data file. (892.7KB, pdf)
Supplementary Figure 9
Click here for additional data file. (6.9MB, pdf)
Supplementary Figure 10
Click here for additional data file. (14.3MB, pdf)
Supplementary Information
Click here for additional data file. (34.4KB, docx)

References

  1. Manolio TA, Collins FS, Cox NJ et al: Finding the missing heritability of complex diseases. Nature 2009; 461: 747–753. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Auer PL, Lettre G: Rare variant association studies: considerations, challenges and opportunities. Genome Med 2015; 7: 16. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Auer PL, Teumer A, Schick U et al: Rare and low-frequency coding variants in CXCR2 and other genes are associated with hematological traits. Nat Genet 2014; 46: 629–634. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Do R, Stitziel NO, Won HH et al: Exome sequencing identifies rare LDLR and APOA5 alleles conferring risk for myocardial infarction. Nature 2014; 518: 102–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Emond MJ, Louie T, Emerson J et al: Exome sequencing of extreme phenotypes identifies DCTN4 as a modifier of chronic Pseudomonas aeruginosa infection in cystic fibrosis. Nat Genet 2012; 44: 886–889. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Huyghe JR, Jackson AU, Fogarty MP et al: Exome array analysis identifies new loci and low-frequency variants influencing insulin processing and secretion. Nat Genet 2013; 45: 197–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Lange LA, Hu Y, Zhang H et al: Whole-exome sequencing identifies rare and low-frequency coding variants associated with LDL cholesterol. Am J Hum Genet 2014; 94: 233–245. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Peloso GM, Auer PL, Bis JC et al: Association of low-frequency and rare coding-sequence variants with blood lipids and coronary heart disease in 56,000 whites and blacks. Am J Hum Genet 2014; 94: 223–232. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Tg, Hdl Working Group of the Exome Sequencing Project NHL, Blood I, Crosby J, Peloso GM et al: Loss-of-function mutations in APOC3, triglycerides, and coronary disease. N Engl J Med 2014; 371: 22–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Lee S, Abecasis GR, Boehnke M et al: Rare-variant association analysis: study designs and statistical tests. Am J Hum Genet 2014; 95: 5–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Lee S, Emond MJ, Bamshad MJ et al: Optimal unified approach for rare-variant association testing with application to small-sample case-control whole-exome sequencing studies. Am J Hum Genet 2012; 91: 224–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Li B, Leal SM: Methods for detecting associations with rare variants for common diseases: application to analysis of sequence data. Am J Hum Genet 2008; 83: 311–321. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Lin DY, Tang ZZ: A general framework for detecting disease associations with rare variants in sequencing studies. Am J Hum Genet 2011; 89: 354–367. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Logsdon BA, Dai JY, Auer PL et al: A variational Bayes discrete mixture test for rare variant association. Genet Epidemiol 2014; 38: 21–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Price AL, Kryukov GV, de Bakker PI et al: Pooled association tests for rare variants in exon-resequencing studies. Am J Hum Genet 2010; 86: 832–838. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Wu MC, Lee S, Cai T et al: Rare-variant association testing for sequencing data with the sequence kernel association test. Am J Hum Genet 2011; 89: 82–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Reiner AP, Lettre G, Nalls MA et al: Genome-wide association study of white blood cell count in 16,388 African Americans: the continental origins and genetic epidemiology network (COGENT). PLoS Genet 2011; 7: e1002108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Schick UM, Auer PL, Bis JC et al: Association of exome sequences with plasma C-reactive protein levels in >9000 participants. Hum Mol Genet 2015; 24: 559–571. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Huber PJ Robust Statistics. Hoboken, N.J 2009.
  20. Auer PL, Wang G, Leal SM: Testing for rare variant associations in the presence of missing data. Genet Epidemiol 2013; 37: 529–538. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Morris AP, Zeggini E: An evaluation of statistical approaches to rare variant analysis in genetic association studies. Genet Epidemiol 2010; 34: 188–193. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Design of the Women's Health Initiative clinical trial and observational study. The Women's Health Initiative Study Group. Control Clin Trials 1998; 19: 61–109. [DOI] [PubMed] [Google Scholar]
  23. Purcell S, Neale B, Todd-Brown K et al: PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet 2007; 81: 559–575. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Beasley TM, Erickson S, Allison DB: Rank-based inverse normal transformations are increasingly used, but are they merited? Behav Genet 2009; 39: 580–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Locke AE, Kahali B, Berndt SI et al: Genetic studies of body mass index yield new insights for obesity biology. Nature 2015; 518: 197–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Buzkova P: Linear regression in genetic association studies. PLoS One 2013; 8: e56976. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kutner MH, Nachtsheim CJ, Neter J et al: Applied Linear Statistical Models. McGraw-Hill/Irwin: New York, NY, 2005. [Google Scholar]
  28. Che R, Motsinger-Reif AA, Brown CC: Loss of power in two-stage residual-outcome regression analysis in genetic association studies. Genet Epidemiol 2012; 36: 890–894. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Demissie S, Cupples LA: Bias due to two-stage residual-outcome regression analysis in genetic association studies. Genet Epidemiol 2011; 35: 592–596. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Shapiro SS, Wilk MB: An Analysis of Variance Test for Normality. Biometrika 1965; 52: 591–611. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Figure 1
Click here for additional data file. (14MB, pdf)
Supplementary Figure 2
Click here for additional data file. (11.3MB, pdf)
Supplementary Figure 3
Click here for additional data file. (4.9MB, pdf)
Supplementary Figure 4
Click here for additional data file. (4.9MB, pdf)
Supplementary Figure 5
Click here for additional data file. (878.4KB, pdf)
Supplementary Figure 6
Click here for additional data file. (8.2MB, pdf)
Supplementary Figure 7
Click here for additional data file. (11.4MB, pdf)
Supplementary Figure 8
Click here for additional data file. (892.7KB, pdf)
Supplementary Figure 9
Click here for additional data file. (6.9MB, pdf)
Supplementary Figure 10
Click here for additional data file. (14.3MB, pdf)
Supplementary Information
Click here for additional data file. (34.4KB, docx)

Articles from European Journal of Human Genetics are provided here courtesy of Nature Publishing Group

RESOURCES