Abstract
Background
Covariate selection to reduce bias in observational data analysis has primarily relied upon statistical criteria to guide researchers. This approach may lead researchers to condition on variables that ultimately increase bias in the effect estimates. The use of directed acyclic graphs (DAGs) aids researchers in constructing thoughtful models based on hypothesized biologic mechanisms to produce the least biased effect estimates possible.
Methods
After providing an overview of different relations in DAGs and the prevailing mechanisms by which conditioning on variables increases or reduces bias in a model, we illustrate examples of DAGs for maternal antidepressants in pregnancy and four separate perinatal outcomes.
Results
By comparing and contrasting the diagrams for maternal antidepressant use in pregnancy and spontaneous abortion, major malformations, preterm birth, and postnatal growth, we illustrate the different conditioning sets required for each model. Moreover, we illustrate why it is not appropriate to condition on the same set of covariates for the same exposure and different perinatal outcomes. We further discuss potential selection biases, over-adjustment of mediators on the causal path, and sufficient sets of conditioning variables.
Conclusion
In our efforts to construct parsimonious models that minimize confounding and selection biases, we must rely upon our scientific knowledge of the causal mechanism. By structuring data collection and analysis around hypothesized DAGs, we ultimately aim to validly estimate the causal effect of interest.
Introduction
In an attempt to make causal inferences from observational data, one must rely on the assumption of conditional exchangeability. Conditional exchangeability generally asserts that there is no unmeasured confounding or lack of comparability resulting from selection between treatment or exposure groups. More specifically, the compared groups are said to be exchangeable if their outcomes would be the same whenever they were subjected to the identical exposure history.1 This untestable assumption requires both an understanding of the causal structure of the relationship between the exposure, outcome and all covariates, and that variables in the causal structure were measured and correctly classified. In perinatal epidemiology, we may lack conditional exchangeability due to confounding or selection biases, and rely on analytical techniques in an effort to estimate the least biased effect estimate from the available data. Approaches to identify and control for confounding in observational studies have been discussed at length.2–4 Often, researchers employ statistical criteria for determining variable selection, primarily through one of three techniques: model selection from stepwise variable addition/subtraction, the use of univariate associations between the exposure/outcome and potential confounders within the data, or a change in estimate approach.3 These techniques rely solely on statistical associations or changes in the estimate or fit of the model to dictate inclusion of covariates, and may unintentionally introduce further bias into the model if non-confounders are included or important confounders are omitted. Moreover, the first two techniques use statistical significance to dictate confounder selection that is heavily reliant on power. Without adequate statistical power, p-values will exhibit wide sample to sample variability.5 The third technique, change in estimate, is dependent upon the other covariates already in the model. Further, in logistic regression models, if the potential confounder is not associated with the outcome, change in estimate criteria may falsely indicate confounding. Such false indication of confounding occurs more often as the strength of the association between covariate and exposure increases.6 Finally, in logistic regression models, changes in the estimate may result from non-collapsibility even in the absence of confounding.7
In an effort to select parsimonious models that incorporate our understanding of the biologic mechanism and causal structure of interest, researchers increasingly construct a type of causal diagram termed a directed acyclic graph (DAG). These diagrams provide a visual aid to the construction of a causal map of the relations of interest and pathways through which systematic bias may arise. Using subject matter knowledge, researchers make assumptions about the causal relations among variables, which are then used to guide data collection and analysis. Consequently, researchers rely on the purported causal mechanism as opposed to statistical associations to identify and address systematic bias.8,9 Although researchers may disagree on the causal structure and hypothesize several candidate DAGs, these relations, not statistical significance, then dictate which covariates to include in the analysis to reduce biases arising from confounding or selection.
Directed acyclic graphs (DAGs)
There are many thorough and accessible texts that illustrate the construction and interpretation of DAGs that readers may refer to. 8–11 In brief, causal diagrams are graphical models for causal relations. Causal DAGs display non-parametric information about the web of causation. As indicated in the name, DAGs are acyclic, meaning they contain no feedback loops, i.e. a variable cannot cause itself. In causal DAGs, single headed arrows encode the causal relations between variables and all common causes of variables are included. In Figure 1, the arrow between X (exposure) and Y (outcome) represents the direct effect of X on Y. Directed paths between variables are noncrossing and nonrepeating sequences in which all connections flow head to tail. All other paths are undirected paths. In Figure 1, a directed path lies from X to Y through M. An undirected path lies from X to Y through Z2. Variables through which a directed path passes are intermediates (e.g. Figure 1, variable M on the path from X→M→Y).
Figure 01.
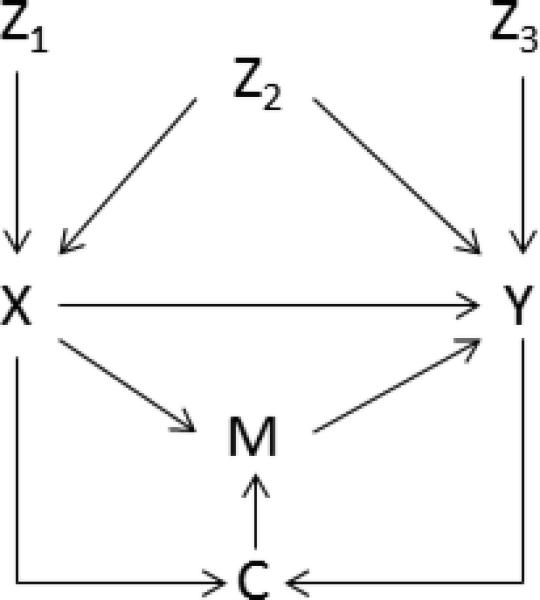
Directed acyclic graph (DAG) of the effects of X (exposure) on Y (outcome).
A variable is a confounder of the effect of exposure on the outcome if it is a common cause of both the exposure and the outcome (e.g. Figure 1, variable Z2). Confounders sit on what are termed “backdoor paths,” because the path from one variable (e.g., the exposure) to the other variable (e.g., the outcome) through the confounder departs against an arrow. An example of a backdoor path in Figure 1 is the path from X to Y through Z2. A variable that has two arrows pointing into it is termed a collider (e.g. Figure 1, variable C). Colliders are path specific, and a variable can be both an intermediate (M on the path from X→M→Y) and a collider (M on the path from X→M←C←Y) depending on which path is being examined. Finally, a path is open, or unblocked, unconditionally if there is no collider on it. Paths with a collider present are unconditionally blocked or closed (e.g. X→C←Y is blocked at C). Conditioning on a noncollider closes the path and removes the association between its adjacent variables (e.g. conditioning on Z2 closes the path from X to Y through Z2), while conditioning on a collider (or the descendent of a collider) opens a path between its adjacent variables (e.g. conditioning on C opens the path from X→C←Y). Finally, a sufficient set of variables is a set of variables that closes all biasing paths between X and Y. This set is minimally sufficient if there is no subset of this set able to control the bias.8,10
This paper will further review the relations that exist in DAGs and conditions in which biases arise, and then will present a motivating example of maternal antidepressant use in pregnancy and four common perinatal outcomes, comparing and contrasting the suggested DAGs.
Adjustment and overadjustment in models
There are many methods one may utilize to minimize bias from a confounder, including stratification by or adjustment for the variable, creation of propensity scores for adjustment9,10 or the use of inverse probability of treatment weights9,10. Irrespective of the method chosen, the following categories indicate which variables in a DAG need be adjusted for, and others for which adjustment could introduce bias.
Confounder- a variable that is associated with the exposure in the source population, a risk factor for the outcome, and are not effects of the exposure or outcome (Figure 1, variable Z2).10 Failure to adjust for confounders may result in a lack of exchangeability between the groups and in a biased estimate of the effect of the exposure on the outcome. In an effort to construct parsimonious models, causal diagrams assist to determine minimally sufficient sets of covariates required to minimize confounding bias.
Collider- a variable is termed a collider if it is on a path where two arrowheads meet. Often encountered in a DAG as selection bias or collider stratification bias (e.g. Berkson's, differential loss-to-follow up, self-selection), stratification by or adjustment of a collider may result in bias that is as strong as confounding bias or may even move the observed effect in the opposite direction of the true effect.10–13
Intermediate- a variable that is an effect of the exposure and that affects the outcome (Figure 1, variable M on the path X→M→Y). Termed “overadjustment,” control of a variable on the causal path from the exposure to the outcome prevents the estimation of the total causal effect.14 Further, if there are unmeasured common causes of the intermediate variable and outcome, conditioning on the intermediate variable will introduce collier stratification bias.10,14
Adjusting for the following two categories of covariates (Figure 1, variables Z1 and Z3) constitutes “unnecessary adjustment.” They do not reside on biasing paths, and their exclusion from statistical models should not change the expectation of the causal effect estimate from exposure to outcome.14 Nonetheless, they are often included in analyses, and may have ramifications on effect estimates.
-
4.
Predictor of the exposure- a variable that is associated with the exposure but not the outcome (e.g. instrumental variable (Figure 1, variable Z1), or strongly associated with exposure and weakly associated with the outcome). These variables should not be adjusted for, as bias amplification may result if there is an unmeasured common cause (confounding) of the exposure-outcome relationship.15,16 However, Myers et. al. noted that the bias resulting from conditioning on an IV is typically smaller than from failing to adjust for a confounder. Therefore, minimizing confounding bias at the risk of adjusting for an IV may be prudent.16
-
5.
Predictor of the outcome- a variable that is associated with the outcome but not the exposure (Figure 1, variable Z3). Conditioning upon these variables may increase precision in the estimate in linear models, although at the expense of degrees of freedom.14,15 However, Robinson and Jewell previously demonstrated that in logistic regression models, such inclusion decreased precision in the estimate.17 Further, in logistic regression models, the crude and marginal odds ratios may differ due to noncollapasbility, confusing interpretation of the results when unnecessary covariates are included.14
Example: maternal antidepressants in pregnancy and perinatal outcomes
To illustrate the use of DAGs in perinatal epidemiology, we will now examine four common perinatal outcomes (spontaneous abortion, major structural malformations, preterm birth, and postnatal growth) with maternal antidepressant use in pregnancy. These examples will show the similarities and subtle differences in the DAGs for different outcomes, resulting in different sufficient sets of covariates necessary to estimate the total causal effects of maternal antidepressants on each outcome. In our causal diagrams, biasing paths (confounders or colliders that have been conditioned upon) are denoted with solid lines. Non-biasing paths that require no adjustment are denoted with dashed edges. These include pathways with variables that would result in overadjustment (intermediates), as well as variables only associated with exposure (maternal antidepressants) or outcome that, as previously discussed, need not be conditioned upon to remove bias. In all of the examples, we assume there is no direct effect of maternal antidepressants and the selected outcomes. For simplicity, we are displaying confounders common across all diagrams, namely maternal age, race/ethnicity, alcohol and tobacco use, and chronic medical conditions, as one variable (C*). Additionally, for brevity, the complex web of relations between potential confounders is not displayed; this level of detail would distract readers from the main points of appropriate control variables. Omission of these additional arrows does not, however, change the conditioning sets that would be required for these DAGs. However, in practice, the full causal model should be considered in order to ascertain minimally sufficient conditioning sets of variables. While these examples are by no means an exhaustive list of factors that may influence the exposure or outcome, we have relied upon previous literature for assessment of potential confounders and colliders.
Spontaneous abortion (SAB)
In Figure 2a we have identified several confounders of the total causal effect of maternal antidepressant use in pregnancy on spontaneous abortion. In this diagram based upon our hypothesized causal mechanisms largely from previous literature, confounders include depression, pre-pregnancy body mass index (BMI), maternal age and race/ethnicity, alcohol or tobacco use, chronic medical conditions, socioeconomic status (SES), prenatal care and folic acid.18,19 Per the proposed diagram, any of the final three covariates would suffice in closing the biasing path through folic acid, although more than one can be included in the model.20
Figure 02.
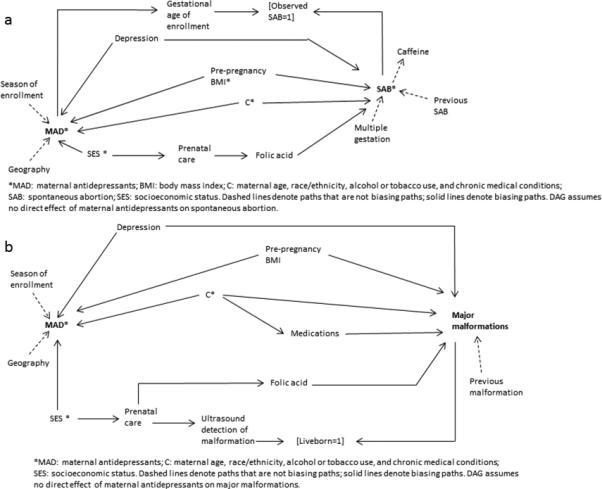
Directed acyclic graphs (DAGs) for (2a) the effects of maternal antidepressants on spontaneous abortion; and (2b) the effects of maternal antidepressants on major structural malformations.
Several publications have noted the possibility of left truncation bias due to the timing of enrollment.22–24 If gestational age of enrollment is differential by exposure, a selection bias may be induced. If women who use antidepressants enroll later and thus have fewer observed spontaneous abortions, the effect estimate may be biased. They are automatically conditioned upon (inducing collider stratification bias) by the absence of “unobserved” spontaneous abortions (denoted in the Fig. 2a DAG by “observed SAB=1”). Different methods to correct for this bias have been proposed, including conditioning upon a continuous variable of gestational age of enrollment24 or employing Cox regression models that incorporate person time into the model.23
Per this DAG and our hypothesized causal mechanisms, we would not adjust for season of enrollment or geography (instrumental variables that in the presence of uncontrolled confounding may amplify bias) or previous spontaneous abortion or multiple gestation (predictors of outcome). As predictors only of spontaneous abortion, the latter variables are not confounding the association of interest and are therefore not necessary in a model. As previously discussed, adjusting for them could reduce precision in logistic regression models. However, if the model employed is one other than logistic regression, their inclusion may increase precision at the expense of degrees of freedom. Thus, inclusion of these variables for the intent of increased precision should be considered against the noted concessions. Of note, several studies have suggested coffee consumption may be a risk factor for spontaneous abortion.18 However, we hypothesize, as have others,21 that the association between coffee and spontaneous abortion could be one of reverse causality, i.e. women undergoing a pregnancy loss that has not yet been recognized may lose their aversion to coffee, and displayed it as such on the diagram.
However, additional consideration may be given for variables such as previous spontaneous abortion. If researchers believe previous spontaneous abortion changed the behavior of women in their current pregnancies with respect to maternal antidepressants (e.g.- they feared antidepressants were associated with their previous spontaneous abortion and therefore discontinued use for this pregnancy) then the DAG would include an arrow from previous spontaneous abortion to maternal antidepressants and one would adjust for previous spontaneous abortion as a confounder. These hypotheses are specific to each exposure and study population and must be considered individually.
Major structural malformations
For the causal effect of maternal antidepressants on major structural malformations, depression, pre-pregnancy BMI, maternal age, race/ethnicity, alcohol/tobacco, chronic medical conditions or medications, and SES, prenatal care or folic acid are all potential confounders 25–27 based upon our hypothesized diagram in Figure 2b.
Here we hypothesize a selection bias that occurs from differential ultrasound detection of malformation by maternal antidepressant use (through an SES/prenatal care pathway) that results when only liveborns are included in analyses. For biases such as this, correction of the estimate is possible if one conditions on the use of ultrasound (or in this example, prenatal care or SES). Eliminating this selection bias through covariate adjustment is possible because selection (at liveborn=1) was dependent on these predictors of exposure, not the exposure itself. Alternatively, if researchers can obtain information on aborted pregnancies, statistical techniques such as inverse probability of censoring weights may be employed.11,28
Preterm birth
From our diagram of pregnancy antidepressant use and preterm birth (Figure 3a), one would adjust for confounding by depression or prenatal stress, maternal age, race/ethnicity, alcohol or tobacco use, and chronic medical conditions, SES or prenatal care.29 One would not adjust for birth defects30 as they are proposed mediators in the path from maternal antidepressants and preterm birth; as such, their inclusion in models would constitute overadjustment. Preeclampsia31 is on both a mediating and biasing pathway and cannot be directly adjusted. However, the confounding bias could be adjusted for using predictors of preeclampsia, such as chronic hypertension or pre-pregnancy BMI.
Figure 03.
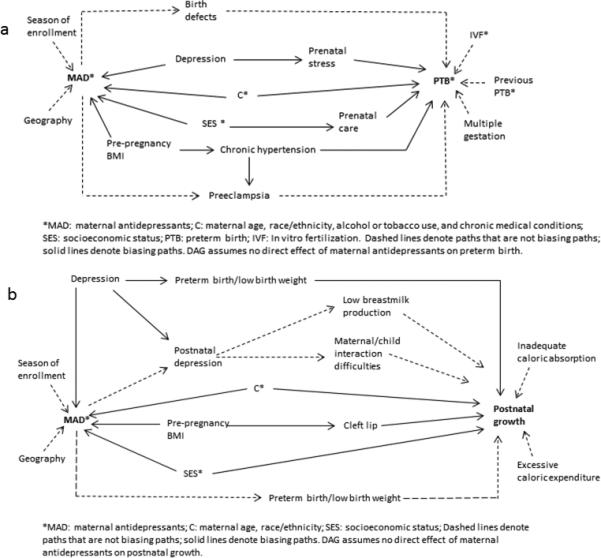
Directed acyclic graphs (DAGs) for (3a) the effects of maternal antidepressants on preterm birth; and (3b) the effects of maternal antidepressants on postnatal growth.
In the DAG of preterm birth we did not include selection bias through gestational age at enrollment as preterm birth tends to occur much later in gestation at a point when many studies have stopped enrolling women. However, if enrollment can happen any time before birth, and differential gestational age of enrollment by exposure is a concern, then the selection bias discussed with spontaneous abortion could also be present for preterm birth (see section on spontaneous abortion). This would require adjustment or the appropriate statistical models as discussed.
Postnatal growth
Our final outcome of postnatal growth was included to demonstrate that outcomes more temporally distant from the exposure require careful consideration of what covariates meet the definition for a confounder. As the temporal distance from exposure to outcome increases, more covariates may reside on mediating pathways, occurring after the exposure. In the diagram for postnatal growth (Figure 3b) we would adjust for maternal depression (or downstream effects including preterm birth/low birth weight (PTB/LBW), maternal age, race/ethnicity, pre-pregnancy BMI or cleft lip, and SES).32,33 Previous literature has suggested maternal antidepressant use in pregnancy may be protective against postpartum depression,34 and is displayed as a mediating pathway in our DAG. As such, effects of postpartum depression such as low breast milk production and maternal/child interactional difficulties would not be appropriate for adjustment. Postnatal factors such as inadequate caloric absorption or excessive caloric expenditure secondary to medical factors would not confound the association with prenatal maternal antidepressant use as they occur after the antidepressant use. Unless they share a common cause with maternal antidepressants in pregnancy, they do not temporally meet the definition of a confounder. Finally, with respect to the mediated path with PTB/LBW at the bottom of the diagram, if researchers hypothesize that these outcomes result from pregnancy antidepressant use, they would be mediators and should not be adjusted. Of note, we hypothesized PTB/LBW as both on a biased path through maternal depression, as well as a mediated path35 resulting from antidepressants. In our diagram, we could adjust for maternal depression and leave PTB/LBW out of the models. However, without a measure of depression or another predictor of PTB/LBW, the researchers could consider the hypothesized strength of the bias resulting from adjusting or not adjusting for PTB/LBW. This consideration could guide their decision for the primary model and a sensitivity analysis could be performed using the other model.
Conclusions
These previous examples are hypothetical and are intended to illustrate the similarities and differences in covariate selection between often overlapping research outcomes. For all four of our outcomes, depression, maternal age, race/ethnicity, pre-pregnancy BMI and SES measures were considered confounders. Maternal alcohol, tobacco and chronic medical conditions were hypothesized confounders of all birth outcomes, but not of postnatal growth, emphasizing the importance of temporality and biologic plausibility. We demonstrated how variables such as preeclampsia and preterm birth can lie on both confounding and mediating pathways, highlighting the importance of careful thought and disease state knowledge when constructing a causal model. Additionally, the use of DAGs helped us illustrate where we believed selection biases could occur. Perinatal epidemiology is particularly vulnerable to left truncation bias from early pregnancy loss or termination as displayed in our DAGs for spontaneous abortion and major malformations. DAGs allowed us to visualize which, if any, variables were at our disposal to correct the bias. Finally, the diagrams guided us in determining whether confounders shared biasing paths (e.g. SES and prenatal care in the models of spontaneous abortion, major malformations and preterm birth), allowing us to correct bias with selected variables rather than including all confounders in adjusted models. This last consideration is particularly of use with small sample sizes where strata become increasingly sparse with increased adjustment.
Biologic mechanisms in the vast majority of birth outcomes research remain elusive and causal models are difficult to construct. The complicated etiologies of these outcomes may result in several candidate DAGs to explore in analyses, which will facilitate research teams in selecting their final model(s). Even if researchers are left with effect estimates that include bias, the knowledge of where the biases are originating from will help to quantify and communicate the limitations, and guide future study design. Ultimately, the thoughtful use of subject matter knowledge combined with an understanding of the implications for adjustment of different variables will guide researchers in their quest to use observational data for causal inference.
Acknowledgements
Kristin Palmsten was supported by a career development award from the Eunice Kennedy Shriver National Institute of Child Health & Human Development, National Institutes of Health (K99HD082412).
References
- 1.Greenland S, Robins JM. Identifiability, exchangeability and confounding revisited. Epidemiol Perspect Innov. 2009;6:4. doi: 10.1186/1742-5573-6-4. doi:10.1186/1742-5573-6-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Robins JM. Data, Design, and Background Knowledge in Etiologic Inference. Epidemiology. 2015;12(3):313–320. doi: 10.1097/00001648-200105000-00011. [DOI] [PubMed] [Google Scholar]
- 3.Hernán M a., Hernández-Diaz S, Werler MM, Mitchell A a. Causal knowledge as a prerequisite for confounding evaluation: An application to birth defects epidemiology. Am J Epidemiol. 2002;155(2):176–184. doi: 10.1093/aje/155.2.176. doi:10.1093/aje/155.2.176. [DOI] [PubMed] [Google Scholar]
- 4.Evans D, Chaix B, Lobbedez T, Verger C, Flahault A. Combining directed acyclic graphs and the change-in-estimate procedure as a novel approach to adjustment-variable selection in epidemiology. BMC Med Res Methodol. 2012;12(1):156. doi: 10.1186/1471-2288-12-156. doi:10.1186/1471-2288-12-156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Halsey LG, Curran-Everett D, Vowler SL, Drummond GB. The fickle P value generates irreproducible results. Nat Methods. 2015;12(3):179–185. doi: 10.1038/nmeth.3288. doi:10.1038/nmeth.3288. [DOI] [PubMed] [Google Scholar]
- 6.Bliss R, Weinberg J, Webster T, Vieira V. Determining the Probability Distribution and Evaluating Sensitivity and False Positive Rate of a Confounder Detection Method Applied To Logistic Regression. J Biomed Biostat. 2013;3(4):142. doi: 10.4172/2155-6180.1000142. doi:10.4172/2155-6180.1000142.Determining. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pearl J, Robins JM, Greenland S. Confounding and Collapsibility in Causal Inference. Stat Sci. 1999;14(1):29–46. doi:10.1214/ss/1009211805. [Google Scholar]
- 8.Greenland S, Pearl J, Robins JM. Causal diagrams for epidemiologic research. Epidemiology. 1999;10(1):37–48. doi:10.1097/00001648-199901000-00008. [PubMed] [Google Scholar]
- 9.Hernán M a., Robins JM. Causal Inference: The Book. Chapman & Hall/CRC; 2015. doi:10.1097/00001648-199311000-00013. [Google Scholar]
- 10.Rothman KJ, Greenland S, Lash TL. Modern Epidemiology. Third Ed. Wolters Kluwer Health/Lippincott Williams & Wilkins; 2008. [Google Scholar]
- 11.Hernán M a, Hernández-Díaz S, Robins JM. A structural approach to selection bias. Epidemiology. 2004;15(5):615–625. doi: 10.1097/01.ede.0000135174.63482.43. doi:10.1097/01.ede.0000135174.63482.43. [DOI] [PubMed] [Google Scholar]
- 12.Whitcomb BW, Schisterman EF, Perkins NJ, Platt RW. Quantification of collider-stratification bias and the birthweight paradox. Paediatr Perinat Epidemiol. 2009;23(5):394–402. doi: 10.1111/j.1365-3016.2009.01053.x. doi:10.1111/j.1365-3016.2009.01053.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wei L, Brookhart MA, Schneeweiss S, Mi X, Setoguchi S. Implications of m bias in epidemiologic studies: A simulation study. Am J Epidemiol. 2012;176(10):938–948. doi: 10.1093/aje/kws165. doi:10.1093/aje/kws165. [DOI] [PubMed] [Google Scholar]
- 14.Schisterman E, Cole S, Platt R. Overadjustment Bias and Unnecessary Adjustment in Epidemiologic Studies. Epidemiology. 2009;20(4):488–495. doi: 10.1097/EDE.0b013e3181a819a1. doi:10.1097/EDE.0b013e3181a819a1.Overadjustment. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ali MS, Groenwold R, Pestman W, et al. Propensity score balance measures in pharmacoepidemiology: a simulation study. Pharmacoepidemiol Drug Saf. 2014;23:802–811. doi: 10.1002/pds.3574. doi:10.1002/pds. [DOI] [PubMed] [Google Scholar]
- 16.Myers J a., Rassen J a., Gagne JJ, et al. Effects of adjusting for instrumental variables on bias and precision of effect estimates. Am J Epidemiol. 2011;174(11):1213–1222. doi: 10.1093/aje/kwr364. doi:10.1093/aje/kwr364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Robinson LD, Jewell NP. Some Surprising Results About Covariate Adjustment in Logistic Regression Models. Int Stat Rev. 1991;58(2):227–240. [Google Scholar]
- 18.Feodor Nilsson S, Andersen PK, Strandberg-Larsen K, Nybo Andersen a. M. Risk factors for miscarriage from a prevention perspective: A nationwide follow-up study. BJOG An Int J Obstet Gynaecol. 2014:1375–1385. doi: 10.1111/1471-0528.12694. doi:10.1111/1471-0528.12694. [DOI] [PubMed] [Google Scholar]
- 19.Bonari L, Pinto N, Ahn E, Einarson A, Steiner RNM, Koren FG. Perinatal Risks of Untreated Depression During Pregnancy. Can J Psychiatry. 2004;49(11) doi: 10.1177/070674370404901103. [DOI] [PubMed] [Google Scholar]
- 20.Fewell Z, Davey Smith G, Sterne J a C. The impact of residual and unmeasured confounding in epidemiologic studies: A simulation study. Am J Epidemiol. 2007;166(6):646–655. doi: 10.1093/aje/kwm165. doi:10.1093/aje/kwm165. [DOI] [PubMed] [Google Scholar]
- 21.Stein Z, Susser M. Miscarriage, Caffeine, and the Epiphenomena of Pregnancy: The Causal Model. Epidemiology. 1991;2(3):163–167. [PubMed] [Google Scholar]
- 22.Daniel S, Koren G, Lunenfeld E, Levy A. Immortal time bias in drug safety cohort studies: spontaneous abortion following nonsteroidal antiinflammatory drug exposure. Am J Obstet Gynecol. 2015;212(3):307.e1–e307.e6. doi: 10.1016/j.ajog.2014.09.028. doi:10.1016/j.ajog.2014.09.028. [DOI] [PubMed] [Google Scholar]
- 23.Howards PP, Hertz-Picciotto I, Poole C. Conditions for bias from differential left truncation. Am J Epidemiol. 2007;165(4):444–452. doi: 10.1093/aje/kwk027. doi:10.1093/aje/kwk027. [DOI] [PubMed] [Google Scholar]
- 24.Margulis A, Mittleman M, Glynn R, Holmes L, Hernandez-Diaz S. Effects of gestational age at enrollment in pregnancy exposure registries. Pharmacoepidemiol Drug Saf. 2015;24:343–352. doi: 10.1002/pds.3731. doi:10.1002/pds. [DOI] [PubMed] [Google Scholar]
- 25.Brent RL. Environmental causes of human congenital malformations: the pediatrician's role in dealing with these complex clinical problems caused by a multiplicity of environmental and genetic factors. Pediatrics. 2004;113(4 Suppl):957–968. doi:10.1542/peds.113.4.S1.957. [PubMed] [Google Scholar]
- 26.Källén B. The Problem of Confounding in Studies of the Effect of Maternal Drug Use on Pregnancy Outcome. Obstet Gynecol Int. 2012;2012:1–16. doi: 10.1155/2012/148616. doi:10.1155/2012/148616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Huybrechts K, Palmsten K, Avorn J, et al. Antidepressant Use in Pregnancy and the Risk of Cardiac Defects. N Engl J Med. 2014;370:2397–2407. doi: 10.1056/NEJMoa1312828. doi:10.1056/NEJMoa1312828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Howards PP, Johnson CY, Honein M a., Flanders WD. Adjusting for Bias Due to Incomplete Case Ascertainment in Case-Control Studies of Birth Defects. Am J Epidemiol. 2015;181(8):595–607. doi: 10.1093/aje/kwu323. doi:10.1093/aje/kwu323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Moutquin JM. Classification and heterogeneity of preterm birth. BJOG An Int J Obstet Gynaecol. 2003;110(SUPPL. 20):30–33. doi: 10.1016/s1470-0328(03)00021-1. doi:10.1016/S1470-0328(03)00021-1. [DOI] [PubMed] [Google Scholar]
- 30.Tuccori M, Testi A, Antonioli L, et al. Safety concerns associated with the use of serotonin reuptake inhibitors and other serotonergic/noradrenergic antidepressants during pregnancy: A review. Clin Ther. 2009;31:1426–1453. doi: 10.1016/j.clinthera.2009.07.009. doi:10.1016/j.clinthera.2009.07.009. [DOI] [PubMed] [Google Scholar]
- 31.Palmsten K, Setoguchi S, Margulis A V, Patrick AR, Hernández-Díaz S. Elevated risk of preeclampsia in pregnant women with depression: Depression or antidepressants? Am J Epidemiol. 2012;175(10):988–997. doi: 10.1093/aje/kwr394. doi:10.1093/aje/kwr394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cole SZ, Lanham JS. Failure to thrive: An update. Am Fam Physician. 2011;83(7):829–834. [PubMed] [Google Scholar]
- 33.Block RW. Failure to Thrive as a Manifestation of Child Neglect. Pediatrics. 2005;116(5):1234–1237. doi: 10.1542/peds.2005-2032. doi:10.1542/peds.2005-2032. [DOI] [PubMed] [Google Scholar]
- 34.Cohen LS, Altshuler LL, Harlow BL, et al. Relapse of Major Depression During Pregnancy in Women Who Maintain or Discontinue Antidepressant Treatment. Tje J Am Med Assoc. 2015;295(5):499–508. doi: 10.1001/jama.295.5.499. [DOI] [PubMed] [Google Scholar]
- 35.Huang H, Coleman S, Bridge J a., Yonkers K, Katon W. A meta-analysis of the relationship between antidepressant use in pregnancy and the risk of preterm birth and low birth weight. Gen Hosp Psychiatry. 2014;36(1):13–18. doi: 10.1016/j.genhosppsych.2013.08.002. doi:10.1016/j.genhosppsych.2013.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]


