Sufficient Cause Representation of the Four-Way Decomposition for Mediation and Interaction

To the Editor

Recent work¹ has shown how a total effect of an exposure on an outcome, in the context of a mediator with which the exposure might interact, could be decomposed into four components: that due to just mediation, that due to just interaction, that due to both mediation and interaction, and that due to neither mediation nor interaction. In this research letter we show how each of these four components can be expressed within the sufficient cause framework allowing for mediation^2,3.

Let A be an exposure, M a mediator, and Y an outcome. For simplicity, we consider the case in which A, M, and Y are all binary. Within the counterfactual framework, we define Y_a as the outcome Y we would have observed if A had been set to a. The total effect is defined by Y₁ – Y₀. We define Y_am as the potential outcome Y if A were set to a, and M were set to m. We define M_a as the potential outcome M if A were set to a. We make consistency assumptions that Y_a =Y and M_a =M when A=a, and that Y_am=Y when A=a and M=m; we also make the composition assumption⁴ that Y_a = Y_aMa.

The four-way decomposition of the total effect can be written as:

$${\mathrm{Y}}_1–{\mathrm{Y}}_0=\mathrm{CDE}+{\mathrm{INT}}^{\mathrm{ref}}+{\mathrm{INT}}^{\mathrm{med}}+\mathrm{PIE}$$

where the four components are as follows: the controlled direct effect (CDE) is given by (Y₁₀ − Y₀₀) and is the component due to neither mediation nor interaction; the reference interaction (INT^ref) is given by (Y₁₁ − Y₁₀ − Y₀₁ + Y₀₀)M₀ and is the component due to interaction but not mediation; the mediated interaction (INT^med) is given by (Y₁₁ − Y₁₀ − Y₀₁ + Y₀₀) (M₁ − M₀) and is the component due to both mediation and interaction; and the pure indirect effect (PIE) is given by (Y₀₁ − Y₀₀) (M₁ − M₀) and is the component due to just mediation, not interaction. The first two components, the controlled direct effect and reference interaction, sum to the direct effect that is generally used in the mediation literature (also referred to as the “pure direct effect”⁵ or one type of “natural direct effect”⁶; and the third and fourth components, the mediated interaction and the pure indirect effect sum to the indirect effect that is generally used in the mediation literature (also referred to as the “total indirect effect”⁵ or one type of “natural indirect effect”⁶. Further discussion of the interpretation of these components, the assumptions needed to estimate them from data on average for a population, and statistical methods to do so are described in further detail in VanderWeele¹.

Here we will relate these four components to the sufficient cause framework allowing for mediation.^5,6,7 A sufficient cause model for a particular outcome posits a collection of different mechanisms each of which is capable of bringing about the outcome under consideration. A particular mechanism operates when some minimal set of actions, events, or states of nature is obtained; when all components required for the mechanism are present, the outcome inevitably occurs. These mechanisms are thus referred to as “sufficient causes” since the conjunction of all the components required for a particular mechanism to operate is sufficient for that outcome; the individual components required for particular mechanisms are then each referred to as “component causes.”

Hafeman² and VanderWeele³ considered the representation of mediation within this sufficient cause framework. Both considered a situation in which the exposure A never prevents the intermediate M or the outcome Y and in which the intermediate M never prevents the outcome Y. Such assumptions are sometimes referred to as monotonicity assumptions and they may or may not be reasonable assumptions in any given context. Under such monotonicity assumptions, there are two possible sufficient causes for the M: one sufficient cause that requires A and possibly some other factors, denoted here by J, to operate; and a second sufficient cause that may operate irrespective of whether A is present, provided some other factors, denoted by K, are present. In the context of exposure A and mediator M, for the outcome Y there are four sufficient causes: one involving both A and M and possibly some other factors F; one involving just A and possibly some other factors C; one involving just M and possibly some other factors B; and one requiring neither A nor M but simply some other factors L. The two sufficient causes for M are thus K and AJ; the four sufficient causes for Y are L, BM, CA, and FAM. Hafeman² and VanderWeele³ discussed the graphical representation⁹ of these sufficient causes which we give in Figure 1 and also the relation of direct and indirect effects to the background components of the sufficient cause model, namely K, J, L, B, C, and F.

Figure 1.

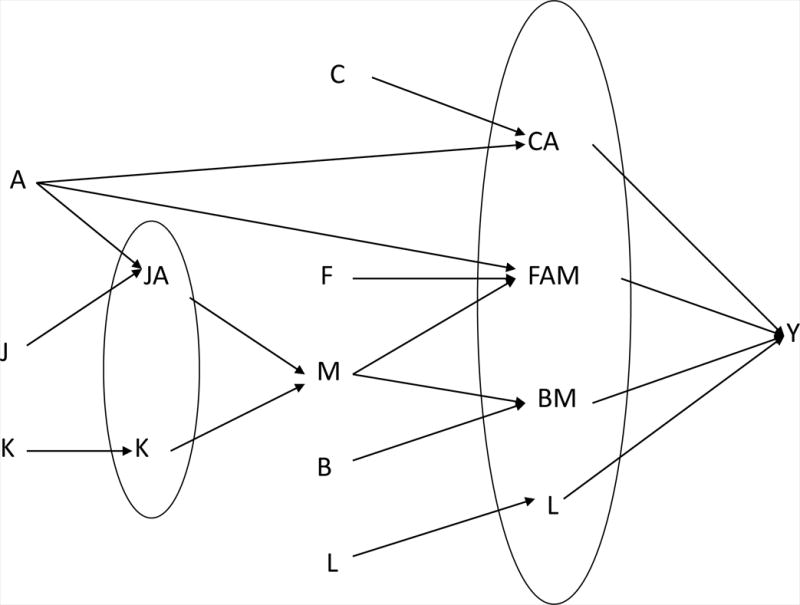
Here we provide similar relations for the components of the four-way decomposition. In the Appendix we show that we can express the average value for a population of each of the four components of the four-way decomposition as:

$$\begin{array}{l}\mathrm{E}[\mathrm{CDE}]=\mathrm{P}(\mathrm{C}=1,\mathrm{L}=0)\\ \mathrm{E}[{\mathrm{INT}}^{\mathrm{ref}}]=\{\mathrm{P}(\mathrm{F}=1,\mathrm{B}=0,\mathrm{C}=0,\mathrm{L}=0)-\mathrm{P}(\mathrm{F}=1,\mathrm{B}=1,\mathrm{C}=1,\mathrm{L}=0)\}\mathrm{P}(\mathrm{K}=1\mathrm{)}\\ \mathrm{E}[{\mathrm{INT}}^{\mathrm{med}}]=\{\mathrm{P}(\mathrm{F}=1,\mathrm{B}=0,\mathrm{C}=0,\mathrm{L}=0)-\mathrm{P}(\mathrm{F}=1,\mathrm{B}=1,\mathrm{C}=1,\mathrm{L}=0)\}\mathrm{P}(\mathrm{J}=1,\mathrm{K}=0)\\ \mathrm{E}[\mathrm{PIE}]=\mathrm{P}(\mathrm{B}=1,\mathrm{L}=0,\mathrm{J}=1,\mathrm{K}=0)\end{array}$$

Several interesting insights emerge from these expressions. For the controlled direct effect (CDE) to be present for an individual, the sufficient cause for Y involving A must be present (C=1) and that involving neither A nor M must be absent (L=0). For the reference interaction to be present for an individual the sufficient cause for M that does not require A must be present (K=1) and then the magnitude of the reference interaction is further determined by the portion of AM causing Y that occurs because K=1. This is the difference between 1) the likelihood of the interactive sufficient cause for Y requiring both A and M being present (F=1) with all other sufficient causes being absent (B=0,C=0,L=0), and 2) the likelihood of all of the sufficient causes for Y being present except that requiring neither A nor M (i.e. F=1,B=1,C=1,L=0). Note that in cases of “competing antagonism”⁹ in which the outcome Y occurs if either A or M or both are present (in Figure 1 if F=1,B=1,C=1), this decreases the magnitude of the reference interaction. This is because, in those cases, the effect of both A and M together is the same as the effect of just A or of just M alone, and thus the effect of both together is smaller than the sum of just A and of just M.

For the mediated interaction to be present for an individual the sufficient cause for M that does not require A must be absent (K=0) and the one requiring A must be present (J=1). Then, the magnitude of the mediated interaction is further determined by the difference between 1) the likelihood of the interactive sufficient cause for Y requiring both A and M being present (F=1) with all other sufficient causes being absent (B=0,C=0,L=0), and 2) the likelihood of all of the sufficient causes for Y being present except that requiring neither A nor M (i.e. F=1,B=1,C=1,L=0). For the pure indirect effect to be present for an individual, the sufficient cause for M that does not require A must be absent (K=0) and the one requiring A must be present (J=1). Then, it also must be the case that the sufficient cause for Y that involves M must be present (B=1) but the one requiring neither A nor M must be absent (K=0).

These expressions describe the four components of the four-way mediation-interaction decomposition in terms of sufficient causes.

Appendix

For a binary variable V, let I(V) denote the indicator function that V=1, and let V’ denote the complement of V i.e. that V=0. Using the counterfactual expression for each of the components of the four-way decomposition we have that:

$$\begin{array}{l}\mathrm{CDE}={\mathrm{Y}}_{10}-{\mathrm{Y}}_{00}=\mathrm{I}(\mathrm{L}\text{or}\mathrm{C})-\mathrm{I}(\mathrm{L})=\mathrm{I}(\mathrm{C}\mathrm{L}\text{'})\\ {\mathrm{INT}}^{\mathrm{ref}}=({\mathrm{Y}}_{11}-{\mathrm{Y}}_{10}-{\mathrm{Y}}_{01}+{\mathrm{Y}}_{00}){\mathrm{M}}_0=\{\mathrm{I}(\mathrm{L}\text{or}\mathrm{C}\text{or}\mathrm{B}\text{or}\mathrm{F})-\mathrm{I}(\mathrm{L}\text{or}\mathrm{C})-\mathrm{I}(\mathrm{L}\text{or}\mathrm{B})+\mathrm{I}(\mathrm{L})\}\mathrm{I}(\mathrm{K})=\{\mathrm{I}(\mathrm{FB}\text{'}\mathrm{C}\text{'}\mathrm{L}\text{'})-\mathrm{I}(\mathrm{FBCL}\text{'})\}\mathrm{I}(\mathrm{K})\\ {\mathrm{INT}}^{\mathrm{med}}=({\mathrm{Y}}_{11}-{\mathrm{Y}}_{10}-{\mathrm{Y}}_{01}+{\mathrm{Y}}_{00})({\mathrm{M}}_1-{\mathrm{M}}_0)=\{\mathrm{I}(\mathrm{L}\text{or}\mathrm{C}\text{or}\mathrm{B}\text{or}\mathrm{F})-\mathrm{I}(\mathrm{L}\text{or}\mathrm{C})-\mathrm{I}(\mathrm{L}\text{or}\mathrm{B})+\mathrm{I}(\mathrm{L})\}\{\mathrm{I}(\mathrm{A}\text{or}\mathrm{K})-\mathrm{I}(\mathrm{K})\}=\{\mathrm{I}(\mathrm{FB}\text{'}\mathrm{C}\text{'}\mathrm{L}\text{'})-\mathrm{I}(\mathrm{FBCL}\text{'})\}\mathrm{I}(\mathrm{AK}\text{'})\\ \mathrm{PIE}=({\mathrm{Y}}_{01}-{\mathrm{Y}}_{00})({\mathrm{M}}_1-{\mathrm{M}}_0)=\{\mathrm{I}(\mathrm{L}\text{or}\mathrm{B})-\mathrm{I}(\mathrm{L})\}\{\mathrm{I}(\mathrm{A}\text{or}\mathrm{K})-\mathrm{I}(\mathrm{K})\}=\mathrm{I}(\mathrm{BL}\text{'}\mathrm{AK}\text{'})\end{array}$$

Thus we have that:

$$\begin{array}{l}\mathrm{E}[\mathrm{CDE}]=\mathrm{P}(\mathrm{C}=1,\mathrm{L}=0)\\ \mathrm{E}[{\mathrm{INT}}^{\mathrm{ref}}]=\{\mathrm{P}(\mathrm{F}=1,\mathrm{B}=0,\mathrm{C}=0,\mathrm{L}=0)-\mathrm{P}(\mathrm{F}=1,\mathrm{B}=1,\mathrm{C}=1,\mathrm{L}=0)\}\mathrm{P}(\mathrm{K}=1)\\ \mathrm{E}[{\mathrm{INT}}^{\mathrm{med}}]=\{\mathrm{P}(\mathrm{F}=1,\mathrm{B}=0,\mathrm{C}=0,\mathrm{L}=0)-\mathrm{P}(\mathrm{F}=1,\mathrm{B}=1,\mathrm{C}=1,\mathrm{L}=0)\}\mathrm{P}(\mathrm{J}=1,\mathrm{K}=0)\\ \mathrm{E}[\mathrm{PIE}]=\mathrm{P}(\mathrm{B}=1,\mathrm{L}=0,\mathrm{J}=1,\mathrm{K}=0)\end{array}$$