Weather explains high annual variation in butterfly dispersal

Abstract

Weather conditions fundamentally affect the activity of short-lived insects. Annual variation in weather is therefore likely to be an important determinant of their between-year variation in dispersal, but conclusive empirical studies are lacking. We studied whether the annual variation of dispersal can be explained by the flight season's weather conditions in a Clouded Apollo (Parnassius mnemosyne) metapopulation. This metapopulation was monitored using the mark–release–recapture method for 12 years. Dispersal was quantified for each monitoring year using three complementary measures: emigration rate (fraction of individuals moving between habitat patches), average residence time in the natal patch, and average distance moved. There was much variation both in dispersal and average weather conditions among the years. Weather variables significantly affected the three measures of dispersal and together with adjusting variables explained 79–91% of the variation observed in dispersal. Different weather variables became selected in the models explaining variation in three dispersal measures apparently because of the notable intercorrelations. In general, dispersal rate increased with increasing temperature, solar radiation, proportion of especially warm days, and butterfly density, and decreased with increasing cloudiness, rainfall, and wind speed. These results help to understand and model annually varying dispersal dynamics of species affected by global warming.

1. Introduction

Dispersal is a key factor affecting distribution and population trends of species [1,2]. It is defined as movements potentially leading to gene flow [3]. The amount of dispersal and the distances moved by dispersing individuals have an important role in population responses to human-induced global changes such as habitat fragmentation and climate change [4]. The frequency of movements between habitat patches may have various effects on spatial population dynamics, which is central to metapopulation theory [5]. Dispersal movements between patches also influence the genetics and distribution of species as well as the evolution of dispersal itself via effects on individual fitness [6,7]. Understanding how intrinsic population biological processes and environmental variables affect dispersal is crucial to successfully managing (meta)populations for conservation and forecasting species responses to global changes [8].

Much empirical research has focused on documenting levels of dispersal between habitat patches and identifying factors affecting it [6,9,10]. Butterflies have been a popular model group in dispersal research [11–13], and a number of intrinsic population and environmental variables have been shown to significantly affect their movements [14]. Variation in dispersal may be sex-specific [15] and density-dependent [16], but it is also affected by species traits [17], landscape structure [12,18–20], and population history [21,22].

Certain features of weather, such as temperature and the amount of sunshine, also fundamentally influence the activity of invertebrates such as butterflies [23,24], but the effects of varying weather conditions on dispersal have been surprisingly little studied. Laboratory studies have documented temperature limits within which butterflies are capable of flying [25,26], and short-term field studies have shown how flight duration and the net displacement rate of individual butterflies increase with increasing temperature and decreasing cloudiness [27–30]. Annual variation in weather could therefore be an important determinant of between-year differences in butterfly dispersal. However, long-term studies documenting annual variation in dispersal activity within metapopulations are scarce [15,31], and conclusive studies on the role of annual weather conditions determining dispersal rates are lacking. This is an important gap in our understanding of the effects of weather on spatial population dynamics, especially given the large impact that recent changes in climate have already caused in various ecosystems worldwide [32,33].

Here, we report a 12-year study documenting large variation in annually observed between-patch movements within a butterfly metapopulation and show that this variation is closely associated with yearly differences in weather conditions (temperature, sunshine, cloudiness, rain, and windiness) during the flight seasons. According to our results, varying weather is the main driver causing variation in annual dispersal rates within the studied metapopulation of the Clouded Apollo butterfly.

2. Material and methods

(a). Study species and system

The Clouded Apollo (Parnassius mnemosyne) is a Palearctic butterfly that is classified as threatened in Finland and elsewhere in Europe [34–36]. In Finland, the Clouded Apollo is a rare inhabitant of traditionally managed flower-rich meadows and pastures accompanied with abundant Corydalis solida, the larval host plant [35].

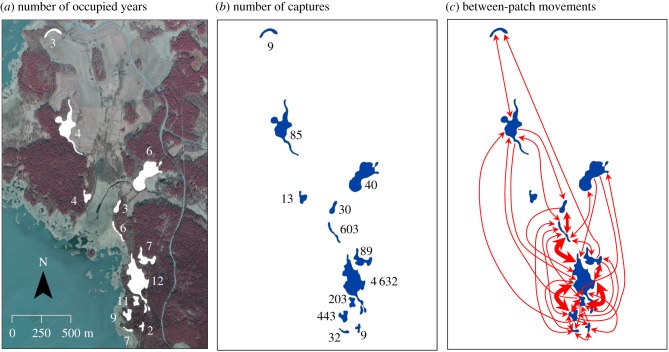
In order to study how annual weather conditions affect butterfly dispersal, we monitored individual movements within an introduced metapopulation of the Clouded Apollo butterfly using the mark–release–recapture (MRR) method during 2004–2015 (electronic supplementary material, table S1). Our study area is located in southern Finland, where the butterfly lives in a network of 12 habitat patches (figure 1). The landscape of the study area consists of a mosaic of forests, cultivated fields, and semi-natural grasslands (for a detailed description of the metapopulation see Kuussaari et al. [37]). During the study period, 2–12 of the patches (mean = 6.1) were annually occupied by the butterfly, with the estimated metapopulation size varying between 98 and 1 122 individuals (mean = 393; figure 1a; electronic supplementary material, table S1 and figure S1).

Figure 1.

Maps of the studied butterfly metapopulation with information on (a) the number of years of butterfly occupancy for the 12 suitable habitat patches plotted on an aerial photograph, (b) total number of butterfly capture events in different patches, and (c) frequency of observed between-patch movements during 2004–2015. Arrows indicate directions of movements and their width indicate the frequency of detected movements between pairs of habitat patches: the narrowest arrow less than 10, medium wide arrow more than 15, and the widest arrow more than 50 movements. (Online version in colour.)

A total of 2 468 Clouded Apollos were marked and 1 308 (53%) individuals recaptured at least once, with annual numbers varying between 56–523 (mean = 206) marked and 33–250 (mean = 109) recaptured individuals during the 12-year period (see figure 1b and electronic supplementary material, table S1, for spatial and annual results). Of all recaptured individuals, 216 (16.5%) were caught for the last time outside their natal patch, with a lot of annual variation in the amount of between-patch movement (electronic supplementary material, table S1). The majority of dispersal movements were observed between relatively closely located patches, but longer (more than 0.5 km) movements were also frequent in some years (figure 1c; electronic supplementary material, figure S2; [37]).

(b). Dispersal variables

We calculated three complementary measures of annual dispersal to study year-to-year variation in butterfly mobility. Firstly, the emigration rate was calculated as the fraction of recaptured individuals observed for the last time outside their natal habitat patch. This measure was based on all recaptured individuals regardless in which habitat patch they were originally marked. Most captures of emigrants were made within other habitat patches suitable for breeding, but a few of them were also made in the intervening areas. Here, as well as in the calculation of the other dispersal measures, each butterfly individual was considered only once. Therefore, the amount of annual between-patch movement reported in the electronic supplementary material, table S1 represents a conservative minimum estimate.

Secondly, we calculated the observed average residence time in the natal habitat patch. This measure was based only on individuals marked and recaptured in the largest (4.1 hectares (ha)) habitat patch which contained the largest local Clouded Apollo population of the metapopulation in every year [37]. This is a complementary measure associated with dispersal, because it describes the tendency of individuals to remain in their natal patch. Residence time and emigration rate measures are inverse to each other, being significantly negatively correlated (Pearson correlation: r = –0.80, p = 0.002, n = 12).

Thirdly, we calculated the average distance moved by individuals based on the distance between the first and last capture point of each recaptured individual. This measure was calculated by combining all recaptured individuals of the whole metapopulation. It is affected by both within- and between-patch movements (electronic supplementary material, figure S2). It correlates positively with the emigration rate (Pearson correlation: r = 0.74, p = 0.006, n = 12) and negatively (though not significantly) with the average residence time (Pearson correlation: r = –0.45, p = 0.14, n = 12).

All three annual dispersal measures were calculated separately for the sexes as well as for their combined data (electronic supplementary material, table S1). However, in the statistical analyses we used the estimates based on the combined data, because variation of annual dispersal was very similar between the two sexes (electronic supplementary material, table S1) with no significant differences except in the residence time. Even though males had on average longer residence times in the natal patch than females (paired t-test: p = 0.008, n = 12), the annual variation was positively correlated (Pearson correlation: r = 0.41, p = 0.41, n = 12) between the sexes. Previous studies have also reported a very similar dispersal tendency of the sexes in the Clouded Apollo [34,38], which supports our approach to combine the data of the sexes.

(c). Weather and adjusting variables

In our analyses, we used daily weather data available from a weather station (Harabacka) located approximately 7 km north of the butterfly study area and run by the Finnish Meteorological Institute. We calculated the annual explanatory weather variables based on the records made only during the yearly observed flight period of the Clouded Apollo in our study area. The timing and length of the butterfly's flight season varied considerably according to the annual weather conditions, with the mean length being 32.4 days (range 24–45), starting date being 1 June (range 24 May–7 June) and the ending date being 4 July (range 26 June–9 July). The following nine weather variables were used to explain between-year differences in butterfly dispersal (for the annual values see the electronic supplementary material, table S2 and figure S1): mean temperature (°C; based on multiple measurements per day), mean daily minimum and maximum temperature (°C), average cloudiness (measured as 0–8/8), mean wind speed (m s⁻¹), mean daily solar radiation (kJ m⁻²), and mean daily rainfall (mm) during the flight season, as well as the proportions of rainy (at least one millimetre of rain per day) and especially warm (more than 25°C) days during the flight season.

In addition to the weather variables, we measured three adjusting variables which might also affect the observed variation in butterfly dispersal (electronic supplementary material, table S2 and figure S1). Firstly, the annually estimated metapopulation size (total number of individuals calculated according to Kuussaari et al. [37]) served as a metapopulation level measure of butterfly density, a factor that has often been shown to impact butterfly dispersal [14,16,38]. Secondly, the annual number of occupied patches measured the spatial component of butterfly occurrence (figure 1a). Thirdly, we used the annual recapture rate of marked butterflies as a measure of study effort, which may also have an effect on dispersal results. This measure correlated strongly with the annual number of days spent in the field (Pearson correlation: r = 0.83, p < 0.001, n = 12), strongly negatively with annual metapopulation size (r = −0.77, p = 0.003, n = 12), and moderately negatively with the annual number of occupied patches (r = −0.51, p = 0.087, n = 12). In addition, metapopulation size and the number of annually occupied patches were strongly correlated (r = 0. 74, p = 0.006, n = 12).

(d). Statistical analyses

In order to explore relationships between the dispersal measures and the explanatory weather and adjusting variables, we calculated single Pearson correlations between each dispersal and explanatory measure. Pearson correlations could be used because all the dispersal measures were normally distributed. As the correlations with explanatory variables were very similar in the two sexes (electronic supplementary material, table S4), we opted to use the dispersal measures based on combined male and female data. To illustrate the correlation structure among the explanatory variables, we also calculated correlations between all explanatory variables (electronic supplementary material, table S3).

As the main analyses, we built statistical models with forward selection (0.05 considered as the threshold p-value for entering and 0.1 for leaving the model) to assess which of the explanatory variables best explain variation in the three dispersal measures. Statistically significant adjusting variables were entered in the model first, after which the weather variables were added using forward selection. The emigration rate was modelled using a generalized linear model (GLM) with a binomial error distribution and a logit link function. Statistical significance of explanatory factors was calculated using χ² test. Annual average residence time and distance moved were modelled based on multiple linear regression with statistical significance of explanatory factors inferred based on t-statistics and the significance of the full model tested using the F-test.

In order to examine the robustness of the results, we also built the models using an alternative way, by always including the adjusting variables in the models before adding the significant weather variables. However, we did not force all three adjusting variables simultaneously into the models for two reasons. Firstly, our adjusting variables were relatively strongly intercorrelated (electronic supplementary material, table S3) and including several collinear predictors could lead to biased results [39,40]. Secondly, it is a general recommendation to include only very few explanatory variables into the models (to avoid overfitting) when the number of independent observations is as low as in our case (i.e. only 12 years of data; see the ‘one in 10 rule’ in Harrell Jr et al. [41]). For these reasons, we built three alternative models for each dispersal measure by forcing each of the adjusting variables separately (one at a time) into the model before adding the significant weather variables. Results for the most important adjusting variable are provided in the Results section, and those for the two alternative models in the electronic supplementary material.

3. Results

There was a lot of variation in both dispersal and average weather conditions among the 12 study years (electronic supplementary material, tables S1 and S2). The butterfly emigration rate varied from 4 to 26%, average residence time from 1.8 to 9.9 days, and average distance moved from 71 to 154 m, but there was no significant linear trend in any of the dispersal measures (electronic supplementary material, figure S1).

All three dispersal measures correlated significantly with several of the nine weather variables (table 1). The emigration rate correlated positively with the temperature variables and the proportion of especially warm days, and negatively with cloudiness, rainfall, and wind speed. The weather variables in turn tended to be intercorrelated with each other (electronic supplementary material, table S3). As expected, the average residence time showed an opposite relationship with weather variables compared with the emigration rate, the residence rate being significantly correlated with seven out of nine weather variables. The average distance moved differed from the first two dispersal measures by being significantly correlated with only two weather (temperature) variables. This difference was at least partly due to the strong positive correlation between average distance moved and the number of occupied patches. Regarding the adjusting variables, annual metapopulation size was significantly correlated with all dispersal variables, indicating that high butterfly density was associated with an elevated emigration rate and short residence time as well as with long average distance moved (table 1).

Table 1.

Pearson correlations between the three dispersal measures and the explanatory adjusting and weather variables (n = 12 years).

explanatory variable	emigration		residence time		distance moved
	r	p-value	r	p-value	r	p-value
adjusting variables
number of occupied patches	0.66	*	−0.42		0.83	***
metapopulation size	0.80	**	−0.60	*	0.74	**
recapture rate	−0.77	**	0.60	*	−0.55
weather variables
average cloudiness	−0.82	**	0.83	***	−0.55
proportion of especially warm days	0.63	*	−0.89	***	0.41
mean daily solar radiation (kJ m−2)	0.56		−0.66	*	0.20
mean daily rainfall (mm)	−0.71	**	0.70	*	−0.48
proportion of rainy days	−0.43		0.53		−0.34
mean daily minimum temperature (°C)	0.71	**	−0.65	*	0.82	**
mean daily maximum temperature (°C)	0.68	*	−0.77	**	0.54
mean temperature (°C)	0.77	**	−0.79	**	0.68	*
mean wind speed (m s−1)	−0.69	*	0.53		−0.44

*p < 0.05, **p < 0.01, ***p < 0.001.

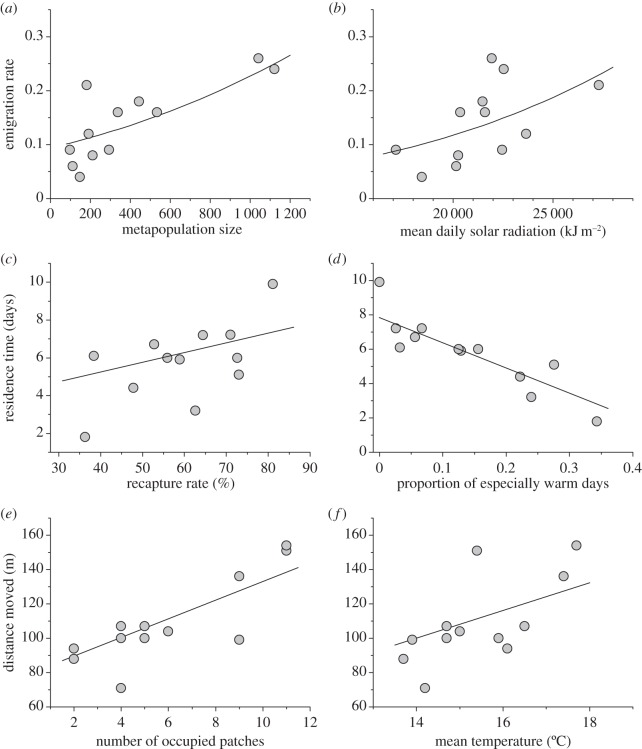
In the statistical models, where significant adjusting variables were entered in the model before the weather variables, one adjusting variable and one weather variable were selected in the final model for each dependent dispersal variable (table 2). The emigration rate increased with both increasing metapopulation size and mean daily solar radiation (figure 2a,b). This model explained 85% of the variation in emigration. The final model for average residence time included recapture rate and the proportion of especially warm days as the selected explanatory variables. This model explained 91% of the variation, the residence time lengthening together with the increasing recapture rate and substantially shortening with the increasing proportion of especially warm days (figure 2c,d). The final model for the average distance moved explained 79% of the variation and included the number of occupied patches together with mean temperature, both of these variables having a positive effect on the observed distances moved (figure 2e,f).

Table 2.

Summary of the modelling results on the factors explaining annual variation in the three dispersal measures. The models were built by entering statistically significant adjusting variables first before testing the significance of the weather variables. (a) The emigration rate was modelled using a generalized linear model (GLM) with a binomial error distribution and a logit link function. (b) Annual average residence times and distances moved were modelled based on multiple linear regression models.

variable	coefficient	d.f.	residual deviance	p-value
(a)
emigration rate
null model		11	55.07
metapopulation size	0.00104	10	17.58	<0.001
mean daily solar radiation	0.00011	9	7.99	0.002
85% of the total deviance explained by the model

variable	coefficient	t	p-value
(b)
residence time
recapture rate	0.056	4.03	0.003
proportion of especially warm days	−14.64	−8.23	<0.001
n, F, P, R2	12, 56.0, <0.001, 0.91
distance moved
number of occupied patches	5.17	4.34	0.002
mean temperature	7.70	2.63	0.027
n, F, P, R2	12, 21.36, <0.001, 0.79

Figure 2.

Relationships between the three dispersal measures and the significant explanatory variables in the statistical models of table 2. Both empirical data points and the predicted lines of the corresponding fitted GLM (a,b) and multiple regression models (c–f) are shown.

The results remained qualitatively very similar, when the two alternative adjusting variables were forced into the model one at a time before the significant weather variables were added (electronic supplementary material, table S5). There was some variation between the different models in the particular weather variables, which became selected, but in eight of the nine built additional models at least one statistically significant weather variable could be added in the model after the forced adjusting variable.

4. Discussion

(a). Weather and dispersal

Our 12-year study revealed high annual variation in butterfly dispersal between habitat patches of a metapopulation. This variation was strongly correlated with several intercorrelated annual weather variables (temperature, sunshine, cloudiness, rainfall, and windiness) measured during the butterfly's flight season. Previously, local weather has been shown to affect the activity and movements in several butterfly species in laboratory [25,26] and short-term field studies [27–30], but to our knowledge this is the first study to convincingly show that this also applies to annual dispersal rates in natural butterfly populations. Over 75% of the observed variation in all three dispersal measures could be explained by the flight season's weather together with intrinsic population factors such as butterfly density and annual pattern of patch occupancy. Based on the results, we conclude that the amount of warm and sunny weather favourable for butterfly activity during the species' flight season is an important driver for year-to-year variation in dispersal of the Clouded Apollo butterfly, and also potentially of many other heliothermic butterfly and insect species.

At first, it may be surprising that the strong relationship between annual weather conditions and butterfly dispersal is insufficiently documented so far, although there are numerous earlier studies on butterfly dispersal. This paucity of previous evidence may be largely due to the general lack of long-term time series documenting variation in dispersal rates. Indeed, despite much empirical research on butterfly dispersal [13,14], studies addressing annual variation in the dispersal rate in the same study system are rare and, therefore, factors affecting such variation have seldom been analysed.

A notable exception is the long-term mark-recapture study of a metapopulation of Proclossiana eunomia in Belgium in which butterfly dispersal between habitat patches was monitored for 19 years [15]. In this species, the dispersal rate varied considerably between years, but in contrast with expectations, the authors could not detect any significant effects of annual weather on the dispersal rate. This was interpreted partly to be due to the substantial effect of butterfly density on emigration rate that varied between the sexes and potentially because the closest weather station was relatively far away. In another long-term study of Parnassius smintheus in Canada, the authors [31] reported high annual variation in the emigration rate during 6 years but did not find any significant weather effects. In our study, the detection of weather effects on the dispersal rate was enabled by the occurrence of several exceptionally warm and sunny (2006, 2011, 2013) as well as cold and rainy (2004, 2014) flight periods during the 12-year study period. In agreement with our results, a number of various observations from short-term studies on butterfly movement and dispersal have suggested that weather may indeed drive dispersal rates (e.g. [22,27,29,30,42,43]).

If the annual variation in dispersal is often high and primarily driven by weather conditions, we can predict high weather-induced annual variability also in colonization rates of empty suitable habitat patches in metapopulations and more generally in the rapidity of expansion of species that are spreading polewards and upwards in mountain slopes under the warming climate [44–46]. Again, there are observations from earlier studies that are in good agreement with these predictions, but systematically collected long-term time series documenting variation in colonization and expansion rates are rare. For example, the introduced population of Proclossiana eunomia in southern France did not manage to colonize new areas until an exceptionally hot and sunny year facilitated a rapid colonization of suitable habitats in the surrounding landscape [47]. Another example is the range expansion of the map butterfly (Araschnia levana) in Finland [48]. This species was observed to expand its range more in warm than in cooler summers, and the annually observed maximum colonization distance was significantly explained by the mean annual late summer temperature.

Regarding our study on the Clouded Apollo, weather conditions correlated significantly (mean daily rainfall and the proportion of rainy days negatively, and mean daily temperature positively; p < 0.05) with annually observed numbers of local colonizations, even though the annual numbers were low (a total of 15 colonizations in 2004–2015). Our dispersal results show that exceptional weather conditions can substantially affect the annual dispersal rates, because the proportion of exceptionally warm days was significantly correlated with both the emigration rate and average residence time. The proportion of especially warm days together with annual recapture rate explained 91% of the high variation in average residence times, with markedly low residence times in years with substantial occurrence of exceptionally warm weather (figure 2d). Nevertheless, there is currently no consensus on the effects of exceptional weather conditions on the colonization process, as was recently pointed out by Malinowska et al. [49]. Thus, more empirical case studies are needed in documenting the effects of extreme weather conditions [50].

(b). Role of intrinsic population variables

In addition to the significant effects of weather, we found that dispersal was higher when the metapopulation size was large and recapture rate low, and that average distances moved were longer when a larger number of patches were occupied by the butterfly. The latter effect is a simple consequence of the larger total occupied landscape area of the butterflies, and of more isolated patches being occupied. The effect of metapopulation size can be interpreted as positively density-dependent dispersal which has often been documented in butterflies [14,16]. This interpretation is also supported by observations from the largest habitat patch of our metapopulation: the emigration rate increased significantly with annual butterfly density (individuals ha⁻¹; linear regression: p = 0.02, r² = 0.39, n = 12) in that local population.

Besides the observation of positively density-dependent emigration, it is possible that the large metapopulation size was also associated with elevated emigration levels from small habitat patches. This is because small patches tended to be occupied by the butterfly only when the metapopulation size was large. A negative relationship between the patch area and emigration rate has been well-established in several butterfly species [51,52] and has also been reported in the Clouded Apollo [38]. We would like to stress however, that the evidence for a strong and robust effect of weather was clear, even if annually varying patch occupancy may have contributed to the observed annual emigration rates. This is indicated by the strong effect of weather on the average residence times. This finding was based only on the data from the largest habitat patch of our study system, but nonetheless, it is in good agreement with the results for emigration rate.

Recapture rate was included in the analyses as an adjusting variable measuring the annual study effort. However, it was strongly negatively correlated with metapopulation size, presumably reflecting the difficulty of getting a large fraction of butterflies recaptured when butterfly density was very high. Therefore, it is probable that it was the large metapopulation size and high butterfly density, and not the low recapture rate, that were ultimately contributing to the high emigration rate observed in some years.

(c). Implications for global change research

If high variation in dispersal, and in range expansion rates caused by varying weather conditions, is a common phenomenon, it has implications on modelling and predicting the effects of climate change on species distributions. For example, average dispersal rates of many insect species might increase with increasing mean temperature and thus facilitate expansion towards areas that have recently become climatically suitable due to climate change [29]. Alternatively, such an effect could be counteracted if average cloudiness would simultaneously increase, especially for heliothermic insects [31]. The results of several recent studies have emphasized the potentially high ecological importance of the variability and extreme weather events compared with average weather conditions [53–56] and the difficulty of predicting the consequences on population dynamics of such climatic changes [50]. Improving our knowledge on the role that average and extreme weather conditions have in governing the annual dispersal rates of ectotherm animals, such as insects, requires further attention. Better knowledge will help develop improved model predictions of the effects of climate change on population dynamics and range shifts of species.

Ethics

The permission to study the threatened and protected butterfly species within a nature reserve was granted by the Uusimaa Centre for Economic Development, Transport, and the Environment in accordance with Finnish law.

Data accessibility

The datasets supporting this article have been uploaded as part of the electronic supplementary material.

Authors' contributions

M.K. designed the study, carried out statistical analyses, and drafted the manuscript. All authors participated in fieldwork. S.R. processed data. S.R., R.K.H., and J.H. helped in study design and in drafting the manuscript.

Competing interests

We have no competing interests.

Funding

Funding was granted by Metsähallitus, the Finnish Ministry of the Environment, Societas Biologica Fennica Vanamo, Societas Entomologica Fennica, and the EU LIFE project titled ‘Improving the Conservation Status of Species-rich Habitats' (LIFE10 NAT/FI/0048).