The cohort effect in childhood disease dynamics

Abstract

The structure of school terms is well known to influence seasonality of transmission rates of childhood infectious diseases in industrialized countries. A less well-studied aspect of school calendars that influences disease dynamics is that all children enter school on the same day each year. Rather than a continuous inflow, there is a sudden increase in the number of susceptible individuals in schools at the start of the school year. Based on the standard susceptible–exposed–infectious–recovered (SEIR) model, we show that school cohort entry alone is sufficient to generate a biennial epidemic pattern, similar to many observed time series of measles incidence. In addition, cohort entry causes an annual decline in the effective transmission that is evident in observed time series, but not in models without the cohort effect. Including both cohort entry and school terms yields a model fit that is significantly closer to observed measles data than is obtained with either cohort entry or school terms alone (and just as good as that obtained with Schenzle's realistic age-structured model). Nevertheless, we find that the bifurcation structure of the periodically forced SEIR model is nearly identical, regardless of whether forcing arises from cohort entry, school terms and any combination of the two. Thus, while detailed time-series fits are substantially improved by including both cohort entry and school terms, the overall qualitative dynamic structure of the SEIR model appears to be insensitive to the origin of periodic forcing.

1. Introduction

Using transmission models to uncover the mechanisms behind observed infectious disease dynamics is a major goal of mathematical epidemiology [1,2]. In the context of recurrent epidemics of childhood diseases such as measles, chicken pox and whooping cough, a large body of research has indicated that seasonal changes in transmission rate are fundamentally important in determining the structure and periodicity of infectious disease time series [1,3–9].

The primary source of transmission seasonality for childhood diseases in industrialized countries appears to be the aggregation of children in schools, which are closed between terms and during summer holidays [3]. Indeed, even crude reconstructions of the transmission rate from incidence data show clear evidence of school term structure [10,11]. Other external influences, such as seasonality of births [12] or weather [13,14] may contribute, but are more difficult to detect (one study indicates that climatic changes affect interannual differences in measles incidence in the UK [15]).

The traditional susceptible–infectious–recovered (SIR) and susceptible–exposed–infectious–recovered (SEIR) modelling frameworks [1,16], including seasonal forcing of the transmission rate, have been used extensively to examine and explain the qualitative dynamics observed for a wide variety of infections in different places and times [4–6,9,17,18]. In addition, detailed quantitative reconstructions of seasonally varying transmission rates for childhood diseases have been achieved, either by extending the Fine and Clarkson method [9,10,19–22] or by using more statistically well-founded inference methods, e.g. (i) the ‘time-series SIR’ (TSIR) framework in which a discrete-time SIR model subject to additive and multiplicative noise is fitted [23], (ii) stochastic epidemic modelling frameworks in which the data are treated as a partially observed Markov process, fitted by particle filtering [24,25], or (iii) deterministic models fitted by generalized profiling, i.e. a combination of trajectory matching and gradient matching [7,26,27]. Other techniques are available for daily incidence data [28,29], but childhood disease incidence has typically been reported weekly.

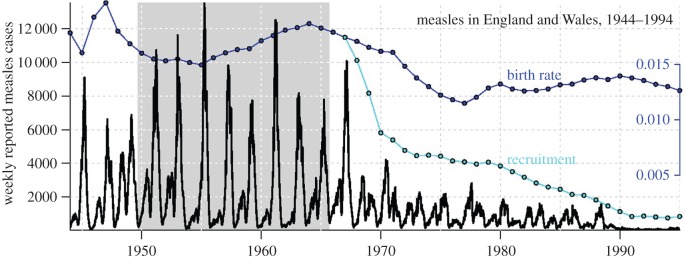
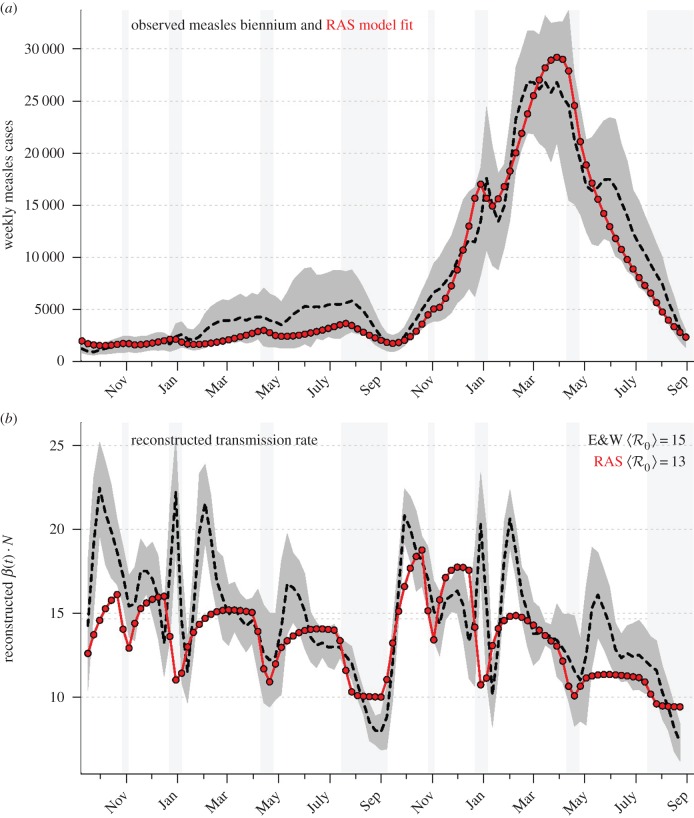
Figure 1 shows the well-known time series of weekly reported measles incidence in 60 major cities of England and Wales (E&W), 1944–1994 [10,11,30–41]. The highlighted period from 1950 to 1964 displays a strictly biennial epidemic cycle, with large and small epidemics in alternate years. It is common to compare a biennial attractor of a deterministic epidemic model with this observed 2-year cycle [37,40,42,43]. Because such attractors are strictly periodic, the observed variation from biennium to biennium must be regarded as random fluctuations about the mean biennium. Figure 2a shows the average measles biennium with a dashed curve (±s.d. in grey). Figure 2b shows the transmission rate as reconstructed with the method of Fine & Clarkson [10].

Figure 1.

Weekly reported measles cases in 60 major cities of England and Wales, 1944–1994, with the biennial period studied by Fine & Clarkson [10] (8 September 1949 to 7 September 1965) highlighted in grey. The per capita annual birth rate and susceptible recruitment rate (birth rate adjusted to account for vaccination [5]) are shown in blue and cyan, respectively. (Online version in colour.)

Figure 2.

(a) Average biennial cycle of reported measles cases in England and Wales, 1950–1964. Mean (dashed) ± s.d. (grey). Best-fit biennial attractor of Schenzle's [37] realistic age-structured (RAS) model (red; see electronic supplementary material, §2). School vacations are indicated with light grey shading. (b) Transmission rate as reconstructed by the method of Fine & Clarkson [10] (see §2.3.5). Colour-coding as in panel (a). Transmission rate reconstructions from other models are shown in figure 3 and in the electronic supplementary material, figures S1 and S2. (Online version in colour.)

The most obvious aspect of reconstructed childhood disease transmission rates such as that shown with a dashed curve in figure 2b is that they are high when school is in session and low otherwise [7,10,11], a feature that can easily be included in simple models using ‘term-time forcing’ [5,17,42]. Another clear aspect of reconstructed transmission rates is that they decline over the course of the school year [7,10], a feature that is not reproduced by the simple term-time forced SEIR model but is reproduced successfully by age-structured models that employ both term-time forcing and annual gradewise movement of school-age cohorts (figure 2, red points [37,40]).

We suggest that the most crucial element of the age-structured models—from the point of view of reproducing the aggregate temporal dynamics of childhood infections in industrialized countries—is the annual, sudden gradewise movement of age cohorts and, moreover, that the key aspect of gradewise movement is the sudden entry of the youngest school-age cohort into schools. This ‘cohort effect’ changes the way new susceptibles enter the system, i.e. each year some proportion of children effectively enter the well-mixed susceptible pool all at once on the first day of school, rather than continuously throughout the year as maternally acquired immunity wanes.

In E&W, the Education Act of 1944 [44] mandates that children must be in school from ages 5 to 16. In practice, this means that children enter school at age four or five.¹ The average age at which measles infection occurred in E&W during the period on which we focus was 4–5 years [1, p. 51], i.e. during the first year of school. Even the extreme approximation that all children entered the susceptible pool on the same day each year may be valid if pre-school children were usually infected by older siblings who were attending school.

In this paper, we show that incorporating the cohort effect in an epidemiological model is easy without introducing any explicit age structure, and that doing so yields an annual decline in the effective (reconstructed) transmission rate, as observed in real measles time series. Moreover, including the cohort effect yields simulation time series that fit observed disease incidence data more closely than standard term-time forced SEIR models. On the other hand, we find that the qualitative dynamic structure of the SEIR model is almost identical if seasonal forcing is implemented only in the transmission rate, only via the cohort effect, or any combination of the two. Consequently, the results of research aiming to understand transitions in the qualitative dynamics of childhood diseases (e.g. via bifurcations) appear to be robust to the detailed implementation of seasonality in the model.

The cohort entry model that we present here was first considered by He [45]. A stochastic version was included in a collection of models used to illustrate plug-and-play inference techniques by He et al. [25].

2. Methods

The standard SEIR model [1] can be expressed as a simple system of nonlinear ordinary differential equations

2.1a

2.1b

2.1c

2.1d

Here, S, E, I and R denote the numbers of susceptible, exposed (infected but not yet infectious), infectious and recovered (immune) individuals. The parameters are the rates of birth (B), per capita death (μ), transmission (β), onset of infectiousness (σ) and recovery (γ). The mean latent and infectious periods are τ_E = 1/σ and τ_I = 1/γ, respectively (for measles, τ_E ≈ 8 days and τ_I ≈ 5 days [1, p. 31]). The total population size is N = S + E + I + R. Disease-induced mortality is not included in equation (2.1) because it has a negligible population-level effect for typical childhood diseases [12]. Note that because equations (2.1a)–(2.1c) do not depend on the recovered class R, equation (2.1d) can be ignored.

The basic reproduction number 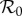(the average number of secondary cases caused by a given primary case in a wholly susceptible population [1,2]) is ([8] and electronic supplementary material, equation (S8))

2.2

The first factor (B/μ) does not normally appear in formulae for 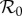because it is usually assumed that B = μN and N is usually absorbed into the transmission rate β. For measles in E&W during the period we examine, [1, p. 70].

2.1. Seasonality of transmission rate

The transmission rate β is not constant for childhood infections. It varies seasonally as a result of the aggregation of children in schools [3]. The term-time forced transmission rate can be written [46]

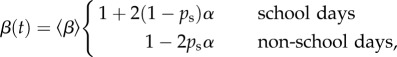2.3

where 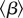is the mean transmission rate, α is the amplitude of forcing and p_s is the proportion of days on which school is in session. (Note that we always use to denote the time average of a quantity.)

2.2. The cohort effect

Early in life, most children have fewer social contacts than they do after entering school at age 4 or 5. This effective shielding from disease exposure is only partial, of course, and some young children become infected before entering school. For simplicity, we suppose that a proportion c of newborns is subject to the cohort effect, meaning complete shielding from disease transmission until entering school, whereas the remaining proportion 1 – c enters the well-mixed population immediately after birth (or, in practice, after maternally acquired immunity wanes, which takes about four months in the case of measles [1]). We refer to the day of the year on which school begins as t₀ (e.g. if school starts on 8 September and we measure time in years, then 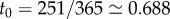). Thus, we implement the cohort effect in the model by replacing the constant annual birth rate B with the function

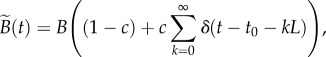2.4

where δ is the Dirac delta function and L is the length of the time interval between cohort entries (normally 1 year). The periodic forcing of the birth term specified in equation (2.4) affects 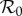(which now depends on the time of year that initial invasion occurs [47]). Instability of the disease-free solution of this non-autonomous SEIR model is determined (approximately, but fairly accurately) by the condition 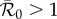, where 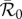refers to the basic reproduction number of the autonomous system obtained by averaging the time-dependent parameters, i.e. using B rather than 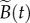and replacing β by 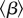in equation (2.2) [47–49].

2.3. Quantitative fits of models to observed time series

2.3.1. Observed measles time series

In the main text, we consider fits to the average biennium of the weekly measles reports in E&W from September 1949 to September 1963. In the electronic supplementary material, we repeat the analysis with three other (city level) measles time series that display a consistent biennial incidence pattern over a similar period:

• (i) weekly reported measles in London, UK, from September 1949 to September 1965 (the same period fitted in [42,43]);

• (ii) weekly reported measles in Liverpool, UK, from September 1945 to September 1965;

• (iii) monthly reported measles in New York City (NYC), USA, from September 1945 to September 1963. To correct for the different lengths of each month in the NYC data, we followed [12] and multiplied each raw data point (reported measles in month j of year i) by

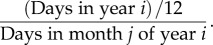
  2.5

2.3.2. Average measles biennium

The observed average biennial pattern (X_obs) and the variance about it (V_obs) can be written [42]

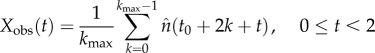2.6

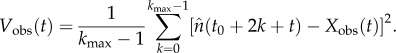2.7

Here, 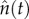refers to the number of notified (reported) measles cases at time t. We took the initial time to be t₀ = 1949.688 (8 September 1949) in E&W and London, and t₀ = 1945.688 (8 September 1945) in Liverpool and NYC. The number of biennia was k_max = 9 in E&W, k_max = 10 in London and NYC, and k_max = 12 in Liverpool (see electronic supplementary material, figure S3 for the four time series).

2.3.3. Simulated measles incidence

To compare the models with the observed data, we solved the SEIR model (equation (2.1)) numerically with initial conditions taken to be a slight random perturbation of 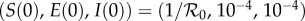. After discarding a 500 year transient to ensure the solution had settled onto an attractor, we defined the simulated number of notified cases at report times t to be

2.8

where Δt is the notification interval (one week or one month), N is the population size (electronic supplementary material, table S1) and η is the notification efficiency (or reporting ratio) for measles [11,37] (electronic supplementary material, table S6). Because γI is the proportional rate at which individuals enter the recovered class (equation (2.1d)), it is a reasonable approximation of the rate at which cases are notified (before adjusting for population size and notification efficiency).

2.3.4. Best fit

Following Keeling & Grenfell [42], we found the parameters of a given deterministic model that yielded an attractor that best fits the observed biennium by minimizing the weighted fitting error

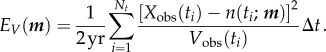2.9

Here, Δt is the reporting interval and N_t is the number of reporting intervals in a biennium (for weekly data, Δt = 1/52 year and N_t = 104). In equation (2.8), we used the notation n(t) for the simulated number of cases at time t; here, we use the more cumbersome notation n(t; m) to emphasize explicitly that the model solution depends on a vector m containing the N_p model parameters that are fitted (e.g. for the cohort-entry, term-time forced SEIR model, 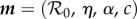and N_p = 4). E_V measures the total deviation of the model's attractor from the observed biennium, relative to the variation in the observed data [42]. Greater weight is given to points where the variation from biennium to biennium is smaller. All the noise in the data is implicitly assumed to arise from observation error as opposed to process error from intrinsic stochasticity.

E_V has a natural likelihood interpretation. Suppose the data point 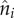observed at biennium time t_i is drawn from a distribution with probability density

2.10

where a_i is a parameter vector associated with distribution d_i. Moreover, suppose that observations at different biennium times, {t_i: i = 1, … , N_t}, are independent. Then, the likelihood of the model (specified by m) given the data, i.e. the probability of obtaining the observed data given the model, is

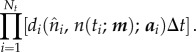2.11

If it is further assumed that the distributions d_i are normal, then

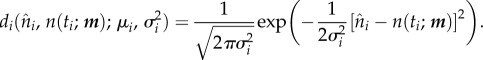2.12

where we have set 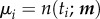. Now, taking 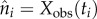and 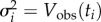, the negative log likelihood is

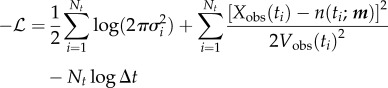2.13a

2.13b

where the constant depends only on the data and not on the model parameters m. Thus, E_V is a scaled and translated version of the negative log likelihood, and minimizing E_V yields a maximum-likelihood estimate of m. Given the likelihood, we can use the Akaike information criterion [50, p. 209] for model selection,

2.14

We compare models via their difference in AIC, so the constant in equation (2.13b) cancels out.

2.3.5. Transmission rate reconstruction

In their study of the aggregate E&W measles times series, Fine & Clarkson [10] reconstructed the seasonally varying transmission rate β(t) using a discrete-time SIR model. The meaning of this ‘reconstruction’ of β(t) is that the ‘reconstructed’ β(t) is the transmission rate that would yield the observed data if the underlying process were exactly a discrete-time SIR model in which the only source of time variation in parameter values is in the transmission rate. Thus, the ‘reconstructed’ β(t) is really an effective transmission rate. The algorithm also ‘reconstructs' (or perhaps more accurately estimates) the unobserved time series of susceptibles.

The discrete-time SIR model that Fine & Clarkson [10] used specifies the number of cases (C_t) and susceptibles (S_t) at times 0,1,2, … , where the time unit is a biweek (14 days), and the mean disease generation time T_g is also assumed to be a biweek (rather than the more precise 13 days). We follow Krylova [19], who found that a slight revision avoids the need to assume the reporting interval is equal to T_g (instead the reporting interval is taken to be a single week, as in reality, and T_g must simply be a multiple of the reporting interval). Assuming the time unit is the reporting interval (one week), the dynamic equations are

2.15a

and

2.15b

where β_t, B_t and V_t denote the transmission rate and numbers of births and vaccinations, respectively, in time interval t, η is the proportion of cases reported and μ is the natural mortality rate. Given time series {β_t}, {B_t} and {V_t}, and initial conditions (S₀, C₀), the discrete dynamic equations (2.15) can be iterated to produce discrete-time trajectories {(S_t, C_t)} [31]. Fine & Clarkson [10] noted that for an observed time series of cases {C_t}, together with an estimated notification efficiency η and initial susceptible proportion S₀, equation (2.15) could instead be used to reconstruct the time series of susceptibles {S_t} and transmission rate {β_t}. This can be achieved by solving equation (2.15a) for β_t, which yields [19, eqn (4.8)]

2.16

We used this method to reconstruct β_t from the E&W time series as well as from time series resulting from simulations of the various models we examined. When reconstructing β_t from a simulation, η and S₀ are known. To compare the reconstructed β_t from a model and from the E&W data, we fitted the model to the data (minimizing E_V as in §2.3.4) and then used the S₀ from the matched trajectory (electronic supplementary material, table S7) and the value of the notification efficiency that yields a piecewise horizontal β_t for the term-time SEIR model (η = 0.71).

The discretization in equation (2.15a) is over the mean generation time T_g (two weeks), which means that cases are integrated over a full generation time T_g and the reconstructed transmission rate β_t is per generation time. Consequently, because 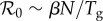, we can interpret β_tN as 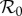and the time-averaged 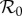can be estimated as .

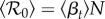2.4. Dynamic structure of the cohort-entry model

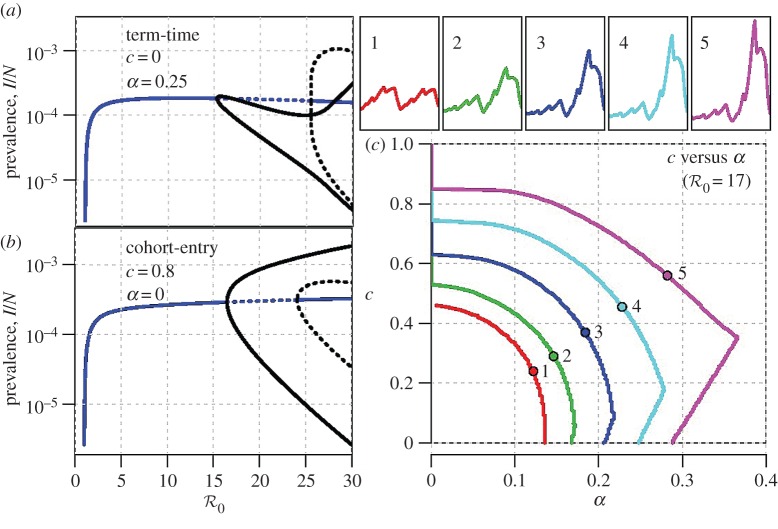
We used standard bifurcation and continuation software (XPPAUT) [51] to construct the bifurcation diagrams shown in figure 5b,c. Solid curves show attractors and dotted curves show repellers. A step-by-step guide to the procedure we used can be found in the electronic supplement to [8].

Figure 5.

Dynamic structure of the term-time and cohort forced SEIR models. (a) The principal branches of the bifurcation tree (as a function of 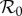) of the term-time forced SEIR measles model (c = 0, α = 0.25), which has been used previously [5,18,46] to predict the dynamic transitions evident in figure 1. (b) The equivalent bifurcation tree for the cohort-entry model (c = 0.8, α = 0). (c) Dynamics in the entire α–c plane for 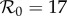. The period-doubling bifurcation occurs on the curve marked 1 (red), whereas the other curves are contours of constant major-to-minor-peak-ratio for the biennial attractor (the ratio is marked on each curve; in London, 1950–1964, this ratio was approx. 5). Time series corresponding to the circled points on these curves are shown in the small numbered panels above panel (c). The equivalents of panel (c) for other values of 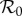are shown in the electronic supplementary material, figure S5. (Online version in colour.)

3. Results

3.1. Qualitative understanding of annual decline in transmission rate

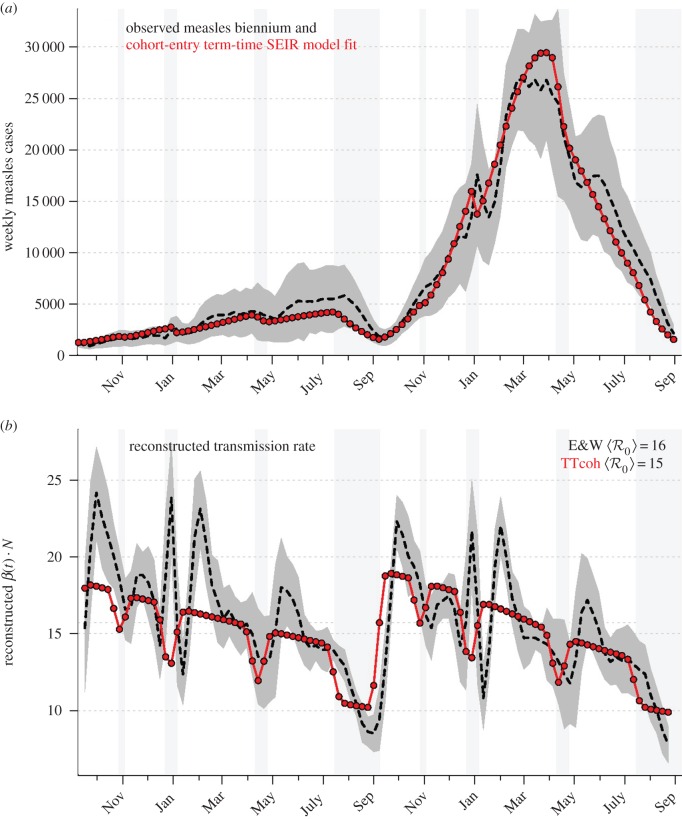
Figure 3 shows the equivalent of figure 2 for the term-time forced SEIR model without age structure, but including the cohort effect as described in §2.2. Visual comparison of the top panels of these figures makes clear, qualitatively, that age structure is not necessary to capture the main features of the observed measles biennium. In addition, comparison of the bottom panels reveals that age structure is not required to capture the observed decline in the reconstructed effective transmission rate β_t over the course of each year.

Figure 3.

Equivalent of figure 2 for the cohort-entry SEIR model with term-time forcing. (Online version in colour.)

Similar figures shown in the electronic supplementary material reinforce the inference that the cause of the annual decline in β_t is the cohort effect. Without the cohort effect, the effective β_t obtained by applying the reconstruction algorithm to solutions of the term-time SEIR model shows no decline (electronic supplementary material, figure S1), whereas without term-time forcing, the effective β_t reconstructed from solutions of the cohort-entry SEIR model shows decline but (unsurprisingly) no dips during school terms (electronic supplementary material, figure S2).

3.2. Quantitative fits of models to observed time series

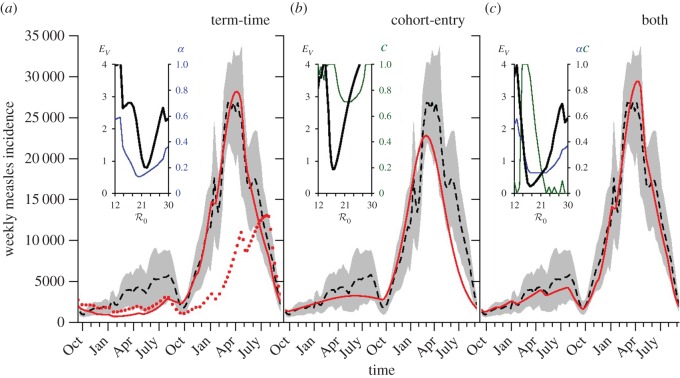
Figure 4 compares the performance of the standard term-time forced SEIR model (figure 4a), the cohort-entry model without school-term forcing (figure 4b) and the full cohort and term-time forced model (figure 4c) in fitting the average E&W measles biennium. As detailed in Methods (§2), we follow previous work [42,43] and assess these deterministic models in terms of their ability to reproduce the average biennium for the period 1950–1964, and quantify the quality of the fits using the weighted fitting error E_V [42].

Figure 4.

SEIR model fits (solid red) of the average measles biennium in England and Wales for the period 1950–1964 (dashed). Best fits were obtained as in previous work [40–43] by minimizing the weighted fitting error E_V (equation (2.9) and [42]). (a) The standard term-time forced SEIR model with forcing amplitude α (the dotted red curve shows the fit obtained by fixing 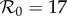([43] and fig. 5.15). (b) The cohort-entry model with cohort proportion c and no school-term forcing. (c) The full cohort and term-time forced model. In each panel, insets show profiles of E_V in black (and the associated minimizing values of α and c in blue and green, respectively) as a function of 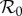. Details are given in §3.2 and §2.3. The analysis is repeated for several city-level measles time series in electronic supplementary material, figure S4. (Online version in colour.)

In each of the three panels of figure 4, the data are shown using a dashed black curve for the mean biennium (X_obs(t), equation (2.6)) and grey shading extending to one standard deviation above and below the mean (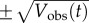, equation (2.7)). For each model, the solid red curve shows the solution (after converging to the attractor) for the parameter set that minimizes E_V.

The inset graphs in each panel show profiles of E_V as a function of 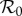, i.e. for each 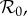we find the values of all other free parameters that minimize E_V (black); thus, the minimum of the plotted E_V profile is the minimum in the full parameter space. The free parameters are the term-time forcing amplitude α, the cohort proportion c and the case notification efficiency η. The values of our focal parameters (α, c) that yield the minimum E_V for each 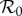are also shown (term-time amplitude α in blue, cohort-entry proportion c in green).

Previous work fitting the term-time forced SEIR model to the same measles incidence time series [42,43] was conducted subject to the constraint that 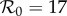, the empirically estimated value [1, p. 70]. The resulting best fit with this constraint (reproducing fig. 5.15 of [43]) is shown as a dotted red curve in figure 4a. Allowing 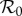to be fitted as well yields the solid red curve in figure 4a, but the fitted value (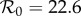) is substantially higher than the empirical value. In contrast, without term-time forcing but with cohort-entry, figure 4b shows a fit that is just as good, with 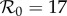arising from the fit rather than being specified in advance. Including both the school-term and cohort effects yields the best fit (lowest E_V), again yielding 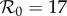without fixing 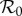in advance. Note that while the cohort effect alone (figure 4b) succeeds in producing a formally good fit to the data, it fails to capture the small-scale temporal fluctuations arising from the three school terms, which are successfully reproduced in figure 4c. Table 1 summarizes the fits shown in figure 4, together with their associated ΔAIC values. The improvement obtained by including the cohort effect in addition to term-time forcing is highly significant.

Table 1.

Parameter estimates obtained by fitting epidemic models to observed weekly measles cases in England and Wales, 1950–1964. Parameters that are not fitted are indicated with ‘—’.

model	c	α		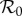η	EV	ΔAIC
term-time (fixed 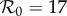)	—	0.25	—	0.25	2.867	270.4
term-time	—	0.15	22.6	0.44	0.813	58.7
cohort-entry	1.00	—	17.2	0.43	0.732	50.3
both	1.00	0.16	17.1	0.49	0.229	0.0
RAS	—	—	13.4a	0.61	0.486	24.7

^aFor the RAS model, 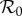was estimated as the mean of the reconstruction in figure 2. The fitted RAS parameters are described in electronic supplementary material, §2.3.

In the electronic supplementary material, we repeat our analysis for several other measles incidence time series (see electronic supplementary material, figure S3) and obtain similar results (see electronic supplementary material, table S6). In addition, a much more elaborate and computationally demanding analysis of fully stochastic implementations of the models [25] also shows that significantly better fits of the detailed time series are achieved by including the cohort-entry effect (AIC_c is improved by more than 12 units).

3.3. Dynamic structure of the cohort-entry model

Predictions of structural changes in epidemic patterns, such as transitions between epidemic cycles of different lengths, depend primarily on qualitative analysis of models (e.g. bifurcation theory) rather than detailed quantitative fits of model-generated time series to case report time series. We therefore consider how the cohort effect influences predictions of bifurcations (e.g. transitions from annual to biennial or more complex dynamics).

Figure 5a shows the principal branches of the bifurcation tree (as a function of 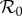) of the term-time forced SEIR measles model (c = 0, α = 0.25), which has been used previously [5,8,9,18,46] to predict the dynamic transitions evident in figure 1. Figure 5b shows the equivalent bifurcation tree for the cohort-entry SEIR model (c = 0.8, α = 0). The topologies of the two bifurcation trees are identical and the positions (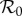) of the bifurcations differ only slightly.² The striking similarity of the strict term-time forced (c = 0) and strict cohort-entry (α = 0) models indicates that qualitative predictions of epidemic structure are very insensitive to the mechanistic origin of periodic seasonal forcing of the system.

Figure 5c summarizes the dynamics in the entire α – c plane for 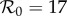. The period-doubling bifurcation occurs on the curve marked 1 (red), whereas the other curves are contours of constant major-to-minor-peak-ratio for the biennial attractor (in London from 1950 to 1964 this ratio was approx. 5). Time series corresponding to the circled points on these curves are shown in the small numbered panels above figure 5c. A comparison of transient dynamics with and without cohort entry is presented in the electronic supplementary material, figure S6.

4. Discussion

In any situation where the rate of contact among children changes significantly when they first enter school, a cohort effect will influence the population dynamics of childhood infectious diseases. In our cohort-entry SEIR model, we formalized this effect using an annual pulse in the birth term; a proportion c of children begins contacting others on the day schools open, whereas the remainder enter the well-mixed population when they are born (equation (2.4)). We have considered the cohort effect in general and in the specific context of measles, a well-studied childhood disease for which lengthy high-quality notification time series exist for a variety of locations.

Complex observed patterns of measles incidence have captured the attention of mathematical ecologists and epidemiologists since the seminal work of Bartlett [52–54] in the 1950s. In an attempt to understand measles dynamics, Schenzle [37] developed a realistic age-structured (RAS) model using a system of 84 differential equations that specify the time variation of the numbers of susceptible (S), exposed (E), infectious (I) and recovered (R) individuals in each of 21 age classes (see electronic supplementary material, §2). The model includes term-time forcing of contacts among school-age children, and entry of a new cohort and gradewise movement at the start of each school year. The RAS model provides a good fit to the averaged biennial cycle of measles epidemics observed in E&W in the pre-vaccine era (1948–1968) [37] and with the fitted parameters does not predict chaotic dynamics [40], in contrast to the simpler sinusoidally forced SEIR model [4].

The global dynamics of the RAS model are, in fact, primarily driven by term-time forcing of the transmission rate, rather than age structure [5]. This realization has made it possible to explain changes in outbreak frequency in many infectious disease time series, using the term-time forced SEIR model or other simple epidemic models [5,8,9,17–19,46].

One aspect of real measles dynamics that is captured by the RAS model but not the simpler term-time forced SEIR model is the decline in the effective (reconstructed) transmission rate β(t) over the course of the school year (figure 2). In this paper, we have shown that the decline in the reconstructed β(t) arises from the cohort effect, not from age structure per se (figure 3).

The cohort-entry SEIR model that we have examined here is essentially equivalent to the two-age-class limit of the RAS model in which there is no transmission in the younger age class. Andreasen & Frommelt [55] presented a different cohort-entry-age-structured model, which has the virtue of being amenable to some useful analytical investigation (unlike the RAS model and the simpler SEIR models considered here). The effects of birth pulses on epidemics in animal populations have been studied previously [49].

Previous work has shown that matching trajectories of the term-time forced SEIR model to the average measles biennium in E&W yields an unrealistically high estimate of the basic reproduction number 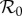[42,43]. We compared the fits obtained using the term-time forced SEIR model (figure 4a) with fits obtained using SEIR models incorporating the cohort-entry effect, both with and without seasonality in the transmission rate (figure 4b,c). We obtained significantly better fits, with an estimated 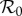closer to the conventional value [1, p. 70], by including the cohort-entry effect. Moreover, when we include both cohort-entry and transmission rate seasonality, the fit to the E&W measles biennium is just as good as that obtained with the RAS model.

We studied the global dynamic structure of the cohort-entry SEIR model and found that the bifurcation tree is topologically equivalent, regardless of whether transmission rate seasonality is included (figure 5). Thus, from the point of view of qualitative dynamics, the source of seasonal forcing may be irrelevant in the SEIR model.

Age-structured models are important and natural tools to use in the development of control strategies for childhood diseases [56], because optimal control strategies are themselves likely to be age-structured. However, when using models that include many biological details, the roles of individual biological mechanisms may be obscured. Our formalization of the cohort-entry SEIR model without explicit age structure has allowed us to reveal that the cohort effect alone is sufficient to generate an annual decline in the effective (reconstructed) transmission rate, as is often observed (cf. figures 2b and 3b; and electronic supplementary material, figures S1 and S2). In addition, our analyses of particular measles time series indicated that the best-fit cohort proportion is large (electronic supplementary material, table S6), suggesting that most children younger than school age are also indirectly subject to the cohort effect, presumably because they interact with older siblings and other schoolchildren.

Data accessibility

All the data studied in this paper are available either from the electronic supplementary material or from the International Infectious Disease Data Archive (IIDDA) at http://iidda.mcmaster.ca.

Authors' contributions

Both authors conceived and carried out the study, drafted the manuscript and gave final approval for publication.

Competing interests

We have no competing interests.

Funding

D.E. was supported by grants from NSERC, CIHR and the J. S. McDonnell Foundation. D.H. was supported by an Early Career Scheme grant from the Hong Kong Research Grant Council (25100114), and a Health and Medical Research Grant from the Hong Kong Food and Health Bureau Research Council (13121382).