Origami mechanical metamaterials based on the Miura-derivative fold patterns

Abstract

This paper presents two new types of origami-inspired mechanical metamaterials based on the Miura-derivative fold patterns that consist of non-identical parallelogram facets. The analytical models to predict dimension changes and deformation kinematics of the proposed metamaterials are developed. Furthermore, by modelling the creases as revolute hinges with certain rotational spring constants, we derived analytical models for stretching and bulk moduli. The analytical models are validated through finite-element simulation results. Numerical examples reveal that the proposed metamaterials possess some intriguing properties, including negative Poisson’s ratios and bulk modulus. The work presented in this paper can provide a highly flexible framework for the design of versatile tunable mechanical metamaterials.

1. Introduction

Metamaterials, the man-made materials with unusual physical properties that arise mainly from the arrangement instead of the properties of constituent structures, have aroused considerable research interest from scientists and engineers in recent years and open up opportunities for many state-of-the-art applications ranging from invisibility cloaks [1–4] to solar photovoltaic [5,6], seismic protection [7], ultra-effective sound absorption [8,9] and mechanical metamaterials [10–14]. In this context, origami, the art of folding a two-dimensional (2D) sheet into a three-dimensional (3D) structure, offers an inspiring source for designing mechanical metamaterials. Of particular interest here are rigid origami where all facets remain unbent with the creases acting as rotational hinges during continuous folding, and a particular fold pattern, known as the Miura pattern, which is constructed from a single repeated parallelogram facet and is both rigid- and flat-foldable. In a pioneering article, Schenk & Guest [15] reported the deformation kinematics of two folded cellular metamaterials based on the folded Miura pattern, which manifest negative in-plane and positive out-of-plane Poisson’s ratios. Wei et al. [16] extended Schenk & Guest’s work by considering the rotational stiffness of the creases and derived the stretching and bending rigidities of Miura-folded metamaterials. Later on, Lv et al. [17] showed that the in-plane Poisson’s ratio of Miura-folded metamaterials can in fact be both positive and negative when the whole size of the Miura pattern instead of the size of a unit cell is taken into account. Silverberg et al. [18] proposed a reprogrammable single-layered origami metamaterial design by introducing pop-through defects into perfect Miura tessellations. More recently, Li & Wang [19] investigated the pressure-dependent multi-stability properties of an individual fluid-filled tubular cell and its dual cell configuration formed by stacking Miura unit cells. Filipov et al. [20] introduced a new orientation to stack Miura patterns into rigid-foldable zipper-coupled tubes from which reconfigurable cellular metamaterials can be built. In addition to the Miura pattern, Waitukaitis et al. [21] studied the multi-stability characteristics of metasheets consisting of periodic rigid degree-four vertices. Eidini & Paulino [22] proposed a new class of cellular folded metamaterials constructed from the rigid-foldable BCH (basic unit cell with hole) pattern that combines origami folding with kirigami.

In this paper, we extend the existing work on classic Miura-folded metamaterials to rigid-foldable Miura-derivative fold patterns [23–25], which comprise quadrilateral facets that are not all identical. We focus here primarily on periodical fold patterns so that the properties of the 3D bulk system can be represented by those of a repeating unit cell, and parallelogram facets because patterns containing non-parallelogram quadrilateral facets will lead to curved or irregular folded shapes [23,24], making it quite challenging if not impossible to use them to design mechanical metamaterials. Our work presented herein leads to metamaterial models that not only include conventional Miura-folded metamaterials as the simplest cases but more importantly can be tailored to exhibit a wide range of mechanical properties which would otherwise be difficult to achieve with existing designs, thus substantially broadening the design space of origami-based mechanical metamaterials.

The layout of this paper is as follows. The geometries of the Miura-derivative unit cell and its stacked unit cell models are first introduced. Based on the stacked unit cell models, two types of Miura-derivative metamaterials are proposed. The analytical models to predict in- and out-of-plane Poisson’s ratios, and stretching and bulk moduli of the proposed metamaterials, are derived and validated with the finite-element (FE) results. The properties of the Miura-derivative metamaterials are discussed through several numerical examples based on a generic piecewise periodic base function. Finally, a brief summary concludes the paper.

2. Unit cell geometry

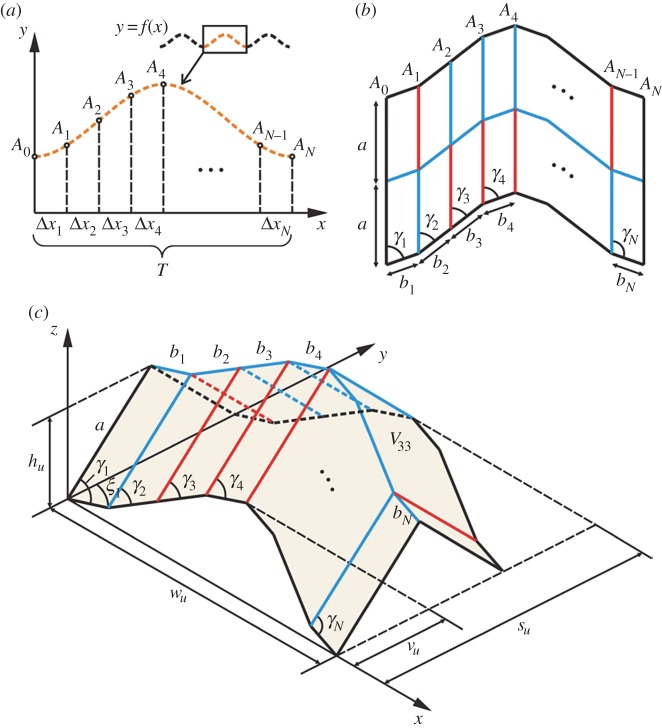
A typical unit cell of the Miura pattern is illustrated in figure 1a, where the mountain and valley creases are indicated by the blue and red lines or vice versa. The pattern can be defined by the longitudinal and transverse crease lengths a and b and an oblique angle γ₁. Without loss of generality, γ₁ is always taken as an acute angle throughout the paper. The other oblique angle γ₂ is determined by γ₁ through the relationship γ₁+γ₂=π because all the parallelogram facets are identical in this case. If γ₂ and b₂ are made independent of γ₁ and b₁, a generalized form of the Miura unit cell can be obtained, as shown in figure 1b. Comparable to the Miura pattern, the generalized form also has one degree of freedom of folding motion that can be characterized by a single parameter. Here, we employ ξ₁∈[0,γ₁] (figure 1c) as the parameter to describe folding. The outer dimensions of the folded pattern, defined by the dimensions of the smallest virtual box that can accommodate the folded pattern, are then given by

$$\begin{array}{rl}w& =\sum _{i=1}^2{b}_i\sqrt{1-{\cos }^2{\gamma }_i\hspace{0.17em}{\sec }^2{\gamma }_1\hspace{0.17em}{\cos }^2{\xi }_1},\end{array}$$ 2.1

$$\begin{array}{rl}s& =\frac{2a\hspace{0.17em}\cos \hspace{0.17em}{\gamma }_1}{\cos \hspace{0.17em}{\xi }_1}+v\end{array}$$ 2.2

$$\begin{array}{rl}\mathrm{and}h& =a\hspace{0.17em}\cos \hspace{0.17em}{\gamma }_1\sqrt{{\tan }^2{\gamma }_1-{\tan }^2{\xi }_1},\end{array}$$ 2.3

where v is determined as

$$v=max\left\{b_1\cos {\xi }_1,\sum _{i=1}^2\frac{b_i\cos {\gamma }_i\cos {\xi }_1}{\cos {\gamma }_1}\right\}.$$ 2.4

The detailed derivation of equations (2.1)–(2.4) is provided in the electronic supplementary material, section A.

Figure 1.

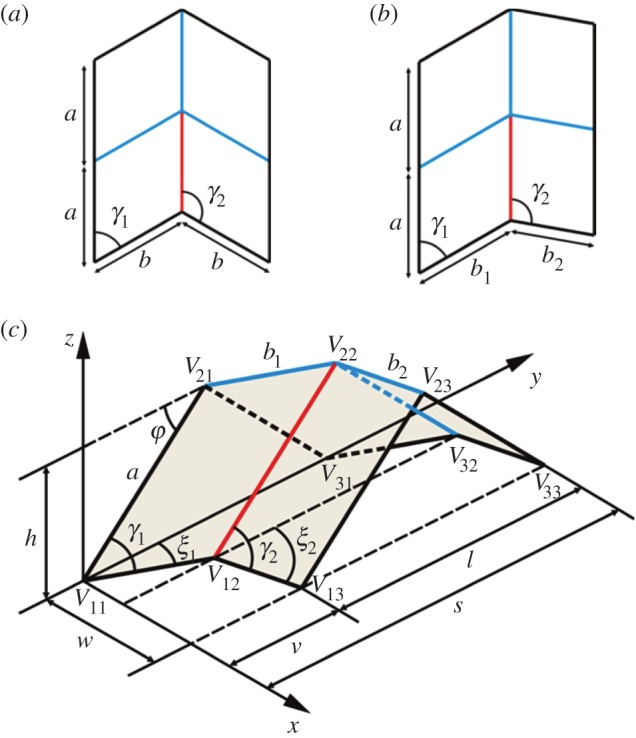
(a) A typical unit cell of the Miura pattern; (b) a generalized Miura unit cell pattern; and (c) the folded state of a generalized Miura unit cell. (Online version in colour.)

Consider now an arbitrary periodic function y=f(x) with period T, which is referred to as the base function in the sequel. A single period of the base function is first discretized into N+1 points A₀, A₁,…,A_N, as shown in figure 2a. Rejoining these points with straight-line segments results in a piecewise polyline, upon which a unit cell of a periodic Miura-derivative pattern can be generated, as shown in figure 2b, where the i-th oblique angle γ_i and the i-th transverse crease length b_i are obtained as

$${\gamma }_i={\tan }^{-1}\left(\frac{\mathrm{\Delta }{x}_i}{f(x_i)-f(x_{i-1})}\right)\text{and}{b}_i=\frac{\mathrm{\Delta }{x}_i}{\sin {\gamma }_i}.$$ 2.5

Figure 2.

(a) A single period of a periodic base function y=f(x) with period T; (b) a unit cell of a periodic Miura-derivative pattern; and (c) the folded state of a Miura-derivative unit cell. (Online version in colour.)

Again, we employ ξ₁∈[0,γ₁] (figure 2c) to parametrize its folding motion. According to equations (2.1) and (2.2), the outer dimensions w_u and s_u of the folded unit cell are obtained as

$$w_u=\sum _{i=1}^N{b}_i\sqrt{1-{\cos }^2{\gamma }_i{\sec }^2{\gamma }_1{\cos }^2{\xi }_1}$$ 2.6

and

$$s_u=\frac{2a\cos {\gamma }_1}{\cos {\xi }_1}+v_u,$$ 2.7

where v_u is determined as

$$v_u=\sum _{i=1}^m\frac{b_i\cos {\gamma }_i\cos {\xi }_1}{\cos {\gamma }_1},$$ 2.8

where m∈[1,N] and $f(x_m)=max\{\hspace{0.17em}f(x_1),\dots ,f(x_N)\}$, and the height h_u=h.

3. Stacked geometry

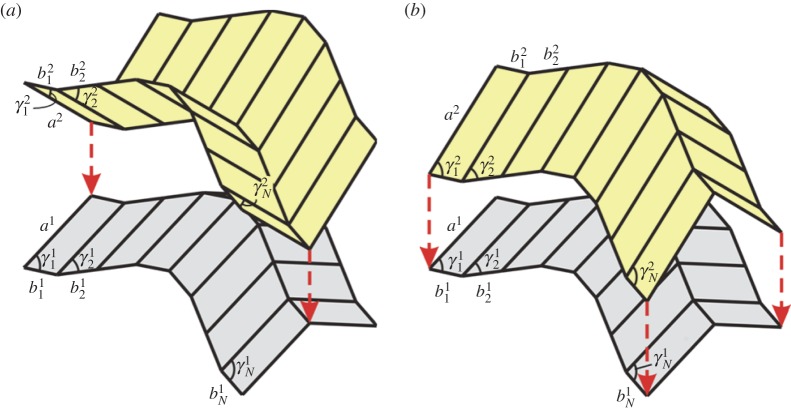
Two or more of the folded Miura-derivative unit cells discussed above of independent heights can be stacked in the z direction, leading to a multi-layered folded structure. There are two types of stacking sequence between successive layers, namely mountain–valley (M–V) stacking and valley–valley (V–V) stacking, as illustrated in figure 3. For both cases, four constraints must be met so that the two layers are practically stackable and the stacked assembly is still rigid-foldable: $b_i^1=b_i^2$, i=1,…,N, $w_u^1=w_u^2$, $s_u^1=s_u^2$, and $v_u^1=v_u^2$, where superscripts 1 and 2 denote the layer numbers. Substituting equations (2.6)–(2.8) into these constraints yields

$$a^1\cos {\gamma }_i^1=a^2\cos {\gamma }_i^2,i=1,\dots ,N.$$ 3.1

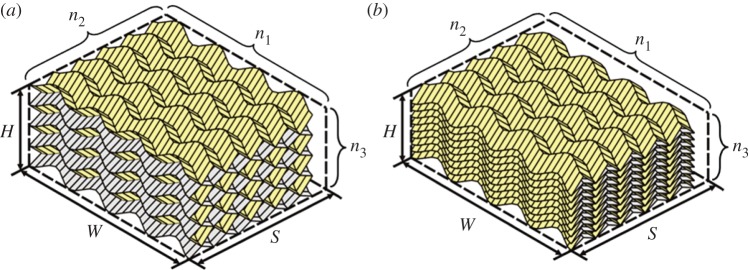
Three-dimensional bulk metamaterials can be constructed by repeating the M–V and/or V–V stacked unit cells in all three orthogonal directions. We focus here on the two generic models shown in figure 4, each having n₁ stacked unit cells in the in-plane transverse (W) direction, n₂ in the in-plane longitudinal (S) direction and n₃ in the stacking (H) direction. Based on the unit cell geometry discussed above, the total outer dimensions of the models can be written as

$$\begin{array}{rl}W{|}_{\mathrm{M}-\mathrm{V}}& =W{|}_{\mathrm{V}-\mathrm{V}}=W=n_1{w}_u^1,\end{array}$$ 3.2

$$\begin{array}{rl}S{|}_{\mathrm{M}-\mathrm{V}}& =S{|}_{\mathrm{V}-\mathrm{V}}=S=n_2{s}_u^1+(1-n_2)v_u^1,\end{array}$$ 3.3

$$\begin{array}{rl}H{|}_{\mathrm{M}-\mathrm{V}}& =n_3(h_u^2+h_u^1)\end{array}$$ 3.4

$$\begin{array}{rl}\mathrm{and}H{|}_{\mathrm{V}-\mathrm{V}}& =h_u^1+n_3(h_u^2-h_u^1),\end{array}$$ 3.5

where it is assumed, without loss of generality, that $h_u^2\ge h_u^1$. The total volume occupied by the bulk system is then obtained as

$$V=W\times S\times H.$$ 3.6

A hand-folded card model of the bulk metamaterials consisting of 3×3×3 M–V stacked unit cells is shown in the electronic supplementary material, movie S1.

Figure 3.

(a) An M–V stacked unit cell; (b) a V–V stacked unit cell. (Online version in colour.)

Figure 4.

(a) M–V and (b) V–V stacked metamaterials consisting of n₁ stacked unit cells in the in-plane transverse (W) direction, n₂ in the in-plane longitudinal (S) direction and n₃ in the stacking (H) direction. (Online version in colour.)

4. Poisson’s ratios of Miura-derivative metamaterials

The deformation of the Miura-derivative metamaterial can be characterized by an in-plane Poisson’s ratio ν_SW=−ε_S/ε_W and two out-of-plane Poisson’s ratios ν_HW=−ε_H/ε_W and ν_HS=−ε_H/ε_S, where ε_W=dW/W, ε_S=dS/S and ε_H=dH/H are the infinitesimal strains in the W, S and H directions, respectively. Using equations (3.2)–(3.5), the Poisson’s ratios are obtained as

$$\begin{array}{rl}{v}_{SW}{|}_{\mathrm{M}-\mathrm{V}}& =v_{SW}{|}_{\mathrm{V}-\mathrm{V}}=-\frac{(2n_2{\alpha }^1\cos {\gamma }_1^1/{\cos }^2{\xi }_1-\sum _{i=1}^m(b_i^1\cos {\gamma }_i^1/\cos {\gamma }_1^1))}{\left(\sum _{i=1}^n\left(n_1{b}_i^1\sec {\gamma }_1^1{\cos }^2{\gamma }_i^1\cos {\xi }_1/\sqrt{{\cos }^2{\gamma }_1^1-{\cos }^2{\gamma }_i^1{\cos }^2{\xi }_1}\right)\right)}\cdot \frac{W}{S},\end{array}$$ 4.1

$$\begin{array}{rl}{v}_{HW}{|}_{\mathrm{M}-\mathrm{V}}& =\frac{n_3{a}^1\left(1/\sqrt{{\tan }^2{\gamma }_1^2-{\tan }^2{\xi }_1}+1/\sqrt{{\tan }^2{\gamma }_1^1-{\tan }^2{\xi }_1}\right)}{\left(\sum _{i=1}^N\left(n_1{b}_i^1{\sec }^2{\gamma }_1^1{\cos }^2{\gamma }_i^1{\cos }^4{\xi }_1/\sqrt{{\cos }^2{\gamma }_1^1-{\cos }^2{\gamma }_i^1{\cos }^2{\xi }_1}\right)\right)}.\frac{W}{H_{\mathrm{M}-\mathrm{V}}},\end{array}$$ 4.2

$$\begin{array}{rl}{v}_{HW}{|}_{\mathrm{V}-\mathrm{V}}& \approx \frac{n_3{a}^1\left(1/\sqrt{{\tan }^2{\gamma }_1^2-{\tan }^2{\xi }_1}-1/\sqrt{{\tan }^2{\gamma }_1^1-{\tan }^2{\xi }_1}\right)}{\left(\sum _{i=1}^N\left(n_1{b}_i^1{\sec }^2{\gamma }_1^1{\cos }^2{\gamma }_i^1{\cos }^4{\xi }_1/\sqrt{{\cos }^2{\gamma }_1^1-{\cos }^2{\gamma }_i^1{\cos }^2{\xi }_1}\right)\right)}.\frac{W}{H_{\mathrm{V}-\mathrm{V}}}\end{array}$$ 4.3

$$\begin{array}{rl}\mathrm{and}{\nu }_{\mathit{\text{HS}}}& =-{\nu }_{\mathit{\text{HW}}}/{\nu }_{\mathit{\text{SW}}},\end{array}$$ 4.4

where it is assumed in equation (4.3) that n₃≫1.

Several immediate findings can be made from equations (4.1)–(4.4). First, for the Poisson’s ratios to be real, the square root terms must be positive. As a result, the range for ξ₁ is obtained as

$$max\{{\chi }_i\}\le {\xi }_1\le min\{{\gamma }_1^j\},i=1,\dots ,N\hspace{0.17em}j=1,2,$$ 4.5

where χ_i equals zero if ${\gamma }_i^1>{\gamma }_1^1$ or ${\cos }^{-1}(|\cos {\gamma }_1^1/\cos {\gamma }_i^1|)$ if ${\gamma }_i^1\le {\gamma }_1^1$. This implies that the Miura-derivative metamaterials are in most cases neither flat-foldable nor developable (i.e. all layers unfold flat at the same time); in other words, their volume will never become zero, a property known as self-locking. Next, ν_WH of the M–V stacked metamaterial is always positive, and hence its height will reduce as it expands in the W direction. On the contrary, ν_WH of the V–V stacked metamaterial is always negative, making it an auxetic material in the W–H plane. Third, the in-plane Poisson’s ratio may transit from a positive value to a negative one when

$$\sum _{i=1}^m{b}_i\cos {\gamma }_i^1>2a^1{\cos }^2{\gamma }_1^1,n_2\le \sum _{i=1}^m\frac{b_i\cos {\gamma }_i^1}{2a^1{\cos }^2{\gamma }_1^1},$$ 4.6

and the critical value for ξ₁ is given by

$${\xi }_1={\cos }^{-1}\sqrt{\frac{2n_2{a}^1{\cos }^2{\gamma }_1^1}{\sum _{i=1}^m{b}_i\cos {\gamma }_i^1}}.$$ 4.7

If inequality (4.6) is not satisfied, the in-plane Poisson’s ratio will always be negative. ν_HS may also change signs under the same condition given by inequality (4.6). Therefore, given that n₂ is sufficiently large, all three Poisson’s ratios of the V–V stacked metamaterial are negative, implying that it expands in all directions, and for the M–V stacked metamaterial, only the in-plane Poisson’s ratio is negative, meaning that the height contracts as the in-plane expansion occurs. Physically, the negative out-of-plane Poisson’s ratios found in the V–V stacked metamaterials arise from the coupled stacking order in which the odd-numbered layers, having a smaller height, are tucked in the even-numbered layers. As the in-plane dimensions of the V–V stacked metamaterials are increased, the separation distance between two adjacent even-numbered layers increases due to flattening of the odd-numbered layers. As a result, the total height of the V–V stacked metamaterial can actually increase, leading to negative out-of-plane Poisson’s ratios.

5. Stretching and bulk moduli of Miura-derivative metamaterials

To derive the stretching and bulk moduli of the Miura-derivative metamaterial when it is modelled as rigid origami, we assume that all longitudinal creases in each layer have a hinge spring constant k₁ per unit length, all transverse creases have a hinge spring constant k₂ per unit length, the elastic energy is stored only in the creases which act as rotational hinges, and the total elastic energy U of the metamaterial is the summation of the elastic energy in each layer. As a result, U can be expressed as

$$U=n_3\sum _{j=1}^2\left(n_2\sum _{i=1}^{n_{1}N-1}{k}_1{a}^j{({\beta }_i^j-{\beta }_{i0}^j)}^2+n_1(2n_2-1)\sum _{i=1}^N\frac{1}{2}{k}_2{b}_i^j{({\alpha }_i^j-{\alpha }_{i0}^j)}^2\right),$$ 5.1

where ${\alpha }_i^j$ and ${\beta }_i^j$ are the dihedral angles of the i-th transverse and longitudinal creases in a Miura-derivative unit cell, respectively, ${\alpha }_{i0}^j$ and ${\beta }_{i0}^j$ are the natural dihedral angles in the undeformed state, and the superscript j denotes the layer number in a stacked unit cell. According to the minimum total potential energy principle, the total potential energy E of the metamaterial is then given by

$$E=U-{\int }_{{\xi }_{10}}^{{\xi }_1}{f}_w\frac{\text{d}W}{\text{d}{\xi }_1^{\prime }}\text{d}{\xi }_1^{\prime }-{\int }_{{\xi }_{10}}^{{\xi }_1}{f}_s\frac{\text{d}S}{\text{d}{\xi }_1^{\prime }}\text{d}{\xi }_1^{\prime }-{\int }_{{\xi }_{10}}^{{\xi }_1}{f}_h\frac{\text{d}H}{\text{d}{\xi }_1^{\prime }}\text{d}{\xi }_1^{\prime },$$ 5.2

where f_w, f_s and f_h are the external forces applied in the W, S and H directions, respectively. The external forces at equilibrium state are then obtained using the condition dE/dξ₁=0, which reads

$$f_w\frac{\text{d}W}{\text{d}{\xi }_1}+f_s\frac{\text{d}S}{\text{d}{\xi }_1}+f_h\frac{\text{d}H}{\text{d}{\xi }_1}=\frac{\text{d}U}{\text{d}{\xi }_1}.$$ 5.3

Using equation (5.3), the uniaxial forces in the W, S and H directions at equilibrium can be determined as

$${\overline{f}}_w=\frac{\text{d}U}{\text{d}{\xi }_1}/\frac{\text{d}W}{\text{d}{\xi }_1},{\overline{f}}_s=\frac{\text{d}U}{\text{d}{\xi }_1}/\frac{\text{d}S}{\text{d}{\xi }_1},{\overline{f}}_h=\frac{\text{d}U}{\text{d}{\xi }_1}/\frac{\text{d}H}{\text{d}{\xi }_1}.$$ 5.4

The stretching moduli of the metamaterial associated with the W, S and H directions are obtained as

$$k_w=\frac{\text{d}{\sigma }_w}{{\epsilon }_W},k_s=\frac{\text{d}{\sigma }_s}{{\epsilon }_s},k_h=\frac{\text{d}{\sigma }_h}{{\epsilon }_h},$$ 5.5

where ${\sigma }_w={\overline{f}}_w/(SH)$, ${\sigma }_s={\overline{f}}_s/(WH)$ and ${\sigma }_h={\overline{f}}_h/(WS)$ are the uniaxial stresses at equilibrium. Finally, the bulk modulus of the metamaterial is obtained as K_V=−dp/(dV/V), where p=−dU/dV is the hydrostatic pressure. The detailed derivations for k_w, k_s, k_h and K_V are provided in the electronic supplementary material, section B.

6. Validation

To validate the analytical models for Poisson’s ratios and moduli discussed above, we simulated the motion of a V–V stacked unit cell FE model in ABAQUS${\hspace{0.17em}}^{\circledR }$ (3DS, France), as shown in figure 5. In the FE model, the oblique angles γ¹ and transverse crease lengths b are taken as

$${\gamma }^1(\text{rad})=[0.97,0.65,0.97,2.17,2.49,2.17]$$ 6.1

and

$$b\hspace{0.17em}(\text{mm})=[6.93,8.49,6.93,6.93,8.49,6.93].$$ 6.2

The longitudinal crease lengths a¹ and a² and the initial folding angle ξ₁₀ are taken as 16 mm and 18 mm and 0.92 rad, respectively. All creases are modelled as revolute hinges with a unified rotational spring constant equal to 0.1 N mm rad⁻¹ mm⁻¹ where two adjacent facets are tied together along their common crease with the rotational degrees of freedom being set free and the torsional spring implemented using a revolute-type connector element inserted at the centre of the crease. The facets are meshed using S4R shell elements with a thickness and average size of 1 mm and are assigned a Young’s modulus equal to 200 GPa. The nodes on the thick dashed and dash-dotted lines are constrained in the z- and x-directions, respectively, and nodes 1 and 2 are constrained in the y-direction. In the load cases for k_w, k_s and k_h, nodes 2, 3 and 4 are displaced along the x, y and z axis, respectively, and the forces acting on them together with the outer dimensions of the model are measured to calculate the Poisson’s ratios and moduli using a central difference algorithm. The Poisson’s ratios versus W curves and the stiffness curves obtained from the FE simulations and the analytical models are shown in figure 6a,b, respectively. Excellent agreement between the FE and analytical results is observed, which provides solid evidence for the validity of the analytical models.

Figure 5.

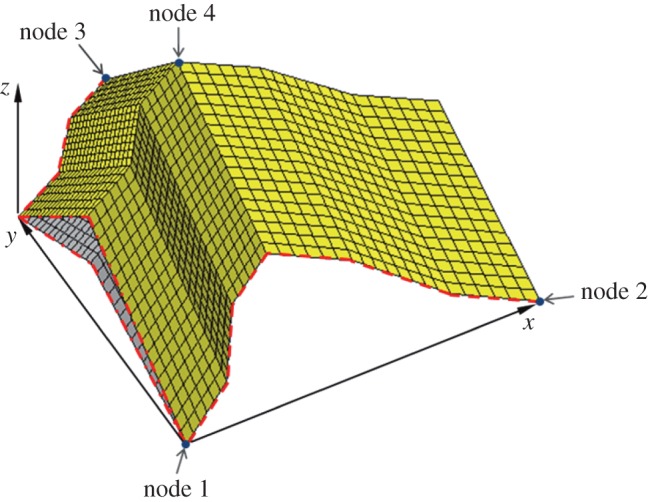
A V–V stacked unit cell FE model. (Online version in colour.)

Figure 6.

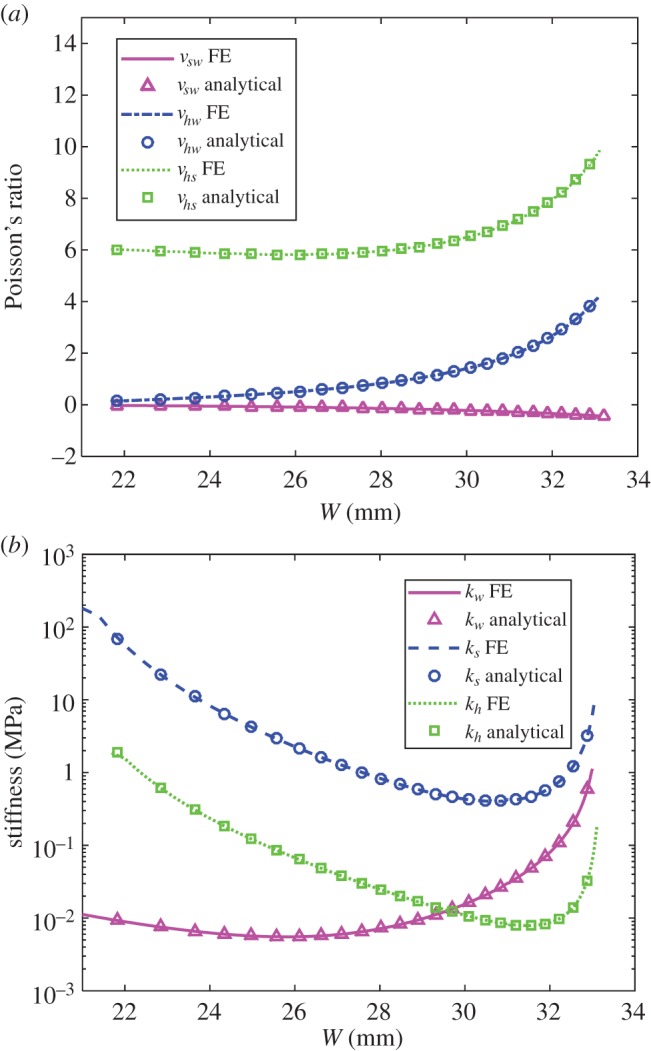
(a) The Poisson’s ratios versus W curves and (b) the stiffness versus W curves obtained from the FE simulations and the analytical models. (Online version in colour.)

7. Examples

To demonstrate the properties of Miura-derivative metamaterials, we consider here a piecewise periodic base function shown in figure 7a. A single period of the base function is naturally discretized into N=2M straight-line segments that have the same projections of length A on the y axis. The acute angles θ_i, i=1,2,…,N, between the straight-line segments and the y axis satisfy the following recursive relationship:

$${({\theta }_{i+1})}^{\lambda }=\left\{\begin{array}{l}{({\theta }_i)}^{\lambda }-\delta ,i=1,2,\dots ,M\\ {({\theta }_i)}^{\lambda }+\delta ,i=M+1,\dots ,N-1,\end{array}\right.$$ 7.1

where ${\theta }_{max}={\theta }_1$, ${\theta }_{min}={\theta }_{M+1}$, λ≠0 and $\delta =({({\theta }_{max})}^{\lambda }-{({\theta }_{min})}^{\lambda })/M$. The i-th oblique angle ${\gamma }_i^1$ and transverse crease length b_i of the first layer are obtained as

$${\gamma }_i^1=\left\{\begin{array}{ll}{\theta }_i,& \text{odd}\hspace{0.17em}i\\ \pi -{\theta }_i,& \text{even}\hspace{0.17em}i\end{array}\right.$$ 7.2

and

$$b_i=\frac{A}{\cos {\theta }_i}.$$ 7.3

Figure 7.

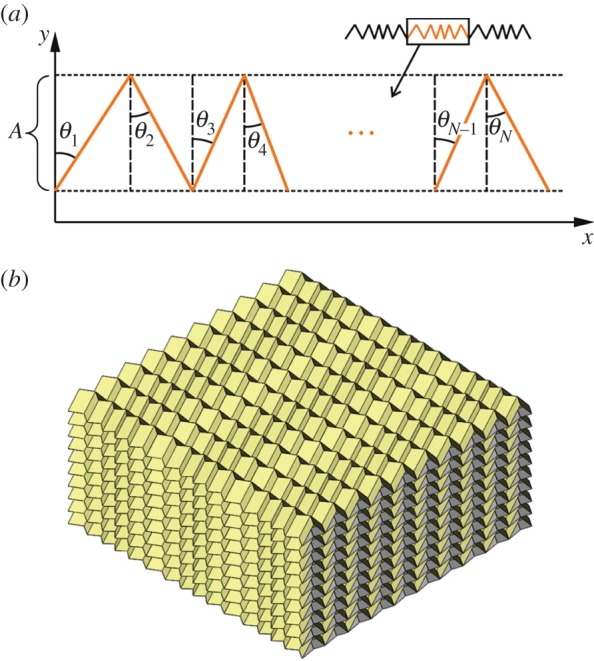
(a) A piecewise periodic base function defined by equation (7.1); and (b) a 3D rendering of the bulk metamaterial corresponding to the base function. (Online version in colour.)

The oblique angles ${\gamma }_i^2$, i=1,2,…,N, of the second layer are then determined using equation (3.1). A 3D rendering of the bulk metamaterial corresponding to the base function is shown in figure 7b.

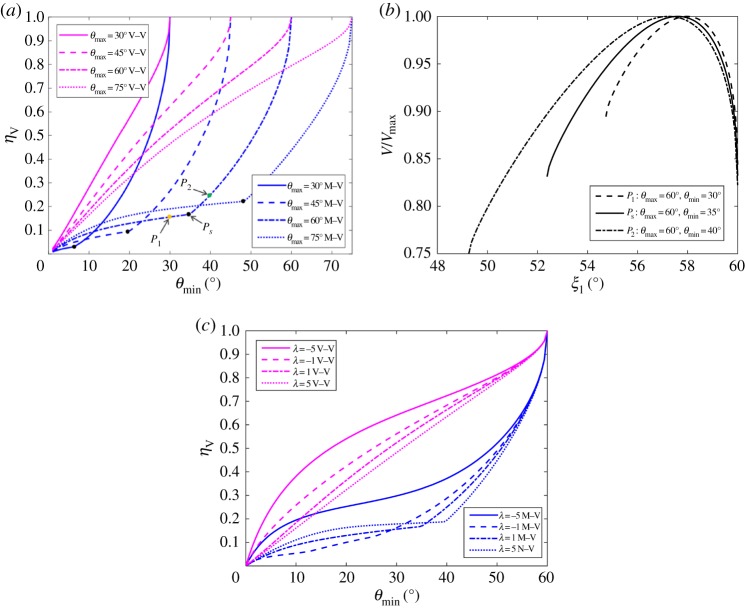
It is shown above that the Miura-derivative metamaterials have auxetic material properties, implying that during motion their volume and density will change. Therefore, the capability of the metamaterial to change its volume is of interest. To investigate this property, we employ here ${\eta }_V=(V_{max}-V_{min})/V_{max}$ as a measurement. Figure 8a shows η_V versus ${\theta }_{min}$ curves with different ${\theta }_{max}$ values ranging from 30° to 75° where λ=1, A=5, N=10, a₁=10, a₂=15 and n_1,2,3=10. The same values for A, N, a₁, a₂ and n_1,2,3 are used throughout this section. It is shown that the V–V stacked metamaterials have larger volume variations than the M–V stacked metamaterials do. For the V–V stacked cases, the volumetric change increases and decreases with the increases in ${\theta }_{min}$ and θ_max, respectively. For the M–V stacked cases, while the volumetric change still increases with the increase in ${\theta }_{min}$, there exist singular points (the black dots) on the curves, before and after which the minimum volume state switches from ${\xi }_1={\xi }_{1max}$ to ${\xi }_1={\xi }_{1min}$ (figure 8b), and the volumetric change increases and then decreases with the increase in ${\theta }_{max}$. Figure 8c shows η_V versus ${\theta }_{min}$ curves with different λ values, where ${\theta }_{max}={60}^{\circ }$. For the V–V stacked cases, the volumetric change increases with the decrease in λ. For the M–V stacked cases, it is noted that singular points only exist for positive λ and the volumetric change decreases with the decrease in λ before the singular points and then increases afterwards.

Figure 8.

(a) η_V versus ${\theta }_{min}$ curves with different ${\theta }_{max}$ values, where λ=1, A=5, N=10, a₁=10, a₂=15 and n_1,2,3=10; (b) $V/V_{max}$ versus ξ₁ curves at P₁, P₂ and P_s; (c) η_V versus ${\theta }_{min}$ curves with different λ values, where ${\theta }_{max}={60}^{\circ }$, A=5, N=10, a₁=10, a₂=15 and n_1,2,3=10. (Online version in colour.)

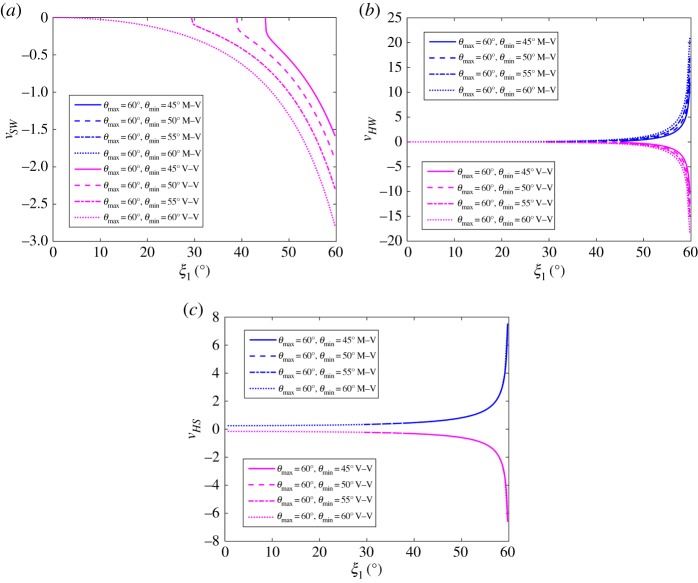
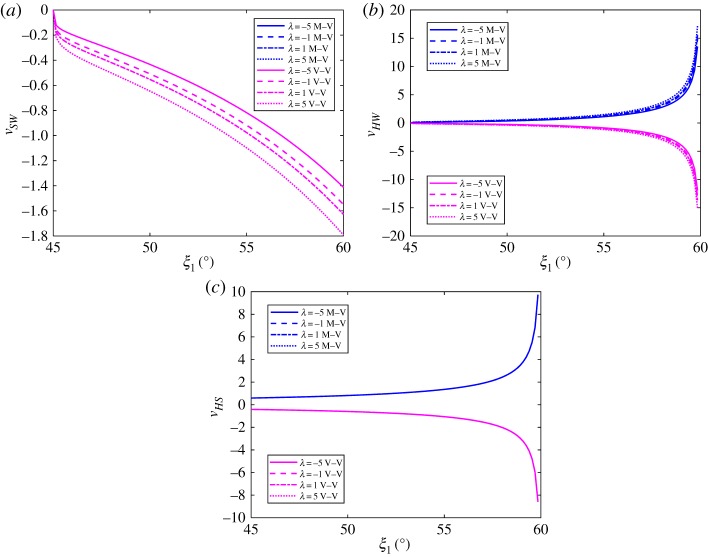
Figure 9 shows the Poisson’s ratios versus ξ₁ curves with different ${\theta }_{min}$ values ranging from 45° to 60° where ${\theta }_{max}={60}^{\circ }$ and λ=1. It is shown that the two out-of-plane Poisson’s ratios of the V–V stacked metamaterials are always opposite to those of the M–V stacked counterparts and slightly lower in magnitude than the latter. For both the M–V and V–V stacked cases, the absolute values of the in-plane Poisson’s ratio ν_SW and the out-of-plane Poisson’s ratio ν_HW increase with the increase in ${\theta }_{min}$ while ${\theta }_{min}$ has negligible influence on ν_HS. The influence of λ on the Poisson’s ratios is illustrated in figure 10, where ${\theta }_{max}={60}^{\circ }$ and ${\theta }_{min}={45}^{\circ }$. It is shown that the ν_SW and ν_HW versus ξ₁ curves become smoother as λ reduces. Again, λ shows no influence on ν_HS.

Figure 9.

(a) ν_SW, (b) ν_HW and (c) ν_HS versus ξ₁ curves with different ${\theta }_{min}$ values, where ${\theta }_{max}={60}^{\circ }$, λ=1, A=5, N=10, a₁=10, a₂=15 and n_1,2,3=10. (Online version in colour.)

Figure 10.

(a) ν_SW, (b) ν_HW and (c) ν_HS versus ξ₁ curves with different λ values, where ${\theta }_{max}={60}^{\circ }$, ${\theta }_{min}={45}^{\circ }$, A = 5, N = 10, a₁=10, a₂=15 and n_1,2,3=10. (Online version in colour.)

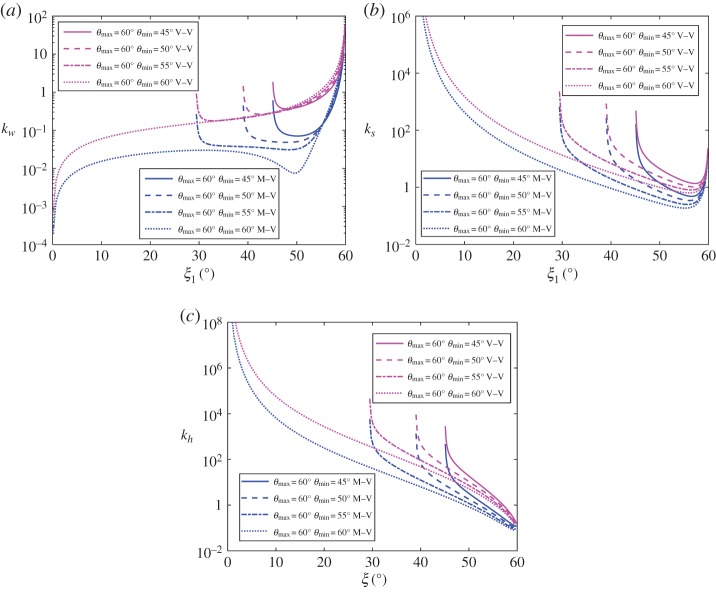
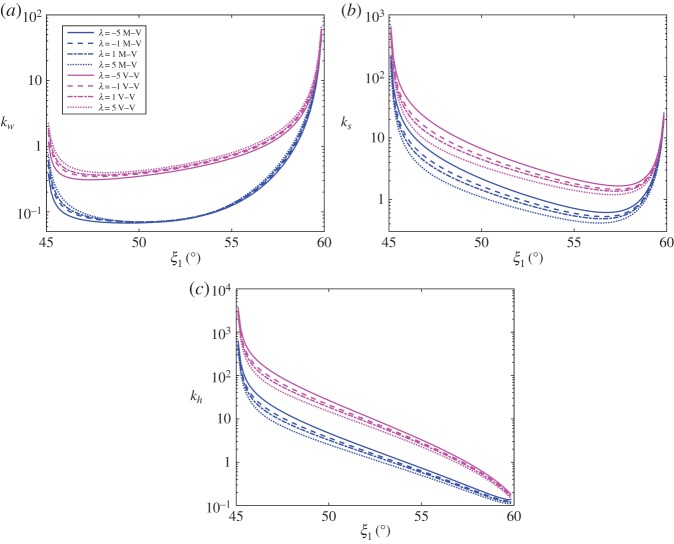
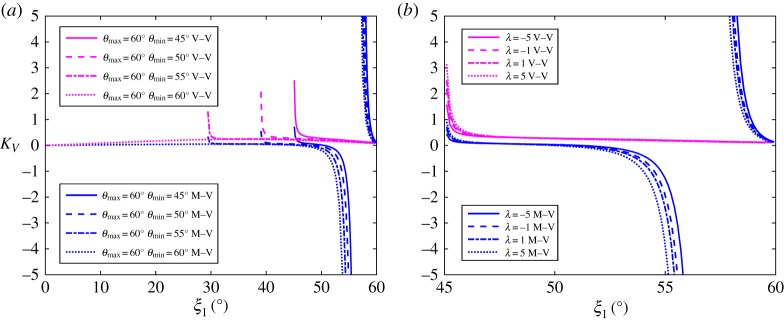
Of particular interest here are the elastic responses of the Miura-derivative metamaterials. Figure 11 shows the stretching moduli versus ξ₁ curves with different ${\theta }_{min}$ values where ${\theta }_{max}={60}^{\circ }$, λ=1 and ξ₁₀=59.5°. It is shown that the V–V stacked metamaterials are generally stiffer than the M–V stacked type. As ${\theta }_{min}$ decreases, the in-plane modulus k_s and the through-the-thickness modulus k_h increase while the in-plane modulus k_w initially decreases. For the standard Miura case, i.e. ${\theta }_{min}={\theta }_{max}$, k_w reduces to zero as ξ₁ decreases, whereas for other cases k_w becomes infinite at both the lower and upper bounds of ξ₁. Figure 12 shows the influences of λ on the stretching moduli, where ${\theta }_{max}={60}^{\circ }$, ${\theta }_{min}={45}^{\circ }$ and ξ₁₀=59.5°. It is shown that k_w increases and k_s and k_h decrease with the increase in λ. Finally, the influence of ${\theta }_{min}$ and λ on the bulk modulus K_v is illustrated in figure 13a,b, respectively. It is shown that K_v increases as ${\theta }_{min}$ decreases while it first increases and then decreases as λ decreases. It is interesting to note that the bulk moduli of the V–V stacked metamaterials are always positive while those of the M–V stacked metamaterials range from negative infinity to positive infinity. This unusual property of the M–V stacked metamaterials arises from the fact that the volume V in this case is not a monotonic function of ξ₁ (figure 8b). Setting dV/dξ₁=0 allows us to determine the critical value of ξ₁ at which the bulk modulus of the M–V stacked metamaterial shifts from $+\mathrm{\infty }$ to $-\mathrm{\infty }$.

Figure 11.

(a) k_w, (b) k_s and (c) k_h versus ξ₁ curves with different ${\theta }_{min}$ values, where ${\theta }_{max}={60}^{\circ }$, λ=1, ξ₁₀=59.5°, A=5, N=10, a₁=10, a₂=15 and n_1,2,3=10. (Online version in colour.)

Figure 12.

(a) k_w, (b) k_s and (c) k_h versus ξ₁ curves with different λ values, where ${\theta }_{max}={60}^{\circ }$, ${\theta }_{min}={45}^{\circ }$, ξ₁₀=59.5°, A=5, N=10, a₁=10, a₂=15 and n_1,2,3=10. (Online version in colour.)

Figure 13.

(a) K_V versus ξ₁ curves with different ${\theta }_{min}$ values, where ${\theta }_{max}={60}^{\circ }$, λ=1, ξ₁₀=59.5°, A=5, N=10, a₁=10, a₂=15 and n_1,2,3=10; (b) K_V versus ξ₁ curves with different λ values, where ${\theta }_{max}={60}^{\circ }$, ${\theta }_{min}={45}^{\circ }$, ξ₁₀=59.5°, A=5, N=10, a₁=10, a₂=15 and n_1,2,3=10. (Online version in colour.)

8. Summary and final remarks

In this paper, we have used patterns consisting of non-identical parallelogram facets to design 3D mechanical metamaterials. Depending on the stacking sequence between successive layers, two types of metamaterials are proposed. We show that the changes in the dimensions of the proposed metamaterials can be parametrized by a single folding parameter ξ₁, based on which the analytical models to predict deformation kinematics characterized by Poisson’s ratios are developed. Moreover, introducing rotational spring constants to the creases that are modelled as revolute hinges enables us to obtain analytical expressions for stretching and bulk moduli of the proposed metamaterials.

The intriguing properties of the Miura-derivative metamaterials are demonstrated through several numerical examples based on a periodic piecewise base function. The main findings include: (i) the Miura-derivative metamaterials possess the self-locking property arising from the restraints on the folding parameter ξ₁, (ii) the V–V stacked metamaterials are subject to greater volume variations and have higher stretching stiffness than the M–V stacked ones, (iii) the V–V stacked metamaterials have negative Poisson’s ratios in all three orthogonal planes whereas only the in-plane Poisson’s ratio of the M–V stacked ones is negative, and (iv) the Miura-derivative metamaterials have infinite stretching and bulk moduli wherein the bulk modulus of the M–V stacked metamaterials even varies from $-\mathrm{\infty }$ to $+\mathrm{\infty }$, which may lead to some unique vibration and acoustic behaviours [26]. In general, the geometric and mechanical properties of the Miura-derivative metamaterials have a broad design space, varying among different sets of base function parameters and folding states, not to mention that there are numerous other possible base function forms that have not been investigated. In this context, our work provides a highly flexible framework for the design of versatile tunable mechanical metamaterials. Moreover, by taking the limit of Δx_i in figure 2a towards zero, the piecewise polyline in figure 2b will eventually convert into a smooth curve of arbitrary shape and the folding of the longitudinal creases into the bending of an infinite narrow strip of the sheet material along each crease. In this manner, the work presented in this paper opens up the opportunity for future study of curved-creased metamaterials.

Data accessibility

The electronic supplementary material is available via http://rspa.royalsocietypublishing.org.

Authors' contributions

X.Z. designed the study, carried out the analysis and drafted the manuscript; S.Z. derived the equations and made the physical model; Z.Y. conceived of the study and commented on the manuscript. All authors gave final approval for publication.

Competing interests

We have no competing interests.

Funding

X.Z. is funded by the National Science Foundation of China (no. 51408357).