Abstract
Understanding response of solids to particle irradiation remains a major materials physics challenge. This applies even to SiC, which is a prototypical nuclear ceramic and wide-band-gap semiconductor material. The lack of predictability is largely related to the complex, dynamic nature of radiation defect formation. Here, we use a novel pulsed-ion-beam method to study dynamic annealing in 4H-SiC ion-bombarded in the temperature range of 25–250 °C. We find that, while the defect recombination efficiency shows an expected monotonic increase with increasing temperature, the defect lifetime exhibits a non-monotonic temperature dependence with a maximum at ~100 °C. This finding indicates a change in the dominant defect interaction mechanism at ~100 °C. The understanding of radiation defect dynamics may suggest new paths to designing radiation-resistant materials.
Silicon carbide (SiC) is an important material for electronics1,2 and nuclear materials3,4 technologies. For both of these applications, the fundamental understanding of radiation damage processes is highly desirable, particularly for practically-relevant irradiation at room temperature (T) and above. For such irradiation conditions, all three main commonly available polymorphs of SiC (3C, 4H, and 6H) exhibit pronounced dynamic annealing (DA)5,6,7,8,9,10,11,12,13,14,15, which refers to migration, recombination, and clustering of radiation-generated point defects during irradiation. The degree of DA increases with increasing sample T. This is evidenced as a reduction in the level of stable post-irradiation disorder or as an increase in the ion dose required to reach a certain level of disorder with increasing T5,6,7,8,10,12,15. The DA also manifests as a dose rate dependence of damage (with all the other irradiation conditions being constant)11,13,14,15. However, due to complexity of radiation defect interaction processes and the lack of direct experimental methods to study them, mechanisms of DA in SiC remain elusive. Indeed, physically very different models of point defect interaction can describe the same experimental T-dependencies of the amorphization dose16. More sophisticated measurements of radiation defect dynamics are needed to unravel the underlying mechanisms.
We have recently demonstrated11,17,18,19 that details of DA can be accessed in pulsed beam experiments when the total ion dose is delivered as a train of equal square pulses with a duration of ton and an instantaneous dose rate of Fon separated by a passive portion of the beam duty cycle of toff (see the inset in Fig. 1). In particular, the dependence of the amount of stable post-irradiation disorder on toff reveals the characteristic time constant of DA (τ) and, hence, the DA rate17. We have successfully applied such a pulsed-beam method to measure τ in Si at room T and in 3C-SiC at 100 °C11,17,19. Here, we report the τ(T) dependence in 4H-SiC bombarded with energetic Ar ions in the T range of 25–250 °C. Our results reveal a non-monotonic τ(T) dependence with a maximum of ~5 ms at ~100 °C, reflecting a change in the dominant DA mechanism at ~100 °C. This result has important practical implications since design strategies for radiation-tolerant materials are determined by the dominant defect formation and DA processes.
Figure 1. Temperature dependence of the ion dose required to reach a damage level of 0.7 in 4H-SiC bombarded with a continuous beam (i.e., toff = 0) of 500 keV Ar ions with a dose rate of 1.7 × 1013 cm−2 s−1.
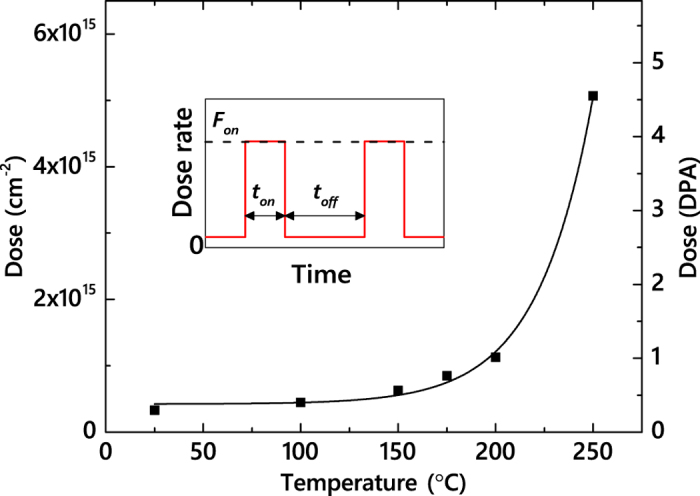
The solid line is an exponential fit to the data. The inset is a schematic of the time dependence of the instantaneous dose rate for pulsed beam irradiation, defining ton, toff, and Fon.
Results and Discussion
Figure 1 shows an exponential T dependence of the dose required to achieve an averaged bulk disorder level (n) of 0.7 (with n = 1 corresponding to complete amorphization) for continuous beam irradiation (i.e., toff = 0) of 4H-SiC. Such a dose increases from 0.2 to 4.3 displacements per atom (DPA) when T is increased from 25 to 250 °C, reflecting the thermally activated nature of DA processes. An increase in the dose required to reach a certain disorder level with increasing T is expected5,6,7,8,9,10,12,15. Indeed, at higher Ts, point defects have higher diffusivity and experience more efficient vacancy-interstitial recombination. We, however, note that the doses revealed by Fig. 1 are smaller than those reported in the previous studies of SiC (refs 5, 6, 7, 8, 9, 10,15) due to a larger dose rate used in the present work. As we discussed in detail in our recent systematic study of the damage buildup in 3C-SiC12, this highlights the dominant role of DA in the formation of stable post-irradiation damage in SiC at elevated Ts. Based on damage buildup data such as shown in Fig. 1, we have chosen ion doses for pulsed beam experiments at different Ts so that, for toff = 0 (i.e., continuous beam irradiation), n is in the range of 0.6–0.8, which is a nonlinear regime of damage buildup with pronounced DA11,12,20.
Figure 2 shows representative depth profiles of relative disorder for bombardment of 4H-SiC with continuous or pulsed beams at Ts of 25, 100, and 250 °C. Each panel of Fig. 2 shows data for cases when all the irradiation conditions are kept constant except for toff. It is seen that, for all three Ts shown, depth profiles are bimodal, with the first small peak at the sample surface and the second major peak in the crystal bulk. The bulk peak (with a height of n) is centered on ~300 nm, which corresponds to the maximum of the nuclear energy loss profile for 500 keV Ar ions. It is also seen from Fig. 2 that n decreases with increasing toff for all three Ts. We have found such a reduction in n with increasing toff in all our measurements at different Ts. Figure 2 further shows that the degree of reduction in n with increasing toff increases dramatically with increasing T. For example, for T = 250 °C [Fig. 2(c)], an increase in toff from 0 to 5 ms results in an ~2.5-fold reduction in n. In contrast, the damage level at the sample surface is independent of toff, suggesting different mechanisms of bulk and surface disordering11,17,19,21.
Figure 2. Selected depth profiles of relative disorder in 4H-SiC bombarded with a pulsed beam of 500 keV Ar ions with Fon = 1.7 × 1013 cm−2 s−1, ton = 1 ms, and different toff values, given in legends (in units of ms), at different temperatures and total doses, also shown in the legends.
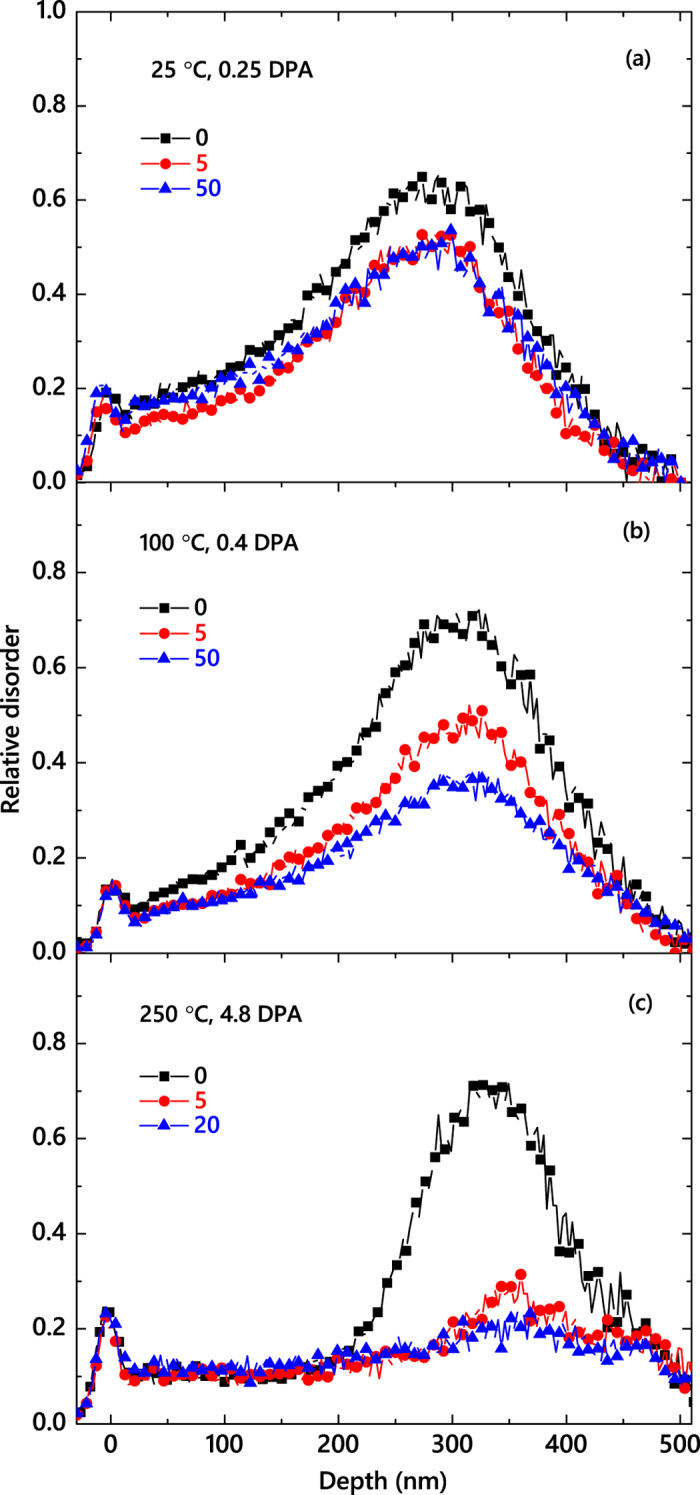
For clarity, only every 5th experimental point is depicted.
Figure 3 summarizes n(toff) dependencies for all the Ts of this study (25–250 °C). It reveals that n monotonically decreases with increasing toff in all these cases. Solid lines in Fig. 3 are fits of the data via the Marquardt-Levenberg algorithm with the second order decay equation 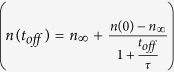 . Here, n∞ is relative disorder for toff ≫ τ. We have found that all the n(toff) dependencies from Fig. 3 obey the second order decay better than the first order (i.e., exponential) decay.
. Here, n∞ is relative disorder for toff ≫ τ. We have found that all the n(toff) dependencies from Fig. 3 obey the second order decay better than the first order (i.e., exponential) decay.
Figure 3. Level of relative bulk disorder in 4H-SiC bombarded with 500 keV Ar ions with Fon = 1.7 × 1013 cm−2 s−1 and ton = 1 ms as a function of the passive portion of the beam duty cycle (toff) at different temperatures, given in the legend (in units of °C).
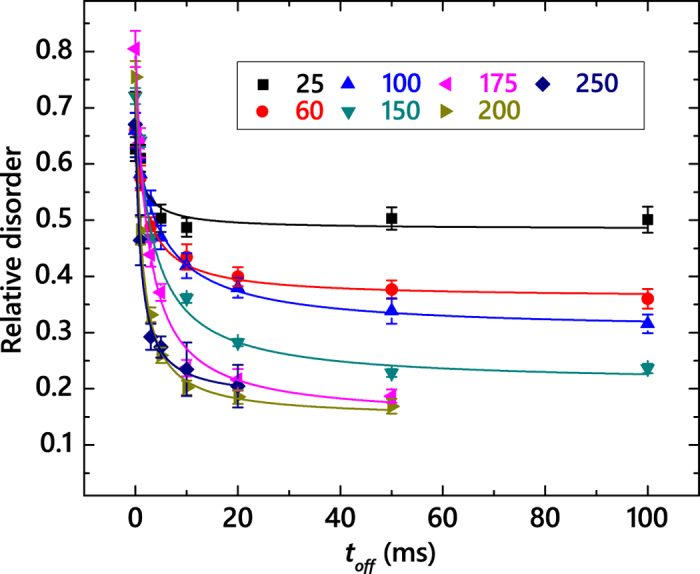
Fitting curves of the data with the second order decay equation are shown by solid lines.
The τ(T) dependence is shown in Fig. 4, revealing a non-monotonic behavior, when τ first rapidly increases with T, reaches a maximum at 100 °C, followed by a monotonic decrease for 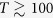 °C. Also plotted in Fig. 4 is the T dependence of the DA efficiency (ξ), which we define as before17:
°C. Also plotted in Fig. 4 is the T dependence of the DA efficiency (ξ), which we define as before17: 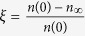 . As discussed in detail recently19, for our choice of Fon and ton, ξ is the magnitude of the dose rate effect; i.e., the difference between n for continuous beam irradiation with dose rates of F = Fon and F → 0. It is seen from Fig. 4 that, in contrast to the τ(T) dependence, ξ increases monotonically with T in the T range of 25–175 °C. At ~175 °C, ξ reaches a maximum of ~80%, followed by a slight decrease at 250 °C. Hence, both τ(T) and ξ(T) dependencies of Fig. 4 are non-trivial, reflecting the complexity of defect interaction processes.
. As discussed in detail recently19, for our choice of Fon and ton, ξ is the magnitude of the dose rate effect; i.e., the difference between n for continuous beam irradiation with dose rates of F = Fon and F → 0. It is seen from Fig. 4 that, in contrast to the τ(T) dependence, ξ increases monotonically with T in the T range of 25–175 °C. At ~175 °C, ξ reaches a maximum of ~80%, followed by a slight decrease at 250 °C. Hence, both τ(T) and ξ(T) dependencies of Fig. 4 are non-trivial, reflecting the complexity of defect interaction processes.
Figure 4. Closed symbols: temperature dependencies of the effective time constant of DA (τ) and the DA efficiency (ξ) for 4H-SiC bombarded with 500 keV Ar ions with Fon = 1.7 × 1013 cm−2 s−1 and ton = 1 ms.
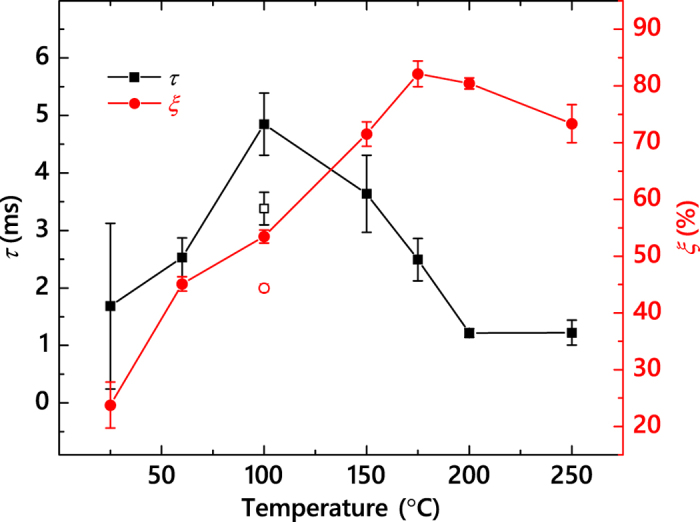
Open symbols show data points for 3C-SiC irradiated at 100 °C with 500 keV Ar ions with Fon = 1.9 × 1013 cm−2 s−1 and ton = 1 ms, taken from ref. 11.
Values of τ revealed by Fig. 4 are in the range of ~1–5 ms. These are orders of magnitude larger than the predictions of molecular dynamics (MD) and kinetic Monte Carlo simulations discussed in our recent paper11. This highlights both the well-known limitations of MD to model long-time defect evolution and the currently limited understanding of radiation defect dynamics in SiC. Interestingly, Fig. 4 also shows one data point available for 3C-SiC at 100 °C (taken from our recent work11), revealing a larger τ for 4H-SiC than for 3C-SiC. This finding is not unexpected, given that DA processes depend on the type and properties of lattice-structure-specific point and extended defects11,12. Values of τ for SiC (Fig. 4) are also comparable to those for Si measured previously for room T bombardment with different ions (~4–13 ms)17,19. Future theoretical studies of defect interaction bench-marked against our pulsed beam data are needed to find out if such similarity in τ values reflects similarity in defect relaxation processes in different materials. Moreover, further systematic measurements of the τ(T) dependencies for 3C-SiC and 6H-SiC will be interesting, revealing similarities and differences in DA of the three main commonly available SiC polymorphs.
A non-monotonic τ(T)-dependence of Fig. 4 reveals the existence of a transition temperature (Tr) of ~100 °C. Such a Tr of 100 °C is not evident from the T dependence of the damage buildup (as shown in Fig. 1 and in numerous previous studies5,6,7,8,10,12,15). Neither is it revealed by the ξ(T) dependence that, as mentioned above, reflects the T dependence of the dose rate effect, also studied previously in traditional measurements with continuous ion beams (or unintentionally scanned beams due to rastering)13,15. A special role of T ~ 100 °C has, however, been noted in a number of previous studies of all three main polymorphs of SiC: 4H-SiC14, 6H-SiC22,23,24,25, and 3C-SiC26,27,28,29, evidenced either as the onset of post-irradiation defect annealing22,23,24,26,27,28, as a rapid decrease in the cross-section of damage production25, as a qualitative change in the radiation resistance of nanocrystalline SiC29, or as a maximum of the concentration of open-volume defects monitored by positron annihilation spectroscopy14. The non-monotonic τ(T)-dependence of Fig. 4 unambiguously shows that qualitatively different defect relaxation processes are dominant above and below a transition temperature (Tr) of ~100 °C.
In order to better understand the mechanism of DA, in Fig. 5, we replot the τ(T) dependence from Fig. 4 in Arrhenius coordinates, with the DA rate defined as 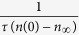 , and with kBT having the usual meaning. For the second order decay process
, and with kBT having the usual meaning. For the second order decay process 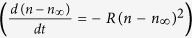 , the decay time constant (τ) depends on the initial concentration of mobile defects, and the decay rate is
, the decay time constant (τ) depends on the initial concentration of mobile defects, and the decay rate is 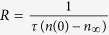 . A regime with a negative effective activation energy (Ea) is clearly seen in Fig. 5 for T ≲ 100 °C. A negative Ea combined with an increase in ξ for T ≲ 100 °C (see Fig. 4) could suggest the dominance of thermally activated processes of defect de-trapping. Indeed, processes of defect trapping and de-trapping that do not involve defect recombination result in an increase in the effective lifetime of mobile defects and, hence, a reduced DA rate characterized by the negative Ea.
. A regime with a negative effective activation energy (Ea) is clearly seen in Fig. 5 for T ≲ 100 °C. A negative Ea combined with an increase in ξ for T ≲ 100 °C (see Fig. 4) could suggest the dominance of thermally activated processes of defect de-trapping. Indeed, processes of defect trapping and de-trapping that do not involve defect recombination result in an increase in the effective lifetime of mobile defects and, hence, a reduced DA rate characterized by the negative Ea.
Figure 5. Arrhenius plot of the DA rate defined as 1/(τ(n(0) − n\infty)) for a second order decay process.
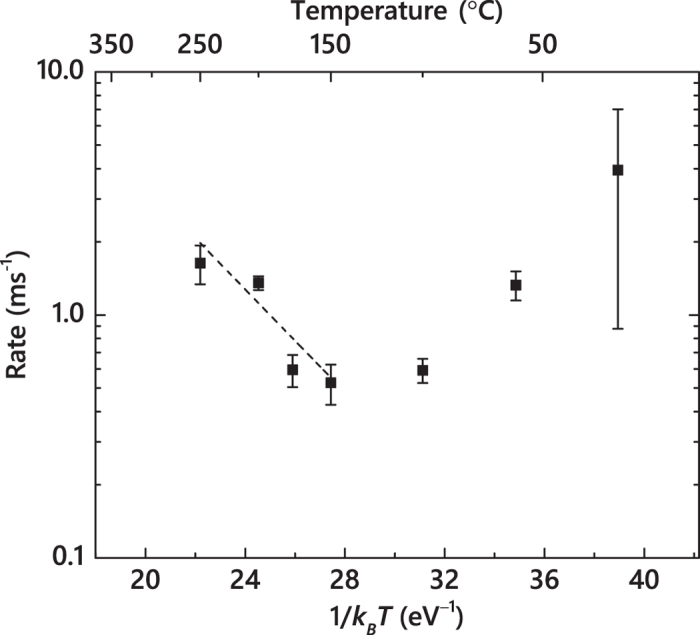
The straight line shows results of linear fitting, revealing an activation energy of 0.25 ± 0.05 eV for the temperature range of 150–250 °C.
At T ≳ 100 °C, thermally activated processes of defect recombination appear to dominate when τ decreases with increasing T. An Arrhenius regime with a positive Ea is seen for the T range of 150–250 °C. Linear fitting of the data gives an Ea and a pre-exponential factor of 0.25 ± 0.05 eV and (5.23 ± 0.62) × 102 Hz, respectively. This Ea value is much smaller than an Ea of 1.3 eV obtained by Kuznetsov et al.13 by the analysis of the T-dependence of the dose rate effect in the T range of 20–225 °C based on the method proposed by Schultz and co-workers30, which is equivalent to the analysis of the ξ(T) dependence of Fig. 4. Such an apparent inconsistency in Ea could be attributed to limitations of the method of Schultz et al.30 Indeed, ξ (i.e., the magnitude of the dose rate effect) reflects the fraction of ballistically-generated Frenkel defects that participate in DA processes for any given Fon rather than the rate of defect interaction. Our Ea of ~0.25 eV is consistent with Ea values for 6H-SiC reported by Weber et al.7,31 from the analysis of the T dependence of the amorphization dose based on the empirical model of Morehead-Crowder32. Dedicated modeling and simulation studies are currently needed to better understand the atomistics of DA and to correlate the apparent activation energies measured here with energetic barriers of specific defect migration and interaction processes in SiC polymorphs.
In conclusion, we have used the pulsed beam method to measure the temperature dependence of both the characteristic time constant (τ) and the efficiency of DA in the Si sublattice of 4H-SiC bombarded with 500 keV Ar ions in the temperature range of 25–250 °C. Results have revealed a non-monotonic T-dependence of τ with a maximum at 100 °C, indicating a change in the dominant DA mechanism at ~100 °C. The Arrhenius regime in the T range of 150–250 °C is described by an activation energy of ~0.25 eV. The details of radiation defect dynamics revealed in this work have important implications for understanding, predicting, and controlling radiation damage in SiC and for benchmarking future theoretical efforts.
Methods
High purity semi-insulating (0001) 4H-SiC single crystals (with a diameter of 100 mm, a resistivity of ≳109 Ω cm, and a nominal micropipe density of <60 cm−2), obtained from Cree, Inc., were bombarded with 500 keV Ar ions at 7° off the [0001] direction in the T range of 25–250 °C. The crystal quality of as-received 4H-SiC wafers was verified by measuring a minimum 2 MeV He ion channeling yield of ~1.6%, consistent across the wafer. The 4 MV ion accelerator (National Electrostatics Corporation, model 4UH) at Lawrence Livermore National Laboratory was used for both ion irradiation and ion beam analysis. To improve thermal contact, the samples were attached to the Ni sample holder with conductive Ag paste. The sample holder temperature was monitored with a chromel/alumel thermocouple (with an accuracy of ±1 °C). All irradiations were performed in a broad beam mode17. Irradiated areas were ~4 × 5 mm2. Ion beam pulsing was achieved by applying high voltage pulses to a pair of parallel plates deflecting the beam in the vertical direction off the final beam defining aperture so that the total dose was split into a train of equal square pulses each with an Fon of ~(1.7 ± 0.05) × 1013 cm−2 s−1 and duration ton = 1 ms. The adjacent pulses were separated by time toff, which was varied between 1 and 100 ms. For irradiation at T ≳ 200 °C that required larger total doses, toff was limited to 20 ms, which was still much larger than the DA time constants at these Ts. A more detailed description of the experimental arrangement can be found elsewhere11,19.
The dependence of lattice damage on toff was studied ex-situ at room temperature by ion channeling. Depth profiles of lattice disorder in the Si sublattice were measured with 2 MeV He ions incident along the [0001] direction and backscattered into a detector at 164 ° relative to the incident beam direction. The spot size of the He beam was ~1.5 × 1.5 mm2. Spectra were analyzed with one of the conventional algorithms33 for extracting the effective number of scattering centers (referred to below as “relative disorder”). Values of averaged bulk disorder (n) were obtained by averaging depth profiles of relative disorder over 10 channels (~25 nm) centered on the bulk damage peak maximum. Error bars of n are standard deviations. Error bars of τ, ξ, and the DA rate are standard errors of the non-linear fitting described above.
The depth profile of vacancies was calculated with the TRIM code (version SRIM-2013.00, full cascade calculations)34 with an atomic concentration of SiC of 9.64 × 1022 atoms cm−3 (ref. 3) and threshold energies for atomic displacements of 20 and 35 eV for C and Si sublattices, respectively35. To convert to DPAs (at the depth corresponding to the maximum of the nuclear energy loss profile), ion doses in 1014 Ar ions cm−2 are multiplied by 0.0898. The projected range and straggle of 500 keV Ar ions are ~320 and ~70 nm, respectively.
Additional Information
How to cite this article: Aji, L. B. B. et al. Non-monotonic temperature dependence of radiation defect dynamics in silicon carbide. Sci. Rep. 6, 30931; doi: 10.1038/srep30931 (2016).
Acknowledgments
This work was funded by the Nuclear Energy Enabling Technology (NEET) Program of the U.S. DOE, Office of Nuclear Energy and performed under the auspices of the U.S. DOE by LLNL under Contract DE-AC52-07NA27344. J.B.W. would like to acknowledge the LGSP for funding.
Footnotes
Author Contributions L.B.B.A. performed the experiments and data analysis with assistance from J.B.W. and wrote the manuscript with input from S.O.K., J.B.W. and L.S.; S.O.K. supervised the project.
References
- Fissel A. Artificially layered heteropolytypic structures based on SiC polytypes: molecular beam epitaxy, characterization and properties. Phys. Rep. 379, 149–255 (2003). [Google Scholar]
- Lohrmann A. et al. Single-photon emitting diode in silicon carbide. Nat. Commun. 6, 7783 (2015). [DOI] [PubMed] [Google Scholar]
- Snead L. L. et al. Handbook of SiC properties for fuel performance modeling. J. Nucl. Mater. 371, 329–377 (2007). [Google Scholar]
- Zhang Y. et al. Ionization-induced annealing of pre-existing defects in silicon carbide. Nat. Commun. 6, 8049 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inui H., Mori H. & Fujita H. Electron-irradiation-induced crystalline to amorphous transition in α-SiC single crystals. Philos. Mag. B 61, 107–124 (1990). [Google Scholar]
- Inui H., Mori H., Suzuki A. & Fujita H. Electron-irradiation-induced crystalline-to-amorphous transition in β-SiC single crystals. Philos. Mag. B 65, 1–14 (1992). [Google Scholar]
- Weber W. J., Wang L. M., Yu N. & Hess N. J. Structure and properties of ion-beam-modified (6H) silicon carbide. Mater. Sci. Eng. A 253, 62–70 (1998). [Google Scholar]
- Zinkle S. J. & Snead L. L. Influence of irradiation spectrum and implanted ions on the amorphization of ceramics. Nucl. Instr. and Meth. B 116, 92–101 (1996). [Google Scholar]
- Wendler E., Bierschenk T., Wesch W., Friedland E. & Malherbe J. B. Temperature dependence of damage formation in Ag ion irradiated 4H-SiC. Nucl. Instr. and Meth. B 268, 2996–3000 (2010). [Google Scholar]
- Matsunaga A., Kinoshita C., Nakai K. & Tomokiyo Y. Radiation-induced amorphization and swelling in ceramics. J. Nucl. Mater. 179–181, 457–460 (1991). [Google Scholar]
- Wallace J. B., Bayu Aji L. B., Shao L. & Kucheyev S. O. Time constant of defect relaxation in ion-irradiated 3C-SiC. Appl. Phys. Lett. 106, 202102 (2015). [Google Scholar]
- Wallace J. B., Bayu Aji L. B., Li T. T., Shao L. & Kucheyev S. O. Damage buildup in Ar-ion-irradiated 3C-SiC at elevated temperatures. J. Appl. Phys. 118, 105705 (2015). [Google Scholar]
- Kuznetsov A. Yu., Wong-Leung J., Hallen A., Jagadish C. & Svensson B. G. Dynamic annealing in ion implanted SiC: Flux versus temperature dependence. J. Appl. Phys. 94, 7112–7115 (2003). [Google Scholar]
- Slotte J. et al. Fluence, flux, and implantation temperature dependence of ion-implantation-induced defect production in 4H-SiC. J. Appl. Phys. 97, 033513 (2005). [Google Scholar]
- Zhang Y. et al. Effects of implantation temperature and ion flux on damage accumulation in Al-implanted 4H-SiC. J. Appl. Phys. 93, 1954–1960 (2003). [Google Scholar]
- Swaminathan N., Morgan D. & Szlufarska I. Ab initio based rate theory model of radiation induced amorphization in β-SiC. J. Nucl. Mater. 414, 431–439 (2011). [Google Scholar]
- Myers M. T., Charnvanichborikarn S., Shao L. & Kucheyev S. O. Pulsed Ion Beam Measurement of the Time Constant of Dynamic Annealing in Si. Phys. Rev. Lett. 109, 095502 (2012). [DOI] [PubMed] [Google Scholar]
- Charnvanichborikarn S., Myers M. T., Shao L. & Kucheyev S. O. Pulsed ion beam measurement of defect diffusion lengths in irradiated solids. J. Phys. Condens. Matter 25, 162203 (2013). [DOI] [PubMed] [Google Scholar]
- Wallace J. B. et al. Radiation defect dynamics in Si at room temperature studied by pulsed ion beams. J. Appl. Phys. 118, 135709 (2015). [Google Scholar]
- Titov A. I. & Carter G. Defect accumulation during room temperature N+ irradiation of silicon. Nucl. Instr. and Meth. B 119, 491–500 (1996). [Google Scholar]
- Titov A. I., Belyakov V. S. & Azarov A. Yu. Formation of surface amorphous layers in semiconductors under low-energy light-ion irradiation: Experiment and theory. Nucl. Instr. and Meth. B 212, 169–178 (2003). [Google Scholar]
- Barklie R. C., Collins M., Holm B., Pacaud Y. & Skorupa W. An EPR study of defects induced in 6H-SiC by ion implantation. J. Electron. Mater. 26, 137–143 (1997). [Google Scholar]
- Dannefaer S. & Kerr D. Positron annihilation investigation of electron irradiation-produced defects in 6H-SiC. Diam. Relat. Mater. 13, 157–165 (2004). [Google Scholar]
- Rempel A. A. & Schaefer H.-E. Irradiation-induced atomic defects in SiC studied by positron annihilation. Appl. Phys. A 61, 51–53 (1995). [Google Scholar]
- Jiang W., Zhang Y. & Weber W. J. Temperature dependence of disorder accumulation and amorphization in Au-ion-irradiated 6H-SiC. Phys. Rev. B 70, 165208 (2004). [Google Scholar]
- Itoh H., Hayakawa N., Nashiyama I. & Sakuma E. Electron spin resonance in electron-irradiated 3C-SiC. J. Appl. Phys. 66, 4529–4531 (1989). [Google Scholar]
- Itoh H. et al. Photoluminescence of radiation induced defects in 3C-SiC epitaxially grown on Si. J. Appl. Phys. 77, 837–842 (1995). [Google Scholar]
- Hallen A. et al. Ion implantation of silicon carbide. Nucl. Instr. and Meth. B 186, 186–194 (2002). [Google Scholar]
- Jamison L., Sridharan K., Shannon S. & Szlufarska I. Temperature and irradiation species dependence of radiation response of nanocrystalline silicon carbide. J. Mater. Res. 29, 2871–2880 (2014). [Google Scholar]
- Schultz P. J., Jagadish C., Ridgway M. C., Elliman R. E. & Williams J. S. Crystalline-to-amorphous transition for Si-ion irradiation of Si(100). Phys. Rev. B 44, 9118–9121 (1991). [DOI] [PubMed] [Google Scholar]
- Weber W. J., Jiang W. & Thevuthasan S. Defect annealing kinetics in irradiated 6H-SiC. Nucl. Instr. and Meth. B 166–167, 410–414 (2000). [Google Scholar]
- Morehead F. F. & Crowder B. L. A model for the formation of amorphous Si by ion bombardment. Radiat. Eff. 6, 27–32 (1970). [Google Scholar]
- Schmid K. Some new aspects for the evaluation of disorder profiles in silicon by backscattering. Radiat. Eff. 17, 201–207 (1973). [Google Scholar]
- Ziegler J. F., Ziegler M. D. & Biersack J. P. SRIM - The stopping and range of ions in matter. Nucl. Instr. and Meth. B 268, 1818–1823 (2010). [Google Scholar]
- Devanathan R., Weber W. J. & Gao F. Atomic scale simulation of defect production in irradiated 3C-SiC. J. Appl. Phys. 90, 2303–2309 (2001). [Google Scholar]


